Abstract
We present pulsed electron-nuclear double resonance (ENDOR) experiments which enable us to characterize the coupling between bismuth donor spin-qubits in Si and the surrounding spin-bath of 29Si impurities which provides the dominant decoherence mechanism (nuclear spin diffusion) at low temperatures (< 16 K). Decoupling from the spin-bath is predicted and cluster correlation expansion simulations show near-complete suppression of spin diffusion, at optimal working points. The suppression takes the form of sharply peaked divergences of the spin diffusion coherence time, in contrast with previously identified broader regions of insensitivity to classical fluctuations. ENDOR data shows anisotropic contributions are comparatively weak, so the form of the divergences is independent of crystal orientation.
I. INTRODUCTION
Quantum decoherence presents a fundamental limitation to the realization of practical quantum computing and of other technological devices which actively exploit quantum phenomena. In 2002, a ground-breaking study established the usefulness of so-called optimal working points (OWPs):1 these are parameter regimes where the system becomes – to first order – insensitive to fluctuations of external classical fields. We consider here the effect of OWPs in a system where decoherence of a central spin system arises from interactions with a fluctuating bath of surrounding spins; a scenario that is of considerable significance in the field of quantum information.2–10
A promising approach for silicon-based quantum information processing (QIP) involves combined electron and nuclear spins of donor atoms in Si, which are amenable to high-fidelity manipulation by means of electron paramagnetic resonance (EPR) and nuclear magnetic resonance (NMR) respectively. Most studies have considered phosphorus (31P) donors in Si.11–22 More recently, several different groups have investigated another Group V donor, 209Bi. These studies not only showed that bismuth donors have similar properties to Si:P, such as long coherence times T2 of the order of several ms at low temperatures (< 16 K),23,24 but that they also offer new possibilities for QIP. For example, strong optical hyperpolarization was demonstrated,23,25 allowing for efficient initialization of the nuclear spin. The Si:Bi spin system has an electron spin S = 1/2 and a large nuclear spin I = 9/2 as well as an atypically strong hyperfine coupling constant, A/2π = 1.4754 GHz. The strong state-mixing occurring for magnetic fields B
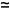 0.1 – 0.6 T where the hyperfine interaction competes with the electronic Zeeman energy, allows transitions which are forbidden at high magnetic fields,26,27 observed recently in Ref. 28. In Refs. 26,27, a set of minima and maxima were found in the f – B parameter space of dipole-allowed transitions at frequencies f. These df/dB = 0 points were identified as OWPs: line narrowing and reduced sensitivity to temporal and spatial noise in B over a broad region of fields (closely related to df/dB = 0 extrema), were found. However, to date, their effectiveness for reducing decoherence in the real environment of a spin-bath remains untested.
0.1 – 0.6 T where the hyperfine interaction competes with the electronic Zeeman energy, allows transitions which are forbidden at high magnetic fields,26,27 observed recently in Ref. 28. In Refs. 26,27, a set of minima and maxima were found in the f – B parameter space of dipole-allowed transitions at frequencies f. These df/dB = 0 points were identified as OWPs: line narrowing and reduced sensitivity to temporal and spatial noise in B over a broad region of fields (closely related to df/dB = 0 extrema), were found. However, to date, their effectiveness for reducing decoherence in the real environment of a spin-bath remains untested.
In natural Si, 4.67% of lattice sites are occupied by the nuclear spin-half 29Si isotope, rather than the spinless 28Si. Flip-flopping of the 29Si spins provides the dominant mechanism of decoherence for both Si:P and Si:Bi systems at low temperatures. The decay of the donor Hahn spin echo for these systems is typically fitted to exp[–t/T2 – (t/TSD)n], where TSD < 1 ms characterizes the nuclear spin diffusion, with n
 2 – 3.29 Other relaxation processes, such as those arising from donor-donor interactions, are represented by T2. Since T2 >> TSD, nuclear spin diffusion remains the main channel of decoherence at low temperatures.30,31
2 – 3.29 Other relaxation processes, such as those arising from donor-donor interactions, are represented by T2. Since T2 >> TSD, nuclear spin diffusion remains the main channel of decoherence at low temperatures.30,31
In this work, we investigate the nature of the Bi-29Si interaction by means of pulsed ENDOR.32 To obtain an ENDOR spectrum, an EPR spin echo is detected as a function of a radio frequency (rf) excitation. When the rf radiation is resonant with an NMR transition, changes are seen in the EPR signal if the populations of the relevant energy levels change. Previous ENDOR studies of Si:Bi used rf frequencies of at least several hundreds of MHz,23,24 and thus could not probe the weak couplings to a spin-bath. In contrast, here, rf frequencies of a few MHz were used. With this approach, we have measured the bismuth spin-bath superhyperfine (SHF) couplings and determined their anisotropy.
We also present the results of cluster correlation expansion (CCE) simulations.29,33 This model has been used with considerable success to model central spin decoherence in Si:P.4,6,7,29 In Ref. 24, weak state-mixing in Si:Bi was investigated by simply allowing for the variation of an effective gyromagnetic ratio. Here we adapt the CCE simulations to include, for the first time, the strong state-mixing seen near the OWPs. A key finding is the demonstration of near-complete suppression of nuclear spin diffusion, even in natural Si: this occurs in extremely narrow regions, where TSD is in effect divergent,34 in contrast to the broader effect expected from the form of df/dB.1 A successful means of controlling decoherence is to employ isotopically enriched samples,4,6,14,19,20,30,31,35–37 which can exhibit long T2 times up to the order of seconds.31 Thus, the OWPs represent a potentially complementary technique, effective for both natural Si and partially enriched samples. In addition, our work suggests that the OWPs may also be effective in suppressing residual effects such as donor-donor interactions which are responsible for shortening T2 times from seconds to the ms timescale.26
II. SPIN HAMILTONIAN
We investigate a spin system with total Hamiltonian:
| 1 |
The first term denotes the isotropic hyperfine interaction between the bismuth electronic and nuclear spins. For Si:Bi, the usual high-field reduction to Ising form cannot be made at the fields of interest here. The second term represents the Zeeman interaction with the external field, including the donor spins and summed over bath spins,
| 2 |
Here, is the electronic Zeeman frequency (μ = 1.857 × 10−23 JT−1) while δBi = 2.486 × 10−4 and δSi = 3.021 × 10−4 are the ratios of the nuclear to electronic Zeeman frequencies for the donor and 29Si spins respectively.
The spin-bath interaction term:
| 3 |
represents the SHF couplings between the donor and bath spins, in general of tensor form (for anisotropic couplings). Finally, dipolar coupling between each pair of 29Si spins is represented by the bath term,
| 4 |
where rnm denotes the relative position vector of bath spins at lattice sites n and m. Writing rnm ≡ r for a pair of spins, the components of the dipolar tensor D are given by,
| 5 |
with μ0 = 4π × 10−7 NA−2 and i, j = x, y, z.
III. ENDOR MEASUREMENTS
The experimental ENDOR studies reported here served to investigate and characterize the isotropic/anisotropic character of the spin-bath interaction term, namely a set of distinct Jn values – SHF couplings – in Eq. (3), corresponding to occupancy of inequivalent lattice sites by 29Si impurities. Pulsed ENDOR experiments were performed using the Davies ENDOR pulse sequence.32,38 We applied the pulse sequence , where the microwave (mw) frequency is chosen to excite one EPR transition and the rf is stochastically varied between 2 – 12 MHz or 2 – 7 MHz to excite all nuclear spin transitions in this region. We used 256 ns long πmw-pulses and a 128 ns long mw-pulse. For optimal signal-to-noise ratio and resolution, we used a πrf-pulse of 10 μs. Pulse delays were set to τ1 = 1 μs, τ2 = 3 μs and τ3 = 1.5 μs and a shot repetition time of 1.3 ms was employed to give a good signal-to-noise ratio. All experiments were carried out at 15 K on an E580 pulsed EPR spectrometer (Bruker Biospin) equipped with pulsed ENDOR accessory (E560DP), a dielectric ring ENDOR resonator (EN4118X-MD4), a liquid helium flow cryostat (Oxford CF935) and an rf amplifier (ENI A-500W). We used a donor concentration of 3 × 1015 cm−3 and the magnetic field was directed perpendicular to the [111] plane.
While not offering the higher frequency resolution attainable with continuous-wave ENDOR,39,40 the pulsed ENDOR measurements permit us to adequately constrain and to demonstrate the reliability of the numerical simulations. In particular, we established that isotropic couplings to the spin-bath dominate the decoherence dynamics. While not the focus of this study, a further motivation is to investigate the feasibility of an alternative possibility for QIP: to simultaneously manipulate the 29Si atoms as spin-half qubits, along with the donors.41
Measured ENDOR spectra at f
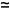 9.755 GHz are presented in Fig. 1, together with a list of SHF couplings. For the magnetic field range B
9.755 GHz are presented in Fig. 1, together with a list of SHF couplings. For the magnetic field range B
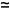 0.1 – 0.6 T in Fig. 1, there is significant mixing of the high-field Si:Bi energy eigenstates |mS, mI
0.1 – 0.6 T in Fig. 1, there is significant mixing of the high-field Si:Bi energy eigenstates |mS, mI . The mixed eigenstates, |±, m
. The mixed eigenstates, |±, m , correspond to doublets (at most) of constant m = mS + mI:
, correspond to doublets (at most) of constant m = mS + mI:
| 6 |
| 7 |
where and m is an integer, –5 ≤ m ≤ 5. Such mixing leads to a complex EPR spectrum for bismuth with df/dB = 0 extrema. The minima correspond to transitions between states corresponding to adjacent avoided level crossings, of which there are four. The disparity between the electronic Zeeman and hyperfine energy scales and SHF energy scales means that the tensor coupling in Eq. (3) reduces to simpler form,
| 8 |
written for coupling to a single 29Si at site l, where and βl = 3Tl sin 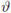 l cos
l cos 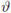 l with aiso,l and Tl the isotropic and anisotropic parts of the molecular-frame SHF tensor respectively and
l with aiso,l and Tl the isotropic and anisotropic parts of the molecular-frame SHF tensor respectively and 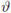 l the angle between the external field and the line connecting the bismuth site and site l. Non-secular terms involving and can be neglected.32 Diagonalization of the resulting 2-dimensional Hamiltonian, and setting Tl = 0 for a purely isotropic coupling leads to a simple expression for the ENDOR resonance frequency for donor level |±, m
l the angle between the external field and the line connecting the bismuth site and site l. Non-secular terms involving and can be neglected.32 Diagonalization of the resulting 2-dimensional Hamiltonian, and setting Tl = 0 for a purely isotropic coupling leads to a simple expression for the ENDOR resonance frequency for donor level |±, m :
:
| 9 |
The above expression is in perfect agreement with full numerical diagonalization. The couplings in Fig. 1 were extracted from the measured spectra by fitting to the data Gaussians of equal width and using Eq. (9). The same expression and a single set of couplings gave excellent agreement with data at 10 different fields. In particular, the observed pattern of half a dozen highest frequency 29Si resonances moving to a minimum at B
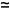 0.2 T, then increasing again, is directly attributable to mixing of the states of the bismuth donor: i.e., here γm(ω0) has a minimum.
0.2 T, then increasing again, is directly attributable to mixing of the states of the bismuth donor: i.e., here γm(ω0) has a minimum.
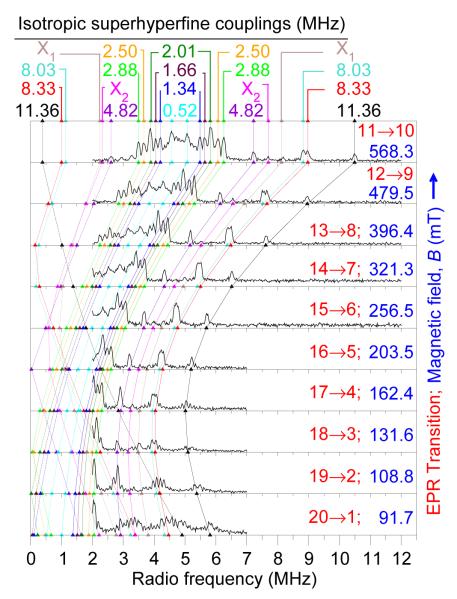
FIG. 1.
(color online) Pulsed ENDOR measured for bismuthdoped silicon with frequency 9.8 GHz at which ten EPR lines are observed, the resonance peaks due to interactions of the donor with 29Si nuclei at inequivalent lattice sites. The isotropic superhyperfine couplings were extracted from the spectrum at the highest magnetic field. As the field is varied, the smooth lines follow the resonance positions according to Eq. (9). Solid and dotted lines distinguish between the two peaks observed for each coupling, each corresponding to one of the two donor levels involved in the EPR transition. Only the peaks labeled X1 and X2, in addition to a third pair not resolved here, were found to show anisotropy from performing ENDOR as a function of crystal orientation.
Ten out of the twelve couplings extracted from data were found to be purely isotropic. The highest-field spectrum was measured for a range of crystal orientations and only three weak intensity lines showed orientation-dependent frequencies and hence anisotropy. Two are indicated by X1 and X2 in Fig. 1: the corresponding two couplings with non-zero anisotropy were found to have (aiso,X1
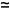 2.8, TX1
2.8, TX1
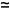 2.4) MHz and (aiso,X2
2.4) MHz and (aiso,X2
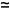 0.4, TX2
0.4, TX2
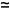 2.8) MHz by fitting the more general form of Eq. (9) with non-zero T. A previous ESEEM (electron spin echo envelope modulation) study identified a single anisotropic coupling,42 attributed to E-shell (nearest neighbor) 29Si. The third line we identify is fitted by coupling constants consistent with the anisotropic coupling in Ref. 42. For most crystal orientations, this line is masked by much higher intensity lines arising from isotropic couplings.
2.8) MHz by fitting the more general form of Eq. (9) with non-zero T. A previous ESEEM (electron spin echo envelope modulation) study identified a single anisotropic coupling,42 attributed to E-shell (nearest neighbor) 29Si. The third line we identify is fitted by coupling constants consistent with the anisotropic coupling in Ref. 42. For most crystal orientations, this line is masked by much higher intensity lines arising from isotropic couplings.
At fields where γm(ω0) becomes small (this occurs close to the df/dB = 0 minima as shown in Refs. 26,27), Eq. (9) tends to the 29Si Zeeman frequency δSiω0. It is straightforward to extend Eq. (9) to the anisotropic case and show that the latter statement also holds for anisotropic couplings. In effect, at these points, the donor might be said to approximately decouple from the bath. For example, for the EPR transition |12 → |9
→ |9 , (labeling the eigenstates |n = 1, 2,…20
, (labeling the eigenstates |n = 1, 2,…20 in increasing order of energy), γm(ω0) = 0 at B = 157.9 mT for level |12
in increasing order of energy), γm(ω0) = 0 at B = 157.9 mT for level |12 and B = 210.5 mT for |9
and B = 210.5 mT for |9 . We note that there is however no B-field value where both the upper and lower levels have γm(ω0) = 0: as we see below, this is not actually essential for complete suppression of spin diffusion. The actual OWP (where df/dB = 0) is at B = 188.0 mT, occurring when
. We note that there is however no B-field value where both the upper and lower levels have γm(ω0) = 0: as we see below, this is not actually essential for complete suppression of spin diffusion. The actual OWP (where df/dB = 0) is at B = 188.0 mT, occurring when
| 10 |
IV. CLUSTER CORRELATION EXPANSION SIMULATIONS
In order to model the full dynamics, we assume that the temperature and donor concentrations are low enough so that phonon-induced decoherence and decoherence due to interactions between donors are negligible. The Hahn spin echo decay of a central donor electron coupled to the bismuth nucleus in a bath of 29Si was calculated using the CCE.33 Denoting the spin echo intensity by L(t), let LS(t) be L(t) computed including only spins in some set or “cluster” of bath spins S. The quantity is defined as,
| 11 |
where the product is over all clusters. Applying this definition to LS(t) and factoring out , an explicit form for the is obtained in terms of the LS(t) and the in subsets of ,
| 12 |
The problem of calculating L(t) is reduced into independent components each for a distinct cluster of bath spins. The exact solution to L(t) is obtained if the from all clusters are combined using Eq. (11) and the approximation to L (t) up to a maximum cluster size of k is defined as,
| 13 |
which involves calculating reduced problems for all clusters each containing at most k spins. Including up to L(k=2)(t) (2-cluster) is a good approximation to L(t) when considering only dipolar interactions in the bath affecting the spin echo, as these are of the order of a few kHz and hence perturbative compared to the SHF interactions in the MHz range involving the donor electron. The CCE is exact, but not always convergent. We calculated the 2-cluster (k = 2) approximation to the CCE and obtained convergence for up to k = 3.
The Hahn echo sequence evolves the combined systembath state to time t = 2τ:
| 14 |
where is the Pauli-X gate acting on the donor and 1B denotes the bath identity. We assume that the time taken for a π-pulse is small compared to τ. The initial state was written as a product of the initial donor and bath states, the former chosen as an equal superposition of states |12 and |9
and |9 . The donor subsystem is recovered after tracing over the bath and the modulus of the normalized off-diagonal element of the donor reduced density matrix is proportional to the intensity of the echo at time t = 2τ. The reduced problem of the 2-cluster bath was solved for each of the four initial 2-product bath states and the average intensity obtained. 2-clusters were formed by pairing 29Si spins separated by up to the 3rd nearest neighbor distance in a diamond cubic lattice of side length 160 Å. Convergence was obtained as the lattice size and the separation between the two bath nuclei were extended. It was assumed that B was large enough to conserve the total 29Si Zeeman energy. Thus, the dipolar interaction between the two bath spins took the form of a combination of Ising () and flip-flop () terms. The Kohn-Luttinger electronic wavefunction was used to calculate the isotropic Fermi contact SHF strength with an ionization energy of 0.069 eV for the bismuth donor. Calculated couplings were of the same order as those obtained from data. The data showed that isotropic couplings predominate; hence anisotropic couplings could be neglected and the simulations are insensitive to orientation. Finally, we obtained the average L(k=2)(t) over 100 spatial configurations of 29Si occupying 4.67% of lattice sites. The resulting decay curves were fitted to exp[–t/T2 – (t/TSD)n], obtaining T2 >> TSD and values of n
. The donor subsystem is recovered after tracing over the bath and the modulus of the normalized off-diagonal element of the donor reduced density matrix is proportional to the intensity of the echo at time t = 2τ. The reduced problem of the 2-cluster bath was solved for each of the four initial 2-product bath states and the average intensity obtained. 2-clusters were formed by pairing 29Si spins separated by up to the 3rd nearest neighbor distance in a diamond cubic lattice of side length 160 Å. Convergence was obtained as the lattice size and the separation between the two bath nuclei were extended. It was assumed that B was large enough to conserve the total 29Si Zeeman energy. Thus, the dipolar interaction between the two bath spins took the form of a combination of Ising () and flip-flop () terms. The Kohn-Luttinger electronic wavefunction was used to calculate the isotropic Fermi contact SHF strength with an ionization energy of 0.069 eV for the bismuth donor. Calculated couplings were of the same order as those obtained from data. The data showed that isotropic couplings predominate; hence anisotropic couplings could be neglected and the simulations are insensitive to orientation. Finally, we obtained the average L(k=2)(t) over 100 spatial configurations of 29Si occupying 4.67% of lattice sites. The resulting decay curves were fitted to exp[–t/T2 – (t/TSD)n], obtaining T2 >> TSD and values of n
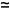 2 – 3.
2 – 3.
V. SUPPRESSION OF NUCLEAR SPIN DIFFUSION
The results of our CCE simulations are presented in Fig. 2. Figure 2(a) shows the behavior around the B = 188.0 mT OWP, associated with the |12 → |9
→ |9 EPR line. The calculated coherence time TSD (orange dashed line) is superposed on a color map showing the SHF spectrum: the latter shows ENDOR spectra simulated as a function of B, using Eq. (9) and centered about the 29Si nuclear Zeeman frequency. Strikingly, as B approaches the OWP, the “comb” of SHF lines narrows to little more than the width of a single line. This suggests a drastic reduction in the value of the SHF couplings, indicating that the bismuth has become largely uncoupled from the 29Si spin-bath.
EPR line. The calculated coherence time TSD (orange dashed line) is superposed on a color map showing the SHF spectrum: the latter shows ENDOR spectra simulated as a function of B, using Eq. (9) and centered about the 29Si nuclear Zeeman frequency. Strikingly, as B approaches the OWP, the “comb” of SHF lines narrows to little more than the width of a single line. This suggests a drastic reduction in the value of the SHF couplings, indicating that the bismuth has become largely uncoupled from the 29Si spin-bath.
FIG. 2.
(color online) Suppression of Bi-29Si spin-bath decoherence for the |12 → |9
→ |9 EPR transition. (a) Simulated ENDOR and nuclear spin diffusion coherence times TSD as a function of magnetic field B, showing collapse of the superhyperfine couplings and a sharp increase in TSD as the field approaches the B = 188.0 mT optimal working point (OWP). The dashed line is a fit. (b) Simulated ENDOR at the B = 188.0 mT OWP (upper panel) and experimental spectrum at 9.755 GHz (lower panel). (c) Calculated donor Hahn spin echo decays from which coherence times in Fig. 2(a) were extracted.
EPR transition. (a) Simulated ENDOR and nuclear spin diffusion coherence times TSD as a function of magnetic field B, showing collapse of the superhyperfine couplings and a sharp increase in TSD as the field approaches the B = 188.0 mT optimal working point (OWP). The dashed line is a fit. (b) Simulated ENDOR at the B = 188.0 mT OWP (upper panel) and experimental spectrum at 9.755 GHz (lower panel). (c) Calculated donor Hahn spin echo decays from which coherence times in Fig. 2(a) were extracted.
The collapse in the SHF couplings is illustrated further in Fig. 2(b). The lower panel shows the measured spectrum at 9.755 GHz. Using our experimentally-determined SHF couplings, the corresponding spectrum at the OWP is shown in the upper panel of Fig. 2(b), demonstrating clearly the line narrowing (corresponding to the same parameters as Fig. 2(a) but at the precise field value of the OWP).
The behavior of TSD is also quite striking and unexpected: the coherence time predicted by CCE simulations increases asymptotically at the OWP by several orders of magnitude. Away from the OWP, the results agree well with experimentally measured values of approximately 0.7 ms.24 In Ref. 24, in a regime of weak state-mixing, simulations using an effective gyromagnetic ratio indicated that TSD was slightly reduced (by about 5%) in a regime corresponding to lower df/dB. The present study on the other hand, (which in contrast to Ref. 24 employed a full treatment of the quantum eigenstate mixing) shows rather an effect very sharply peaked about the OWP: nuclear spin diffusion is predicted to be largely suppressed, but over an extremely narrow magnetic field range.
Figure 2(c) shows a sample of CCE spin echo decays from which TSD times were extracted, and also serves to further illustrate the sharp increase in TSD. Similar suppression is present for other OWPs in Si:Bi. There are df/dB = 0 minima for the |15 → |6
→ |6 , |14
, |14 → |7
→ |7 , |13
, |13 → |8
→ |8 , |12
, |12 → |9
→ |9 and |11
and |11 → |8
→ |8 transitions in the frequency range 5 – 7.5 GHz and two maxima for |12
transitions in the frequency range 5 – 7.5 GHz and two maxima for |12 → |11
→ |11 and |9
and |9 → |8
→ |8 close to 1 GHz. The decoupling from the spin-bath is also expected to lead to suppression of decoherence arising from the interaction with a bath of donors.26
close to 1 GHz. The decoupling from the spin-bath is also expected to lead to suppression of decoherence arising from the interaction with a bath of donors.26
VI. CONCLUSIONS
In conclusion, we present the first measurements of the isotropic SHF couplings which dominate the interaction between a bismuth donor and a bath of 29Si impurities. We further demonstrate the suppression of couplings at OWPs. Finally, the spin echo decay of the donor is calculated as a many-body problem and sharp divergence of the spin diffusion time is observed at an OWP. Our study motivates experimental EPR studies in the range 5 – 7.5 GHz corresponding to the regions of suppressed decoherence.
ACKNOWLEDGMENTS
We acknowledge Bernard Pajot for the Si:Bi crystal used here and thank the EPSRC for financial support through the COMPASSS grant. GWM is supported by the Royal Commission for the Exhibition of 1851. Sandia National Laboratories is a multiprogram laboratory operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.
Footnotes
PACS numbers: 76.70.Dx, 76.30.–v, 03.65.Yz, 03.67.Lx
References
- 1.Vion D, Aassime A, Cottet A, Joyez P, Pothier H, Urbina C, Esteve D, Devoret MH. Science. 2002;296:886. doi: 10.1126/science.1069372. [DOI] [PubMed] [Google Scholar]
- 2.de Sousa R, Das Sarma S. Phys. Rev. B. 2003;67:033301. [Google Scholar]
- 3.de Sousa R, Das Sarma S. Phys. Rev. B. 2003;68:115322. [Google Scholar]
- 4.Abe E, Itoh KM, Isoya J, Yamasaki S. Phys. Rev. B. 2004;70:033204. [Google Scholar]
- 5.Takahashi S, Hanson R, van Tol J, Sherwin MS, Awschalom DD. Phys. Rev. Lett. 2008;101:047601. doi: 10.1103/PhysRevLett.101.047601. [DOI] [PubMed] [Google Scholar]
- 6.Abe E, Tyryshkin AM, Tojo S, Morton JJL, Witzel WM, Fujimoto A, Ager JW, Haller EE, Isoya J, Lyon SA, Thewalt MLW, Itoh KM. Phys. Rev. B. 2010;82:121201(R). [Google Scholar]
- 7.Witzel WM, Carroll MS, Morello A, Cywinski L, Das Sarma S. Phys. Rev. Lett. 2010;105:187602. doi: 10.1103/PhysRevLett.105.187602. [DOI] [PubMed] [Google Scholar]
- 8.Bar-Gill N, Pham LM, Belthangady C, Le Sage D, Cappellaro P, Maze JR, Lukin MD, Yacoby A, Walsworth R. Nat. Commun. 2012;3:858. doi: 10.1038/ncomms1856. [DOI] [PubMed] [Google Scholar]
- 9.Zhao N, Ho SW, Liu RB. Phys. Rev. B. 2012;85:115303. [Google Scholar]
- 10.de Lange G, van der Sar T, Blok M, Wang Z-H, Dobrovitski V, Hanson Ronald. Sci. Rep. 2012;2:382. doi: 10.1038/srep00382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kane BE. Nature. 1998;393:133. [Google Scholar]
- 12.Schofield SR, Curson NJ, Simmons MY, Rueß FJ, Hallam T, Oberbeck L, Clark RG. Phys. Rev. Lett. 2003;91:136104. doi: 10.1103/PhysRevLett.91.136104. [DOI] [PubMed] [Google Scholar]
- 13.Stoneham AM, Fisher AJ, Greenland PT. J. Phys.: Condens. Matter. 2003;15:L447. [Google Scholar]
- 14.Tyryshkin AM, Lyon SA, Astashkin AV, Raitsimring AM. Phys. Rev. B. 2003;68:193207. [Google Scholar]
- 15.Fu K-MC, Ladd TD, Santori C, Yamamoto Y. Phys. Rev. B. 2004;69:125306. [Google Scholar]
- 16.Morley GW, McCamey DR, Seipel HA, Brunel L-C, van Tol J, Boehme C. Phys. Rev. Lett. 2008;101:207602. doi: 10.1103/PhysRevLett.101.207602. [DOI] [PubMed] [Google Scholar]
- 17.Morello A, Pla JJ, Zwanenburg FA, Chan KW, Tan KY, Huebl H, Möttönen M, Nugroho CD, Yang C, van Donkelaar JA, Alves ADC, Jamieson DN, Escott CC, Hollenberg LCL, Clark RG, Dzurak AS. Nature. 2010;467:687. doi: 10.1038/nature09392. [DOI] [PubMed] [Google Scholar]
- 18.Greenland PT, Lynch SA, van der Meer AFG, Murdin BN, Pidgeon CR, Redlich B, Vinh NQ, Aeppli G. Nature. 2010;465:1057. doi: 10.1038/nature09112. [DOI] [PubMed] [Google Scholar]
- 19.Simmons S, Brown RM, Riemann H, Abrosimov NV, Becker P, Pohl H-J, Thewalt MLW, Itoh KM, Morton JJL. Nature. 2011;470:69. doi: 10.1038/nature09696. [DOI] [PubMed] [Google Scholar]
- 20.Steger M, Sekiguchi T, Yang A, Saeedi K, Hayden ME, Thewalt MLW, Itoh KM, Riemann H, Abrosimov NV, Becker P, Pohl H-J. J. Appl. Phys. 2011;109:102411. [Google Scholar]
- 21.Dreher L, Hoehne F, Stutzmann M, Brandt MS. Phys. Rev. Lett. 2012;108:027602. doi: 10.1103/PhysRevLett.108.027602. [DOI] [PubMed] [Google Scholar]
- 22.Fuechsle M, Miwa JA, Mahapatra S, Ryu H, Lee S, Warschkow O, Hollenberg LCL, Klimeck G, Simmons MY. Nature Nanotech. 2012;7:242. doi: 10.1038/nnano.2012.21. [DOI] [PubMed] [Google Scholar]
- 23.Morley GW, Warner M, Stoneham AM, Greenland PT, van Tol J, Kay CWM, Aeppli G. Nature Mater. 2010;9:725–729. doi: 10.1038/nmat2828. [DOI] [PubMed] [Google Scholar]
- 24.George RE, Witzel W, Riemann H, Abrosimov NV, Nötzel N, Thewalt MLW, Morton JJL. Phys. Rev. Lett. 2010;105:067601. doi: 10.1103/PhysRevLett.105.067601. [DOI] [PubMed] [Google Scholar]
- 25.Sekiguchi T, Steger M, Saeedi K, Thewalt MLW, Riemann H, Abrosimov NV, Nötzel N. Phys. Rev. Lett. 2010;104:137402. doi: 10.1103/PhysRevLett.104.137402. [DOI] [PubMed] [Google Scholar]
- 26.Mohammady MH, Morley GW, Monteiro TS. Phys. Rev. Lett. 2010;105:067602. doi: 10.1103/PhysRevLett.105.067602. [DOI] [PubMed] [Google Scholar]
- 27.Mohammady MH, Morley GW, Nazir A, Monteiro TS. Phys. Rev. B. 2012;85:094404. [Google Scholar]
- 28.Morley GW, Lueders P, Mohammady MH, Balian SJ, Aeppli G, Kay CWM, Witzel WM, Jeschke G, Monteiro TS. e-print arXiv:1109.4269 (unpublished)
- 29.Witzel WM, Das Sarma S. Phys. Rev. B. 2006;74:035322. [Google Scholar]
- 30.Tyryshkin AM, Morton JJL, Benjamin SC, Ardavan A, Briggs GAD, Ager JW, Lyon SA. J. Phys.: Condens. Matter. 2006;18:S783. [Google Scholar]
- 31.Tyryshkin AM, Tojo S, Morton JJL, Riemann H, Abrosimov NV, Becker P, Pohl H-J, Schenkel T, Thewalt MLW, Itoh KM, Lyon SA. Nature Mater. 2012;11:143. doi: 10.1038/nmat3182. [DOI] [PubMed] [Google Scholar]
- 32.Schweiger A, Jeschke G. Principles of Pulse paramagnetic resonance. Oxford University Press; Great Clarendon Street, Oxford, UK: 2001. [Google Scholar]
- 33.Yang W, Liu RB. Phys. Rev. B. 2008;78:085315. [Google Scholar]; Yang W, Liu RB. ibid. 2008;78:129901(E). [Google Scholar]; Yang W, Liu RB. ibid. 2009;79:115320. [Google Scholar]
- 34.In the sense that decay of the spin echo is no longer discernible in our converged cluster calculations.
- 35.Steger M, Saeedi K, Thewalt MLW, Morton JJL, Riemann H, Abrosimov NV, Becker P, Pohl H-J. Science. 2012;336:1280. doi: 10.1126/science.1217635. [DOI] [PubMed] [Google Scholar]
- 36.Weis CD, Lo CC, Lang V, Tyryshkin AM, George RE, Yu KM, Bokor J, Lyon SA, Morton JJL, Schenkel T. e-print arXiv:1202.1560 (unpublished)
- 37.Wolfowicz G, Simmons S, Tyryshkin AM, George RE, Riemann H, Abrosimov NV, Becker P, Pohl H-J, Lyon SA, Thewalt MLW, Morton JJL. e-print arXiv:1207.3776 (unpublished)
- 38.Although Mims ENDOR offers higher selectivity to small SHF couplings, it would suffer from blind spots.
- 39.Feher G. Phys. Rev. 1959;114:1219. [Google Scholar]
- 40.Hale EB, Mieher RL. Phys. Rev. 1969;184:739. [Google Scholar]
- 41.Akhtar W, Filidou V, Sekiguchi T, Kawakami E, Itahashi T, Vlasenko L, Morton JJL, Itoh KM. Phys. Rev. Lett. 2012;108:097601. doi: 10.1103/PhysRevLett.108.097601. [DOI] [PubMed] [Google Scholar]
- 42.Belli M, Fanciulli M, Abrosimov NV. Phys. Rev. B. 2011;83:235204. [Google Scholar]