The Impact of Mutation and Gene Conversion on the Local Diversification of Antigen Genes in African Trypanosomes

Abstract

Patterns of genetic diversity in parasite antigen gene families hold important information about their potential to generate antigenic variation within and between hosts. The evolution of such gene families is typically driven by gene duplication, followed by point mutation and gene conversion. There is great interest in estimating the rates of these processes from molecular sequences for understanding the evolution of the pathogen and its significance for infection processes. In this study, a series of models are constructed to investigate hypotheses about the nucleotide diversity patterns between closely related gene sequences from the antigen gene archive of the African trypanosome, the protozoan parasite causative of human sleeping sickness in Equatorial Africa. We use a hidden Markov model approach to identify two scales of diversification: clustering of sequence mismatches, a putative indicator of gene conversion events with other lower-identity donor genes in the archive, and at a sparser scale, isolated mismatches, likely arising from independent point mutations. In addition to quantifying the respective probabilities of occurrence of these two processes, our approach yields estimates for the gene conversion tract length distribution and the average diversity contributed locally by conversion events. Model fitting is conducted using a Bayesian framework. We find that diversifying gene conversion events with lower-identity partners occur at least five times less frequently than point mutations on variant surface glycoprotein (VSG) pairs, and the average imported conversion tract is between 14 and 25 nucleotides long. However, because of the high diversity introduced by gene conversion, the two processes have almost equal impact on the per-nucleotide rate of sequence diversification between VSG subfamily members. We are able to disentangle the most likely locations of point mutations and conversions on each aligned gene pair.

Introduction

The African trypanosome, a protozoan pathogen prevalent in Equatorial Africa is the causative agent of human sleeping sickness. Despite extensive research efforts, the development of vaccines against this parasite remains a challenge. This is mainly due to trypanosome antigenic variation, a complex process whereby the parasite switches expression of its variant surface glycoprotein (VSG) genes during infection, in a largely unpredictable manner. As antibodies arise against an antigenic variant, parasites that have switched to another variant survive and can proliferate, continuing the infection. Trypanosomes contain a large family of >1,600 VSG genes, involved in antigenic variation (Morrison et al. 2009). These genes are genetically diverse and their products are antigenically diverse. Although just a single VSG gene from this repertoire is expressed by the trypanosome at any time, the other silent genes undergo evolutionary changes in an incremental manner, thought to facilitate future immune evasion of this parasite.

In this context, studying the dynamic mechanisms that generate and maintain diversity within such antigen repertoires is crucial. Multigene families, such as the VSG antigen repertoire of trypanosomes, are groups of genes that include multiple copies generated by duplication from a common ancestor gene, usually serving a similar function. To understand the biological function of gene families, one needs to examine their evolutionary histories. Typically, multigene families diversify through a variety of mutational mechanisms, prominent among which are base substitutions, insertions–deletions (indels), and intergenic conversions through overwriting one sequence with a copy of another. Although conversion reduces globally the diversity between sequences, it can potentially increase it locally (within subfamilies), in particular by introducing one diverged sequence adjacent to another (Parham and Ohta 1996; Martinsohn et al. 1999; Ohta 2010). Diversification of gene family members has the potential to expand the range of biological functions served by the entire gene family.

The nearly completed sequencing of the African trypanosome genome (Berriman et al. 2005) provides unprecedented opportunities to explore the effects of such processes on the antigen gene family of this parasite. The VSG archive evolves through whole-gene duplication followed by divergence through point mutation and recombination events. As individual VSGs are rarely expressed, they are under low direct selection. It seems likely that the archive is under second-order selection (Weber 1996), through the evolution of mechanisms for high intrinsic mutation rates across the entire coding sequence (Marcello and Barry 2007). As the archive is located in subtelomeres, which undergo promiscuous ectopic recombination, most VSGs are able to interact recombinationally, independently of locus. Consequently, gene conversion has also an important role to play in genetic diversification of silent antigen copies.

The target of antibodies is typically the N-terminal domain of the VSG genes, whose main feature is hypervariability: modal peptide identity across N-domains is <25%. However, multiple DNA sequence alignments have revealed that the archive is structured, with ∼40% of VSGs occurring as high-identity pairs or triplets of >50% peptide identity (Marcello and Barry 2007). The presence of such antigen gene groupings, consisting mainly of pseudogenes, and their genetic similarity, facilitate the processes of homology-driven recombination, whereby successful novel mosaic VSGs are formed and expressed in the chronic stages of trypanosome infections. Despite its role in the generation, disruption, and maintenance of gene similarity, the extent to which recombination occurs in the antigen gene archive of African trypanosomes remains largely unknown.

To track and characterize the mutational events that diversify this archive, there is a need for a mechanistic parametric analysis of these processes. An interesting question, central to mosaic gene formation in African trypanosomes, is how do highly similar, newly arisen, archive subgroups diverge? Presumably, similarity between two archival copies indicates short divergence time since duplication. However, what is the relative contribution of point mutation and gene conversion, early in the course of this evolution? Quantifying the rates of these evolutionary processes may be key for addressing more complicated questions about the underlying mechanisms involved and their maintenance by selective forces.

The function of the VSG gene family is fundamental to the life history of trypanosomes. Determining the extent to which pathogen genes recombine has been considered one of the central problems to map mutations that determine parasite phenotypes, such as immune evasion or pathogenicity (Awadalla 2003). Naturally, recombination must occur at various temporal and spatial scales, e.g., within the pathogen genome and between genomes, within the same strain and between strains, potentially serving a different function, and leaving a different signature at each scale.

In this study, we aim to unravel the short-term divergence of duplicated genes within an antigen gene family, resulting from the interplay between point mutation and gene conversion. We develop a general mathematical model that describes changes to aligned gene pairs, by individual point mutation events and by conversion from donor genes in the gene family. The model relies entirely on patterns of identity and mismatches between pairs of aligned sequences, without needing or using any explicit information about the donors that have contributed the genetic material. We are interested only indirectly in detecting the locations of conversion events. A key assumption is that imported conversion tracts differ from the original sequence they replace due to their higher density of nucleotide mismatches. At the temporal scale soon after gene duplication, both point mutation and gene conversion imports from third-party donors in the gene family have a diversifying effect on newly arisen gene pairs.

We apply this modeling framework to pairwise alignment data from small VSG subfamilies, whose gene members display high pairwise nucleotide identity. Such high identity indicates recent gene duplication, followed by moderate discernible diversification. Our method estimates the probabilities of point mutation and gene conversion, the average diversity introduced by gene conversion events and their tract length distribution. We find evidence for a higher frequency of point mutations, compared with gene conversion events, although the resulting per-nucleotide rate of substitution is almost the same for the two processes. Although there are differences in the number of events inferred on each gene pair, the VSG pairs considered exhibit the same size distribution of conversion fragments, characterized by a short average length and a rate of substitution much higher than that of nonrecombined regions. In conclusion, we suggest that patterns of diversity in N-domains of African trypanosome VSG genes may reflect a dynamic in which point mutation and gene conversion are kept at a balance, which could facilitate antigenic dissimilarity, yet without disrupting substantially the homology structure so fundamental to the formation and expression of mosaic genes during chronic-phase infection.

Methods

Gene Isolates

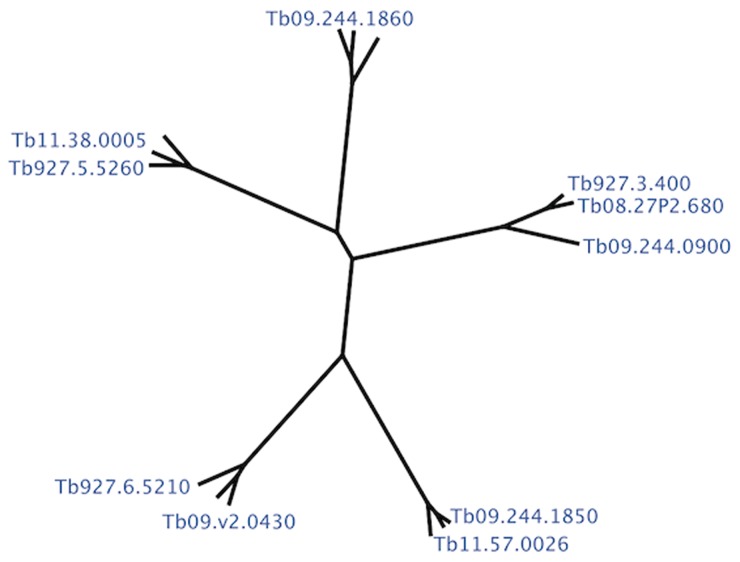
We examined a VSG data set consisting of five triplets of high-identity VSG genes, from the antigen gene archive of African trypanosomes (fig. 1). The 15 genes were obtained from the trypanosome VSG database (http://www.vsgdb.net), with the members of each triplet being 1) Tb927.5.5260, Tb09.160.0100, Tb11.38.0005; 2) Tb09.244.1860, Tb11.57.0027, Tb09.244.0130; 3) Tb927.3.400, Tb08.27P2.680, Tb09.244. 0900; 4) Tb09.244.1850, Tb09.244.0 140, Tb11.57.0026; and 5) Tb09.v2.0430, Tb09.v4.0178, Tb927.6.5210. In the chronic stages of trypanosome infection, such highly related genes can recombine with expressed genes and form novel mosaic genes that can sustain parasite antigenic variation. Given the importance of N-domain hypervariability in determining the epitopes essential for antigenic variation of this parasite, our analysis is restricted to the N-domain encoding regions of these genes (supplementary material SI1, Supplementary Material online, for details). The pairwise alignments used in the analysis were performed by CLUSTALW (Thompson et al. 1994), aligning the three genes of each triplet separately and subsequently retaining only the N-domain encoding regions, comprising ∼1,050 nucleotides on average. Pairwise nucleotide identity within the same triplet ranges between 80% and 90%, whereas gene comparisons across triplets display a much lower identity of approximately 50%. Because we are interested in understanding the evolutionary processes that diversify high-identity gene pairs, we consider only pairwise alignments within the same triplet (3 pairs per triplet), thus obtaining a total of 15 pairwise alignments.

Fig. 1.

Data phylogenetic structure. The phylogenetic tree of the five VSG triplets considered in our study. A total of 15 VSG sequences from the antigen gene archive of African trypanosomes were extracted from the VSG database (http://www.vsgdb.net) and multiply aligned by CLUSTALw. The close relatedness between genes within the same triplet suggests recent divergence from a common ancestor.

Model Formulation

Patterns of nucleotide diversity within each gene pair can be simplified into numerical vectors taking the values of 0 and 1 at each alignment position, to denote a mismatch or an identical nucleotide respectively. From left to right along each alignment, regions of low mismatch density are assumed to be affected only by point mutation, whereas regions of high mismatch density are considered as possible locations where a conversion with an outside donor may have occurred. To distinguish between these two spatial patterns: the higher rate of diversity within conversion tracts and the sparsity of mismatches introduced by point mutation, we develop a simple probabilistic model as follows.

We denote each pairwise alignment by a vector X⁽ⁿ⁾, n = 1, . . N, of length L, where each element X_i⁽ⁿ⁾ takes the values of 0 or 1, to indicate, respectively, a mismatch or identity at nucleotide position i between the two genes. N is the number of gene pairs we analyze. Assuming mutational processes occur at fixed rates per nucleotide, we represent point mutation by a Bernoulli process. For gene conversion events, we assume a parallel Bernoulli process with fixed probability of occurrence per nucleotide, given by λ_begin. A mismatch is positioned at the leftmost border of a conversion with probability λ_begin per nucleotide, denoting the initiation of the converted region. Within the imported conversion tracts, we assume there are only two possible events: either an internal mismatch is introduced with probability μ per nucleotide or the conversion terminates with an end mismatch with probability λ_end per nucleotide. This formulation implies that a conversion tract is imported noninterrupted and always delimited by two mismatches at its borders. In the alignment regions between conversions, there are two possible events: either a point mutation occurs, altering the sequence with probability m per nucleotide (m < μ) or a new conversion is initiated with probability λ_begin. Implicitly, we make the simplifying assumption that conversion events are nonoverlapping, which might lead to an underestimation of the real conversion event probability and an overestimation of the conversion tract length. The average relative number of conversion and point mutation events that occur on each alignment depends directly on the ratio λ_begin/m.

The simulation of this process can be carried out on an event-by-event basis (supplementary material SI2, Supplementary Material online), essentially similar to the Gillespie algorithm (Gillespie 1977). The memoryless property of the process ensures the distances to the next event, i.e., to the next mismatch, are geometrically distributed with parameter corresponding to the total probability of events that can happen at the current point. As a consequence, the resulting conversion lengths, defined (conservatively) by the distance from the first to the last mismatch inside conversion tracts, follow a geometric distribution with parameter λ_end. The geometric tract length distribution appears to describe well the mechanistic basis of gene conversion and has been applied previously (Hilliker et al. 1994; Betran et al. 1997; Didelot and Falush 2007).

Estimation of Mutation and Gene Conversion Probabilities

Instead of focusing on mismatches themselves and their locations, it is more convenient to transform the data into intermismatch distances. Suppose alignment X⁽ⁿ⁾ has M mismatches. We can thus consider on any alignment that each observation y_i(i = 1, … M) of “waiting-times” (distances) to the next mismatch is associated with an unobserved hidden state s_i = k, k ∈ {1, 2}: 1, corresponding to a between-conversion region, and 2, corresponding to a “within conversion region”. Conditioned on the type of the hidden state, each y_i observation is assumed to be independently drawn from a geometric distribution: Φ_k(d) = P( y_i = d|s_i = k) = (1−λ_k)^d−1λ_k, with parameters λ₁ = λ_begin + m, for between-cluster distances, and λ₂ = μ + λ_end, for within-cluster distances, where d = 1,2,3, … L − 1.

This model is an example of a large class of models known as Hidden Markov Models (HMM) (Durbin et al. 1998), widely used in biological sequence analysis. The numerical values of intermismatch distances we observe are generated by hidden states, forming an ordered sequence where the probability of the next state depends only on the current state. The transition matrix between states 1 and 2 in our model is given by:

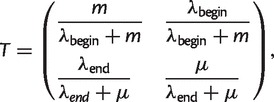(1)

where entry T_1,2 = P(s_i = 2|s_i−1 = 1) and so on, expressing the probabilities for the mismatches to persist within the same conversion or to jump between conversions. Given the four basic parameters (λ_begin, λ_end, μ, and m), the transition probabilities T_i,j and the two geometric distributions for the next-mismatch segment lengths (“emission” probabilities) are uniquely determined. Conditioned on the sequence of hidden states S = {s_i, i = 1, … , M}, the likelihood of the data y = {y_i, i = 1, … M} on each alignment is:

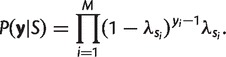(2)

The joint probability of the observations and a particular hidden path is given by:

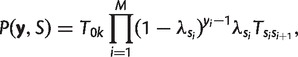(3)

where T_0k is the transition probability from an artificially introduced initial state to state k and can be thought of as the probability of starting in state k. Because many different hidden paths can give rise to the same sequence of observations y, to obtain the full likelihood of y, we must consider and sum over all possible sequences of hidden states. We do not impose a priori any information about the hidden states.

Given the observations of next-mismatch distances in N closely related pairs of gene sequences, we wish to infer the genetic parameters (λ_begin, λ_end, μ and m) that are most likely to have generated the diversity pattern. Each aligned gene pair within the same triplet is treated as an independent realization of the stochastic process describing the evolutionary dynamics of recently duplicated genes. This implies the total likelihood of the data becomes a product over the individual alignment likelihoods. Such a simplifying assumption about independence between the gene pairs in our data set should introduce no bias in our estimates, although it could potentially underestimate the associated standard deviations. The fact that we consider all gene pairs within each triplet: (i,j), (j,k), and (i,k), allows each conversion and mutation event that has occurred on one of the triplet members, e.g., on gene i, to be counted twice, if detected correctly, because it should appear on both alignments with the other members (i,j) and (i,k). Reassuringly, numerical simulations confirm an accuracy of event detection ≥80%, even for short conversion tracts, the only difficulty arising in the estimation of imported tract lengths, where the identifiability of all mismatches imported from outside is more challenging.

Testing Different Hypotheses

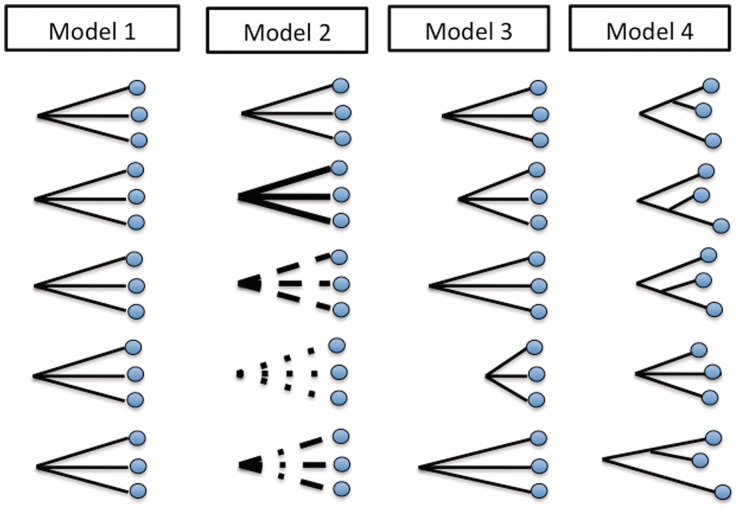
We construct different models to investigate competing hypotheses on the same data set. Each model is based on different assumptions about the origin of differences across aligned pairs (fig. 2). In the following, we present results for four models that we consider most relevant and biologically plausible:

1. Global fit model: The simplest hypothesis is the one where the same parameter values apply to all (N = 15) closely related pairs simultaneously. All gene pairs can be thought to derive from the same process, thus sharing the same probability of conversion, conversion length distribution, point mutation probability, and the same mismatch density per conversion. This model results in four parameters that should explain the mismatch pattern of every pairwise alignment.

2. Triplet fits: Alternatively, the data may be seen as a collection of five completely independent triplets, each governed by its own set of parameters (λ_begin, λ_end, μ, and m). This formulation entails 5 × 4 = 20 parameters in total.

3. Triplet ages: The data may consist of five partially related triplets, which are governed by the same density of mismatches within conversions μ and same probability of conversion termination λ_end but differ in the time elapsed since sharing a common ancestor, thus display triplet-specific point mutation probability m and triplet-specific conversion event probability λ_begin. Under the convention that the latter probabilities scale by the same factor in each triplet relative to the first triplet, we can introduce a new parameter in the model, namely the relative “age” of each triplet. Triplet 1 gets assigned age A₁ = 1. Then, for the other triplets (2, … N/3 − 1), the “ages” relative to the first triplet A_triplet can be inferred. It is sufficient to parameterize the model in terms of λ_begin and m only for the first triplet and A₂, A₃, A₄, and A₅. Such a model has 4 + 4 = 8 parameters, which are estimated jointly across all data. When “ages” are included, the triplet-specific probability of conversion initiation per nucleotide λ_begin and the triplet-specific probability of point mutation per nucleotide m, after scaling become the products λ_begin A_triplet and mA_triplet, in the range [0,1]. Intuitively, in aligned pairs from an “older” triplet, we should expect more conversion events and more point mutation events on average compared to a “younger” triplet. This model considers the scenario that all three genes within the same triplet have arisen at the same time from a common ancestor.

4. Individual ages: Here we consider the case where each gene pair shares the same μ and λ_end with the other gene pairs but differs in λ_begin and m. Assuming that the probabilities of conversion and point mutation events scale equally among gene pairs, we can introduce again a scaling parameter, similar to a pair-specific “age” relative to pair 1. This yields a set of four primary parameters governing the reference pair/alignment and 14 = N − 1 parameters for the relative “ages” of the other gene pairs. For these other alignments, the pair-specific parameters λ_begin and m become the products of the corresponding parameters in the reference pair, multiplied (as in the triplet ages model) by their relative age A_i,i = 2, … N. The total number of parameters here is 4 + 14 = 18. This model also results in the same conversion tract length distribution and the same density of mismatches per conversion across all gene pairs, while allowing for variability in divergence time from one same common ancestor.

Fig. 2.

Model diagrams. The four models differ in the assumptions they make about the nature of the evolutionary processes (depicted by line type) and the divergence time between the compared sequences (depicted by line length). Model 1 assumes point mutation and conversion are governed by the same parameters on all gene pairs, and each pair within a triplet shares the same “age” with other pairs. Model 2 assumes distinct triplet-specific probabilities of genetic processes, and it allows for triplet-specific conversion length distribution and conversion mismatch density. Model 3 assumes the processes occur universally at equal rates across triplets, including conversion length distribution and mismatch density; however, the divergence time of each triplet may be different. Model 4 assumes equal process rates across gene pairs, but it allows for within-triplet variation in divergence time.

Inference Procedure and Model Selection

We adopt a Bayesian approach that allows us to estimate explicitly the transition probabilities between large-scale and small-scale next-mismatch distances and the probability distributions associated with each of these states. In addition, this approach enables us to include any prior knowledge about the process and to quantify the statistical uncertainty associated with our data. Because the posterior distributions themselves are impossible to get analytically, we implement the Metropolis–Hastings Algorithm, one of the simplest Monte Carlo Markov Chain (MCMC) sampling techniques (Gilks et al. 1996), to obtain numerically the probability distributions of model parameters. We reparameterize the model from (λ_begin, λ_end, μ, m) to the more convenient form θ = ( p₁, p₂, λ₂, ε), yielding the following transition and emission probabilities in the HMM:

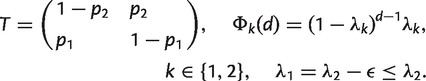We can recover explicitly the genetic parameters from: λ_begin = p₂λ₁; m = (1 − p₂) λ₁; λ_end = p₁λ₂; μ = (1 − p₁)λ₂, after the auxiliary composite parameters θ = (p₁,p₂,λ₂,ε) have been estimated. Notice that θ varies across the four models considered. For example, in Model 4, θ = (p₁,p₂,λ₂,ε₁,ε₂,…ε₁₅), where the index of ε runs through all gene pairs. Then, the relative ages are obtained as A_i = λ_begin (i)/λ_begin (1) = m(i)/m(1), where λ_begin (1) and m(1) are the estimated probabilities in the reference gene pair.

The algorithm is implemented in MATLAB (MathWorks, 2010) and its performance evaluated on simulated data (supplementary material SI3, Supplementary Material online). We use uniform priors U(0,1) for all parameters, truncating to the range [0,1] where parameters are probabilities. For calculating the overall likelihood of each sequence of observations, posterior HMM decoding is used (Durbin et al. 1998), taking into account all possible hidden paths that might have generated the intermismatch distances.

MCMC sampling starts with an initial guess of the parameter values θ₀. Then a new guess is generated from a proposal distribution, e.g., a multivariate normal distribution centred at the current value of the parameters N(θ_old, σ²). The new likelihood of the data is calculated for the new parameter values θ_new. If the new likelihood exceeds the old one, θ_new is accepted with probability 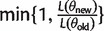, otherwise it is rejected. The covariance matrix of the proposal distribution is tuned to optimize the speed of convergence to the stationary distribution. In our case, σ² was between 0.00025 and 0.0025. This yielded an acceptance rate in the range [0.15,0.5] .

For each model, we ran three MCMC chains from different starting points, until no autocorrelation remained and convergence to the stationary distributions in parameter sample paths was reached. To check convergence, the Gelman–Rubin convergence statistic, as modified by Brooks and Gelman (1998), was monitored. After the burn-in period, which generally consisted of 10,000 iterations, the Markov chains continued to run for 50,000 further iterations. For every parameter, the posterior was thus obtained from a sample of 3 × 50,000 independent MCMC observations.

Model selection was performed on the basis of the Deviance Information Criterion (DIC) (Spiegelhalter et al. 2002), the Bayesian analog of the Akaike's Information Criterion from maximum likelihood methods. Generally, models with lower DIC are preferred over models with higher DIC, although this is not always a strict criterion for model choice (supplementary material SI4, Supplementary Material online). As independent goodness-of-fit tests, we compared the original data set and the simulated data generated with estimated parameters, by checking higher order characteristics such as pair-correlation functions (Illian et al. 2008) and next-mismatch distance cumulative distributions. These tests are explained in more detail in the supplementary material (supplementary material SI6, Supplementary Material online).

Results

We tested the performance of our Bayesian algorithm on simulated mismatch data for different parameter combinations, acting on the same sequence length as the N-domains we considered in our study (supplementary material SI3, Supplementary Material online). Even with small sample sizes of simulated mismatch sequences, our algorithm was able to retrieve within the 90% inferred credibility interval the true parameter values for all four genetic parameters of the baseline model. Furthermore, the average accuracy of the “decoded” types of intermismatch regions was >85%. As the sample size of simulated data increases, both the precision of the method and the accuracy of the posterior decoding increase, with the mean of the inferred posterior distributions approaching the true parameter value. The algorithm performs better when the difference between mismatch density within converted regions (μ) and mutation probability (m) is higher, independently of the conversion tract length.

Estimates of Mutation and Conversion Probabilities

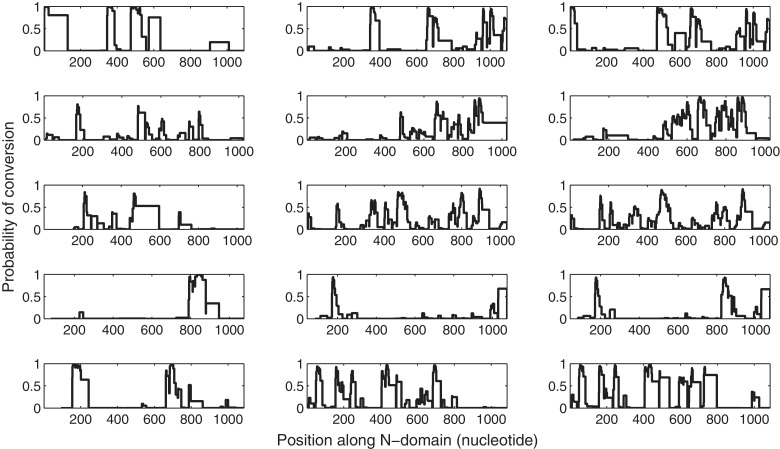
In Model 1, the estimated mean probability of conversion was estimated to be 0.0099 per base pair, whereas the mean probability of point mutation was estimated to be 0.0410, i.e., about four times higher. This suggests that mutation events are more frequent than conversion events with other members of the gene archive in the short time scale after duplication. In Model 2, we considered the case of each triplet being governed by distinct values of parameters. We found that the estimated λ_begin was in the range 0.0038–0.0175 across triplets, a result not very far from the estimate obtained with Model 1. The point mutation probability also showed some variation 0.0325–0.0623, but the values predicted for each triplet stayed within the same order of magnitude. The ratio m/λ_begin increased slightly in Model 3, ≈4.7, strengthening the dominance of the point mutation process. In Model 4, because the effective event probabilities on each gene pair are obtained by the baseline values in the reference pair multiplied by the corresponding relative ages, the λ_begin and m values are pair specific. The values inferred in this model for the reference pair are lower than the values obtained in Model 1, for example. The ratio m/λ_begin, however, is invariant across gene pairs and independent of their relative ages. We observe that point mutations in this last model occur five times more frequently than conversion events (table 1). Note that to obtain the conversion event and mutation probability per gene per nucleotide, the obtained estimates across all models need to be divided by 2. The posterior probabilities associated with the location of imported gene conversion tracts for Model 4 are shown in figure 3.

Table 1.

Parameter Estimates Obtained for Model 4.

Parameter	5% Confidence Bound	Mean	95% Confidence Bound
λbegin (pair 1)	0.0021	0.0035	0.0052
λend	0.0400	0.0551	0.0718
μ	0.2611	0.2877	0.3127
m (pair 1)	0.0124	0.0191	0.0270
A2	1.4725	2.3980	3.6719
A3	1.5531	2.5507	3.9701
A4	1.8741	2.9923	4.5708
A5	2.6478	4.2168	6.3249
A6	1.7537	2.9912	4.6698
A7	1.3536	2.3153	3.5950
A8	3.0133	4.7650	7.1719
A9	3.3190	5.2838	8.0093
A10	0.5063	0.9645	1.5966
A11	1.6073	2.6257	4.0232
A12	1.6795	2.7357	4.1687
A13	1.0776	1.8165	2.8530
A14	1.9615	3.2001	4.8341
A15	1.5089	2.5283	3.9155

Fig. 3.

The posterior probabilities of gene conversion tracts in Model 4. This model gives results, which are the best among the four models considered, on the basis of both DIC and log likelihood. Because a Bayesian approach is adopted, the uncertainty around the most likely hidden path is given in the posterior probabilities of each inter-mismatch segment being of type within or between conversion. The triplets of closely related genes are presented in each row panel in the order (1,2), (1,3), (2,3) for each triplet.

Gene Conversion Tract Length

The average conversion length predicted by all models is notably small, compared with the total length of the sequences analyzed. Model 1 predicts a mean imported tract length of 1/0.0387 ≈25 nucleotides, thus about 2.5% of the total gene length. This increases in Model 2, where for λ_end, the mean range was 0.0126–0.0836, implying more variable conversion lengths between 12 and 80 nucleotides. Model 3 fixes again the conversion tract length across triplets, with the mean estimated to be ∼21 nucleotides. By allowing conversion probabilities to vary across pairs, Model 4 supports even shorter gene conversions, ranging in mean from 14 to 25 nucleotides, with an average of approximately 18 nucleotides (fig. 4). Naturally, the assumption of the geometric distribution of imported tract lengths implies that the inferred conversions do vary in length within the same alignment and across alignments; however, a common feature remains a high mismatch frequency within conversions, which helps to distinguish converted regions from nonconverted regions.

Fig. 4.

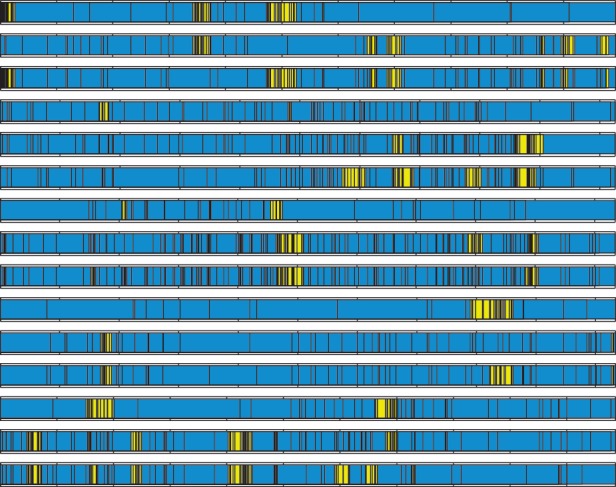
The most likely conversion tracts from Model 4. The 15 high-identity VSG alignments are listed in the order (1,2), (1,3), (2,3) for each triplet. The bars refer to mismatches between nucleotides in the N-domains of the two sequences. The most likely conversion tracts (highlighted in yellow) were estimated by the “decoding” algorithm using the means of the posteriors in table 1. Between-conversion regions are given in blue.

Genetic Diversity Introduced by Gene Conversion

The density of mismatches within conversion tracts gives information about the potential donors with which the given genes might have interacted in the course of their evolution. We estimated the density to be μ = 0.2552 in Model 1, which suggests a large contribution from conversion events with other archive genes in introducing genetic novelty to recently duplicated sequences. In Model 2, the mean density of mismatches per conversion varied across triplets, ranging from 0.2043 to 0.3469; however, its global average, ∼0.26, was consistent with the value of μ predicted by the first model. An increase in the estimate of μ is observed with Model 3, where the diversity within converted tracts is ∼27%. We notice that in Model 4 (table 1), the frequency of mismatches introduced by gene conversion is estimated to be even higher, ∼0.29. A comparison with the average density of mismatches observed in nonconverted regions by the ratio μ/m, which significantly exceeds 1 across all models, suggests a very diverse pool of donor genes in the archive.

Estimates of Relative Divergence Time

The only models that allowed for variation in divergence time from a common ancestor between and within triplets were, respectively, Model 3 and Model 4. In Model 3, which assumed each triplet had a different “age” relative to the first triplet of genes, we obtained mean estimates for the relative “ages” ranging from 1.09 to 2.05, a result that supports a moderate variation between triplets in divergence time from the most recent common ancestor. In Model 4, which allowed each gene pair to be characterized by a different evolutionary “age” relative to the reference gene pair (1), more variation in estimated ages than in Model 3 emerged, with an approximate range from 0.96 (gene pair 10) to 5.28 (gene pair 9). These values strongly correlated (correlation coefficient 0.85) with differences in pairwise identity between gene pairs. In any case, this variation is still within a factor of 5, which is unsurprising given the fact that all the gene pairs within triplets display similar levels of nucleotide identity (≈90.7%), suggesting a short divergence overall from their common ancestor in the archive.

Assessing Different Models

The models we considered are nested within each other, and due to the differences in their underlying assumptions, the estimates of the genetic parameters and the DIC and log-likelihood values across models show variation (table 2). However, all models agree on the estimates for the density of mismatches per conversion μ and the per-nucleotide probability of conversion termination λ_end. This is reassuring as the two parameters are expected to remain invariant under all hypotheses. For all parameters, the posteriors obtained are generally unimodal and symmetric around the mean, resembling the normal distribution (supplementary material SI5, Supplementary Material online, for details).

Table 2.

Summary of Model Selection Criteria.

Model	Number of parameters	Log likelihood	DIC
1. Global fit	4	−4430.8	8232.8
2. Triplet fits	20	−4399.4	8140.4
3. Triplet ages	8	−4414.2	8188.4
4. Individual ages	18	−4390.5	8136.1

Note.—The model with the lowest DIC/log likelihood is best to fit the data.

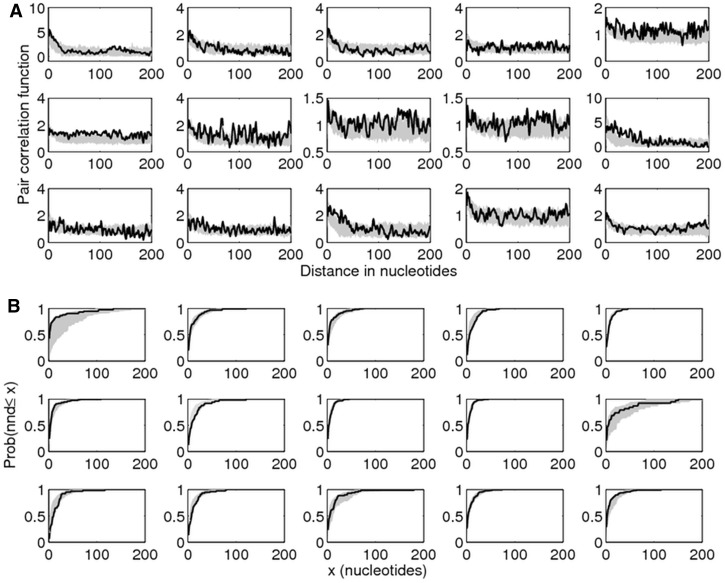
DIC values for each model indicated that rank order performance of these four formulations supports Model 4 as the best model, despite its large number of parameters, followed by Model 2, Model 3, and Model 1. Applying the Viterbi algorithm (Forney 1973) within the framework of Model 4, to the observed mismatch patterns on all 15 alignments, we were able to “decode” the most likely hidden path, thus obtaining the most likely locations of point mutations and conversion tracts, shown in figure 4. As expected, the empirical conversion lengths obtained from this maximum-likelihood decoding fit well the theoretical geometric distribution with parameter E[λ_end] predicted by our model. Further, as independent goodness-of-fit tests, we compared pair correlation functions in the original data set with pair correlation functions (Illian et al. 2008) of simulated data for the best model. We also compared the cumulative distribution of next-mismatch distances in the real data and in simulated data with estimated parameters, to verify the quality of fit of Model 4. As shown in figure 5, simulated statistics very closely matched the statistics from the original data set, demonstrating the usefulness of the individual ages model in capturing the diversity pattern displayed by our data set of closely-related VSG pairs.

Fig. 5.

Goodness-of-fit tests for Model 4 using higher order statistics. (A) Pair correlation functions, denoting the density g(r) of mismatches at distance r from each other (supplementary material SI6, Supplementary Material online). (B) Cumulative next-mismatch distance distribution. The gray shaded area represents 95% credibility intervals for the modeled mismatch patterns (100 replicates, with mean estimates for each parameter as in table 1). The lines represent the respective statistics of observed mismatches from the data set. The panels show the VSG gene pairs in the order 1–5 (row 1), 6–10 (row 2), and 11–15 (row 3).

Discussion

We have presented a general modeling framework that can describe pairwise identity patterns within gene families and an inference framework that can disentangle two genetic processes: gene conversion with partners outside the family and point mutation. Although applied to the VSG genes of African trypanosomes, our approach has several advantages that may apply to other, similar contexts: 1) it uses abstract, global-level information about mismatch occurrence between two aligned gene sequences, without requiring specific information about the underlying DNA; 2) it accounts for the spatial ordering of the identity pattern; 3) it allows direct estimation of switching rates between two different scales: short and long intermismatch distances; 4) it provides a means of quantifying the mutational processes that mechanistically give rise to clustered identity pattern on a pairwise alignment; 5) its results can be applied to the case when another process acts instead of gene conversion but with the same systematic effect of introducing clustered mismatches (e.g., localized point hypermutation, such as in immunoglobulin gene somatic hypermutation); and 6) it can be readily extended through the incorporation of additional factors that may influence the nature of evolutionary processes.

Of many computational approaches currently available for detecting gene conversion, the most prominent apply phylogeny-based methods (e.g., recHMM [Westesson and Holmes 2009]) that identify gene conversions by finding breakpoints that change the tree topology and similarity-based methods, which search for segments of unusually high similarity within two homologous sequences in the set (e.g., GeneConv [Sawyer 1989]). These approaches are powerful in detecting recombination events, especially when the potential set of donor sequences is known, when the recombination tracts are long and the number of data is large. However, they are usually of a less-parametric nature, thus making it difficult to explicitly link them to the mechanistic processes involved. Rather than replacing these models, we see our method as a potentially valuable extension to existing approaches for generating new insight into the relative roles of mutation and gene conversion in a new context, genetic diversification of antigen families, and for parameterizing their underlying mechanisms.

Among the existing parametric approaches that estimate recombination, our approach is most similar to the one adopted by Didelot and Falush (2007). There are parallels in the construction of the HMM, in the higher substitution rate of recombination and geometric distribution of converted regions that both approaches assume. Furthermore, neither approach attempts to model the origin of imported DNA explicitly. However, the primary difference with our approach is that we do not adopt an underlying coalescent model and make no assumptions about the underlying demographic processes or the strength of selection that may be acting. A coalescent approach can be very useful in some cases, but it inevitably requires more assumptions. Therefore our method, although simpler, is likely to provide robust results even when the nature of past demographic history and selection are unknown. Instead of inferring the entire genealogy and branching events, we consider systematically several discrete possibilities about the ways in which evolutionary processes such as gene conversion and point mutation might have acted to shape the identity patterns between highly related genes in a multigene family. In contrast to the multilocus sequence data, which is the main target of the algorithm by Didelot and Falush (2007), to compare different bacterial strains, the algorithm we propose is more suited to deal with relationships between genes of the same organism. Because of this difference in scale of resolution, the conversion tracts we model are intrinsically of much smaller size.

Through our analysis, we find that the patterns of pairwise diversity between highly related VSG genes can be explained by two processes: one that results from importation of genetic material existing elsewhere in the archive and one that generates diversity de novo from within. All models considered reveal that the probability of importing a conversion tract from outside is lower than the probability of undergoing point mutation, which by virtue of m < μ serves to slow down overall diversification of these pairs. We do not impose additional mechanisms behind clustering. In our context, it is highly likely that clustering of mismatches reflects conversion events with third-party older donors, because: first, there is no reason to expect that different regions of the N-domains of VSG genes should evolve at different mutation rates; second, there is no evidence that the mutation rate is bimodal or that it might switch from one value to another so frequently and stochastically as we observe in our data; and third, the difference of the substitution rate by a factor of 14, in converted and nonconverted regions, as observed in our model, cannot be easily attributed to variation in the mutation process alone.

Gene conversion from other donor genes in the archive could be restricted due to several factors, one possibility being pairwise homology requirements which might be satisfied by only a few donor candidates. Finding the donors of these imported fragments may be challenging for several reasons. First, and in this particular example, although the trypanosome genome is available, only about two thirds of the VSG genes have been assembled; second, the donors may have themselves changed since the conversion event, thus to match the sequence of the putative converted region with the sequence of the actual donor may be far from trivial.

Combining the estimate for average mismatch density within converted regions, μ ≈ 0.29, obtained from Model 4, with the average conversion length given by 1/λ_end ≈18, we estimate the average number of mismatches contributed by one gene conversion into the alignment is rough ∼5.2. This implies that the relative contribution of gene conversion on pairwise diversity between two genes, on a per-nucleotide basis, is ∼0.96 times that of point-mutation. Thus, although on an event basis, point mutation is apparently much more prominent than conversion, on a per-nucleotide basis, the two processes are of roughly equal importance for sequence diversification.

Model 4 ranked as the best model by our model selection procedure, suggesting the inclusion of relative ages of gene pairs holds key information that explains the variance in the sample we considered. Reassuringly, the estimated ages have a small mean of 2.83 and a small standard deviation, confirming a relatively minor variation, expected among gene pairs that share similar pairwise identity. Notably, Model 4 supports short conversion tracts, between 14 and 25 nucleotides in length, geometrically distributed with mean equal to 18 nucleotides, much lower than the total length of the N-domain. This characteristic small scale resembles human major histocompatibility complex gene conversion events, which display a mode of 14 nucleotides (range: 2–35) (Parham et al. 1995), inevitably arising from a mechanistic basis in the recombination pathway involved. Conceivably, the observed length range can serve to maximize effective alteration in VSG epitopes and slow down the pace of archive homogenization globally.

From visual inspection of the mismatch patterns, one can also notice regions of unusually low mismatch density, besides regions of high mismatch density on the aligned pairs. Although neglected in this analysis, such high-identity regions are potentially indicative of within-pair recombination and could be addressed in future studies. It may be that the short range of mismatch clustering we observe reflects the difference between those conversion events that occur and those that persist over evolutionary time. Perhaps, the actual imported regions from third-party donor genes in the archive are longer than our current estimates suggest, but frequent within-pair gene conversion can act to break them down, thus interrupting the highly diverse regions imported from outside, by regions of sparser diversity generated from within.

Clearly, an important aspect of VSG archive evolution that this framework may elucidate is the divergence between subsets of a multigene family. The assumption that gene conversion by external donors introduces diversity to a recently duplicated gene pair through a cluster of mismatches can be translated into a hypothesis for the divergence time of the entire family relative to the high-identity subfamily in consideration. It is worth noting that pairwise identity between recently duplicated genes is higher than sequence identity of an arbitrary gene pair from the archive. This results in a higher density of mismatches in the regions where the sequence has been mutated from outside through conversion, rather than changed from within, through point mutation. If one assumes that point mutation happens at the same rate across all VSG genes, as would occur in second-order selection (Weber 1996) and indeed appears to be the case (Hutchison et al. 2007; Marcello and Barry 2007; Jackson et al. 2010), the difference in mismatch density within (μ) and between conversions (m) should be attributable to differences in evolutionary time, an avenue calling for further investigation.

Furthermore, our inferred mean density of mismatches per conversion, approximately equal to 0.25, is considerably lower than the mean frequency of nucleotide mismatches measured across the whole archive, which is very high (≈0.75), thus conversion appears to be biased toward more similar donor genes. As argued earlier, it is difficult to account for this effect through direct selection of the sequence of individual VSGs. A reason for this preferential use of more homologous tracts might lie in the need to introduce a region from the corresponding donor VSG, so that, for example, the characteristic cysteine pattern of the protein is conserved, rather than being disrupted by random conversion from any region of a donor gene. By using sequence “decoding” as a first step, the most likely locations of conversions and point mutations along each alignment can then be used to map these recombination “hotspots” to the actual underlying genetic content.

To be able to transform our estimated point mutation and conversion probabilities into actual rates, i.e., probabilities per unit of time (or per generation), one would need information on the precise time since duplication of the reference gene pair at least. Once the real evolutionary age of the reference gene pair (with A_i = 1) is established, its λ_begin and m parameters could be scaled and subsequently the other pair-specific observed probabilities updated. So far, the time information has been missing but could become available through longitudinal sequencing of field isolates, at which time it could inform the proposed formalism and transform the present estimates to dynamic parameters of evolutionary processes, making them comparable with estimates derived from other methods.

In our models, we assumed that the density of mismatches in each conversion is the same and fixed. Such a rigid assumption might not always hold, as gene conversion donors in the rest of the archive may come from particular subfamilies, each having had its own rate of divergence, thereby contributing a distinct mismatch clustering density. A more general framework in that case, to accommodate this phenomenon, could be to model the mean density of mismatches per conversion, μ, through a probability distribution.

Another simplifying assumption in our study is the spatial homogeneity in the occurrence of point mutations and conversions. It is possible that formulations and inference frameworks accounting for spatial bias might bring additional insight into the nature and constraints of gene diversification. Finally, by considering conversion length distributions different from the geometric distribution assumed here, one might represent other mechanisms governing gene conversion. A negative binomial distribution could, for example, allow longer conversions to be more frequent, but the memorylessness property would be lost. More flexible distributions would require more sophisticated modeling and possibly a larger data set, but such alternatives could be explored to better disentangle the various spatial scales that characterize genetic diversity in different settings. Nonetheless, the model presented here provides a framework that can easily be built upon as more data become available, offering a valuable tool for a more parametric understanding of genetic diversification processes at the level of a multigene family.

Supplementary Material

Supplementary materials SI1–SI6 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).