Root-Growth Behavior of the Arabidopsis Mutant rgr1

Abstract

In this study we investigated the kinetics of the gravitropic response of the Arabidopsis mutant rgr1 (reduced root gravitropism). Although the rate of curvature in rgr1, which is allelic to axr4, was smaller than in the wild type (ecotype Wassilewskija), curvature was initiated in the same region of the root, the distal elongation zone. The time lag for the response was unaffected in the mutant; however, the gravitropic response of rgr1 contained a feature not found in the wild type: when roots growing along the surface of an agar plate were gravistimulated, there was often an upward curvature that initiated in the central elongation zone. Because this response was dependent on the tactile environment of the root, it most likely resulted from the superposition of the waving/coiling phenomenon onto the gravitropic response. We found that the frequency of the waving pattern and circumnutation, a cyclic endogenous pattern of root growth, was the same in rgr1 and in the wild type, so the waving/coiling phenomenon is likely governed by circumnutation patterns. The amplitudes of these oscillations may then be selectively amplified by tactile stimulation to provide a directional preference to the slanting.

Although plant roots appear superficially to be symmetrical, their growth patterns can be asymmetrical. An example of asymmetrical growth patterns in a seemingly symmetrical environment is the skewed, wavy pattern observed in the roots of some ecotypes of Arabidopsis grown on inclined plates of agar (Okada and Shimura, 1990, 1992; Simmons et al., 1995a; also see Fig. 1A). The waving pattern is caused by a series of bends in the root that alternate in direction. The skew arises from a nonrandom preference by the root in the direction of bending relative to the vertical. There is a strict correlation between the direction of curvature for each bend of the root and the orientation (left or right) of the helical spirals formed by epidermal cell files, suggesting that the pattern is caused by a succession of left- and right-oriented processes (Rutherford and Masson, 1996). The pattern of wavy growth has been suggested to result primarily from an interaction of gravitropism and thigmotropism (Okada and Shimura, 1990, 1992) or from an interaction of gravitropism and circumnutation (Maher and Martindale, 1980; Simmons et al., 1995b).

Figure 1.

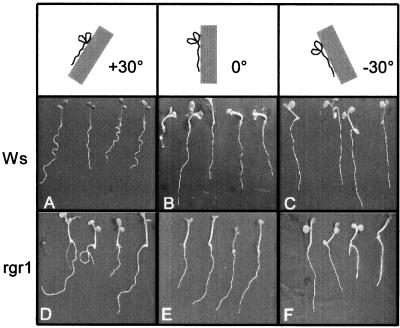
Waving/coiling patterns for seedlings of wild type (ecotype Wassilewskija [Ws]) and rgr1. The roots are growing on the surface of agar (1%, w/v) plates. A to C, Wild-type seedlings growing on plates tilted by angles of +30°, 0°, or −30°. D to F, rgr1 seedlings oriented at the same angles.

In the former model it is postulated that thigmotropism of the root tip causes a reversal in the direction of rotation of cell files and, therefore, a reversal in the direction of tip growth. Subsequent thigmostimulation of the root tip results in another reversal of cell-file rotation, causing the root to grow in a wavy pattern along the agar surface. Gravitropic sensitivity provides thigmostimulation by giving the root a tendency to grow into the agar.

According to the circumnutation/gravitropism model, the wavy pattern of root growth on inclined surfaces results from an endogenous pattern of root growth (circumnutation) interacting with the gravitropic response, which causes the roots to grow downward. Because root circumnutation usually has a chirality favoring the clockwise direction, as viewed looking downward along the root axis (Baillaud, 1962; Johnsson, 1997, and refs. therein), circumnutation may be able to provide the directional preference for the wavy growth. However, this slanting preference did not occur in roots embedded in agar, on a soft agar surface, or on a surface slanted so that gravitropism tended to pull the roots away from the agar surface (Rutherford and Masson, 1996; also see Fig. 1C). Therefore, asymmetrical mechanical stimulation, which these treatments minimize, is involved in the slanting response in some manner.

Because gravitropism serves an important role in these models of the waving pattern of growth, we wanted to investigate the relationships between this waving phenomenon and gravitropism and other growth behaviors in the gravitropism-deficient mutant rgr1 (reduced root gravitropism). The mutant was isolated from the DuPont T-DNA insertional mutagenesis collection in the Arabidopsis Wassilewskija ecotype by Simmons et al. (1995a) and is allelic to the axr4 mutant isolated by Hobbie and Estelle (1995). Primary roots of these mutants are characterized by reduced gravitropism, as indicated by a slower rate of gravitropic curvature (Hobbie and Estelle, 1995) and more random orientation about the vertical after gravitropic response (Simmons et al., 1995a). This confirms the importance of gravitropism in the waving phenomenon, because the roots of rgr1 seedlings grown on inclined surfaces do not form wavy patterns, but instead form circular coils that have the same directional preference as the wild-type slanting preference (Simmons et al., 1995b; Fig. 1D). Roots of rgr1 seedlings also exhibit resistance to growth inhibition by auxin, which may explain their reduced gravitropic sensitivity.

We have developed an automated video-digitizer system for detailed measurement of the growth and curvature of roots of Arabidopsis. We used this new system to compare the kinetics of gravitropism and other growth behaviors between the roots of rgr1 and wild-type seedlings in a series of different tactile environments. These comparisons provide insight into the basis of the waving/coiling growth phenomenon.

MATERIALS AND METHODS

Plant Material

Seeds of Arabidopsis of either the wild type (ecotype Wassilewskija) or the mutant rgr1 were surface-sterilized by agitation in a 5.25% (v/v) NaOCl solution for 5 min, followed by several rinses in distilled water. Seeds were sown in a row (three to five seeds per row) on sterile agar (1%, w/v) in Petri dishes (60 mm in diameter, 15 mm in height) sealed with laboratory film (Parafilm, American Can, Greenwich, CT). The agar medium contained 1% (w/v) Suc, one-half-strength Murashige-Skoog medium (Murashige and Skoog, 1962), and 1 mm Mes, pH 5.8. The rows of seeds were placed on the agar surface perpendicular to the cylindrical axis of the dish so that the roots would grow along the surface or on a surface parallel to the axis, so that the roots would grow downward through the agar. The Petri dishes were either placed immediately in a culture room under continuous white light from fluorescent lamps (F30T8-CW, Sylvania) with a fluence rate of approximately 47 μm m⁻² s⁻¹ at a temperature of 23°C, or they were refrigerated at 4°C for 1 to 6 d before being transferred to the culture room. The Petri dishes were placed vertically or at the indicated angle of tilt and used for experimentation when the seedlings were 4 to 5 d old.

Video-Digitizer System

The seedlings were viewed by a CCD (charge-coupled device) camera (Marshall Electronics, Culver City, CA) connected to a computer via a frame-grabber circuit board (ImageNation, Beaverton, OR). The roots were illuminated from behind with a fiber-optic illuminator (Fiber Lite, Leica) or with an IR light-emitting diode (Radio Shack, Fort Worth, TX). No difference in growth or response was observed between the two light conditions.

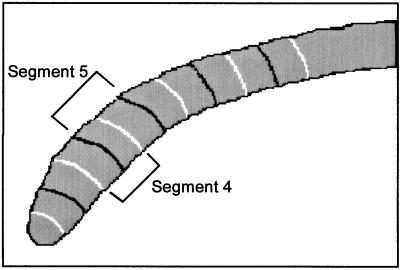
The growth behavior of the roots was analyzed using a modified version of the Multi-ADAPT software described by Ishikawa and Evans (1997). The new version of ADAPT measures the rate of elongation of the opposite flanks of the root as well as the angles (relative to vertical) of different segments of the root, defined by their distance from the root tip. The software determines total elongation on opposite sides of the root by tracing the root edges from the calculated root-tip position to the position of fixed reference points in the nonelongating region. Regression of the changes in length of a side gives its elongation rate. ADAPT defines segments of the root by searching along arcs of fixed radius for the edges of the root (Fig. 2). A particular segment can then be described by a line segment connecting the midpoints of the arcs defining the boundaries of the segment. The angle of this line segment from the vertical is then calculated as a function of time.

Figure 2.

Logic of custom software for measurement of length and segment angles of roots. A key feature of the software is its ability to identify the edges of the root based on a user-defined threshold luminous intensity and record that pixel location. Black and white arcs denote segment limits as determined by the search routine of the software. The size of each segment is selected by the user and input as a searching radius. Black arcs indicate the limits of odd-numbered segments (1, 3, 5, etc.) and white arcs indicate the limits of even-numbered segments (2, 4, 6, etc.). Segment angle was determined by first finding the line connecting the edge points of the root at a given search distance, then determining the angle of the line connecting the midpoints of the two limit lines relative to vertical. The overlapping process used to define segment limits increases the resolution of angle measurement. By definition the segments remain a fixed distance relative to the root tip as the root elongates. Total length of each edge is measured from the tip to a user-defined basal point in the mature region of the root.

Interaction of Gravitropism and Tactile Stimulation

For the gravitropism experiments, root growth was first analyzed by the digitizer system with the seedling oriented vertically. The Petri dish containing the seedling was then rotated 90° in either a clockwise or a counterclockwise direction, and data collection was resumed. To determine the extent to which tactile stimulation of the root as a result of contact with the agar surface influenced the gravitropic response, gravitropism was measured both with the root growing along the surface of the agar and with the root growing through a solid block of agar. To minimize tactile stimulation, we also examined growth and gravitropism of roots growing in a liquid medium or in humid air. To create these conditions of minimal stimulation, we cut a small cube out of the agar block, just below the tip of the root. This created an open cavity, which was then covered with a layer of agar. For some experiments the cavity was filled with a liquid medium (one-half-strength Murashige-Skoog medium plus 1 mm Mes, pH 5.8).

Circumnutation and Calculation of Curvature

To observe the direction of circumnutation in a horizontal plane, root growth was measured in two perpendicular planes by placing two cameras at right angles to one another. The direction of curvature in the horizontal plane was then found by plotting the angle of the root tip in one plane in relation to the angle in the other. The curvature (the reciprocal of the radius of curvature) of points along this curve was calculated using seven-point quadratic numerical differentiation formulae, as described by Silk and Erickson (1978).

Conventions of Terminology

Angle of Plate Orientation

For purposes of this report, plates oriented vertically with the roots growing downward were assigned an angle of 0; plates tilted so that the gravity vector pointed from the root toward the agar surface were assigned positive values of tilt; and plates inclined so that the gravity vector was away from the surface were assigned negative values.

Direction of Asymmetric Growth and Plate Rotation

For this report we assumed that the viewer's perspective is looking at the seedling through the Petri dish cover with the seedling in front of the agar surface. From this perspective the directions of rotation are consistent with those in previous reports of root coiling (Mirza, 1987; Simmons et al., 1995b). It is from this same frame of reference that we refer to the directional preference of the wavy growth pattern as slanting to the left.

RESULTS

Gravitropism and the Waving Response

The wavy growth pattern of a wild-type root growing along an inclined plane has a directional preference to the left (Okada and Shimura, 1990), which shifts the root's direction of growth away from the gravity vector; therefore, gravitropism should play a role in the wavy growth pattern. Indeed, the magnitude of waving and of directional preference are dependent on the angle of incline (Fig. 1, A–C). They are also angle dependent in rgr1, but the “waves” change to coils at positive angles (Fig. 1, D–F). To investigate the interactions of gravitropism and waving/coiling, we analyzed the kinetics of gravitropism after seedlings were reoriented to a horizontal position with a clockwise or a counterclockwise rotation.

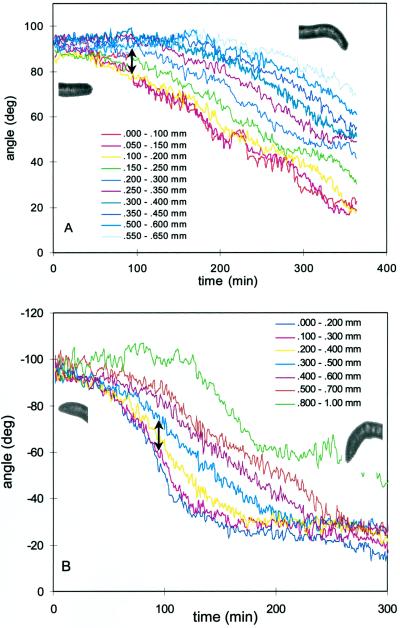
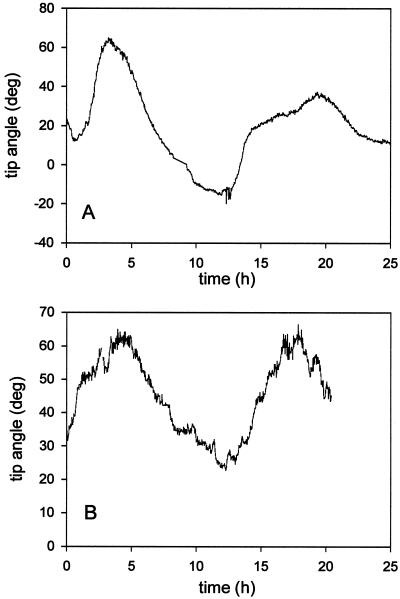
For roots of wild-type seedlings, the gravitropic responses after counterclockwise rotation (gravitropism and slanting are in the same direction; Fig. 3A) and clockwise rotation (responses have opposing directional preferences; Fig. 3B) were similar. In both cases, downward curvature was initiated in a region 200 to 300 μm from the root tip. It is in this region that roots show a characteristic divergence of orientation angle after gravistimulation (segments shown by arrows in Fig. 3). Segments apical to this region show a change in angle attributable to the change of their basal neighbor, whereas segments basal to this region do not show curvature until growth causes the curvature to migrate back into these segments. Because we were able to localize the region of initial downward curvature, we calculated the time lag until curvature initiation as the time until the difference in angle between a segment apical to and a segment basal to the region of curvature reached 5% of the maximal difference minus the initial difference in angle. The difference in direction of gravistimulation did not cause a statistically significant difference in the time lag (Table I), which averaged 27 min. As a measure of the magnitude of the growth response, we also calculated the average rate of curvature for the 2 h immediately after the time lag. The mean rate of curvature was 18° h⁻¹, with no significant difference between clockwise and counterclockwise treatments (Table I). Therefore, the directional preference of the waving was not strong enough to interfere with the wild-type gravitropic response.

Figure 3.

Kinetics of the gravitropic response of a representative root of a wild-type seedling growing along the surface of a vertically oriented agar plate. Different-colored lines represent segments located at the stated distances from the tip. Arrows show the range of segments where the initial curvature originates. Inset images show the root curvature that the data characterize. A, Root gravistimulated by a counterclockwise rotation of 90°. B, Root gravistimulated by a clockwise rotation of 90°. Not all segments are plotted. deg, Degrees.

Table I.

Comparative gravitropism kinetics for roots of wild-type and rgr1 seedlings growing on the surface of vertically oriented agar plates

Seedling Type	Clockwise		Counterclockwise
	Lag	Rate	Lag	Rate
	min	° h−1	min	° h−1
Wild type	22  ± 6 (n = 4)	22  ± 8 (n = 4)	29  ± 13 (n = 10)	16  ± 5 (n = 10)
rgr1	25  ± 8 (n = 10)	2  ± 6a(n = 10)	22  ± 8 (n = 8)	8  ± 5a(n = 8)

Values are ± sd.

^aSignificant difference (P < 0.05). 

The kinetics of the gravitropic response for the roots of rgr1, however, did depend on the direction of rotation (Fig. 4). Seedlings rotated counterclockwise bent downward because of the initial curvature in the region 200 to 300 μm from the tip (Fig. 4A). This response is similar to that of the wild type, except for the reduced rate of curvature (Table I). However, for seedlings rotated clockwise, 63% of the roots showed upward curvature (Fig. 4B). This upward bending originates in the central elongation zone, farther back from the tip than the site of major downward curvature, which was found in the same location as in the wild type. Because of this upward curvature in roots rotated clockwise, there was a difference in the mean rates of curvature for the clockwise and counterclockwise treatments (Table I). The time lags for the gravitropic response were unaffected in rgr1 (Table I).

Figure 4.

Kinetics of the gravitropic response of a representative root of a rgr1 seedling growing along the surface of a vertically oriented agar plate. Different-colored lines represent segments located at the stated distances from the tip. Arrows show the segments where the initial curvature originates. Inset images show the root curvature that the data characterize. A, Root gravistimulated by a counterclockwise rotation of 90°. Arrow shows the range of segments involved in the initial downward curvature. B, Root gravistimulated by a clockwise rotation of 90°. Arrow shows the upward curvature of the more basipetal segments, whereas the gravitropic response of more apical segments dampens this upward curvature. deg, Degrees.

The roots of rgr1 showed a growth feature not found in the wild type: upward curvature in the central elongation zone. This feature has a clockwise directional preference, which is the same directionality found in the coiling response of rgr1. To determine whether the upward curvature was a true component of the gravitropic response or if it was part of the root-coiling pattern superimposed on the gravitropic response, we measured gravitropic kinetics under different tactile environments.

Upward Curvature and Altered Tactile and Light Environments

To test the behavior of rgr1 under a more uniform tactile environment, we measured the gravitropic response of roots growing through solid blocks of agar. Figure 5 shows the time course for the gravitropic response for such a root after clockwise reorientation. There was no initial upward curvature in the central elongation zone of roots growing through solid agar. However, downward curvature occurred just as it did in roots growing along the surface (initiating 200–300 μm from the root tip). This suggests that an asymmetrical tactile environment is necessary for the upward-curvature component of the growth pattern. It is also consistent with the upward curvature being part of the root-coiling phenomenon, which also disappears when the root is embedded in agar (Rutherford and Masson, 1996), rather than being a part of the gravitropic response.

Figure 5.

Kinetics of the gravitropic response of a representative root of rgr1 growing through a block of agar. The root was gravistimulated by a clockwise rotation. The different lines represent segments located at the stated distances from the tip. deg, Degrees.

To minimize the overall tactile stimulation, we also observed root behavior while the roots were growing in a liquid medium or in a chamber of humid air. The pattern of growth after clockwise stimulation was similar to that of roots growing in solid agar, with no upward curvature (E. Turk, unpublished data). To rule out light as a signal for upward curvature, we compared the behavior of a root growing along the agar surface after gravistimulation when the light source was in front of the plate and when it was behind it. We also measured the kinetics of gravitropism when the seedlings were exposed to no light during the experiment (except IR radiation for imaging by the camera). The upward bending pattern does not depend on the type of light treatment provided (E. Turk, unpublished data).

Circumnutation

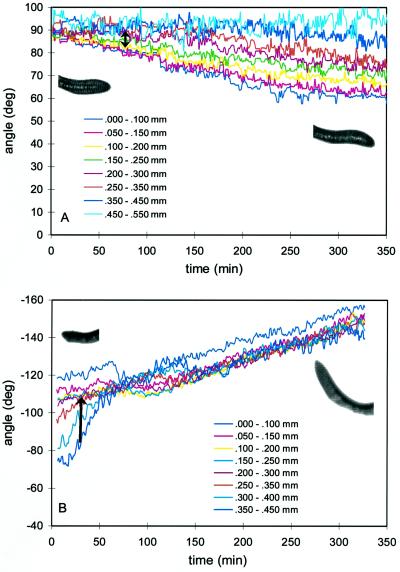
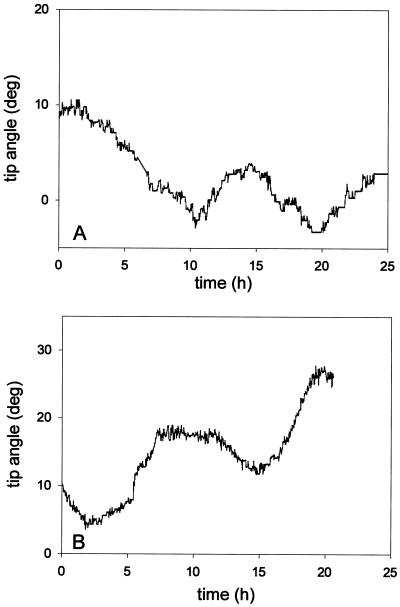
One model of the wavy growth phenomenon suggests that endogenous oscillations in the growth direction, called circumnutation, drive the pattern. Selective amplification of the pattern in an asymmetrical tactile environment could then create a directional preference. Therefore, we investigated roots growing vertically through a solid volume of agar for periodic oscillations in the root-tip direction. Roots of both wild type and rgr1 showed periodic oscillations in tip angle, with similar periods of 11.9 ± 1.1 h (mean ± se; n = 10) and 11.0 ± 1.7 h (n = 5), respectively (Fig. 6). Although the amplitude of the circumnutation seems variable, there was no obvious difference in the amplitude of the responses between rgr1 and wild-type seedlings. Therefore, the magnitude of the circumnutation was not dependent on the strength of the root's gravitropic response. There was no long-term directional preference evident in roots growing through agar.

Figure 6.

Circumnutation patterns for roots growing through a block of agar. Data for the root-tip segment of a wild-type (A) and a rgr1 seedling (B) are plotted. deg, Degrees.

This pattern of circumnutation in a uniform tactile environment (Fig. 6) is very similar to the kinetics of the wavy growth pattern of a root growing along the agar surface (Fig. 7). We measured the periodicity of this pattern as 11.1 ± 2.1 h (n = 7) and 12.0 ± 2.2 h (n = 5) for rgr1 and wild type, respectively, which is not significantly different from the circumnutation period. There was, however, a long-term directional preference for the root tip to stay to the left of vertical in roots growing along the surface, which can be seen by the shift in the angle of the axis of oscillations away from 0 (Fig. 7).

Figure 7.

Waving growth pattern for roots growing along the surface of an agar plate. The root-tip angle is plotted for a representative wild-type (A) and a rgr1 root (B). deg, Degrees.

To determine if the circumnutation behavior had any directional preference, we used two perpendicular cameras to measure the three-dimensional growth of rgr1 roots through solid agar. Although both clockwise and counterclockwise growth was observed, most root growth was in a counterclockwise direction, as viewed from above. If there was no directional preference to circumnutation, we would expect no mean curvature. However, the observed mean curvature was 1.2 ± 0.4 milliradians⁻¹ (mean ± se; n = 10) and 1.8 ± 0. 7 milliradians⁻¹ (n = 7) for rgr1 and wild type, respectively, a significant difference from the theoretical mean (P < 0.05). Therefore, we found chirality to circumnutation, even in a homogeneous tactile environment.

DISCUSSION

These investigations of root behavior illustrate the complexities in growth kinetics that can occur as a result of the interactions of separate growth responses. Roots of rgr1 seedlings tended to slant to the left when growing on vertical plates. This slanting contributed to the observed gravitropism kinetics in a manner dependent on the direction of rotation (Fig. 4), suggesting that the relative magnitudes of the early curvature responses in rgr1 and the wild type may not have accurately reflected the difference in the strengths of the true gravitropic response. This was made more evident by the fact that the kinetics of the overall response of wild-type roots were not dependent on the direction of gravistimulation. Therefore, the magnitude of the gravitropic response in the wild type varied with the direction of rotation and offset the slanting preference of the root.

The interaction between slanting and gravitropism also illustrates the difficulty in calculating time lags based solely on changes in the angle of the root tip. Because we were able to localize the initial downward curvature to the region 200 to 300 μm from the tip, we could calculate time lags based on changes in angle occurring in this region only, excluding from consideration curvature arising farther back in the root, where the slanting phenomenon arises. The region initiating downward curvature corresponds to the location of the distal elongation zone (Mullen et al., 1998), showing that rgr1 roots have a functional distal elongation zone. The upward curvature in gravistimulated rgr1 roots occurred in the central elongation zone, which is consistent with the location of major bending in waving/coiling growth (Okada and Shimura, 1990).

The lack of upward curvature after clockwise gravistimulation of rgr1 roots growing in more uniform tactile environments (Fig. 5) provides further evidence that the upward curvature is not a true component of gravitropism, but is a part of the wavy growth pattern. These results provide further evidence that an asymmetrical tactile environment is necessary for the establishment of a directional preference to the waving/coiling phenomenon.

The similarity in the frequencies of the wavy growth pattern and the circumnutation pattern of roots growing in uniform tactile environments (Figs. 6 and 7) suggests that circumnutation may be the driving force behind the induction of tactile stimulation. Differences in growth rate also had no direct correlation with the period of the oscillations, which is in agreement with previous observations (Johnsson, 1979). The frequency of waving remained the same despite differences in growth rate between roots growing on the surface of agar and those growing in the agar, or between rgr1 and wild-type roots growing in agar (J.L. Mullen and E. Turk, unpublished data).

An alternative to the model that circumnutation drives the waving pattern is the idea that a series of gravitropic and thigmotropic responses are sufficient to create the pattern. However, it seems unlikely that this scenario could explain the similarity in the frequency of the waving pattern in rgr1 and wild type, given their difference in gravitropic response. It is also difficult to explain the directional preference with such a model. Therefore, to account for all aspects of the waving/coiling phenomenon, both circumnutation and thigmostimulation are necessary components. In this combined model of the waving/coiling phenomenon, it is circumnutation that drives the pattern of wavy growth. Leftward slanting arose when the counterclockwise chirality of circumnutation caused differential thigmostimulation in an asymmetric tactile environment. Because of the chirality, the root was growing to the left at the point of greatest tactile stimulation. This thigmostimulation can manifest itself as an alteration in circumnutational amplitude. Further investigation into the nature of the three-dimensional circumnutation process may aid in the understanding of the tactile forces involved. The genetic analysis of mutants may also provide clues to the basis of the chirality. For example, sku mutants of Arabidopsis show increased magnitude of directional preference (Rutherford and Masson, 1996), and Marinelli et al. (1997) found mutants with inverted chirality.

Whether the growth pattern takes the form of waving or coiling is based on whether the amount of bending in the clockwise direction during a half-wavelength of the pattern is equal to the amount in a counterclockwise direction during the successive half-wavelength. For waving to occur, the sum of the gravitropic response and the thigmoresponse must be the same during clockwise and counterclockwise bending. Because the tactile stimulation is direction-dependent, the gravitropic response must be modulated to maintain a constant overall response, as seen for wild-type roots in Figure 3. The reduced gravitropic response of rgr1 is unable to counter the differential thigmoresponse, so the amount of clockwise curvature is greater than the amount in the counterclockwise direction and the waving pattern switches to one of coiling.