Linear Spring-Damper Model of the Hypertonic Elbow: Reliability and Validity

Abstract

Hypertonia of the elbow joint complex is common in individuals with stroke and is related to the magnitude of the torque response (described by position dependent parameters) during constant velocity extensions. The objective of this study was to model position and velocity dependent characteristics of hypertonia. For both the more and less affected arms in 17 persons with chronic stroke, we measured the torque response to constant velocity stretches (30–180 deg/sec). The responses were combined in position-velocity space and parameters of stiffness, damping, and offset angle were determined from a linear spring-damper model of the torque profile. The model was assessed at three levels: (1) ability to describe the combined torque profile variance, (2) reliability of parameters, and (3) validity of parameters (i.e., clinical correlation). Model parameters fit the torque profiles of both arm groups well and exhibited day-to-day reliability. Stiffness (r=0.820), damping (r=0.816), and ‘viscoelasticity’ (r=0.909), a composite parameter index developed posthoc, were highly correlated to a manual assessment of hypertonia (Modified Ashworth Scale). Mechanically determined parameters of hypertonia graded along a continuum may have better discriminatory power than manual assessments and thus, may be better at tracking recovery and evaluating interventions.

Introduction

Spasticity has been defined as ‘… a velocity dependent increase in the tonic stretch reflex (muscle tone) with exaggerated tendon reflexes …’ (Lance, 1980). Spasticity may contribute to both impaired motion (Katz & Rymer, 1989) and reduced functional independence (Carey & Burghardt, 1993). Hypertonia is the increase in joint resistance to passive movement and results from spasticity (i.e., hyperactivity of the stretch reflex) and/or changes in the viscoelastic characteristics of muscular and connective tissues (Katz & Rymer, 1989). The Modified Ashworth Scale (MAS) (Bohannon & Smith, 1987) is the primary clinical measure of hypertonia. The MAS subjectively grades the sensation of resistance felt by an examiner (i.e., ‘tone’) when manipulating a relaxed joint through its passive range of motion. Limited reproducibility and resolution of the MAS (Pandyan et al., 1999) has been a motivating factor for objectively quantifying hypertonia through biomechanical evaluations of the torque response to passive movement. The most well used biomechanical alternatives to manual assessment are the ‘pendulum test’ (e.g., Lin & Rymer, 1991), sinusoidal motion (e.g., Agarwal & Gottlieb, 1977; Lehmann et al., 1989), and ramp and hold stretches (e.g., Powers et al., 1989; Katz et al., 1992; Given et al., 1995).

In a ramp and hold stretch, a relaxed joint is stretched at a constant angular velocity over a predetermined angular displacement and hypertonia is quantified by the resistive torque generated by the stretched muscle (Powers et al., 1988; Katz & Rymer, 1989; Given et al., 1995). As ramp changes of position correspond to functional disturbances and avoid cyclical stretching effects, the magnitude and time course of responses during testing are highly related to the joint’s natural behaviour (Kearney & Hunter, 1990). The response during these stretches has been characterized by the threshold angle at which torque begins to rise, the slope of the angle-torque (stiffness) curve, and the peak resistive torque (Powers et al., 1988; Damiano et al., 2002). These biomechanical parameters correlate with clinical measures of hypertonia (Katz et al., 1992) and are dependent on the angular velocity of the passive stretch (Ju et al., 2000; Damiano et al., 2002).

The neuromuscular behaviour of a healthy joint system (i.e., connective tissues, muscles, etc.) is commonly parameterized by not only position dependent (i.e., stiffness) but also velocity dependent (i.e., damping) terms (Kearney & Hunter, 1990). The mechanical response of hypertonic joints has yet to be described as such, despite its dependence on stretch velocity. These parameters would be useful for characterizing the resistance that is felt by clinicians during manual assessments and could be determined by combining the torque responses to ramp and hold stretches at a variety of velocities within a spring-damper model. If these parameters are reliable between days and are related to clinical measures (i.e., are valid) they would be useful for measuring recovery and evaluating interventions. In this study, we examined the mechanical response of elbow flexors of persons with hypertonia due to chronic stroke to determine (1) the ability of a linear spring-damper model to describe passive resistance, (2) the test-retest reliability of model parameters between days, (3) the relationship of these parameters and a composite parameter to a clinical assessment of spasticity.

Methods

GROUP DESCRIPTION AND CLINICAL EVALUATION

Seventeen older adults (Mean Age=61.8, SD=5.84, Range=49–72 years; 11 males and 6 females) with chronic stroke (Mean time since injury=3.9, SD=2.2, Range=1–8 years) were recruited from the community with inclusion criteria of: 1) a minimum of one year post-stroke, 2) present with hemiparesis secondary to first cerebrovascular accident, 3) able to provide informed consent, 4) able to follow one and two step commands and 5) able to voluntarily flex/abduct their shoulder 45 degrees and extend their elbow 30 degrees. Exclusion criteria were any neurological condition aside from the stroke and any musculoskeletal conditions which might affect upper extremity function. The study protocol was approved by the local university and hospital ethics committees.

The upper extremity portion of the Fugl-Meyer motor scale (Fugl-Meyer et al., 1975) was used to describe motor impairment of the more affected arm. The mean score was 37.5/66 (SD=18.3, Range=13–64). Elbow flexor muscle tone was assessed by extending the participant’s elbow over its entire range of motion and graded according to the MAS (Bohannon & Smith, 1987). The mean score of the more affected arm was 1.4 (SD=1.1, Range=0–4).

EXPERIMENTAL SETUP

We measured the velocity dependent resistance of elbow flexors of the more and less affected arm using a seated isokinetic dynamometer system (KinCom, Chattanooga, TN) in passive mode. Isokinetic dynamometers can passively rotate joints in the same posture that is used during manual joint assessments of the MAS. These devices have been used to assess spasticity in both the lower (e.g., Lamontagne et al., 1997) and upper (e.g., Schmit et al., 2000) extremities in persons with chronic stroke.

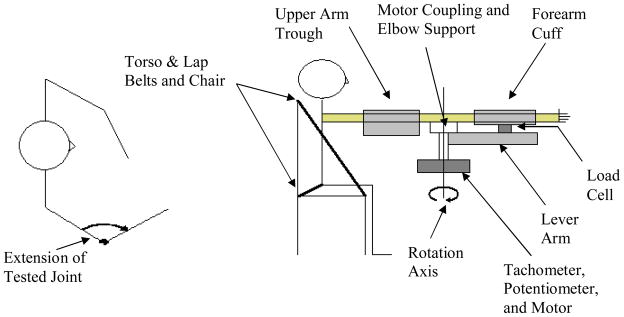
Subjects were seated with the torso supported by crossing lap belts and the upper arm rigidly stabilized by a trough so that the shoulder was abducted and flexed to 80° and 45° (i.e., gravitationally neutral elbow flexion/extension). The forearm was fastened in mid pronation/supination by an adjustable cuff attached to the lever arm of the dynamometer (see figure 1). The cuff was wrapped snugly around to the forearm to minimize forces related to the human-cuff interaction (i.e., compression of cuff material and soft tissue of the forearm). The flexion-extension axis of the elbow was aligned to the rotary axis of the motor and the start and stop angles of the motor were adjusted to the full passive range of the more affected arm. The same angular range was used for tests of the less affected arm.

Figure 1.

Schematic of testing apparatus (not to scale). The transverse view on the left shows the testing direction while the side view on the right describes the testing apparatus.

Observations of the hypertonic torque response over broad angular ranges are preferable to smaller ranges (Schmit et al., 1999). Full elbow extension was defined as 180°. The start elbow angle ranged from 60 to 80 degrees while the stop elbow angle ranged from 140 to 165 degrees. Ramp and hold extensions were applied to the elbow through its available passive range at speeds of 30, 60, 90, 120, 150, and 180°/sec. The tested joint was protected from hyperextension by (1) mechanical stops, (2) a failsafe motor shutdown, and (3) and an emergency stop. Custom designed software was used to directly sampled angles from the potentiometer, angular velocity signals from the tachometer, and force readings from the load cell at 600 Hz; the rotational resistance (i.e., torque) was found by multiplying force readings by the distance between the elbow joint center and the contact point of the load cell. Three trials, separated by 1-minute breaks, were conducted at each speed. Ten of the participants were tested a second time 2–3 days following the first assessment to establish between-day reliability.

ANALYSIS OF RESISTANCE PROFILES

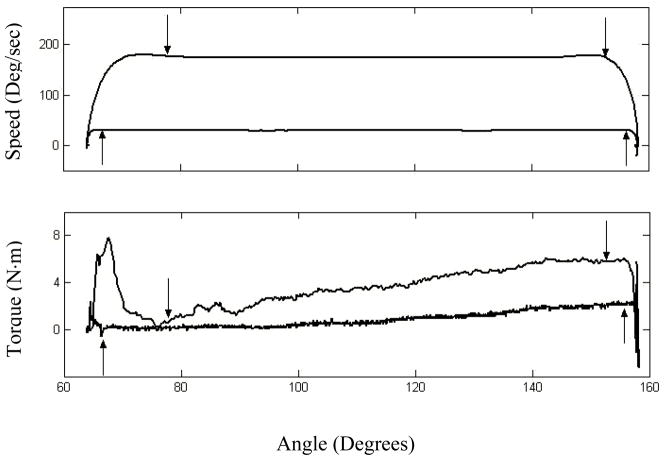
For each trial, the torque resistance-angle profile was windowed for the region of constant rotation speed (i.e., zero inertial dependent torque) (Lamontagne et al., 1997); the windowed region decreased slightly with speed because of prolonged acceleration effects (see figure 2). [Insert Figure 2 About Here]

Figure 2.

Windowing of raw profiles for low and high speeds. Speed and torque-resistance profiles are shown in the upper and lower graphics respectively. Upward pointing arrows denote the windowed region for 30 deg/sec and downward pointing arrows denote the windowed region for 180 deg/sec.

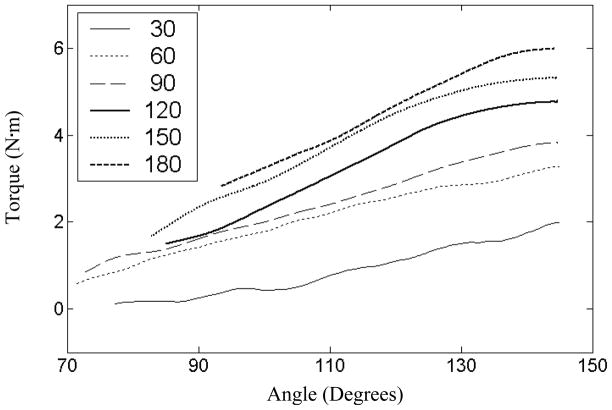
The rotational torque resistance of the elbow was ensemble averaged over three trials at each extension speed; ensemble-averaging reduced artifacts and preserved the highly repeatable shape and magnitude characteristics of individual trial profiles. In addition to verifying a positive association of passive torque resistance with extension angle and speed, preliminary analysis of torque resistance-angle profile families (i.e., the set of torque resistance-angle profiles to increasing extension speeds) identified three key response characteristics (see figure 3). Firstly, the majority of torque-resistance-angle profile families consisted of near parallel torque resistance-angle profiles; this parallel relationship within families suggested that the interaction effect between speed and position on passive resistance was minor. Secondly, individual resistance-angle profiles were consistent with the classic linear hypertonic response to stretching of the elbow (e.g., Given et al., 1995). Finally, a linear effect of velocity was indicated by increases of resistance that were proportional to increases in extension speed at each extension angle.

Figure 3.

Family of torque resistance-angle profiles for the more affected arm of one subject (SR09). Extension speeds vary from 30 to 180 deg/sec. Profiles are near parallel and increase with both angle and speed.

Given the predominant linear characteristics of profiles, we constructed a linear spring-damper model in terms of the angular position, θ, and the angular velocity, dθ/dt to describe the passive torque response, τ to extensions (see equation 1).

$$\tau (\theta ,d\theta /dt)=k\theta +bd\theta /dt+{\tau }_0=k(\theta -{\theta }_0)+bd\theta /dt$$ (Equation 1)

Here, k is the stiffness, b is the damping, and τ₀ is a constant; the constant, τ₀, was then converted into offset angle (i.e., spring displacement), θ₀. The offset angle can be interpreted as the spring-damper analogue of the threshold angle that is used in spring-offset models. Stiffness (N•m/deg), damping (N•m•sec/deg), and angular offset (deg) parameters were found by applying a least-squares fit of the spring-damper model to position, velocity, and torque data; this least-squares method was independent of starting parameters and search paradigm because of the linearity of the model (Strang, 1988). Specifically, the fit solved for x (stiffness, damping, and angular offset parameters) by minimizing the total squared error, E², between model estimates and measured values of torque (b) for position and velocity data (A) (i.e., E²=||Ax−b||²) (Strang, 1988). To facilitate comparisons between subjects and account for the effect of elbow flexor muscle mass on passive resistance (Given et al., 1995), both stiffness and damping parameters were normalized by participant mass.

STATISTICAL ANALYSIS

For both the more and less affected arms of each subject, the ability of the linear spring-damper model to describe passive resistance torque data was measured by the squared multiple correlation, R², goodness of fit measure (Tabachnick, 2001). Relative reliability using intraclass correlations, ICC(1,1) (Shrout & Fleiss, 1979) and absolute reliability using the standard error of measurement (SEM) (Eliasziw et al., 1994) was determined between days for stiffness, damping, and offset angle parameters; the ICC was used in the SEM calculation and SEMs were expressed as a percentage of mean scores. Subsequent analyses used parameter values from tests on the first day.

Concurrent and construct validity were tested for the parameters. The most common evidence in support of construct validity is provided when a test can discriminate between conditions known to have the trait and those who do not (Portney & Watkins, 2000). The effect of arm condition (i.e., more versus less affected arm) on parameters of normalized stiffness, normalized damping, and offset angle was assessed by two-tailed t-tests. T-tests were conducted with equal variances not assumed because a preliminary Levene’s Test of Equality of Variance indicated that arm condition had an effect on variance. Concurrent validity is the relationship of one measure to another and is quantified by correlation (Portney and Watkins, 2000; Streiner & Norman, 1995). The relationship between clinical hypertonia, as measured by the MAS, with parameters of offset angle, stiffness, and damping was calculated by Spearman rank correlations. The robustness of the correlations was quantified by the leverage of influential data points (i.e., effect of removing a data point) (Wilcox, 1998). Correlation leverage (CL) was documented by the range of correlations that occurred when single data points were removed. Non-parametric correlations were used because of the non-normal distribution of scores and the non-equivalence of MAS ordinal grade intervals. For purposes of statistical coding, ‘1+’ on the MAS was assigned a value of 1.5. All statistical tests were conducted at a significance level of p=.05.

Results

SURFACE PARAMETER FIT AND RELIABILITY

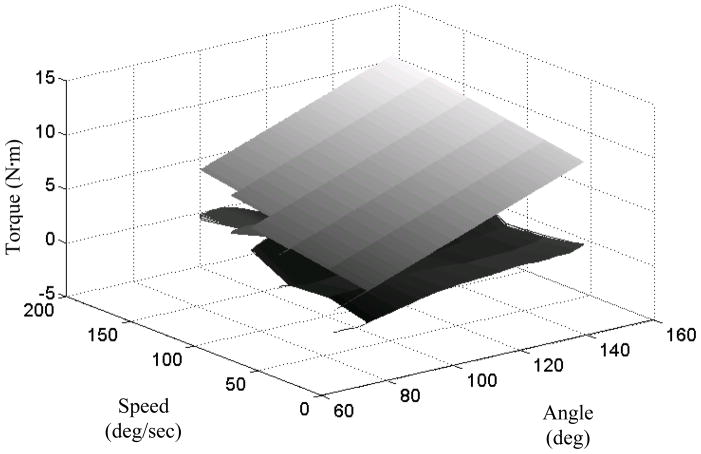
Across all the subjects, the R² values of the model fit to the torque profile for the less affected arm ranged from 0.58 to 0.96 with a mean value of 0.83. For the more affected arm, R² values ranged from 0.79 to 0.99 with a mean value of 0.94. Typical features of the linear spring-damper model fit are illustrated by figure 4. The between-day reliabilities of model parameters are in table 1.

Figure 4.

Passive resistance data fit to linear spring-damper model for the more affected arm of one subject (SR18). The upper curve is the least squares fit to extensions at different speeds. Residuals are plotted on the lower curve. The model slightly overestimates response torque for combinations of fast speed/small angle and slow speed/large angle while it slightly underestimates response torque for slow speed/small angle (i.e., angle-speed interaction). Residuals are near zero elsewhere.

Table 1.

Between day reliability of Surface Parameters

Parameter	More Affected		Less Affected
	ICC	% SEM	ICC	% SEM
Stiffness	.983	9.9	.909	21.0
Damping	.862	28.5	.882	37.0
Offset	.740	18.6	.902	8.2

COMPARISON OF SIDES

There was a significant effect of arm condition on stiffness, t(32)=3.56, p<.05, with the mean stiffness of the more affected arm (4.81*10^-4 N•m/deg•kg) greater than twice that of the less affected arm (2.08*10^-4 N•m/deg•kg). There was also a significant effect of arm condition on damping, t(32)=2.32, p<.05, with the mean damping of the more affected arm (14.38*10^-5 N•m•sec/deg•kg) also greater than twice that of the less affected arm (6.29*10^-5 N•m•sec/deg•kg). There was also a significant effect of arm condition on the offset angle, t(32)=2.55, p<.05, with the mean offset angle of the more affected arm (76.1 deg) reduced from that of the less affected arm (107.4 deg). Resistive viscous and elastic forces can be computed from spring-damper model parameters given body mass, forearm length, and a specified extension angle and velocity. Consider a person exhibiting the mean spring-damper parameter values above, weighing 100 kg with a forearm length of 0.25 m, whose elbow is extended to 120 deg at a velocity of 100 deg/sec. For the more affected arm the resulting viscous and elastic resistances would be 5.8 N and 8.4 N respectively. Parameters of the less affected arm translate as smaller viscous and elastic forces of 2.5 N and 1.0 N.

PARAMETER RELATIONSHIPS TO CLINICAL MEASURES OF HYPERTONIA

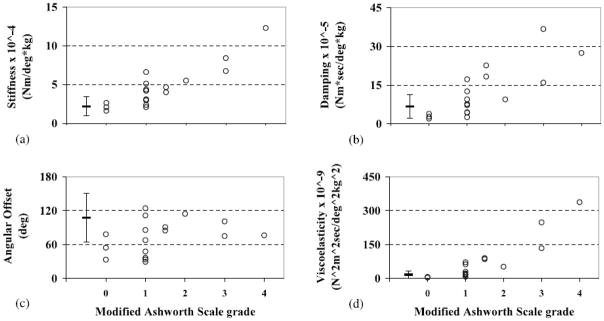
The MAS was not significantly correlated, p>.05, with the offset angle (r=0.408; CL = 0.289 – 0.446) but was significantly correlated, p<.001, with stiffness (r=0.820; CL = 0.765–0.848) and damping (r=0.816; CL = 0.766 – 0.853). Given the complexity of interpreting many mechanical parameters of hypertonia simultaneously, clinicians may find it easier to grade hypertonia by a single measure. This motivated us to generate a composite descriptor of muscle tone, ‘viscoelasticity’, by multiplying stiffness and damping parameters. A combined score is advantageous because the intrinsic randomness of related variables is reduced when they are combined; multiplication of parameters (as opposed to addition) generates scores that are unbiased to parameter units. The MAS was significantly correlated, p<.001, with viscoelasticity (r=0.909; CL = 0.882 – 0.939). Parameter values are graphed against the MAS in figure 5.

Figure 5.

Scatterplots of the MAS versus mechanical parameters of (a) stiffness, (b) damping, (c) angular offset, and (d) viscoelasticity for the more affected arm ‘○’ and the distribution of mechanical parameters for the less affected arm (mean and standard error bars on left of each graph).

Discussion

The purpose of this study was to test the reliability and validity of a linear spring-damper model of elbow flexor hypertonicity in persons with chronic stroke. Spring-damper parameters fit resistive torque profiles well, were reliable between days, and were capable of differentiating hypertonia from normal muscle tone. Stiffness, damping, and viscoelasticity, but not offset angle, were strongly and robustly correlated with increases in hypertonia as graded by the MAS. These results were found in our dataset which had a wide distribution of elbow flexor MAS scores.

The smaller number of data points at higher MAS grades may have reduced the power of our correlation analysis. However, the tight range of correlations found when potentially influential data points were removed demonstrates robust relationships between mechanical parameters and clinical scores of hypertonia. Furthermore, the distribution of our dataset is similar to many studies (e.g., Watkins et al., 2002; Johnson, 2002; Katz et al., 1992) which indicate that only a small percentage of individuals with chronic stroke exhibit scores at the upper two levels of the MAS under passive extension of the elbow. A second limitation of this study is that we did not use electromyography to identify the presence of hyperactive stretch reflexes. The identification of hyperactive stretch reflexes has been used to separate the mechanical contribution of hyperreflexia from the changes to the intrinsic viscoelastic characteristics of soft tissues (i.e., muscle and tendon) (Zhang et al., 1997). Subdividing hypertonicity, however, may not be practical or of clinical use as the reflex response has been shown to be insignificant when compared to changes in the natural viscoelastic joint resisitance (Lee et al., 1987). A final limitation of this study is that our spring-damper model did not accommodate for possible non-linear features of the response profile. While the addition of nonlinear terms may have potentially improved the model fit to response data, it is unlikely that nonlinear parameters would improve the model’s already excellent clinical correspondence (i.e., correlations) to hypertonia.

Our spring-damper model of hypertonicity compares favorably with other biomechanical studies. On average, 90% of the variance (R²) in the torque response profile was explained by the three spring-damper parameters. With the addition of a single damping parameter to account for changing extension velocities, our model is capable of explaining a percentage of variance that is similar to linear parameterizations (84%) of torque responses at isolated velocities (Pandyan et al., 2001). Although it is not possible to make exact comparisons between different studies due to different subject characteristics and protocols, the ability of the linear spring-damper model to explain a similar percentage of variance calculated from single speeds suggests that that the relationship between response torque and stretch velocity can be characterized as linear. The few hypertonic profiles that demonstrated reduced response linearity (i.e., smaller R² values) may have been associated with a ‘catch’. Catches are a transient increase in the passive resistive torque, are non-linear with position, and their fit to linear functions is reduced (Pandyan et al., 2001). The validity of this spring-damper model is limited to the direction, angles and speeds that lie within the testing range as geometrical constraints (i.e., bone contact) and a different rotation direction will cause the hypertonic response to diverge from linearity.

Reliable measures are crucial for determining changes that may occur during natural recovery or as a result of therapeutic intervention. Despite this, there is little information on the reliability of biomechanical and neurophysiological measures of hypertonia between days. In our study, the relative reliabilities of stiffness (ICC=0.983) and damping (ICC=0.862) parameters but not the offset angle (ICC=0.740) were high in comparison to the reliability calculated for the MAS (Kappa=0.826) (Bohannon & Smith, 1987); reliability calculations by Kappa and ICC statistics are similar or identical (Streiner & Norman, 1995). There was more variability in the absolute reliability of damping (28.5%) than offset (18.6%) and stiffness (9.9%). Whereas damping is a velocity dependent parameter, both offset and stiffness parameter are position dependent. Thus, it is possible that increased variability in damping estimates is related to the resolution of torque data which is decreased across speeds (6 speeds) when compared to data across angles (several hundred data points).

Construct validity of the spring-damper model was demonstrated by the sensitivity of its parameters to arm condition (i.e., more versus less affected arm) and concurrent validity was demonstrated by the high correlation of parameters with clinical measures of hypertonia. In addition to finding a correlation of stiffness with the MAS (0.820) that is comparable to those previously reported (0.778–0.873, Katz et al., 1992), this is the first study to show a correlation between the MAS and a damping parameter (0.816). We also found that compressing mechanical parameters into a single biomechanical index, ‘viscoelasticity’ can improve clinical correlations (r=0.909). Other methods of compressing biomechanical parameters such as principal components analysis may be useful in isolating a single index, particularly if several mechanical parameters are determined from the torque response to stretch.

We expected that in hypertonic elbow flexors, mechanical parameters values would shift so as to cause a more resistive spring-damper model (i.e., increases in stiffness and damping and a decrease in offset angle). This was the case for stiffness and damping parameters, as both were larger in the presence of hypertonia and both increased with its clinical grading. In addition, elbow flexors graded as having ‘normal’ muscle tone had comparable stiffness and damping parameters to the less affected arm. While the offset angle was significantly smaller for hypertonic elbow flexors, it was not as reliable as stiffness and damping measures and did not decrease with increasing clinical grades as we had anticipated. This unexpected result may have been due to non-linear features of the torque response profile that were not taken into account by the linear model or the slight bias of the offset angle calculation to the larger amounts of data available at lower extension velocities. However, the high goodness of fit measures associated with the spring-damper model, particularly in the more affected arm, would suggest that these are not problems. Alternatively, the differences in start angle between participants may have affected the response mechanics and the onset of the stretch reflex (Wolf et al., 1996) and thus, the calculation of the offset angle. A third possibility is that clinical gradings of hypertonia may not be related to the angle at which resistance is first felt but to the sensations associated with stiffness and damping.

CONCLUSION

Combining the torque responses of a variety of angular position-velocity combinations can lead to improvements in the mechanical characterization of a hypertonic joint. A spring-damper model describes both the position and velocity dependence of hypertonia with parameters that are strongly correlated to clinical measures. The increased resolution of these mechanical descriptors could be useful for detecting small but clinically meaningful changes in hypertonia for which the Ashworth and MAS scales are insensitive.