Sequential interaction of chloride and proton ions with the fast gate steer the voltage-dependent gating in ClC-2 chloride channels

Abstract

The interaction of either H⁺ or Cl⁻ ions with the fast gate is the major source of voltage (V_m) dependence in ClC Cl⁻ channels. However, the mechanism by which these ions confer V_m dependence to the ClC-2 Cl⁻ channel remains unclear. By determining the V_m dependence of normalized conductance (G_norm(V_m)), an index of open probability, ClC-2 gating was studied at different [H⁺]_i, [H⁺]_o and [Cl⁻]_i. Changing [H⁺]_i by five orders of magnitude whilst [Cl⁻]_i/[Cl⁻]_o = 140/140 or 10/140 mm slightly shifted G_norm(V_m) to negative V_m without altering the onset kinetics; however, channel closing was slower at acidic pH_i. A similar change in [H⁺]_o with [Cl⁻]_i/[Cl⁻]_o = 140/140 mm enhanced G_norm in a bell-shaped manner and shifted G_norm(V_m) curves to positive V_m. Importantly, G_norm was >0 with [H⁺]_o = 10⁻¹⁰ m but channel closing was slower when [H⁺]_o or [Cl⁻]_i increased implying that ClC-2 was opened without protonation and that external H⁺ and/or internal Cl⁻ ions stabilized the open conformation. The analysis of kinetics and steady-state properties at different [H⁺]_o and [Cl⁻]_i was carried out using a gating Scheme coupled to Cl⁻ permeation. Unlike previous results showing V_m-dependent protonation, our analysis revealed that fast gate protonation was V_m and Cl⁻ independent and the equilibrium constant for closed–open transition of unprotonated channels was facilitated by elevated [Cl⁻]_i in a V_m-dependent manner. Hence a V_m dependence of pore occupancy by Cl⁻ induces a conformational change in unprotonated closed channels, before the pore opens, and the open conformation is stabilized by Cl⁻ occupancy and V_m-independent protonation.

Key points

• Plasma membrane ClC-2 chloride channels are widely distributed in our body and are important for vision and fertility.

• ClC-2 channels are gated by changes in transmembrane voltage despite of lacking a voltage sensor device. It has been hypothesized that the interaction of an external proton with the gating machinery is responsible for voltage-dependent gating.

• Here we used electrophysiological recordings and quantitative analysis under different external proton and internal chloride concentrations and found that the voltage dependence of gating is due to interaction between the passing chloride ion and the permeation pathway, with the external proton stabilizing the open state of the channel.

Introduction

Opening and closing of the two independent permeation pathways in homodimeric ClC chloride channels is controlled by two fast acting gates and one slow acting gate (Miller & White, 1984; Richard & Miller, 1990; Accardi & Pusch, 2000; Zúñiga et al. 2004; De Santiago et al. 2005). Despite the lack of an intrinsic voltage sensor typically present in cation channels (Bezanilla 2008), gating in ClC channels is triggered by voltage (V_m) and is dependent on changes in [H⁺] and [Cl⁻] (Hanke & Miller, 1983; Pusch et al. 1995; Chen & Miller, 1996; Rychkov et al. 1996; Fahlke et al. 1997a; Pusch et al. 1999; Chen & Chen, 2001). A fast gate, also known as protopore gate, is formed by a carboxyl side chain (–CH₂–CH₂–COO⁻) of a conserved glutamic (E) residue located in the permeation pathway (Fahlke et al. 1997b; Dutzler et al. 2002). Based on the structural homology of channel pores with the anion pathway structure of the EcClC Cl⁻/H⁺ exchanger (Dutzler et al. 2002), it has been proposed that in the closed state the side chain physically occludes the permeation pathway by protruding into the channel pore whilst in the open state the side chain lines the pore snorkelling toward the extracellular side. Accordingly, mutating E166 in ClC-0, E232 in ClC-1 and E207 or E213 in ClC-2 removes fast gating and also the sensitivity of gating to Cl⁻ and H⁺ ions (Dutzler et al. 2003; Estévez et al. 2003; Niemeyer et al. 2003; Zúñiga et al. 2004; De Santiago et al. 2005). These observations indicate that opening of the fast gate is an essential step in ClC Cl⁻ channel gating and this process is dependent on both Cl⁻ and H⁺ ions. However, the underlying mechanism by which H⁺ and Cl⁻ ions contribute to gating appears to be slightly different in each channel despite their structural similarities.

In ClC-0 (the prototype ClC Cl⁻ channel amenable to single channel analysis and probably the best understood channel), extracellular acidic pH enhanced the minimal open probability at negative voltage in a V_m-independent manner, resulting in a single channel open probability of nearly 1 at all voltages without altering the single channel current (Chen & Chen, 2001). Similar results were seen with ClC-1 (Rychkov et al. 1996). In contrast, intracellular acidic pH shifted to more negative voltages the activation curve yielding V_m-dependent gating (Traverso et al. 2006; Zifarelli et al. 2008). Furthermore, it has been proposed that H⁺ from either side of the membrane must induce slow gate opening and cross the membrane to be able to gate ClC-0 (Lisal & Maduke, 2008, but see Picollo & Pusch, 2005). However, the widely expressed ClC-2 (Thiemann et al. 1992) has a complex response to variations in extracellular proton concentration ([H⁺]_o) and the effects of changes in intracellular protons ([H⁺]_i) remain undetermined. Channel opening (determined by calculating conductance, G_norm) steadily increases with [H⁺]_o increments in the low range; however, G_norm decreases with further [H⁺]_o increments (Arreola et al. 2002). Such behaviour is due to titration of side chains of two residues: a glutamic acid (E207 in guinea pig ClC-2 or E213 in mouse ClC-2) whose side chain forms the fast gate and histidine 513 (guinea pig ClC-2) located in one of the extracellular loops (Niemeyer et al. 2003, 2009), respectively. Mutating H513 in guinea pig ClC-2 channel abolished the inhibitory effect of high [H⁺]_o without affecting the enhancement of G_norm by low increments in [H⁺]_o. Similarly, the precise role of Cl⁻ ions in the V_m-dependent gating is not well understood. It has been proposed that extracellular Cl⁻ allosterically modulate the interaction between intracellular H⁺ and the fast gate in ClC-0 (Miller, 2006; Traverso et al. 2006; Zifarelli et al. 2008).

Following the hypothesis of V_m-dependent gating of ClC-0 due to protonation of the side chain of the gating glutamate by intracellular H⁺ and the analysis of G_norm([H⁺]_o) curves at different V_m in H513 ClC-2 mutant channel, a hypothesis for V_m-dependent gating of ClC-2 based on V_m-dependent titration of the side chain of the gating glutamate by extracellular H⁺ was proposed (Niemeyer et al. 2009). In this hypothesis, intracellular Cl⁻ would allosterically modulate the protonation reaction. If the fast gate is within the electrical field, the open probability is strictly dependent on [H⁺] and the closing rate must be independent of [H⁺]. However, if the gate is within the electrical field then either extracellular H⁺ or intracellular Cl⁻ ions can be potentially responsible for V_m-dependent gating of ClC-2 and hence the mechanism by which intracellular Cl⁻ ions contribute to ClC-2 gating should be thoroughly analysed. Interestingly, in ClC-Ka and ClC-Kb, the kidney Cl⁻ channels that lack fast gate, high [H⁺]_o also abolished Cl⁻ current (Gradogna et al. 2010). A homologous histidine is present in all ClC channels in a highly conserved region located between transmembrane segments P and Q. But mutating this residue renders ClC-Ka non-functional (Gradogna et al. 2010) without altering the gating behaviour and Zn²⁺ sensitivity in ClC-1 (Kürz et al. 1999). Recently, we showed that exposing mouse ClC-2 to increasing [Cl⁻]_i facilitated the V_m-dependent activation (G_norm(V_m) curve) and slowed down the fast gate closing. These processes displayed anomalous mole-fraction behaviour in Cl⁻/SCN⁻ mixtures indicating that multi-ion occupancy of the ClC-2 pore was important for channel gating (Sanchez-Rodriguez et al. 2010). Furthermore, Cl⁻, Br⁻ and SCN⁻ drove gating and slowed channel closing following the same sequence SCN⁻ > Br⁻ > Cl⁻ as the sequence found for binding site occupancy in ClC-ec1 (Lobet & Dutzler, 2006; Picollo et al. 2009). Based on the strong homology of the anion pathway composition of ClC exchangers and channels (Estévez et al. 2003; Bisset et al. 2005; Engh et al. 2007) we presumed that ClC-2 has three anion binding sites (S_int, S_cent and S_ext), just like the ones identified by X-ray crystallography in the ClC-ec1 Cl⁻/H⁺ exchanger (Dutzler et al. 2002, 2003). We also presumed that binding site occupancy by permeant anions was critical to ClC-2 gating. In this scenario pore occupancy and/or Cl⁻ movement between sites can be V_m-dependent events and thus could confer the V_m dependence, as has been proposed in ClC-0 (Engh et al. 2007). To gain further insights into the ClC-2 gating, in this work we reanalysed the contribution of both Cl⁻ and H⁺ to gating. Our data analysis and modelling suggest a V_m-dependent interaction of intracellular Cl⁻ ions with the fast gate as the major step conferring V_m dependence to ClC-2 channels.

Methods

Cell culture, transient transfection and electrophysiological recordings

HEK cells transfected with mouse ClC-2 cDNA were cultured and used to record whole cell Cl⁻ current (I_Cl(t)) as previously described (De Santiago et al. 2005; Sanchez-Rodriguez et al. 2010). Briefly, I_Cl(t) was recorded after a 5–6 min equilibration period. Step voltages (from +60 to –200 mV in 20 mV increments) delivered from the holding potential and returned to +60 mV were used to open ClC-2 channels. Throughout the experiment, the cells were maintained at 0 mV. All experiments were performed at ambient temperature (21–23°C).

Recording solutions

The standard external solution contained (in mm): TEA-Cl 139, CaCl₂ 0.5 and d-mannitol 100. The standard internal solution contained (in mm): TEA-Cl 140 and EGTA 20. The pH of both solutions was adjusted to 7.3 using 20 mm Hepes with TEA-OH. External and internal test solutions with different pH values were prepared by adding 20 mm of phthalate (pH 4.0 and 4.8), Mes (pH 5.5 and 6.4), Hepes (pH 7.3 and 8.2), Ampso (pH 9.1) or Caps (pH 10). Internal solutions with different [Cl⁻] were prepared by adding adequate amounts of TEA-Cl to obtain the desired [Cl⁻] without restoring ionic strength. Average tonicity, adjusted with d-mannitol, of external and internal solutions was 387.9 ± 1.9 and 347.3 ± 2.6 mosmol kg⁻¹, respectively.

Analysis

Since [Cl⁻]_i is critical to ClC-2 gating, we only included data with the reversal potential (V_r) near the predicted Nernst potential for Cl⁻ (E_Cl) and nearly identical G_norm–V_m and instantaneous tail current (I_tail)–V_m curves (for details on this inclusion criteria see Sanchez-Rodriguez et al. 2010). When solutions with different [Cl⁻] were tested, the V_m values were corrected for junction potential errors estimated using pCLAMP (Molecular Devices, Sunnyvale, CA, USA) or series resistance errors. G_norm was estimated as described before (De Santiago et al. 2005; Sanchez-Rodriguez et al. 2010). Briefly, whole cell Cl⁻ conductance (G = I_Cl/(V_m–V_r)) were plotted as a function of V_m and fitted with a Boltzmann function to estimate maximum G. Maximum G was then used to normalize the corresponding G–V_m relationship. G_norm(V_m) curves at different [H⁺]_i were obtained by normalizing each G vs. V_m curve against its own maximum G and then pooled. G_norm(V_m) curves at different [H⁺]_o were obtained by normalizing individual G vs. V_m curve to its corresponding maximum G obtained under control condition [H⁺]_o = 10^−7.3 m and then pooled. The resulting curves described the voltage dependence of apparent open probability (P_A(V_m)) in terms of normalized conductance. G_norm(V_m) curves were fitted to a Boltzmann function (eqn (1)):

(1)

where A is a scaling factor, z is the apparent charge, F is the Faraday constant, R is the gas constant, T is the temperature and V_1/2 is the V_m needed to reach G_norm = A/2. I_Cl(t) values at each V_m value under different conditions ([H⁺] or [Cl⁻]) were fitted with eqn (2):

(2)

where A_f and A_s are the relative weights of fast and slow components and τ_f and τ_s are their corresponding time constants (De Santiago et al. 2005). Macroscopic closing time constants (τ_C) were calculated by fitting G_norm(t) at +60 mV traces with eqn (3):

(3)

where y₀ is G_norm at t = 0 and y₁+y₀ is G_norm in steady-state. Means ± SEM are given or plotted and the number of experiments is indicated by n.

Modelling ClC-2 gating

Different models were built using the software IonChannelLab (http://www.jadesantiago.com/Electrophysiology/IonChannelLab/) (De Santiago-Castillo et al. 2010). To estimate and constrain the rate constant values for each model, we performed a global fit procedure using the program IChMASCOT (http://www.jadesantiago.com/Electrophysiology/IChMASCOT/) where I_Cl(t) and G_norm(V_m) curves obtained at different [H⁺]_i, different [Cl⁻]_i and different [Cl⁻]_o (from Sanchez-Rodriguez et al. 2010) were fitted to each model. See Supplemental Material for details. Then IonChannelLab was used to evaluate the ability of each model and their corresponding set of rate constants to reproduce the properties of ClC-2, I_Cl(t), G_norm(V_m) at different [Cl⁻]_i and [H⁺]_o, I_tail, and V_1/2([Cl⁻]_i, [H⁺]_o).

Results

[H⁺] dependence of ClC-2 gating

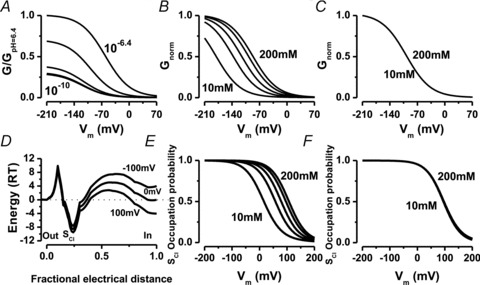
Data from V_m-dependent protonation of guinea pig ClC-2 by extracellular H⁺ (Niemeyer et al. 2009) and V_m-dependent protonation by intracellular H⁺ of ClC-0 (Miller, 2006; Traverso et al. 2006; Zifarelli et al. 2008) suggest that the fast gate might be located half way through the electrical field. If so, then intracellular H⁺ ions would also induce V_m-dependent gating in ClC-2. To test this possibility, experiments changing the [H⁺]_i from 10^−4.0 to 10^−9.1 m were carried out under conditions of symmetrical [Cl⁻] (140 mm) and constant [H⁺]_o (10^−7.3 m). Figure 1A shows whole cell Cl⁻ current traces (I_Cl(t)) obtained from different cells dialysed with solutions containing the indicated [H⁺]_i (in m) while changing the membrane potential (V_m) between +40 and –160 mV in increments of 40 mV. The onset of I_Cl(t) appeared to be similar when [H⁺]_i was between 10^−5.5 and 10^−9.1 m, but it became slower at [H⁺]_i 10^−4.0 m. This is summarized in Fig. 1B where the fast (open circles) and slow (open squares) time constants for currents measured at –120 mV are plotted as a function of [H⁺]_i. In contrast, the time constant of closing (τ_c) at +60 mV (Fig. 1C) and the absolute amplitude of whole cell current (Fig. 1D) decreased as [H⁺]_i increased.

Figure 1. Regulation of I_Cl through ClC-2 by [H⁺]_i.

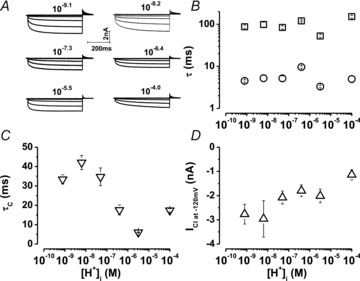
A, representative I_Cl(t) recordings obtained from 6 different cells dialysed with internal solutions whose [H⁺] (in m) was adjusted to the indicated values. Currents were recorded from −160 to +40 mV, in 40 mV increments. Horizontal (200 ms) and vertical (2 nA) bars are valid for all records. [H⁺]_o = 10^−7.3 m and [Cl⁻]_i = [Cl⁻]_o = 140 mm. B, fast (open circles) and slow (open squares) time constants as a function of [H⁺]_i were obtained by fitting eqn (2) to the onset phase of I_Cl(t). C, time constants of closing as a function of [H⁺]_i were obtained by fitting eqn (3) to the offset phase of I_Cl(t) at +60 mV. D, total I_Cl at −120 mV as a function of [H⁺]_i. n = 5–11 different cells.

To determine the effects of [H⁺]_i on the V_m dependence of apparent open probability (measured as normalized conductance, G_norm) we constructed G_norm(V_m) curves at each [H⁺]_i while [Cl⁻]_o = [Cl⁻]_i = 140 mm (Fig. 2A). The shape of these curves was quite similar, but their position shifted along the V_m axis as [H⁺]_i increased. Since varying [H⁺]_i has little effect on the onset kinetics, a double pulse protocol was used to determine the V_m dependence of the open probability of the fast gate P_P (De Santiago et al. 2005) in order to assay its H⁺ dependence. As with G_norm(V_m), the position of P_P(V_m) curves on the V_m axis varied as [H⁺]_i increased (Fig. 2B). Data in Fig. 2A and B were fitted with Boltzmann eqn (1) (continuous lines) to determine the V_m needed to reach 50% of G_norm or P_P (V_1/2) and their apparent charge value (z). Figure 2C summarizes the effects of [H⁺]_i on V_1/2 of G_norm (filled circles) or V_1/2 of P_P (open circles) and the apparent charge (z) of G_norm (filled circles) and P_P (open circles). There was a shift of V_1/2 of G_norm curves to more negative potentials as [H⁺]_i increased from 10^−9.1 to 10^−5.5 m, but then a further increase in [H⁺]_i up to 10⁻⁴ m shifted the V_1/2 value back to a slightly less negative potential. A similar behaviour was observed for V_1/2 values for P_P at the [H⁺]_i tested. Also, the estimated apparent charge z for both G_norm and P_P was nearly constant, ∼–1, at all [H⁺]_i. We then reasoned that if intracellular H⁺ ions activate ClC-2, then extracellular H⁺ ions would not increase G_norm. This was not the case; when pH_o was decreased from 7.3 to 6.4 while keeping pH_i at 6.4 and [Cl⁻]_i = [Cl⁻]_o = 140 mm, the G_norm(V_m) curve was shifted by +28.4 mV, a value similar to that observed when pH_i was set to 7.3 (see Fig. 3). We have previously shown that lowering [Cl⁻]_i to 10 mm unmasks the effect of [Cl⁻]_o on G_norm(V_m) (Sanchez-Rodriguez et al. 2010). Hence, we wondered if keeping the apparent open probability low by lowering [Cl⁻]_i would favour regulation of G_norm(V_m) by high [H⁺]_i. However, compared to [Cl⁻]_i = 140 mm, pH_i of 4.8 did not change the position of the G_norm(V_m) curves when [Cl⁻]_i was 10 mm. V_1/2 values were –152 mV and –154 mV, with 10 mm (n = 3) and 140 mm (n = 3) [Cl⁻]_i, respectively. In contrast, lowering pH_o from 7.3 to 6.4 with [Cl⁻]_o = 140 mm and [Cl⁻]_i constant at 10 mm (n = 3) increased G_norm and shifted G_norm(V_m) curves to the right by +29 mV (Fig. 2D), suggesting that high [H⁺]_i failed to activate ClC-2. Thus, taken together, these data show that increasing [H⁺]_i decreased the total current, sped up channel closing and had little effect on V_m-dependent gating of ClC-2.

Figure 2. ClC-2 gating at different [H⁺]_i.

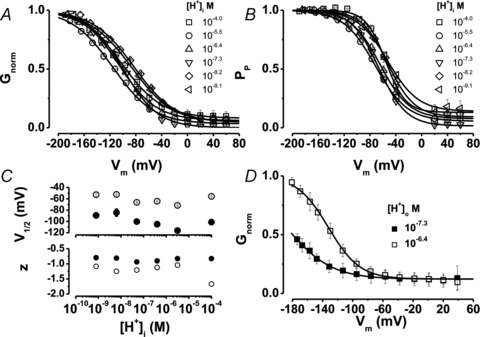
A, G_norm(V_m) curves at different [H⁺]_i. B, P_P(V_m) curves at different [H⁺]_i. [H⁺]_i (in m) and number of experiments were: 10^−9.1, 9 (⊲); 10^−8.2, 5 (⋄); 10^−7.3, 11 (▿); 10^−6.4, 11 (▵); 10^−5.5, 11 (○); 10^−4.0, 7 (□). Continuous lines in A and B are fits with Boltzmann eqn (1). C, estimated V_1/2 and z values obtained by fitting with eqn (1) individual G_norm(V_m) or P_P(V_m) curves. Open symbols are parameters for G_norm(V_m) curves while filled symbols are parameters corresponding to P_P(V_m) curves. D, G_norm(V_m) curves obtained from cells bathed first in a solution with pH 7.3 (filled squares) and then switched to a solution with pH 6.4 (open squares). The [Cl⁻]_i and pH_i were 10 mm and 6.4, respectively. [Cl⁻]_o was 140 mm.

Figure 3. Effect of [H⁺]_o on ClC-2 gating.

A, I_Cl(t) recordings obtained from 4 different cells exposed first to control solution containing [H⁺]_o = 10^−7.3 m (left traces) and then to a test solution (right traces) whose [H⁺]_o was adjusted to the indicated values (in m). Horizontal bars = 100 ms, valid for all recordings. Vertical bar = 2 nA is valid for control recordings and that at 10^−6.4 m H⁺; vertical bar = 0.5 nA is valid for all remaining recordings. pH_i 7.3 and [Cl⁻]_i = [Cl⁻]_o = 140 mm. Currents displayed were sampled at V_m: −160 to +40 mV in 20 mV increments for 10^−6.4, 10^−8.2 and 10^−9.1 m H⁺, and from −200 to +40 for 10⁻¹⁰ m H⁺ in 40 mV increments. B, G_norm(V_m) curves at different [H⁺]_o constructed using data like those shown in A. Continuous lines are fits with Boltzmann eqn (1) used to estimate V_1/2 and z values. n = 4 (10⁻¹⁰, ◆),5 (10^−9.1, ▸), 5 (10^−8.2, ◂), 11 (10^−7.3, ▾), and 6 (10^−6.4, ▴). C, V_1/2 values at different [H⁺]_o. D, z values at different [H⁺]_o.

In contrast to the effects of [H⁺]_i, Fig. 3 displays the effects of increasing [H⁺]_o on ClC-2 gating (Arreola et al. 2002; Niemeyer et al. 2009). Figure 3A shows I_Cl(t) recordings at V_m ranging from +60 to –160 mV at the indicated [H⁺]_o. Traces on the left side are the control recordings taken at [H⁺]_o = 10^−7.3 m and traces on the right side are the corresponding recordings taken from the same cell after the [H⁺]_o was changed. Increasing [H⁺]_o gradually increased I_Cl. Note that a sizable I_Cl was recorded with [H⁺]_o = 10⁻¹⁰ m; at –160 and –200 mV, the ratio I_Cl at pH 10 to I_Cl at pH 7.3 was 0.25 and 0.35, respectively. Supplementary Figs S1 and S2 show that a [H⁺]_o > 10^−6.4 m decrease the current size. Interestingly, wild-type ClC-2 channels did not lose rectification at all [H⁺]_o as indicated by the decay of the tail current to 0 (Fig. 3A). Figure 3B shows G_norm(V_m) curves at each [H⁺]_o. In all conditions, curves show a maximum at negative V_m while at positive values G_norm was very close to 0 reflecting the characteristic rectification of ClC-2. Maximum G_norm was achieved at [H⁺]_o = 10^−6.4 m and further decrements or increments in [H⁺]_o gradually decreased G_norm at all V_m (see also Supplementary Figs S1 and S2). However note that at –200 mV with [H⁺]_o = 10⁻¹⁰ m (filled diamonds) the G_norm was ∼0.33 indicating that ClC-2 was opened by V_m under adverse protonation conditions. The position of G_norm(V_m) curves on the V_m axis, measured by V_1/2 (eqn (1)), varied in a bell-shaped fashion with the [H⁺]_o (Fig. 3C). At low and high [H⁺]_o, V_1/2 was around –140 mV but shifted to less negative V_m when the [H⁺]_o approached a physiological range. In contrast, z did not change with [H⁺]_o (Fig. 3D).

In addition to the effects on G_norm(V_m) described above, increasing [H⁺]_o hampered ClC-2 closing indicating that external H⁺ ions interacted with the fast gate. We show this by analysing the kinetics of I_tail recorded at +60 mV (Fig. 4) which reflects the closing of the fast gate (De Santiago et al. 2005) under symmetrical [Cl⁻] of 140 mm. Figure 4A shows time courses of normalized whole cell conductance (G_norm) at –110 and +60 mV from a cell exposed to increasing [H⁺]_o (green = 10^−10.2 m; grey = 10^−9.1 m; red = 10^−7.3 m; light blue = 10^−6.4 m). The analysis of G_norm(t) using a single exponential function (dashed black lines) revealed that the opening became faster by increasing [H⁺]_o (Fig. 4B). In contrast, the G_norm at +60 mV reflecting the time course of channel closing was slower as [H⁺]_o increased (Fig. 4C). Overall, these observations suggest that ClC-2 is opened without protonation and the fast gate is stabilized in the open state by extracellular H⁺ ions.

Figure 4. External H⁺ ions hinder channel closing.

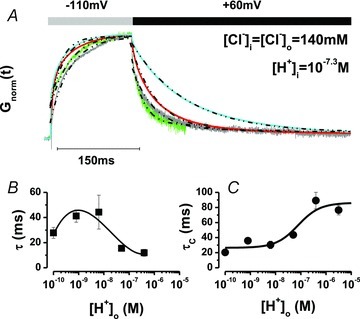
A, time course of G_norm at −110 (channel opening) and +60 (channel closing) mV and at different [H⁺]_o (10^−10.2 m green; 10^−9.1 m grey; 10^−7.3 m red; 10^−6.4 m light blue). Each trace is the average of four independent records. Broken lines at the top of the G_norm at −110 mV and +60 mV are fits with a mono-exponential function used to calculate the activation time constant (τ) or the closing time constant (τ_C) at each [H⁺]_o. B, τvs.[H⁺]_o curve. C, τ_C vs.[H⁺]_o curve. For each pH_o 5 < n < 9. pH_i 7.3 and [Cl⁻]_i = [Cl⁻]_o = 140 mm.

Analysis of intracellular Cl⁻ and extracellular H⁺ ions effects on V_m-dependent gating

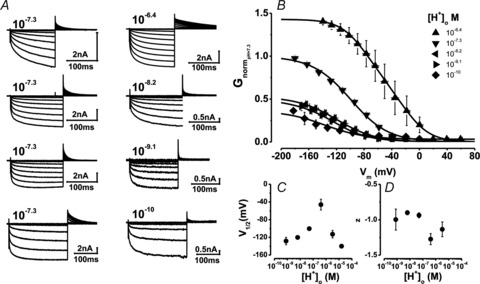
For the most part ClC-2 gating was not altered by changing either [Cl⁻]_o (Sanchez-Rodriguez et al. 2010) or [H⁺]_i, although the latter was expected to enhance gating. Since ClC-2 was opened by hyperpolarization at [H⁺]_o insufficient to induce protonation, we then re-evaluated the effects on V_m-dependent gating of [Cl⁻]_i, a known facilitator of ClC-2 gating (Pusch et al. 1999; Sanchez-Rodriguez et al. 2010) at different [H⁺]_o. Figure 5A–D displays sets of G_norm(V_m) curves obtained from cells with [Cl⁻]_i fixed at 40 (Fig. 5A), 80 (Fig. 5B), 140 (Fig. 5C), and 200 mm (Fig. 5D) and bathed in external solutions whose [H⁺]_o was adjusted to 10^−9.1 (filled inverted triangles), 10^−8.4 (filled triangles), 10^−7.3 (filled circles), and 10^−6.4 m (filled squares). For clarity, G_norm(V_m) curves at acidic pH_o (5.5 and 4.8) are not shown (Supplementary Fig. S1 shows curves at all pH_o). At any given V_m or [Cl⁻]_i, G_norm increased when [H⁺]_o increased from 10^−9.1 to 10^−6.4 m. Although these data seem to be compatible with protonation of a binding site, S₁ (representing protonation of the fast gate which enhances G_norm), we find that protonation was insufficient to entirely explain these curves and those shown in Fig. 4. If ClC-2 gating is triggered solely by protonation of the fast gate 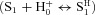, then G_norm should be 0 when [H⁺]_o is low and channel closing should be independent on [H⁺]_o. This was not the case; at any [Cl⁻], G_norm was >0 at low [H⁺]_o (Fig. 5A–D) and ClC-2 closing slowed down in the presence of high [H⁺]_o and high [Cl⁻]_i (Fig. 5G).

Figure 5. V_m-dependent gating of ClC-2 at different [H⁺]_o and [Cl⁻]_i ions.

A, B, C and D, families of G_norm(V_m) curves at different [H⁺]_o from cells dialysed with 40 (A, 5 < n < 9), 80 (B, 4 < n < 10), 140 (C, 4 < n < 11) and 200 (D, 4 < n < 8) mm Cl⁻. [H⁺]_o were: 10^−9.1 (▾), 10^−8.4 (▴), 10^−7.3 (•;), and 10^−6.4 m (▪). The [H⁺]_i = 10^−7.3 m and [Cl⁻]_o = 140 mm was the same in all cases. Note that G_norm was >0 when the [H⁺]_o was 10^−9.1 m in all cases. Continuous lines are fits with eqn (6) (from Scheme II) used to calculate pK_O and β_o/α₀ ratio. The resulting parameters were: [Cl⁻]_i = 40 mm: B = 2.95, A = 1492, z = −1.02, pK_O = 7.8, z_h = −0.017; [Cl⁻]_i = 80 mm: B = 5.59, A = 350, z = −0.89, pK_O = 7.9, z_h = −0.016; [Cl⁻]_i = 140 mm: B = 3.2, A = 255, z = −0.83, pK_O = 7.96, z_h = 0; [Cl⁻]_i = 200 mm: B = 3.1, A = 68.8, z = −0.71, pK_O = 8.0, z_h = 0.008. SEM were similar for all V_m and for clarity only high and low [H⁺]_o are included. E, pK_O vs. V_m at different [Cl⁻]_i. F, β₀/α₀ ratio vs. V_m curves for C↔O transition (Scheme II) at different [Cl⁻]_i. Continuous lines are fits using eqn (7) with z = −0.79, −0.75, −0.75 and −1.13 for 40, 80, 140 and 200 mm Cl⁻, respectively. G, τ_C vs.[H⁺]_o at different [Cl⁻]_i. Continuous lines are fits with eqn (9). For E, F and G curves [Cl⁻]_i was (in mm): (□ = 40; ○ = 80; ▵ = 140, and ▿ = 200 mm). Triangles and inverted triangles plotted at +60 mV in panel E are pK_o values obtained from fitting eqn (9) to data shown in panel G.

To gain insights into alternative mechanisms by which both H⁺ and Cl⁻ ions drive the V_m-dependent gating of ClC-2 we took an approach identical to that applied to uncover the flip mechanism of partial agonist on ligand gated channels (Lape et al. 2008). Different kinetic schemes based on different putative gating mechanisms were tested for their ability to describe I_Cl(t), G_norm(V_m) and τ_C at different [H⁺]_o and [Cl⁻]_i. We reasoned that the increased G_norm caused by high [H⁺]_o can be explained by assuming that protonation of closed channel favours the opening transitions (Supplementary Table 1). Another possibility is that protonation occurs when the channels are open and this stabilizes the open state (Schemes I and II). To quantitatively test these possibilities, two groups of kinetic Schemes were constructed based on these assumptions and a kinetic analysis was conducted.

The simplest two states kinetic scheme aimed to describe ClC-2 opening by protonation (Supplementary Table 1, row 1) gave a poor description of [H⁺]_o dependence of G_norm(V_m) curves and did not predict the effect seen on the channel closing. Several variations of this scheme were also tested including those based on ideas like: protonation does not lead immediately to the open state or the channel can transit to two open states after protonation (rows 2 and 3 of Supplementary Table I). The kinetic scheme proposed by Niemeyer and co-workers (Niemeyer et al. 2009) that includes Cl⁻ binding was also tested (row 4). The handicap of protonation schemes is that they predicted a constant value for τ_C (Supplemental Table 1, column 3) contrary to the experimental observation (Fig. 4C and 5G).

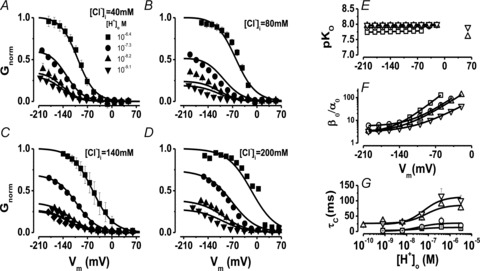
Since the idea that protonation of closed channel could favour channel opening did not work we considered that the open state was stabilized by protonation. The simplest sequential Scheme included one closed and two open states with the protonation reaction placed in the transition O↔O_H (Scheme I):

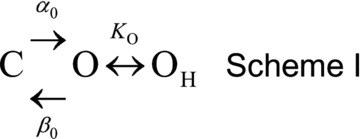
The open probability (P_O) for channels behaving as Scheme I is given by:

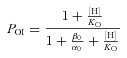(4)

To obtain the H⁺, Cl⁻ and V_m dependence of equilibrium (K_O) and rate (α_O, β_O) constants, eqn (4) was fitted to G_norm([H⁺]) curves at each [Cl⁻]_i and V_m. However, the off-line correction of V_m precluded construction of G_norm([H⁺]) curves at each V_m. To circumvent this problem, we used the Boltzmann fits of corrected G_norm(V_m) curves (as those shown in Fig. 3B) to generate corrected G_norm([H⁺]) curves at each [Cl⁻]_i and V_m and then eqn (4) was used to fit the resulting curves (continuous lines, Supplementary Fig. S1A). Alternatively, the H⁺ and Cl⁻ dependence of gating according to Scheme I can be studied by applying the Eyring rate theory (Eyring et al. 1949) which proposes that transition rate constants vary exponentially with V_m (see eqns (7) and (8) below). For this case, eqn (4) was fitted to G_norm(V_m) curves obtained at pH greater than or equal to 6.4 to determine K_O, α_O and β_O (Supplementary Fig. S1B, continuous lines). Scheme I gave a good description of G_norm([H⁺]_o) and G_norm(V_m) (Fig. S1A and B) and both methods used to extract the parameter values gave similar pK₀ (Supplementary Fig. S1C). Importantly, Scheme I predicted that the protonation constant (K₀) was V_m independent (Fig. S1C) while the ratio β₀/α₀ controlling the C↔O transition increased as V_m became positive (Supplementary Fig. S1D). For channels closing as described in Scheme I, τ_C is given by:

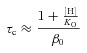(5)

which indicates that τ_C will linearly increase as [H⁺]_o increases (Supplementary Fig. S1E). Figures 4C and 5G show that this was not the case, at high [H⁺]_o, τ_C levels off. The finite value of τ_C at acidic pH_o indicates that the channel can transit through the protonated open state and reach the close state, although with more difficulty. To take this into account, a protonated closed state (C_H) was added to connect the protonated open state (O_H) and the closed state (C) (Scheme II):

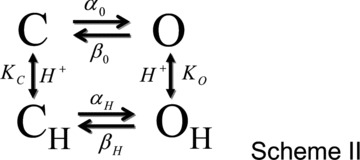
Scheme II is similar to that proposed by Hanke and Miller to explain the H⁺ dependence of ClC-0 (Hanke & Miller, 1983). Channels behaving according to Scheme II can transit from the C (closed unprotonated) to the O (open unprotonated) state with rate constants α₀ and β₀ or from state C_H (closed protonated) to state O_H (open protonated) with rate constants α_H and β_H. Equilibrium constants for protonation of C and O states are K_C and K_O, respectively. The P_O equation for a channel gating according to Scheme II is given by:

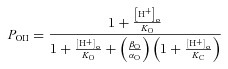(6)

To obtain the H⁺, Cl⁻ and V_m dependence of equilibrium (K_O, K_C) and rate (α_O, β_O) constants for Scheme II, the same procedure above described for Scheme I was applied. First, eqn (6), without any assumption, was used to fit the corrected G_norm([H⁺]_o) (Supplementary Fig. S2A,) with pK_C = 5 since the fit did not converge or was not modified with 1 < pK_C < 5. Second, we assumed that rate constants for C ↔ O transition and the equilibrium constant of protonation of closed channels varied exponentially with V_m and were given by eqns (7) and (8):

(7)

(8)

where A+B is the β₀/α₀ratio at 0 mV, f is an allosteric factor to account for the protonation reaction, k_o is the equilibrium constant of protonation of open channels at 0 mV and z or z_h is the apparent charge. Then eqn (6), with V_m-dependent rate constants, was used to fit the corrected G_norm(V_m) curves at [H⁺]_o up to 10^−9.1 m (Supplementary Fig. S2B) and the results were compared to those obtained with the first approach. Supplementary Fig. S2C and 2D shows that both approaches returned nearly identical values for pK_o and the β₀/α₀ ratio, although pK_o was V_m independent while the β₀/α₀ ratio displayed V_m dependence. Since both approaches returned the same results, a full analysis of the G_norm(V_m) at different [H⁺]_o and [Cl⁻]_i using eqn (6) was carried out to determine the H⁺, Cl⁻ and V_m dependence of K_O, K_C, α_O and β_O (Fig. 5A–D, continuous lines). It is important to remark that a single set of parameters (see Fig. 5) for each [Cl⁻]_i tested was sufficient to fit all G_norm(V_m) curves at such [Cl⁻]_i. Figure 5E shows the pK_O values obtained using eqn (6) without any assumption (symbols) or assuming a V_m dependence on β₀/α₀ (continous lines). The equilibrium constant for the protonation reaction O↔O_H in Scheme II, was both V_m and [Cl⁻]_i independent with values around 7.8. Since G_norm was >0 at [H⁺]_o = 10⁻¹⁰ m and pK_C < pK_O (f = 64 in eqn (8)), this suggested that the most likely transitions leading to the open conformation are C↔O↔O_H. In addition, given that the O↔O_H transition is V_m and Cl⁻ independent, then the transition C↔O should be V_m and/or Cl⁻ dependent in order for ClC-2 to have V_m-dependent gating. In agreement with this idea, the β₀/α₀ ratio increased from a limiting value of ∼3.5, as V_m became positive and was shifted to more positive V_m by increasing [Cl⁻]_i with z = –0.79, –0.75, –0.75, –1.13 for 40 (open squares), 80 (open circles), 140 (open triangles) and 200 (open inverted triangles) mm[Cl⁻]_i, respectively. Overall, these data suggested that Cl⁻ acted on a site located within the electrical field and such interaction was responsible for V_m-dependent gating in ClC-2. Finally, for channels returning to a fully closed conformation according to Scheme II, the τ_C as a function of [H⁺]_o was approximated by:

(9)

Unlike Scheme I, Scheme II described well the [H⁺]₀ and [Cl⁻]_i dependency of the closing rate. Data in Fig. 5G were fitted using eqn (9) with a pK_O value of 8.5, 8.2, 7.5 and 7.7 for 40 mm (open squares), 80 mm (open circles), 140 mm (open triangles) and 200 mm (open inverted triangles) [Cl⁻]_i, respectively. These values were plotted in Fig. 5E (open inverted triangles and open triangles at +60 mV) and corresponded well with those expected by extrapolating the pK_o(V_m) curves to +60 mV. Taken together our findings support the hypothesis that external H⁺ ions interacted with the fast gate in a V_m-independent manner and that ClC-2 remains in the open conformation for longer times when [H⁺]_o and [Cl⁻]_i are increased since both these ions hinder closing of the fast gate.

Simulating the voltage dependence of ClC2 based on gating Scheme II

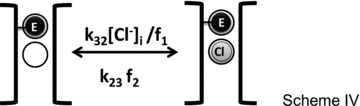
Our final aim was to develop a minimal model able to reproduce the gating of mouse ClC-2. Since our data and their analysis show that permeant anions interacted with the fast gate and extracellular H⁺ stabilized the open conformation, our minimal model was based on these interactions and ignored any other effects on the common gate. Models 1 and 2 based on Schemes I and II, respectively, were tested in detail to assess their ability to reproduce the kinetics and steady state properties of ClC-2 gating. To take into account the dependence of gating on the permeant Cl⁻ ion, it was necessary to develop coupled gating/permeation models. Given the absence of structural data for ClC-2 channels, we assumed for simplicity that the fast gate and Cl⁻ share the permeation pathway by presumably occupying the so-called external (S_ext) and central (S_cen) binding sites described for the ClC Cl⁻/H⁺ exchanger (Dutzler et al. 2003). Scheme III describes the occupancy by either extracellular or intracellular Cl⁻ (grey sphere) of an open pore (black brackets). The fast gate is represented by the black sphere and S_cen and S_ext binding sites by black circles.

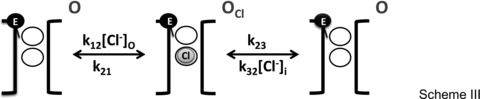
Once a Cl⁻ ion occupies the pore with rate constants k₁₂[Cl⁻]_o and k₃₂[Cl⁻]_i, it can exit the pore with rate constants k₂₁ and k₂₃. Alternatively, an intracellular Cl⁻ ion can occupy a closed pore with rate constants k₃[Cl⁻]_i/f and leave it with rate constant k₂₃f as shown by Scheme IV. These rate constants are assumed to vary in an exponential manner with voltage and hence carry the voltage dependence of gating transitions.

Thus, full Model 1 (Supplementary Fig. S3A) based on Scheme I considered transitions between empty or Cl⁻ occupied pores. In the closed states, the fast gate is blocking the conduction pathway. In the open states, the fast gate swings towards the extracellular side and then becomes protonated. The full open state is when a Cl⁻ occupies the pore and the fast gate is protonated by extracellular H⁺ (O_Cl,H). Model 1 was built using the software IonChannelLab (De Santiago-Castillo et al. 2010) and served to perform a global fit of I_Cl(t), G_norm(V_m) curves and τ_c([H⁺]_o) data using ICHMASCOT. The rate constants for each transition that were obtained this way were then used to simulate kinetics and steady-state properties of ClC-2. Simulations with Model 1 were able to reproduce I_Cl(t) (Supplementary Fig. S3B), the [Cl⁻]_i and [Cl⁻]_o dependence of G_norm(t) and τ_c (Supplementary Fig. S3C and D). Also, Model 1, described the [H⁺]_o, [Cl⁻]_i and [Cl⁻]_o dependencies of G_norm(V_m) (Supplementary Fig. S4A–C). However, as expected, the model failed to reproduce the time course of channel closing at high [H⁺]_o (Supplementary Fig. S5). The model failed because it does not allow transitions to the close state from the protonated states.

Model 2 assumed that (a) Cl⁻ interacts with the fast gate in a V_m-dependent manner according to Scheme II to facilitate the C↔O transition. The parallel shifts of P_P and G_norm at different [Cl⁻]_i (Sanchez-Rodriguez et al. 2010) and the modest contribution of the slow gate to ClC-2 gating (De Santiago et al. 2005; Yusef et al. 2006) support this assumption; (b) S_ext is near the extracellular side as suggested by the ClC-ec1 structure (Dutzler et al. 2003; Lisal & Maduke, 2008) and by the V_m-independent effects of extracellular H⁺ and V_m-dependent effects of intracellular Cl⁻ on G_norm(V_m); (c) H⁺ and Cl⁻ regulate ClC-2 gating by hindering the fast gate closing. Figure 6A depicts the complete Model 2 in two levels where C and O represent closed and open states. The pore was represented by blue brackets whilst the fast gate, represented by the red sphere, was placed within the pore, closer to the extracellular side. The front level represents the gating transitions (just as Scheme II) in the absence of Cl⁻ whilst the back level represents the corresponding transitions after one intracellular Cl⁻ occupies the pore. The fast gate can be protonated by extracellular H⁺ (blue sphere) and this reaction stabilizes the open conformations (O_H and O_Cl,H). Transition rate constants α and β control the C↔O transition in the absence of Cl⁻ and H⁺. When similar transitions occurred in the presence of Cl⁻ (C^Cl↔O^Cl), or H⁺ (C_H↔O_H), or both (C_Cl,H↔O_Cl,H), α_o and β_o rate constants are weighed by allosteric factors f₁ and f₂ or by f_H to account for the Cl⁻–fast gate interaction within the pore and for the protonation state of the fast gate, respectively. K^H_C ( = K^H_O×f²_H) and K^H_O are equilibrium constants for protonation in closed and open channels, respectively. Note that the equilibrium constant of protonation of either closed or open pores was independent of pore occupancy by Cl⁻. An additional feature of Model 2 is that microscopic reversibility is maintained for cycles C–C^Cl–C_H^Cl–C_H, C^Cl–O^Cl–O_H^Cl–C_H^Cl, O^Cl–O–O_H–O_H^Cl, but not for cycles C–C_Cl–O^Cl–O and C_H–C_H^Cl–O_H^Cl–O_H. A broken microscopic reversibility is expected if gating is coupled to ion permeation (Chen & Miller, 1996). k^Cl_C(+/−) and k^Cl_O(+/−) are rate constants controlling transitions resulting from binding (+) or unbinding (–) of one Cl⁻ ion to open or closed channel pore according to Schemes III and IV, respectively. These rate constants are given by:

Figure 6. Model 2 for ClC-2 gating.

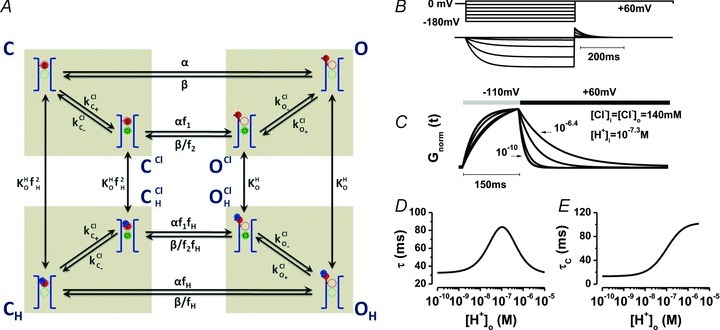
A, kinetic model built according to Scheme II that couples movement of the fast gate to Cl⁻ occupancy of the pore_. Rectangular boxes indicate four conformations: C = closed unprotonated, O = open unprotonated, C_H = closed protonated and O_H = open protonated. S_cen and S_ext anion binding sites are represented by dashed green and red circles, respectively. Cl⁻ is represented by a green sphere, H⁺ by a blue sphere and the fast gate by a red sphere. Protonation of the fast gate by 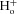is indicated by a blue sphere attach to a red sphere. Transitions between Cl⁻-free and Cl⁻-bound states are dictated by V_m-dependent rate constants. Transitions between unprotonated and protonated states are characterized by V_m-independent equilibrium constants 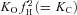and K_O, respectively. Fast gate is open by electrostatic repulsion when either a Cl⁻ (f₁ = 151) or H⁺ ion is bound (f_H = 8.46). B, simulated ionic currents from +60 mV to −180 mV, in 40 mV increments according to the voltage protocol shown on top. I_Cl(t) were simulated for [Cl⁻]_i = [Cl⁻]_o = 140 mm, pH_o = pH_i = 7.3. C, simulated time course of G_norm at −110 and +60 with [H⁺]_o from = 10⁻¹⁰ m to = 10^−6.4 m. D, opening time constant vs.[H⁺]_o. E, closing time constant vs.[H⁺]_o. Simulations were done using the parameter set listed in Table 1.

(10)

(11)

(12)

(13)

Model 2 was built using the software IonChannelLab (De Santiago-Castillo et al. 2010) and then used to perform a global fit of I_Cl(t), G_norm(V_m) curves and τ_c([H⁺]_o) data using ICHMASCOT in order to extract the rate constants for the transitions depicted in Model 2. Table 1 shows the corresponding rate constants obtained this way. These rate constants were fed into IonChannelLab (De Santiago-Castillo et al. 2010), to simulate ClC-2 channel kinetics and steady-state properties. Figure 6B shows the simulated I_Cl(t) according to the voltage protocol depicted on top. As with real channels, simulated I_Cl(t) displayed strong inward rectification, slow activation and large tail currents at +60 mV. The reversal potentials of simulated instantaneous current–voltage relations followed the Nernst potential for Cl⁻ ions, as is expected for a perfect selective channel. Model 2 also reproduced the effects of [H⁺]_o on the onset and offset kinetics. Figure 6C displays simulated G_norm vs. time traces obtained using a V_m step to –110 mV followed by step to +60 mV at different [H⁺]_o. As with the experiment, the onset kinetics display a bell shape (Fig. 6D) while the offset kinetics slowed down (Fig. 6E) as [H⁺]_o increased. Furthermore, Model 2 was able to reproduce experimental data describing the effects of external [H⁺]_o (Fig. 7A), and [Cl⁻]_i (Fig. 7B) on G_norm(V_m) curves. Importantly, when [Cl⁻]_i was fixed at 140 mm and [Cl⁻]_o was varied between 10 and 200 mm, no change was predicted on G_norm(V_m) curves (Fig. 7C), just as observed experimentally (Sanchez-Rodriguez et al. 2010). The underlying explanation for the effects of Cl⁻ ions on V_m-dependent ClC-2 gating is shown in Fig. 7D and E. The probability of one intracellular Cl⁻ ion occupying the pore decreases as V_m becomes positive but increases as [Cl⁻]_i increases (Fig. 7E). By contrast varying [Cl⁻]_o between 10 and 200 mm with 140 mm[Cl⁻]_i does not alter the probability of pore occupancy (Fig. 7F). These distinct effects of permeant Cl⁻ are because an incoming Cl⁻ ion experience a larger energy barrier (∼10 RT) when approaching from outside than when approaching from the inside (Fig. 7D). These simulations show that Model 2 reproduces most of the experimental observations regarding the H⁺ and Cl⁻ dependence of ClC-2 gating.

Table 1.

Equilibrium constants, rate constants and allosteric parameters determined by global fitting of experimental data using Model 2

Parameter	Value or expression	Parameter	Value or expression
k12		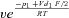pK	7.9
k21		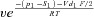α	0.06 s−1
k23		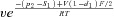β	229 s−1
k32		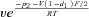f1	151.6
p1	10 RT	f2	8.4
p2	5 RT	fH	8.46
s1	−5 RT
d1	0.2

ν = kT/h, where k, T and h are the Boltzmann constant, temperature and the Planck constant, respectively. The p_i, S_i and d_i parameters represent the barrier high, well depth and fractional electrical distance from extracellular media, respectively (see Fig. 6D). These values or expressions were used in the simulations shown in Figs 6 and 7.

Figure 7. Simulation of steady-state properties of ClC-2 gating under different ionic conditions according to Model 2.

A, G_norm(V_m) dependence on [H⁺]_o (from 10⁻¹⁰ to 10^−6.4 m) was simulated using Model 2. B, simulations of the dependence on [Cl⁻]_i (from 10 to 200 mm) of the G_norm(V_m) curve. C, lack of effect of [Cl⁻]_o on G_norm(V_m). Curves were simulated using [Cl⁻]_o ranging between 10 and 200 mm. D, energy barriers experienced by a Cl⁻ ion going through the permeation pathway in ClC-2 at the indicated V_m. Energy profiles were calculated considering that permeation and gating are coupled as described by Model 2. E, voltage dependence of probability of ClC-2 pore occupancy by Cl⁻ at the indicated [Cl⁻]_i. F, voltage dependence of probability of ClC-2 pore occupancy by Cl⁻ is independent of [Cl⁻]_o. All simulations were done using the parameter set listed in Table 1.

Discussion

Soon after solving the structure of EcClC by X-ray diffraction (Dutzler et al. 2003), it was recognized that a glutamic acid residue located in the permeation pathway and its interaction with H⁺ and/or Cl⁻ ions was fundamental for voltage gating in all ClC Cl⁻ channels. A large body of data show that indeed H⁺ and Cl⁻ ions do participate in voltage gating in ClC Cl⁻ channels and that the side chain of a pore glutamic acid is forming the fast gate. However, the mechanism by which these ions confer voltage dependence is a matter of debate despite structural similarities among ClC channels.

We have previously shown that intracellular permeant anions contributed to mouse ClC-2 gating by interacting and then facilitating the opening of the fast gate opening (Sanchez-Rodriguez et al. 2010). This suggested that permeant anions play an active role in voltage gating. In the present work additional data that support the idea that Cl⁻ ions interact in a V_m-dependent manner with the fast gate are presented. Thus, we proposed that Cl⁻ is important for V_m-dependent gating in ClC-2. We observed that channel opening increased as [H⁺]_o increased but not when [H⁺]_i increased, that channel opening was larger than 0 (G_norm = 0.3) when [H⁺]_o was very low (10⁻¹⁰ m) and that I_tail kinetics which reflect closing of the fast gate became slower when [H⁺]_o increased. The analysis using Scheme II showed no evidence for V_m-dependent protonation of ClC-2; instead, the rate constants for a C↔O transition were sensitive to both V_m and permeant intracellular Cl⁻. These later observations are contrary to what is expected (strict dependence of channel opening on [H⁺]_o, G_norm almost 0 with low [H⁺]_o and closing kinetics independent of [H⁺]_o) if ClC-2 gating is dictated solely by V_m-dependent protonation of the fast gate caused by extracellular H⁺. Interestingly, the ratio β₀/α₀ for C↔O transition increased from an apparent limiting value of 3.5; this suggests that even when [H⁺]_o would be quite low, the channel can be opened by strong hyperpolarizations. We proposed that V_m-dependent gating is conferred by a V_m-dependent interaction between Cl⁻ and the fast gate with subsequent protonation by extracellular H⁺ helping to stabilize the open conformation. This idea nicely unified the effects of both intracellular Cl⁻ and extracellular H⁺ on gating and our model based on this idea reproduced the V_m-dependent gating of ClC-2.

Recently, a kinetic model for Cl⁻/H⁺ exchanger was proposed based on three functional states (two closed and one open) whose atomic structures were solved by x-ray crystallography (Dutzler et al. 2002, 2003; Feng et al. 2010). In that model, the binding of an intracellular H⁺ to the side chain of E148 induces a displacement of the side chain towards the extracellular side and turns on the forward mode of the exchanger. In contrast, intracellular Cl⁻ induces the backward mode but the unprotonated E148 side chain suffers the same conformational change, a displacement towards the extracellular side. Since, ClC Cl⁻ channels are both structurally and functionally related to ClC Cl⁻/H⁺ exchangers, it is tempting to speculate that the intracellular Cl⁻-dependent gating of ClC-2 described in this work proceeds by a mechanism similar to that induced by intracellular Cl⁻ in the exchanger. In this hypothetical setting, the fast gate will be sitting on S_ext near the outside vestibule of ClC-2, just like suggested for ClC-0 (Bisset et al. 2005; Lisal & Maduke, 2008). That way, an extracellular H⁺ would interact with the fast gate outside the electrical field while an intracellular Cl⁻ will travel nearly the entire pathway – sensing the electrical field – before reaching the fast gate. Data simulation with Model 2 indicates that pore occupancy is V_m dependent, i.e. at negative V_m the pore will be occupied by Cl⁻. This will repel the fast gate and additional entry of intracellular Cl⁻ would further push outwardly any Cl⁻ ions already sitting in the pore with the consequent swing of the unprotonated fast gate toward the extracellular side. Once the gate reaches this new conformation the extracellular H⁺ can bind to the gate to stabilize its open conformation. This would represent the full open/conductive state of ClC-2 and Cl⁻ would flow towards the extracellular space. Consequently, Cl⁻ will hamper closing simply because the likelihood that S_cent and/or S_ext are occupied rise as the [Cl⁻]_i is increased. When V_m is switched to positive values, the pore will eventually be emptied of Cl⁻. Under this condition, closing of the fast gate will be dependent on dissociation of the H⁺ into the extracellular space. In this way, Cl⁻ is able to flow without H⁺ permeation (see also Picollo & Pusch, 2005) and the fast gate of ClC-2 is able to close even at high [H⁺]_o as experimentally observed. In summary, this gating mechanism explains how pore occupancy contributes to the V_m dependence of gating.

Although the mechanism, V_m-dependent chlorination followed by V_m-independent protonation, described by Model 2 captured most of the V_m dependence of ClC-2 gating and predicted G_norm vs. pH curves similar to those published by Niemeyer et al. (2009), it is still insufficient and cannot rule out for certain that external H⁺ interacted with the fast gate in a V_m-dependent manner. Model 2 is an over-simplification since the effects of Cl⁻ and H⁺ on the common gate were ignored and the anomalous mole fraction behaviour cannot be reproduced. Also, the observation that the ratio β_O/α_O cannot be described as a single exponential function of voltage – as expected for a process described by rate theory – implies that our model has some limitations, such as a limited number of transitions. An additional problem in developing sound quantitative models that help understand the gating of ClC-2 Cl⁻ channel is the uncertainty of the fast gate location within the pore and within the electrical field. On one hand, the structure of the ClC-ec1 Cl⁻/H⁺ exchanger used for homology modelling of ClC channels suggests that the physical location of the side chain of the gating glutamate would be near the outside entry of the pore (Dutzler et al. 2003). If this is the case, then external Cl⁻ and H⁺ ions would affect gating in a V_m-independent manner, whilst intracellular Cl⁻ and H⁺ ions would have to travel most of the electrical field to reach the of the side chain of the gating glutamate and in doing so, the protonation and chlorination reactions will be V_m dependent, a critical step for V_m-dependent gating. This scenario seems to be likely in ClC-0 (Chen & Chen, 2001; Traverso et al. 2006; Lísal & Maduke, 2008). On the other hand, theoretical analysis of EcClC structure or of the homology model for ClC-0 using Poisson–Boltzmann theory suggests that the side chain of the glutamic acid forming the fast gate may be half way within the electrical field (Faraldo-Gomez & Roux, 2004; Engh et al. 2007. If so, then the electrical field will alter the effective concentration of both H⁺ and Cl⁻ around the fast gate and thus both ions could alter gating in a V_m-dependent manner. Our analysis suggests that the fast gate would be located near the extracellular side of the channel. In fact, Model 2 reproduced most of the data using an electrical distance of 0.2 for location of the fast gate. Despite of this, we cannot rule out the possibility that the gate is deeper within the electrical field. But even so, the gating process will position the fast gate near the exit side where an extracellular H⁺ can bind to it. Either way, with a fast gate closer to the exit side or deep in the permeation pathway, an intracellular Cl⁻ ion would need to travel within the electrical field to reach the fast gate and this is essential for V_m-dependent gating in ClC-2. To conclusively demonstrate the physical location of the fast gate of ClC-2 and its interaction with H⁺ and Cl⁻ ions, additional structural data and theoretical analysis are needed.

The present results are compatible with those we previously published using fresh dissociated rat parotid acinar cells (Arreola et al. 2002). For example, at –100 mV and pH 9.0, I_Cl,pH9.0/I_Cl,pH7.3 was 0.21 in acinar cells; in the present data G_norm was 0.1 with pH 9 at –100 mV and rose to nearly 0.3 at –200 mV. Although Niemeyer et al. (2009) reported a ratio value close to 0.5 at pH 9 and –170 mV they reached a different conclusion about V_m dependence. We wonder about possible experimental differences that may explain dissimilar conclusions. The primary sequence of mouse ClC-2 clone used in this work is quite similar (96% identity) to Cavia porcellus ClC-2 used by Niemeyer and co-workers. Although residues 77–86 were deleted in C. porcellus ClC-2, its behaviour is quite similar to the wild-type channel. Another fundamental difference is the analytical method used to extract the equilibrium constant for protonation. In our case, we considered that the channel can be opened via the unprotonated open state 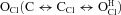or via the protonated closed state 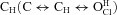but we make no assumption about V_m dependence on any rate constant. In addition, we took into account changes in kinetics resulting from variations in either [Cl⁻]_i or [H⁺]_o. In contrast, Niemeyer et al. (2009) extracted the equilibrium constant of protonation from steady-state gating parameters assuming that the channel would open in a single step 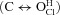triggered solely by protonation of the fast gate. This later case is a lump version of a more general mechanism comprising V_m-dependent and V_m-independent steps and certainly the resulting apparent equilibrium constant for protonation will be V_m dependent just because the gating is V_m dependent.

Is ClC-2 gating completely independent of [H⁺]_i? We do not think so. G_norm(V_m) curves shifted along the V_m axis, channel closing was sped up and total I_Cl decreased when pH_i was decreased. These are indications that gating is also altered by pH_i. However, all effects of pH_i were opposite to those expected for a gating facilitator. Recently, it was proposed that ClC-0 channels are opened by intracellular H⁺ produced by water dissociation within the channel pore whereas the OH⁻ anion may occupy either S_int or S_ext sites (Zifarelli et al. 2008). We wonder if the effect of alkaline pH_i on ClC-2 was the result of OH⁻ interaction with the channel pore just like the interaction of intracellular Cl⁻ (Sanchez-Rodriguez et al. 2010). If so, then the same mechanism that explains the effects of intracellular Cl⁻ would explain the effects of pH_i including a positive shift of the V_1/2 parameter, a slower channel closing and current increase caused when [OH⁻]_i increased at alkaline pH_i.

In conclusion, we hypothesized that under physiological conditions, ClC-2 would frequently reach the full open conformation state via the unprotonated open state and that intracellular Cl⁻ would favour this transition by occupying the pore in a V_m-dependent manner. Extracellular H⁺, on the other hand, would stabilize the open state due to a V_m-independent protonation reaction taking place after the fast gate swings towards the extracellular media. Thus, stabilization of the open state and V_m-dependent occupancy of anion binding sites will determine the open time duration and the V_m dependence of ClC-2 gating.

Author contributions

J.E.S.R. designed research, performed research and wrote the paper. J.A.C.V. analysed and modelled data. P.G.N.D. performed research and analysed data. A.C.C. performed research and analysed data. J.A.D.S.C. designed research, analysed and modelled data and wrote the paper. J.A. designed research, analysed data and wrote the paper. All authors approved the final version for publication.

Author's present address

J. E. Sánchez-Rodríguez: Department of Biochemistry and Molecular Biology, University of Chicago.

Supplementary material

Supplemental Figure S 1

Supplemental Figure S 2

Supplemental Figure S 3

Supplemental Figure S 4

Supplemental Figure S 5

Supplemental Table 1.