Abstract
Severe brain damage is often followed by serious complications. Quantitative measurements, such as regional volume and surface area under various conditions, are essential for understanding functional changes in the brain and assessing prognosis. The affected brain tissue is variable, hence traditional imaging methods are not always applicable and automatic methods may not be able to match the individual observer. Stereological techniques are alternative tools in the quantitative description of biological structures, and have been increasingly applied to the human brain. In the present study, we applied stereological techniques to representative CT and MRI brain scans from five patients to describe how stereological methods, when applied to scans of trauma patients, can provide a useful supplement to the estimation of structural brain changes in head injuries. The reliability of the estimates was tested by obtaining repeated intra- and interobserver estimates of selected subdivisions of the brain in patients with acute head injury, as well as in an MR phantom. The estimates of different subdivisions showed a coefficient of variation (CV) below 12% in the patients and below 7% for phantom estimation. The validity of phantom estimates was tested by the average deviation from the true geometric values, and was below 10%. The stereological methods were compared with more traditional region-based methods performed on medical imaging, which showed a CV below 7% and bias below 14%. It is concluded that the stereological estimates may be useful tools in head injury quantification.
Despite the impressive volume of basic quantitative data that has been provided from the healthy and diseased human brain [1–4], there is still a limited basic knowledge about quantitative relationships, such as the regional volume and surface area of the human brain under various conditions. Design-based stereological methods enable us to overcome the methodological pitfalls from earlier studies, and have been applied to the human brain previously [5–7]. Stereology is based on systematic uniformly random sampling (SURS) (i.e. sampling with a random start followed by systematic sampling) [8], which, at least in principle, leads to an unbiased estimate of volume. Furthermore, the investigator determines the precision of the estimates. The methods are easy to implement and have an obvious efficiency in terms of workload and precision [9]. The extent of sampling can be adjusted to the most efficient level, with respect to precision and effort, if the object is intercepted by a series of SURS parallel sections and the corresponding cross-sectional areas estimated by point counting [8]. The principle of SURS sectioning can also be extended to include other estimates, e.g. surface area and length estimations. On two-dimensional (2D) sections, the surface area of a structure is reduced to a structure boundary and, because it is not efficient (in terms of workload) to trace the whole boundary, we count intersections between test lines [10].
In the MRI field, stereology has proven itself to be highly efficient [11–13]. Roberts et al [14] used stereology to measure brain tumours, whereas Fernández-Viadero et al [15] found stereology to be an efficient and objective tool with which to obtain brain volumes in elders with dementia. The authors concluded that stereology should assist in diagnostic and follow-up evaluation of the disease. Joe et al [16] found stereology to be superior to ellipsoid-based measurements, with higher interobserver reliability, in a study of uterine volumetry using MRI, whereas Bendel et al [17] used stereology to investigate temporomesial volume loss in subarachnoid haemorrhage patients. They found atrophy in temporomesial structures following subarachnoid haemorrhage; however, they did not report any volumetric measurements, only a percentage increase/decrease after correction for head size. Keller et al [18] used stereology to estimate asymmetry in Boca's area on MR images. The precision of quantitative MRI has been assessed in vivo in only a few studies. Jelsing et al [19] estimated pig brain volumes in vivo using MRI and the corresponding volumes in vitro. The authors demonstrated that it is possible to obtain consistent estimates of brain volumes using MRI and stereology for in vivo quantitative analysis. However, they found that the accuracy of MRI volumetry was extremely sensitive to the variable interpretation of grey/white matter intensity. Therefore, differences in observer interpretation should always be taken into account in quantitative studies, whether based on CT or MRI.
The aim of the present study was to demonstrate the feasibility of stereological quantification on medical images from patients with severe head injury, which enables estimates of geometric quantities to be obtained with a moderate workload. Brain parameters and volumes from imaging (MR) are usually estimated using automated segmentation methods. However, these methods require standardisation or normalisation of brain images. Brain tissue suffering from severe head injury is very inhomogeneous (i.e. the signal intensity and contrast), and can therefore usually not be standardised. Another widely used technique for quantifying volumes from medical images is the region of interest (ROI), whereby the ROI is drawn manually. Depending on the structure of interest, this may be time-consuming and thus not as efficient as stereology. Hence, we applied stereological methods for measuring volumes in several regions of the affected brains, and validated the use of stereology in head injury imaging. Before the volume estimation in patients with head injury, we applied both stereological and ROI techniques to an MRI phantom with known volumes and surfaces for comparison of efficiency in terms of workload and precision.
Methods and materials
The brain scans used in this study were derived from a large database collected by the Co-operative Study on Brain Injury Depolarizations (COSBID), a multicentre study of acute brain injury in humans. Five subjects were chosen with a primary diagnosis of aneurysmal subarachnoid haemorrhage, especially selected to represent the high degree of variation in the amount of damaged tissue. Images from acute CT and both subacute and follow-up T1 weighted MRI at different stages were included for all five cases (see Table 1 for scanning information). Imaging was performed at different centres and hence with different scanners. Before the analysis of images from human subjects, images from an MR phantom (T1 weighted MR) (Figure 1a) with known volume were used to test the precision of the estimates. The phantom consisted of Magphan spherical phantoms (Magphan® EMR051; The Phantom Laboratory, Salem, NY) with spherical structures of diameter 1 cm, 1.5 cm, 3 cm, 6 cm and 20 cm. In total, there were 158 structures of 1 cm in diameter, 2 structures of 1.5 cm in diameter, 4 structures of 3 cm in diameter, and a single structure of each 6 cm and 20 cm in diameter. In contrast to the variability in the estimates of the phantom, the precision of the estimates on the different subdivisions of the traumatised brain is a product of both the variability of the stereological estimates and the quality of the scans.
Table 1. Scanning parameters.
| Patient | Day | Scanner mode | Sequence | Scanner type | Voxel dimensions (mm3) |
| 1 | 5 | CT | GE Lightspeed Pro 16 | 0.49×0.49×5.00 | |
| 15 | MR | 3D T1 | Philips 1.5T | 0.45×0.45×6.00 | |
| 2 | 4 | CT | GE Lightspeed 4 slice | 0.43×0.43×7.00 | |
| 59 | MR | 3D T1 | GE Signa Horizon 1.5T | 0.47×0.47×7.50 | |
| 3 | 5 | CT | Lightspeed 16 | 0.45×0.45×10.00 | |
| 459 | MR | 3D T1 | Signa Excite 1.5T | 1.10×1.10×1.10 | |
| 4 | 4 | CT | GE Lightspeed 4 slice | 0.43×0.43×7.50 | |
| 21 | MR | 3D T1 | GE Signa Horizon 1.5T | 0.45×0.45×7.50 | |
| 5 | 1 | CT | GE Lightspeed 4 slice | 0.43×0.43×7.50 | |
| 17 | MR | 3D T1 | GE Signa Horizon 1.5T | 0.47×0.47×7.50 | |
| Phantom | MR | 3D MPRAGE | Siemens 3T | 1.31×1.31×1.5 |
3D, three-dimensional. MPRAGE, magnetisation prepared rapid acquisition gradient echo.
Figure 1.
MR phantom estimation. Five objects of different diameter are shown in (a). Purple = 20 cm diameter; green = 6 cm diameter; red = 3 cm diameter; yellow = 1.5 cm diameter, and turquoise = 1 cm diameter. (b) Point counting grids with difference area per point for volume estimation. This is an example for the phantom 1 cm in diameter. (c) As the phantoms are spherical and isotropic, perpendicular test lines were used to estimate surface. Only red lines intersect with the surface. This is an example for a phantom 6 cm in diameter.
The Cavalieri estimator
Over each set of CT/MR scanning images, a counting grid was placed at random over a sub-sampled set of images, approximately 10 per specimen. All volumes were estimated from Cavalieri's principle [9] (modified in [20]):
 |
(1) |
where V is the total volume of each brain compartment, t is the distance between scan planes, a(p) is equal to a predetermined, known and constant area per point (distance between points) (mm2), and σP is the number of points hitting the compartment.
Surface areas were estimated from the following equation:
 |
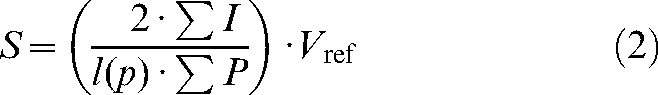(2) |
where S is total surface area of the structure, Vref is the reference volume (neocortex or phantom), σI is the total number of intersections of a testline and the structure (pial surface of neocortex or phantom border), l(p) is the test line length per point, and σP is the total number of the points hitting the structure (neocortex or phantom).
When combining Equations 1 and 2 this simplifies to:
 |
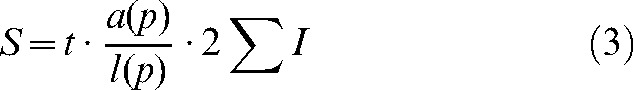(3) |
when the area and volume are known.
The average neocortical thickness can be calculated from:
 |
(4) |
The above equation assumes that the pial surface is isotropic. The test lines used for the estimation of the surface area were 2D isotropic, uniform, random (IUR) straight test lines. The estimator of pial surface area, as opposed to the other stereological techniques used in this study, is thus not based strictly on unbiased principles because the brains were sliced in parallel frontal slices. The actual bias in the estimates of the highly convoluted pial surface area is, however, too small to be detected [21]. A sampling scheme involving 150–200 point counts in approximately 10 sections has been shown previously to provide a coefficient of error (CE) of ∼6–8% [22] (see also section on error prediction below).
Pre-processing and volume estimation of CT and MRI data
All data analysis was done using the general-purpose image analysis software RIP (available on request) programmed in MATLAB (Mathworks Inc, Natick, MA USA). By means of RIP, the stereological probes (points and test lines) were superimposed upon the CT or MR sections. The images were displayed using consistent image and display levels on a monitor with fixed hardware contrast settings. The RIP software, however, allows user subjectivity to determine contrast and magnification parameters when assessing difficult border points and test lines. Before any stereological measurements were made, a Cavalieri sample was extracted from the complete set, and grids of systematically spaced points were placed over the 2D set of images by the RIP program. Grid points were displayed point by point.
The analysis of phantom volume based on ROIs was also performed in RIP by adjusting an intensity threshold level and manually selecting objects in three-dimensional (3D) space, corresponding to each phantom structure. From this inclusion criterion, the number of voxels was found, and volume could be calculated as voxels multiplied by voxel dimensions.
MR phantom
See Table 1 for the scanning parameters. The stereological volume estimator was obtained for the different phantoms using different point counting grids for different phantom diameters, aiming to obtain an average of ∼150–200 points hitting the phantom structure. As an example, for a phantom diameter of 1 cm, a 4 × 4 voxel grid was chosen, resulting in a grid point spacing of 5.3 mm × 5.3 mm (4 × 1.3 mm and 4 × 1.3 mm) (Figure 1b). For each phantom, there was a different number of images in the Cavalieri sample. The mean number of images per Cavalieri sample was 13.7, ensuring 10–12 sections for each phantom, and the mean number of total points counted was 162 (range, 111–212). Two estimates were made for each diameter by the same observer (intraobserver), whereas a second observer provided a separate set of estimates (interobserver). Surface area was estimated using a grid with test lines on the scanning images and then counting all intersections with lines and the outer border of the phantom surface. As the MR phantoms were spherical, isotropic perpendicular test lines were used to ensure the maximum effect of point counting (Figure 1c). There was no training of observers for the phantom study, but the same Cavalieri sample and point grid spacing was used for all estimates.
Human subjects
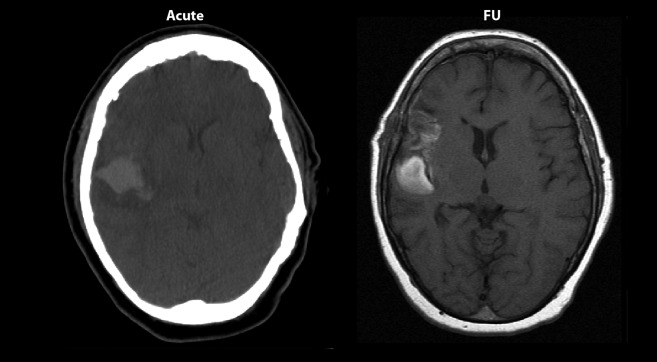
As this is an international collaboration project, different scanners were used for the five patients (see Table 1 for scanning parameters). This was done so that the contribution of variance that comes from using different scanners with different contrast is included in the variance of the estimates in this study. A random start position of the first section was ensured by the random position of the patient in the scanner. The mean number of images per Cavalieri sample was 10.9, ensuring 10–12 sections for each brain compartment volume, except when pathological changes were occasionally present on a lower number of sections, in which case at least 5 images were always included. All scanning sets in which it was possible to identify pathological changes were subdivided into “unaffected tissue”, “lesion” and “haemorrhage”. For both CT and MRI, unaffected tissue was defined as tissue that appeared free of damage. Lesion was defined as affected tissue that appeared darker than unaffected tissue. Haematoma was defined as clear white profiles within the cerebrum. Intraventricular haemorrhage was not included. The subdivisions (unaffected, lesion and haematoma) were categorised into two stages: acute and follow-up. An example is given in Figure 2.
Figure 2.
Scanning image examples. Acute (CT) and follow-up (FU) (MR) scanning images from Patient 2.
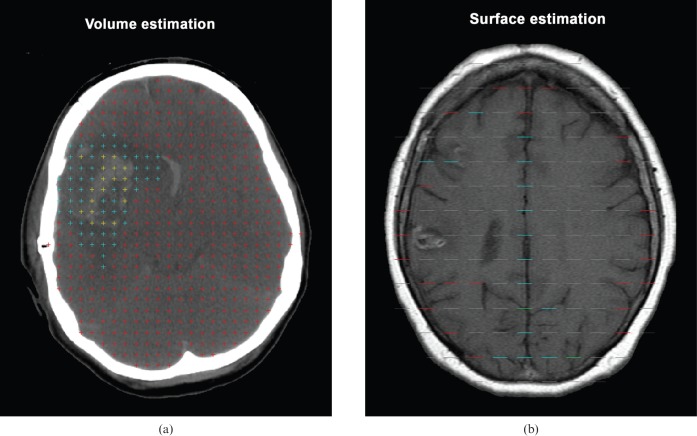
Grid points were displayed point by point and for each point assigned to specific brain compartments by means of different colour codes, aiming for an average of 150 points in total hitting the smallest region (Figure 3a). Owing to the variation in size of the pathological changes from patient to patient, the point spacing was optimised for each patient. As an example, for Patient 2, an 11 × 11 voxel grid was chosen, resulting in a grid point spacing of 5.2 mm × 5.2 mm (11 × 0.47 mm and 11 × 0.47 mm). The surface area was estimated using grids with test lines on the scanning images and counting all intersections with lines and the outer border of the neocortex (Figure 3b). The surface area and neocortical thickness could be obtained only from MR scans, as it was not possible to distinguish between grey and white matter on CT scans. Training of the two observers was required to obtain agreement with the definition of the different tissue division (i.e. unaffected tissue, lesion and haematoma).
Figure 3.
Stereological grids. (a) Points used for volume estimation (Cavalieri's method). All brains were divided into unaffected tissue (red), lesion (turquoise) and haematoma (yellow) and were counted simultaneously. (b) Test lines used for surface estimation. All intersections between the borders of neocortical matter and the test line were counted. Red = one intersection; turquoise = two intersections; and green = three intersections. It was assumed that there was isotropy.
Computer-simulated stereology
Computer simulations of different brain compartments were made using the BrainWeb (see http:\\www.bic.mni.mcgill.ca\brainweb\anatomic_normal.html) anatomical brain model to show the number of total points needed to obtain reliable estimates. The brain compartments were grey matter, white matter, cerebrospinal fluid and total intracranial volume. A probabilistic map of each compartment was downloaded from BrainWeb, and automated point counting was performed using a code developed in MatLab (MathWorks Inc). An in-plane point spacing, varying between 1 mm and 30 mm, and 10 slices equally spaced over the entire brain were used. All possible in-plane grid positions and 10 starting slice positions were tested, enabling the calculation of a coefficient of variation (CV; see below) for each grid density. In total, approximately 42 000 separate counts were performed. Points were assigned to a given compartment if the BrainWeb probability for that compartment was more than 50, and the total volume was calculated according to Equation 1. The intracranial volume was defined as the sum of probability images for grey and white matter and cerebrospinal fluid.
Error prediction
The precision of the estimate of the total volume from a single systematic sample [P1, P2,… Pn] is not a trivial problem because the observations are, in general, not independent [23, 24]. This theory has been adapted to stereology [9, 25]. The error predictor was estimated as the CE [20, 26]. In short, CE was calculated as a function of the so-called “noise effect”, also known as the point counting variance, and the SURS variance for sums of areas, σa [20]. The noise effect is the uncertainty in the estimate that comes from point counting:
 |
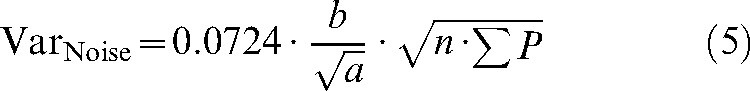(5) |
where 0.0724 is a constant, n is the number of sections, b/√a is the average profile shape (see nomogram [5]), and σP is the number of points counted in total for a given object over all slices. Using the nomogram, b/√a is set to 3 for the spherical MR phantom, 35 for unaffected tissue, and 9 for lesions and haematoma. The SURS variance arises from the fact that repeated estimates based on different sets of sections will vary as a consequence of the different sum of areas in the different sections:
 |
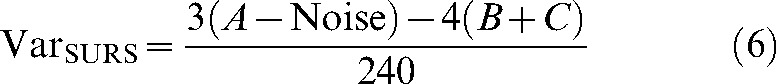(6) |
where
 |
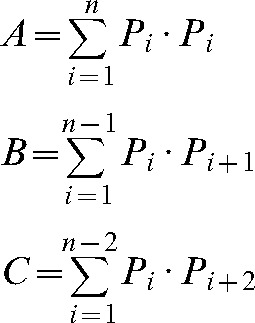Pi is the number of points counted for the object in the ith slice and n is the number of slices. CE(σP) is the total sampling variance and is calculated as:
 |
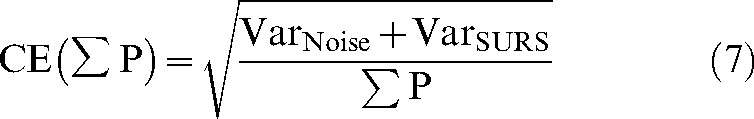(7) |
For biological structures, the sampling is considered optimal when CE is about half the total CV, as CV2 = CV2biological + CV2observer + CEestimated [9]. For non-biological structures such as an MR phantom, CVbiological is zero.
Two different approaches were taken to test the precision of the method: (i) the intra-observer variability following volume estimates performed by a single observer; and (ii) the interobserver variability of volume estimates from two different observers. The variability is measured as the within-subject standard deviation, σw, and found as σw2, the within-subject variance:
 |
(8) |
where G is the number of subjects and d is the difference between two subsequent measurements. The empirical CV was calculated as:
 |
(9) |
where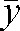 
is the mean of the two measurements.
The difference between estimated and geometrically calculated values in phantom estimation was described as:
 |
(10) |
Results
Phantom measurements
Volume and surface estimation in the MR phantom of five different objects are shown in Table 2. Two different approaches were performed for estimating the volume of the phantoms: Cavalieri's method and the ROI.
Table 2. Intra- and interobserver variability for the MR phantom.
| Diameter (cm) | ||||||
| 1.0 | 1.5 | 3.0 | 6.0 | 20.0 | ||
| Geometric volume | 82.7 | 3.50 | 56.6 | 113 | 4189 | |
| Cavalieri volume | ||||||
| Observer 1 | 1 | 83.5 | 3.3 | 57.4 | 109 | 3898 |
| 2 | 88.7 | 3 | 53.3 | 112 | 3642 | |
| CE (intra) | 1.90 | 2.23 | 2.75 | 2.36 | 1.13 | |
| CV (intra) | 4.27 | 6.73 | 5.24 | 1.92 | 4.80 | |
| Average deviation | 3.95 | −11.11 | −2.26 | −2.26 | −11.11 | |
| Observer 2 | 83.8 | 3.19 | 57.2 | 120 | 4014 | |
| CE (inter) | 0.90 | 2.31 | 1.03 | 1.81 | 2.36 | |
| CV (inter) | 0.25 | 2.40 | 0.25 | 6.79 | 2.13 | |
| ROI volume | ||||||
| Observer 1 | 1 | 97.9 | 3.80 | 58.7 | 103 | 4168 |
| 2 | 95.4 | 3.55 | 60.9 | 104 | 4249 | |
| CV (intra) | 1.85 | 4.98 | 2.55 | 0.68 | 1.35 | |
| Average deviation | 14.4 | 4.76 | 5.35 | −9.18 | 0.46 | |
| Observer 2 | 94 | 3.64 | 65.3 | 116 | 4948 | |
| CV (inter) | 2.87 | 3.04 | 7.53 | 8.39 | 12.1 | |
| Geometric surface area | 496 | 14.1 | 113 | 113 | 1257 | |
| Surface | ||||||
| Observer 1 | 1 | 512 | 14.7 | 105 | 101 | 1221 |
| 2 | 567 | 15.2 | 111 | 108 | 1116 | |
| CE (intra) | 1.58 | 3.84 | 2.03 | 2.03 | 1.84 | |
| CV (intra) | 7.21 | 2.36 | 3.93 | 4.74 | 6.35 | |
| Average deviation | 8.06 | 5.69 | −4.63 | −8.13 | −7.57 | |
| Observer 2 | 547 | 15.1 | 96.8 | 98.1 | 1258 | |
| CE (inter) | 2.36 | 2.80 | 1.75 | 1.43 | 2.80 | |
| CV (inter) | 4.49 | 1.87 | 5.98 | 2.13 | 2.08 | |
Volume is in measured in cm3 and was found using Equation 1; surface area is measured in cm2 and found using Equation 2. CE is calculated using Equation 7. CV is calculated using Equation 9. Average deviation is calculated using Equation 10.
CE, coefficient of error; CV, coefficient of variation; CE (intra), mean CE for Observer 1; CE (inter), mean CE for both observers; CV (intra), intraobserver variability, the variance for the two estimates made by Observer 1; CV (inter), interobserver variability (Observer 1 against Observer 2) using the first estimate from Observer 1 and the estimate from Observer 2.
Reliability of measurements
Reliability expressed as the intra- and interobserver CV can be found in Table 2. For Cavalieri's method, intra- and interobserver variability was about the same, whereas interobserver variability was higher for ROI measurements. Intraobserver variability for surface estimation was lower than interobserver variability.
Validity of measurements
Both the volumes and surfaces of the phantoms were known before scanning and are shown as geometric values in Table 2. The table shows that the ROI method shows a higher average deviation from geometric values than had Cavalieri's; however, the deviations varied considerably. Deviation did not vary as much for surface estimation.
Measurements of human pathological changes
The volume estimates, as well as the variation in the pathological changes, can be seen in Table 3. These values show that the size of the damaged areas is variable (inhomogeneous). Taking Patient 2 as an example (follow-up taken 3 months post ictus), it can be seen from the table that the lesion had a volume of 37.8 cm3 on acute CT, whereas it was 24 cm3 in the follow-up scan. Haematoma volume was about the same in the acute (18.2 cm3) as the follow-up stage (19.6 cm3). The mean thickness of cortex was between 2.07 mm and 2.61 mm in these five brains.
Table 3. Intra- and interobserver variability for patient subjects.
| Patient no. | |||||||
| 1 | 2 | 3 | 4 | 5 | |||
| CT | |||||||
| Unaffected tissue volume | Observer 1 | 1 | 1134 | 1129 | 1027 | 959 | 731 |
| 2 | 1114 | 1063 | 1019 | 943 | 726 | ||
| CE | 1.27 | 0.56 | 0.57 | 1.78 | 1.17 | ||
| CV (intra) | 4.77 | ||||||
| Observer 2 | 1 | 1233 | 1225 | 1037 | 968 | 779 | |
| CE | 0.76 | 0.59 | 0.56 | 1.31 | 1.51 | ||
| CV (inter) | 10.5 | ||||||
| Lesion volume | Observer 1 | 1 | 102 | 37.8 | 19.4 | 30.4 | 43.1 |
| 2 | 94.9 | 41.5 | 18.2 | 31.2 | 41.5 | ||
| CE | 1.47 | 2.48 | 3.57 | 1.27 | 1.14 | ||
| CV (intra) | 4.79 | ||||||
| Observer 2 | 97.8 | 39.7 | 18.3 | 25.7 | 45 | ||
| CE | 1.51 | 2.60 | 3.21 | 5.64 | 3.88 | ||
| CV(inter) | 5.51 | ||||||
| Haematoma volume | Observer 1 | 1 | 33.9 | 18.2 | 10.2 | 5.62 | 5.93 |
| 2 | 36.5 | 19.5 | 11.4 | 6.03 | 6.86 | ||
| CE | 3.16 | 3.33 | 4.64 | 9.97 | 7.83 | ||
| CV (intra) | 7.06 | ||||||
| Observer 2 | 35.7 | 18.9 | 10.8 | 4.89 | 5.3 | ||
| CE | 3.44 | 2.96 | 4.76 | 1.88 | 1.84 | ||
| CV(inter) | 4.75 | ||||||
| MR | |||||||
| Unaffected tissue volume | Observer 1 | 1 | 1034 | 931 | 860 | 944 | 924 |
| 2 | 1008 | 902 | 847 | 939 | 898 | ||
| CE | 2.57 | 0.43 | 3.16 | 1.99 | 1.58 | ||
| CV (intra) | 4.35 | ||||||
| Observer 2 | 1004 | 1001 | 897 | 984 | 965 | ||
| CE | 0.90 | 1.10 | 0.32 | 1.22 | 1.41 | ||
| CV (inter) | 6.76 | ||||||
| Lesion volume | Observer 1 | 1 | 167 | 24 | 81,6 | 53.9 | 26.4 |
| 2 | 175 | 25.1 | 87.3 | 56.9 | 29.7 | ||
| CE | 3.58 | 2.47 | 3.57 | 7.85 | 8.95 | ||
| CV (intra) | 11.9 | ||||||
| Observer 2 | 160 | 27.7 | 85.3 | 50.4 | 18.6 | ||
| CE | 2.26 | 3.37 | 4.75 | 4.63 | 3.84 | ||
| CV (inter) | 6.4 | ||||||
| Haematoma volume | Observer 1 | 1 | 60.2 | 19.6 | – | 31.4 | 5.57 |
| 2 | 63 | 20.5 | – | 33.4 | 5.2 | ||
| CE | 7.18 | 6.39 | – | 6.41 | 4.07 | ||
| CV (intra) | 7.29 | ||||||
| Observer 2 | 70.7 | 20.3 | – | 30.4 | 4.08 | ||
| CE | 3.78 | 4.47 | – | 3.15 | 2.56 | ||
| CV(inter) | 7.02 | ||||||
| Surface | Observer 1 | 1 | 1651 | 1650 | 1418 | 2256 | 1639 |
| 2 | 1694 | 1566 | 1326 | 2063 | 1750 | ||
| CE | 3.80 | 3.76 | 4.04 | 6.25 | 7.21 | ||
| CV (intra) | 5.16 | ||||||
| Observer 2 | 1673 | 1608 | 1372 | 2140 | 1983 | ||
| CE | 2.19 | 1.94 | 0.84 | 3.71 | 3.87 | ||
| CV (inter) | 8.85 | ||||||
| Cortical thickness | Observer 1 | 1 | 2.41 | 2.44 | 2.35 | 2.07 | 2.61 |
| 2 | 2.43 | 2.57 | 2.51 | 2.27 | 2.44 | ||
| CV(intra) | 5.76 | ||||||
| Observer 2 | 2.42 | 2.5 | 2.43 | 2.19 | 2.16 | ||
| CV(inter) | 3.12 | ||||||
Volume is measured in cm3 and was found using Equation 1; surface is measured in cm2 and found using Equation 2; and cortical thickness is measured in mm and found according to Equation 4. CV is calculated using Equation 9.
CE, the mean coefficient of error for both observers; CV, coefficient of variation; CV (intra), the intraobserver variability, the variance for the two estimates made by Observer 1; CV (inter), the interobserver variability (Observer 1 against Observer 2) using the first estimate from Observer 1 and the estimate from Observer 2.
Reliability of measurements
Both intra- and interobserver variability for the patient subjects are shown in Table 3. There was no large difference between the CV of volume estimates for CT and MR in the unaffected tissue, but interobserver variability was higher than intrao-bserver variability. For lesions, interobserver variability was higher than intraobserver variability in CT images, whereas the opposite was the case for MR images.
Intraobserver haematoma variability was highest on both CT and MR estimations. For surface estimation, the highest variability was seen between observers (interobserver variability), whereas the intraobserver variability was highest for cortical thickness.
Variance of repeated estimates on computer simulation
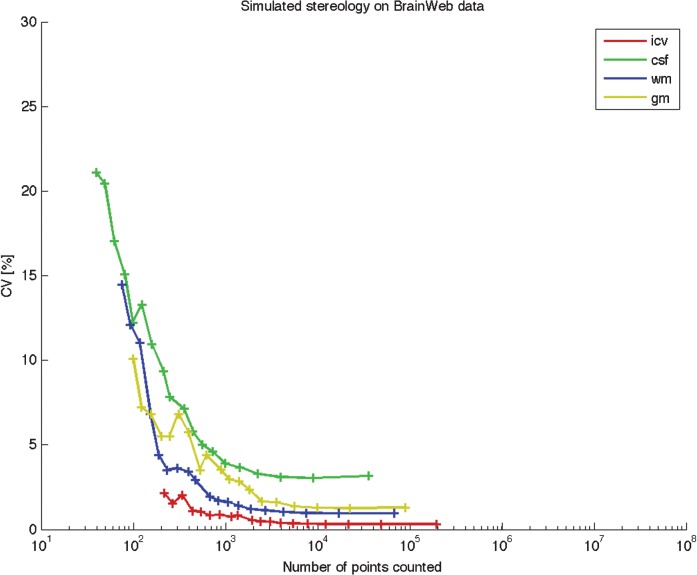
Figure 4 shows the CV of repeated estimates as a function of the total number of points hitting each compartment. For white matter and intracranial volume, the variance of repeated estimates lies below 5% when 200 points are counted. More counted points are required for grey matter and cerebrospinal fluid to gain a variance below 5%.
Figure 4.
Simulated stereology on BrainWeb data. Automated point counting was performed of different brain compartments using the BrainWeb anatomical brain model. All possible grid positions and 10 starting slice positions were tested using an in-plane point spacing varying between 1 mm and 30 mm, and 10 slices equally spaced over the entire brain. Points were assigned to a given compartment if the BrainWeb probability for that compartment was more than 50. The total volume for each compartment was calculated using Equation 1, and CV for each grid density was calculated according to Equation 9. gm, grey matter; wm, white matter; csf, cerebrospinal fluid; icv, total intracranial volume.
Discussion
Fully automatic methods may be a desirable goal in future studies to reduce subjectivity and to increase precision in terms of re-test reliability [27, 28]. However, when measuring structural changes in brain tissue that displays patient-specific and uneven changes (i.e. subarachnoid haemorrhagic lesions), no automatic methods can yet replace the individual observer.
We found that the Cavalieri method showed good reliability for phantom estimation (CV<7%), whereas the validity (average deviation) of the phantom estimates was below 4%; however, two estimates (1.5 cm and 20 cm in diameter) varied by 10% from the geometric value. Reliability of the ROI method was below 7% and validity below 9.5%; however, one estimate varied by 12% from the geometric value. For surface estimation, CV was below 7.5% and the average deviation was below 8.5%. This part of the study shows the reliability from the observers' estimate to the true geometric value. For the patients, there is, of course, no true geometric value of the different tissue volumes, only the observers' estimates. Hence, the phantom study was performed to show the reproducibility of the method.
The reliability of the measurements on patients showed that the intra-observer variability for two repeated measures on the five patients showed a variation below 7% for CT and 10% for MRI. The interobserver variability between two different observers showed a higher variance of 12% for CT and approximately the same for MR (≤8%). This is considered acceptable considering the inhomogeneity of the damaged tissue. Therefore, we conclude that the reliability test shows that the method is accurate, and that it is possible to obtain reliable and consistent estimates of brain volumes and surfaces using stereology on both CT and MR scanning images. For the individual subdivisions, there was no clear picture of whether intra- or interobserver variability was highest, or on which scanning modality (CT or MR). This is probably due to the low sample size (n = 5).
Stereological efficiency
The advantages of the stereological tools include adjustment of the precision required for each specific study, limiting the workload to a necessary minimum. The investigator, not a computer, makes the decision about which point to include and which to exclude. The method is easy to implement, and the measurements provided by the standard software can be tested and thus evaluated by the investigators. Compared with the prevalent semi-quantitative methods for brain parameter and volume estimation, stereology is indifferent to shape and homogeneity. Conversely, usual methods such as voxel-based morphometry require standardisation or normalisation of brain images and cannot, in a meaningful way, be applied to images of brain suffering from severe head trauma. The two different approaches (stereology and ROI) for estimating phantom volumes showed the same accuracy from estimations to known volumes. However, when dealing with damaged tissue, the ROI method cannot be used semi-automatically, as used in this study in the spherical phantoms. The observer would have to manually draw ROIs on all image slices, which would be very time consuming.
Stereology is an effective tool with which to estimate lesions in these patients, as an individual design can be performed for each brain.
Precision
As there is a high biological variation in brain tissue, particularly following brain injury, sampling is considered optimal when CE is about half of the CV [9]. Choice of grid size depends on both the desired precision as well as the efficiency of the point counting. For the volume estimation on patients, we have included estimations based on counting from 150 points upwards. As previously mentioned in a number of stereological papers, a sampling scheme involving 100–200 counts on approximately 10 sections provides a precision with a CE of 6–8% [29, 22]. For the patients, we chose to estimate the three subdivisions simultaneously. This sometimes resulted in counting more than 150–200 points over each individual region, thus obtaining estimates with CEs lower than 6%. However, by quantifying the subdivisions at the same time, the observer assigned each point to a certain subdivision, and hence eliminated the risk of assigning the same point to two different subdivisions. Figure 4 shows that it does not pay to count more than about 200 points, as the variance of the repeated estimates does not decrease with increasing point counts. For a section spacing of 10 mm, the variance is stable from about 2000 points and above, and seems to be determined by the section to section difference in the object.
Average cortical thickness has previously been reported to be 2.69 mm on post-mortem brains [3], which is somewhat higher than the mean (2.45 mm) in this study. This could be caused by differences in the definitions of the various compartments in histology/MRI or by the small number of cases in this study.
Limitations of the study
An optimal way to detect and quantify volume loss caused by injury to the brain would include comparisons of volume on admission or, even better, before haemorrhage. Haemorrhage itself may cause several problems, as acute and sub-acute haematoma measured on CT and MR, respectively, cannot be compared. On CT, the haematoma appears bright owing to the higher CT density of the coagel than the brain tissue. On T1 weighted MRI, the appearance of the haematoma is largely determined by methaemoglobin, which is visible in the sub-acute phase and several months following, even after the haematoma on CT is long gone. However, this limitation is not important for the method, only for interpretation of results. When the haematoma is close to the skull vault, this may cause problems, as it can be difficult to determine haematoma from skull. Intraventricular haemorrhage was not included in the study, as this does not represent true haemorrhagic volume.
Other limitations are that these critically ill patients cannot always be scanned in the acute phase and that the brain parenchyma may be swollen because of cytotoxic or vasogenic oedema and hyperperfusion. This oedema could not be registered. Furthermore, there may be displacements caused by mass effect from the haematoma or hydrocephalus. Evidently, these problems must be taken into account in the evaluation of the scanning images and in the comparison of sequential volume estimates. Further limitations include resolution problems associated within CT in particularly, but also the MR images, which usually have a resolution of millimetres. Both CT- and MR-generated images are in principle a true depiction of the structure of interest, but a number of technical problems and biological restraints compromise the precision and accuracy of both scanning techniques for quantitative studies, such as the limited resolution, partial volume effect, magnetic field and radiofrequency non-uniformity, movements of the subject (including those from respiration and heart beat), variable intensity of some structures and absence of clear boundaries between different areas. All of these uncertainties are reflected directly as noise in the estimates of volume and can only be reduced by an optimisation of the technical quality of the images. If the quality of the scanning images is low because of, for example, low resolution, it should be taken into account in the point-counting procedure. There is no gain in knowledge by increasing the workload to get a very precise volume estimate from a scanning image where it is difficult to determine the various regions. For the same reason, MR images are preferred to CT images. It would have been helpful to have had multiple scans (both CT and MRI) of the same individual at the same time to determine how reliable each method is when estimated from different imaging modalities (when the lesion/tissue would be expected not to change). However, as the five patients included in this study were critically ill, it was not possible.
Furthermore, some injuries such as diffuse axonal injury will not be detected using the stereological approach, and this may cause some sort of injury volume underestimation. For diffuse axonal injury detection, diffusion tensor imaging and diffusion will be most helpful, although more time consuming.
Conclusions
In the present study, we demonstrated that it is possible to obtain estimates of both different-sized MR phantoms, as well as small compartments of severe brain injury, using a combination of medical imaging and stereology for in vivo quantitative analysis. Stereology is an alternative tool with a quantitative structural basis for the evaluation of severe brain injury on scanning images when other semi-automated volume estimation methods are not applicable. It is also a fast and efficient way to estimate volume. This may help in future studies to optimise treatment and benefit the outcome of patients suffering from severe brain trauma.
Footnotes
Funding: Copenhagen University Hospital Bispebjerg; Aase and Ejnar Danielsen's Foundation; The Dagmar Marshall Foundation; and Agnes and Poul Friis' Foundation
References
- 1.Regeur L, Pakkenberg B. Optimizing sampling designs for volume measurements of components of human brain using a stereological method. J Microsc 1989;155:113–21 [DOI] [PubMed] [Google Scholar]
- 2.Andersen BB, Korbo L, Pakkenberg B. A quantitative study of the human cerebellum with unbiased stereological techniques. J Comp Neurol 1992;326:549–60 [DOI] [PubMed] [Google Scholar]
- 3.Pakkenberg B, Gundersen HJG. Neocortical neuron number in humans: effect of sex and age. J Comp Neurol 1997;384:312–20 [PubMed] [Google Scholar]
- 4.Korbo L, West M. No loss of hippocampal neurons in AIDS patients. Acta Neuropathol (Berl) 2000;99:529–33 [DOI] [PubMed] [Google Scholar]
- 5.Mayhew TM, Mwamengele GL, Dantzer V. Comparative morphometry of the mammalian brain: estimates of cerebral volumes and cortical surface areas obtained from macroscopic slices. J Anat 1990;172:191–200 [PMC free article] [PubMed] [Google Scholar]
- 6.Mayhew TM, Mwamengele GL, Dantzer V. Stereological and allometric studies on mammalian cerebral cortex with implications for medical brain imaging. J Anat 1996;189:177–84 [PMC free article] [PubMed] [Google Scholar]
- 7.Holm IE, West MJ. Hippocampus of the domestic pig: a stereological study of the subdivisional volumes and neuron numbers. Hippocampus 1994;4:115–26 [DOI] [PubMed] [Google Scholar]
- 8.Gundersen HJG. The smooth fractionator. J Microsc 2002;207:191–210 [DOI] [PubMed] [Google Scholar]
- 9.Gundersen HJG, Jensen EB. The efficiency of systematic sampling in stereology and its prediction. J Microsc 1987;147:229–63 [DOI] [PubMed] [Google Scholar]
- 10.Baddeley AJ, Gundersen HJG, Cruz-Orive LM. Estimation of surface area from vertical sections. J Microsc 1986;142:259–76 [DOI] [PubMed] [Google Scholar]
- 11.Roberts N, Gardern A, Cruz-Orive L, Reid N, Whitehouse G, Edwards R. Estimation of fetal volume by magnetic resonance imaging and stereology. J Microsc 1994;171:239–55 [DOI] [PubMed] [Google Scholar]
- 12.Ronan L, Doherty CP, Delanty N, Thornton J, Fitzsimons M. Quantitative MRI: a reliable protocol for measurements of cerebral gyrification using stereology. J Magn Reson Imaging 2006;24:265–72 [DOI] [PubMed] [Google Scholar]
- 13.Karstoft K, Lødrup AB, Dissing TH, Sørensen TS, Nyengaard JR, Pedersen M. Different strategies for MRI measurements of renal cortical volume. J Magn Reson Imaging 2007;26:1564–71 [DOI] [PubMed] [Google Scholar]
- 14.Roberts N, Puddephat MJ, McMulty V. The benefit of stereology for quantitative radiology. Br J Radiol 2000;73:679–97 [DOI] [PubMed] [Google Scholar]
- 15.Fernández-Viadero C, González-Mandly A, Verduga R, Crespo D, Cruz-Orive LM. Stereology as a tool to estimate brain volume and cortical atrophy in elders with dementia. Rev Esp Geriatr Gerontol 2008;43:32–43 [DOI] [PubMed] [Google Scholar]
- 16.Joe BN, Suh J, Hildebold CF, Hovsepian DM, Johnston B, Bae KT. MR volumetric measurements of the myomatous uterus: improved reliability of stereology over linear measurements. Acad Radiol 2007;14:455–62 [DOI] [PubMed] [Google Scholar]
- 17.Bendel P, Koivisto M, Hänninen T, Kolehmainen A, Könönen M, Hurskainen H, et al. Subarachnoid hemorrhage is followed by temporomesial volume loss. MRI volumetric study. Neurology 2006;67:575–82 [DOI] [PubMed] [Google Scholar]
- 18.Keller SS, Highley JR, Garcia-Finana M, Sluming V, Rezaie R, Roberts N. Sulcal variability, stereological measurement and asymmetry of Broca's area on MR images. J Anat 2007;211:534–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jelsing J, Rostrup E, Markenroth K, Paulson OB, Gundersen HJG, Hemmingsen R, et al. Assesment of in vivo MR imaging compared to physical sections in vitro — a quantitative study of brain volumes using stereology. NeuroImage 2005;26:57–65 [DOI] [PubMed] [Google Scholar]
- 20.Gundersen HJG, Jensen EB, Kiêv K, Nielsen J. The efficiency of systematic sampling in stereology - reconsidered. J Microsc 1999;193:199–211 [DOI] [PubMed] [Google Scholar]
- 21.Øster S, Christoffersen P, Gundersen HJG, Nielsen JO, Pakkenberg B, Pedersen C. Cerebral atrophy in AIDS: a stereological study. Acta Neuropathol (Berl) 1993;85:617–22 [DOI] [PubMed] [Google Scholar]
- 22.West MJ. Stereological precision and bias. Trends Neurosci 1999;22:51–61 [DOI] [PubMed] [Google Scholar]
- 23.Matheron G. Les variables régionalisées et leur estimation. Masson et cie, Paris, France: 1965. [Google Scholar]
- 24.Matheron G. The theory of regionalized variables and its applications. Les Cahiers du Centre de Morphologie Mathématique de Fontainebleau no. 5. 1971 Paris School of Mines Publication, Paris, France. [Google Scholar]
- 25.Cruz-Orive LM. On the precision of systematic sampling: a review of Matheron's transitive methods. J Microsc 1989;153:315–33 [Google Scholar]
- 26.Kiêu K, Souchet S, Istas J. Precision of systematic sampling and transitive methods. J Statist Plan Inf 1999;77:263–79 [Google Scholar]
- 27.Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA 2000;97:11050–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Eskildsen SF, østergaard LR. Active surface approach for extraction of the human cerebral cortex from MRI. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv 2006;9:823–30 [PubMed] [Google Scholar]
- 29.Gundersen HJG. Stereology of arbitrary particles. A review of unbiased numbers and the size of estimators and the presentation of some new ones. In memory of William R. Thompson. J Microsc 1986;143:3–45 [PubMed] [Google Scholar]