The apparent increase in the β-parameter of the linear quadratic model with increased linear energy transfer during fast neutron irradiation

Abstract

The issue of whether the β-parameter of the linear quadratic model changes with linear energy transfer (LET) remains controversial. Retrospective analysis of UK fast neutron experimental data using human cell lines at Clatterbridge shows that the β-parameter of the linear quadratic model probably does increase with LET during neutron irradiation. For cells without a deficiency in DNA damage repair and for experiments in which β-parameter estimates were considered to be unreliably low, a provisional relationship of β_H = 1.82 β_L was found (where the suffixes refer to high and low LET exposures, respectively). This implies that √β increases by around 1.35 in the specific case of 62.5 MeV neutrons relative to 4 MeV X-rays. Increments in the β-parameter with LET influence the relative biological effect (RBE), especially at high doses per fraction. Large fractions are being used in experimental carbon ion therapy, in which broadly similar RBE values to fast neutrons are found. These interesting findings after fast neutron exposure need to be studied further for applications in charged particle beam therapy using light ions, which is presently undergoing a worldwide expansion.

Charged particle radiotherapy offers considerable promise because of the excellent dose distribution achieved owing to the Bragg peak effect [1–4]. However, it is important to take into account the relative biological effect (RBE) when the ionisation events at the microscopic level are especially close, i.e. if the linear energy transfer (LET) is high compared with the megavoltage X-rays.

RBE is defined as the ratio of dose of a test radiation to a control radiation, such as cobalt γ-rays or megavoltage X-rays, required to achieve the same bio-effect. RBE varies with dose per fraction in radiotherapy, such that, at very low doses, RBE approaches a maximum value (R_max). This is expressed, in terms of the linear quadratic model of radiation effect, as the ratio of the α-parameters, whereas, at very high doses, it approaches R_min, the ratio of the square roots of the β-parameters (where the suffixes L and H refer to low and high LET radiation, respectively) as follows [5, 6]:

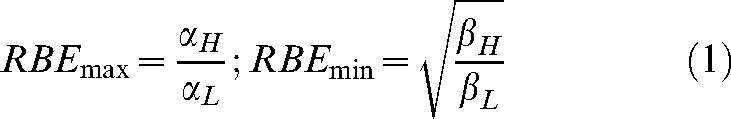(1)

At all intermediate doses per fraction, the RBE has an intermediate value between these limits.

There is some controversy regarding the theoretical prediction from microdosimetry considerations by Goodhead [7] that both α- and β-parameters increase with LET in order to fit experimental data. It is clear that the largest effect with LET is an increment in α [8]; longstanding in vivo experience has shown an increase in the α/β ratio or reduced fractionation sensitivity with the use of high-LET radiations, such as neutrons [9]. Some experiments have failed to show an increment in β with LET, e.g. Chapman et al [10, 11] showed no increase in √β with LET in plateau-arrested Chinese hamster ovary (CHO) cells. In contrast, experiments in Japan showed a probable increase in the β-parameter [12]. Further evidence from fast neutron studies in vivo has shown that, at the higher dose ranges needed for bio-effects in normal tissues, the value of RBE tends to reach an asymptotic lower (minimum) level, which exceeds unity in the higher dose range [7]. This provides an apparent justification for β increasing with LET. However, historical animal experiments can be criticised because dose cannot be increased further than certain biological limits (associated with death or severe radiation effects), and also because variations in experimental techniques, such as the use of priming doses, could influence the measured RBE.

One alternative method for investigating this enigma is to use previously published experimental data of human cell line irradiation using megavoltage X-rays and fast neutrons on the Clatterbridge cyclotron [8]. These data were used to determine α and β values and the RBE, but are amenable to further analysis.

Methods and materials

The original Clatterbridge data, consisting of 20 human cell lines irradiated separately using 62.5 MeV neutrons and 4 MeV X-rays, were re-analysed by plotting β values at low and high LET using the same scaling on the ordinate and abscissa. The null hypothesis for no difference with LET should describe a slope of gradient unity, or equal means or median values in both sets. Should β increase with LET, then the slope of the association should be described by a line with a slope significantly greater than unity. Furthermore, the mean β value should be significantly elevated at high LET vs low LET. The form of the β distributions was found to be non-gaussian, but log transformation did produce a gaussian distribution, and the paired t-test was performed on such data. A least-squares-fit program was used to provide the best linear fit to the data. Owing to the inherent difficulties in measuring β when α is large (e.g. because of a deficiency in DNA damage repair), especially in the case of repair-deficient cell lines or when experimental values are highly abnormal, the censoring of data is required. The entire data set is termed Group A. In Group B, three low values of β (<0.001 Gy⁻²) were eliminated, as well as two very high data points for which β was considered to be very large (0.77 Gy⁻² and 0.136 Gy⁻²), after neutron exposure (Figure 1). With one exception (i.e. the HX34 line, for which the increment in β was from 0.018 Gy⁻² to 0.136 Gy⁻²), the data points eliminated did have high X-ray and neutron α-parameters, which would indicate a significant deficiency in DNA damage repair. Further details of the irradiated cells are contained in the Clatterbridge publication [8].

Figure 1.

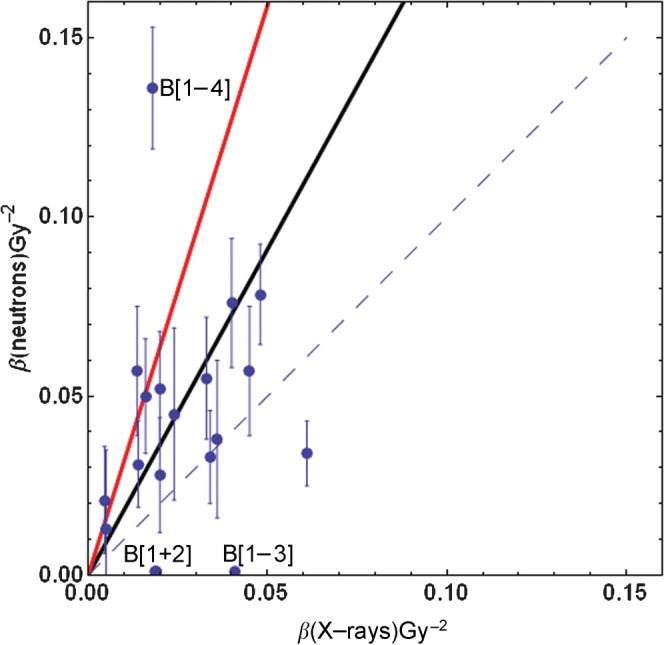
A plot of mean β values (with standard errors) for 4 MeV megavoltage X-rays and 62.5 MeV fast neutrons published by Britten et al [8]. The dashed line indicates no change (β_H = β_L); the red line is the fit for all data points (Group A); and the black line is the fit for Group B. Note that there is a superimposition of two data points in the apparent point, which has the lowermost value of β (X-rays) and is labelled B [1+2]. The censored data points for Group B are B [1–4] and one further cell line that cannot be displayed because β was 0.77 Gy⁻² for neutrons in the AT5 line. Standard errors were not measurable for the three very low β estimations points for B [1–3].

The fitted lines were calculated using the non-linear best-fit program on Mathematica (Wolfram Champaign, IL USA).

Results

Figure 1 shows the entire data set, in which there is a preponderance of points situated above the null hypothesis, which is illustrated by the dashed line. The data points that are later censored are those labelled B [1–4] and the ataxia telangiectasia cell line AT5, which had a neutron β value of 0.77 Gy⁻² (this line cannot be displayed on Figure 1 but is included in the analysis within Group A). The summary of the data analysis is presented in Table 1. The skewed nature of the β-parameter distribution is reflected in the differences between the means and the medians. Statistically significant changes are found in both groups by application of the distribution-free sign test and for Group B when the paired t-test is performed on log-transformed data. These tests are for two-tailed distributions, which consider that β could increase or decrease with LET; the probabilities can be halved for a one-tailed hypothesis, e.g. that β increases with LET.

Table 1. Results obtained for Groups A (uncensored) and B (censored) (data contained in Figure 1); the p-values are for two-tailed tests.

	Group A (n = 20)	Group B (n = 15)
Mean X-ray βL (Gy−2)	0.029	0.028
Mean neutron βH (Gy−2)	0.0789	0.075
Median X-ray βL (Gy−2)	0.022	0.024
Median neutron βH (Gy−2)	0.042	0.045
Ratio of means (βH/βL)	2.772	2.694
Ratio of medians (βH/βL)	1.886	1.875
“Best fit” linear equation (95% confidence intervals of slope parameter)	βH = 3.18 βL [1.020, 5.335]	βH = 1.82 βL [−0.410, 4.054]
Log-transformed paired t-test (two-tailed)	p>0.4	p<0.01
Sign test	p<0.05	p<0.01

Discussion

Experimental measurement of the β-parameter is difficult for several reasons. Although line fitting and non-linear regression methods can be used to provide direct estimates of the parameters from cell survival curves, such in vitro experiments are possible only over a range of survival between 1.0 and 0.0001. The α-parameter dominates the initial part of the survival curve, and α and β cell kill become equal at a dose given by the α/β ratio, which usually varies between 2 Gy and 10 Gy in most circumstances. In general, the α/β ratio increases with cellular proliferation rates. Cells with large α values will cause inaccuracies in the estimation of the β-parameter using mathematical techniques. In addition, experimental conditions that might lead to reduced colony survival, independent of the radiation received, will lower the survival fraction. This will cause a steeper slope and an enhanced curvature, especially if this source of error has occurred in experiments within the higher dose range; in this situation, β will be overestimated. The overall accuracy of survival statistics is also less reliable at the high-dose low-survival end of the survival curve because of the logarithmic scaling; thus, any source of additional error in this region could cause marked changes in the β estimate. Other methods to estimate the recovery ratio (i.e. the ratio of the survival fractions, which is related to β) include Fe Plots [6, 11] or split dose experiments. Considerable care is required to obtain accurate β-parameter values, usually measured as typical values of 0.02–0.04 Gy⁻². Some authors recommend measurement of √β in Gy, which is larger and linked to dose, rather than dose squared.

The Clatterbridge data show a statistically significant association between β_L and β_H using the sign test, and also when using the log-transformed paired t-test, after the data are censored for extreme outliers. Detailed experiments confined to one cell type might not detect a significant difference in β with LET because there is considerable variation between cell lines in the entire data set. It is also possible that some cell types do express an increment in β with LET, whereas others do not. Another interpretation would be that the magnitude of the effect may also vary between different cell lines. In addition, the effect may differ among species, owing to different chromosomal structures and numbers, so that CHO cells, as used by Chapman et al [10, 11], may not be the best model to simulate human high-LET radiation effects, despite their convenience in the laboratory.

Experimental growth conditions may also influence the estimation of the β-parameter. The Clatterbridge data set experiments were performed in logarithmic growth conditions. Different β responses are found in cells during plateau growth conditions, in which the ratio of α/β is likely to be reduced and β effects become relatively more important. The G1 arrested cells used by Chapman et al [10, 11] would have recourse to all of the available forms of DNA repair, whereas cells irradiated later in the G2 and M stages would not, and all forms of repair would be truncated by mitosis.

Further studies are warranted in this field because of the huge range of LET and RBE values encountered in particle therapy and the potential scope for errors in biological dose estimation, which far exceeds that of physical doses [13]. The approaches used in various countries are provided in detail in a recent International Commission on Radiation Units/International Atomic Energy Agency report [14], but there is little attention paid to the combined concepts of RBE_max and RBE_min, with variable RBE between these limits.

Ideally, well-designed studies using multiple human cell lines should be tested using a range of LET values, with minimal γ-ray “contamination” owing to particle collisions with other materials.

The present study suggests that, for the spectrum of LET provided by a mixed fast neutron and γ field, the β-parameter increases by a factor of around 1.7–1.9 for fast neutrons.

It must be noted that, for more specific and higher values of LET, the magnitude of change in β may differ, and so the present results should not be used to predict ion beam RBE values. The energy spectrum of the Clatterbridge beam has not been characterised, but it is likely to be between 30 keV μM⁻¹ and 80 keV μM⁻¹ because of the RBE values obtained [8]. It is also unclear whether the increase in β is maintained at higher values of LET or if it falls again at extremely high LET values, as is generally the case with RBE. The author is not aware of any data which show a second peak caused by a rise and fall in β at a different turnover point compared with RBE in data sets for which LET is varied. This suggests that either the increase in β follows the same overall pattern as that of α (i.e. both have the same LET values for turnover points) or that the elevation of β is maintained at very high LET, thus ensuring that the RBE never falls to unity, despite the fall in α from overkill effects. This explanation might also suggest that the increase in β is caused by secondary delta-rays.

Further experiments are required to test these hypotheses, especially at specific LET values for ion beam therapy and over a wider range of LET than that of fast neutrons.