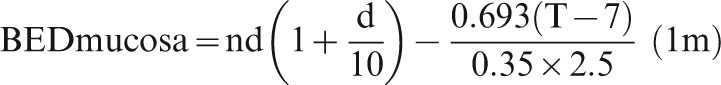Abstract
In 1989 the British Journal of Radiology published a review proposing the term biologically effective dose (BED), based on linear quadratic cell survival in radiobiology. It aimed to indicate quantitatively the biological effect of any radiotherapy treatment, taking account of changes in dose-per-fraction or dose rate, total dose and (the new factor) overall time. How has it done so far? Acceptable clinical results have been generally reported using BED, and it is in increasing use, although sometimes mistaken for “biologically equivalent dose”, from which it differs by large factors, as explained here. The continuously bending nature of the linear quadratic curve has been questioned but BED has worked well for comparing treatments in many modalities, including some with large fractions. Two important improvements occurred in the BED formula. First, in 1999, high linear energy transfer (LET) radiation was included; second, in 2003, when time parameters for acute mucosal tolerance were proposed, optimum overall times could then be “triangulated” to optimise tumour BED and cell kill. This occurs only when both early and late BEDs meet their full constraints simultaneously. New methods of dose delivery (intensity modulated radiation therapy, stereotactic body radiation therapy, protons, tomotherapy, rapid arc and cyberknife) use a few large fractions and obviously oppose well-known fractionation schedules. Careful biological modelling is required to balance the differing trends of fraction size and local dose gradient, as explained in the discussion “How Fractionation Really Works”. BED is now used for dose escalation studies, radiochemotherapy, brachytherapy, high-LET particle beams, radionuclide-targeted therapy, and for quantifying any treatments using ionising radiation.
In 1989 the British Journal of Radiology (BJR) published an article [1] that introduced the term BED, biologically effective dose, as a linear quadratic (LQ)-based formula with an overall time factor included, to replace Dr Frank Ellis's (1969) nominal standard dose (NSD) and the Orton and Ellis (1973) time–dose factor (TDF) tables.
| (1) |
Where n fractions of d Gy are given in an overall time of T days and tumour repopulation doesn't start until day Tk (using k for kick-off, or onset, of the delayed repopulation during fractionated irradiation).
Dr Ellis had designed NSD as a much-needed concept, distinct from physical dose, because dose alone obviously fails to represent the effect on biological tissues if it is delivered in one instead of 30 daily fractions, or at a different dose rate or radiation quality. NSD was for normal tissues only; repopulation had been discovered in tumours in rats and mice but was thought not to occur in human tumours during continued “daily” irradiation, until nearly a decade later (“Labelling indices go to zero...” Tubiana, oral comment in a conference in Rome, 1969). The main contribution of BED was just to add a simple overall time factor on to the equally simple LQ equation, log cell kill = αd+ βd2, which had been in regular, but not universal, use in radiotherapy since before 1980. Somehow, BED stuck and continues to be useful. Does it need modifying yet? Its record, of mainly avoiding accidental overdoses for late complications, has remained intact for nearly 30 years because those effects of late complications didn't depend on overall time, but only on dose-per-fraction if intervals between fractions were more than 6 h.
Three big steps
Since 1989, three main changes have occurred. The first was the gradual lifting of the late-tolerance complications constraint EQD3/2 (equivalent doses as 2-Gy fractions for α/β = 3 Gy, known also as NTD) from about 66 to 70 Gy in head and neck (H&N) and non-small-cell lung cancer (NSCLC) (the rapidly repopulating tumours) and from about 64 to 78 Gy EQD3/2 in prostate radiotherapy with definite volume constraints. (See Table 1 for an explanation of the subscripts.) All this has been accomplished with much use of the BED concept, with acceptable clinical results. Intensity modulated radiation therapy (IMRT) and stereotactic body radiation therapy (SBRT) are currently writing new values of constraint doses.
Table 1. The linear quadratic (LQ) dose terms used.
| BED: biologically effective dose (of a given schedule): the total dose required to give the same log cell kill as the schedule being studied, at an infinitely low dose-rate or with infinitely small fractions well spaced out; now with an overall time factor for repopulation during continued irradiation |
| ETD: extrapolated tolerance dose, and later ERD: extrapolated response dose. Exactly the same concept defined by Barendsen [12] in 1982 but without the overall time factor explicitly included |
| EQD: equivalent total dose in 2-Gy fraction. Or NTD, normalised total dose, normalised to 2-Gy fractions. The total dose in 2-Gy fractions that would give the same log cell kill as the given schedule. It is this that is the biologically equivalent dose, which should not be abbreviated to BED. In previous literature EQD has been called NTD (normalised total dose at 2-Gy fractions) |
| Because BED = total dose×RE, then EQD[α/β] /2 = BED[α/β]/RE[α/β]/2α/β, α/β ratio of the tissue; [α/β]/2, dose per fraction used |
Relationship:  Eqn (2) Eqn (2) |
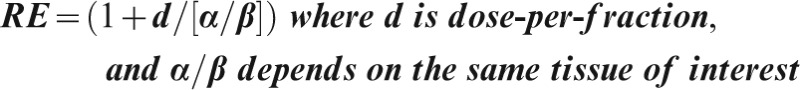 Eqn (3) Eqn (3) |
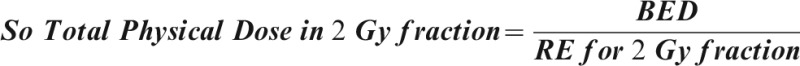 Eqn (4) Eqn (4) |
For a late-reacting tissue a BED in Gy3 must be divided by 1+2/3 = 1.67 to find its EDQ3 /2, using the same “late” α/β ratio, 3 Gy. For a central nervous system or kidney BED in Gy2, divide by 1+2/2 = 2.0 to obtain its EQD2/2.
For an early-responding tissue, a BED in Gy10 must be divided by 1+2/10 = 1.2 to find its EQD10 /2, using this “early” α/β ratio of 10 Gy. And so on for any tissue, using the same α/β ratio as that chosen to calculate its BED in the first place.
A BED can most conveniently be identified simply by a single subscript meaning the α/β ratio of the relevant tissue; thus, Gy10 for early complications, Gy3 for late complications, or Gy2 for late complications in central nervous system or kidney.
Any EQD can be identified most securely by two subscripts, the first showing the α/β ratio of the relevant tissue and the second showing the equivalent dose per fraction, usually 2 Gy for an EQD, but occasionally another equivalent as stated. Thus for an irradiation of 30F×2 Gy = 60 Gy, a BED of 100 Gy3 = 60 Gy EQD3/2 is delivered to the late-reacting tissues, but a BED of 72 Gy10 = 60 Gy10/2 EQD10/2 is delivered simultaneously to acutely reacting types of tissue. The BEDs are different in the two tissues in the same beam, but the EQDs are equal, being all “normalised” to the 2-Gy fraction size at the two different α/β‚s because two different tissues.
This BED formula has also been used to predict the effects on tumours of changes in fractionation, with remarkable agreement across a wide range of internationally developed schedules. All of the best schedules for H&N radiotherapy now deliver 11.0–11.2 log10 cell kill in this modelling: no more, no less, as shown below. This constancy speaks well for the reliability of Equation (1). 11 log10 means that the proportion of surviving cells would be reduced from approximately 109 cells per gram of tissue to a chance of one cell in 100 tumours surviving the irradiation. These figures are approximate only, but they ensure an exceedingly good chance of tumour control.
The second main change was the spreading of BED outside its obvious uses in external beam X-ray scheduling studies, to evaluate equivalent radiation doses in other treatment modalities starting with high LET radiotherapy, brachytherapy at high and low dose rates, radiochemotherapy and duration of palliation, etc. [A1–A31].
The third main change is that in 2003 acute reactions were found to have some credible parameters in a similar BED formula, so that predictions of acute tolerance doses could then be matched to clinical data for volumes above a few square centimetres of mucosa irradiated as a tolerance prediction. This acute mucosal BED formula is now being used to evaluate the effects of chemoradiotherapy on tumours with some success compared with radiation-only acute reactions. The important result of this step is that a full explanation of how multifraction radiotherapy works in optimising tumour cell kill has, at last, become possible.
BED has been used in almost every field of radiotherapy, including high-LET and high and low dose rates and targeted nuclide radiotherapy. To avoid a wildly unfocused story of the way that basic understanding has gradually developed of the mechanisms and opportunities of fractionated radiotherapy, I have concentrated mostly on H&N radiotherapy (H&N RT). These tumour sites allow reasonably complete clinical results to be obtained in fewer years than most other sites except lung cancer, which has more complexities in interpretation of results. Appendix B contains some of the grains of insight gathered during the hunt for “How fractionation actually works” to optimise overall time for maximum tumour cell kill.
Advantages and disadvantages of BED use
An occasional disadvantage is that BED is confused with “biologically equivalent dose”, which it definitely is not: not until after the biologically effective dose (which it is) has been divided by 1.2, or 1.67, or 2.0, depending on whether the tissue under discussion was early or late responding or was in the central nervous system, as explained in Table 1. This problem could be solved by renaming these BED units, as discussed at the end of this review. Its many advantages are that it enables different radiotherapy schedules to be compared, after clinical use in explaining different results, and even before use to design clinical trials more efficiently than by guesswork, however inspired. It was successfully used to design animal experiments by the present author, with appropriate different parameters, before writing that 1989 review [1].
A step backwards?
Correspondence within the past three years has questioned whether the simple LQ curve should be straightened beyond an arbitrary dose of 7 Gy. This was suggested because of some scattered and non-mature two- and three-year results from SBRT treatments of NSCLC on which no reliance should yet be placed [2]. In practice, a good straightening can be simulated in the original simple LQ curve simply by assuming that α/β for lung tumours is 20 instead of 10 Gy; I do this now for NSCLC tumours. There is good biological evidence that such higher values of the α/β ratio are found in rapidly repopulating tumours, for example in tumours of the larynx, [3] where a ratio of α/β = 15 Gy was estimated, with even higher α/β values of 35 or 50 Gy found in other rapidly growing tumours.
However, even before there is any real evidence that a straightening is required, both Curtis [4] and Gilbert et al [5] had pointed out that the simple two-term LQ equation was an approximation of the exponential expansion that could be calculated to further terms (with appropriate coefficients to be derived from reliable clinical data). A small negative “gamma dose-cubed” term could do that elegantly, as pointed out by Douglas and Fowler [6]. Such an additional coefficient might well be derived from clinical results with doses of 8–24 Gy as used in SBRT, but to date sufficiently reliable clinical data have not been analysed.
Origins of the BED formula
A LQ response for radiation effects was not new in radiobiology [7], but it had not been shown to be applicable to fractionated radiotherapy until Douglas and Fowler [6] did so in 1976 with multifraction experiments on the skin of mouse feet comfortably restrained without anaesthetic. We used LQ to analyse the data instead of the generally preferred multitarget or multihit models of cell killing. Arguments about the shape of mammalian cell survival curves ended with the self-defeating multihit prediction of zero slope at very small doses, which could obviously not be true. One of the leaders in cell culture at the time was Dr GW (Eddie) Barendsen at Rijswijk in The Netherlands. He was respected but when he obtained in 1962 mammalian cell survival curves in vitro, which appeared to be LQ down to 10−4 cell survival in vitro [8], he was not generally believed (he was, after all, originally a physicist!). Such curves were most plausibly related to the phases of the cell cycle by the biophysical “lethal/potentially lethal” model of Curtis [4] 24 years later, and others.
In 1980 Withers et al [9] had discovered, with groundbreaking insight, that the major difference between early responding, fast turning-over mammalian tissues and the late-responding, slowly proliferating tissues was in the steepness of their response to changes in the dose-per-fraction. Instead of plotting dose–response curves as effect against increasing fraction number, he plotted them against decreasing dose-per-fraction, which went the same way with overall time as increasing fraction numbers, and then the difference was obvious. Nobody was more forward-thinking than Rod Withers and his colleagues in Houston, Howard Thames and Lester Peters. They found a ready explanation for the steepness effect by a change in the ratio of initial slope to the higher-dose slope of the relevant cell survival curves; that meant a change in the ratio of α to β of the LQ cell survival curve. This important difference between acute and late normal-tissue radiation damage was soon accepted by the radiation oncology community, and this difference made logical sense. LQ modelling was being widely used to plan improved fractionation schedules in the mid-1980s [10, 11].
Dr Eddie Barendsen made the biggest step in formulating the usefulness of the LQ algorithm in 1982 [12]. This was when “the genie came out of the bottle” for me! I based the present BED concept firmly on his concept of an extrapolated tolerance dose defined [12] as “That dose which, if given at infinitely small doses per fraction or at infinitely low dose rate, would give the same log cell kill (LCK) as the schedule being considered.” His ETD was soon renamed “extrapolated response dose” (ERD) when it was realised that it applied to all types of biological effect and not just to tolerance of normal tissues. ERD is still used, especially by Dutch scientists, as is appropriate. It uses the simplest form of LQ algorithm to calculate LCK, E = αd+βd2.
Eddie Barendsen's other major contribution in 1982 was to choose to divide E by α instead of by β to define a quantity (proportional to LCK) that had dimensions of dose instead of dose squared.
The LQ formula was criticised at the time “because it didn't have a time factor”, although it was enormously useful for schedules of similar overall time, and for all questions of late complications because they depended little on overall time of treatment. However, attachment to the old multitarget survival curve concept did not die easily, especially in the USA. When I moved from the Gray Laboratory to Wisconsin in 1988, every resident in radiation oncology in the USA seemed to have a little book of NSD-TDF tables (Orton and Ellis time–dose factors) in his white coat pocket, although by 1983 the LQ description of log cell kill had been used to point out the superiority of two fractions a day over one fraction a day in radiotherapy schedules [10].
The cell kineticists and radiobiologists whose insights contributed directly to my derivation of Equation (1) included Rod Withers [9, 13], Eddie Barendsen [8,12], Howard Thames [10], Bruce Douglas [6] and Barry Michael, plus Liz Travis and Sue Tucker [14] and Jan van der Geijn [15], who suggested the subtraction term for repopulation; not forgetting Julie Denekamp and Fiona Stewart (by being sceptical about any equations in biology, so keep them simple!).
I have described this precursor background so that the derivation of the BED Equation (1) can be seen clearly to depend on many previous contributors. I joined in “climbing on the shoulders of others”, adding just a third time component out of the four (see below).
The BED formula
Log cell kill was calculated by the simple LQ formula α1d+α2d2 [12]. To derive the BED formula intended to replace Ellis's NSD and TDF calculations, I took this simple formula, converted Barendsen's ratio a1/a2 to α/β because of its well-known radiobiological relevance [9, 10], added the negative term recently suggested by Travis and Tucker [14] and by Van de Geijn [15] (actually in the British Journal of Radiology earlier in 1989), and simply wrote down this formula:
| (1) |
Where n fractions of d Gy are given in an overall time of T days and repopulation (with a cell doubling time Tp) doesn't start until day Tk (using k for kick-off for the delayed repopulation during irradiation). It should be noted that the repopulation term followed Withers et al [13] in assuming a constant repopulation rate, i.e. a constant cell doubling time Tp up to the end of the radiation treatment. It should be noted that Tp is a little shorter than Tpot (potential doubling time measured before the tumour has received any cytotoxic treatment), as illustrated in Figure 1. Thames and Withers [16], and others had carried out tests for the equal effect of each equal dose fraction before the time Tk.
Figure 1.
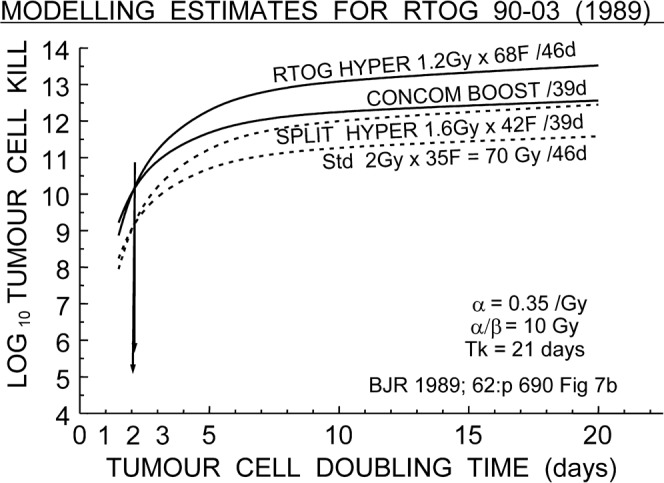
Estimated tumour log cell kill plotted vs tumour cell doubling time Tp during radiotherapy of the four schedules in the Radiation Therapy Oncology Group 90-03 clinical trial [27, 28]. The start of repopulation Tk was assumed to be 21 days. The rapid decrease of tumour effect as doubling time decreases is obvious, with two pairs of the schedules predicted to give identical results at two different levels of cell kill, but both at Tp = 2 days only, at the crossover points. Redrawn from log cell kill Figure 7 of Fowler 1989 [1].
For some reason BED was taken up more widely than ETD or ERD. Although it's sadly clear that not all radiation workers are sufficiently well educated in this basic part of their subject, so it bears repeating now at the 20-year mark that BED does NOT mean “biologically equivalent dose”, although it is sometimes used very wrongly as if it did, and that can lead to dose errors by factors of 1.2 or 1.67 or 2 (Table 1). BED means strictly what Equation (1) above says, and it is a biologically effective dose for a tissue with a particular α/β ratio only.
The most important part of this LQ algorithm is the basic Barendsen formula:
| (2) |
| (2) |
If the irradiation lasts more than a few minutes,
| (2a) |
where g is the dose rate factor for intracellular repair of radiation lesions [7]:
| (2b) |
where μ = 0.693/T½ and T = duration of irradiation (h). T½ is often taken as 1.5 h, or in a 2-component repair model as 60% at 0.4 h+ 40% at 4 h. All time components depend on α/β inversely, as Equation (2a) shows. This gets us into the fascinating prospect that a slowly delivered IMRT fraction of 35 or 45 min might spare late complications by repair of about 10% of the BED3, but would spare most tumours (with α/β ∼10 or 20 Gy) by much less.
In any LQ calculation, RE is the first term that you calculate, and once you have calculated RE you have an instant view of how much more radiation damage your schedule can do to tissue compared with just the obvious physical dose number. It may be modified also by chemical, biological or genetic radiosensitisers or radioprotectors, and particularly by repopulation or by dose rate, but the damage begins with total dose×RE and there is still no escaping this basic relationship.
The role of the British Journal of Radiology
The BJR has played a large part in these developments, starting with the first tentative mention of LQ in relation to radiotherapy [17, 18]. Then followed many fractionation animal experiments [19] and early modelling [4–7], including the first published mention of the crucial mouse skin experiments [20]. This was even before the more often quoted Radiation Research reference [6], and the definitive experiments demonstrating the delayed onset time Tk in skin of mice as early as 1973 [21].
These were followed in the mid-1980s by a series of brilliant biomathematical papers by Dr Roger Dale [22–24]. They are frequently quoted today because they untangled the two aspects of the time factor that were considered the most important factors until the animal experiments about repopulation [6, 9–13, 19–21] brought those into focus as well. The two earlier factors concerned falling dose rates rather than the third time factor, overall treatment time: they were repair of intracellular radiation damage (with half-times of an hour or so), and the half-lives of the radionuclides used to deliver many kinds of brachytherapy [22–25]. Dale and Jones [25] introduced a fourth time factor, that of changes in tumour size leading to frank changes of dosimetry from any implanted sources. It is to be expected that more information on this factor will be forthcoming as image-guided radiation therapy (IGRT) grows in use. Roger Dale and Bleddyn Jones have gone on to publish a library of papers that are important in radiotherapy modelling and therapeutic insight, with References 22 and 25 as still basic essential reading for any radiobiology scientist. It will be a detrimental change if the teaching of radiotherapy principles, and of oncology generally, ever fails to include such seminal papers. That has been a fluctuating danger for the past 25 years.
A search for titles including “modelling” in the BJR archives (kindly carried out by the BIR librarian Susanne Smith) back to their digitised date of 1928, listed 47 titles, reduced to 40 by excluding all before 1989 and all diagnostic topics. Of these 40, about half were relevant to radiobiology or physics and clinical oncology. My select list of References 17–26 contains some of the most influential ones on LQ modelling. Other important applications of BED are listed in Appendix A, together with many more BJR references.
I remember an early occasion when it was astonishing to discover, from looking only at the REs, that doubling the dose-rate from the traditional low dose-rate of 42–80 rads (cGy) per hour, which the International Commission on Radiological Units casually appeared to regard as equally effective “LDR”, was actually biologically equivalent to increasing daily fraction size from 2 Gy to 4 Gy per fraction, which clinicians would rightly be much more reluctant to do! Consideration of this modelling steers us away from such simplistic divisions into categories of LDR vs HDR (high dose rate).
Hyperfractionation or accelerated radiotherapy for head and neck RT?
In 1989, this was a major controversy in the radiotherapy of head and neck (H&N) cancer. The 1989 BJR review [1] examined the implications for a number of well-known H&N schedules, presenting graphs of the expected LCK as a function of the repopulation rate of malignant tumour cells, from doubling times of Tp = 1.5–20 days. The most uncertain parameters were Tk and Tp in Equation (1) above, so the graphs were constructed to plot the result as LCK against Tp, having chosen a Tk of 21 or 28 days from published human tumour determinations in the range 18–32 days, knowing that repopulation is detectable in animal tumours within a few days after irradiation, which suggests earlier rather than later. The other parameters chosen for this modelling were unexceptional, being those required for a reasonable chance of tumour control at the schedules then used, as described in the original 1989 paper [1].
Four of those schedules were tested synchronously in the Radiation Therapy Oncology Group (RTOG) 90-03 clinical trial of 1300 patients with advanced H&N cancer, which reported results in 2000 [27, 28]. The 1989 paper had shown unequivocally that two of the schedules were strong and two were weak (Table 2), but could make no more accurate prediction about tumour results until both the kick-off time Tk and the actual repopulation doubling time Tp (during continuing radiotherapy, as derived from analysis of clinical data) were known to some extent. Other studies of schedules with varied overall times had suggested that Tp (actual cell doubling times during radiotherapy) was as rapid as about three days [13]; i.e. shorter than the median Tpot of five days obtained from unirradiated pre-treatment tumour cell proliferation by flow cytometry. Which could be wrong?
Table 2. The four arms of the clinical trial Radiation Therapy Oncology Group (RTOG) 90-03 [17].
| Schedule | Total |
Overall |
Tumour time-corrected |
Late complications |
Acute mucosal |
|
| Dose (Gy) | Time (days) | EQD (Gy) | Log10 cell kill | EQD Gy (aim <70) | EQD Gy (<49–52.5) | |
| (1) HFX: 1.2 Gy×68 F | 81.6 | 45 | 73.0 | 11.1 | 66.6 | 51.0 |
| (2) Concom boost: 1.8×30F + 1.5 × 12F | 72 | 39 | 72.4 | 11.0 | 67.8 | 49.2 |
| (3) CC Wang split AFX: 1.6 Gy×42F | 67.2 | 39 | 65.8 | 10.0 | 61.7 | 43.8 |
| (4) Control: 2 Gy×35 F | 70 | 46 | 70 | 10.2 | 70 | 44.3 |
AFX, accelerated and split course; EQD, equivalent dose in 2 Gy fractions; HFX, hyperfractionated.
Modelled assuming α = 0.35 Gy, α/β = 10 for tumour and mucosa, α/β = 3 for late complications, Tk = 21 days for tumour and Tk = 7 days for acute mucosa. Tp = 3 days for tumour and 2.5 days for mucosa. Schedules 1 and 2 are the “strong” schedules and Schedules 3 and 4 are “weak”, as shown in the tumour log10 cell kill column.
The results [27, 28] answered that question clearly. The two weak schedules gave coincident results of 46% loco-regional tumour control (LRC) at two years, but the two strong schedules gave coincident results of 54% LRC, significantly different by 8% at p = 0.02. Later follow-up showed the difference to be 7% at seven years (41–42% vs 48–49%) (see also [27, 28]). The strong schedules were concomitant boost and the RTOG hyperfractionation of 68F×1.2 Gy b.i.d. ( = 2F/day). The weak schedules were the standard 35F×2 Gy = 70 Gy in seven weeks and the hyperfractionated 42F×1.6 Gy b.i.d. = 67.2 Gy but with a central split of two weeks. No gratitude was expressed (or expected) that this modelling had been able to pick out the two weakest and the two strongest schedules 11 years before the two-year clinical results were obtained. But an important scientific point was established in 2000 [27, 28]. A glance at the graphs in Figure 7b of the 1989 review [1], redrawn here as Figure 1 (note the two arrows), shows that these two coincidences were predicted to occur only if the clonogenic cell doubling times were close to two days for both the weak and the strong pairs of schedules. Even if the kick-off times were changed over the whole likely range from Tk = 0–32 days coincidences still occurred at Tp = 1.8–2.3 days only (not shown). These results of modelling supported the faster doubling times being derived from other clinical studies where delayed treatments were giving lower tumour control results in H&N patients at 1.5–2% LRC per day of lengthening, and confirmed that strong measures had to be taken to avoid delays in treatment once started. This was one of the important changes that LQ modelling brought to practical radiotherapy in 1996 [29, A8].
Small, encouraging steps
During the next years the colleagues I visited several times in Uruguay strengthened the “weak” schedule of 1.6 Gy b.i.d. (10F/week), described above. This was achieved by gradually reducing the gap to zero, using a slight modification of this BED formula and deciding near the end of each patient's treatment whether to add one or two fractions of 1.6 Gy, or instead to wait a day before adding another one or two fractions or none. The improved results were published in 2001 [30] and showed with 1007 H&N patients an increase at five years of 19% LRC for T3–4 patients treated b.i.d. over 40 days compared with their previous 5F per week schedule which was a median length of 13 days longer. There was no significant increase in either late or acute reactions. Also in 2001, other colleagues, Lee et al in Hong Kong [31], had found that shortening the treatment of nasopharyngeal carcinoma by one week had increased progression-free survival from 63% to 74% at 3 years (p = 0.02) as Equation (1) had suggested. Much later, in 2003, Overgaard et al [32] also gained 12% LRC in advanced H&N patients by saving a week of overall time when they used 6F instead of 5F per week with the same 33 fractions of 2 Gy. The tumour BEDs predicted by Equation (1) also matched the small (about 5%, statistically insignificant) gains in LRC found in H&N radiotherapy for the CHART Continuous hyperfractionated accelerated radiation therapy MR UK trial [33] and Trans-Tasman Radiation Oncology Group [34] clinical trials, and for the larger success of CHART in improving on the LRC of their 60-Gy control arm in 2-Gy fractions then used for NSCLC [35].
It became obvious to me that all of the good fractionation schedules in various countries were giving remarkably similar tumour BEDs for H&N radiotherapy, all yielding the narrow range 11.0–11.2 LCK on my scale of assumed parameters [36]. This narrow range of the modelled BED and EQD tumour values is a strong suggestion that the tumour modelling is giving reliable results for the overall times of four to seven weeks for the rather rapidly repopulating tumours in H&N and presumably in non-small cell lung cancer (NSCLC).
Late complications Gy3 BEDs were not the limiting constraint
It was also shown that the limiting BEDs were clearly not those for late complications, but were possibly those for acute BEDS. We return to this important point later. A hint can be seen in Table 2. The four schedules in the RTOG 90-03 trial show that three of the four late complications EQDs (derived from late Gy3 BEDs by dividing by 1.67) are comfortably below the nominal constraint level of 70 Gy in 2-Gy fractions, whereas one of the acute mucosal BEDs and EQDs (for HFX) was above the middle of the grey zone level at 61 Gy10 (or 51 Gy EQD, obtained by dividing the BED in Gy10 by 1.2) [37]. The grey zone of acute mucosal tolerance is described in detail below, but it represents a region of total doses from 59 Gy to 63 Gy10 wide (49–52.5 Gy10/2 EQD). This means that doses near the bottom of that range signify a low probability of serious reactions, but those at the top signify higher probabilities.
Table 3 presents good evidence for the relevance of Equation (1), with the altered parameters chosen specifically for acute mucosal reactions, notably Tk = 7 days instead of the Tk of more than 20 days in tumours [37]. Schedules are listed that were too “hot” (numbered 1) acutely when first used and so were soon moderated by the originating clinicians to become tolerable (numbered 2). Since these schedules were radiation only with no chemotherapy added, they provide a good check on the modelling [37] because they show that all of the acute mucosal BEDs and corresponding EQDs came down from above to just below the grey zone of acute constraint of BED = 63 Gy10 or EQD = 52.5 Gy [37]. Even better confirmation of the BED formula modified for acute mucosal reactions is obtained from a schedule using 1.3 Gy at 2F/day×60F = 78 Gy [38], but in 42 days instead of the neat and obvious 39 days overall time. At 39 days the mucosal BED was 62.8 Gy10, close to the top of the grey zone, but at 42 days was at the middle of the zone, 60.4 Gy10, and therefore much safer.
Table 3. “Hot” schedules (1), now moderated (2) by the originators.
| Dose/fraction×number of fractions | Total dose (Gy) | Overall time (days) | Tumour log10 cell kill estimate | Late complications aim <70 EQD Gy | Acute mucosal aim <49–52.5 EQD Gy | Yes or no | ||
| Gortec 1 2F/d | 2 Gy×32F | 10F/week | 64 | 21 | 11.5 | 64.2 | 54.1 | No |
| Gortec 2 2F/d | 1.75×36F | 10F/week | 63 | 23 | 11.05 | 60.0 | 51.2 | Y |
| Cair 1 | 2 Gy×35F | 7F/week | 70 | 34 | 11.5 | 70+ | 52.2 | ? |
| Cair 2 | 1.8 Gy×39F | 7F/week | 70.2 | 39 | 10.9 | 67.2 | 48.6 | Y |
| Harde 1 2F/d | 1.2Gy×20F+1.6×10F+1.4×20F+2 Gy×4F | 76 | 33 | 12.01 | 67.0 | 55.2 | No | |
| Harde 2 2F/d | 1.2 Gy×36F+ 1.5 Gy×20F | 73.2 | 37 | 11.0 | 63.6 | 49.0 | Y | |
| Sanguinetti 1 | 1.3 Gy×60F | 2F/d | 78 | 39 | 11.6 | 67.1 | 52.3 | No |
| Sanguinetti 2 | 1.3 Gy×60F | 2F/d | 78 | 42 | 11.3 | 67.1 | 50.3 | Y |
| Escalation study 2F/day | All Yes | |||||||
| Leborgne et al Hyperfr no gap different OvTs | 1.6 Gy×42F | 67.2 | 29 | 11.05 | 61.8 | 50.4 | Y | |
| Leborgne et al 1 | 1.6 Gy×43F | 68.8 | 30 | 11.2 | 63.3 | 52.8 | No | |
| Leborgne et al 2 | 1.6 Gy×43F | 68.8 | 31 | 11.1 | 62.5 | 52.1 | Y | |
| Leborgne et al 1 | 1.6 Gy×44F | 70.4 | 30 | 11.5 | 64.7 | 52.8 | No | |
| Leborgne et al 2 | 1.6 Gy×44F | All 2F/d | 70.4 | 33 | 11.2 | 64.7 | 50.9 | Y |
Original references can be found in References 19, 25, 27 or 35.
Tumour Tk assumed, 21 days; Tp, 3 days; acute mucosiits Tk = 7 days and Tp = 2.5 days; both with α = 0.35 Gy−1 and α/β = 10 Gy. EQD, equivalent dose; OvT, optimum overall times.
It is now well known that the limiting tolerance reactions for altered fractionation for H&N radiotherapy are the acute reactions, mucositis and dysphagia. We have learnt to avoid late complications by respecting the late BEDs corresponding to 70 Gy of 2-Gy fractions (EQD3/2), which is 117 Gy3, together with 45–50 Gy (EQD2/2) for spinal cord, which is a late BED of 90–100 Gy2. (Table 1 describes the terminology Gy3/2, etc.)
By reviewing all the H&N schedules that we could collect, together with the published reports of the acute reactions of Grades 1–3 and higher, Fowler et al [39] proposed a “Grey Zone” of 59–63 Gy10 (corresponding to EQD10/2 = 49–52.5 Gy10/2). Within this zone any H&N schedule should lie as a prediction for new schedules. This was confirmed by the five published schedules in Table 3. The fifth schedule shows the RTOG “hyperfractination with a gap”, after the gap had been gradually reduced to zero by Leborgne et al's [30] careful testing of Equation (1). This was a major test of the BED concept at the time, starting in the mid-1990s.
Tests for any X-ray radiotherapy schedule
Table 4 therefore lists the three separate calculations that are now recommended for each schedule to be investigated in its main radiobiological aspects of (1) late complications, (2) tumour BED or EQD or estimated log cell kill, and (3) acute mucosal BED or EQD in relation to the “tolerance grey zone”. The ratio of the tumour BED to the late BED, or even more clearly tumour EQD to the late EQD, is a good therapeutic ratio. The ratio of a calculated tumour BED (usually with α/β = 10 Gy) to a late complications BED (α/β = 3 Gy usually, but α/β = 2 Gy for CNS (central nervous system) and kidney had been used before the BED formula as a very rough approximation, but that was one of the reasons for introducing BED with an overall time factor.
Table 4. The three sets of biologically effective dose (BED) calculations to analyse any schedule with the parameters regularly used by the author.
| 1. Ensure late complication constraints are not overdosed: late BED3≤117 Gy3≤EQD3/2 70 Gy unless volume reduced, e.g. 80 Gy ∼EQD3/2 for 2 cm3. No overall time factor normally assumed. α/β = 3 Gy, or 2 Gy for central nervous system and kidney |
| 2. Tumour BED 10 = nd(1+d/[α/β])−0.693 (T−Tk)/0.35 Tp, [1] with Tk = 21–32 days and Tp = 3 days for lung or head and neck cancer. α = 0.35, occasionally 0.3 Gy−1 where stated. For most tumours α/β = 10 Gy, but prostate cancer α/β = 1.5 to 2 Gy, breast cancer α/β = 4 Gy, malignant melanoma α/β = 0.6 Gy, non-small-cell lung cancer α/β = 20 Gy. Log10 cell kill = BED Gy10×0.152 and EQD10/2 Gy×0.1266.3 normal mucosa |
| 3. Acute BED10 = nd(1+d/10)−0.693 (T−7d)/0.35×2.5d [37] < = grey zone of 59−63 Gy10 = 49–52.5 EQD10/2. Derived from oropharyngeal data; possibly applies to rectal mucosa too, with the commonly applied volume limitations used in prostate radiotherapy [39] |
EQD, equivalent dose in 2 Gy fractions.
The grey zone for mucosa requires further clinical verification but is well worth calculating before any new schedule is tried on patients; it has been used to guide some new dose escalation steps in H&N radiotherapy, and recently to compare acute responses in chemoradiotherapy (Appendix A).
Equation 1 for acute mucosa reduces then simply to:
The subscript “am” stands for acute mucosa. There is preliminary evidence that the same acute grey zone of tolerance dose might also apply to the other end of the gastrointestinal tract, to rectal mucosa, especially in the treatments of prostate radiotherapy where tight volume constraints are now well known [39, 40].
After these successes with acute mucosal BED we should now ask whether the simple “linear” (exponentially) form of repopulation, following (Withers et al's dog leg [13]) in Equation (1), is still adequate, or whether we should allow for an expected (and long alleged) accelerated repopulation towards the end of a schedule. Table 5 lists the three formulae that have been proposed for this [37, 40, 41]. The second of these references shows a clinical graph with a very slight upward curvature of accumulated acute damage at the end of the schedule. It differs by less than 4% from the predictions of tolerance EQDs of the present Equation (1am) [37].
Table 5. The three proposed acute mucosal bed tolerance dose estimation systems.
| 1. Fowler JF, Harari PM, Leborgne F, Leborgne JH [37] | |
| |
| Similar to Equation (1), but with Tk = 7 days and Tp = 2.5 days. α/β = !0 Gy and α = 0.35 Gy−1 as before. This assumes a constant rate of repopulation as an average over the time T−Tk.) The term (T–Tk)/Tp gives the average number of cell doublings in the time T–Tk days available for repopulation | |
| 2. Strigari l, Arcangeli G, Arcangeli S et al [40] | |
| Their Figure 3 shows a clinically derived curve bending upwards by 4% above a straight line, for rectal toxicity during conventional or hypofractionated radiotherapy for prostate cancer. This is in reasonable agreement with Equation (1am). Their formula is somewhat less simple algebraically | |
| 3. Fenwick [41] | |
| BEDmucos. = 69.5×(T/32.2)/sin (T/32.2)–3.5 Gy10 | |
| This formula curves upwards at the end – I believe too sharply unless modified |
How fractionated radiotherapy works: obtaining maximum optimum tumour cell kill
It is obvious that in a situation like H&N radiotherapy where malignant tissues cannot be reliably separated from normal mucosal tissues by a steep dose gradient, a high tumour dose can only be achieved when both the late and early tolerance constraint doses are delivered simultaneously. This is hard to achieve with altered schedules but happens quite closely with doses per fraction of about 2 Gy given 5 times a week for 44–46 days, as explained in detail in Reference 42. This happy coincidence accounts for the long popularity of this scheduling; but earlier modelling, based only on late BEDs in Gy3 vs tumour repopulation, had suggested in 1990 that shorter overall times should be tried so as to avoid tumour repopulation [43]. The snag was that acute reactions became the limiting factors in the shorter schedules [44] and there were no ways of modelling those acute tolerance doses until after 2003, when a good value for their mucosal Tk was found.
Against this trend was the modelling showing that smaller doses per fraction enabled higher total doses to be given for the same late tolerance, and several fractions per day could achieve this without the excessive overall times. However, mucosal reactions again became limiting [44]. Three fractions a day were too many: perhaps 2F/day would do better? Much clinical effort has been put into these obviously contradictory approaches, with no indication whatever of any type of optimum overall time (Figure 2) until very recently, 2008 [42] and here; the present paper is a shortened story of that unravelling of trends.
Figure 2.
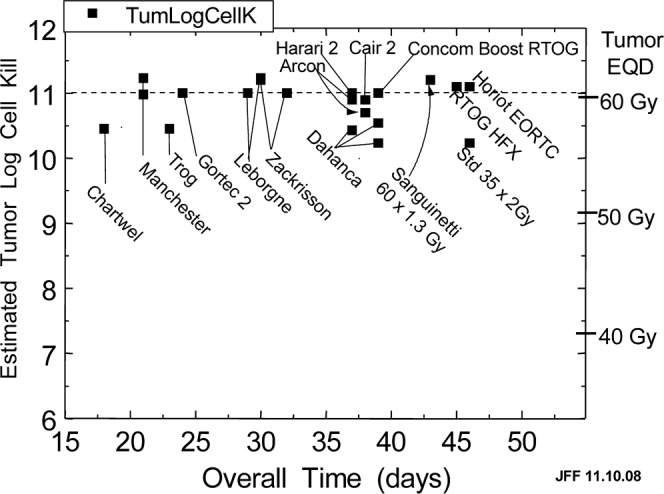
The lack of any obvious optimum overall time in head and neck radiotherapy with radiation only. The square points show the estimated tumour log10 cell kill for schedules used in 14 centres worldwide and the schedule of 2 Gy×35F = 70 Gy in 7 weeks commonly used as control. The best schedules are predicted to give 11.0 to 11.2 logs of cell kill assuming α/β = 10 Gy, α = 0.35 Gy−1, Tk = 21 days, Tp = 3 days.
Estimating kick-off time Tk for acute mucosal reaction
One of the two main innovations in LQ modelling since 1989 was the accumulation of data on fractionation schedules that led to the concept of the “Grey Zone” for acute mucositis tolerability in 2003 [37]. Those authors had narrowed the choice of Tk for oral mucosa down to “between 5 and 10 days”, but the strong V-shaped curve from cell counts in human mucosal biopsies pinned down Tk to a clearly determined seven days in a watershed paper [45]. This work enabled the parameters for this modification of Equation (1am) to be settled. Labelled cells, indicating proliferating cells, fell rapidly to about 10% at seven days after starting irradiation with 2-Gy fractions, and then began to rise sharply. This finding alters the concept of Tk somewhat from “start of repopulation” to “time at which repopulating cells become obvious”. But it conforms to the concept of Tk as defined in tumour observations [1, 13, 37, 45].
The time at which mid-grey zone is reached defines the practical overall time
It was therefore not until 2003 that an acute mucosal constraint could be defined [37], so that a meaningful calculation of an optimum overall treatment time for altered fractionation could be attempted, with both late and early constraints. For this acute constraint we could use the middle of the acute grey zone: (61 Gy10 = EQD of 51 Gy10/2), being safely below the possible upper boundary of 63 Gy10 or 52.5 Gy EQD10/2.
An attempt at predicting realistic optimum overall times (OvT) was made, finally, in 2008, together with an explanation of how fractionation really works [42]. Why did it all take so long? It took my final retirement from Madison for me to have the time to complete the many calculations of each “practical overall time for any fraction number”, as described below.
Optimum overall time for H&N radiotherapy: solution of a puzzle
Figure 2 shows a plot of the estimated tumour EQDs/LCKs delivered by many of the best schedules internationally, and a few nearly-best also. The best ones lie on or just above the straight dotted line at 11 LCK and the others less than 1 log10 below. There is obviously no indication of anything resembling an optimum “hump”, which indicates how confused the field has been, including me [36, 43], until now [42].
The following solutions were only arrived at by calculating the maximum tumour BEDs for every number of fractions from one fraction of 17.3 Gy to 115 fractions of 0.8 Gy, given on five treatment days a week. All of them had the same late BED of 117 Gy3, corresponding to the EQD3/2 of 70 Gy. This late constraint determined the exact fraction size of each of the 115 schedules, with no time factor involved.
For each schedule, the maximum possible tumour dose is only obtained when both the acute and the late dose constraints are delivered simultaneously. It's too easy to decide on some round-figure dose-per-fraction and so instead to score a near-miss in dose per fractions, which is a much bigger miss in total dose. To match equal acute mucosal BEDs (in Gy10) with the late constraint was therefore tedious.
First I set up the ordinary, 5F/week, expected number of days for the number of fractions, and calculated the predicted acute mucosal BED. If this exceeded our chosen acute constraint of the middle of the grey zone ( = EQD10/2 of 51.0 Gy), I then had to extend the overall time a few days to bring down the calculated acute BED to the constraint EQD of 51.0 Gy or slightly below (or go to 2F/d with smaller fraction size in a different time frame). This was more like knitting than like the final moves in a game of chess against a slippery opponent! That's why anyone had to be retired to do enough of these fractionated schedules to define the overall time curve. It's also not a coincidence that the first paper under discussion, [1], was written just after I had retired from the Gray Laboratory in 1988, before I got “busy again” with day-to-day matters.
The resulting “practical overall time” of the knitting/chess moves for each number of fractions was then recorded. I had a list of fraction numbers and sizes, all limited by the same late and early constraint doses of 70 EQD3/2 and 51 EQD10/2 values, and each with the overall time that gave the closest acute constraint EQD just below 51 Gy EQD [42]. Each of those recorded schedules would then deliver the maximum tumour BED (and EQD) which could be obtained with that number of fractions in five treatment days a week. This principle is not limited to H&N patients.
These results should be clinically reliable for any tumour site where the late tolerance dose is 70 Gy in 2-Gy fractions and the acute tolerance depends on mucosal tissues. The acute constraint at 51 Gy EQD10/2 is cautiously below the maximum of 52.5 Gy at the top of the grey zone. The listed schedules here and in Reference 42 could be tried in any new clinical trial with no more than a few patients treated at perhaps one fraction less than those listed, as a doubly cautious mini-escalation test for any centre. But increasing fraction size, even very slightly, could lead to strong acute reactions, unless extra overall time was allowed, which would decrease tumour control by the equivalent of 1–2 Gy/day [29]. Finally, the maximum tumour EQD was calculated at the “practical overall time” for each schedule, using the tumour Tk of 21 days [46], and the resulting log10 cell kill was estimated. “Practical” meant that Saturdays and Sundays were not allowed to be treatment days.
Distinction between carcinomas and acutely reacting normal tissues that drives the optimum fractionation is not limited to H&N tumours
It was the big difference in the two values of Tk between tumour and mucosa that was the important factor in determining this “practical overall time” result. The values of Tp of 3 and 2.5 days average cell-doubling times respectively made relatively little difference.
Figure 3 shows a simple graph by Arvidson et al [47] of gradually increasing tumour effect (specified as the estimated progression-free survival of patients treated with an imaginary series of schedules with two fractions given on each of five days a week, up to 60 fractions in six weeks (39 days)). The fraction size for each schedule was adjusted to deliver always the same late constraint BED in Gy3 or total EQD10/2. The two-day dips (due to no irradiation at weekends) are obvious, but the point is that the tumour effect continues to rise week after week although progressively less rapidly. It is this gradual rise in tumour effect as the fraction sizes become successively smaller and overall time longer that has attracted users to move to longer and longer overall times in spite of the detriment of tumour repopulation, because the weekly increase in tumour radiation damage continues to exceed the loss by repopulation damage. It shows that “hyperfraction does work best”, until overall times become so long that they are inconvenient, or doses per fraction become so low that they cannot counteract the repopulation rate in the tumours of about 0.7 Gy EQD10/2 per day. This is an average approximate rate of loss of tumour effect every day, translating to 7/5×0.7 = 0.98 Gy EQD10/2 if irradiated on five treatment days a week, as a minimum useful treatment rate. Hyperfractionation will continue to improve when more and smaller fractions are given, down to fraction sizes of approximately this small; that is how multifractionation works. Radiotherapy goes on being more “efficient” (defined as tumour BED divided by late BED, that is BED10/2 divided by BED3/2) for more and smaller fractions, down to this limit, if anyone had the time and patience.
Figure 3.
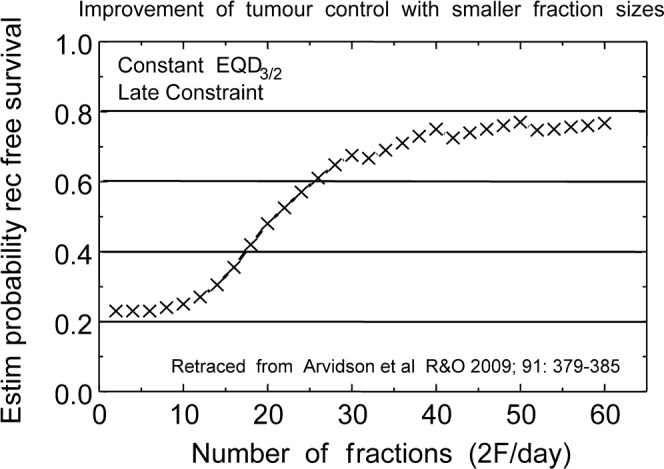
Estimated biochemical recurrence-free survival of patients treated with an imaginary series of schedules with 2F given on each of 5 days a week, up to 60F in 6 weeks (39 days), calculated from Equation (1) assuming Tp = 4 days doubling time and Tk = 14 days. The fraction size for each schedule was adjusted to deliver always the same late constraint biologically effective dose in Gy3 or total EQD3/2. The 2-day gaps at weekends are obvious, but the accumulated effect on tumours continues to rise with successive weeks. (Replotted from Arvidson et al [47].
Old-fashioned low dose rates and permanent implants have this magical advantage of being the only radiation modality that approaches 100% therapeutic ratio (because all REs tend to 1.0 for X-rays (or strictly to RBEmax) at low doses per fraction. Even radium at 7000 cGy/week was 18% short of that for tumour effects. That brings its RE of 1.18 very close to the RE of 1.2 for external beam acute reactions and most tumours, which is just the standard conventional expectation. There was some rationale, as well as tradition, when experienced radiation oncologists expressed reservations as HDR came in. Although I did not hear it expressed as clearly as this at the time. “Is HDR high risk for high throughput?” is how it was put, although HDR has become useful, with large dose reductions and good geometry [25, 48, 49, A19, A20, A28, A29].
So, provided that α/β for tumours is so much larger than for late complications, and that tumour repopulation averages no more than about 0.7 Gy/day, multifraction radiotherapy (hyperfractionation) is advantageous in principle. This principle makes pulsed dose rates (PDRs) more attractive, but PDR is available in convenient form only as pulsed brachytherapy.
But are there any optimum overall times at smaller fraction numbers, closer to the onset time of tumour cell repopulation Tk perhaps?
The solution of the puzzle: yes, there are clear optimum overall times
It should be emphasised that the following solutions are not limited to H&N RT – they apply to any tumours that repopulate fairly fast, probably most carcinomas except prostate, gliomas and some breast tumours.
Figure 4 shows my 2008 graph of those “maximum possible tumour EQDs” for any fraction number, all with the same late and early constraint doses. Tumour EQDs are scaled on the left axis and corresponding LCK on the right axis, with all schedules plotted against increasing fraction number, regardless of overall time. The crosses are the highest resulting tumour EQDs obtainable for each number of fractions. The circles are the highest acute mucosal EQDs obtainable, all for the same constraint BED and EQD values. For the tumour EQDs clear optimum ‘humps’ are now obvious, the downward slopes being due to tumour repopulation after both the constraints had been reached [42]. It is interesting that the two types of schedule, 1F/day and 2F/day (both at five days/week), are distinctly separate. However, they would join up as a kind of non-constant “ridge”, which is what had been confusing the subject of “optimum overall time” in earlier publications [36, 43].
Figure 4.
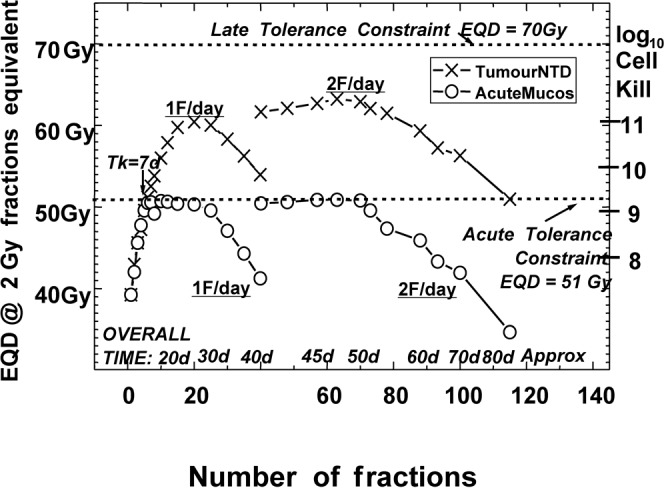
Each schedule is represented by one X (tumour equivalent dose (EQD)10/2) and one O (acute mucosal EQD10/2 below it), plotted against fraction number only. The circles show the maximum estimated acute mucosal EQDs given by choosing overall times according to 1F or 2F on weekdays only, and then extending overall time where necessary to the shortest “practical OvT” that keeps the acute mucosal EQD 10/2 not greater than 51.0 Gy. (Reproduced from Fowler 2008 [42]). The separate families of points for 1F or 2F per day were then obvious.
In Figure 5 the same data are plotted against practical overall time and this is the important result: with the same late constraint, and (after about five fractions) also for their acute constraint of 51 Gy EQD10/2. It is shown how these acute EQDs (circles) can be maintained close to the constraint level for many days by lengthening the overall time, which could not be seen in Figure 4 because overall time was not plotted there. Figure 5 illustrates what might be called “constructive lengthening”, when for each extra day the tumour EQD10/2 goes up a little instead of down.
Figure 5.
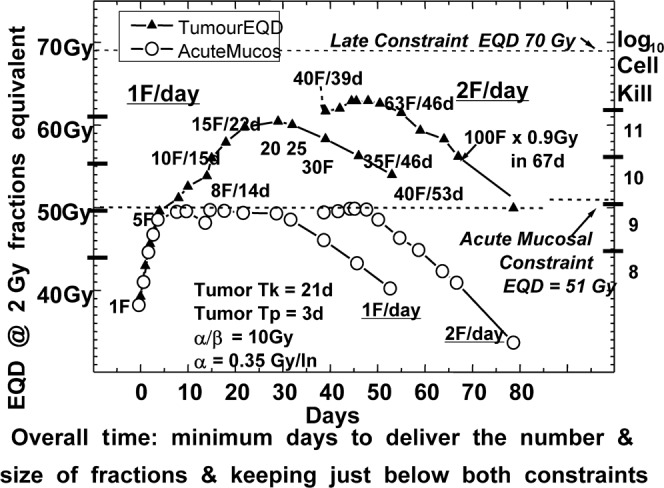
The same data as in Figure 4 plotted against practical overall time (the minimum overall time that keeps acute mucosal equivalent dose (EQD)10/2 at or below 51 Gy). X, Tumour EQD; O, acute mucosal EQD. Optimum tumour EQDs for 2F/day are higher than those for 1F/day by 4 Gy EQD and 0.3 log10 cell kill. The plotted curves fall when the late constraint dose is reached (Reproduced from Fowler [42] 2008).
These curves are slightly irregular, subject to the weekend gaps and of overall time being integral days instead of continuous time. Local tumour maxima are often but not always on a Friday. Both types of schedule have their main tumour maxima appreciably later than the intuitive expectation of Tk days, until we look (see [42]) at even shorter doubling times for Tp than the presently plotted three days.
Figure 6 shows the same data, with only the tumour EQDs, cleaned up and some good schedules labelled. Table 6 summarises the best schedules in the 1F/day and 2F/day schedules. The slightly extended overall times should be noted, as making them shorter would mean being more risky above the acute constraint.
Figure 6.
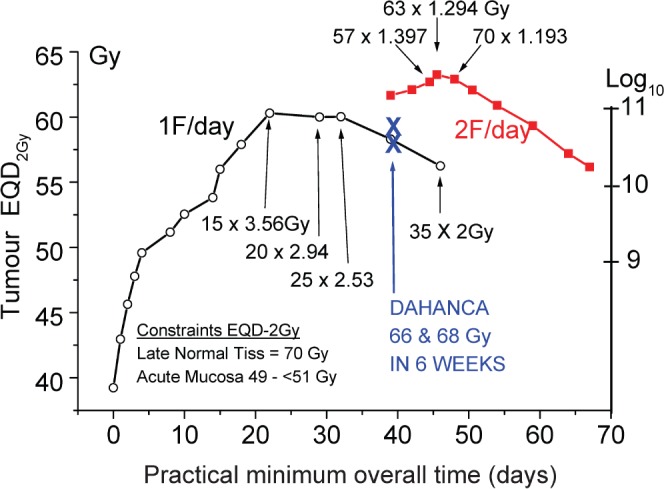
The same data for tumour EQD and log-cell kill as in Figures 4 and 5, cleaned up and the best schedules labelled. They are also listed in Table 6 slightly more legibly with mandatory minimum overall times listed too. It is interesting how much better we can do than with 35 factions of 2 Gy in 7 weeks, even without adding chemotherapy.
Table 6. Recommended optimum head and neck schedules and some other tumours from the present modelling (Figure 6).
| Late constraints are always 70 Gy EQD with α/β = 3 Gy and no time factor. Acute mucosal constraints are 51 Gy EQD with α/β = 10 Gy, α = 0.35 Gy−1, Tk = 7d, Tp = 2.5d. (Equation 1m) | |
| Two fractions a day should ideally be used, as: | These overall times must not be shortened by even one day without dropping at least one fraction |
| 1.4 Gy×57F = 79.8 Gy/45 days, not 39 days | These overall times cannot be shortened without risk of acute complications |
| 1.3 Gy×60F = 78 Gy/42 days, not 39 days | |
| 1.2 Gy×70F = 84 Gy/49 days, not 45 days | |
| If only one fraction a day can be given, these are the best schedules to use: | |
| 3.41 Gy×16F = 54.56 Gy/23 days, not 21 days | |
| 2.94 Gy×20F = 58.8 Gy/27 or 28 days | |
| 2.53 Gy×25F = 63.25/31 or 32 days | |
| If 2F/day can be used, the tumour EQDs will be 2–4 fractions of 2 Gy greater than 1F/day | |
Some of the finer points arising from all this modelling for optimum overall times, and from the new understanding of how fractionation works, are summarised in Appendix B.
Conclusions
The considerable gains between the 2F/day and 1F/day schedules are discussed in Appendix B. These points are relevant when we consider protons, SBRT and radiosurgery that have a propensity for short schedules with very large doses per fraction. These are based at best on more rapid dose gradients from tumour to surrounding normal tissue or, at worst on, cost considerations.
So the modelling suggests (rather strongly) that two fractions a day is the best practical compromise for external beam radiation, with PDRs as an interesting competitor in the wings, even if it is used outside “office hours.” With present technology, it is only available as brachytherapy, which has some of its own good physical dose gradients.
Although both parts of Equation (1) are the most obvious mathematical simplifications of what could be longer series of terms, it does appear to work fairly well. To date, Equation (1) has been useful, both for tumours and for acute mucosa, as well as for late complications. There is still more to be done by using this modelling.
It has come to my attention that a new radiobiological unit is being suggested for deterministic clinical radiation reactions (as distinct from stochastic events). It would honour a former colleague appropriately and would also avoid the confusion mentioned above that BED could be mistaken for biologically equivalent dose instead of its defined meaning of biologially effective dose.
This suggestion was made within the last year by a group from MIRD [50] and is under consideration by the ICRU and IAEA. It would be called the Barendsen (Bv) in honour of his many scientific contributions, as emphasised in the present account, that Eddie Barendsen has made, from his obtaining of LQ shaped cell survival curves in the early 1960s to the finding of rapid repopulation in human-origin tumours implanted into rats at a time when it was not known that repopulation is common in tumours during continued irradiation, and culminating in the concept of using the initial slopes of cell survival curves to define the log cell kill which is the basic concept of the present BED as explained above [12].
I support this proposal with great pleasure [15], especially as it will be able to discriminate clearly between this concept as Barendsen Units (Bd) proportional to log cell kill, for specific tissues as designated by their α/β ratios, distinct from that of EQD2, which is the biologically equivalent dose in 2 Gy fractions in ordinary Gy units of dose.
APPENDIX A
Other applications of BED
Other applications than “How fractionation with X-ray beams really works”
The concept of BED has been applied to many modalities of cancer treatment, as we have said. Many of the following references pay further tribute to the continuing role of the BJR, as well as to the scientific enterprise and energy of my erstwhile colleagues Professors Roger Dale and Bleddyn Jones, whom I thank for adding to these references.
High LET radiotherapy
An important BED formula development was made in 1999 for high-let radiotherapy (high ionizing density), i.e. neutrons, heavy-particle beams and some radioactive nuclides. Dale & Jones [A1] explained how the “(1+…)” in Equations (1) and (2) for BED and RE in the main text should be simply replaced by the term “(RBEM+…)”. RBE varies inversely with dose per fraction and dose rate, with RBEM to be determined at low doses per fraction or lowest dose-rates. This is an echo of the definition of BED (or ERD) itself and separates out the non-linear, repairable, biological effects from the linear, non-repairable effects. Previously, the changes in RBE were known only empirically in terms of the different shapes of the two types of cell survival curve. A very curved shape indicates low vs nearly straight for high-LET radiation. RBEs can now be better quantified during their variations with dose per fraction [A2–A4].
General modelling for radiotherapy
The specific reference to changes of tumour dose with time as a result of shrinkage of tumour volume were first quantified in 1994 in the BJR [A5]. In the 1999 groundbreaking discovery that prostate tumours have a very low α/β ratio [A6], Dale's important equations [22] played an essential role and in the ensuing arguments [A1, A7].
The team of Jones and Dale has dealt also with many other topics in conventional radiotherapy [A8, A9], including duration of palliation [A10] and evaluating treatment errors [A11]. A general discussion of the utility of BED in clinical practice for medically knowledgeable but not so mathematically enthusiastic readers is given in Reference A12.
Radiochemotherapy
Concomitant chemotherapy with radiotherapy, with or without surgery, is current standard practice for advanced H&N cancer and other tumour sites. BED analysis has been used to assess the proportion of total tumour effect provided by either modality if used alone or in escalation of either alone [A13–A15].
Several authors are also investigating whether the observed increase of acute (or late) complications from chemotherapy is greater or less than the increase if radiotherapy alone at escalated total dose was used using Equation (1) for tumour BED, and Equation (1am) for the increases in acute mucosal reactions reported clinically [A16–A18]. Although the δ% increases in mucosal scores are broadly similar, with wide spread, a balance in favour of radiochemotherapy seems to be emerging at the time of writing (May 2010).
Ca cervix uteri
I had been aware since the 1950s that the British results in Ca cervix were regarded by American and French radiation oncologists as “in need of improvement”. One of the first clinical science lectures I ever heard as a young radiation physicist was by Dr Gilbert Fletcher from Houston when he visited Newcastle-upon-Tyne in 1955, and he spoke memorably on how to achieve better results with his method. Fast forward 33 years, and I was confronted in Madison, USA, with a newly purchased HDR afterloading machine intended for Ca Cervix treatments, and Dr Dee Buchler saying “what doses can we give to be safe and effective?” She was a highly experienced radiation oncologist and also a surgeon, and she was asking me? She quickly understood that any HDR schedule could give the same tumour BED (with a large dose reduction) as her previous LDR (traditional low dose rate). However either the late complications BED would be too high or the tumour BED might be too low – both effects could not be matched at HDR. Her surgeon's instincts won: “I don't want to risk tumour recurrence.” The ultimate results were clarified and published by Dr Dan Petereit, using eventually slightly smaller doses [A19]. LQ came into the discussions but BED did not arrive until a year later, partly indeed as the result of our having an “ERD” without yet having overall time allowed for [A19]. It was Dr Rachelle Lanciano, from Fox Chase, who first identified repopulation in Ca cervix and told me, although the first publication of it was from Toronto.
My first collaboration with the late Dr Felix Leborgne from Uruguay was for medium dose rate brachytherapy of Ca cervix [A20]. He had such good data for his stepped sequence of dose escalation that the LQ analysis enabled a moderate schedule to be designed that was subsequently used in Montevideo for many years, with acceptable results [A21–A22]. Further, the resulting rectal “tolerance BEDs” turned out to be consistent with the corrected Manchester dose levels and with those from France [A23], and with the toe of an unusually complete dose–response curve in human patients from Canada [A24], modelling by LQ and the T1/2 repair half-time of about 2 h learnt from the Leborne rectal results. A “tolerance” level of 10% grade 3 rectal reactions, accepted during the 1990s, although not today, corresponded to 125–130 Gy3 before rectal volume constraints were introduced about 2002 from the prostate experiences [39]. These concerns about late complications do not involve the latter half of Equation (1), because it is accepted that late complications are reduced little, if at all, by longer overall treatment times. But for tumour effects [A25] the whole BED Equation (1) is necessary, because for almost every type of tumour (except prostate up to 8 weeks) overall time is an important variable.
Non-small-cell lung cancer
Long after it was known that most types of carcinoma had pre-treatment Tpot values less than about 10 days, few determinations of the expected similar or slightly shorter doubling times of repopulation during radiotherapy, called Tp, had been made. To determine Tp requires data, preferably from controlled clinical trials, of the effect of extending overall time without altering dose-per-fraction. Several RTOG trials of lung cancer were available in 2000, and my colleague statistician Dr Rick Chappell and I determined that the value of Tp for NSCLC was as short as three days [A26], similar to the average value found for H&N tumours [13]. This was another case of “Why did it take so long?”
Applying this through the BED Equation (1) to lung tumour modelling [A27] showed at once that if the overall treatment times for lung cancer could be reduced from 6 or 7 weeks to 2.5–3 weeks, the abysmally low 3-year survival rates could be doubled to 40–50%. About four centres had used this approach and had shown that it worked [A27, A33–A36], but it has too rarely been exploited. At the same time some conventional “daily” dose escalation trials had reached over 80 Gy in daily doses of 2 Gy, but in 9 weeks, giving well-founded anxieties of too long overall times. Thus began in the early 2000s a series of attempts through the National Institutes of Health to achieve at least this level of success [A27]. One method in Amsterdam used two fractions a day. The BED Equation (1) was central to all of these.
These initiatives were trumped in 2004 by Dr Bob Timmerman's revolutionary use of stereotactic body radiotherapy [A29], based on a Swedish expansion of their brain physiology work, to use three fractions of about 20 Gy each in 2 weeks [A28, A29] and results are only now being published [A29, A32]. I was concerned in all of these with BED and EQD, and the trick for tolerance seems to be to keep the average BED in both lungs, excluding the prescribed treatment volume (PTV), below a value close to 33 Gy3 which is an EQD 3/2 of about 20 Gy in 2-Gy fractions, normalised using α/β = 3 Gy, averaged from every voxel. Although the safety aspects did not involve the overall time part of BED, they were vital to be checked first, largely from Amsterdam [A31]. Tumour comparisons [A27–A29, A32] certainly involve the overall time part of Equation (1), hence the controversy about LQ mentioned at the beginning of this review [32], which is still to be resolved.
APPENDIX B
Discussion on “How fractionation really works”
1. Figures 3 and 5 explain how the “momentum towards longer overall times” encouraged the trend to schedules as long as six or seven weeks. This is in spite of 2F/day (at about half the 1F/d previous overall times) providing better tumour control, before any analysis such as the present one could explain why. Smaller fraction sizes will always enable higher total doses to be tolerated, but the competing balance of longer overall times loses tumour control because of repopulation. Modelling is necessary to quantify this balance [42]. Two fractions a day are about right.
2. It is worth noting that the recent thorough remodelling of parameters for limited-stage small-cell-carcinoma of the lung by Arvidson et al [47] found α/β = 11.9 Gy, Tp = 4 days and Tk = 14 days. Not bad “general agreement for most tumours” over 20 years, except that Tk appears here notably shorter than the 21 days assumed for the Fowler modelling here. Arvidson et al also considered incomplete repair in 2F/day. Using their modelling for two half-times of repair of 0.4 and 4 h, an increase of about 10% for late and 5% for tumour and early appears likely in BED or EQD for the 6-h intervals of 2F/d. Overnight incomplete repair of ∼1% would accumulate for four nights, but not beyond a two-day weekend. So let's just add these percentages to late BEDs and stop worrying, but continue to look for more evidence. Some modern 2F/day schedules are working already at 5–10% below my 70 Gy EQD3/10, constraint with only marginally less than optimal tumour control (Tables 2 and 3).
3. The important practical conclusion is that 2F/day provides more tumour damage than 1F/day (for the same normal tissue risks) by 4–9 Gy total dose EQD, that is by two to four 2-Gy fractions, with the greater gain for the slower-repopulating tumours. The best tumour EQD10/2 and cell kill will be found with the smallest doses per fraction, down to an average EQD of about 1 Gy per day, below which repopulation (in H&N and many other) tumours might not be cancelled out.
5. For any number of fractions, the optimum tumour LCK can only be obtained when both the acute and the late constraint doses are fully delivered. (This is obvious but somewhat hard to achieve except by the Leborgne method of observing every patient in the last few days of a treatment. Or by the present modelling.)
6. Optimum tumour cell kill occurs at the Tk related time of, or soon after, 21–32 days if 2-Gy fractions are given five times a week, and at a range of times from 42 to 50 days if two smaller fractions are given each day (see Figure 6). The maximum tumour damage is 4–5 Gy EQD higher for 2F/d than for 1F/d (therefore debatably worthwhile), but rising to a 10-Gy superiority in favour of 2F/day at an overall time of about 50 days if repopulation is slower than 3 days, i.e. if doubling times Tp are longer than 3 days.
7. No optimum OvT can be shorter than Tk, when tumour repopulation begins. This has implications for some SBRT, proton or cyberknife schedules, although in practice it suggests “not shorter than about 2 weeks” as far as we yet know. Five fractions in 5 days seems too short to achieve highest tolerable doses (Figures 4–6).
8. Most tumours will have optimum overall times at least a week or two longer than their Tk day.
9. With the exception of the few fastest-repopulating tumours, such as those with Tp of 3 days or less, whose optimum OvTs are then just at Tk days, then “repopulation rules.”
10. And with the exception of tumours with smaller α/β ratios than the late constraint α/β of 3 Gy, of which the outstanding example is prostate cancer [49] with breast cancer being near a cusp of no difference in its α/β ratios, and malignant melanoma with α/β ∼0.6 Gy [48].
11. More than two fractions a day suffer from two disadvantages: the possibility of incomplete repair in normal tissues (see note 2 above) and the inconvenience to patients and departmental planning. However, pulsed brachytherapy has dealt head-on with incomplete repair, even if its algorithms need further clinical confirmation.
12. If we do not know the values of Tk or Tp well enough, in individual tumours or in tumour types, that is a challenge to be able to measure them.
References to the appendices
- A1.Dale RG, Jones B. The assessment of RBE effects using the concept of biologically effective dose. Int J Radiat Oncol Biol Phys 1999;43:639–45 [DOI] [PubMed] [Google Scholar]
- A2.Dale RG, Carabe-Ferandez A. the radiobiology of conventional radiotherapy and its application to radionuclide therapy. Cancer Biother Radiopharm 2005;20:47–51 [DOI] [PubMed] [Google Scholar]
- A3.Carabe-Fernandez A, Dale RG, Jones B. The incorporation of the concept of minimum RBE (RBEmin) into the linear-quadratic model and the potential for improved radiobiological analysis of high-LET treatments. Int J Radiat Biol 2007;83:27–39 [DOI] [PubMed] [Google Scholar]
- A4.Jones B, Carabe-Fernandez A, Dale RG. Calculation of high-LET radiotherapy dose required for compensation of overall treatment time extensions. Br J Radiol 2005;79:254–7 [DOI] [PubMed] [Google Scholar]
- A5.Dale RG, Jones B, Coles IP. The effect of tumour shrinkage on the biological effectiveness of permanent brachytherapy implants. Br J Radiol 1994;67:639–45 [DOI] [PubMed] [Google Scholar]
- A6.Brenner DL, Hall EJ. Fractionation and protraction for radiotherapy of prostate carcinoma. Int J Radiat Oncol Biol Phys 1999;43:1095–101 [DOI] [PubMed] [Google Scholar]
- A7.Chappell R, Fowler JF, Ritter MA. In response to Drs Dale and Jones: “Is α/β for prostate tumours really low? In regard to Fowler et al IROBP 2001 50:1021–1031” [Letter]. Int J Radiat Oncol Biol Phys 2002;52:1427–8 [DOI] [PubMed] [Google Scholar]
- A8.Dale RG, Hendry JH, Jones B., et al Practical methods for compensating for missed treatment days in radiotherapy, with particular reference to head & neck schedules. Clin Oncol 2002;14:382–393 (Update of [29]). [DOI] [PubMed] [Google Scholar]
- A9.Jones B, Dale RG, Gaya A. Linear quadratic modelling of increased late normal tissue effects in special clinical situations. Int J Radiat Oncol Biol Phys 2006;64:948–953 [DOI] [PubMed] [Google Scholar]
- A10.Jones B, Cominos M, Dale RG. Application of the Biological Effective Dose (BED) to estimate the duration of symptomatic relief and repopulation dose equivalent in palliative radiotherapy and chemotherapy. Int J Radiat Oncol Biol Phys 2003;55:736–742 [DOI] [PubMed] [Google Scholar]
- A11.Jones B, Dale RG. Radiobiological compensation of treatment errors in radiotherapy. Br J Radiol 2008;81:323–326 [DOI] [PubMed] [Google Scholar]
- A12.Jones , B , Dale RG, Deehan C, Hopkins KI, Morgan DAL. The role of biologically effective dose (BED) in Clinical Oncology. Clin Oncol (UK RCR) 2001;13:71–81 [DOI] [PubMed] [Google Scholar]
- A13.Jones B., Dale RG The potential for mathematical modelling in the assessment of the radiation dose equivalent of cytotoxic chemotherapy given concomitantly with radiotherapy. Br J Radiol 2005;78:939–944 [DOI] [PubMed] [Google Scholar]
- A14.Jones B, Dale RG, Gaya A. Linear quadratic modelling in the assessment of the radiation dose equivalent of cytotoxic chemotherapy given concomitantly with radiotherapy. Br J Radiol 2005;79:254–257 [DOI] [PubMed] [Google Scholar]
- A15.Plataniotis GA, Dale RG. Use of concept of chemotherapy-equivalent biologically effective dose to provide quantitative evaluation of contribution of chemotherapy to local tumor control in chemoradiotherapy cervical cancer trials. Int J Radiat Oncol Biol Phys 2008;72:1538–1543 [DOI] [PubMed] [Google Scholar]
- A16.Fowler J. Correction to Kasibhatla et al. How much radiation is the chemotherapy worth in advanced head and neck cancer? (IJROBP 2007;68:1491–1495). Int J Radiat Oncol Biol Phys 2008;71:326–329 [DOI] [PubMed] [Google Scholar]
- A17.Lee I, Eisbruch A. Mucositis versus tumor control: the therapeutic index of adding chemotherapy to irradiation of head and neck cancer. Int J Radiat Oncol Biol Phys 2009;75:1060–1063 [DOI] [PubMed] [Google Scholar]
- A18.Hartley A, Sanghera P, Glaholm J., et al Radiobiological modelling of the therapeutic ratio for the addition of synchronous chemotherapy to radiotherapy in locally advanced squamous cell carcinoma of the head and neck. Clin Oncol 2009 Oncology (UK RCR) 2010;22:125–130 [DOI] [PubMed] [Google Scholar]
- A19.Petereit DG, Sarkaria JN, Chappell R, Fowler JF, Hartmann , Kinsella TJ, et al. The adverse effect of treatment prolongation in cervical carcinoma. Int J Radiat Oncol Biol Phys 1995;32:1301–7 [DOI] [PubMed] [Google Scholar]
- A20.Leborgne F, Fowler JF, Leborgne JH, Zubizarreta E, Chappell Fractionation in medium dose rate brachytherapy of cancer of the cervix. Int J Radiat Oncol Biol Phys 1996;35:907–14 [DOI] [PubMed] [Google Scholar]
- A21.Leborgne F, Fowler JF, Leborgne JH, Zubizareta E, Curuchquin R. Medium–dose-rate brachytherapy of cancer of the cervix: preliminary results of a prospectively designed schedule based on the linear quadratic model. Int J Radiat Oncol Biol Phys 1999;43:1061–4 [DOI] [PubMed] [Google Scholar]
- A22.Leborgne , F , Fowler JF, Leborgne JH., et al Biologically Effective Doses in medium dose rate brachytherapy of cancer of the cervix. Radiat Oncol Invest 1997;5:289–99 [DOI] [PubMed] [Google Scholar]
- A23.Fowler JF. Dose reduction factors when increasing dose in LDR or MDR brachytherapy of carcinoma of the cervix. Radiother Oncol 1997;45:49–54 [DOI] [PubMed] [Google Scholar]
- A24.Clark BG, Souhami L. Roman TN, Chappell R, Evans MDC, Fowler JF. The prediction of late rectal complications in patients treated with high dose-rate brachytherapy for carcinoma of the cervix using the linear quadratic model. Int J Radiat Oncol Biol Phys 1997;38:989–93 [DOI] [PubMed] [Google Scholar]
- A25.Gasinska A, Fowler JF, Lind BK., et al Influence of overall treatment time and radiobiological parameters on biologically effective doses in cervical cancer patients treated with radiation therapy alone. Acta Oncol 2004;43:657–66 [DOI] [PubMed] [Google Scholar]
- A26.Fowler JF, Chappell R. Non-small cell lung tumors repopulate rapidly during radiation therapy [Letter]. Int J Radiat Oncol Biol Phys 2000;46:516–17 [DOI] [PubMed] [Google Scholar]
- A27.Mehta M, Scrimger R, Mackie R., et al A new approach to dose escalation in non-small-cell lung cancer. Int J Radiat Oncol Biol Phys 2001;49:22–3 [DOI] [PubMed] [Google Scholar]
- A28.Fowler JF, Tome W, Fenwick J, Meta M. Stereotactic body radiotherapy: a challenge to conventional radiation oncology. Int J Radiat Oncol Biol Phys 2004;60:1241–56 [DOI] [PubMed] [Google Scholar]
- A29.Timmerman R, Paulus R, Galvin J, Michalski J, Straube W, Bradley J, et al. RTOG 0236: Stereo-tactic body radiotherapy to treat medically inoperable early stage lung cancer patients. J Am Med Assoc 2010;303:11 1070–1076 [Google Scholar]
- A30.Bradley J, Bae K, Graham M, Byhardt R, Govindan R, Fowler J, et al. doi: 10.1200/JCO.2009.27.1205. Primary analysis of phase II of a phase I/II dose intensification study using three dimensional conformal radiation therapy and concurrent chemotherapy for oatients with inoperable, non-smalll cell lung cancer. Radiation Oncology Group (RTOG 0117). J Clin Oncol 2010. Published ahead of print on April 5th, 2010 as10.1200/JCO.2009.27.1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A31.Seppenwoolde Y, Lebesque J, de Jaeger K., et al Comparing different NTCP models that predict the incidence of radiation pneumonitis. Int J Radiat Oncol Biol Phys 2003;55:724–35 [DOI] [PubMed] [Google Scholar]
- A32.Chi A, Welsh J, Fowler J, Tome W, Meta M. Stereotactic body radiation therapy in non-small-cell lung cancer: linking radiobiologic modeling and clinical outcome. Am J Clin Oncol. doi: 10.1097/COC.0b013e3181df4b3f. 2010 Accepted 19 Feb 2010. [DOI] [PubMed] [Google Scholar]
- A33.Slotman BJ, Antonosse LE, Njo KH. Limited field irradiation in early stage (T1-2 N0) non-small cell lung cancer. Radiother Oncol 1996;41:41–44 [DOI] [PubMed] [Google Scholar]
- A34.Maguire J, Marks LB, Sibley GS, Herndon SE, 2nd, Clough RW, Light KL., et al 73.6 Gy and beyond; hyperfractionated, accelerated radiotherapy for non-small cell lung cancer. J Clin Oncol 2001;19:705–11 [DOI] [PubMed] [Google Scholar]
- A35.Cheung PCF, Yeung LTF, Basrur V, Ung YC, Balogh J, Danjoux CE. Accelerated hypofraction for early-stage non-small cell lung cancer. Int J Radiat Oncol Biol Phys 2002;54:1014–1023 [DOI] [PubMed] [Google Scholar]
- A36.Mehta MP, Wang W, Johnson D, Wagner H, Schiller J, Veeder M, et al. Induction chemotherapy followed by standard thoracic radiotherapy vs hyperfractionated accelerated radiotherapy for patients with unresectable stage IIIA and B non-small-cell lung cancer: phase III study of the eastern cooperative oncology group (ECOG 2597). Int J Radiat Oncol Biol Phys 2003;57:S14. [DOI] [PubMed] [Google Scholar]
Footnotes
The author has no financial conflict of interest.
References
- 1.Fowler JF. A Review: The linear quadratic formula and progress in fractionated radiotherapy. Br J Radiol 1989;62:679–675 [DOI] [PubMed] [Google Scholar]
- 2.Park CS, Papiez L, Zhang S, Story M, Timmerman RD. Universal survival curve and single fraction equivalent dose: useful tools in understanding potency of ablative radiotherapy. Int J Radiat Oncol Biol Phys 2008;70:847–52 [DOI] [PubMed] [Google Scholar]
- 3.Maciejewski B, Withers HR, Taylor JMG, et al. Dose fractionation and regeneration in radiotherapy for cancer of the oral cavity and oropharynx: tumor dose-response and repopulation. Int J Radiat Oncol Biol Phys 1989;16:831–43 [DOI] [PubMed] [Google Scholar]
- 4.Curtis SB. Lethal and potentially lethal lesions induced by radiation – a unified repair model. Radiat Res 1986;106:252–70 [PubMed] [Google Scholar]
- 5.Gilbert CW, Hendry JH, Major D. The approximation in the formulation for survival of S = exp – (αd+βd2). Int J Radiat Biol;37:469–71 [DOI] [PubMed] [Google Scholar]
- 6.Douglas BG, Fowler JF. The effect of multiple small doses of X-rays on skin reactions in the mouse and a basic interpretation. Radiat Res 1976;66:401–26 [PubMed] [Google Scholar]
- 7.Lea DE, Catcheside DG. The mechanism of the induction by radiation of chromosome aberrations in Tradescantia. J Genet 1942;$$:216–45 [Google Scholar]
- 8.Barendsen GW. Dose-survival curves of human cells in tissue culture irradiated with alpha-, beta, 20-KV X- and 200KV X-radiation. Nature 1962;193:1153–5 [DOI] [PubMed] [Google Scholar]
- 9.Withers HR, Thames HD, Peters LJ. Differences in the fractionation response of acutely and late-responding tissues. In: Kärcher KH, et al., editors. Progress in radio-oncology II. New York, NY: Raven Press, 1982: 287–96 [Google Scholar]
- 10.Thames HD, Peters LJ, Withers HR, Fletcher GH. Accelerated fractionation vs hyperfractionation : rationales for several treatments per day. Int J Radiat Oncol Biol Phys 1983;9:127–38 [DOI] [PubMed] [Google Scholar]
- 11.Fowler JF. Brief summary of radiobiological principles in fractionated radiotherapy. Sem Radiat Oncol 1992;2:16–21 [Google Scholar]
- 12.Barendsen GW. Dose fractionation, dose rate, and isoeffect relationships for normal tissue responses. Int J Radiat Oncol Biol Phys 1982;8:1981–97 [DOI] [PubMed] [Google Scholar]
- 13.Withers HR, Taylor JMG, Maciejewski B. The hazard of accelerated tumor clonogen repopulation during radiotherapy. Acta Oncol 1988;27:131–46 [DOI] [PubMed] [Google Scholar]
- 14.Travis EL, Tucker SL. Isoeffect models and fractionated radiation therapy. Int J Radiat Oncol Biol Phys 1987;13:283–7 [DOI] [PubMed] [Google Scholar]
- 15.Van deGeijn J. Incorporating the time factor into the linear quadratic model [letter]. Br J Radiol;62:296–8 [DOI] [PubMed] [Google Scholar]
- 16.Thames HD, Withers HR. Tests of equal effect per fraction and estimation of initial clonogen number in microcolony assays of survival after fractionated irradiation. Br J Radiol 1980;53:1071–7 [DOI] [PubMed] [Google Scholar]
- 17.Fowler JF, Stern BE. Dose-rate factors in integral dose estimations [letter]. Br J Radiol 1958;31:316 [Google Scholar]
- 18.Fowler JF, Stern BE. Dose-rate effects: some theoretical and practical considerations. Br J Radiol 1960;33:389–95; 58 [DOI] [PubMed] [Google Scholar]
- 19.Fowler JF, Morgan RL, Silvester JA, et al. Experiments with fractionated X-ray treatment of the skin of pigs. I fractionation up to 28 days. Br J Radiol 1963;36:188–96 [DOI] [PubMed] [Google Scholar]
- 20.Douglas BG, Fowler JF. Fractionation schedules and a quadratic dose effect relationship [letter]. Br J Radiol 1975;48:502–3 [DOI] [PubMed] [Google Scholar]
- 21.Denekamp J. Changes in the rate of repopulation during multifraction irradiation of mouse skin. Br J Radiol 1973;46:381–7 [DOI] [PubMed] [Google Scholar]
- 22.Dale RG. The application of the linear-quadratic dose-effect equation to fractionated and protracted radiotherapy. Br J Radiol 1985;58:515–8 [DOI] [PubMed] [Google Scholar]
- 23.Dale RG. The application of the linear-quadratic model to fractionated radiotherapy when there is incomplete normal tissue recovery between fractions, and possible implications for treatments involving multiple fractions per day. Br J Radiol 1986;59:919–27 [DOI] [PubMed] [Google Scholar]
- 24.Dale RG. Possible dose rate dependence of recovery kinetics as deduced from a preliminary analysis of the effects of fractionated irradiations at varying dose rates. Br J Radiol 1988;61:153–7 [DOI] [PubMed] [Google Scholar]
- 25.Dale RG, Jones B. The clinical radiobiology of brachytherapy. Br J Radiol 1998;71:465–83 [DOI] [PubMed] [Google Scholar]
- 26.Armpilia CI, Dale RG, Jones B. Determination of the optimum dose per fraction in fractionated radiotherapy when there is delayed onset of tumour repopulation during treatment. Br J Radiol 2004;77:765–7 [DOI] [PubMed] [Google Scholar]
- 27.Fu KK, Pajak TF, Trotti A, et al. A Radiation Therapy Oncology Group (RTOG) phase III randomized study to compare hyperfraction and two variants of accelerated fractionation to standard fractionation radiotherapy for head and neck squamous cell carcinomas: first report of RTOG 90–03. Int J Radiat Oncol Biol Phys 2000;48:7–16 [DOI] [PubMed] [Google Scholar]
- 28.Trotti , et al. Long term outcomes of RTOG 90-03. Int J Radiat Oncol Biol Phys 2005;63:S70–1 [Google Scholar]
- 29.Hendry JH, Bentzen SM, Dale RG, et al. A modelled comparison of the effects of using different ways to compensate for missed treatment days in radiotherapy. Clin Oncol 1996;8:297–307 (Updated in 2002, see A8.) [DOI] [PubMed] [Google Scholar]
- 30.Leborgne F, Leborgne JH, Zubizaretta E, Fowler JF, Mezzera J. Accelerated hyperfractionated irradiation for advanced head and neck cancer: effect of shortening the median treatment duration by 13 days. Head Neck 2001;23:661–8 [DOI] [PubMed] [Google Scholar]
- 31.Lee AWM, Sze W-M, Yau T-K, et al. Retrospective analysis on treating nasopharyngeal carcinoma with accelerated fractionation (6 fractions per week) in comparison with conventional fractionation (5 fractions per week): report on 3-year tumor control and normal tissue toxicity. Radiother Oncol 2001;58:121–30 [DOI] [PubMed] [Google Scholar]
- 32.Overgaard J, Hansen HS, Lena S, et al. Five compared with six fractions per week of conventional radiotherapy of squamous cell carcinomas of head and neck: DAHANCA 6 & 7 randomised controlled trial. Lancet 2003;362:933–40 [DOI] [PubMed] [Google Scholar]
- 33.Saunders M, Rojas AM, Dische S. CHART revisited: a conservative approach for advanced head and neck cancer. Clin Oncol (RCR) 2008;20:127–33 [DOI] [PubMed] [Google Scholar]
- 34.Poulsen MG, Denham JW, Peters LJ, et al. A randomized trial of accelerated and conventional radiotherapy for stage III and IV squamous carcinoma of the head and neck: a Trans-Tasman Radiation Oncology Group Study. Radiother Oncol 2001;60:113–22 [DOI] [PubMed] [Google Scholar]
- 35.Saunders MI, Dische S, Barrett A, et al. Continuous, hyperfractionated, accelerated radiotherapy (CHART) versus conventional radiotherapy in non-small-cell lung cancer: mature data from the randomized multicentre trial. Radiother Oncol 1999;52:137–48 [DOI] [PubMed] [Google Scholar]
- 36.Fowler JF. Practical time–dose evaluation, or how to stop worrying and love LQ. In: Levitt SH, Purdy JA, Perez CA, Vijayakumar S, editors. Technical basis of radiation therapy, 4th revised edition. Heidelberg: Springer-Verlag, 2006:3–31 [Google Scholar]
- 37.Fowler JF, Harari PM, Leborgne F, Leborgne JH. Acute radiation reactions in oral and pharyngeal mucosa: tolerable levels in altered fractionation schedules. Radiother Oncol 2003;69:161–8 [DOI] [PubMed] [Google Scholar]
- 38.Sanguinetti G, Sosa M, Endres E, et al. Hyperfractionated IMRT (HF-IMRT) alone for locally advanced oropharyngeal carcinoma: a phase I study. Radiother Oncol 2004;73(Suppl 1):S300 [Google Scholar]
- 39.Huang EH, Pollack A, Levy Y, et al. Late rectal toxicity: dose–volume effects of conformal radiotherapy for prostate cancer. Int J Radiat Oncol Biol Phys 2002;54:1314–21 [DOI] [PubMed] [Google Scholar]
- 40.Strigari L, Arcangeli G, Arcangeli S, et al. Mathematical model for evaluating incidence of acute reactal toxicity during conventional or hypofractionated radiotherapy courses for prostate cancer. Int J Radiat Oncol Biol Phys 2009;73:1454–60 [DOI] [PubMed] [Google Scholar]
- 41.Fenwick J. Early mucosal reactions during and after head-and-neck radiotherapy. Int J Radiat Oncol Biol Phys 2008;71:625–34 [DOI] [PubMed] [Google Scholar]
- 42.Fowler JF. Optimum overall times II: Extended modelling for head and neck radiotherapy. Clin Oncol (RCR) 2008;20:113–26 [DOI] [PubMed] [Google Scholar]
- 43.Fowler JF. How worthwhile are short schedules in radiotherapy? Radiother Oncol 1990;18:165–81 [DOI] [PubMed] [Google Scholar]
- 44.Kaanders JHAM, van derKogel AJ, Ang KK. Altered fractionation: limited by mucosal reactions? Radiother Oncol 2002;22:81–91 [DOI] [PubMed] [Google Scholar]
- 45.Dörr W, Hamilton CS, Boyd T, et al. Radiation induced changes in cellularity and proliferation in human oralmucosa. Int J Radiat Oncol Biol Phys 2002;52:911–17 [DOI] [PubMed] [Google Scholar]
- 46.Roberts SA, Hendry JH. Time factors in larynx tumour radiotherapy: lag times ad intertumour heterogeneity in clinical data sets from four centers. Int J Radiat Oncol Biol Phys 1999;45:1247–57 [DOI] [PubMed] [Google Scholar]
- 47.Arvidson NB, Khunyia D, Tome WA. Dose escalation model for limited-stage small-cell lung cancer. Radiother Oncol 2009;91:379–85 [DOI] [PubMed] [Google Scholar]
- 48.Bentzen SM, Overgaard J, Thames HD, et al. Clinical radiobiology of malignant melanoma. Radiother Oncol 1989;16:169–82 [DOI] [PubMed] [Google Scholar]
- 49.Fowler JF. The radiobiology of prostate cancer : new aspects of fractionated radiotherapy. Acta Oncol 2005;44:265–75 [DOI] [PubMed] [Google Scholar]
- 50.Sgouros G, Howell RW, Bolch WE, Fisher DR. doi: 10.2967/jnumed.108.057398. MIRD Commentary: Proposed name for a dosimetry unit applicable to deterministic biological effects – The Barendsen (Bd) [DOI] [PubMed] [Google Scholar]
- 51.Fowler JF, Dale RG. When is a BED not a BED? – When it's an EQDQ! [Letter] IJROBP. Accepted 5 May 2010. [Google Scholar]