Monte Carlo radiotherapy simulations of accelerated repopulation and reoxygenation for hypoxic head and neck cancer

Abstract

Objective

A temporal Monte Carlo tumour growth and radiotherapy effect model (HYP-RT) simulating hypoxia in head and neck cancer has been developed and used to analyse parameters influencing cell kill during conventionally fractionated radiotherapy. The model was designed to simulate individual cell division up to 10⁸ cells, while incorporating radiobiological effects, including accelerated repopulation and reoxygenation during treatment.

Method

Reoxygenation of hypoxic tumours has been modelled using randomised increments of oxygen to tumour cells after each treatment fraction. The process of accelerated repopulation has been modelled by increasing the symmetrical stem cell division probability. Both phenomena were onset immediately or after a number of weeks of simulated treatment.

Results

The extra dose required to control (total cell kill) hypoxic vs oxic tumours was 15–25% (8–20 Gy for 5×2 Gy per week) depending on the timing of accelerated repopulation onset. Reoxygenation of hypoxic tumours resulted in resensitisation and reduction in total dose required by approximately 10%, depending on the time of onset. When modelled simultaneously, accelerated repopulation and reoxygenation affected cell kill in hypoxic tumours in a similar manner to when the phenomena were modelled individually; however, the degree was altered, with non-additive results. Simulation results were in good agreement with standard linear quadratic theory; however, differed for more complex comparisons where hypoxia, reoxygenation as well as accelerated repopulation effects were considered.

Conclusion

Simulations have quantitatively confirmed the need for patient individualisation in radiotherapy for hypoxic head and neck tumours, and have shown the benefits of modelling complex and dynamic processes using Monte Carlo methods.

Tumour hypoxia and radiotherapy

Multiple studies have shown that hypoxia decreases the sensitivity of cells to ionising radiation and affects tumour cells as well as healthy cells in vitro and in vivo [1-3]. Head and neck cancers often exhibit regions of tumour hypoxia; approximately 70% of locally advanced tumours present with hypoxic regions at diagnosis [4,5]. Currently, radiotherapy is used as the sole radical treatment modality for approximately 50% of head and neck tumours. The tumour control probability (TCP) rates are approximately 80% for early-stage head and neck squamous cell carcinoma; however, this probability drops significantly (often below 50%) for locally advanced disease [6-8].

It has been shown in clinical trials that some cancer types, including head and neck cancer, show improved outcomes when hyper-fractionated and/or accelerated radiation treatment schedules are used. Some trials have shown that stratifying patients for tumour oxygen related parameters had a significant impact on prognosis [6,9]. However, owing to the time constraints involved in treatment individualisation as well as the complexity and logistics of obtaining, interpreting and using specific patient biological data, it is still common practice to use the conventional 2 Gy per day, 5 days per week radiotherapy scheduling despite the benefits of altered fractionation schedules. These statistics show that research is required to investigate the impact of hypoxia and the process of reoxygenation (ROx) during therapy, to quantify the potential benefits to outcome that may be achieved by individualising radiotherapy treatment.

Accelerated repopulation during radiotherapy

In tumours of epithelial origin, repopulation after trauma, such as a dose of irradiation, may occur through rapid cell division of the surviving cell population. In a tumour system this rapid repopulation has a detrimental effect on tumour control, especially if the total planned treatment time is extensive [10]. On average, published reports conclude that head and neck squamous cell carcinoma (HNSCC) accelerated repopulation (AR) onset time or “kick off” time is approximately 2–4 weeks into therapy, but could be as late as 5 weeks into therapy [11].

There are a number of theories on the mechanisms that contribute towards AR. The key cellular mechanism is the increase in the probability of the clonogenic tumour stem cells to produce two clonogenic daughter cells upon division; this is called the stem cell symmetrical division probability [10,12]. In normal tissue this probability is very low and symmetrical division only occurs when cell replacement is required. Other mechanisms of AR include a decrease in the average cell cycle time (CCT), recruitment of the cells from the G0 quiescent phase and dedifferentiation of cells to a more “stem-like” state.

It is likely that a number of these mechanisms are induced together; however, their times of onset require further study [10^,12-14]. In this work symmetrical stem cell division has been modelled as the sole mechanism of AR. The factor increase in symmetrical division compared with the normal division rate is not well known and may differ for every tumour. The modelling of this effect has therefore been analysed in detail through implementation of a factor, called the AR boost factor. Of particular interest were the most plausible AR boost factor values and the time of onset for AR, which may be a gradual process on the microscopic/cellular level initiated earlier than 2–5 weeks into treatment [15].

Tumour and treatment modelling

An efficient way to complement results from clinical trials is to predict the effect of tumour-related parameters on biological mechanisms and treatment efficacy using computer models. Models that can predict the effect of individualised tumour properties on treatment outcome after conventional and altered radiation treatment schedules are of value in the pursuit of individualisation of radiotherapy planning based on the individual tumour.

Results from models are reproducible and can take into account the statistical nature of the biology through the use of probability distributions and Monte Carlo (stochastic) techniques. Compared with clinical trials, computer models have the potential to benefit the user in terms of time efficiency and resource requirements. In addition, model input parameters may be tailored to the individual or a population subset to provide a personalised prediction of tumour growth or treatment response to a variety of radiotherapy treatment options and an estimate on how tumour parameters affect outcome.

When considering tumour hypoxia, computer models are particularly advantageous as there is a wide distribution of oxygenation levels among cells in most tumours. Monte Carlo modelling allows the entire range of oxygen levels (oxygenation histogram) to be used to assign cellular oxygen levels and this distribution can be changed in time to simulate the changing oxygenation dynamics during therapy.

Stochastic computer tumour models were first developed in the early 1980s and 1990s by groups Donaghey et al, Duechting and Vogelsaenger, Smolle and Stettner, and Kocher [16-20]. These were the first models to peruse individual (or grouped) cell division using Monte Carlo methods, to grow a tumour and simulate radiotherapy, and in some cases start to implement oxygenation-related parameters. Hypoxia modelling has been built on work from the mid-1990s when the initial hypoxia-related experimental and mathematical models were researched by Elkind et al, Tannock and Steel, and Thomlinson and Gray [21-23]. This initial work proved that hypoxia exists in tumour systems and that the diffusion distance of oxygen from blood vessels was directly related to cellular oxygenation. Currently, work is being pursued by researchers, such as Stamatakos and Dionysiou, Antipas, Sovik and Dasu, using mathematical [24-28], as well as Monte Carlo techniques. However, the Monte Carlo technique is becoming more common for modelling tumour growth and subsequent radiation-induced cell kill, and is proving to be especially useful for modelling the oxygenation levels of dynamic biological systems.

The present article presents a temporal stochastic computer model for propagating individual cells to simulate tumour growth, and subsequent conventional fractionated radiotherapy treatment. Analysis of conventional radiotherapy treatment schedule outcomes are relevant because many radiotherapy centres continue to prescribe the 2 Gy per day, 5 days per week dose schedule, and do not have the resources to routinely treat patients with 6 days per week or multiple fraction per day schedule.

A detailed description of the theory behind the tumour growth algorithm of the model has been reported upon previously [29], therefore, this report will consist of a brief overview of the current version of the model and then describe in more depth those parameters used in the current study to analyse the impact of AR and ROx alone or simultaneously on cell kill during simulated radiotherapy.

Aims

The current work aims to analyse the tumour and treatment parameters used within the HYP-RT model in terms of the effect on the number fractions (5×2 Gy per week) required to control tumours of various oxygenation levels. The parameters analysed are those controlling AR, ROx and the difference in the number of fractions required to eliminate all cells compared with having 1 or 5 cells remaining.

The results of these simulations are compared with linear quadratic (LQ) theory and clinical trial data to validate the HYP-RT model. Future publications regarding this model will aim to broaden the analysis for alternative schedules including many of the hyperfractionated and accelerated schedules used in HNSCC clinical trials.

Methods and materials

The HYP-RT model has been designed based on the biology of epithelial tissue to simulate HNSCC tumour growth and radiotherapy. The algorithms employ Monte Carlo methods to predict the number of 2 Gy treatment fractions required to kill all cells that have the potential to grow back the tumour. Tumour hypoxia is modelled using individual cell oxygen assignment based on published Eppendorf partial pressure of oxygen (pO₂) histograms, which have a known effect on tumour CCT and radiosensitivity. Algorithms have also been developed to simulate the process of gradual ROx and cellular repopulation as well as AR between treatment fractions.

Hypoxic tumour growth and radiotherapy in the model

Oxic tumours have been modelled in the current work using a uniform distribution of pO₂ values ranging from 5–100 mmHg. To model a biologically relevant range of tumour cell pO₂ values for hypoxic tumours, HNSCC Eppendorf probe results were identified in the literature and normalised to create probability distributions [30-32]. The moderately and severely hypoxic pO₂ histograms used in the model are shown in Figure 1. For comparison, normal tissue oxygenation levels in non-diseased tissue are in the range of 20–100 mmHg, with an average of 40 mmHg in the head and neck region [30, 31, 32].

Figure 1.

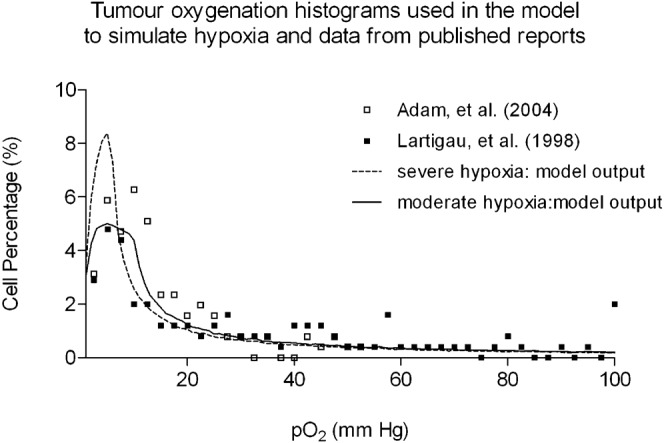
The distribution of oxygen levels used to simulate moderate and severe hypoxia (black and dashed curves) compared with literature reports [30–32]. The scattered distributions represent the pO₂ histogram outputs from the model when using a log-normal random number generator.

In the model cells are considered on an individual basis and are classed as either clonogenic cells (S cells, stem cells), as transit cells (T cells, limited to a few generations of division), differentiating cells (D1 or D2 cells) or fully differentiated cells (D3 cells). Stem cells may be in a G0 quiescent phase. All cycling cells are assigned a CCT (Gaussian distribution) and an oxygenation value. The progress of the tumour can be tracked at any time during growth and during radiotherapy from a single stem cell.

Oxygenation has been modelled to alter CCT [33,34] with cell cycle arrest occuring at a 1 mmHg. Arrested cells are eliminated using a half-life of 4 days (if not reoxygenated), a value which can be adjusted by the modeller if desired [35]. Cellular parameters and other processes in the algorithm that required randomisation use a Gaussian, uniform or exponential probability distribution. Random number generation was performed using the Ziggurat algorithm, which generates a pseudorandom number sequence with 32-bit precision [36].

The radiotherapy algorithm was developed to simulate fractionated therapy of 5×2 Gy per week (no weekends), assuming that a uniform dose is delivered to the tumour. LQ theory was implemented to define the average cycling cell survival probability using the standard surviving fraction (SF) equation based on alpha and beta parameters. The probability of cell kill is assessed for each individual cell in the population for each dose fraction, based on LQ theory. However, before cell death is implemented the probability is altered to take into account the current oxygenation level for each cell based on the oxygen enhancement ratio reported by Kirkpatrick et al [37].

To model gradual tumour ROx during treatment, a method of implementing small pO₂ increases was designed using a randomised binomial theory-based approach. After ROx is onset in the model, a ROx event is programmed to occur after each dose fraction (by default the number of increments is equated to the total cell number at the time). These events involve calculating the probability of each cell receiving between zero and four pO₂ increments. The probability of 5 or more increments was below 0.5% and disregarded. The ROx process is carried out by calculating the pO₂ increase required for each cell and then increasing the oxygen level of each cell by the increment number multiplied by the pO₂ increment size (default of 3 mmHg). This process was designed to be dependent on the current cell number and the most recent fraction dose. ROx events were set to occur a few hours after each treatment fraction (default of 4 h [38]). Oxygen increment size was set to ensure that when tumours had reduced to approximately 1–2 mm in diameter the pO₂ histogram resembled the oxic tumour distribution (an approximate uniform distribution ranging from 5–100 mmHg).

AR was modelled by increasing the symmetrical stem cell division probability (S_percent) with a multiplicative factor called the “AR boost factor”. The S_percent parameter was set to a default value of 3% during tumour growth and the beginning of treatment, which has been justified in a previous report [29].

The default AR boost factor value of 10 was determined to be the most plausible value for this parameter based on the corresponding decrease in tumour doubling time (e.g. for random seed 333: from 35 to 65 days before the boost decreased to 1 to 5 days after the boost, depending on oxygenation status) and an analysis of the extra dose per fraction required to kill the extra cells that had propagated as a result of AR (published data reporting values between 0.5–1.0 Gy per fraction [10, 39–42]). The comparison of the doses per fraction have not been disclosed here and will form part of a separate report.

An AR boost factor of 10 was expected to yield the most suitable effect on cell growth. This was based on the commonly reported theory of AR causing the tumour growth rate to increase by approximately 10 times (reducing the potential doubling time of the tumour if all stem cells (T_pot) from 10–20 days pre-treatment to as low as 2 days, and thereby approaching the stem cell division time [10,13]). In this study an AR boost factor of 10 decreased tumour doubling times by approximately 10–15 times. For example, for moderately hypoxic tumours the tumour doubling time decreased from approximately 65 days before AR onset to approximately 4.4 days after AR onset, and for oxic tumours from approximately 37 days down to 3.7 days (all standard division errors less than 1 day when averaging over 5 simulations with different random number seeds). For moderately hypoxic tumours these doubling times are a good match to published data [10].

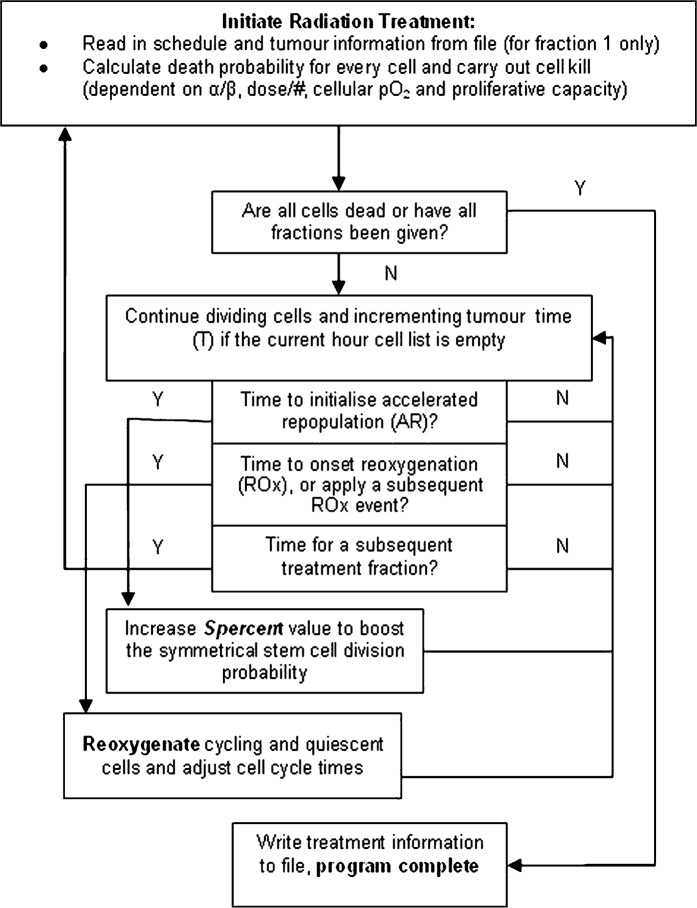
Fundamental tumour growth and radiation algorithm parameters are summarised in Table 1. A flow chart of the radiotherapy algorithm is shown in Figure 2. Outlining the basic process required to treat a grown tumour, apply hypoxia and simulate AR and ROx until tumour control has been achieved.

Table 1. Cellular and algorithm design-based parameters in the HYP-RT model used to simulate tumour growth and fractionated radiotherapy.

Parameter	Default	User input	Range	References	Comments
Cell total	108	Yes	Up to 108	N/A	Tumour cell limit in the growth algorithm.
Cell cycle time (stem cell)	27 h	No	Gaussian, sigma = 3 h	Indirect: Begg et al [43], Mantel et al [44], Steel [45], Wilson et al [46]	The G0 phase adds to the length to the stem cell cycle time. Infinite division capability of these cells.
Cell cycle time (transit cell)	33 h	No	Gaussian, sigma = 3 h	Gaussian, sigma = 6 h	Limited to 2–4 generations of division.
Differentiating time: D1 and D2 cells	D1: 36 hD2: 36 h	No	Uniform: range of 24–48 h	Indirect: Wilson et al [46], Potten et al [47]	Estimated based on 1–2 week cell turnover in epithelial tissue.
Fully differentiated D3 cell natural death rate	D3: 80%	No	Constant	Indirect: Steel [45] (approximately 85% cell loss factor)	This cell loss rate for the fully differentiated cells means that the total average cell loss is approximately 85% for the whole population where TD is approximately 40–45 days.
Stem cell division products i.e. the S:T:D1 ratio	S = 3% T = 87% D1 = 10%	Yes	Constant	Steel [45]	This ratio produces an approximate 1% stem cell population in the tumour
Low oxygen limit for cell cycle arrest	1 mmHg	Yes	Constant	Indirect: Alarcon [34], Ljungkvist et al [48]	Hypoxia induced quiescence is initiated at this pO2.
Percentage of cells exiting the cell cycle (with pO2 <1 mmHg)	50%	Yes	1–100%	N/A	Set so that the total number of hypoxia induced quiescent cells (<1 mmHg) = 3%, in line with the pO2 specific histogram used.
Hypoxic cell half-life (due to necrosis: pO2 <1 to 2 mmHg)	4 days	Yes	Constant	Durand and Sham [35], Ljungkvist [48]	4–10 day hypoxic cell lifetime in human colon carcinoma spheroids, 2 days in HNSCC xenografts.
AR onset time after RT initialisation (weeks)	No AR	Yes	0, 1, 2, 3	Withers et al [10], Marcu et al [12], Maciejewski et al [40], Peters and Withers [49], Terhaard et al [50], Trott [51], Trott and Kummermehr [52]	The number weeks into RT that AR is initiated, 2–4 weeks observed in references, however in this small tumour system. “0” weeks is used by default to initiate the microscopic response.
ROx onset time after RT initialisation (weeks)	No ROx	Yes	0, 1, 2, 3	N/A	The number of weeks into RT that ROx is initiated. This is an extremely variable parameter and open to user input.
Time of ROx after a particular RT fraction	4 h	Yes	1 to 23	Ljungkvist et al [38]	Factor increase in stem cell symmetrical division due to AR.
AR Spercent, factor increase in the symmetrical stem cell division probability	10	Yes	1.1 to 30.0	Marcu et al [12], Steel [45], Marcu et al [53]
ROx induced incremental increases in pO2	3 mmHg	Yes	1 to 5	N/A	pO2 increment size during randomised ROx after a RT fraction (linearly SF dependent), set to obtain full oxygenation by approximately 1 to 2 mm tumour diameter.
Alpha (LQ model)	0.3	Yes	0.1 to 1.0	Horiot et al [54], Stuschke and Thames [55]	Used in SF calculations (LQ equation).
Beta (LQ model)	0.03	Yes	0.01 to 0.1	Horiot et al [54], Stuschke and Thames [55]	Used in SF calculations (LQ equation).

RT, radiotherapy; ROx, reoxygenation; SF, surviving fraction; AR, accelerated repopulation; LQ, linear quadratic; HNSCC, head and neck small cell carcinoma.

Figure 2.

A flow diagram of the fractionated radiotherapy algorithm where initiation of treatment is followed by continual cell growth between subsequent treatment fractions. Accelerated repopulation is initiated once and ROx events are initiated and repeated at regular intervals after each subsequent fraction until the tumour is fully reoxygenated. Treatment is complete when either the number of desired fractions has been delivered or total cell death is achieved.

Tumour model parameter analysis

In a parametric analysis of the model, various parameter combinations were compared in terms of the number of 2 Gy fractions required to kill the tumour. Previous reports have concentrated on the tumour growth parameters (including the S_percentparameter, hypoxic tumour growth rates for various pO₂ histograms. The current analysis validates the default AR boost factor and the impact of all onset times of AR and ROx on cell kill for tumours of varying oxygenation levels.

Although clonogenic stems cells are traditionally thought to be the cells responsible for local treatment failure in radiotherapy, in this work the number of fractions required to kill all stem, transit and level one differentiating cells, as well as hypoxic cells, were analysed. These are cells that normally reside in the “basal” or lower layer of the epithelium in healthy tissue. This approach was taken because hypoxia may cause genetic mutations in cells as a result of the altered environmental conditions; this assists in dedifferentiation (to become more “stem-like”), which may threaten tumour control [56,57].

To assess quantitative statistical error, multiple simulation batch runs were simulated using different initial random seed number. This was applied to the tumour growth and to the treatment simulations that followed. Batch runs were also used to assess the impact of parameter values (within plausible ranges) for all fundamental tumour parameters while keeping other parameters constant, and for combinations of parameters that were likely to be dependent on each other.

All tumour growth and treatment data (recorded every 1000 h of tumour time during growth and at every fraction or ROx event) were written to file dose. Data included the different cell type percentages in the population, the timing of full ROx, the tumour growth rate and the pO₂ histogram for the total cell population. The post growth or treatment analyses were performed using a Java program with a graphical user interface, to access the data files and display the results of single simulations or batch run simulations.

Model assumptions

Where possible, literature values of tumour properties have been used from oropharynx HNSCC clinical trials and experimental work. However, it is possible to input parameters values suitable for other tumour sites. Owing to the limitation of the available experimental data in the literature and the complex nature of the system being modelled, it was necessary to make a number of assumptions.

Temporal tumour modelling can not been used to model blood vessel systems, which requires a spatial dimension. The HYP-RT model randomises the oxygenation assignment to cells, but cannot bias particular tumour regions or cell types into having higher oxygen levels than other regions or cells.

Where random number generation and probability distributions were used, assumptions including the truncating of the distributions and fitting biological data to smooth Gaussian, uniform or exponential curves were necessary. Hypoxia has been reported to affect the rate of cell differentiation [56] and radiosensitivity of cells when newly reoxygenated [58]; however, these effects have not been modelled. Model updates planned for future include cellular repair of sublethally damaged cells and cell death that can occur over a finite period of time.

Comparison of simulation to linear quadratic theory

LQ theory was used to determine the number of fractions required to reduce the cell number to below one cell, to compare with HYP-RT model predictions. To incorporate AR into this comparison, the standard LQ equation was adjusted with a time factor (Equation 1), which includes a kick off time variable (T_K), the potential doubling time (T_pot) and the total treatment time (t), where N₀ represents the initial number of cells and N represents the remaining number of cells [59]. An initial cell number of 10⁸ was used for all calculations and the T_K and T_potparameters were assigned values of 2–3 weeks and 4 days, respectively.

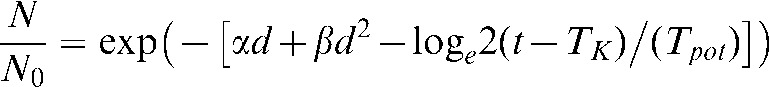(1)

Use of the LQ equation with OER modification was also included in the comparison between LQ theory and the HYP-RT model (Equation 2) [59, 60]. The LQ calculations were performed assuming a uniform hypoxic cell population, and hence a single q value representing the dose-modifying factor of hypoxic cells (Equation 3).

(2)

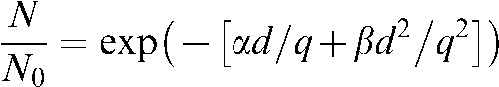(3)

The LQ equation with time factor and OER modification (Equation 4) was further implemented in the analysis, using the same range of q and T_K values as stated above.

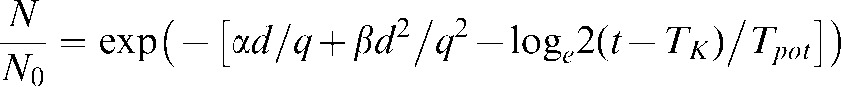(4)

To equate LQ results with HYP-RT results, a 3% hypoxic population (representing cells in the 0–1 mmHg range, having a low OER and hence high q value (2.0)), and a 97% oxic cell population was included in the LQ analysis (Equation 5) with h representing the hypoxic percentage of cells in the very low 0–1 mmHg range. No further assessment was made in terms of applying ROx modifying factors and functions because too many parameter assumptions would have been required.

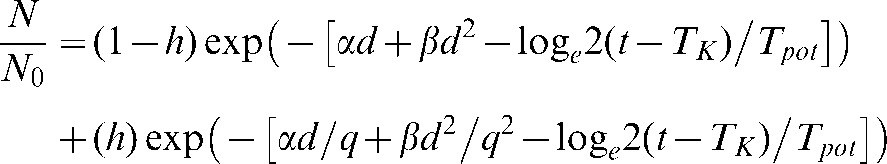(5)

Statistical analysis

All simulations were repeated for virtual tumours grown using different random seed number, to allow for the random statistical variations. For this analysis three tumours of each oxygenation category (oxic, moderately hypoxic and severely hypoxic) were grown using three random seed numbers. These tumours were then treated with a further three random number seeds for each parameter set investigated. This resulted in a total of nine simulations per parameter set and provided consistent error margins when comparing sets of averaged cell kill results.

Errors presented in the results in the text and figures are the standard deviations from nine simulations. Statistical significance has been analysed using a two-tailed t-test method (paired test if indicated) using a confidence interval of 95% (significant for p<0.05). Correlation has been assessed through linear regression (Pearson) with a confidence interval of 95%. Linear fit gradients and Pearson r values are presented with standard deviations and 95% confidence intervals, respectively. All data were processed using the statistical software package Prism 5 (v5.02, GraphPad Software Inc San Diego, CA).

Results

Results of tumour growth and radiotherapy simulations using the HYP-RT Monte Carlo model are presented as the number of fractions required to kill all tumour cells (all S, T and D1 cells). All results correspond to simulated conventional radiotherapy (5×2 Gy per week) of tumours consisting of 100 million cells.

Oxic tumour radiotherapy and accelerated repopulation

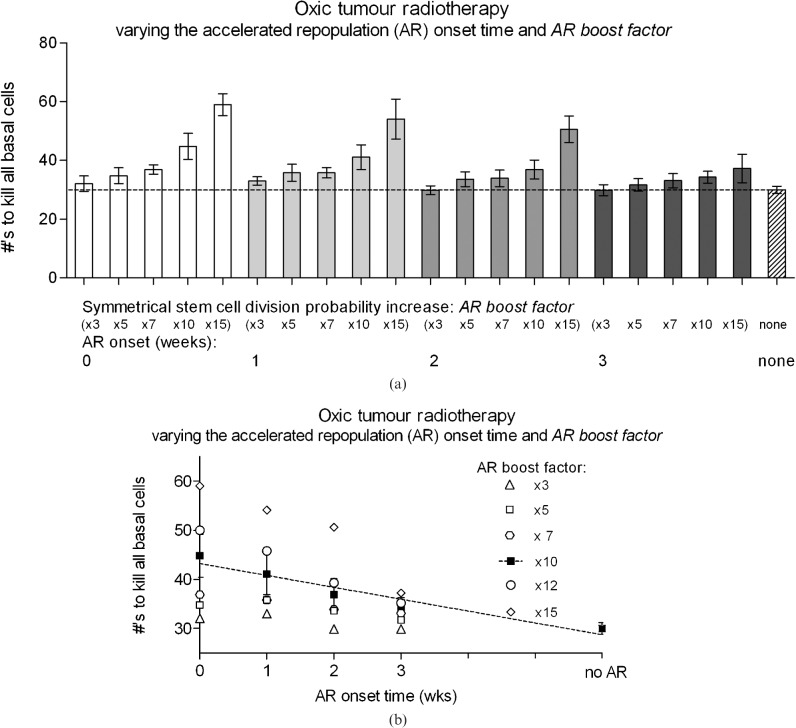
To analyse the effects of AR on cell kill, the symmetrical stem cell division probability (S_percent) was increased by the AR boost factor from ×3 to ×15. Figure 3a illustrates the change in the number of fractions required to kill all S, T and D1 cells as well as stem cells alone, for AR onset times ranging from 0 (immediate onset) to 3 weeks. With an AR boost factor of 10 or greater, the onset times of 2 weeks or less significantly affected the number of fractions required for total cell kill compared with the no AR case. For an AR boost factor of 10, no statistical difference in the number of required fractions was found compared to having no AR simulated. An AR boost factor value of 15 was found to be too high because of the extreme fraction number (>40) that resulted. These fraction numbers were outside of the estimated range deemed “normal” for head and neck tumours (or of even bigger diameter/cell number than that modelled here), corresponding to required total doses between 80 and 120 Gy in 8–12 weeks.

Figure 3.

The number of conventional radiotherapy fractions (5×2 Gy per week) required to kill all basal cells in oxic tumours, where the symmetrical stem cell division probability increase “boost factor” is, (a) varied from 3–15 and (b) plotted for boost factors ranging from 3–15. Note that treatment with no AR took 6 weeks (30 fractions).

From these results a value of 10 was deemed to be the most plausible AR boost factor. This result is in accordance with a previous sensitivity study that aimed to validate the AR boost factor through calculations of the extra dose per fraction required to account for AR. In this conventional fraction study an AR boost factor of 10 resulted in average equivalent doses per fraction of 2.6 Gy, which was in agreement with literature values ranging from 2.5–3.0 Gy per fraction [10,29,39,40,42,61]. Note that some radiotherapy plus concomitant chemotherapy schedules may have the effect of delaying tumour AR; however, this mechanism has not been considered for this report.

The total doses required to achieve 100% tumour control in the current study ranged from 62–108 Gy for hypoxic tumours (depending on ROx and AR onset times). These doses are reasonable considering the 70 Gy often prescribed in conventional schemes compared with the equivalent dose in 2 Gy fractions (EQD2) of 54–82 Gy (α/β = 10 Gy) and biological effective doses (BED with time correction) of 63–75 Gy (α/β = 10 Gy, α = 0.35 Gy^-1, T_pot = 4 days) calculated based on HNSCC clinical trials (i.e. with improvements in LC or reduction in toxicity) [62–67].

For AR onset times greater than 3 weeks and an AR boost factor of 10, no significant difference in fraction number could be detected compared with the no AR simulations. Note the exponential shape of the fraction number results for a fixed AR onset time and an increasing S_percentvalue. This shape was expected owing to the corresponding increase in exponential cell growth when the symmetrical division probability for stem cells was increased.

Linearity of AR onset time vs fraction number was relatively high (Pearson r² value of 0.93) using an AR boost factor value of 10 (Figure 3b), this corresponding to a 2.4 ± 0.4 average reduction in the number of fractions required for each week that AR onset was delayed.

Hypoxic tumour radiotherapy

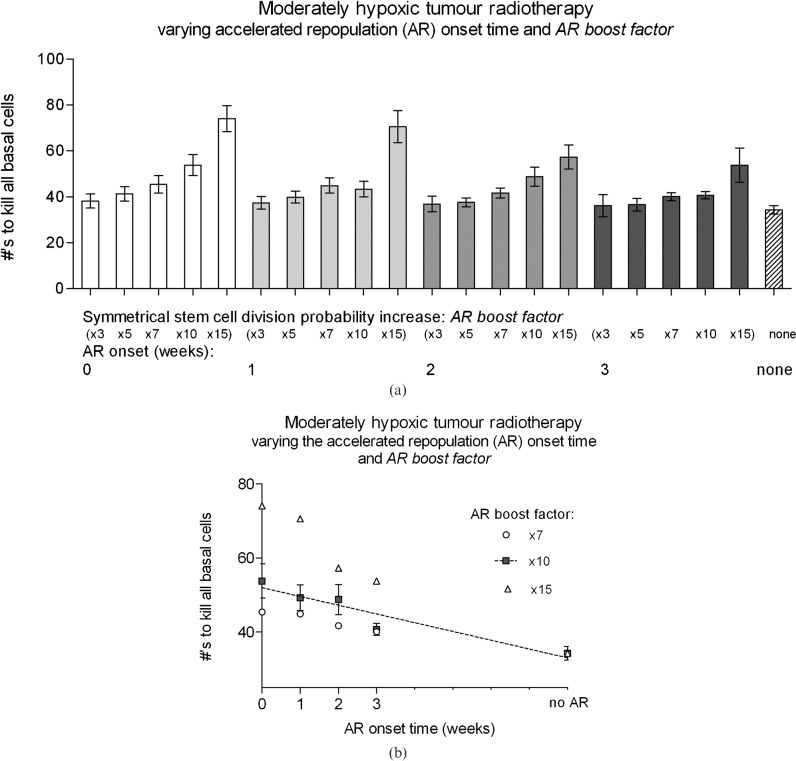
For moderately hypoxic tumours, the timing of AR onset affected cell kill with similar trends to the oxic tumour case, but by a reduced amount. Simulation results are shown in Figure 4a, where the AR boost factor was varied from 3–15. Linearity of the required number of fractions vs onset time for an AR boost factor of 10 was reduced compared with oxic tumour simulations (Pearson r² value of 0.9), with onset time vs total treatment time presented for a limited AR boost factor range between 7 and 15 (Figure 4b). For each week that AR onset was prolonged, the number of fractions reduced by 2.4 ± 0.5 (approximately 5 Gy per week), which was in accordance with oxic simulations.

Figure 4.

A comparison of the average number of conventional radiotherapy fractions (5×2 Gy per week) required for moderately hypoxic tumours, with accelerated repopulation (AR) onset at 0–3 weeks after the start of radiotherapy for a symmetrical stem cell division probability AR boost factor, (a) ranging from 3–15, and (b) ranging from 7–15, with no reoxygenation (ROx) simulated.

ROx had the effect of decreasing the number of required fractions to kill all cells (radiosensitising) as the onset time decreased (Figure 5). The response was linear with a Pearson r² factor of 0.91. The required dose increased by 6.6 ± 3.6 Gy (11%) when comparing the 0 week (immediate) ROx onset with no ROx onset. For each week that ROx onset was delayed the number of required fractions increased by 0.4 ± 0.1 (approximately 1 Gy per week).

Figure 5.

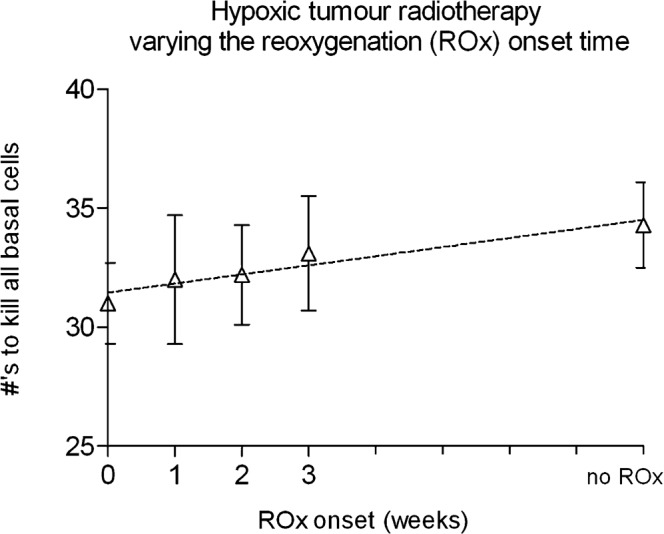
A comparison of the average number of conventional radiotherapy fractions (5×2 Gy per week) required for local control of moderately hypoxic tumours of 10⁸ cells, modelled with increasing reoxygenation (ROx) onset times, including the no ROx case with no accelerated repopulation considered.

The timing of ROx applied after each does fraction was analysed for the impact on the required fraction number for total cell kill. No significant difference was found when ROx was onset 4 h (default value) after a dose fraction or after 12, 24 or 48 h after a dose fraction.

Analysis of radiotherapy fractionation modelling both accelerated repopulation and reoxygenation

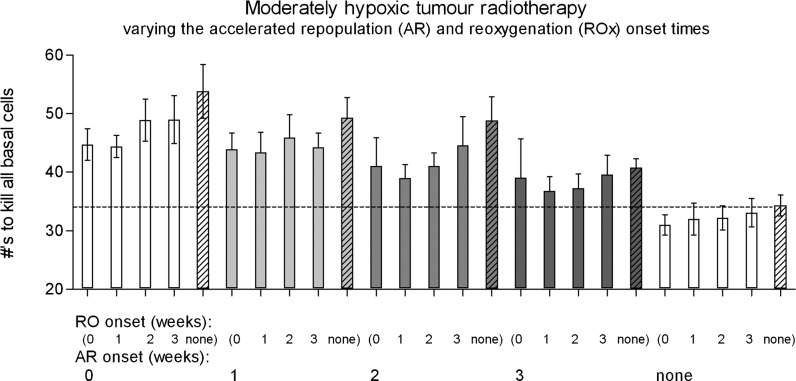
When considering ROx as well as AR for hypoxic tumours, the impact of AR on cell kill was decreased compared with no AR for all ROx onset times. Figure 6 shows all combinations of AR and ROx onset times ranging from 0–3 weeks and including the no AR and no ROx cases.

Figure 6.

Moderately hypoxic tumour conventional radiotherapy (5×2 Gy per week) fraction numbers required to achieve local control, varying the onset time of accelerated repopulation (AR) and reoxygenation (ROx) from 0–3 weeks, including the no AR and no ROx cases (striped columns). A dotted line represents the standard number of fractions for the no AR and no ROx case.

Whenever AR was modelled along with ROx, the required fractions to control the tumours always increased compared with the standard no AR case (in a similar trend to the oxic case). The maximum dose increase owing solely to AR in hypoxic tumours was approximately 55%, compared with the no AR case. The impact of AR was much larger compared with the impact of ROx in hypoxic tumours. ROx could only offset the extra cell growth caused by AR, for AR onset at 3 weeks or later together with early ROx. ROx-related radiosensitisation only provided an overall dose reduction advantage when ROx was onset at 0 or 1 week and when no AR was simulated.

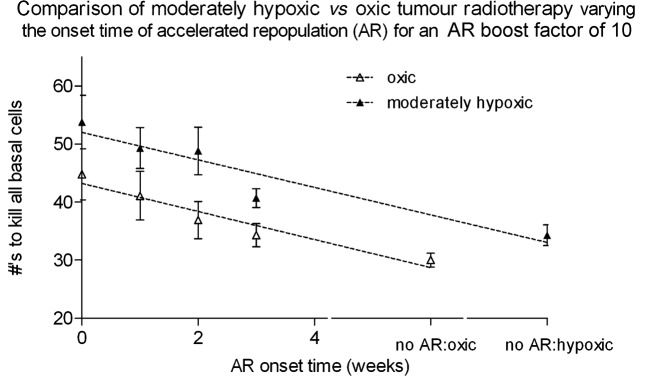
Comparison of moderately hypoxic and oxic tumours

Individual AR onset time results are shown in Figure 7, outlining the difference between oxic and moderately hypoxic tumour simulations. On average it took an extra 16 ± 6 Gy to kill moderately hypoxic tumours (4–12 fractions, or 0.8–2.4 weeks) compared with oxic tumours. This dose difference is plausible, considering the high proportion of cells (50%) in the hypoxic tumours that had low oxygenation levels below 10 mmHg (equating to low OER values of 1.0–2.0, compared with 2.5–3.0 when oxic), and therefore an increased radioresistance.

Figure 7.

A comparison of the average number of radiotherapy fractions (5×2 Gy per week) required for moderately hypoxic vs oxic tumours. The onset on accelerated repopulation (AR) is varied 0 (immediate onset) to 3 weeks after the start of radiotherapy, and with a constant symmetrical stem cell division probability AR boost factor of 10. The no AR case corresponds to the time of total cell kill without AR applied (after 6 or 8 weeks of radiotherapy for oxic and hypoxic tumours respectively).

For both tumour types, AR onset time had a linear effect on cell kill (Pearson r² values of 0.93 and 0.90 for oxic and moderately hypoxic tumours, respectively). Both linear fits showed significant non-zero gradients of −3.6 ± 1.2 and −3.8 ± 0.9 fractions, for every week that AR onset was delayed, for oxic and moderately hypoxic linear fits, respectively.

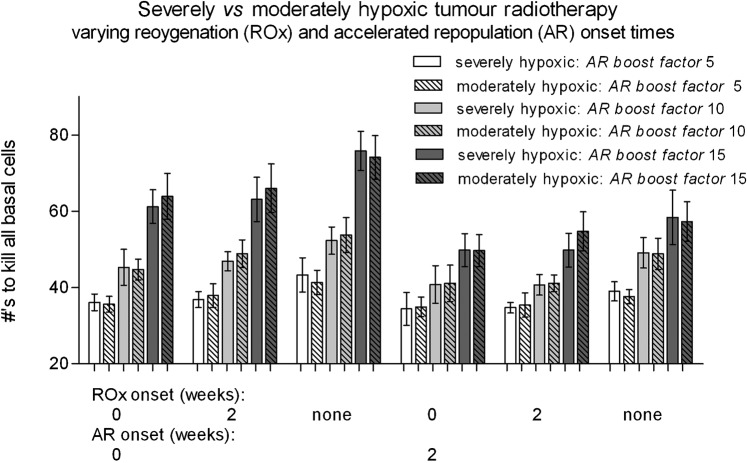
There was no significant difference between the moderately and severely hypoxic tumour simulations for all AR and ROx onset times (Figure 8). This was an unexpected result considering the increase in the percentage of cells in the lower region of the applied severe hypoxic pO₂ histogram compared with the moderate case (approximately 10% higher cell number in the 0–5 mmHg and 0–10 mmHg oxygenation ranges). However, these results show that despite having more hypoxic cells in the cell population, a greater hypoxic percentage must be required to make a difference to the simulation outcomes above the inherent statistical error in the model.

Figure 8.

A comparison of the average number of radiotherapy fractions (5×2 Gy per week) required for severely hypoxic vs moderately hypoxic tumours, for onset times of accelerated repopulation (AR) and reoxygenation (ROx) between 0 to 2 weeks. No significant difference was found between these two tumour types, using the moderately and severely hypoxic tumour oxygenation histograms shown in Figure 1.

Similar AR and ROx onset trends were observed for the severely hypoxic tumours compared with moderately hypoxic tumours; for example, the AR onset time has a linearly increasing effect on the required fractions with decreasing onset week, and the ROx sensitising the tumour with decreasing onset week.

Analysis of cell numbers and cell types near the completion of radiotherapy

Using standard Poisson theory (TCP = e^−a, where a is the number of clonogenic cells remaining) TCP is reduced from 100% to 37% if 1 clonogenic cell remains after treatment completion, and is reduced to below 1% if 5 or more clonogenic cells remain after treatment. In the HYP-RT model, the number of fractions required to kill all but 1 or all but 5 cells was reduced significantly compared with the dose required to kill all cells. Data averaged from specific simulation sets are presented in Table 2. Data such as this is important if simulation results are to be used for TCP predictions.

Table 2. The number of fraction (2 Gy per fraction) reductions required to kill all cells (stem+transit+Level 1 differentiating vs stem only), compared with killing all but 1 or 5 cells, averaged over multiple simulations varying the random number seed and accelerated repopulation and reoxygenation onset times (average of no onset and 0 and 2 week onset for each effect).

Reduction in the number of 2 Gy fractions required to kill tumour cells
	0 cells remainingcompared with 1 cell remaining		0 cells remainingcompared with 5 cells remaining
	Number of fractions	Dose (Gy)	Number of fractions	Dose (Gy)
Stem+transit+Level 1 differentiating cells	0.70 ± 0.36	1.4 ± 0.7	3.00 ± 1.15	6.0 ± 2.3
Stem cells only	2.13 ± 0.68	4.3 ± 1.4	5.65 ± 1.23	11.3 ± 2.5

Overall, the trend observed for a set of moderately hypoxic tumour radiotherapy simulations, showed that the average difference between killing all of the stem, transit and Level 1 differentiating cells vs stem cells only was 2.2 fractions; however, this was within the statistical error (4–8 Gy).

Simulation vs linear quadratic theory

The standard LQ model predicts the need for 26 fractions in 5.2 weeks for a 10⁸cell tumour (2 Gy per fraction, α/β = 10 Gy). The LQ model with time factor modification predicts between 31 and 34 fractions in 6.2–7 weeks, when implementing a time factor (AR onset time) of 3 and 2 weeks, respectively (T_pot = 4 days).

In comparison, the HYP-RT simulations of oxic tumours required 27 ± 2 fractions in 5.4 weeks, with no AR and 33–35 ± 3 fractions in 6.6–7 weeks, for AR onset times of 2–3 weeks. These oxic tumour results correlate with the killing of stem cells only, with results shown in the upper section of Table 3.

Table 3. Comparison of the HYP-RT model with linear quadratic theory in terms of the required number of 2 Gy fractions to kill a 10⁸ cell tumour, for oxic and hypoxic tumours with accelerated repopulation (AR) time factor considerations. Linear quadratic results for the hypoxic cases have been assigned a q value to represent the dose modification factor due to low oxygenation.

Fractions (2 Gy) required to kill all stem cells in a 108 cell tumour
	Time factor settings: for accelerated repopulation (AR)	HYP-RT model: moderately hypoxic pO2 distribution	Linear quadratic theory: cell kill down to less than 1 cell
Oxic tumours
1.	No time factor	27 ± 2	26
2.	No AR time factor (2 to 3 weeks AR onset)	33–35 ± 3	31–34
Hypoxic Tumours
1.	No AR time factor	33 ± 3	32 (LQ: q = 1.182*)
		OR
		29–32 ± 3
		(with added ROx at 0–2 weeks)
2.	With AR time factor (2–3 weeks AR onset)	41–49 ± 3	42–45 (LQ: q = 1.182*)
		OR
		37–41 ± 3
		(with added ROx at 0–2 weeks)
3.	No AR time factor		32 (LQ: q = 1.2)
4.	No AR time factor		38 (LQ: q = 1.4)
5.	No AR time factor		44 (LQ: q = 1.6)
6.	No AR time factor		50 (LQ: q = 1.8)
7.	No AR time factor		56 (LQ: q = 2.0)
8.	No AR time factor		46 (LQ: 3% q = 2.0, 97% q = 1, to represent the approximately 3% 1 mmHg or less mmHg population in the pO2 distribution)
9.	AR time factor (2–3 weeks AR onset)		93–100 (LQ: 3% q = 2.0, 97% q = 1, to represent the approximately 3% 1 mmHg or less mmHg population in the pO2 distribution)

*an average equivalent q value of 1.182 corresponded to the average cell population pO₂ value in the moderately hypoxic tumour pO₂ histogram.

For hypoxic LQ calculations vs the HYP-RT model, the use of an average q value in the LQ model, for the cases of no AR (no time factor) as well as AR onset at 2–3 weeks, resulted in good agreement between the two models. Adjusting the q value had a very large impact on LQ results, even for conservative q estimates, as shown in the lower section of Table 3. When using the LQ equation to model a small hypoxic component of the tumour (3% used to best match the 0–1 mmHg population in the HYP-RT modelled pO₂ distribution, with a q value of 2, results from the 2 different models were no longer in agreement (rows 8 and 9 of Table 3).

Discussion

Predictions of cell kill for oxic and hypoxic tumours

When applying an AR boost factor of 10 for conventional schedule simulation of 5×2 Gy per week, the required number of fractions increased in oxic tumours from 30 for no AR onset to 34 for late onset (3 weeks), and to 45 fractions for early onset (0 weeks). Overall, the maximum impact of AR corresponded to a 30 ± 6 Gy increase (3 week difference) in the total dose required to control a tumour.

For the same parameters in hypoxic tumour simulations, the required number of fractions increased from 34 for no AR onset to 41 for late onset at 3 weeks, and then to 54 fractions at early onset (0 weeks). This resulted in a maximum dose increase of 40 ± 8 Gy as a result of AR. This was a slightly greater dose difference than for the oxic case in absolute terms, but a smaller relative difference. Overall this difference was not significant and therefore it was concluded that the effects of AR were not influenced by tumour oxygenation in this study.

ROx alone in hypoxic tumour simulations decreased the required fractions significantly from 31 for immediate onset, 33 for late 2 week onset and 34 if no ROx was onset (±2 fractions). With no AR considered, immediate ROx onset in hypoxic tumours cancelled out the effect of having a hypoxic tumour compared with an oxic tumour within statistical error, assuming that all cells reoxygenate before the end of treatment.

ROx of hypoxic tumours at weeks 2 and 3 were similar in terms of the required fractions (no significant difference) for most AR onset times. In these cases it is possible that the benefit of reoxygenating the tumour was overcome by the extra cells that were propagated due to the rapid repopulation after AR onset.

Early onset AR required the same number of fractions in oxic and hypoxic tumours if ROx was onset in the hypoxic tumour immediately. The model predicted that AR effects may be overcome in hypoxic tumours if ROx is initiated early. Findings such as these may lead to renewed interest and investigation into chemical/mechanical ROx methods of head and neck tumour undergoing radiotherapy if they start immediately after treatment initiation.

AR had a much greater influence on cell kill compared with ROx using the modelling methods previously explained for each of these phenomena. With AR onset at 0 weeks compared with ROx onset at 0 weeks (in separate simulations) there was a +20 vs a −3 fraction difference compared with no onset of each effect. With AR onset at 2 weeks compared with ROx onset at 2 weeks there was a +15 fraction difference in comparison to the −2 fraction difference of the no onset of each effect. Moreover, AR and ROx were not additive effects (could not sum the individual effects if simulated individually). With AR and ROx both onset at 0 weeks, the required fractions increased by 11 (compared with an increase of 20 and a decrease of 3 when simulated at 0 weeks individually).

When AR and ROx were onset together early in the treatment course there was an early increase in the oxic stem cell population from quiescent cells returning to the cell cycle and an average decrease in CCT. These processes resulted in a greater number of stem cells available for symmetrical division and therefore an increasing percentage of oxic/reoxygenating stem cells in the population to repopulate the tumour and consequently a requirement of a higher total dose for tumour control. This is in contrast to some reports indicating that AR is not very important when ROx is present [68]. These facts outline the complexity of these two dynamic and dependent effects, for which Monte Carlo modelling is extremely useful.

As the total dose required to kill all cells in a moderately hypoxic tumour was over 100 Gy for the case of immediate AR onset and no ROx, this combination of parameters was not considered plausible from this study, considering routine clinical prescription doses of 60–80 Gy in 6–8 weeks. However, in real tumours where AR does occur early and the flow of oxygen back into the tumour during shrinkage is greatly restricted, it is conceivable that a very high dose, such as 100 Gy, would be necessary. Clinical evidence of this will need to be determined through specific oxygenation testing of a cohort of patients with hypoxic tumours (and perhaps further stratified/selected based on stem cell clonogenic properties and surrounding tissue pressures/restrictions that may restrict ROx).

Radiotherapy results for moderately hypoxic tumours were not significantly different from severely hypoxic tumours. This may be because the severe hypoxia does not make a difference to the treatment outcome for the way in which the pO₂ histograms were defined (within statistical error), or that the mechanism of oxygen level assignment and ROx was not sufficient and biased the results. A change to the pO₂ histogram was investigated to increase the percentage of cells in the very hypoxic range (0 to 1 mmHg) to assess treatment fraction requirements. It was found that raising the cells in this low pO₂ group above the earlier value of approximately 3% (pO₂ histogram y-axis intercept) had the effect of stopping tumour growth before 10⁸ cells were reached. Growth may have stopped because the cells in this group were no longer dividing, and/or because these cells had a finite life span (half-life of 4 days), where as cycling cells continued to replicate unless undergoing differentiation into non-cycling cell types. Further work will aim to model different variations in the pO₂ histogram for severe hypoxia to assess the point at which the two tumour types have significantly different results (by varying the histogram shape, peak height, percentage of cells below 2.5 or 5.0 mmHg, etc).

A small change in the hypoxic cell half-life for cells that have become quiescent owing to low oxygenation, greatly impacted upon the results for hypoxic tumours. Care should be taken with this parameter and if possible tailored to the specific cell type modelled.

The simulations involving the analysis of the difference in fractions required for 0, 1 and 5 cells remaining at the end of treatment showed that in the last 1 to 5 fractions, although cell kill is minimal, they are crucial for the killing of the last few cells that could potentially grow back the tumour. On average an extra one to two fractions were required to kill the last cell and three to five fractions were required to kill the last five cells.

Comparison of HYP-RT results with HNSCC clinical trials and linear quadratic theory

Compared with patients in the conventional schedule arm of clinical trials and basic LQ theory, the number of fractions required in simulations was in good agreement for the oxic tumour case. In a selection of large trials from 1990 to 2004 the average local control (LC) rate for HNSCC was 40–50% (2 Gy per day, 5 days per week for 6.5–8 weeks, i.e. 32–40 fractions and LC rates reported at 2–5 years), with a decrease in LC for advanced stage tumours and for tumours of larger size and faster cell proliferation [13^,54^,63^,69-71]. The total doses from oxic tumour simulations of 69–90 Gy in 6.9–9 weeks were also comparable with the BEDs calculated from HNSCC alternate fractionation clinical trials in the range 63–75 Gy with time correction in the BED formula [59]. This agreement aids in the validation of the HYP-RT model in terms of the basic cell division, cell kill and repopulation mechanisms. Simulation doses are likely to be higher in this comparison because of the 100% TCP simulated (approximately 6 Gy required to kill the last 5 cells found in this simulation study).

An unavoidable limitation of the comparison of model results with human data is the varying tumour oxygenation levels present in the patient groups and the number of cells in each of their tumours, which may have approached up to 10¹⁰–10¹¹ cells. Further, the exact number of fractions required to kill all tumour cells from the trials cannot be readily obtained for simple model comparisons. The reported average LC percentages at 2–5 years are the closest results that can be compared with the model and can be roughly equated to the average remaining tumour cell number using the Poisson model, where 50% LC corresponds to 0.7 cells remaining, i.e. 70% of tumours having 1 cell remaining to potentially regrow the tumour. It is therefore reasonable to expect a higher number of required fractions to control tumours in a real patient group if a significant proportion of the tumours are hypoxic.

A small number of trials have specifically aimed to analyse individual tumour properties, such as oxygenation status and the property of tumour control using radiotherapy. There is evidence in these trial reports of the significant negative impact of low oxygenation in HNSCCs on LC [5^,72-75]. Unfortunately, averaging these trial results and equating this difference to the number of fraction required to kill all cells in the model or with LQ theory is very difficult because studies report upon the hypoxic status in different ways. They may show the difference in outcome for tumours above vs below a mean or median pO₂ level, correlate LC with the percentage of cells below a pO₂ threshold (e.g. 2.5 mmHg), correlate outcome with any presence of hypoxia (i.e. positron emission tomography (PET) imaging) or a number of other methods.

For example, a small trial reported by Richin et al [5], presented LC results that were based on dividing patients into groups above and below the median percentage of cells below 2.5 mmHg (median of 15%). The 35 patients all received 70 Gy in 2 Gy fractions. This resulted in a 33% vs 77% LC rate [5]. Using Poisson theory, the average remaining cell number in each of the LC groups would have been approximately 1 and 0.3 cells for the 33% and 77% LC groups, respectively. This is a very large difference in outcome for a very small change in cell number. LQ theory predicted an extra 2–3 fractions were required to bring the remaining cell number in the 33% group equal to that in the 77% group. This fraction number would be up to three times greater if the remaining few cells had very low oxygenation. This equates to a 4–6 Gy increase for oxic remaining cells and up to 12–18 Gy increase for hypoxic remaining cells. In the HYP-RT model, hypoxia had the impact of increasing the required dose by 16±6 Gy for all AR onset times, which reduced as ROx was simulated with earlier onset times.

For hypoxic tumours the HYP-RT model, LQ theory and clinical trial data were not all in agreement. The LQ theory used was relatively basic in terms of the single q value representing the hypoxic cell population, which resulted in an extremely sharp increase in the required fraction number with an increasing q value. The fraction requirements predicted with LQ theory were very high compared with the standard human treatment schedules and indicated that a hypoxic cell percentage of less than 10% is likely to exist in real tumours when considering very low oxygenation levels (approximate q value of 2). To account for this, either a smaller percentage of such cells must exist in the tumour or there must be a spread of oxygenation levels where only a very small percentage of cells fall within the extremely low oxygenation region (0–1 mmHg).

Presumably, ROx occurs in most real tumours to some degree and decreases the average q value of the cell population, and hence the fraction number required would be lower than results in this study. An estimate of this reduction is difficult to obtain without in vivo pre- and interfraction oxygenation data. The LQ model predicted over 100 fractions for the hypoxic tumour case with AR time factor considerations and a 3% extreme hypoxic cell population (q value of 2.0). For comparison, the HYP-RT model predicted 40 fractions for the moderate hypoxia tumour case, and up to 45 fractions using an AR onset time of 14 days, and 55 fractions with an immediate AR onset and no ROx. Note that these modelling results relate to a pO₂ histogram with 3% of cells in the 0–1 mmHg range, and 7% of cells in the 0–2 mmHg range.

Sources of error and model limitations

Limitations of the model arise from the non-geometrical nature of the individual cell data storage. This is assumed to be adequate for tumours having random and uniformly spread cellular oxygenation values. AR is modelled by a single mechanism (increase in the symmetrical division probability). Currently, the modelling of ROx is based on achieving full ROx when the tumour has reduced to 1–2 mm in diameter. ROx rates are likely to vary during tumour shrinkage, resulting in full oxygenation at varying tumour diameters depending on the blood vessel system and integrity near treatment completion. In some cases full ROx may never be achieved. This could be partially accounted for in future versions of the model by inducing a ROx rate based purely on current tumour diameter and adding an option to completely reoxygenate or not depending on existing knowledge of the specific tumour blood vessel supply and surrounding tissues for PET, MRI or ultrasound imaging of the tumour.

Features such as the modelling of “gradual cell death” may be considered in future versions which will include modelling abortive divisions where sterilised stem cells remain alive but only divide into transit and differentiated cells for a limited number of generations [28,76]. This death mechanism may have an impact on tumour oxygenation if the pO₂ distribution and ROx mechanisms can be linked more closely to the changing tumour volume.

Although the model was designed with epithelial cell hierarchy in mind, other tumour types may form part of future uses of this model if the relative percentages of cell types are changed, i.e. the basic cell division structure is maintained but the relative number of stem, transit and differentiated/differentiating cells are changed. Changing the stem cell percentage above 6% and with a small differentiated cell compartment have not been analysed in detail in the work at the current time, and therefore future studies changing cell percentages would need to carefully set cell division-based parameters to obtain plausible tumour doubling times for the tumour type being simulated.

Conclusion

The Monte Carlo HYP-RT model has been used to analyse the effects of ROx and AR (and some of their associated parameters) on cell kill for a 10⁸ cell tumour and conventional radiotherapy. Three different oxygenation levels were included in the study defined as oxic, moderately and severely hypoxic. Of all the 3 oxygenation histograms used, AR was the most dominant effect and ROx effects became important for hypoxic tumours with onset at 2 weeks or earlier after the start of treatment.

AR and ROx were not necessarily additive when simulated together compared with separately for most combinations of onset times effects. ROx of hypoxic tumours counteracted the effects of hypoxic tumour radioresistance if ROx was onset early (within the first week). The half-life of quiescent hypoxic cells did not significantly impact upon cell kill, only the timing of full tumour reoxygenation. For hypoxic tumour simulations, the last one to three fractions accounted for the killing of the tumour cell and the last two to six fractions accounted for the killing of the last five cells. These figures highlight the extreme importance of completing/scheduling fractions adequately if a high TCP is to be achieved.

From the validation study, the oxic tumour HYP-RT simulation agreed with LQ theory (oxygen and time factor modification where relevant) and clinical trials, but for hypoxic tumours Monte Carlo modelling gave more realistic results and could handle the complicated and probabilistic type parameters needed to model ROx.

The HYP-RT model provided an efficient tool for the analysis of AR and ROx and their impact on cell kill during conventionally fractionated radiotherapy. The model will now be used for further research to explore altered clinical trial fractionation schedules and to investigate new fractionation schedules to reveal optimum treatment strategies for tumours with specific oxygenation histograms and repopulation related characteristics.