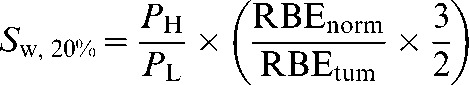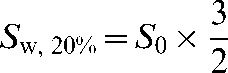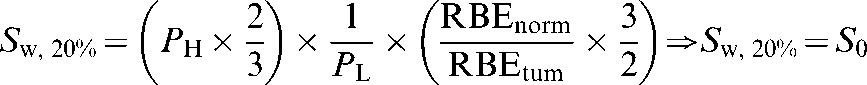The potential impact of relative biological effectiveness uncertainty on charged particle treatment prescriptions

Abstract

There continues to be uncertainty regarding the relative biological effectiveness (RBE) values that should be used in charged particle radiotherapy (CPT) prescriptions using protons and heavier ions. This uncertainty could potentially offset the physical dose advantage gained by exploiting the Bragg peak effect and it needs to be clearly understood by clinicians and physicists. This paper introduces a combined radiobiological and physical sparing factor (S). This factor includes the ratio of the most relevant physical doses in tumour and normal tissues in combination with their respective RBE values and can be extended to contain the uncertainties in RBE. S factors can be used to study, in a simplified way for tentative modelling, those clinical situations in which high-linear energy transfer (LET) irradiations are likely to prove preferable over their low-LET counterparts for a matched tumour iso-effect. In cases where CPT achieves an excellent degree of normal tissue sparing, the radiobiological factors become less important and any uncertainties in the tumour and healthy tissue RBE values are correspondingly less problematic. When less normal tissue sparing can be achieved, however, the RBE uncertainties assume greater relevance and will affect the reliability of the dose-prescription methodology. More research is required to provide accurate RBE estimation, focusing attention on the associated statistical uncertainties and potential differences in RBE between different tissue types.

Conventional megavoltage X-ray therapy almost invariably makes use of physical dose planning to identify the best achievable dose distributions. For any given physical dose plan, manipulation of the treatment fractionation (total dose, fraction size, overall time etc.) may then be used to secure further improvements in the therapeutic index. Fractionation allows sub-lethal radiation damage in all irradiated tissues to be repaired between fractions, with the overall repair capacity varying between tissues and tumour types. As late-responding normal tissues usually possess more repair capacity than do tumours, the use of small or modest-sized fractions, rather than larger fractions, is more likely to spare such tissues preferentially. This consideration is particularly important when treatment volumes are large, or if they extend significantly into critical normal tissues such as the spinal cord, lung, kidney, bowel etc.

In contrast to conventional X-ray therapy, charged particle therapy (CPT) using hadrons (such as protons) or heavier ions (such as helium or carbon) entails the use of Bragg peaks to deposit dose far more selectively in tumours, with a potentially large reduction in normal tissue dose. CPT dose prescriptions must take account of the changed relative biological effectiveness (RBE) as, compared with X-rays, less physical dose is required to produce a given biological effect. RBEs vary from around an average of 1.1 for protons to 1.4–5.0 or more for helium or carbon ions [1,2]. These high RBEs are a consequence of raised linear energy transfer (LET), which in simple terms represents the local intensity of energy transfer by ionisation on a microscopic scale, normally expressed in units of kiloelectronvolts per micrometre. Owing to the enhanced complexity of deoxyribonucleic acid (DNA) damage that occurs with increased LET, however, cellular DNA repair mechanisms are less effective for radiation with higher RBE values. This means that treatment dose plans involving high-LET radiation are less fraction-size-dependent than those for megavoltage X-ray therapy. Nevertheless, some residual fractionation effect will remain in most clinical applications of high-LET radiotherapy because CPT inherently involves a mixture of low- and high-LET radiation present before the Bragg peak and high-LET radiation present within the Bragg peak.

The analysis used here makes use of the linear quadratic (LQ) formulation for low- and high-LET radiations, and allows for the systematic change in RBE that occurs with changing dose per fraction. This follows from including two fundamental RBE parameters within biological effective dose (BED) equations: the maximum RBE value (RBE_max) at near zero fraction dose and the lower limit of RBE (RBE_min) at very high fraction dose [3,4]. These RBE parameters are shown within the BED equation in Appendix A as Equation A1. These two parameters can be used to calculate a “working” RBE at a specified dose per fraction. The classical definition of RBE is the ratio of doses for the two forms of radiation when given as a single fraction or in equal numbers of fractions. In the case of multiple fractions, the ratio of iso-effect total doses can be used to express a different “fractionated RBE”. However, use of the BED method allows calculation of both dose per fraction and fraction numbers required for high- and low-LET iso-effects.

We intend that this article should be understood by both clinical physicists and medical personnel and hence we have used a necessarily simplified approach, but one which expresses ideas with potential clinical relevance. This approach has similarities to the US and Japanese practical guidelines for proton and ion beam therapy, where constraints are defined routinely at well-defined tissue points, such as the spinal cord surface, mid-spinal cord or optic chiasm, or using the maximum allowable skin dose. The use of volume-related models to predict normal tissue complication probabilities are not used in this article because of their requirement for many additional assumptions and their lack of validation in clinical practice.

Methods

The terminology below uses suffixes of L and H for low- and high-LET, respectively. Let the tumour dose per fraction at the prescription point be z_H for high-LET and z_L for low-LET radiations. As RBE is the ratio of the low- to high-LET single doses (or dose per fraction) necessary for a given biological iso-effect, then the required value of z_H in the high-LET case may be calculated from the RBE specific to the tumour volume (RBE_tum) by:

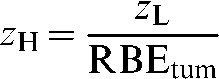(1)

Equation 1 represents the iso-effective dose conversion required when the fraction number is the same for both the high- and low-LET cases. In practice, when the fraction numbers differ, RBE_tum can be determined by application of Equation A2, which calculates the RBE required for use in Equation 1.

In most forms of radiotherapy, but especially in CPT, a degree of physical normal tissue sparing is expected, such that the physical dose (d_H) to a critical region of normal tissue (e.g. the maximum or modal dose given to a clinically relevant normal tissue point or volume according to local anatomical constraints) is given by:

(2)

where P_H is the physical sparing factor of high-LET radiation and is the fraction of the tumour dose (z_H) that is delivered to the normal tissue. Ideally, P_H should be as small as possible. For low-LET radiation, the associated sparing will probably be less, i.e. the physical sparing factor (P_L) will be greater than P_H. For example, if a vertebral tumour is given a dose z_L by low LET or z_H by high LET, the dose at the surface of the spinal cord a few millimetres away might be P_H×z_H=d_H in the high-LET case and P_L×z_L=d_L in the low-LET case.

Using Equations 1 and 2, the normal tissue high-LET dose per fraction, d_H, can be converted back to an equivalent low-LET dose per fraction, (d_Leq) by use of the normal tissue RBE (RBE_norm)_, to give:

(3)

where z_H×P_H replaces d_H, which is itself obtained from the prescription dose z_H by multiplying it by the high-LET sparing factor P_H (Equation 2).

Then by substituting z_H from Equation 1:

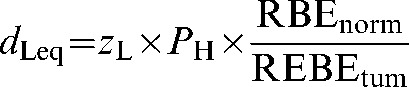(4)

For the low-LET radiation, the normal tissue dose is:

(5)

where P_L is the physical sparing factor for low-LET radiation and P_H<P_L in most circumstances. Combining Equations 4 and 5 and rearranging the terms leads to:

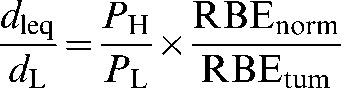(6)

which can be written as:

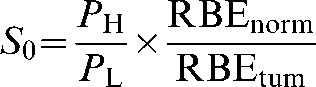(7)

where S₀=d_Leq/d_L and represents the combined physical and radiobiological sparing. S₀, which could also be called the biological sparing advantage factor, needs to be as small as possible for particle therapy to have advantage over conventional X-ray therapy. It is clear that the precise value of S₀ not only will depend on the physical dose sparing ratio but will also be highly sensitive to errors made in estimating RBE for both tumours and normal tissue, especially as the RBEs are themselves dependent on fraction size and tissue cell kinetics. To give an S factor that includes error terms (S_I), the errors in the estimation of RBE values can be incorporated as multiplicative terms on the normal tissue and tumour RBEs values (defined as Error_d and Error_Z, respectively):

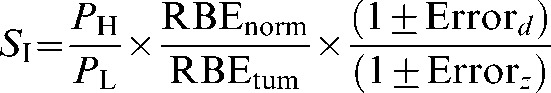(8)

The error term can be treated simply as a factor from 0 to 1 or as a percentage change. For example, if the RBE is assumed to be 3, while it is actually 1.5 in a particular tissue of interest, this represents a 50% error, whereas if the actual RBE is 6, there is a 100% error. In Equation 8, such an error of 50% would be included as a factor of 0.5, an error of 30% as 0.3 etc. For the high-LET case to be advantageous relative to low-LET, S_I must be less than unity, and for optimal healthy tissue sparing, S_I should be kept as low as possible.

Modelling parameter assumptions

The examples in this paper are not intended for practical use, but rather to illustrate the general principles involved.

For such purposes, it is assumed that:

carbon: RBE_max=9.8, RBE_min=1.3

protons: RBE_max=3.3, RBE_min=1.0.

These values are based on V79 cell line data [5,6], where α and β were investigated as functions of LET for carbon ions and protons, respectively (in both cases compared with X-ray radiation). RBE_max and RBE_min were calculated for all LET values investigated in the papers, and the values considered here correspond to the LETs associated with the greatest differential between RBE_max and RBE_min. These were 153.5 keV μm^–1 for carbon and 20 keV μm^–1 for protons. V79 cells probably provide a poor representation of human cells in vivo, but it must be stressed that there is a lack of available data on this topic, and the values employed here are for illustrative purposes. For protons, an RBE_max of 3.6 may be applicable to the last few millimetres of a Bragg peak only. For this reason, the following (realistic spread out Bragg peak) RBE_max parameters are also considered, where an error increment of 10% is applied to the standard clinical RBE values of 1.1 for protons and 3 for carbon ions, so that for most practical situations we assume:

carbon: RBE_max=3.3, RBE_min=1.3

protons: RBE_max=1.2, RBE_min=1.0.

In both cases, RBE_min is maintained at the estimates indicated above (from [5,6]). In the absence of further data, the RBE values were assumed to be the same in the normal tissue and the tumour but with use of generic, low-LET, α/β values of 3 Gy for normal tissues and 10 Gy for tumours, unless otherwise stated.

The equations given in Appendix A (A3–A6) provide a working RBE function that expresses an effective dose multiplying factor as the ratio of the dose per fraction for low LET divided by the high-LET dose per fraction. These calculations utilise the fractional doses for both low- and high-LET radiations. In the case of unequal fractions, the total dose provides the working RBE: the dose per fraction is multiplied by the number of fractions in each case. For inclusion within the S factor, however, the ratios of RBEs are required for the normal and tumour tissues, as shown in Equation 8 above. These ratios can be expressed as:

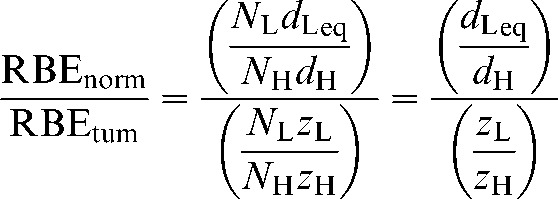(9)

So, it is only necessary to include the ratios of the dose per fraction within the S factor, although the solution for dose per fraction in the normal tissue and tumour cases will include the relevant fraction numbers as given in Equations A2 and A5.

The sequence of the computer programming to obtain S is given at the end of Appendix A.

Results and worked examples

Considering the effects of errors

To assume a worst-case scenario, from Equation 8 let the errors be of equal magnitude and include a positive error on the numerator (increasing the assumed normal tissue RBE) and a negative error on the denominator (decreasing the assumed tumour RBE). This gives:

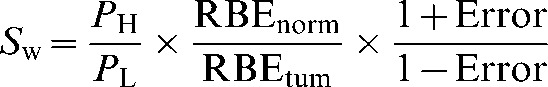(10)

where S_w now represents the worst-case scenario for equal errors on both healthy tissue and tumour RBE values. Uncertainties in RBE values might also prove favourable and a best-case scenario, S_b (where the signs of the errors in the numerator and denominator are reversed) can also be considered. The two extremes are shown in Figure 1, where equal physical sparing for both the high- and low-LET radiations has been assumed (P_H=P_L).

Figure 1.

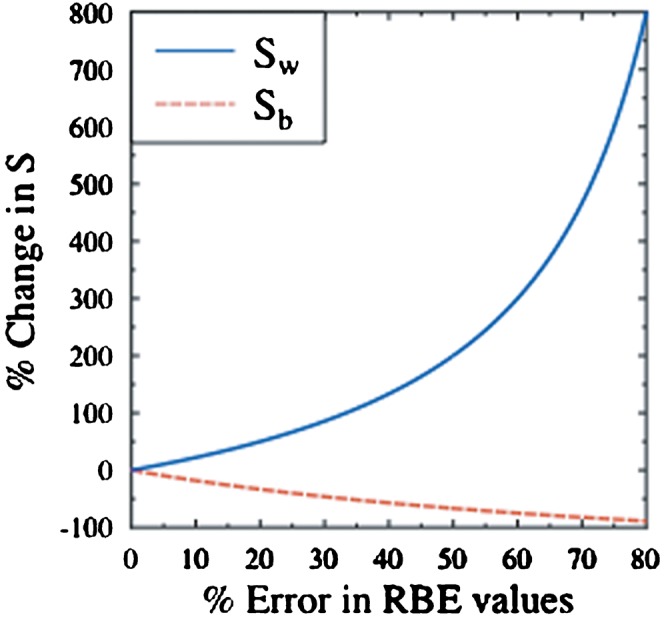
The percentage change in S as a function of the percentage errors in relative biological effectiveness (RBE) for the best- (S_b) and worst-case (S_w) scenarios, where the RBE errors are assumed to be equal for both normal tissue and tumour and with P_H set equal to P_L. P_H, physical sparing factor of high linear energy transformation; P_L, physical sparing factor of low linear energy transformation.

Figure 1 shows that relatively modest errors in assumed RBE values can potentially change the S factors by significant amounts. For example, in the case of S_w, a 20% error in both normal tissue and tumour RBE values would increase S by 50%. For high-LET therapy to remain the better treatment option in the presence of such errors, a new requirement would be placed on the high-LET physical dose sparing factor (P_H): it would have to be reduced by a factor of one-third (as shown in Table 1). This example highlights the interplay between physical dose sparing and RBE uncertainty. If incorrect RBE values (as in the worst-case scenario) are used in dose prescriptions, then increased reliance is placed on the dose sparing capability of high-LET radiation to provide the desired improvement over the low-LET case. In such instances, alternative low-LET therapies, such as X-ray-based intensity modulated radiotherapy, may be a less speculative treatment option because there is no reliance on RBE estimation.

Table 1. Worked example.

Applying 20% errors to Equation 10: (10)

gives: (11)

substituting S0, the S value assumed prior to the consideration of RBE errors (Equation 7) into Equation 11: (12)

Thus, for S0 to be maintained in the case of Sw,20%, the high-LET physical dose sparing factor, PH, would have to be reduced by one-third: (13)

H, high-LET transformation; L, low-LET transformation; LET, linear energy transfer; norm, normal tissue RBE; P, physical sparing factor; RBE, relative biological effectiveness; S, sparing factor; tum, tumour volume RBE; w, worst-case scenario.

Magnitude of RBE errors

Paganetti et al [7] concluded (from experimental in vitro and in vivo data) that a generic RBE value of 1.1 for proton therapy could reasonably be employed. This conclusion was based on the desirability of using a “one-number” RBE correction factor in clinical protocols. However, the RBE value was obtained using fast-growing cells and tissue assays with high α/β ratios. Such experiments may not adequately provide the true RBEs for late reacting issues, which have low α/β ratios. The need for further work to reduce the uncertainty in RBE values for specific tissue, dose per fraction, proton energy etc. was also highlighted by the group. They found the average RBE value at mid spread-out Bragg peak in vivo to be 1.1, but their data had a range of 0.7–1.6 (i.e. −36% to +45% relative to 1.1). Taking these percentages and applying them as errors to both normal tissue and tumour RBEs as in Equation 9, in the best case the S factor would be reduced by 64%, and in the worst case it would be increased by ≈127%.

The effects of fractionation

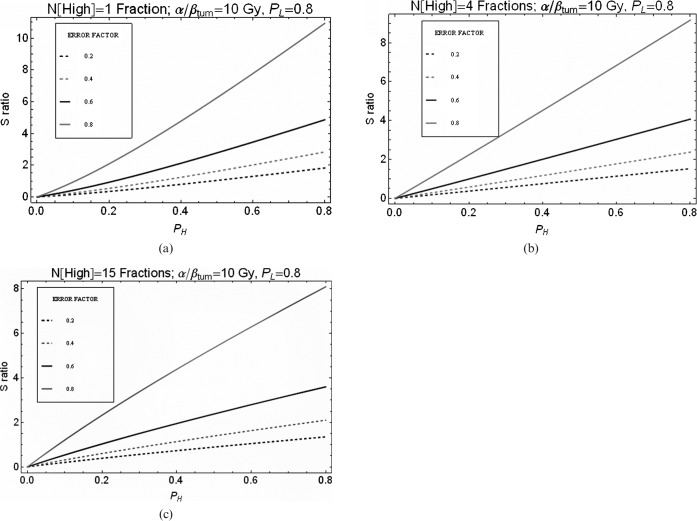
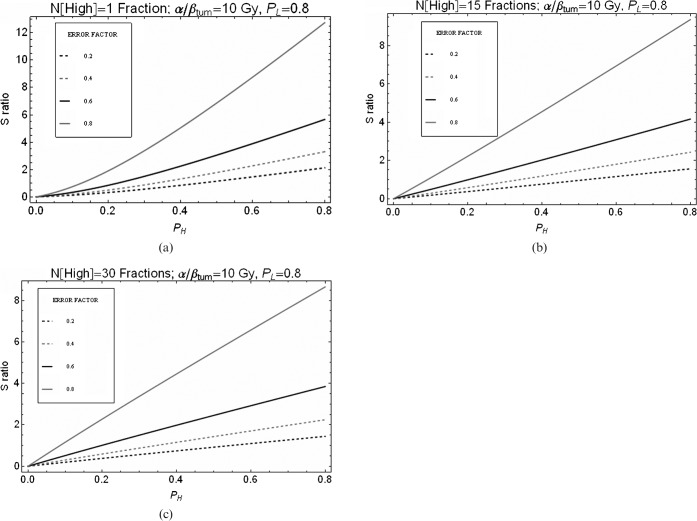
Using the LQ (linear quadratic model of radiation effect)-based equations given in Appendix A and the RBE_max and RBE_min values quoted in the methods section, the combined radiobiological and physical normal tissue sparing factor, S (as defined in Equation 8 and referred to as S in all further plots), was determined for different numbers of high-LET fractions (Figures 2–5). In each case, the number of low-LET fractions was maintained at 30 using a dose of 2 Gy per fraction and the high-LET dose per fraction gave the same tumour BED. The effect of increasing the number of fractions for carbon ions is shown in Figure 2 for a range of assumed errors in RBE where 0.2, for example, indicates a 20% error set in the worst-case direction. For assumed RBE errors of 20%, and where P_L is 0.8, then to maintain an S ratio below unity, P_H values below approximately 0.5 are required for the single fraction case (Figure 2a), P_H values of below approximately 0.6 for the 4-fractions case (Figure 2b) and P_H values of approximately 0.7 for the 15-fractions case (Figure 2c). In general, the S values for all levels of error improve with fractionation. Similarly, for the proton examples, we obtain S ratios below unity for P_H values of <0.45, 0.5 and 0.6 for fraction numbers of 1, 15 and 30, respectively (Figure 3).

Figure 2.

Relationship between S ratio and degree of normal sparing (P_H) achieved by carbon ions for variation in error of relative biological effectiveness (RBE) used. P_L is assumed to be 0.8. The “ERROR FACTOR” key describes the assumed error in RBE where 0.2, for example, indicates a 20% error set in the worst-case direction. (a) Only 1 high linear energy transfer (LET) fraction, (b) 4 high-LET fractions or (c) 15 high-LET fractions were used to give an iso-effective tumour dose equivalent to that given by 30 fractions of 2 Gy of low-LET X-rays.

Figure 5.

Relationship between S ratio and degree of normal tissue sparing achieved by (a) carbon ions and (b) protons for variations in tumour α/β ratio. P_L is assumed to be 0.8. RBE, relative biological effectiveness.

Figure 3.

Relationship between S ratio and degree of normal sparing (P_H) achieved by protons for variations in error of relative biological effectiveness (RBE) used. P_L is assumed to be 0.8. The “ERROR FACTOR” key describes the assumed error in RBE where 0.2, for example, indicates a 20% error set in the worst-case direction. (a) Only one high linear energy transfer (LET) fraction, (b) 15 high-LET fractions or (c) 30 high-LET fractions were used to give an iso-effective tumour dose equivalent to that given by 30 fractions of 2 Gy of low-LET X-rays.

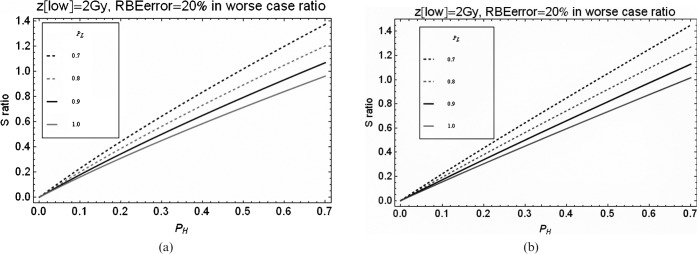
The influence of a change in the X-ray normal tissue sparing ratio (P_L) is shown for carbon and protons in Figure 4. The achievement of good sparing with X-rays requires even greater sparing with CPT if these therapies are to provide a therapeutic improvement; for example, if X-rays achieve a sparing factor of 0.7, sparing factors of less than 0.5 and 0.45 are needed for CPT involving carbon and protons, respectively (assuming that the RBE estimates are unfavourable and in the worse direction by 20%).

Figure 4.

(a) Relationship between S ratio and the degree of normal-tissue sparing for carbon ions (P_H) at varying amounts of X-ray sparing of normal tissues (P_L). 15 high linear energy transfer (LET) carbon fractions were given compared with 30 treatments of low-LET X-ray radiation (at 2 Gy dose per fraction). (b) Relationship between S ratio and the degree of normal tissue sparing for protons (P_H) at varying amounts of X-ray sparing of normal tissues (P_L). 30 “high LET” proton treatments were given, the same as for low-LET X-rays.

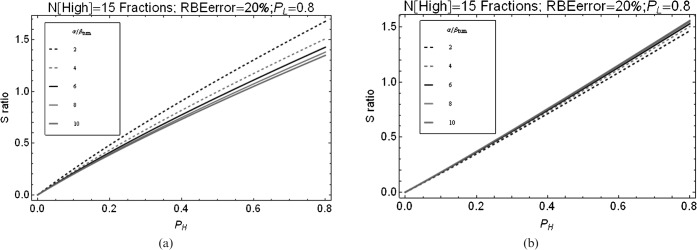
The separate influence of tumour α/β ratio on the S ratio is shown for carbon and protons in Figure 5. The variation of S with changing α/β ratio is greater for carbon ions than for protons because of the larger range of RBE values for carbon. The proton relationship shifts towards the carbon relationship if extreme hypofractionation is used, in which case the lowest α/β tumour ratio becomes the lowest curve (such graphics are not reproduced here because of space restrictions). For iso-effective tumour control (without accounting for repopulation), the increment in S is greatest for low fraction numbers. This shows that fractionation processes continue to exert a change in S.

It is clear that hypofractionation is capable of providing good therapeutic ratios provided that the normal tissue sparing is good. When good physical dose sparing cannot be achieved with high-LET radiation, increased fraction numbers are likely to be a better option. In most cases, the modelled worst-case scenario (derived using Equation 8) implies that hypofractionation will be justified only if a very good P_H of ≤0.3 can be achieved (i.e. if the physical dose to the clinically relevant volume of healthy tissue is ≤30% of the tumour prescription dose). Even better degrees of sparing are required if the RBE uncertainty is greater. If the error in RBE may operate in the opposite direction, however, these constraints will not be so marked but other dangers may ensue. For example, if RBE is generally underestimated in both tumour and normal tissue, then the tumour dose will be greater than expected. Should the Bragg peaks be inadvertently located within normal tissue (or include normal tissue as an intended margin) in such cases, however, normal tissue would be overdosed. The level of uncertainty in RBE that should be accepted has yet to be decided on an international basis.

Discussion

This provisional study has shown only a small number of the many complex interactions that affect treatment planning. Further modelling along these lines should aid the process of treatment plan acceptance when there is a choice between CPT and X-ray therapy. The overall process of prescribing high-LET CPT is more complex than that for megavoltage X-ray-based radiotherapy and must include consideration of RBE, which is itself related to dose and modified by local LET values. Because of this, greater care and a good appreciation of radiobiological effects are required to ensure that CPT is administered optimally. The literature currently contains active discussion regarding both the potential merits of using variable rather than fixed RBE values and the role of fractionated vs single-dose RBEs [1,2,7-12]. We have adopted a definition of RBE that is based on the ratio of high- and low-LET radiations in the dose per fraction rather than in the total dose because dose per fraction is a single entity rather than a combination of two parameters. Total doses can be misleading if not qualified by dose per fraction.

Although the S factor contains the essential parameters for tentative modelling purposes, it is not intended for direct clinical application; rather it represents the possible form of an (as yet) incomplete methodology that contains both fractionation and RBE effects. The S factor can, in principle, be extended to more complex volume-based situations. Importantly, it also allows for the calculation of an iso-effective high-LET fraction dose when the number of high-LET fractions differs from the number of low-LET fractions, while taking into account the classical definition of RBE. The normal tissue RBE term within S, if found using the equations given in Appendix A, will contain the normal tissue-sparing factor as dose per fraction determines RBE. This does not undermine the validity of this approach as long as these parameters are included and RBE values are not just assumed.

Despite the dose improvements afforded by the Bragg peak effect, there are severe limitations in the knowledge of accurate RBE values in most situations. Dale et al [13] have warned that the lack of radiobiological precision in RBE is in marked contrast to the expectation that physical dosimetry will be of a high standard, dosimetric errors of >10% being legally reportable in the UK and an expected attainment of 3% accuracy being the norm. Our study shows, however, that when the degree of normal-tissue sparing with CPT is excellent, the radiobiological factors become less important. Another issue is the possibility that late-reacting normal tissues and slow-growing tumours could have a different (and higher) RBE value from that of acute-reacting normal tissues and rapidly growing tumours [3]. If this is so, then additional fractionation sensitivity constraints will be required and we are currently working on this.

RBE exerts a very significant influence on the degree of radiobiological normal-tissue sparing that can be achieved in high-LET therapy, and it has been shown here that errors in RBE determination can mean that the true degree of sparing may be very different from that which might otherwise be assumed. Consequently, it is necessary to take the uncertainty in RBE into account, because the error may reduce the apparent benefit of reduced physical dose to normal tissues afforded by high-LET radiations. In many CPT applications, the physical dose sparing may be so good that uncertainties in RBE will have only trivial impact on the treatment outcome. When significant volumes of normal tissue are included in a high-LET high-dose target region, however, these tissues could be unintentionally overdosed if the RBE of the slowly dividing normal tissues is significantly higher than that of the tumour. Even in apparently satisfactory situations where a small degree of physical dose sparing is achievable by using CPT, the apparent benefit could be over-ridden by wide uncertainties in RBE estimation.

Although the methodology used here is essentially simplistic, it is useful for the purposes of illustrative modelling. In reality, more than one organ at risk of complication will be present and the principles contained in this study will need to be extended to include effects in a three-dimensional situation within the human body.

For a complete and reliable decision-making process, it will be necessary to know how RBE varies with fractionation and LET in different tissue types. This requirement would need considerable investment of resources to uncover the most appropriate values in typical situations and, more so, in individuals, with use of predictive modelling. It may be that such knowledge will always be incomplete. In this case, the acceptable dose in normal tissues must include realistic RBE values within expected limits of accuracy, so that the clinician is alerted to the range of equivalent doses with reasonable statistical accuracy.

The accurate prediction of RBE values remains an essential long-term objective in this field. Various microdosimetric systems currently claim to achieve this [14,15], but they involve multiple assumptions and are essentially incomplete, with limitations at high dose. Some have been found wanting when tested empirically [16] and there is a tendency for these methods to underestimate RBE. Ideally, they should be capable of predicting uncertainties in RBE and not only point estimates of RBE. Further research is required to achieve this goal.

Any estimation of RBE will include multiple uncertainties ranging from those associated with the estimation of physical dose using different dosemeters to biological variation. Typical values for the means and standard errors (SEs) of RBEs for protons are small [7]: mean of 1.22 and SE of 0.02 for in vitro systems and mean of 1.10 and SE of 0.01 for in vivo systems. For fast neutrons, the RBEs in vivo are typically approximately 3 with an SE of approximately 0.1–0.2 [17]. An interesting study of carbon ion RBE carried out in Germany and Japan showed mean RBE values of 1.879 and SE of 0.074 in Germany, and mean RBE values of 1.906 and SE of 0.13 in Japan [18]. In all cases, exceptions involving much larger variations are found and thus SEs are not as informative as 95% confidence limits in these circumstances. Furthermore, these data are all from carefully controlled laboratory studies, often using inbred animals or selected cell lines, that will not adequately reflect the variation between different human patients and across different organ systems.

One potential method of overcoming the RBE uncertainty would be to re-analyse a large number of CPT-treated patients in terms of physical dose and LET and ion species (with reference to both particle charge and mass) in order to build up a new experience of tissue tolerances and tumour control probabilities without the need for prospective assumptions about RBE. With sufficient retrospective information, it might be possible to proceed with safe CPT without excessive reliance on experimental or theoretical RBE values.

Our findings demonstrate the continuing influence of fractionation in the sparing of normal tissues at high LET. It has been shown that the use of high fraction numbers becomes increasingly important when excellent physical dose sparing cannot be achieved with high-LET radiation. Thus, the trend to lower fraction numbers, for example to extreme limits of one, two and four fractions using carbon ions in Japan, could prove problematic if good overall (physical plus radiobiological) sparing cannot be achieved. This issue also imposes a demand for better predictive modelling in order to provide a secure basis for decision making and appropriate patient selection [19]. Until RBE can be predicted with good accuracy, probable errors in RBE estimation should be included as additional constraints in the treatment-planning process. Physicists and clinicians embarking on CPT need to familiarise themselves with these concepts, and further research must be encouraged if CPT is to be used in the most optimal way.

Appendix A

Tumour RBE values are found by solving the iso-effective BED relationship for z_L (the low-LET tumour dose per fraction). Variables within this relationship are the assumed RBE limits of RBE_max (the RBE at very low dose per fraction) and RBE_min (the RBE at very large dose per fraction), both designated by the prefix “tum”.

For iso-effective conditions, low-LET BED = high-LET BED, so,

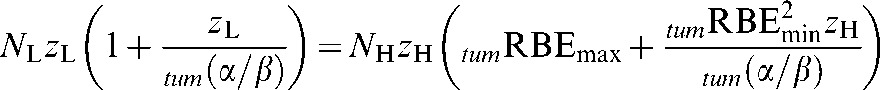(A1)

where N_L is the number of low-LET fractions, N_H is the number of high-LET fractions, z_L is the low-LET tumour dose per fraction, z_H is the high-LET tumour dose per fraction and _tum(α/β) is for the low-LET tumour case. The value of z_H is the solution of Equation A1, that is:

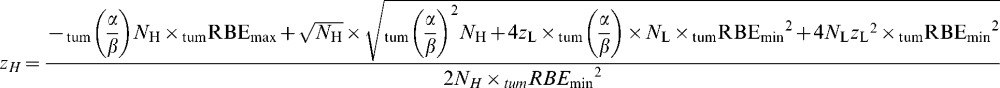(A2)

It should be noted that if N_L=N_H the last equation will not contain these fractionation numbers, since they will cancel in Equation 1.

It then follows that the “working” tumour RBE is z_L divided by z_H, so

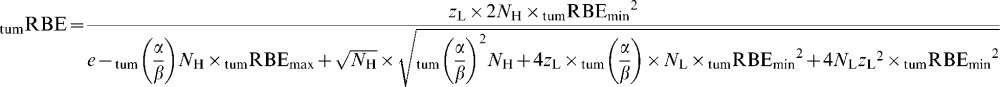(A3)

Similarly, for normal tissues, using the prefixes “norm”, the iso-effect is defined by

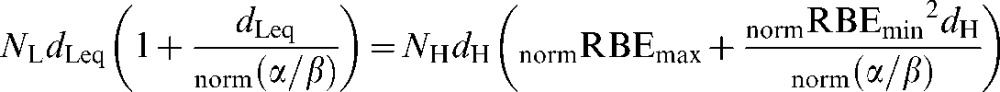(A4)

where d_H is the high-LET normal tissue dose per fraction and _norm(α/β) is for the low-LET normal tissue.

Then the “working” RBE (defined here as d_Leq/d_H ) is given by the solution of Equation A3 for d_Leq, which is:

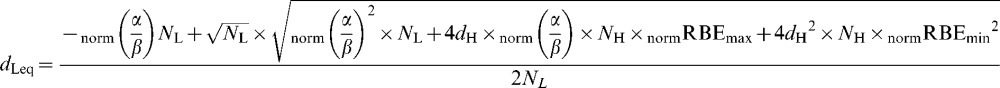(A5)

It then follows that the “working” RBE of the normal tissues is given by d_Leq divided by d_H, which is

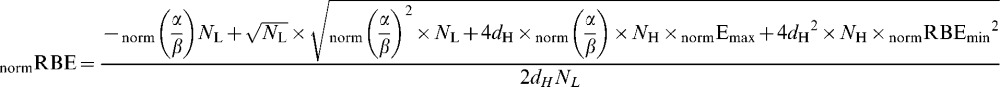(A6)

In both tumour and normal tissue cases, the RBE concept can be extended to schedules that have different fractionation plans (i.e. where N_L is different from N_H). Then, the “fractionated RBE” will be:

(low-LET dose per fraction × number of low-LET fractions) divided by (high-LET dose per fraction × number of high-LET fractions). However, the working RBE in terms of dose per fraction (i.e. Equations A3 and A6) can be used in Equation 8 because the fraction numbers cancel, as explained above.

Programming sequence for calculating S:

1. Set z_L as the prescribed tumour dose and find z_H using equation A2.

2. Find the working tumour RBE from Equation A3.

3. Find d_H by multiplying z_H by P_H.

4. Find d_Leq from equation A5 and then the working normal tissue RBE from Equation A6.

5. S is found from Equation 8 by allocation of the physical sparing factors and the two working RBEs together with an RBE error.