Accelerator science in medical physics

Abstract

The use of cyclotrons and synchrotrons to accelerate charged particles in hospital settings for the purpose of cancer therapy is increasing. Consequently, there is a growing demand from medical physicists, radiographers, physicians and oncologists for articles that explain the basic physical concepts of these technologies. There are unique advantages and disadvantages to all methods of acceleration. Several promising alternative methods of accelerating particles also have to be considered since they will become increasingly available with time; however, there are still many technical problems with these that require solving. This article serves as an introduction to this complex area of physics, and will be of benefit to those engaged in cancer therapy, or who intend to acquire such technologies in the future.

There is growing public awareness of particle accelerators in science owing, in part, to the publicity surrounding the Large Hadron Collider at CERN [1] in Geneva, although protons can be accelerated to high energies at several accelerator laboratories around the world. However, there are many other applications of lower particle energies, especially in medical physics. The general public is largely unaware that the greatest use of particle accelerators worldwide is within hospitals. 5–15 MeV electrons are used to generate megavoltage X-rays or deliver these electrons, without prior collision, from a linear-accelerator to treat cancer.

The recent expansion, in several countries, in charged particle therapy (CPT), which uses protons and light ions to treat cancer has been achieved using relatively conventional, cyclotron or synchrotron accelerator technology [2–4]. Cyclotrons have been used in medicine for many years, especially for radioisotope production. The commercial manufacture of cyclotrons and synchrotrons for radiotherapy by several companies over the past decade has allowed turnkey centres within hospital cancer centres to be installed. Consequently there is a need for medical physicists and oncologists to be aware of the basic principles of CPT accelerator systems, how the equipment operates and the potential impact of new technologies in this area. This article attempts to explain some of these aspects for the benefit of multidisciplinary hospital staff. A glossary of terms frequently used by accelerator physicists is included as an appendix.

Basic concepts

Motion of charged particle in electric and magnetic field

In most particle accelerators, an electric field is used to accelerate the charged particles, while a magnetic field is applied to guide the particle through the accelerating structure. In this section, the motion of a charged particle under the influence of these two fields is briefly described.

A particle with charge (q) in an electric field (E) will experience a directional force (F) (using vector symbols):

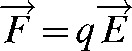(1)

and will be accelerated in a direction that depends on the sign of the charge. For example, a positively charged proton will accelerate towards the negative terminal of the electric field, i.e. the cathode. The velocity (v) acquired by the particle can be expressed as:

(2)

where m is the mass of the particle and 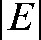is the magnitude of the electric field regardless of its polarity. Also the particle will gain kinetic energy (T) given by:

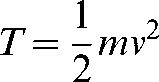(3)

In contrast, a charged particle will not acquire any kinetic energy from a magnetic field, but there will be a change in the direction of its velocity. The motion of the particle, with velocity v, in a magnetic field is governed by the so-called Lorentz force (F_L) as:

(4)

where B is the magnetic field (in units of Tesla).

If the magnetic field is applied perpendicular to the particle motion then the magnetic force will be orthogonal to the magnetic field and to the velocity. The deflection of the particle is illustrated in Figure 1.

Figure 1.

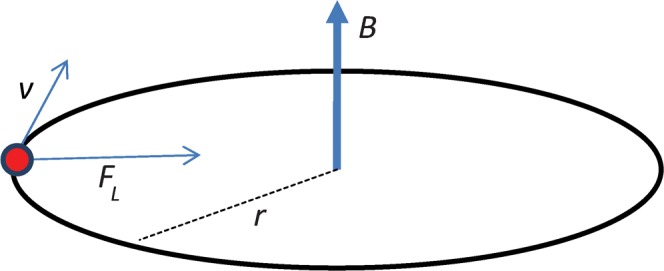
The motion of a positive charged particle in magnetic field. The particle is deflected perpendicular to both the direction of instantaneous velocity (v) and magnetic field (B). F_L, Lorenz force; r, radius of curvature.

This force, 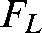, provides the centripetal acceleration necessary to keep the particle moving in a circle and in the plane perpendicular to the magnetic field direction, so that:

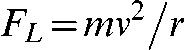(5)

where r is the radius of curvature. Thus:

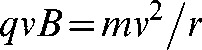(6)

or:

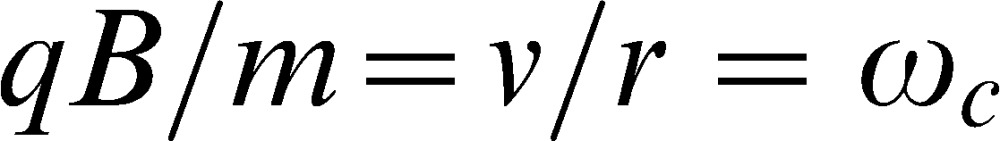(7)

where ω_c is the angular velocity:

The cyclotron frequency (f_c) at which the particle completes a circular path is:

(8)

Then, Equation 8 can be re-arranged as:

(9)

where p is the momentum mv. Here, 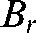is known as the magnetic rigidity, which is a measure of the reluctance of the particle to be bent in a curve in the presence of a magnetic field. As a consequence, a much greater magnetic field will be required to keep a carbon ion, which is approximately 12 times the mass of a proton, in the same orbit as a proton of the same velocity.

Relativistic effects

The above analysis is correct when the velocity of the particle is small relative to the velocity of light. However, when the velocity approaches that of light, the effects of special relativity need to be taken into account. For example, a proton accelerated to 250 MeV (the energy needed to just pass through the human body) will move with a velocity of approximately 60% that of light. To take account of relativistic effects, it is necessary to replace the definition of the momentum by its relativistic equivalent:

(10)

where 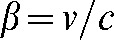and .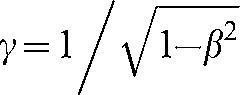

It is also necessary to change the definition of the kinetic energy (T). In relativity, the total energy of a particle is given by 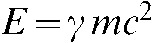and the kinetic energy is given by 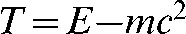(it can be easily shown that when , this definition of the kinetic energy reduces to that of Equation 3).

Cyclotrons and synchrotrons

Although it is possible, in principle, to build a linear accelerator to accelerate protons and light ions, such as carbon, the length required (determined by the achievable accelerating gradients) has in general been considered excessive; however, recent advances in the development of high-gradient accelerating cavities might mean that these become competitive in future. Therefore, the present generation of CPT centres use either a cyclotron or a synchrotron.

Cyclotrons

A simple cyclotron consists of a large circular magnet providing a constant magnetic field across the gap between the pole-faces. A schematic diagram of a cyclotron is shown in Figure 2. A particle is injected into the magnetic field with an initial velocity, somewhere near the centre of the magnet, inside two “dee” (D) shaped hollow electrodes, which are placed between the poles of the magnet. While the particle is inside the D, it is shielded from the electric field (i.e. in a Faraday cage), so that only the magnetic force applies, and the particle moves along a circular path. A potential difference is established between the two Ds, so that each time the particle crosses from one D to the other, it sees a small accelerating voltage and moves outwards, following a new orbit at a slightly larger radius. During the time that the particle is inside the D, the polarity of the voltage is changed, so that it is continually accelerated. The frequency with which the accelerating voltage must be changed is the cyclotron frequency defined in Equation 8; for practical cyclotrons this frequency is in the megahertz range, and is usually referred to as radiofrequency (RF). Eventually, the radius will reach a maximum value, determined by the radius of the magnet pole faces, and the particle will escape.

Figure 2.

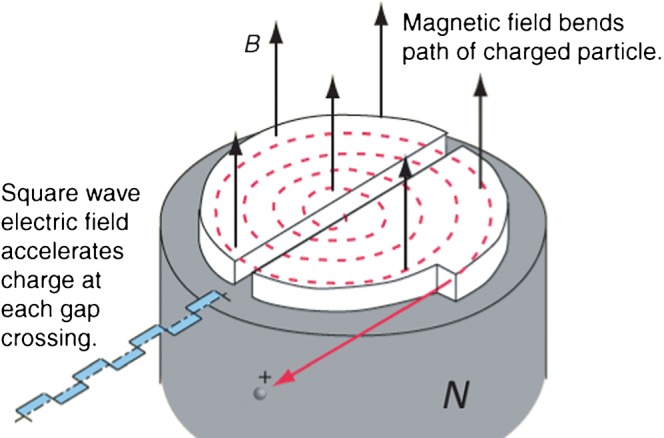
A schematic diagram that shows the particle motion in a simple cyclotron. B, magnetic field; N, polarity of the field.

This description so far ignores relativistic effects, which become significant when the proton kinetic energy is larger than approximately 15 MeV. To reach higher energies, it is necessary either to modify the magnetic field as a function of the radius or to vary the accelerating RF. Most modern cyclotrons use a modified magnetic field shape to keep the cyclotron frequency constant, by ensuring that the time taken for a particle to complete a revolution is constant. This type of machine is known as an isochronous cyclotron, which provides continuous beam output with high intensity. Alternatively, the decrease in rotation frequency of the ions owing to relativity can be synchronised to the RF leading to the synchrocyclotron, keeping the magnetic field constant.

Orbit stability

Charged particles (ions) travel a long distance in the cyclotron before reaching the maximum energy. It is very challenging to keep them in their equilibrium orbit (orbital stability) for various reasons, including the distribution of initial energies, positions and directions of the particles at injection, and effects such as collisions with residual gas molecules in the cavity; ions tend to deviate from the equilibrium orbit during rotation. Therefore, corrective steering forces should be applied, to correct for up–down (axial) and left–right (radial) deviations.

The isochronous cyclotron

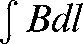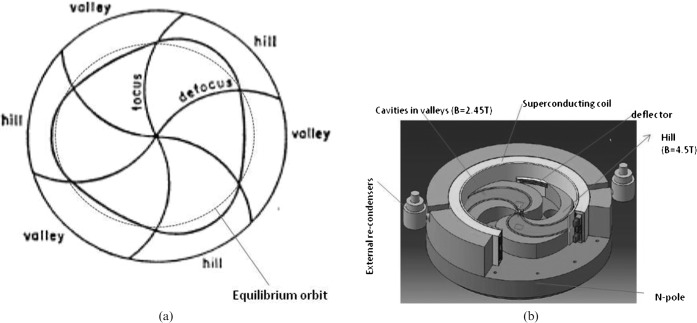
An isochronous cyclotron employs a magnetic field that increases with radius to compensate for the relativistic effects. In fact, what is important is the strength of the magnetic field multiplied by the path length in the magnetic field traverse by the particle (often referred to as the integral Bdl or ). For a particle moving in a uniform magnetic field at a radius (r) from the centre turning through an angle θ, the integral Bdl is . By carefully shaping the pole-faces, and in particular by having a shorter magnetic path length near the centre of the magnet, it is possible to ensure that the cyclotron frequency remains constant. This arrangement (Figure 3) is called a separated sector cyclotron.

Figure 3.

(a) The orbit or a particle in an isochronous cyclotron; alternating strong and weak azimuthal regions are created (“sectors” or “hills and valleys”) to provide axial focusing to offset the defocusing effect owing to radially increasing magnetic field. (b) Cross-section of an IBA C400 isochronous cyclotron, which can accelerate protons (approximately 265 MeV) and light ions up to carbon (400 MeV u⁻¹).

The separated sector cyclotron has another advantage; in the discussion of the simple cyclotron, it was assumed that all of the particles entered the magnetic field region near the centre of the magnet with just the right energy, position and direction to follow the ideal spiralling orbit to the point of extraction. However, in reality, the particles will have a distribution of energies, positions and directions, and each of the particles in a group of particles (the bunch) will follow its own path, scattered around the ideal orbit. Now, it might be thought that there would be a tendency for the particles to diverge as they accelerate; however, by shaping the magnetic field, it is possible to focus the bunch, both horizontally and vertically, so that it remains relatively compact. In a separated sector cyclotron, it is possible to shape the remaining pole-pieces to enhance this focusing effect, as indicated in Figure 3.

Synchrotrons

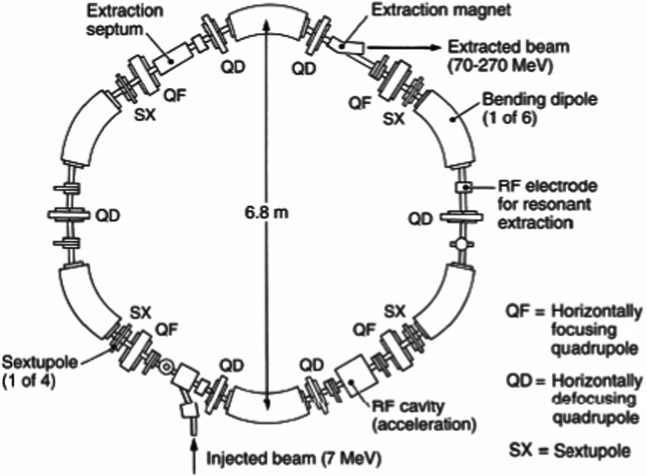
The main limitation of the cyclotron is that as the energy increases so does the size of the magnet, and relativistic effects mean that the Bdl effect has to increase even faster. As a result, the synchrotron was developed with a fixed particle orbital radius. To achieve this, the magnetic field must vary as the particles accelerate (Equation 7). At very high energies (when the velocity is close to the speed of light), the RF is constant, but at lower energies (such as those needed for proton and light ion therapy) the RF must vary, in synchronisation with the energy and the magnetic fields. While this is clearly a more complicated accelerator, the advantage is that the magnets and the RF cavities are much smaller, and therefore cheaper. A schematic diagram of a synchrotron is shown in Figure 4.

Figure 4.

Schematic diagram of HITACHI 250 MeV proton synchrotron. It consists of one RF cavity for acceleration and six bending dipole magnets to drive the particle in circular orbit. Quadruple magnets are used for focusing. RF, radiofrequency.

Generally, a linear accelerator is used to pre-accelerate the ion (typically to a few mega-electron volts), which is then injected into the synchrotron ring. When the ion transits through the RF cavity, it is accelerated, acquiring energy and increased velocity. The magnetic field of the bending magnet needs to be increased to match this increase in velocity to keep particles in a fixed orbit. Therefore, unlike the cyclotron where the particle spirals outward with increasing energy under the action of constant magnetic field, the synchrotron accelerates the particle at a constant trajectory even when the particle energy increases. Unlike the cyclotron, where a magnetic field is applied within the circular orbit of the beam, in the synchrotron the guide field can be provided by a narrow ring of magnets. Dipole magnets are used to bend the beam to follow the circular orbit.

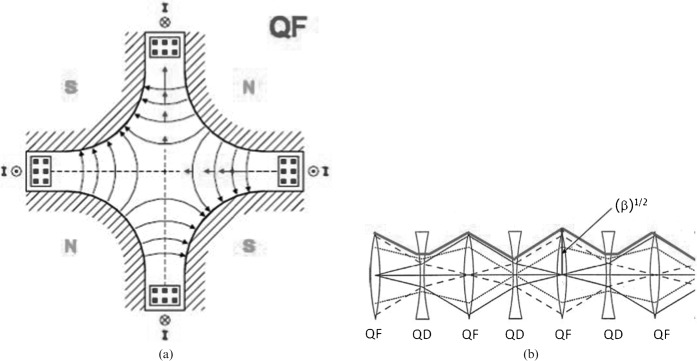
As noted for the cyclotron, not all of the particles have exactly the right energy, position and direction to follow the desired orbit. Although the bending magnets have a weak focusing effect in the horizontal plane, the real advance came with the invention of strong focusing in the 1950s. In strong focusing, quadrupole magnets (a magnet consisting of four poles) spaced around the ring between the bending magnets continually focus and defocus the beam. This happens because quadrupoles have an odd behaviour, compared with optical lenses. A spherical optical lens focuses in both planes—horizontally and vertically. However, if a quadrupole focuses in one plane (say the horizontal plane), it defocuses in the other (vertical) plane (Figure 5). It can easily be shown that the combination of two lenses of equal strength, one focusing and one defocusing, has a net focusing defect. By constantly focusing and defocusing around the ring, it is possible to keep the transverse size of the particle bunch small, leading to small aperture (and therefore cheaper) magnets.

Figure 5.

(a) Magnetic force lines owing to a focusing dipole magnet which focuses the particle in horizontal plane while defocuses in other plane. (b) Alternative focusing and defocusing quadruple represented using a lens analogy. The net effect is focusing in both directions. QD, horizontally defocusing quadrupole; QF, horizontally focusing quadrupole.

The individual particles are constantly changing their position (x,y) and angle (x',y') relative to the on-axis on-momentum particle on the ideal orbit, each particle describing an ellipse in the horizontal (x,x') and vertical (y,y') planes. This is called the phase space. The area swept by the ensemble of particles in the two transverse phase space planes is called the emittance (ε), and is a fundamentally important parameter of the accelerator. The particle motions around the ideal orbit are called betatron oscillations, and the main characteristic is described by the β-function, which varies around the circumference of the machine. At any point, the physical size of the beam in the horizontal (vertical) plane is given by:

The discussion above assumes that the main components’ (dipole and quadrupole) magnets are perfectly constructed. However, real magnets of finite length always have higher multipole components, and there is also dispersion in the magnets owing to the finite distribution of momenta. These can be (partially) compensated by including higher-order multipole magnets (e.g. sextupoles with six pole faces) in the design.

When the beam reaches the desired energy, it must be extracted into an external beam-line and transported to where it is needed. One method uses kicker and septum magnets. A kicker magnet, which has a very fast rise time, is used to divert the entire beam to the transport line, where a septum is a magnetic (or sometimes electrostatic) device for deflecting a beam, or part of it, from its normal path. It can be used to split the proton beam into two beams, so that one of the beams can be extracted while the other beam stays in orbit. Other extraction mechanisms can be used, such as the RF driven extraction, where the betatron oscillations are enhanced, sending the beam into the septum.

Comparisons between cyclotrons and synchrotrons

The typical clinical requirements for particle therapy are shown in Table 1. Comparisons of different accelerators for particle therapy can be found in the literature [5], although not recently, but there are several good generic textbooks [6, 7]. Cyclotrons are considered simple to operate, very reliable and compact. They deliver a continuous output with higher beam current in the order of microamperes. But their major drawback is that the output energy is constant—at the maximum attainable energy of the device—and passive degraders are required to reduce the energy and provide the range of energies required to treat a tumour. This process occurs outside the cyclotron and before entry of the beam to the treatment room, since there is unwanted neutron production. Some modern cyclotrons use very powerful superconducting magnets, which makes them very compact. The first superconducting cyclotron started operating at the Paul Scherrer Institute in 2007 [250 MeV by Accel, Varian (Varian Medical Systems, Palo Alto, CA)]. Further developments include the Still River Company (Still River Systems, Littleton, MA) [8] superconducting synchrocyclotron weighing only 20 t, which is one-tenth of a conventional machine and can be mounted on treatment gantry in the patient room, but which must incorporate sufficient shielding to minimise neutron contamination. Commercially available cyclotrons can accelerate protons only to the clinical range of energies at the present time. With progress in superconducting technology, many groups are trying to develop a cyclotron for heavy ion therapy where energies of >400 MV per nucleon are required.

Table 1. Typical clinical requirements for particle therapy using protons and carbon ions.

Parameter	Value	Units
Extraction energy (proton) (min, max)	60, 240	MeV
Extraction energy (carbon) (min, max)	110, 450	MeV u−1
Energy step (protons) (at min, at max)	5, 1	MeV
Energy step (carbon) (at min, at max)	15, 6	MeV u−1
Energy resolution ΔE/E (at min, at max)	3.5, 1.8	%
Voxel size (min, max)	4×4×4, 10×10×10	mm
Smallest field of view (min, max)	100×100, 250×250	mm
Clinical dose rate (protons) (min, max)	2, >10	Gy min−1
Clinical dose rate (carbon) (min, max)	2, >10	Gy min−1
Cycle rate (min, max)	0.5, 2	kHz
Bunch charge (protons) (min, max)	1.6, 16	pC
Bunch charge (carbon) (min, max)	300, 3000	fC
Bunch charge stability and bunch charge measurement accuracy	<10	%

max, maximum; min, minimum.

The pure synchrotron has the advantage of variable energy extraction but requires beam injection and complex beam extraction systems, so that only particles with the required energies are used. No degradation process is necessary. The beam current is less than that of a cyclotron and is of the order of nano amperes when averaged over the acceleration cycle, thus producing significantly longer treatment times. However, recent technological advances, particularly in beam extraction, may mean that these accelerators could be less complicated and more efficient with reduced cost. Previously, synchrotrons were available only in physics laboratories; now all heavy ion centres that currently operate around the world employ a synchrotron for particle acceleration.

Future accelerators

As well as some combinations of cyclotrons with a final linear proton or ion accelerator known as the cyclinac [9], there are several projects that aim to develop different forms of more compact and efficient systems, as described below. These are not placed in any particular order, e.g. time to completion, which remains undetermined in each case owing to the additional research and prototype construction required in each case.

Fixed field alternating gradient accelerator

Fixed field alternating gradient (FFAG) accelerators use a magnetic field that does not change with time, but does contain field gradients along the radial direction. Owing to the fixed magnetic field (as in a cyclotron), the FFAG accelerator can accelerate particles very rapidly, which results in high currents, while the magnetic gradient (as used in a synchrotron) allows a variable energy output. The FFAG accelerator appears to combine the best features of cyclotrons and synchrotrons, and the particles assume a different orbital pathway on each rotation and can be extracted from a unique position. Using non-scaling FFAG (NS-FFAG) techniques, where the magnetic field gradient is further modified to contain the particles in smaller closed orbits and by employing superconducting magnets, the accelerator foot print and gantry size can be reduced considerably. The UK is pioneering the development of NS-FFAG technology with the Engineering and Physical Sciences Research Council-funded Particle Accelerator for Medical Applications project, which aims to design a complete hadron therapy facility for protons and light ions [10].

Dielectric wall accelerator

The dielectric wall accelerator (DWA) is another new concept for very compact proton therapy acceleration. It is expected to be small enough (approximately 2.5 m) to fit in a conventional linear accelerator vault and capable of producing very high current in short pulses (<1 ns). Both the proton energy and beam intensity can be varied simultaneously. The DWA comprises a hollow vacuum tube whose walls consist of a very good insulator (dielectric), which can withstand a high electric field gradient. It uses a fast switched high-voltage transmission line to generate pulsed electric fields inside the acceleration tube. An accelerating electric field gradient is achieved by use of alternating insulators and conductors [11]. A programme to develop DWA for clinical application is currently underway, but clinically relevant energies are yet to be achieved.

Laser driven particle accelerator

Another promising particle accelerator is based on the laser plasma accelerator. These use a high intensity (>10¹⁹ W cm⁻²) short pulse (<1 ps) laser beam to generate high energy particles. When the laser beam is incident on a thin target (often metallic foils or plastic discs of a few micrometres thickness or even a water or oil droplet), high-energy electrons are injected into the target. A fraction of these relativistic electrons will escape from the target, it being charged to very high potentials. The resultant electric field (approximately 10¹² V m⁻¹) will accelerate particles emerging from the target material to high energies. A laser driven accelerator has the potential to produce high-intensity beams with some superior beam characteristics. However, the maximum proton energy achieved so far is up to approximately 70–100 MeV. There are further challenges, such as how to produce the required energy variability, monochromaticity etc. [12]. It is an active area of research, with the UK at its forefront [13]. In principle, laser particle production has some attractive advantages, for example it allows changes in the ion type and energy range by varying the shape and composition of the target material. Laser light can be deflected by mirror systems into treatment rooms and target systems near to the patient, so that beam transmission and gantry costs should be sharply reduced.

Conclusion

The rapid increase in charged particle therapy worldwide imposes a demand for a better understanding of accelerator techniques amid the medical and allied professional groups. It is self-evident that many large hospitals will eventually contain proton and ion beam accelerators and that the choice of equipment will pose dilemmas when different methods of accelerating particles become available.

Appendix A: Glossary of terms

Beam dump

A massive object used to absorb an unwanted beam and dissipate the resulting heat. Dumps for high intensity beams are usually composed of large water-cooled metal blocks. They must be shielded from the surrounding environment owing to the extreme radioactivity induced by the absorbed beam.

Beamline (transport line)

A series of magnets and vacuum pipe that carry the proton beam from one portion of the accelerator to another.

Blow up

A relatively sudden and usually catastrophic increase in beam size that is generally caused by some magnetic field error driving the beam to resonance.

Bunch

A group of particles that are injected, accelerated and extracted together. Within the bunch, the particles (which can be hundreds of millions) have similar energies, positions and directions, and the individual particles move around relative to the bunch centroid through acceleration.

Dipole magnet

A dipole magnet has a magnet field in one direction (usually vertical) and is used to steer the charged particles around the accelerator along a circular path.

Emittance

The area in phase space occupied by a particle beam. The units are millimetre-milliradians for transverse emittance and electron volts-second for longitudinal emittance.

Injection (extraction)

The controlled insertion (removal) of bunches into (from) one stage of the accelerator from (into) the next stage.

Kicker magnet

Very fast rise time magnet used to divert the entire beam at once.

Phase space

A six-dimensional space consisting of a particle's position (x, y and z) and divergence (x', y' and z'). Phase space is generally represented in two dimensions by plotting position on the horizontal axis and the corresponding divergence on the vertical axis.

Phase stability

Phase stability enables particles to be accelerated to their final energy. The voltage waveform for the accelerating electric field is sinusoidal. Particles in an accelerator do not advance side by side but are spread out into a column. Therefore, if the front end of such a column reaches the accelerating gap when the voltage is at its maximum, all later particles experience less voltage and thus less acceleration. Consequently the column lengthens and ultimately many of the particles are decelerated because they arrive at the gap when the electric field is directed in the opposite way. If the phase φ of a synchronous particle (frequency of RF = frequency of revolution) is within certain limits then the accelerating voltage can accelerate particles that enter the gap with FDF (a triple magnet arrangement for focusing defocusing and focusing the beam), thus giving a stability.

Quadrupole magnet

A quadrupole magnet has four poles, arranged around as N-S-N-S. The action of a quadrupole magnet on a charged particle is similar to that of a lens on a light ray. However, whereas an optical lens focuses or defocuses in both planes, a quadrupole lens focuses in one plane (say the horizontal plane) and defocuses in the orthogonal plane (the vertical plane). A combination of two quadrupoles, one rotated through 90° relative to the other, has a net focusing in both planes.

Resonance

Usually used to mean “betatron resonance” when talking about an accelerator; it occurs when some perturbing force in the accelerator distorts the orbit in a periodic way, causing the betatron oscillations to grow larger and larger, until the beam is lost or perhaps extracted.

Radiofrequency cavity

The acceleration of the particles takes place in an accelerator component at certain points around the accelerator called a cavity, in which a variable (RF) electric field is generated.

Septum

A septum is an accelerator component (usually a dipole magnet, but sometimes electrostatic), which channels a bunch into (from) the circular orbit from an external injection (extraction) beam line.

Superconducting magnet

This is a magnet whose coils are made from superconducting material. Superconducting magnets reach much higher magnetic fields than conventional iron/copper magnets at a much lower electrical power cost. They must be cooled to 4 K, which is achieved by a continual flow of liquid helium through the magnets.