Revisiting the ultra-high dose rate effect: implications for charged particle radiotherapy using protons and light ions

Abstract

Objective

To reinvestigate ultra-high dose rate radiation (UHDRR) radiobiology and consider potential implications for hadrontherapy.

Methods

A literature search of cellular UHDRR exposures was performed. Standard oxygen diffusion equations were used to estimate the time taken to replace UHDRR-related oxygen depletion. Dose rates from conventional and novel methods of hadrontherapy accelerators were considered, including spot scanning beam delivery, which intensifies dose rate.

Results

The literature findings were that, for X-ray and electron dose rates of around 10⁹ Gy s^–1, 5–10 Gy depletes cellular oxygen, significantly changing the radiosensitivity of cells already in low oxygen tension (around 3 mmHg or 0.4 kPa). The time taken to reverse the oxygen depletion of such cells is estimated to be over 20–30 s at distances of over 100 μm from a tumour blood vessel. In this time window, tumours have a higher hypoxic fraction (capable of reducing tumour control), so the next application of radiation within the same fraction should be at a time that exceeds these estimates in the case of scanned beams or with ultra-fast laser-generated particles.

Conclusion

This study has potential implications for particle therapy, including laser-generated particles, where dose rate is greatly increased. Conventional accelerators probably do not achieve the critical UHDRR conditions. However, specific UHDRR oxygen depletion experiments using proton and ion beams are indicated.

Ionising radiation exposure of biological systems produces very rapid physical and chemical changes that are later processed into biological damage. The main sequence of chemical events is ionisation of water and production of a range of free radicals, which interact with key biological targets such as DNA. Both the yield and variety of free radicals are enhanced by the presence of oxygen, which also increases the subsequent stability of the chemical changes in biomolecules, a process known as fixation of damage [1]. The availability of ultra-high dose rates in various physics laboratories, together with improved cell culture techniques, allowed scientists to investigate the potential impact of radiation delivered within the time frame of most of the chemical processes (ranging from 10 ps to 50 μs). For mammalian cellular and chromosomal systems, interesting results were published by several authors between 1967 and 1978. These led to the conclusion that ultra-high dose rates would not necessarily be advantageous and might have adverse consequences because of local oxygen depletion [2-9], with very low oxygen tensions causing significant cellular radioresistance and being capable of reducing local cancer “cure”.

These experiments were aimed at investigating the role of X-rays and electrons in radiotherapy. The results also required interpretation in terms of how normal tissue and tumour responses might change, especially if the former received lower doses than the latter during radiotherapy. Of special concern was the occurrence of very low oxygen tensions within parts of many malignant tumours, which contribute to cellular radioresistance. Further decrements in oxygen tension caused by very high dose rates appeared to increase the proportion of radiologically hypoxic cells with low radiosensitivities, as seen by shallower slopes on the radiation cell survival curves beyond certain critical doses. The classic relationship between the change in radiosensitivity and oxygen tension is non-linear, with a steep gradient between ∼0.75 and 7.5 mmHg (∼0.1 and 1 kPa), changing radiosensitivity by a factor of two or more (pp. 207–8 of [10]). In this paper, oxygen tensions will be quoted in both mmHg and kPa because the older publications use the former units.

Currently, there is increasing clinical use of charged particle therapy (CPT) using protons and light ions in the treatment of cancer [11-13]. Due to the Bragg peak effect, the tumour dose can be increased in many situations while reducing, or eliminating, the dose to some normal tissues. Within the Bragg peak, there are particle mass- and particle charge-dependent increases in the local intensity of ionisation on a microscopic scale (referred to as linear energy transfer, or LET), which in turn results in a higher relative biological effect (or RBE). Both LET and RBE are reduced by spreading out many Bragg peaks to cover a tumour target, which then includes more low-LET parts of the beam away from the peak. The local complexity—or clustering—of high-LET biological damage differs from that of megavoltage X-rays and electrons, and probably accounts for RBE as clustered damage is more difficult to repair by cellular enzymatic processes (p. 69 of [10]). In practice the same biological effects can be achieved with low- and high-LET radiations by reduction of the high-LET dose in accordance with the RBE of the particle. A further feature is that the extent of oxygen sensitisation on cellular radiosensitivity is reduced for some forms of CPT (e.g. particles with atomic numbers greater than 2), but such an effect is considerably reduced by spreading out of the Bragg peaks, although even a mild reduction in oxygen dependency could be advantageous in the case of carbon ion therapy [13].

Particle acceleration for CPT is usually achieved using cyclotrons or synchrotrons. The former, due to their fast cycling and larger beam current characteristics, provide higher dose rates than the latter. More advanced accelerator designs, such as the non-scaling fixed-field alternating gradient (NS-FFAG) and dielectric wall accelerators [14-16], could, in principle, deliver much higher dose rates, with the potential advantage of shorter patient treatment times and some degree of improved throughput, even though set-up time is usually longer than treatment time. Personal observations of synchrotron treatments in Japan can take over 2 h to deliver a single radical fraction, although at least half of the time is taken up by positioning of patients and verification of each of four different treatment fields. Another important issue is that beam delivery by means of scanned pencil beams (sometimes referred to as raster or “spot scanning” beams) ensures that a small volume of tissue (usually measuring ∼4 mm³) receives the entire dose output within a few milliseconds. This is in marked contrast to the use of a broadened, passively scattered beam delivered to the entire target volume simultaneously, but at a lower dose rate.

Currently, two different schemes are employed for pencil beam scanning. In discrete spot scanning the beam is switched off when moving between successive spots, and the dose delivered by each spot is often determined by the beam “on time” at that particular spot. Raster scanning employs a pencil beam, which is continuously moving at constant speed, and dose profiling can be further improved by beam intensity modulation.

The conduct of spot scanning can be varied so that lower doses are given at each “spot” exposure, but each tumour spot region is then retreated at a slightly later time, a technique referred to as “repainting”. Any such delay between successive spots in the same location within the same treatment fraction allows a short time for diffusion of oxygen to oxygen-depleted sites in situations of chronic (diffusion-related) hypoxia, and also the possibility that temporarily “closed” blood vessels could reopen and relieve acute hypoxia. The rationale usually given for repainting a tumour is the reduction of uncertainty in dose deposition rather than for physico-chemical reasons. The conversion of beam intensity to dose rate is not straightforward for spot scanning technique and there are only average dose rate measurements or estimates in the literature, rather than instantaneous dose rates for each spot. For a NS-FFAG accelerator in spot scanning mode, tentative calculations show that a 100 ns bunch of 10⁶ proton particles can provide a dose of 1 Gy (RBE) (the gray-equivalent dose, which contains an RBE correction) and a dose rate in the deepest volume element (or voxel measuring 5 mm³) of 2.07×10⁸ Gy s^–1. These parameters are below the critical requirements for oxygen depletion for electrons and X-rays, which are provided below. However, since the dose profile of each spot follows a Gaussian distribution and spots are partially overlapped, then the instantaneous dose rate will vary with position in the treated volume, and there will be considerable uncertainty.

Further technological developments include laser particle production [17,18]. Here, the laser pulses are very short (picoseconds) and are capable of a high dose per pulse (>10¹⁰ Gy s^–1). The design of future laser-based systems should take into account radiobiological concerns regarding potential oxygen depletion in hypoxic tumour zones and should aim to minimise any potential disadvantages associated with ultra-high dose rate effects.

Methods and modelling assumptions

A literature review of ultra-high radiation dose rates provided experimental cell survival data for changes in dose and dose rate in aerated and hypoxic conditions. These data provide useful parameters for simulating the spot scanning or any rapid pulsed radiation techniques, and are summarised in Table 1.

Table 1. Literature review on ultra-high dose experiments in tumour systems.

Authors (dates)	Experimental system	Oxygen depletion dose, etc.	Radiation type	Dose rate	Pulse duration
Town et al (1967) [2]	HeLa S-3 cells	Above 9 Gy exposure; effect lost for second pulse 2.5×10−3 s later	15 MeV electrons	3.5×107 Gy s–1	1.3 μs
Prempree et al (1969) [3]	Human lymphocyte chromosomal aberrations	Reduction in yield described	X-rays	4.8×108 Gy s–1	n/a
Nias et al (1969) [4]	HeLa	7 Gy	8–14 MeV electron	<1.8×107 Gy s–1	1 μs
Berry et al (1969) [5]	HeLa S-3oxi and CHL-F	5–10 Gy for short pulses	2 MV X-rays up; 3.7 MV X-rays:	109 Gy s–1, up to 1010 Gy s–1	7 ns pulse, 50 ns pulse
Berry et al (1972) [6]	2 HeLa lines and murine leukaemia	5–10 Gy; partly hypoxic cells develop radiolo-gical hypoxia above 5 Gy	400 KeV electrons at dose rate	109 Gy s–1	3 ns
Purrot et al (1977) [7]	Chromosomal aberrations in human lymphocytes	No increase in yield	15 MeV electrons	5×106 Gy s–1	1 μs
Ling et al (1978) [8]	CHO cells	12 Gy depletion dose; oxygen diffusion to single cells significant after 3×10−3 s	Electrons	109 Gy s–1	3 ns
Watts et al (1978) [9]	Cultured V-79 cells	Oxygen diffusion to single cells significant after 1–2×10–3 s	400 keV electrons	109 Gy s–1	n/a

CHO, Chinese hamster ovary; n/a, not available.

The standard oxygen diffusion equations used are summarised in Appendix A. Ling et al [8] used two electron pulses of 3 ns duration and a high dose rate of 10⁹ Gy s^–1 to obtain survival curves for Chinese hamster ovary (CHO) cells at ∼0.44% oxygen concentration (around 3 mmHg or 0.4 kPa), and the data obtained from those experiments are used for the estimation of reoxygenation times at various parts in this paper.

Within a 4 cm³ tumour volume, tumour subvolumes of 4 mm³ (commonly used in spot scanning techniques) are assumed to contain regions of diffusion-related hypoxia. The relationship between oxygen tension and radiosensitivity is given in Appendix B. Typical values of K in the literature are 0.5–4 mmHg (0.07–0.53 kPa) [19], and a value of 1 mmHg (0.13 kPa) was used in this study.

Mathematica (Wolfram, Champaign, IL) software was used to simulate the diffusion of oxygen into hypoxic regions.

Local reoxygenation after its depletion by ultra-high dose rate irradiation

Assuming oxygen is almost completely depleted in cells at low oxygen tension as a result of high-dose rate irradiation, the estimated time taken to reoxygenate at different distances from a blood vessel is calculated using the diffusion equation given in Appendix A. The value of the diffusion co-efficient is taken as D=2×10⁻⁵ cm² s⁻¹ and initial oxygen concentration of C₀=0.44%.

However, there is the additional complication that red blood cell (erythrocyte) oxygen might also be partially depleted, although to a lesser extent than in other tissues since erythrocytes do not metabolise oxygen. Erythrocytes release oxygen quickly in response to local hypoxia, but the process can change with pH and other chemical factors. It is not known what the effect of radiation on release of oxygen from haemoglobin might be for those erythrocytes that are already severely depleted, having already traversed along tumour blood vessels. Should erythrocytes be severely depleted of oxygen, a further short delay of a few seconds would be required for perfusion of unirradiated blood to replace irradiated blood within the tumour. The magnitude of this reperfusion time would depend on the ambient tumour blood flow, interstitial pressure and the architecture of the vascular network itself. A further issue is that oxygen gradients occur between the vessel and the hypoxic region, but oxygen will be partially depleted at all distances, and it is assumed that intracellular metabolism will also extract oxygen at a constant rate, thus causing further depletion. Complete restoration of the pre-irradiation oxygen gradient values will only be achieved by diffusion of new oxygen along the entire distance from the vessel. Areas of intermediate oxygenation can replenish the outer hypoxic areas, but only at their own expense. The estimation of the time for restoration of the pre-treatment oxygen level given by the equation in Appendix A probably represents a maximum value. For the present purpose, and until specific experiments can be done to determine the actual times, we should assume the “worst case” scenario that these calculated times provide the lowermost time limit, such that treatments should exceed these values in order to allow reasonable time for complete restoration of the pre-treatment oxygen concentrations.

Results

The collected literature on ultra-high dose rate cell survival effects shows some general findings, as shown in Table 1. In the case of low-LET X-rays and electrons, a critical dose of 5–10 Gy is sufficient to deplete cellular oxygen at dose rates of around 10⁹ Gy s^–1. There are no data on protons and heavy ions.

The change in radiosensitivity due to oxygen depletion is plotted on a semi-log scale in Figure 1. In this way, a sigmoidal relationship is seen with a marked depletion effect occurring at a critical range of oxygen tension between the two black points on the curve.

Figure 1.

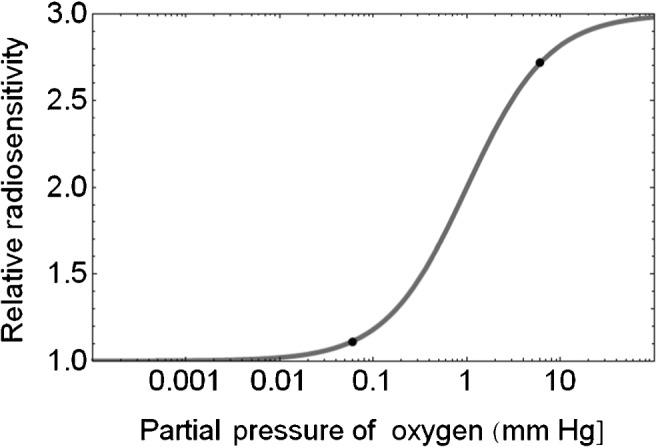
Plot of relative radiosensitivity with changes in partial pressure of oxygen. The critical oxygen depletion range is indicated by the two black points (changing from an oxygen pressure of 3 to 0.06 mmHg reduces the relative radiosensitivity from around 2.7 to 1.1) and is compatible with the changes of radiosensitivity described by multiple authors in Table 1.

Oxygen dose-depletion kinetics are not well established, but we assume (tentatively) a first order (exponential) decay process such as

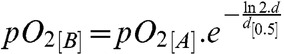(1)

where d is the dose and d_[0.5] is the dose required for a 50% reduction in the unirradiated initial pO_2[A] to a radiation depleted value of pO_2[B].

If we assume the changes in pO₂ between the two black points in Figure 1 (from around 3 mmHg to 0.06 mmHg, which represents approximately six reductions of 50%) of pO₂. If this is achieved by a dose of 5 Gy, then the value of d_[0.5] is found to be d_[0.5]=0.89 Gy. For a dose of 6 Gy to achieve the same effect we obtain d_[0.5] of 1.06 Gy. If a more simple linear depletion of oxygen with dose is assumed (where pO_2[B]=pO_2[A]–z.d, where z is a linear depletion coefficient, then the same degree of reduction would occur by z=0.59% Gy⁻¹ for a dose of 5 Gy and by z=0.49% Gy⁻¹for a dose of 6 Gy, and so on. In the absence of specific data, these calculations provide a rough guide to the effect of dose on oxygen depletion. It is then self-evident that doses of radiation even higher than 5–6 Gy will not produce such changes in radiosensitivity if given to cells/tissues at much higher oxygen tensions such as 10%, because of flatness of the curve at higher oxygen tensions.

Reoxygenation effect during spot scanning

Modern proton and ion therapy centres employ spot scanning dose delivery techniques, where a narrow pencil beam (of ∼4 mm width) is used to scan the treatment volume and deposit dose in small voxels to achieve the desired dose conformity. Fast scanning magnets are used to move the beam across the most distal layer initially and then less deep layers of the tumour are scanned by gradual reduction in beam energy. The dwell time per spot is variable and is greater for the distal portion of a target compared with its proximal part, because the beam irradiating the distal edge will contribute some dose to the proximal region. However, for tentative modelling purposes an average value is assumed. The beam can be either switched off when moving between the consecutive spots (“discrete spot scanning”) [20], or the beam is moved to the next voxel without turning it off (“raster scanning”) [21]. Discrete spot scanning may offer some advantages in terms of reoxygenation, as the beam is off between spots, allowing some more time for rediffusion of oxygen before the same voxel is treated again. There is no standard system for spot scanning—treatment times vary with tumour size, depth and the “repainting” policy used.

For a target volume v cm³ consisting of linear dimensions d_x (depth of target), d_y (width of target) and d_z (height of target) in three planes, a spot volume of s cm³, then the number of spots (n) required will be v/s. To simplify our assumptions, if the time to deliver each spot is, on average, t_av s, the time between successive spots is t_a s for discrete spot scanning (in contrast to continuous raster scanning) and t_b is the time to change particle energy for m different depths found from the dimension d_x, then the overall treatment will be delivered in a time T, where

(2)

Assuming an average time of 10 ms per spot, and that 5 ms is the dead time between spots and 50 ms the time for energy change, then to cover a 4 cm³ target by successive spots, the elapsed time T will be approximately 15.4 s. Should the tumour be repainted, then T will increase, although the time per spot will be reduced.

This is shorter than the calculated time required to fully reoxygenate a hypoxic area at a distance exceeding 100 μm from a blood vessel (as shown in Figure 2). This is not considered to be a serious problem for fractionated proton therapy at conventional dose rates and where the dose per fraction is only 2 Gy, since there should be insufficient oxygen depletion because a dose of 5 Gy is not reached. For doses larger than 5 Gy, some degree of caution is required. But dose rate is also relevant: it is around 2×10³ Gy s^–1 for standard cyclotron accelerators used in spot scanning mode, so that significant oxygen depletion should not occur according to the data given in Table 1, although some caution is required since the data sets in the literature (Table 1) do not use protons.

Figure 2.

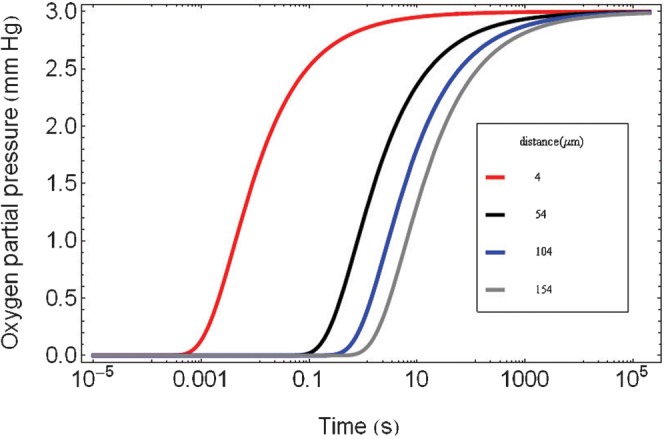
Theoretical plot of local reoxygenation by the diffusion process with elapsed time after ultra-high dose rate irradiation for cells at various assumed distances from a blood vessel using Equation (A2) given in Appendix A.

Impact of oxygen depletion on the percentage of radiologically hypoxic cells

If a tumour contains a hypoxic fraction of h% of cells, which, by microelectrode studies, are usually bounded between 0 and 2.5 mmHg (0–0.33kPa), then if there are x% of cells in the next category (2.5–5 mmHg, or 0.33–0.67kPa), then, by using equation (1) and a D_[0.5] of 0.89 Gy⁻¹, the average tension of 3.75 mmHg (0.5kPa) will fall after 5 Gy ultra-high dose rate exposure to be 0.076 mmHg. Cells at this oxygen tension will be radiologically hypoxic (as shown in Figure 1). Cells at the upper boundary of 5 mmHg (0.67kPa) will become depleted to a level of 0.101 mmHg, which again is radiologically hypoxic. Thus the entire cell population in the range 2.5–5 mmHg (0.33–0.67 kPa) will become radiologically hypoxic, and the hypoxic fraction will become at least (h+x)%. For example, if h=10% and x=7%, the effect of a dose over 5 Gy would be to produce a new hypoxic fraction (h) of 17%. Such changes in hypoxia can, in principle, influence tumour cell kill and cure in extensive modelling studies, as well as contribute to worse clinical outcomes in terms of local tumour control [22-26].

Discussion

The previously published ultra-high dose radiation data sets provide useful information, although they use different physical and biological experimental conditions. Only low-LET electrons and X-rays have been used and in a limited range of cell lines. We have considered the influence of oxygen depletion in regions that have diffusion-related hypoxia (sometimes referred to as chronic hypoxia). The changes in oxygen considered in this paper cover a wide range of radiosensitivity modulation (as between the two points of interest in Figure 1). Lesser degrees of oxygen depletion may also occur, such as from the uppermost point to halfway between the two points (that is from 3 mmHg to around 1 mmHg), which would reduce the relative radiosensitivities from 2.75 to 2.

For acute hypoxia caused by cyclical variations in tumour blood perfusion, there are issues about the reliability of invasive microelectrode measurements [9,26], although there is some promise that non-invasive techniques such as 19F MRI may provide more reliable data. For example, Magat et al [27] have recently used this technique in murine tumours, which showed spontaneous fluctuation at a rate of one cycle per 12–47 min. If such rates were to be confirmed in humans these times would be far longer than most radiotherapy exposures and ultra-high dose rates would have no impact on these dynamics. Acute hypoxia would need to be compensated for by dose fractionation and or the use of radiosensitisers and vasodilator drugs [28].

Experiments in normal tissues are more limited. For example, the work of Hendry et al in 1982 [29] used pulsed electrons delivered in less than 4.5 s to cause resistance to mouse tail necrosis, which was characteristic of oxygen depletion of the target cells from a natural hypoxia state where the oxygen concentration is between 3 and 6 μM. Restoration of pre-treatment oxygen levels was evident at times longer than 20 s, which is compatible with the diffusion results obtained above.

There is renewed interest in dose rate effect in linear accelerator-based X-ray treatment, because dose rate increases when the flattening filter is removed. In such cases, maximum dose rate can typically increase from 29.91 Gy min^–1 to instantaneous pulse dose rates in the pulse of up to 338 Gy s^–1, but which showed no significant effect on cell survival [30] such as would be expected from our literature review. Another group has shown a marked dose rate effect between 6 and 24 Gy min^–1 in glioblastoma lines [31], which shows how some cell types have repair rate coefficients that are sensitive to temporal patterns of dose delivery. These dose rates are far below those required for oxygen depletion.

Because the previous ultra-high dose experiments used electrons or X-rays in a limited range of cell lines, there is consequently an urgent need to study a variety of human cell lines and animal tissues using heavier particles, such as protons, helium and carbon ions. It is important to establish the relevant range of dose for oxygen depletion for high- and low-LET particles (both within and outside Bragg peaks), and when the LET is mixed by spreading out the peaks. The degree of change in the survival curve slopes will also be different in high-LET beams, due to the lower dependency on oxygen for cell killing. Monolayer cell cultures will allow rapid oxygen replacement by diffusion, but in reality longer distances, such as 50–170 μm, will be encountered in human tumours [32], so it will be necessary to use tumour spheroids and in vivo experimental systems such as human tumours growing in immune-deficient hosts.

Recently, some investigators have used laser-generated particle beams (LGPB) and found no change in cell surviving fraction for ultra-high dose rates [33,34] (using 20 ns pulses), but since the experiments were performed using well-oxygenated cells, this result is not surprising. Careful LGPB experiments need to be done in low-oxygen-tension conditions, as in the work of Berry et al [6] and Ling et al [8]. For treatments using LGPB, keeping the dose to below 5 Gy per fraction would appear reasonable if no “repainting” is to be used. Repainting with an appropriate time-lag to allow for rediffusion of oxygen into depleted oxygen sites (of at least 20–30 s) would appear to be indicated when a dose per fraction above 5 Gy is used. It remains to be seen whether LGPB will be delivered by covering larger (mixed energy spectrum) tumour areas combined with smaller areas closer to the classic spot scanning technique. The choice of dose and number of subexposures within a fraction to each region of the tumour would need to be determined carefully, bearing in mind the possibility of oxygen depletion at critical levels of dose and dose rate.

Another intriguing issue is the possibility that nascent oxygen can be formed within the tracks of high-LET particle beams [35,36], so that oxygen depletion at low LET might be reversed in very high LET conditions. The inverse relationship between RBE and dose per fraction is a further complication, which could potentially influence the magnitude of the oxygen effect in high-LET beams: further work is required in this respect, with real-time monitoring of oxygen tensions. There is evidence that, for X-rays, there is a reduction in the oxygen enhancement ratio as the exposure dose is reduced [23]. The magnitude and direction of changes in radiosensitivity due to oxygen depletion or replenishment effects, as well as the influence of the more complex DNA damage and its repair proficiency during high-LET charged particle exposures, remains to be determined. However, if we assume a worst case scenario of, for example, an order of magnitude change in the dose rate and dose requirement for oxygen depletion by high-LET particles, then we might expect oxygen depletion with doses as low as 0.5–1 Gy and at dose rates above 10⁸ Gy s^–1 rather than 10⁹ Gy s^–1. Specific experiments need to be performed to ascertain the kinetics of oxygen depletion with dose and dose rate for high-LET radiations, and their relevance to modern radiotherapy. The reduced dependency for oxygen in the production of lethal radiation effects with high-LET particle beams also needs to be considered. It is possible that any high-LET-related oxygen depletion will be more local within the cell, owing to microdosimetry effects such as increased clustering of DNA damage, but that such changes will not change radiosensitivity by the same degree as in the case of low-LET radiations. Such arguments are speculative; experimental evidence is required to resolve these issues.

It is concluded that the interaction of RBE, LET and dose-rate dependent oxygen depletion effects need to be studied further. More extensive modelling is certainly required, but needs to be based on specific hadron charged particle beam experimental data, which is not currently available. The correct kinetics of dose-related oxygen depletion, together with times to restore oxygen concentration, are required in order to make further progress. This is not a trivial issue, because of the important implications for cancer therapy. Carefully designed experiments are required on accelerator systems capable of ultra-high dose rate exposures of cells, tumour spheroids, and intact tumours using protons and heavier charged ions, with real-time monitoring of oxygen tensions, together with separate studies of cell survival and other surrogates of radiation-induced damage under such conditions. In short, a renaissance of ultra-high dose rate radiobiology is indicated with a complete analysis of dose rate-related issues arising in proton and ion beam therapy, so that no patient might be disadvantaged by oxygen depletion contributing to radioresistance and failure of tumour control.

Appendix A

Assuming that oxygen is nearly completely depleted due to high-dose rate irradiation, the time taken to fully replace the oxygen depletion can be estimated using a classic diffusion equation. The oxygen diffusion equation is normally expressed as:

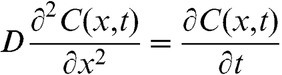(A1)

where D, x and t are the oxygen diffusion coefficient in tissue, distance to the capillaries and time, respectively.

The solution for Equation (A1) can be obtained as:

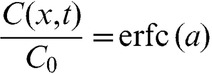(A2)

where 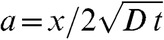and erfc is the complementary error function.

Appendix B

The relationship between relative radiosensitivity (RR) and oxygen tension can be expressed as:

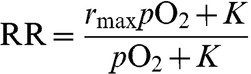(B1)

where PO₂ is the oxygen tension, K is the parameter that defines the value of pO₂ at which the radiosensitivity is “halfway” between r_max, the maximum value, and the baseline value of 1 [19,23].