Dilemmas concerning dose distribution and the influence of relative biological effect in proton beam therapy of medulloblastoma

Abstract

Objective

To improve medulloblastoma proton therapy. Although considered ideal for proton therapy, there are potential disadvantages. Expected benefits include reduced radiation-induced cancer and circulatory complications, while avoiding small brain volumes of dose in-homogeneity when compared with conventional X-rays. Several aspects of proton therapy might contribute to reduced tumour control due to (a) the use of more homogenous dose levels which can result in under-dosage, (b) differences in relative biological effectiveness (RBE) between that prescription RBE of 1.1 and the RBE of brain and spinal cord (likely to exceed 1.1) and in medulloblastoma cells (where RBE is likely to be below 1.1). Such changes, although speculative for RBE, might result in potential underdosage of tumour cells and a higher bio-effect in brain tissue.

Methods

Dose distributions for X-ray and proton treatment are compared, with allocation of likely RBE values for fast growing medullolastoma cells and stable central nervous system tissue.

Results

These physical and radiobiological factors are shown to combine to give a higher risk of tumour recurrence with further risks on tumour control when dose reduction schedules used for X-ray therapy are replicated for proton therapy for “low-risk” patients.

Conclusion

The dose distributions and prescribed doses of proton therapy, taking into account RBE, in children and adults with medulloblastoma, need to be reconsidered.

The medulloblastoma tumour, which most commonly arises in childhood, is normally treated by subtotal surgical excision, with or without cytotoxic chemotherapy, but always with post-operative radiotherapy to the whole brain and spinal column, which results in impressive cure rates of around 70–80%. The highest radiation dose is given to the posterior fossa of the brain where the tumour originates, but a lower dose is given to the remaining brain and spinal cord tissues using X-rays or protons [1-4] because of the risk of later tumour growth in these regions as a consequence of tumour cells deposited on neural surfaces due to spread of the tumour via the cerebrospinal fluid (CSF). Unlike X-rays, a posterior spinal proton beam using a selected energy range does not incur an “exit beam” dose to organs anterior to the spinal tissues, and so reduces the risk of future carcinogenesis [5], circulatory complications [6] and potentially some cases of female infertility. Such complications can occur after a relatively low dose of X-ray exposure, such as in the 5–30 Gy range.

Proton therapy dose distributions depend on the Bragg peak effect and can be delivered using broad “passively scattered” beams or by multiple individual pencil beams. Spread of the tumour from the primary site occurs through the CSF to other areas of the brain or spine. The aim of proton therapy is to deliver a homogeneous dose across the brain and spinal cord. The CSF-containing regions must be included, especially the cisterns and ventricles of the brain, and all subarachnoid spaces, including the space between the surface of the brain and the meninges, while avoiding structures that cannot be infiltrated by the tumour cells such as the inner ear (cochlea). These regions were formerly treated to X-ray doses of 34–36 Gy in 20 fractions, but in some “low-risk” cases a lower X-ray dose of 23–24 Gy is now used [1-4]. The site of the original tumour in the anterior part of the cerebellum is usually “boosted” to a dose of up to 54–55 Gy, which is close to the neural tolerance of the adjacent brainstem which must be included to the full dose.

Prescription of proton therapy and the influence of relative biological effect

The relative biological effect (RBE) concept is based on the ratio of doses required for the same biological effect when using a low linear energy transfer (LET) radiation—such as megavoltage X-rays—and a radiation that has higher LET values. The standard medical proton prescription includes an RBE of 1.1, which means that the delivered physical dose is reduced by dividing by 1.1, representing a 9.1% reduction in physical dose compared with megavoltage X-rays. This figure is arrived at from a range of experiments using in vitro and in vivo assays, which use short-term rapidly proliferating assays with a low fractionation sensitivity [7-9]. The data show considerable variation, with so many values lower and higher than 1.1, that 1.1 can be considered to be a median value for the doses and cell lines used. Some investigators have found higher values of RBE in the case of lower energy proton beams and in more restricted parts of the beam (namely towards the end of the Bragg peak [10,11]), with indications that RBE increases with X-ray radioresistance. Also, RBE values lower than 1.1, such as 1.05, are well documented for a variety of cellular and tissue assays [9]. Proton RBE values for fraction-sensitive late-reacting tissues such as the brain and kidney have not been investigated. In the absence of such information, there is a real possibility that higher RBE values can occur in mature stable tissues such as the brain.

The relationship between the low-LET fractionation sensitivity (which is inversely related to the α/β ratio of the linear quadratic model of radiation effect) and RBE is of special interest. Theoreticians have argued that RBE will be related to the low-LET α/β ratio [7,12]. Increasing RBE values at smaller doses per fraction are mainly due to the increasing repair of sublethal damage that occurs when the control X-ray cells/tissues are irradiated and are proportional to the α/β ratio: cells and tissue systems with low α/β values have a greater capacity for repair, and consequently should have a higher RBE. A recent analysis of in vitro cell lines and in vivo tissue data exposed to fast neutrons has shown an inverse correlation between the low LET α/β and the RBE_max, which is the RBE at near zero dose [13]. In contrast, the RBE_min (the RBE at very high dose) appears to correlate directly with the square root of α/β. The net effect is that tissues with low α/β values of around 2 Gy (typical of the central nervous system) have the highest RBE values and show the most significant change in RBE with dose per fraction compared with lower RBE values, and little change in RBE with dose per fraction for tissues or tumours with α/β values of 8–15 Gy (which are more typical of acute skin reactions or the response of a fast-growing tumour). Although it remains controversial as to whether proton RBE changes with dose per fraction (and, if so, by how much), scaling of the RBE changes found using fast neutrons down to typical proton RBE values does suggest that significant changes might occur, again with an important dependency on low-LET α/β values in the low dose per fraction range (1.4–1.8 Gy) used in clinical proton therapy of medulloblastoma. Jones et al [13] also showed that RBEs of 1.2 or higher might be found in the brain. Also, the rapidly growing and highly radiosensitive medulloblastoma has a high α/β value, which favours a low RBE.

However, until further experiments can be done using the critical normal tissues such as the brain and spinal cord, it is reasonable to consider some physical dose and clinical radiobiology assumptions, both of which produce dilemmas within the treatment planning and prescription process, as described below.

Methods and materials

Physical dose distributions

Dose distributions across the cranium are compared for two opposed lateral 5-MeV X-ray fields in the widest part of the cranium and protons, which are assumed to deliver a uniform dose across the brain.

Plots are generated using XiO planning software (Elekta, Stockholm, Sweden) and Mathematica (Wolfram Research, Champaign, IL).

The X-ray dose gradient, from a posterior 6-MV X-ray field, across the spinal tissues and meningeal surfaces is considered to be sufficiently small compared with a relatively uniform proton “spread-out Bragg peak”, such that the physical spinal dose can be arranged to be equal in both treatment types. A dose per fraction of 1.7 Gy is normally used for X-ray cranio spinal therapy given to a total dose of 34 Gy in 20 fractions. The given proton dose is then 1.7/1.1=1.54 Gy (when using an RBE of 1.1).

Relative biological effect values

The published α/β for medulloblastoma is 28 Gy [14]. It is highly radiosensitive with indications that the RBE will be low. From the article referred to above by Jones et al [13], and using the same symbols, further tentative modelling can be used to estimate likely values of proton RBE. By setting an RBE of 1.1 for rapidly growing assay systems with an assumed α/β=10 Gy, at a proton dose of 1.54 Gy with RBE_min=K+B√(α/β), where it is reasonable to assume that B is small and smaller than in the neutron analysis [13] and will exert only a small effect on the RBE at 1.8 Gy, it is then possible to estimate the value of A in RBE_max=C+A/(α/β) for high-energy protons. If it is assumed that the value of C is likely to be only slightly greater than unity (e.g. 1.02), then the value of A can be estimated by using the equations given in Appendix A for an RBE of 1.1, where the average α/β=10 Gy.

For an assumed B=0.02, A is estimated to be 0.92; then for α/β=28 Gy, the RBE at 1.7 Gy is 1.06; for α/β=2 Gy, the RBE at 1.8 Gy is 1.19.

From these calculations RBE values of 1.06 and 1.2 are assumed for medulloblastoma cells and CNS, respectively, in the arguments that follow.

Results

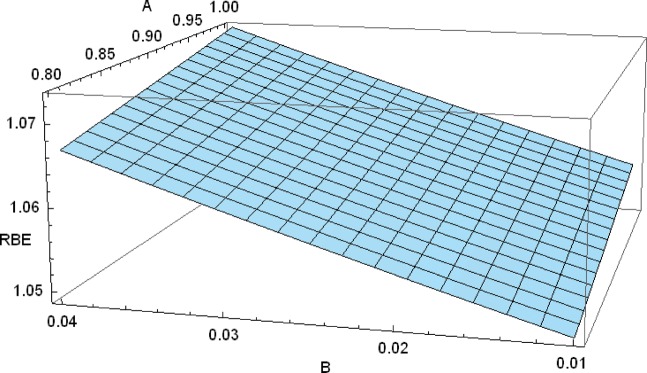
The influence of variation in the assumed parameters A and B (which are scaled downwards from the fast neutron results [13]) on the RBE is shown in Figure 1. Changes in A between 0.8 and 1 change RBE by around 0.005, and changes in B between 0.01 and 0.04 change RBE by less than 0.015. These estimates need further refinement by experiment to determine RBE values more accurately.

Figure 1.

Three-dimensional plot of relative biological effectiveness (RBE) and parameters A and B, which link α/β with RBE_max and RBE_min, respectively.

The influence of physical dose distribution and RBE are considered separately for medulloblastoma cells in the spinal cord and brain tissues.

The spinal cord

Here the dose is relatively uniform across the spinal cord for both X-rays and protons. It is assumed that the RBE of spinal tissues (α/β=2 Gy) is 1.2; the medical prescription is based on an RBE of 1.1 and the medulloblastoma has a high α/β, resulting in an RBE of only 1.06.

Consequently, in comparison with megavoltage X-rays, the dose per fraction will be reduced by nearly 10%, but the effective dose in spinal neurological tissue needs to be reduced by around 17% for an RBE of 1.2 to obtain the same effect/risk. To have the same effect on tumour cells the proton physical dose should be reduced by around 6% for an RBE of 1.06 rather than nearly 10% for an RBE of 1.1. It can be appreciated from the above that the therapeutic ratio is reversed for protons compared with X-rays: we could experience reduced tumour control and/or more tissue side effects with protons if the assumed RBE values of 1.06 and 1.2 occur in the tumour and CNS, respectively. Fortunately, doses of 34 Gy and the lower doses around 24 Gy, used for low-risk patients, are all below spinal tolerance (normally assumed to be between 40 Gy in 2 Gy fractions for long sections of the spine), so that a small increment in the physical dose of, say, 5% (an increase from 1.7 to 1.785 Gy for X-ray doses) is unlikely to produce spinal paralysis when the same number of fractions is given, although it remains a possible side effect over 10–20 years. In this context, the use of neoadjuvant and concomitant chemotherapy may lower neural tolerance, producing some uncertainty about the toxicity thresholds.

The results are dependent on the assumptions used above: until specific experiments are performed, it is possible that the brain and spinal cord RBE might be as high as 1.25 at a dose of 1.54 Gy per fraction, as well as the tumour RBE being as low as 1.02 or 1.03 at the prescription surface. An RBE of 1.1 used in the prescription would then incur a greater reversal in the therapeutic ratio: around a 14% effective increase in spinal cord dose and a 7% reduction in tumour dose per fraction.

The brain

The whole brain

Here megavoltage X-rays will be given by parallel opposed lateral fields, which result in a subtle but significant non-homogeneous dose. The dose gradient will be greatest for larger tissue separations over the flat surfaces of the skull, where the tissue immediately beneath the meninges will receive the higher dose. Areas of higher dose will also occur in relation to convexities of the skull, and where the entry-to-exit tissue separation is smaller. Such differences will be larger for older children or adults since this distance will increase. The widest tissue separation occurs in the temporoparietal region. The dose is usually prescribed at the minimum level, namely in the anatomical midline, although some radiotherapy departments may prefer to use the maximum subcutaneous dose concept, which will be at the depth of obtaining beam electronic equilibrium (around 1.4 cm deep to the skin for a 6-MeV X-ray beam).

In the former case, should the proton beam be used to match the minimum dose on the X-ray plan (and uniformly across the brain), then the X-ray plan will inevitably contain higher regions of dose than with protons. The excess dose is usually in the 2–4% range, depending on the separation and shape of the skull bones (Figure 2). The excess dose nearest to the skull includes the subarachnoid spaces near to the meninges, which are a site of potential tumour cell metastases. The clinical oncologists and physicists should then consider whether it would be better to prescribe a higher dose of homogeneous proton therapy, as shown in Figure 3, but this would mean slight overdosage of other areas of the brain, especially if—as in the spinal case above—the brain RBE exceeds that used in the prescription process. Figure 3 shows the dilemma in a schematic graphical form: should one prescribe the proton dose to match the minimum, the average or the maximum X-ray dose? Or, alternatively, should the spot scanning techniques be used to recreate the original non-homogeneous X-ray dose distribution? Another solution would be to use X-rays for the wide cranial fields and only use protons for the posterior fossa boost. There also needs to be a high degree of confidence in the proton particle range in order to ensure good coverage of the inner meningeal surfaces from the contralateral side, as well as ensuring full electronic equilibrium of the entry beam on the same side, while also sparing skin/scalp to a certain extent. Even X-ray therapy can sometimes deposit a lower dose at the meningeal surface when the surface-to-meningeal distance is less than or around 1.4–1.5 cm, as may occur in the temporoparietal region in young children when using a 6 MeV beam, since full electronic equilibrium will not have been established at that depth. This may be a further problem in this region of the skull, where the bone thickness is smallest, as seen in Figure 4.

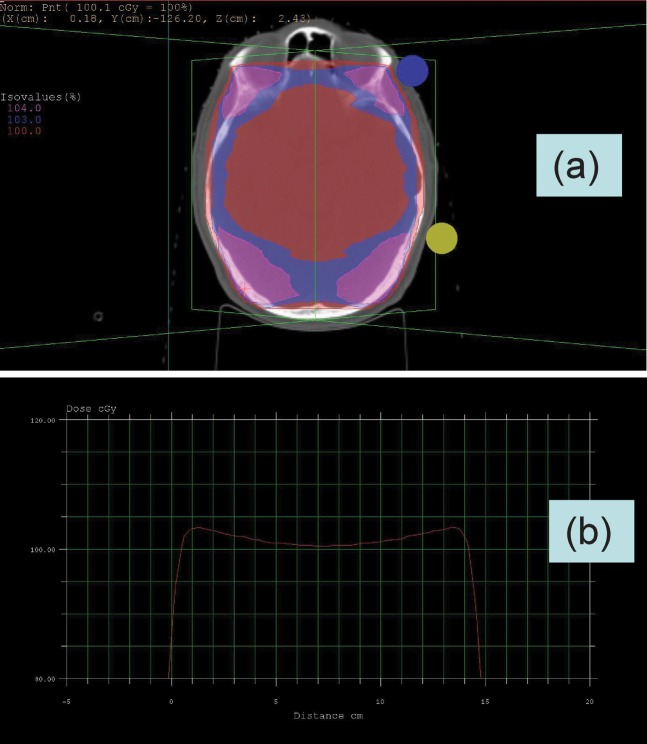
Figure 2.

(a) Dose distribution across brain in temporoparietal region for parallel opposed fields using 6 MeV X-rays, showing non-uniformity of dose with excess dose near to the brain surfaces and in more anterior and posterior areas. (b) Dose profile across widest section of the plan shown in (a) where the maximum dose is 103%. Normally the dose is prescribed at midline, although could be prescribed as a maximum subcutaneous dose at 104%, which is shown in (a) more anteriorly.

Figure 3.

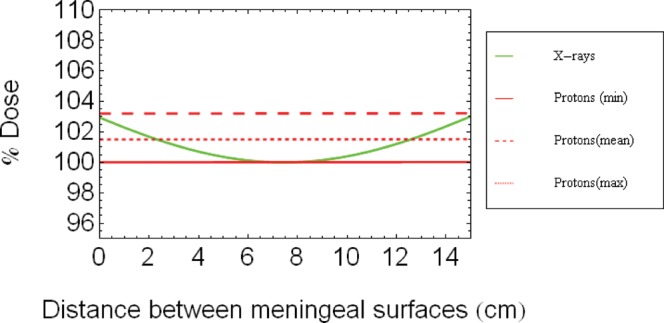
Schematic diagram of depth dose profiles for X-rays and protons (assuming the proton dose is homogeneous) between two parallel opposed lateral fields for tissues between the meningeal surfaces. The plot does not show the dose decreases that occur close to the surface of the patient's skull owing to the breakdown of electronic equilibrium, but which are shown in Figure 2b.

The posterior fossa and temporal lobe regions

This region can, in the case of megavoltage X-rays, be boosted by a three-field conformal plan or by various intensity-modulated radiotherapy techniques. Again we have a potential discrepancy based on the brain RBE exceeding the prescription RBE, and also the issue of dose homogeneity. In the past the use of wedge compensators for obtaining a more homogeneous dose across the posterior fossa and its inclusion of the posterior aspect of the temporal lobe were associated with enhanced tumour recurrence within the posterior fossa [H Sack, 1996, personal communication]. However, the spot scanning (multiple pencil beam technique) could be used to create a deliberate non-homogeneous preferential dose distribution based on primary site and CSF spaces where the risk of recurrence is highest.

An MRI scan of an 8-year-old child treated by proton therapy to a spinal and whole-brain dose of 24 Gy-eq is shown in Figure 4. A recurrent tumour is seen on the surface of the brain in a region which would have received a slightly higher dose if treated by X-rays. It is speculative as to whether RBE has also contributed to this recurrence. Additional reasons might be (1) that full electronic equilibrium was not achieved from the ipsilateral entry beam (mesh type immobilisation masks also allow less build-up), or (2) that the Bragg peaks delivered from the contralateral side could have a shorter range than expected, especially if the treatment plan aims to spare scalp tissue.

Figure 4.

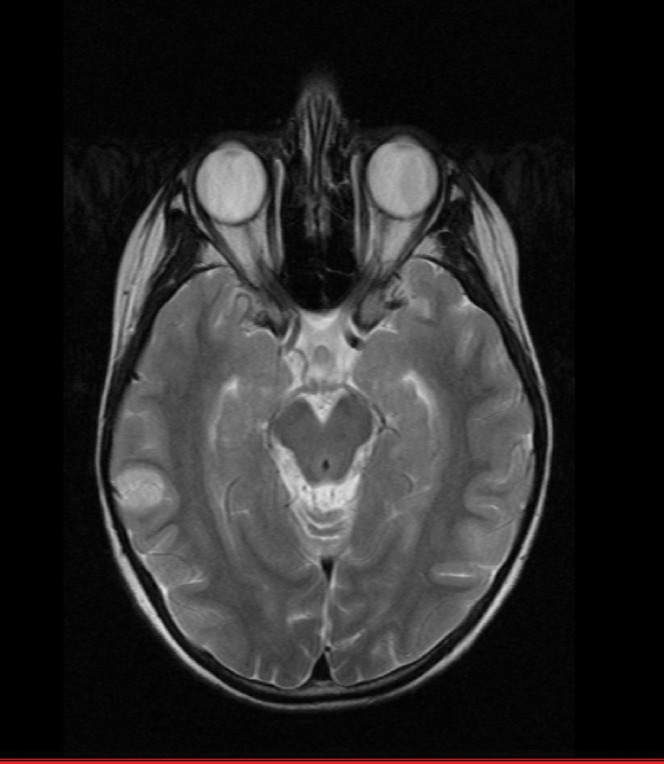
Recurrence of medulloblastoma in an 8-year-old child after using low-dose fractionated treatment to 24 Gy and relative biological effectiveness=1.1. The recurrence is in superficial brain tissue at the level of maximum tissue separation and where the skull bone (black) is of minimum thickness.

Discussion

Medulloblastoma is often quoted as the tumour class that is most suitable for proton beam radiotherapy. The comparative descriptions of medulloblastoma treatments given above show the limitation of present knowledge as to what might be the optimal technique and, consequently, the need for considerable research into several aspects of proton beam therapy. Without better knowledge of RBE the therapeutic ratio may be reversed, especially in the case of fast-growing tumours with high α/β ratios and which are situated in the CNS, which has a very low α/β ratio of 2 Gy.

According to our hypothesis, particle therapy—in general terms—will only be as effective as X-rays, in terms of tumour control, if an enhanced dose (greater than that given using RBE=1.1) can be given, but this will incur slightly higher risks of detrimental side effects to the brain and spinal tissues, although in the case of medulloblastoma the doses given at the present time with X-rays are below neural tolerance. If this is not possible (for example owing to significant normal tissue encroachment into the planning target volume in a less radiosensitive tumour), then giving the same dose to such a normal tissue structure and to the tumour will be disadvantageous if the RBE is lower in the tumour than in the normal tissue and where the prescribed dose has used an intermediate RBE value.

One possible solution to this problem is to preferentially sensitise the tumour cell and increase its fractionation sensitivity. In terms of the linear quadratic model this implies preferential sensitisation of the β parameter. There is evidence that high-LET radiations sensitise the α parameter to a greater degree than the β parameter [15]. There is already evidence that some drugs or treatment strategies can, in susceptible cells, achieve β sensitisation [16,17], and consequently a lower α/β ratio, with enhanced fractionation sensitivity. Drugs with such properties would be useful with X-ray treatment also. However, there would be several requirements for successful applications:

• an adequate cerebrospinal fluid concentration of the drug

• safe administration over an entire course of treatment (or at least a substantial part of it)

• lack of normal tissue sensitisation

• low bone marrow toxicity.

In most treatments, care is still taken to achieve dose uniformity within the radiotherapy target volume. In fact this is a legacy of former megavoltage techniques that has carried over to modern protocols. Such practice was by and large designed to defend against inadvertent overdosage in normal tissues when radiotherapy was planned using one cross-sectional plane in the absence of full three-dimensional (3D) dose distributions. In such circumstances, excess dose regions might inadvertently extend into normal tissues and cause enhanced complications. In the specific case of particle therapy, a better dose distribution in 3D is obtainable; consequently, homogeneity across the target is less important. Non-homogeneity of dose, resulting in additional tumour dose, may be advantageous: tumour cure probability may be enhanced by deliberate increase of the internal dose gradient within a tumour, as long as this is confined within the gross tumour volume. This represents the deliberate use of an internal dose gradient such as occurs in brachytherapy and some other rotational or multisource γ-ray techniques.

With so many subtle dose distribution and radiobiological differences between megavoltage X-ray and proton beam therapy, it is difficult to envisage true equipoise within a clinical trial: an RBE iso-effect can only be generated for one tissue or for the tumour, and at one dose level. Priority must be given to the maintenance of tumour control in protocol and clinical trial design. Until more detailed knowledge of RBE is acquired, more pragmatic trials (perhaps using different RBE values, and therefore different dosage) should be allowed to determine the magnitude of overall benefit provided by proton beams. There is a good background of well-organised international clinical studies for X-ray based radiotherapy of medulloblastoma, which can be used to compare the results of proton beam treatments. These studies should be used to compare the patterns of relapses for both modalities. However, determination of the optimal dose distribution and RBE values, even in the absence of randomised studies, will be both difficult and time-consuming, but necessary. In order to show the potential advantages in terms of the reduced malignant induction and circulatory risks, life-long follow-up (preferably to 30 years or more) will be required. Then it will be possible to assess the true benefit of proton beam therapy, balanced against the neural effects of slightly higher proton doses to the spine and CNS in order to overcome the likely RBE disadvantages.

There should be no complacency about the treatment of medulloblastoma patients: although it is a radiosensitive tumour with an α/β ratio of 28.9 Gy [14], the dose response curve is claimed to be steep [18] compared with other cancers, so that small changes in dose may confer significant clinical effects. Dose reduction in the low-risk category may not be required to the same extent as for X-rays because of the absence of dose to many important organ systems. Recurrent tumour almost inevitably leads to the death of the patient. Also, practitioners need to consider dose compensation for rapid tumour proliferation during time delays incurred before and during treatment in order to achieve optimal tumour control [19-21].

To summarise, there is an urgent need for research to identify:

1. The anatomical distribution of relapse in medulloblastoma patients treated by proton therapy compared with X-rays.

2. Better knowledge of RBE in different tissues and tumour types, especially those at the extremes of fraction sensitivity reflected in the low-LET α/β ratio.

3. The most appropriate non-homogeneous proton dose distributions and prescribed doses tailored to prevent tumour recurrences.