Quantifying the Erlenmeyer flask deformity

Abstract

Objective

Erlenmeyer flask deformity is a common radiological finding in patients with Gaucher′s disease; however, no definition of this deformity exists and the reported prevalence of the deformity varies widely. To devise an easily applied definition of this deformity, we investigated a cohort of knee radiographs in which there was consensus between three experienced radiologists as to the presence or absence of Erlenmeyer flask morphology.

Methods

Using the presence or absence of Erlenmeyer flask morphology as a benchmark, we measured the diameter of the femur at the level of the physeal scar and serially at defined intervals along the metadiaphysis.

Results

A measured ratio in excess of 0.57 between the diameter of the femoral shaft 4 cm from the physis to the diameter of the physeal baseline itself on a frontal radiograph of the knee predicted the Erlenmeyer flask deformity with 95.6% sensitivity and 100% specificity in our series of 43 independently diagnosed adults with Gaucher′s disease. Application of this method to the distal femur detected the Erlenmeyer flask deformity reproducibly and was simple to carry out.

Conclusion

Unlike diagnostic assignments based on subjective review, our simple procedure for identifying the modelling deformity is based on robust quantitative measurement: it should facilitate comparative studies between different groups of patients, and may allow more rigorous exploration of the pathogenesis of the complex osseous manifestations of Gaucher′s disease to be undertaken.

Gaucher′s disease is a rare autosomal recessive disease due to deficiency in the lysosomal enzyme β-glucocerebrosidase; this leads to accumulation of glucocerebroside in tissue macrophages of multiple organs [1,2]. The most common non-neuropathic form (94%) is characterised by hepatosplenomegaly, anaemia and thrombocytopenia, as well as prominent skeletal manifestations and marrow infiltration [3]. The osseous manifestations of Gaucher′s disease include lytic lesions, osteoporosis, osteonecrosis and growth disturbance with modelling abnormalities including Erlenmeyer flask deformity [4].

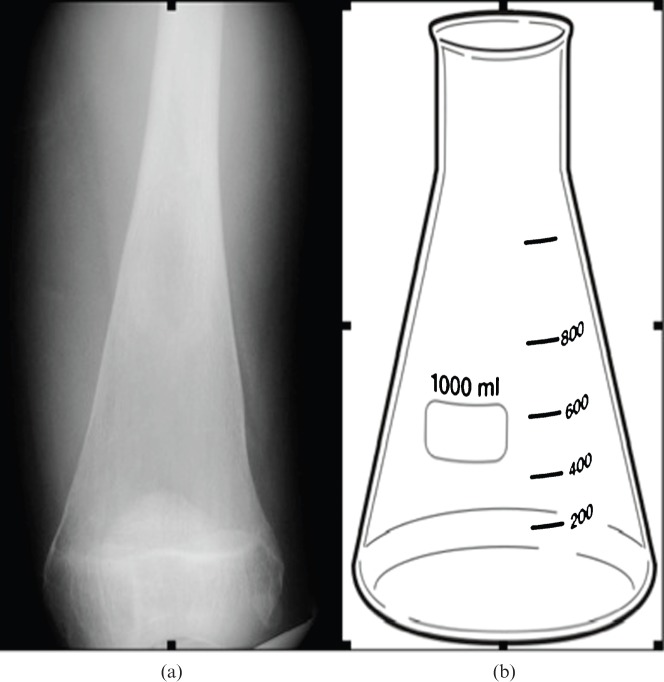
The Erlenmeyer flask deformity of the distal femur is so named because of its resemblance to a glass flask (Figure 1) invented by the distinguished German chemist Emil Richard August Carl Erlenmeyer (1825–1909). The deformity, due to undertubulation of the distal diametaphysis of the distal femur, is classically associated with Gaucher′s disease [5,6]. A similar appearance has also been described in osteoclastic defects causing osteopetrosis, as well as diverse conditions including Niemann–Pick diseases A and B, rickets, chronic anaemias, fibrous dysplasia, heavy metal poisoning, metaphyseal dysplasia, Down′s syndrome, achondroplasia and juvenile inflammatory arthritis [7].

Figure 1.

(a) Radiograph of the distal femur obtained from a patient with Gaucher′s disease and (b) comparison illustration of an Erlenmeyer flask.

The presence of Erlenmeyer flask deformity implies involvement in childhood when the skeleton is developing and is an important diagnostic indicator of disease. The frequency of the Erlenmeyer flask deformity in Gaucher′s disease has been reported to be between 44% and 61% of patients [8-10]. However, since there is no rigorous definition of the abnormality and its designation has relied on qualitative and subjective assessments by individual radiologists, the true prevalence in Gaucher′s disease is unknown.

The aim of this study was to develop a validated and easily applied measurement to determine the presence of the Erlenmeyer flask deformity in Gaucher′s disease. Several components in this study were used to define the abnormality. Initially, a group of patients whose radiographs could be assigned positive or negative for the presence of the Erlenmeyer flask deformity was determined by consensus. Those radiographs from patients with independently diagnosed Gaucher′s disease that were unequivocally considered to have the features positive or negative for the Erlenmeyer flask deformity were taken as the benchmark.

Next, the interobserver agreement of a series of measurements was carried out to ensure that a reliable determination of the radiological geometry could be obtained consistently.

From these measurements a series of ratios were obtained that could be compared with the pre-defined benchmark. Finally, this ratio was used to determine the prevalence of the Erlenmeyer flask deformity in the study population.

The outcome of this study is an accessible means to determine the presence or absence of the Erlenmeyer flask abnormality based on simple measurements that can be readily applied to radiographs that include views of the distal femur in patients with Gaucher′s disease.

Methods

The first part of the study investigated the agreement between experienced radiologists in determining the presence of an Erlenmeyer flask deformity. Given the absence of a pre-determined benchmark, this was also used to identify a group of patients whose radiographs could be unequivocally assigned to a positive or negative category for the Erlenmeyer flask deformity.

The study population was taken randomly from the radiographs available from adults under the care of a single national referral centre for lysosomal diseases, designated for the diagnosis and treatment of Gaucher′s disease since 1997 by the Department of Health (England); 145 patients have been referred over a 20-year period. All patients had been independently diagnosed with Gaucher′s disease on the basis of deficient acid β-glucosidase activity in peripheral blood leukocytes, as determined in an approved diagnostic reference laboratory; for most patients, diagnostic genotyping of the cognate human GBA-1 gene was also available.

The study was performed as a retrospective review of previously acquired radiographs that were made anonymous prior to review. Because there were no implications for the patients involved, formal ethics approval was not obtained.

Radiographs of the knee and distal femur were presented randomly to three senior radiologists experienced in musculoskeletal radiology. The radiologists were blinded to each other's assessment. The study cohort included 80 knees obtained from 43 patients with Gaucher′s disease, as well as 25 knees from 23 patients without Gaucher′s disease, included as controls. In total there were therefore radiographic images of 105 knees from 66 patients. There were 59 male and 46 female knee radiographs, with age range 15–89 years (mean 49 years). Three of the radiographs obtained were not suitable for inclusion because they excluded a region required for subsequent measurement. Radiographs were classified by each radiologist as positive, negative or uncertain for the presence of Erlenmeyer flask deformity. Accuracies were calculated with exact Pearson–Clopper 95% confidence intervals [10]. Only the unequivocal cases were taken forward to the second and third phases of the study.

The second phase of the study was designed to establish a robust and easily reproduced measurement that could be applied to radiographs to establish the presence of Erlenmeyer flask deformity. All available knee radiographs were subjected to a series of measurements by two observers. Measurements were obtained of the width of the physeal plate and then of the perpendicular width of the distal femoral diametaphysis 2, 4, 6, 8 and 10 cm from the physeal plate. The ratio of the diametaphysis measurement to the physeal plate was calculated. When the physeal scar was indistinct, the base measurement was obtained along a line connecting the junction of the concave and convex portions of the metaphysis, which corresponds to the position of the original growth plate and is a consistent feature that is easily identified (Figure 2).

Figure 2.

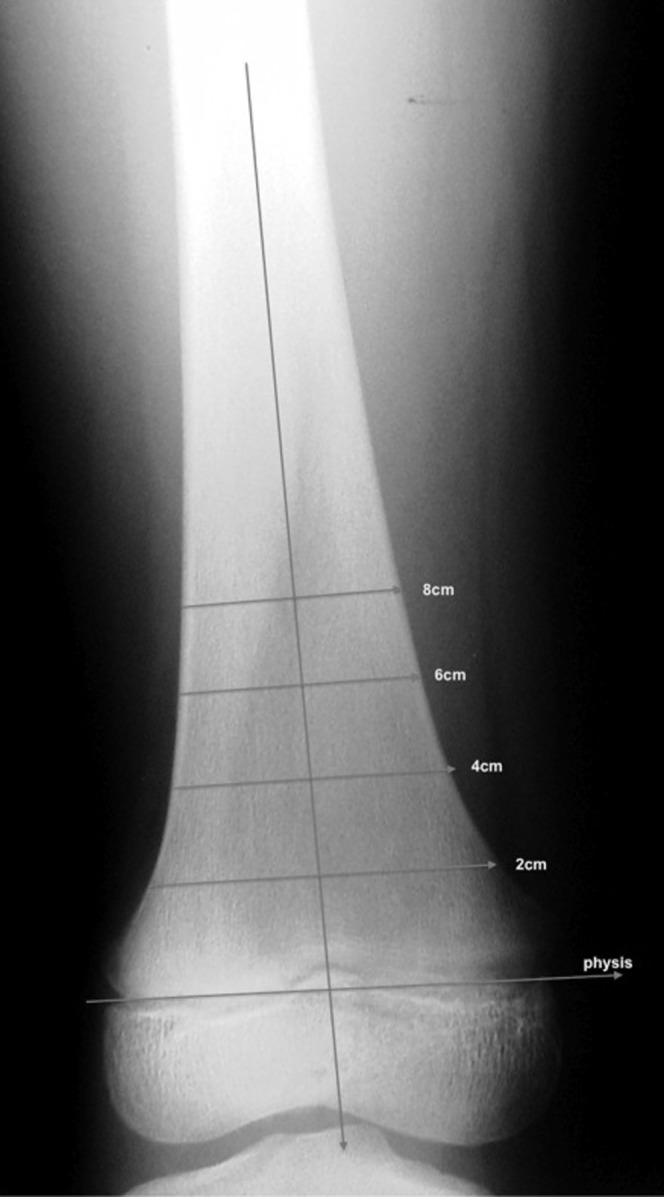
Radiograph with overlaying lines demonstrating where the location measurements were obtained.

The interobserver variation (of obtained measurements and of the derived ratios) between the two observers of obtained measurements was calculated using Bland and Altman's limits of agreement analysis [11]. Using logistic regression analysis of the various ratios, the best measurement cut-point for the presence of Erlenmeyer flask deformity was assessed relative to previously determined unequivocal positive or negative cases.

Using this cut-point, the cases that had not been agreed upon were reassessed to deduce the prevalence of Erlenmeyer flask deformity in this population.

Results

The initial part of the study presented 102 knee radiographs (80 from patients with Gaucher′s disease) for review by 3 experienced radiologists. The results of independent assessment were:

• 27 cases in which all three agreed the film was positive for Erlenmeyer flask deformity

• 37 cases in which all three agreed the film was negative for Erlenmeyer flask deformity

• 38 cases in which there was no consensus.

Accuracies were calculated along with 95% confidence intervals. Results are shown in Table 1. Although analysis of agreement is an important pre-requisite, to be further utilised in the study, the immediate purpose was to define a cohort of radiographs where consensus for the Erlenmeyer flask deformity had been reached.

Table 1. Analysis of agreement of independent assessment of radiographs. Radiologists 2 and 3 were compared with Radiologist 1.

Rater	Accuracy	Estimate % (95% CI)
Radiologist 2 (n=76)	Sensitivity	100.0 (88.4, 100.0)
	Specificity	80.4 (66.1, 90.6)
	Positive predictive value	76.9 (60.7, 88.9)
	Negative predictive value	100.0 (90.5, 100.0)
	Overall proportion correct	88.2 (78.7, 94.4)
Radiologist 3 (n=79)	Sensitivity	90.0 (73.5, 97.9)
	Specificity	89.8 (77.8, 96.6)
	Positive predictive value	84.4 (67.2, 94.7)
	Negative predictive value	93.6 (82.5, 98.7)
	Overall proportion correct	89.9 (81.0, 95.5)

CI, confidence interval.

The second phase of the study involved a series of measurements obtained at regular intervals along the distal femur by two observers. Interobserver agreement was calculated using Bland and Altman's limits of agreement analysis. Table 2 shows the mean difference and limits of agreement, and their 95% confidence intervals, for each set of measurements. Table 3 shows the mean difference in ratios obtained, as well as limits of agreement and their 95% confidence intervals. Analyses were carried out in SPSS v.13.0 (SPSS Inc., Chicago, IL).

Table 2. Comparison of independent measurements.

Measurement	Mean difference	Lower limit of agreement (95%CI)	Upper limit of agreement (95%CI)
Base	−1.47	−7.23 (−8.21, −6.24)	4.29 (3.30, 5.27)
2 cm	−1.58	−7.44 (−8.44, −6.43)	4.28 (3.28, 5.29)
4 cm	−0.67	−4.55 (−5.22, −3.89)	3.22 (2.55, 3.88)
6 cm	−0.64	−3.01 (−3.41, −2.60)	1.73 (1.33, 2.14)
8 cm	−0.69	−3.74 (−4.28, −3.20)	2.37 (1.83, 2.91)
10 cm	−0.90	−3.23 (−3.65, −2.82)	1.43 (1.01, 1.85)
15 cm	−0.54	−2.54 (−2.92, −2.16)	1.47 (1.09, 1.85)
Midshaft	−0.79	−3.84 (−4.43, −3.25)	2.26 (1.67, 2.85)

CI, confidence interval.

Table 3. Comparison of calculated ratios between observers.

Measurement	Mean difference	Lower limit of agreement (95%CI)	Upper limit of agreement (95%CI)
2 cm:base	−0.007	−0.072 (−0.083, −0.061)	0.058 (0.047, 0.069)
4 cm:base	0.002	−0.046 (−0.054, −0.038)	0.050 (0.042, 0.058)
6 cm:base	0.001	−0.035 (−0.041, −0.029)	0.037 (0.031, 0.043)
8 cm:base	−0.00005	−0.040 (−0.047, −0.033)	0.039 (0.032, 0.046)
10 cm:base	−0.004	−0.036 (−0.042, −0.031)	0.029 (0.023, 0.035)
15 cm:base	−0.001	−0.030 (−0.036, −0.025)	0.029 (0.023, 0.034)
Midshaft:base	−0.004	−0.050 (−0.059, −0.041)	0.041 (0.032, 0.050)

CI, confidence interval.

It was apparent that ratios obtained from measurements made at 2, 4 and 6 cm had potential utility for defining the Erlenmeyer flask deformity. Measurements obtained further along the diaphysis were clearly beyond the limit of the skeletal deformity. Logistic regression analysis, with Erlenmeyer flask deformity (agreed by consensus to be either present or absent) as the outcome and the three ratios (2, 3 and 4 cm:base) as the explanatory variables, was used to calculate the best cut-point (to two decimal places) from this cohort in one of the ratios. The results for all three ratios investigated are given in Table 4.

Table 4. Analysis of the accuracy of the obtained ratios in determine Erlenmeyer flask deformity.

Ratio	Accuracy (95% CI)
2 cm:base (cut-point=0.70)	Sensitivity 88.9% (70.8%, 97.6%)
	Specificity 91.9% (78.1%, 98.3%)
	PPV 88.9% (70.8%, 97.6%)
	NPV 91.9% (78.1%, 98.3%)
	Correct 90.6% (80.7%, 96.5%)
4 cm:base (cut-point=0.58)	Sensitivity 95.6% (75.7%, 99.1%)
	Specificity 100.0% (90.5%, 100.0%)
	PPV 100.0% (86.3%, 100.0%)
	NPV 94.9% (82.7%, 99.4%)
	Correct 96.9% (89.2%, 99.6%)
6 cm:base (cut-point=0.54)	Sensitivity 88.9% (70.8%, 97.6%)
	Specificity 97.3% (85.8%, 99.9%)
	PPV 96.0% (79.6%, 99.9%)
	NPV 92.3% (79.1%, 98.4%)
	Correct 93.8% (84.8%, 98.3%)

NPV, negative predictive value; PPV, positive predictive value.

With reference to a described receiver operator characteristic (ROC) curve obtained from the three logistic regressions, the ratio of 4 cm:base gave the best classification of the patients with Gaucher′s disease. This has the largest area under the curve (AUC=0.96, compared with AUC=0.95 for both 2 and 6 cm:base).

Taking the ratio of 4 cm:base of ≥0.58 as positive for the Erlenmeyer flask category gave the best combination of sensitivity and specificity. When this criterion was applied to the hitherto unclassified patients with Gaucher′s disease, it gave 19 positive and 19 negative cases.

Using this ratio the total number of knee radiographs positive for Erlenmeyer flask deformity was 46 out of 102. By excluding radiographs from the control patients (none of whom had Erlenmeyer flask deformity by consensus or ratio measurement), the prevalence of Erlenmeyer flask deformity in the study population of patients with Gaucher′s disease was determined as 57.5%.

Discussion

The first phase of the study showed that the level of agreement between experienced radiologists in determination of the Erlenmeyer flask abnormality is of the order of 90%. The centre where the study was performed is a national referral centre for the treatment of Gaucher′s disease; as a result, the number of patients would be much higher than is likely to be encountered by a radiologist in a non-specialist centre. Hence, the high level of concordance may not be generally applicable.

The measurements in this study were obtained before introduction of the Picture Archive and Communications System (PACS; Centricity™, GE Healthcare, Waukesha, WI) system. A transparent overlay template was used to obtain measurements and to determine interobserver variability. Using this technique the interobserver variability is low (of the order of 1 mm). Currently employed PACS workstations have readily available tools to allow this measurement to be carried out. Although interobserver variability was not formally assessed on a PACS workstation, there is no reason to suppose that this technology would increase the error of measurement.

By using a ratio of >0.58 at 4 cm from the physeal plate, the sensitivity for diagnosing Erlenmeyer flask deformity was determined to be 95.6%, with a high degree of specificity (100% in this study). This measurement is sufficiently robust and accurate to be employed for comparing different populations or groups of patients with Gaucher′s disease.

The method is clearly limited by the availability of suitable radiographs from patients with Gaucher′s disease, since the measurements depend on views of the knee and distal femur. Patients with Gaucher′s disease who had not undergone a knee radiograph could not be included, so theoretically a selection bias towards symptomatic patients might affect the apparent prevalence of the skeletal deformity. However, it is impossible to confirm that the prevalence of Erlenmeyer flask deformity is the same in patients who had undergone radiography as in those who had not had suitable imaging.

Technical factors also limit the accuracy of the measurements undertaken. Depending on where the X-ray beam is centred (as well as any variation in the standard tube–film distance) there will be a slight magnification or error in measurement angle. The calculation of ratios serves to reduce this error. Determination of the ratios in patients with significant valgus or varus deformity is more likely to be inaccurate. The measurements performed did not attempt to account for this error, and the operationally useful results obtained suggest that it is not necessary to attempt corrections for this error to obtain useful ratios.

Our study was performed in adult patients with Gaucher′s disease, in whom the degree of variation in overall bone length is more limited than in children. The measurements were obtained at pre-determined regular increments. While obtaining measurements at a proportion relative to the total bone size would theoretically be ideal, in routine clinical practice radiographs are limited to the distal femur and knee, rather than the whole femur.

In the radiographs available for review, full-length images of the femur were not available, so an alternative approach to measurement at variable proportions of the total bone length was not possible. In children, who have more marked variability in bone size, an alternative approach of measuring the diametaphyseal width at a certain length along the femur relative to the physeal width may be more appropriate. This was not assessed in our study.

Conclusion

Although Erlenmeyer flask deformity is frequently mentioned in relation to Gaucher′s disease, no formal definition of the radiological finding exists. We have devised an easily applied measurement that shows a high degree of interobserver accuracy and which is both sensitive and specific for the diagnosis of this skeletal deformity. This involves relating the diameter of the distal femoral shaft 4 cm from a baseline to the diameter of the baseline on a frontal radiograph of the knee. A ratio in excess of 0.57 implies the presence of Erlenmeyer flask deformity with 95.6% sensitivity and 100% specificity in our series.