Towards Automatic Quantitative Quality Control for MRI

Abstract

Quality and consistency of clinical and research data collected from Magnetic Resonance Imaging (MRI) scanners may become suspect due to a wide variety of common factors including, experimental changes, hardware degradation, hardware replacement, software updates, personnel changes, and observed imaging artifacts. Standard practice limits quality analysis to visual assessment by a researcher/clinician or a quantitative quality control based upon phantoms which may not be timely, cannot account for differing experimental protocol (e.g. gradient timings and strengths), and may not be pertinent to the data or experimental question at hand. This paper presents a parallel processing pipeline developed towards experiment specific automatic quantitative quality control of MRI data using diffusion tensor imaging (DTI) as an experimental test case. The pipeline consists of automatic identification of DTI scans run on the MRI scanner, calculation of DTI contrasts from the data, implementation of modern statistical methods (wild bootstrap and SIMEX) to assess variance and bias in DTI contrasts, and quality assessment via power calculations and normative values. For this pipeline, a DTI specific power calculation analysis is developed as well as the first incorporation of bias estimates in DTI data to improve statistical analysis.

1. INTRODUCTION

Standard practice for quantitative quality control of magnetic resonance imaging (MRI) data is currently restricted to phantom studies, which primarily evaluate B_o and B₁ field homogeneity (scanner produced magnetic fields), and receiver coil sensitivity [1]. Although useful in evaluating basic scanner stability and improving overall scanner performance, phantom analysis may not be timely and cannot provide data-specific quality analysis. Such common events as patient motion, daily magnetic field drift, parameter tweaking, software updates, or hardware ‘glitches’, will not be captured by intermittent phantom studies yet these occurrences can drastically impact data quality. Additionally, phantom studies cannot assist the researcher in deciding if suspect data is of a sufficient quality to answer an experimental question at hand. An automatic data-specific quality analysis pipeline can be used to address these issues and provide additional early warning about experimental specific scanner problems.

Diffusion Tensor Imaging (DTI) provides an excellent test case for a data specific quality analysis pipeline. DTI is an invaluable state of the art MRI method which measures water diffusion in vivo as a means to interrogate cytoarchitecture and elucidate neuronal fiber tracks [2]. Currently, DTI is the only in vivo method capable of measuring anatomical connectivity at a level that is beginning to rival its only alternative, histology. As such, DTI contrasts are quantitatively valuable and quality analysis becomes increasingly important. DTI data is particularly large, involving up to one hundred brain volumes, each with scores of slices, and experimental protocols are gradient intensive and subject to gradient amplifier difficulties and heating artifacts. DTI processing involves model fitting procedures — the SNR properties of the starting imaging data do not carry through in an easily tractable manner to the final DTI estimated contrasts. Furthermore, DTI contrasts are known to contain bias [3], particularly fractional anisotropy (FA) investigated herein, and as of yet this bias has remained unaccounted for in quantitative analysis of empirical data.

This article presents a pipeline for quality analysis of DTI data through use of two methods, power calculations and normative values. Power calculations, although arguably naïve, are fundamental to grant proposals and ubiquitous in the literature, making the statistical tool easily accessible to clinical researchers. In a quality control setting, power calculations can be used to evaluate if data is of sufficient quality to probe a desired effect size in a hypothesis testing scenario. A simplifying but deeply informative assumption would be to assume that all n data sets would be collected at the same variability and bias level of the observed dataset. An insufficient power at the desired effect size or adverse changes over the duration of a study (often years) can provide prompt warning of the need for experimental adjustments or scanner performance evaluation. Meanwhile, normative values provide an opportunity for long period monitoring of an experimental study. In this case, important DTI values are automatically processed and stored and expected distributional properties of these values can be established. In this method, normative values organic the specific scanner/experimental protocol/processing method, can be established. By comparing histograms from individual datasets to the group histogram, questions of data compatibility and stability can be answered.

Four important challenges towards DTI data specific quality analysis using power calculations and normative values are (i) measuring variability of an individual data-set, (ii) estimating and incorporating contrast bias, and (iii) a system that links to the scanner and automatically processes and analyses the dataset in a time efficient manner. Here we present solutions to these challenges by combining (i) wild bootstrap analysis to estimate variability from a single dataset [4] and (ii) simulation extrapolation (SIMEX) to evaluate bias [5].

2. THEORY

The theory section provides (2.1) background in DTI, (2.2) bootstrap applied to DTI to measure FA variance, (2.3) SIMEX applied to DTI to measure FA bias, and (2.4) incorporation of bias into power calculations for DTI. The first three sections address topics that have been presented in detail previously by this lab and by others. These sections are then kept as brief as possible.

2.1 Diffusion Tensor Imaging [2]

Diffusion tensor imaging is a method to measure the three dimensional diffusion coefficient of water, D, in vivo. To do so, diffusion gradients are applied in sequence along various directions, g, resulting in a series of diffusion weighted images (DWI). Each gradient attenuates the water signal in proportion to the diffusion coefficient of water along that gradient direction. Attenuation in each DWI is measured in relation to a control image, symbolized as S_o, and for a single voxel the diffusion equation for a DTI experiment is,

$${\text{DWI}}_j={\mathrm{S}}_{\mathrm{o}}\text{exp}(-b{\mathbf{g}}_{\mathit{j}}^{\mathbf{T}}·\mathbf{D}·{\mathbf{g}}_{\mathit{j}})$$ (1)

where j indexes the diffusion gradient number and b is an experimental dependent parameter reflecting gradient strength and timing. The diffusion coefficient D is a 3×3 tensor and in the simplest and most commonly employed model represents the covariance matrix of the trivariate Gaussion probability distribution for finding a water molecule at a distance Δd from a starting point, (x,y,z) after time Δt. D is commonly in units of mm²/s. The Eigenvectors of D describe the three principle axis of the trivariate Gaussian while the three Eigenvalues, (λ₁ λ₂ λ₃), represent the one dimensional diffusion coefficient along each principle axis. An invaluable and ubiquitous diffusion tensor contrast is fractional anisotropy, which ranges from 0 to 1 and measures the extent of diffusion anisotropy, FA = 1 being unidirectional diffusion and FA = 0 being perfectly isotropic diffusion.

$$\text{FA}=\sqrt{\frac{3}{2}\frac{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2{({\lambda }_3-\overline{\lambda })}^2}{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$ (2)

Note that FA greater than 1 may occur if negative Eigenvalues (which do not represent physical diffusion processes but may result from experimental noise) are permitted.

2.2 SIMEX on DTI to measure bias [6, 7]

The premise of SIMEX is conceptually simple. Bias can be understood by adding noise to data in incremental amounts and measuring the resulting contrast. The trend in the contrast with added noise should enable prediction of the contrast with ‘removed’ noise. For simplicity, the following description assumes a single DTI experiment is performed (e.g. single subject, one DTI dataset) and describes the single-voxel case, though the analysis can be extended to multiple experiments and multiple voxels. In the following, bold lettering represents a vector or function. Let x refer to the collection of DWI and S_o images (Eq. 1), and let x_T be a truth data set described by zero experimental noise, σ_E = 0. Let the function F map dataset x to the contrast FA. Then the experimentally observed data x_obs and corresponding FA_obs is described by,

$${\mathbf{x}}_{\mathbf{\text{obs}}}={\mathbf{x}}_{\mathbf{T}}+{\mathrm{\sigma }}_{\mathrm{E}}\mathbf{Z};{\text{FA}}_{\text{obs}}=\mathbf{F}({\mathbf{x}}_{\mathbf{\text{obs}}})$$ (3)

where Z is a vector length j+1 of standard normal error values. The noise distribution of x_obs is technically Rician, however for SNR >5, which is nearly always the case for clinical and research scans, the Gaussian becomes an excellent approximation [8]. For the simulation step of SIMEX, Gaussian synthetic noise of variance ωσ_E² is added (in implementation for DTI data, Rician noise is used to x_obs. Letting U_k be a j+1 vector of random drawings from a standard normal we have,

$${\mathbf{x}}_{\mathit{k}}(\mathrm{\omega })={\mathbf{x}}_{\mathbf{\text{obs}}}+{\mathrm{\omega }}^{1/2}{\mathrm{\sigma }}_{\mathrm{E}}{\mathbf{U}}_{\mathit{k}};{\text{FA}}_{\mathit{k}}(\mathrm{\omega })=\mathbf{F}({\mathbf{x}}_{\mathit{k}}(\mathrm{\omega })).$$ (4)

For R different ω_r, the process is repeated K times to evaluate the expectation value of FA(ω_r).

$$\mathbf{E}(\text{FA}({\mathrm{\omega }}_r))\approx \overline{\text{FA}}({\mathrm{\omega }}_r)=\frac{1}{K}{\displaystyle {\sum }_{k=1}^K}{\text{FA}}_k({\mathrm{\omega }}_r)$$ (5)

Observe from Eq. 4 that the variance of x_k(ω) is exactly described by σ_E(1+ω), and the variance of x_k(ω) is zero when ω = −1 and therefore so to is FA_k(−1). The case of ω = −1 cannot be reached through simulation, as this represents the impossible tasks of removing noise, however it can be reached throughfitting of $\overline{\text{FA}}({\mathrm{\omega }}_r)$ followed by extrapolation to ω = −1. In the extrapolation step, the set of R + 1 FA values, $\{{\text{FA}}_{\text{obs}},\overline{\text{FA}}({\mathrm{\omega }}_r)|\underset{r=1}{R}\}$ are fit with an approximating function, $\widetilde{\text{FA}}(\mathrm{\omega })$, in this case a polynomial order 2. The new SIMEX estimate of FA, FA_SMX, is then calculated through extrapolation to ω = −1. The bias in the original FA_obs estimate, B_FA, can then be estimated.

$${\text{FA}}_{\text{SMX}}=\widetilde{\text{FA}}(-1);{\mathrm{B}}_{\text{FA}}={\text{FA}}_{\text{obs}}-{\text{FA}}_{\text{SMX}}$$ (6)

2.3 Wild Bootstrap on DTI data to measure variance[4]

The bootstrap method to estimate variance from a single dataset first creates a simulated population based upon that dataset. Let X_obs be the set DWI_j/S_o for a single voxel (capitalized to distinguish from the similar x_obs described above in section 2.2) and let D be the diffusion tensor calculated from X_obs using Eq.1. A model-fit data set X_mf can then be created by solving for a new DWIj/S_o using the fitted diffusion tensor D. The model error vector ε is composed of the elements X_obs − X_mf. Synthetic bootstrap data X_bs and synthetic bootstrap FA values, FA_bs, can then be made by resampling with replacement the errors from ε.

$${\mathbf{X}}_{\mathbf{\text{bs}}}^{(\mathit{m})}={\mathbf{X}}_{\mathbf{\text{mf}}}+{\mathbf{\alpha }}_{\mathit{m}}{\mathbf{\epsilon }}_{\mathit{m}}^{\mathbf{*}};{\text{FA}}_{\text{bs}}^{(m)}=\mathbf{F}({\mathbf{X}}_{\mathbf{\text{bs}}}^{(\mathit{m})})$$ (4)

Here, ${\mathbf{\epsilon }}_{\mathit{m}}^{*}$ is a vector of length j whose elements are created by random sampling with replacement from ε, α is a vector of length j whose elements are randomly chosen from the set {−1 1}, F is a mapping from X to FA, and m = 1,2,‥M indexes the bootstrap number. Note that errors are resampled in imaging space and are resampled along a constant voxel (e.g. errors from one voxel are not used on a different voxel). Once a population of $M{\mathbf{\text{FA}}}_{\mathbf{\text{bs}}}^{(\mathbf{m})}$ is simulated, the bootstrap estimated variance, σ_bs, of the original FA_obs is calculated.

$${\mathrm{\sigma }}_{\text{bs}}=\text{var}\left(\left\{{\text{FA}}_{\text{bs}}^{(m)}|\begin{array}{c}\hfill M\hfill \\ \hfill m=1\hfill \end{array}\right\}\right)$$ (8)

2.4 Power Calculations with Bias

Bias is well known to exist in DTI data [3, 9]. The presence of bias in data changes the true power, 1-β_T and true alpha rate, α_T, of a hypothesis test away from the nominal power, 1- β_nom, and the nominal alpha rate α_nom of the hypothesis test. Although this is well known, a literature and textbook search yielded no readily available equations. Here we derive α_T and 1-β_T for a two sided Z-test run with ignored bias B. Let x̄ be the average of n observations drawn from a normally distributed population with mean μ and standard deviation σ. Let μ be an estimate of μ_T. Without bias, μ = μ_T and x̄ limits to μ_T as n approaches infinity. In the presence of bias B, μ = μ_T + B and x̄ limits to μ and not μ_T as n approaches infinity. Define the null hypothesis as μ_T = f, and the alternative hypothesis as μ_T ≠ f. The null hypothesis is rejected under the condition that $\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}>{\mathrm{Z}}_{1-\raisebox{1ex}{${\mathrm{\alpha }}_{\text{nom}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\text{ or }\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}<{\mathrm{Z}}_{1-\raisebox{1ex}{${\mathrm{\alpha }}_{\text{nom}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, where Z_a is defined as the inverse cumulative distribution function of a standard normal evaluated at a, Φ⁻¹(a).

Alpha-rate

The nominal alpha rate is defined as the probability of falsely rejecting the null. It is therefore defined under the given condition μ_T = f.

$$\text{Pr}\left(\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}>{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}\cup \frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}<-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}|{\mathrm{\mu }}_{\mathrm{T}}=f\right)={\alpha }_{\mathit{\text{nom}}}$$ (9)

Here, P is the probability function. When bias B is present, the given condition, μ_T = f leads to μ = f + B. The true alpha rate for a test run with the nominal alpha rate defined as in Eq. 9 becomes

$$\text{Pr}\left(\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}>{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}\cup \frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}<-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}|\mathrm{\mu }=f+{\mathrm{B}}_{\text{FA}}\right)={\alpha }_T$$ (10)

Using the fact that $\frac{\overline{\mathrm{x}}-(f+B)}{\mathrm{\sigma }/\sqrt{n}}$ is sampled from a standard normal, the analytic solution for α_T is easily obtained.

$$1-\mathrm{\Phi }\left({\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{B\sqrt{n}}{\mathrm{\sigma }}\right)+\mathrm{\Phi }\left(-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{B\sqrt{n}}{\mathrm{\sigma }}\right)={\alpha }_T$$ (11)

Power analysis

The nominal power for a given effect size, ES, is defined as the probability of correctly rejecting the null when μ_T = f + ES.

$$\mathit{\text{Pr}}\left(\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}>{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}\cup \frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}<-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}|{\mathrm{\mu }}_{\mathrm{T}}=f+\text{ES}\right)=1-{\mathrm{\beta }}_{\text{nom}}$$ (12)

The probability function is solved using the fact that $\frac{\overline{x}-f-\text{ES}}{\mathrm{\sigma }/\sqrt{n}}$ is sampled from a standard normal,

$$1-\mathrm{\Phi }\left({\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{\text{ES}\sqrt{n}}{\mathrm{\sigma }}\right)+\mathrm{\Phi }\left(-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{\text{ES}\sqrt{n}}{\mathrm{\sigma }}\right)=1-{\mathrm{\beta }}_{\text{nom}}$$ (13)

When bias B is present, the given condition μ_T = f +ES leads to μ = f+ ES +B and the true power for a test with nominal power as in Eq. 12 is,

$$\mathrm{P}\left(\frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}>{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}\cup \frac{\overline{x}-f}{\mathrm{\sigma }/\sqrt{n}}\mathrm{<}-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}|\mathrm{\mu }=f+\text{ES}+B\right)=1-{\mathrm{\beta }}_{\mathrm{T}}$$ (14)

The probability function is solved using the fact that $\frac{\overline{x}-f-(\text{ES}+B)}{\mathrm{\sigma }/\sqrt{n}}$ is sampled from a standard normal,

$$1-\mathrm{\Phi }\left({\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{(\text{ES}+B)\sqrt{n}}{\mathrm{\sigma }}\right)+\mathrm{\Phi }\left(-{\mathrm{Z}}_{1-{\mathrm{\alpha }}_{\text{nom}}/2}-\frac{(\text{ES}+B)\sqrt{n}}{\mathrm{\sigma }}\right)=1-{\mathrm{\beta }}_{\mathrm{T}}$$ (15)

3. METHODS AND RESULTS

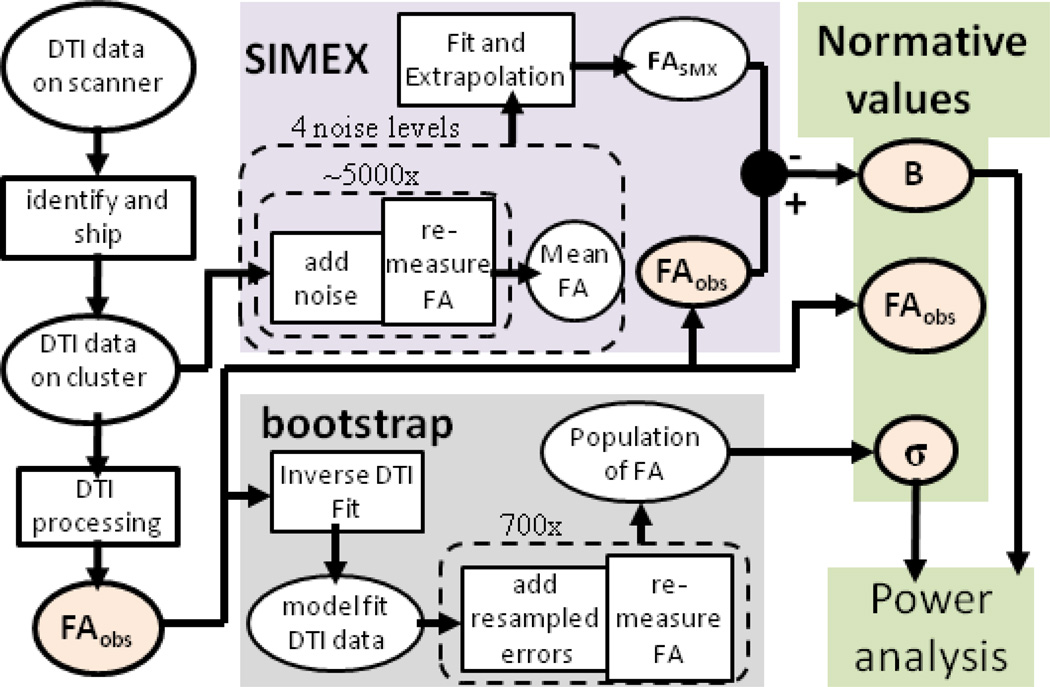
Figure 1 shows the near future completed pipeline for dataset specific quality analysis in DTI. Herein we present the methods and results for nearly all pieces of the Figure 1 pipeline. Two incomplete parts of the pipeline are the pipeline beginning and the pipeline end. The pipeline begins with data collected on the scanner being shipped to a cluster for analysis. Although the infrastructure for detection and automatic DTI processing is in place, for efficiency we use as a test case previously acquired data available online (see below). The end of the pipeline uses power analysis and normative values for quality analysis. Here we present first pass methods of visualizing and interpreting these results, but much information is contained in these values and further investigation is required before a more optimal output and statistical analysis is designed. Unless otherwise stated, all processing and analysis was performed in Matlab 2010 (Mathworks, Natick, MA).

Figure 1.

Flow chart of quality analysis pipeline. The flow chart begins in the upper left corner with data collected on the scanner. The data undergoes DTI processing followed by analysis with SIMEX to measure bias, B_FA, and bootstrap to measure the variance of FA, σ_bs. These parameters are then kept for the development of normative values and for power analyses.

3.1 Experimental DTI Dataset and Pre-processing

Data were downloaded from the Multi-Modal MRI Reproducibility study [10] available online at www.nitrc.org. The dataset consists of 21 DTI datasets each repeated twice for a total of 42 DTI datasets. Full collection details are provided in the reference. Briefly, the DTI data was collected using a multi-slice, single-shot, echo planar imaging (EPI) sequence. Thirty two gradient directions were used with a b-value = 700 s/mm² (j = 32, b = 700, (Eq. 1)). Five S_o images were collected and averaged to form a single S_o image. The resulting images consisted of sixty-five transverse slices with a field of view = 212 × 212 mm, reconstructed to 256 × 256 voxels. Each voxel size is 0.83 × 0.83 × 2.2 mm. Matched DTI dataset pairs were registered to the same space through affine registration to an S_o target image and data were automatically masked and the brain volume isolated. Registration and masking were performed using FSL (FMRIB, Oxford, UK). Individual case inspection revealed that automatic masking was mostly successful but most images had less restrictive masking than optimal. The experimental error, σ_E (Eq. 3) was estimated at each voxel using the 32 differences of DWI between paired datasets. Assuming approximate normality for the empirical noise, σ_E² = Var(DWI(scan 1) − DWI(repeat scan))/2, where Var is the variance function.

3.2 Calculation of FA_obs, B_FA, and σ_bs (Figure 2)

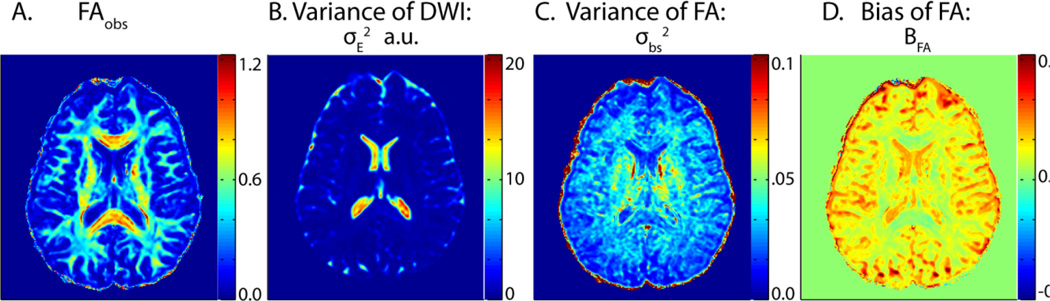
Figure 2.

Three important parameters produced through the pipeline and the initial data variance. All images are from the dataset ‘Session01’ slice 36. (A) The FA values calculated from the initial tensor fit. (B) DWI variance for Session01 and its repeat scan Session25. (C) The bootstrap estimated variance of FA_obs. (D) The SIMEX estimated bias.

Following the flowchart, first data underwent DTI processing. Diffusion tensor estimates were calculated by fitting the model (Eq. 1) to the data using a simple LLMMSE. FA_obs for each voxel was then calculated according to Eq.2. Moving upwards along the flowchart, SIMEX was then performed to estimate the bias B_FA. For the simulation step, noise added to the data (Eq. 4) was Rician distributed, which is approximately Gaussian for SNR > 5 [8]. (ω_r) was averaged from K = 2000, 4000, 6000, and 8000 iterations for ω = 2, 4, 6, and 8 respectively (Eqs. 4–5). The resulting set of (ω_r) was fit to a polynomial of order 2 and the fit equation, (ω), extrapolated to ω = −1, producing FA_SMX. The SIMEX estimated bias, , was then calculated (Eq. 6). Travelling next to the lower path on the flowchart, bootstrap analysis was run in order to calculate the bootstrap estimated variance, σ_bs. The bootstrap method herein follows the methodology described in the theory section and used 700 iterations to calculate σ_bs. Example output of FA_obs, B_FA, and σ_bs² for a mid-brain slice is shown in Figure 2, together with the spatial map of the estimated experimental variance for the DWI, σ_E².

3.3 Power Analysis (Figure 3)

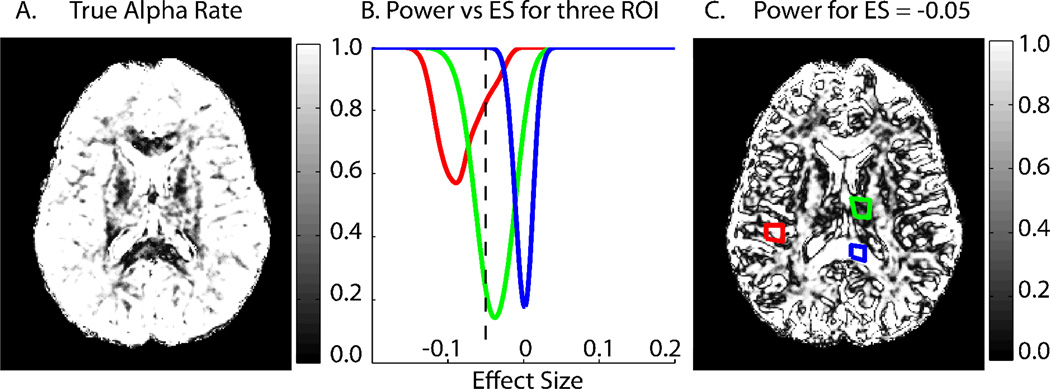
Figure 3.

Power analyses incorporating bias. Values represent a ‘worst case scenario’ as described in materials and methods. Data shown are from dataset ‘Session01’ slice 36. The colorscale values for (A) are shared with the Y-axis for (B). (A) The true alpha rate for a hypothesis test with alpha = .05 and uncorrected bias. (B) The average power for three ROIs at various effect sizes. Gray matter (red) represents a low σ_bs high B_FA case, deep gray matter (green) represents high σ_bs and medium B_FA while white matter (blue) represents low σ_bs and near zero B_FA. Note the white matter plot (blue) is symmetric, as is expected of an unbiased estimator. The dashed black line corresponds to an effect size, ES = −.05. (C) The power for ES = −.05. The three ROI used to create the plots in (B) are shown.

The power analysis herein is framed by the statistically tractable and meaningful question, ‘if all datasets in the study were collected at the measured data quality level, what is the power and alpha rate for a two sided hypothesis test at effect size ES?’. The specific hypothesis test is as described in the theory section with the test population being a hypothetical cohort with variance σ_bs and bias B_FA and an adjustable sample size of n=15. Although the hypothesis test is not between two groups, as is usually the case with a DTI study, the power analysis for this hypothesis test represents a worst case scenario. Owing to the correlation between bias and FA, it is likely that two compared groups would have similar bias values. This hypothesis test assumes no bias in the comparison constant f, thus reflecting an upperlimit for the largest bias discrepancy in a comparison study. With σ_bs and bias B_FA, α_T (Eq. 11) is calculated (Figure 3A). Power is then analyzed for an array of effect sizes and demonstrated for regions of interest ROI (Figure 3B). The power for all voxels within a slice at a specific effect size can also be visualized (Figure 3B). These images not only provide information on quality of the DTI dataset, but also represent the first graphical representation of power analysis for DTI and emphasize the potentially serious impact of bias on power and alpha rates.

3.4 Normative Values (Figure 4)

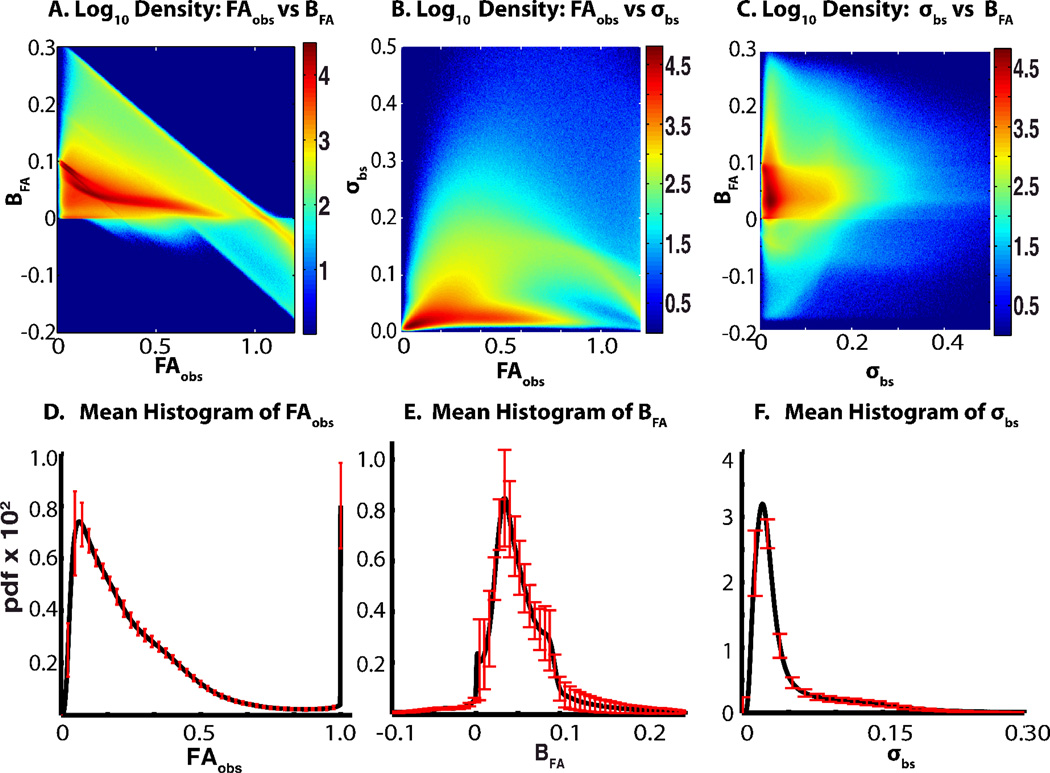
Figure 4.

Distribution of FA_obs, B_FA, σ_bs, and their histograms. Density of individual parameters (A–C) represents 55.7 × 10⁶ values and the colorbar scale represents the log₁₀ of the total number of values found in each region. The distribution of histograms (D–E) represents 42 histograms each from the 42 datasets, red error bars show the standard deviation of that bin. Before averaging, each bin value was normalized by the total number of voxels processed in that dataset. In all cases, the standard deviations are shown on a downsampled number of bins for ease of viewing.

The FA_obs, B_FA, and σ_bs for each voxel in the 42 different DTI images collectively form a massive dataset, consisting of over 55 million values for each parameter. Three two way comparisons formed from all pairs of FA, B_FA and σ_bs are shown in Figure 4A–C. Histograms for each parameter were constructed for each of the 42 DTI datasets using fixed b in widths and centers. For FA_obs 481 bins were used with evenly spaced centers ranging from 0 to 1.2, for B_FA 1201 bins were used with evenly spaced centers ranging from −2 to .4, and for σ_bs 1818 bins ranging from .0011 to 2 were used. Bin widths were roughly based on the equation 3.5σ/55.7², (σ is standard deviation) and bin upper and lower limits were placed near minimum and maximum values. The average of each bin for each parameter are shown in Figure 4D–F together with evenly spaced standard deviations of a bin subset. .

4. DISCUSSION

Current practice for quantitative quality control in MRI can be improved through the use of quality analysis of experimental data itself. Here we demonstrate important steps towards creating a quality analysis pipeline for DTI data. The processing incorporates both the previously established bootstrap analysis for DTI metrics and, as bias is a known problem in DTI contrasts, the novel usage of SIMEX to estimate bias in those metrics. Although both bootstrap and SIMEX are computationally expensive, involving hundreds to thousands of loops per voxel (Figure 1), these methods are highly parallelizable and become timely and feasible with the incorporation of cluster computing. By incorporating these methods into an automatic pipeline, not only can these values be made available to the researcher for prompt feedback, but can also be stored for the creation of normative values or other applications such as comparisons between different experimental methods.

A first look at the power analysis and normative values from the pipeline offers some interesting insights. The pipeline incorporates power analysis in order to provide quantitative values that would be useful in deciding the levels of FA values that are distinguishable at the variability and bias level of the tested dataset. Accounting for bias or even estimating bias is not yet standard practice in DTI as bias estimation methods have only most recently been introduced. However, bias in the DTI data examined here proved to have surprisingly severe effects on power and alpha rate of the pipeline hypothesis test (Figure 2). As mentioned in materials in methods, this is a worst case scenario. But the analysis also provides strong confidence in the alpha and power rate for the predominantly unbiased and low variance white matter. The density plots (Figure 4A–C) offers a first insight into the surprising effect on alpha rate. Bias correlates more strongly with FA_obs than with σ_bc, causing substantial bias at σ_bc levels insufficient to mask the impact of bias. The normative histograms (Figure 4D–F) offer a comparison method for testing if a new dataset collected using the same DTI sequence is ‘reasonable’ and already suggest interesting patterns. For example. the large spike at FA_obs = 1.0 in Figure 4D represent a cluster of voxels with negative Eigenvalues.

Remaining steps in the pipeline are to (1) streamline through addition and removal of useful values (e.g. incorporation of a model fit error map and/or quantify patient motion through the affine registration), (2) to investigate, likely using cluster analysis methods, interesting and potentially useful properties of the growing normative values, and (3) test on live data with researcher/clinician feedback. The basic method described herein and its future development should prove translatable to other areas of MRI experiments, e.g., BOLD or VASO, allowing automatic feedback on data quality and experimentally stability.