Abstract
Objective
This study sought to determine the relationship between BMI fluctuation and cardiovascular disease phenotypes, diabetes, and depression and the role of genetic and environmental factors in individual differences in BMI fluctuation using the extended twin-family model (ETFM).
Study Design and Methods
This study included 14,763 twins and their relatives. Health and Lifestyle Questionnaires were obtained from 28,492 individuals from the Virginia 30,000 dataset including twins, parents, siblings, spouses, and children of twins. Self-report cardiovascular disease, diabetes, and depression data were available. From self-reported height and weight, BMI fluctuation was calculated as the difference between highest and lowest BMI after age 18, for individuals 18–80 years. Logistic regression analyses were used to determine the relationship between BMI fluctuation and disease status. The ETFM was used to estimate the significance and contribution of genetic and environmental factors, cultural transmission, and assortative mating components to BMI fluctuation, while controlling for age. We tested sex differences in additive and dominant genetic effects, parental, non-parental, twin, and unique environmental effects.
Results
BMI fluctuation was highly associated with disease status, independent of BMI. Genetic effects accounted for ~34% of variance in BMI fluctuation in males and ~43% of variance in females. The majority of the variance was accounted for by environmental factors, about a third of which were shared among twins. Assortative mating, and cultural transmission accounted for only a small proportion of variance in this phenotype.
Conclusions
Since there are substantial health risks associated with BMI fluctuation and environmental components of BMI fluctuation account for over 60% of variance in males and over 50% of variance in females, environmental risk factors may be appropriate targets to reduce BMI fluctuation.
Keywords: BMI, Chronic Disease, Weight change, Heritability, Family Studies
Introduction
Body mass index (BMI) in overweight and obese ranges are associated with adverse health outcomes including type 2 diabetes mellitus, hypertension, cardiovascular disease, and stroke (Field et al. 2001; Seidell et al. 1989). A “J” or “U” shaped relationship between BMI and mortality has been consistently found (Reis et al. 2009; Freedman et al. 2006) suggesting that BMI at either end of the spectrum is associated with increased risk of morbidity and mortality. The relationship between BMI and mortality appears to differ by age. In the Freedman et al. (2006) study, the risk for mortality began to increase at 30 kg/m2 for males and 25 kg/m2 for females over 55 years, compared with 23 kg/m2 for males and 21 kg/m2 for females under 55 years (Freedman et al. 2006). Overweight and underweight male adolescents have an increased risk for mortality as adults (38 years later) compared with normal weight male adolescents (Neovius et al. 2009). A BMI over 30 kg/m2 in males aged 18 years is associated with increased risk for mortality 14 years later (Yarnell et al. 2000). Therefore, even at relatively young ages there is a substantial association between BMI and mortality. These data suggest important age effects on the relationship between BMI and mortality.
Obesity is also a significant public health burden and is associated with increased health care costs (Finkelstein et al. 2010; Lightwood et al. 2009), lost productivity (Finkelstein et al. 2010; Lightwood et al. 2009), and overall poor quality of life (Schwimmer et al. 2003). These factors have prompted public health efforts and initiatives to promote weight loss. However, weight loss attempts are largely unsuccessful over the long-term (Jeffery et al. 2000; Wing and Phelan 2005). Results from one study indicated that only 20% of individuals are successful in maintaining a 10% weight loss for one year (Wing and Phelan 2005). If sustained weight loss is unsuccessful and weight is regained, this may lead to another dieting attempt. Therefore, this high percentage of unsuccessful dieting attempts (weight loss followed by weight regain), may lead to large BMI fluctuations (large differences between high and low BMI).
Large BMI fluctuations appear to be associated with adverse health outcomes but evidence is limited. Independent of obesity, large fluctuations in weight are associated with increased disease and death, specifically cardiovascular diseases (Lissner et al. 1991; Blair et al. 1993; Lee and Paffenbarger 1992; Diaz et al. 2005) and metabolic syndrome components (Zhang et al. 2005). Diaz and colleagues note increased mortality in individuals who experienced weight loss (Diaz et al. 2005) suggesting this relationship is not solely based on weight gain. This suggests that BMI fluctuation may also have an influence on overall health. Further research is needed to determine the impact of BMI fluctuation on specific diseases while controlling for BMI, age, and sex which are known to influence disease status.
While the contribution of genes and environment to individual differences in BMI has been investigated in numerous studies, to the best of the authors' knowledge no twin and extended twin-family model (ETFM) studies have yet been conducted on BMI fluctuation. Understanding the magnitude of genetic and environmental sources of variation can provide additional knowledge about this phenotype. The aim of the current study is to 1) determine the relationship between BMI fluctuation and a variety of medical conditions and depression while controlling for current BMI, age, and sex and 2) to use ETFM to determine which factors are important components in the variation of BMI fluctuation.
Methods and Materials
Virginia 30,000
Data come from the Virginia 30,000 twin sample which has been described elsewhere (Truett et al. 1994; Maes et al. 2006). Briefly, this is a Caucasian sample which contains data from 14,763 twins, ascertained from two sources: 1) public birth records for twins born in Virginia between 1915 and 1971 (5,287 individuals) and 2) responses to an advertisement in the American Association of Retired Persons newsletter (9,476 individuals). Median family income for this sample was slightly higher than the 1985 median Caucasian family income (Truett et al. 1994). Twins who chose to participate were mailed a 16-page `Health and Lifestyles' questionnaire (HLS), and asked to provide names and addresses of family members including spouses, siblings, parents and children for the follow-up study of relatives of twins. This provided information on 88 sex-specific biological and social relationships. Completed questionnaires were obtained from 69.8% of twins and 44.7% of relatives. The complete sample included 28,492 individuals (8567 extended kinships), 42% were male. For the current study individuals aged 18 years to 80 years were included. This yielded a sample of 26,808 individuals (94.1% of the original sample): 11,028 males and 15,780 females.
Zygosity Determination
Zygosity determination was based on questions asking how often the twin was confused for the cotwin as a child (Truett et al. 1994; Maes et al. 2006); this method has been validated showing 95% agreement with zygosity determination based on blood typing (Eaves et al. 1989).
BMI Fluctuation
On the HLS, participants were asked questions regarding their height and their current, highest (non-pregnancy), and lowest weight after age 18. Current, highest, and lowest BMI were calculated as current, highest, and lowest weight (kg)/ height (m2). BMI fluctuation was calculated as the difference between highest and lowest BMI. Individuals (n= 492; 1.7%) with BMI fluctuations falling three or more standard deviations from the mean were removed because these values were likely erroneous or indicative of a disease state (e.g. cancer, anorexia nervosa, thyroid disorder).
Disease
The HLS contained questions about self-reported disease status. Participants were asked if they had heart failure, heart attack, stroke, angina, and high blood pressure [“diagnosed or treated by a physician”]. Response options were `yes' and `no' for each item. From responses to these questions, an “any cardiovascular disease” variable was constructed. If participants answered yes to presence of any one of heart failure, heart attack, stroke, angina, or high blood pressure, the participant was considered to have cardiovascular disease; otherwise they were not. For diabetes, participants were asked whether they had diabetes “diagnosed or treated by a physician;” thus both type 1 and type 2 diabetes were included. Participants were also asked whether they had had depression diagnosed or treated by a physician. In the current sample the same 346 participants were missing information on cardiovascular disease, diabetes, and depression.
Statistical Analyses
Using the entire sample, logistic regression analyses were performed separately for any cardiovascular disease, heart failure, heart attack, stroke, angina, hypertension, diabetes, and depression, controlling for current BMI, age, and sex. Number of children and pregnancies did not influence results so were not included in final analyses. Generalized estimating equation corrections were applied to control for non-independence of the data due to inclusion of related individuals. These analyses were conducted in SAS 9.2 (SAS Institute Inc. 2004).
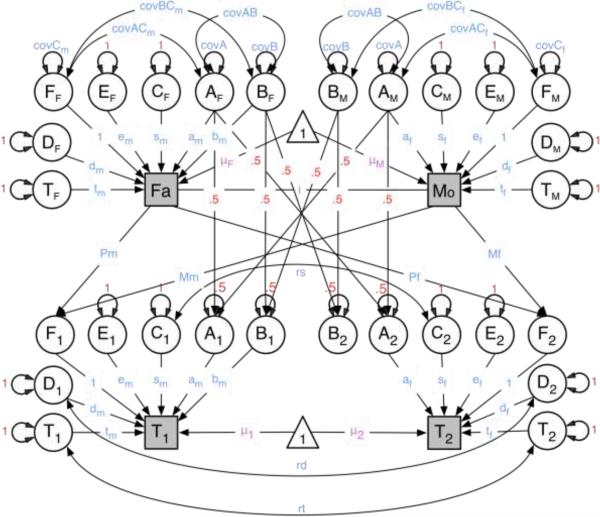
Structural equation modeling was performed to estimate the contributions of genetic and environmental factors to BMI fluctuation; raw continuous data were used. With availability of data on twins and their first and second-degree relatives (parents, siblings, spouses, and children), familial correlations were estimated by maximum likelihood. Next, an ETFM (Keller et al. 2009; Maes et al. 2009), which builds on the classical twin design (Neale and Cardon 1992; Neale and Maes 1998), was used. The ETFM allows for the simultaneous estimation of sex-specific additive and dominant genetic and shared and non-shared environmental factors in the presence of assortative mating. Genetic factors can be divided into additive genetic factors [(A), shared entirely by monozygotic (MZ) twins and on average 50% by dizygotic (DZ) twins], and dominant genetic factors [(D), shared entirely by MZ twins and 25% by DZ twins]. There are two main environmental sources of variance; common environmental factors (C) which are those shared by both members of a twin pair regardless of zygosity and specific environmental factors (E) which are unique to each twin and include measurement error (Neale and Cardon 1992; Neale and Maes 1998). While in classic twin models, C and D are confounded, all sources can be estimated simultaneously in the ETFM. This model is further able to partition the shared environmental variance in factors shared with parents (cultural transmission), non-parental shared sibling and twin environmental factors. The presence of spousal pairs and other relatives through marriage allows the effects of assortative mating to be taken into account.
Qualitative and quantitative sex differences are incorporated in the model. Qualitative sex differences are those in which the genes responsible for the phenotype differ in males and females while quantitative sex differences are those in which the magnitude of the genetic effect is different across the sexes. The base ETFM was further modified to allow for age regression on the mean values for BMI fluctuation.
Parameters of the ETFM were estimated from patterns of twin and family resemblance. Parameters estimates and their 95% confidence intervals were obtained using a maximum likelihood approach. Submodels were fitted to determine the most parsimonious model that did not fit significantly worse than the full model using likelihood ratio tests. The difference in minus twice the log-likelihood (−2LL) between two nested models is distributed as a chi-square with degrees of freedom (df) equal to the difference between the df's of the two models. The following rationale was used for fitting submodels. First, we evaluated the significance of qualitative sex differences; this test of whether the same factors are operating in both sexes was implemented by fixing the correlations between the male and female factors to one. The test was done for dominance, twin, and sibling environments. Qualitative differences for the additive component are modeled as male-specific additive genetic factors which can be dropped from the model to test their significance. Secondly, we tested for quantitative sex differences by equating the magnitudes of the male and female additive and dominant genetic effects, sibling, twin and unique environment, and cultural transmission. Third, we tested the significance of each of the sources of variance as well as assortment. Lastly, we removed the effects of age regression. Akaike information criterion (AIC) and −2LL were used to determine the best fit model. The best fit model was the most parsimonious model, as indicated by the lowest value for AIC, that did not fit significantly worse than the full model. Figure 1 contains a graphical representation of the full model for opposite-sex twins and their parents. All statistical analyses were conducted in the R software version 2.12.2 (R Development Core Team 2010); all structural equational modeling was conducted using OpenMx version 1.03 (Boker et al. 2010).
Figure 1. Extended-Twin Family Model for opposite-sex twins and their parents.
Note: T=special twin environment; D=non-additive genetic effects; E=unique environmental effects; C=common environmental effects; A=additive genetic effects; B=male specific genetic effects; Fa=father; Mo=mother; tm=special twin environment-males; dm=non-additive genes-males; em=unique environment and error-males; sm=special sibling environment-males; am=additive genetic effects-males; bm=male-specific genetic effects; i=assortative mating; tf=special twin environment-females; df=non-additive genes-females; ef=unique environment and error-females; sf=special sibling environment-females; af=additive genetic effects-females;T1=twin 1; T2=Twin2; rd=correlation between non-additive genetic effects in males and females; rt=correlation between special twin environment in males and females; rs=correlation between common environmental factors in males and females.
Results
The mean age of the sample was 48.6(16.9) years. BMI fluctuation ranged from 0.00 kg/m2 to 16.84 kg/m2. After controlling for current BMI, age, and sex, BMI fluctuation significantly predicted presence of any cardiovascular disease, heart failure, heart attack, stroke, angina, hypertension, diabetes, and depression; p-value <0.001 for all diseases. BMI fluctuation more strongly predicted disease than current BMI for all diseases phenotypes except hypertension where BMI more strongly predicted hypertension. Results of logistic regression equations are shown in Table 1. Although BMI fluctuation and current BMI are highly correlated, BMI fluctuation remained a significant predictor of disease when BMI and all other covariates were included. It should be noted that current BMI was inversely correlated with heart failure. This may be because congestive heart failure is often associated with low current BMI.
Table 1.
Logistic regression for BMI Fluctuation and Disease Phenotypes
| Disease | BMI Fluctuation β (SE) | χ 2 | p | BMI β (SE) | χ 2 | p | Age β (SE) | χ 2 | p | Sex* β (SE) | χ 2 | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heart Failure | 0.43 (0.07) | 26.42 | <0.001 | −0.37 (0.11) | 11.84 | 0.001 | 1.26 (0.09) | 175.83 | <0.001 | −0.65 (0.12) | 27.24 | <0.001 |
| Heart Attack | 0.31 (0.05) | 38.54 | <0.001 | −0.11 (0.06) | 3.55 | 0.06 | 1.36 (0.05) | 549.43 | <0.001 | −1.32 (0.08) | 254.85 | <0.001 |
| Stroke | 0.38 (0.07) | 21.56 | <0.001 | −0.18 (0.09) | 3.49 | 0.07 | 1.39 (0.09) | 220.14 | <0.001 | −0.58 (0.11) | 25.66 | <0.001 |
| Angina | 0.32 (0.04) | 69.05 | <0.001 | −0.03 (0.04) | 0.56 | 0.46 | 1.05 (0.04) | 599.01 | <0.001 | −0.54 (0.06) | 77.93 | <0.001 |
| HTN | 0.26 (0.02) | 121.74 | <0.001 | 0.33 (0.03) | 150.13 | <0.001 | 1.02 (0.03) | 1724.38 | <0.001 | −0.05 (0.04) | 1.87 | 0.18 |
| DM | 0.57 (0.05) | 117.61 | <0.001 | −0.01 (0.05) | 0.01 | 0.94 | 0.75 (0.05) | 252.71 | <0.001 | −0.35 (0.07) | 20.90 | <0.001 |
| CVD | 0.31 (0.02) | 188.36 | <0.001 | 0.23 (0.03) | 75.99 | <0.001 | 1.13 (0.02) | 2137.65 | <0.001 | 0.25 (0.04) | 50.46 | <0.001 |
| Dep | 0.46 (0.03) | 168.67 | <0.001 | 0.31 (0.04) | 65.99 | <0.001 | 0.02 (0.02) | 0.71 | 0.40 | 0.59 (0.06) | 118.36 | <0.001 |
note: BMI=body mass index; HTN=high blood pressure; DM=diabetes mellitus; Dep=depression; CVD=cardiovascular disease (composite of all cardiovascular diseases); SE=standard error;
males=1 females=0- referent group=females
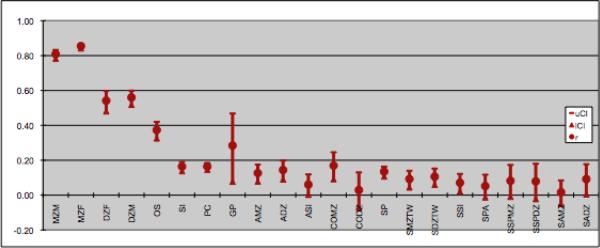
Maximum likelihood estimates of the correlations between relatives are presented in Figure 2. Except for twin correlations, all correlations could be equated across sex within each type of genetic and social relatedness. These correlations showed that twins were more similar than any other familial or social relationships. As expected, MZ twins were the most highly correlated of all relatives. The pattern of correlations was roughly consistent with decreased correlations for decreased level of relatedness. Table 2 shows model fit statistics for the full extended twin-family model and submodels. The full twin model included age regression on BMI fluctuation means. Next, the significance of qualitative and quantitative sex-differences, and age regression was tested. All were significant except for the qualitative sex differences. Additive genetic factors, dominance genetic factors in females, unique and twin environmental factors all contributed significantly to variance of BMI fluctuation.
Figure 2. Correlations between relationships for body mass index fluctuation.
note: mzm=monozygotic male twins; mzf=monozygotic female twins; dzf=dizygotic female twins; dzm=dizygotic male twins; os=opposite sex twins; si=sibling; pc=parent/child; gp=grandparent;; amz= avuncular/monozygotic twin; adz=avuncular/dizygotic twin; asi=avuncular/sibling; comz=cousin/monozygotic twin; codz=cousin/dizygotic twin; sp=spouse; smztw=spouse/monozygotic twin; sdztwin= spouse/dizygotic twin; ssi=spouse/sibling; spa=spouse/parent; sspmz=sibling/spouce monozygotic twin; sspdz=sibling/spouce dizygotic twin; samz=spouce/avuncular monozygotic twin; sadz=spouce/avuncular dizygotic twin
Table 2.
Fit Statistics for the Extended-Twin Family (ETFM) Model with Age moderation for BMI Fluctuation
| Model | df | −2LL | Δ χ 2 | Δdf | p | AIC |
|---|---|---|---|---|---|---|
| 1. Full * | 21838 | 109337.93 | n/a | n/a | n/a | 65661.93 |
| 2. No qualitative sex differences | 21842 | 109345.23 | 7.30 | 4 | 0.12 | 65661.23 |
| 3. No qualitative or quantitative sex differences | 21850 | 109559.09 | 221.16 | 12 | 0.00 | 65859.09 |
| 4. No qualitative sex difference or genetic quantitative sex differences | 21844 | 109364.39 | 24.46 | 6 | 0.00 | 65676.39 |
| 5. No qualitative sex difference or environmental quantitative sex differences | 21848 | 109361.83 | 23.90 | 10 | 0.01 | 65665.83 |
| 6. No qualitative sex difference or cultural transmission quantitative sex differences | 21845 | 109353.40 | 15.47 | 7 | 0.03 | 65664.40 |
| 7. No qualitative sex differences or assortative mating | 21843 | 109423.23 | 85.29 | 5 | 0.00 | 65737.23 |
| 8. No qualitative sex differences or age moderation | 21844 | 110345.04 | 1007.11 | 6 | 0.00 | 66657.04 |
note: BMI=body mass index; AIC=Akaike information Criterion; n/a=not applicable
all models are compared to the full model
Results from the bolded model are presented
The confidence intervals for sex-specific genes, male dominant genetic factors, sibling environment, assortative mating, and cultural transmission contained zero, indicating that these parameters did not contribute significantly to the variance of this phenotype in this study. However, to provide the most comprehensive unbiased results, parameter estimates are presented for the full model even though this was not the most parsimonious model based on AIC. Means, parameter estimates and 95% confidence intervals for the full model are provided in Table 3.
Table 3.
Parameter estimates for the Extended-Twin Family (ETFMM) Model with Age moderation for BMI Fluctuation
| Means | Estimate-Male (95% Confidence Interval) | Estimate-Female (95% Confidence Interval) |
|---|---|---|
| Parents of twins | 3.4 (3.1–3.7) | 4.6 (4.3–4.9) |
| Twins, Spouses, Siblings | 3.1 (2.9–3.3) | 3.5 (3.2–3.7) |
| Children of twins | 3.2 (3.0–3.4) | 4.0 (3.7–4.2) |
| Variance Components | Estimate-Male (95% Confidence Interval) | Estimate-Female (95% Confidence Interval) |
|---|---|---|
| Additive genetic | 0.31 (0.02–0.43) | 0.15 (0.01–0.38) |
| Dominant genetic | 0.01 (0.00–0.22) | 0.29 (0.10–0.41) |
| Sex-specific genetic | 0.02 (0.00–0.28) | Not Applicable |
| Assortative mating | 0.01 (0.00–0.02) | 0.01 (0.00–0.02) |
| Sibling environment | 0.00 (0.00–0.08) | 0.02 (0.00–0.08) |
| Twin environment | 0.22 (0.13–0.32) | 0.15 (0.09–0.22) |
| Unique environment | 0.43 (0.38–0.48) | 0.37 (0.34–0.40) |
| Cultural transmission | 0.01 (0.00–0.02) | 0.02 (0.00–0.06) |
The variance in BMI fluctuation was accounted for more by environmental than genetic factors for males and females (Table 3). For both males and females the largest source of variance was the unique environment, which explained about 40% of the variance. The main source of shared environmental variance of BMI fluctuation was twin environment contributing between 22 and 15% of the variance in males and females, respectively. A small non-significant amount of cultural transmission existed and parameter estimates suggested a positive influence from mothers' phenotype to their daughters' phenotype and a negative influence from fathers' phenotype to their sons' phenotype.
Sex-specific genes accounted only for a very small amount (<2%) of the variance in this phenotype; this indicated that mostly the same genes contributed to the variance of BMI fluctuation in both sexes, but the magnitudes of their effects were different. In males the genetic factors accounted for ~34% of the variance in BMI fluctuation; this was largely due to additive genetic effects. In females, genetic factors accounted for ~43% of the variance in BMI, largely due to dominant genetic effects.
The age regression on the mean values for BMI fluctuation was significant. The β value from the regression coefficient was 5.38 for males and 4.67 for females. As individuals age, BMI variation increased with larger effects in males than females.
Discussion
Previous research has shown that both current BMI (Freedman et al. 2006; Whitlock et al. 2009; Fontaine et al. 2003) and BMI fluctuations (Lissner et al. 1991; Blair et al. 1993; Lee and Paffenbarger 1992; Diaz et al. 2005) are associated with numerous adverse health outcomes. While it is well known that obesity is associated with disease, results from the current study provide more evidence that BMI fluctuation, independent of current BMI was also significantly associated with a variety of cardiovascular disease phenotypes, diabetes, and depression.
The relationships between BMI fluctuation and cardiovascular phenotypes, diabetes, and depression suggests that BMI fluctuation could be a useful predictor of many disorders. Cardiovascular disease phenotypes are all positively associated with BMI fluctuation. This suggests that higher fluctuation in BMI are associated with greater likelihood of suffering from cardiovascular diseases. Similarly, diabetes is positively associated with BMI fluctuation, suggesting that changes in BMI are also associated with increased incidences of diabetes. In addition to BMI fluctuation's association with medical disorders, it is associated with at least one psychiatric phenotype, depression. Higher BMI fluctuation is associated with higher endorsement of depression. This could be due to weight fluctuations (either weight gain or weight loss) during depressive episodes. Therefore, it might be worth assessing individuals with high levels of BMI fluctuation for depression. Further, it is not surprising that current BMI is inversely associated with depression given that depression can be characterized by gain or loss of weight. BMI fluctuation is relatively inexpensive to collect and may provide additional information relevant to health status.
The role of genes and environment in the variance of current BMI has been widely investigated. However, much less is known about their relative contributions to BMI fluctuation, nor, whether the magnitude of the genetic and environmental contributions to variance of current BMI and BMI fluctuation are similar. Results of this study suggested there are some differences in the magnitude of sources contributing to variance in current BMI and BMI fluctuation. There are several possible explanations for these differences.
First, our results suggest that BMI fluctuation has a lower heritability than BMI (Stunkard et al. 1986; Allison et al. 1996; Maes et al. 1997). This suggests that while current BMI is largely influenced by genetic factors which cannot be changed, changing the environment may be exceptionally helpful in reducing BMI fluctuation. If individuals are not fighting against a strong genetic disposition towards a given phenotype, it is potentially easier to prevent the manifestation of a certain phenotype. Results from this study suggest that changing the environment could substantially influence BMI fluctuation. However, it is also possible that there is greater error of measurement in assessing BMI fluctuation than there is in BMI, and this would manifest as greater environmental variation in our analyses. Improving the measurement of BMI fluctuation (such as by measured height and weight at frequent intervals across the lifespan) could help resolve this paradox.
Second, while the same genetic and environmental influences may be responsible for both BMI fluctuation and current BMI, it is also possible that these phenotypes do not share all of these influences. If (partly) different genetic and/or environmental influences are contributing to these phenotypes, this could help explain the differences in magnitude of the contribution of different sources of variation and possibly why current BMI and BMI fluctuation are both predictive of disease risk independently of one another and while controlling for one another.
Third, the motivation to alter current BMI if at either BMI extreme could be environmentally driven. Societal norms and ideals would likely push individuals with low or high BMI values to attempt to alter BMI. However, it is well known that weight change is difficult to maintain (Wing and Phelan 2005). Therefore, individuals may be motivated by environmental factors to alter weight, but have difficulty maintaining these changes, due to their genetic predisposition. This might result in large BMI fluctuations.
Results of this study suggest that unlike current BMI, there is a substantial environmental component to BMI fluctuation. Therefore, altering environmental factors could reduce BMI fluctuation. The current study also suggests that altering BMI fluctuation could thereby reduce adverse health consequences associated with BMI fluctuation. However, additional studies are needed to confirm this notion. In conjunction with what is known about current BMI, results from this study suggest that a balance might need to be reached between reducing current high BMI and reducing large BMI fluctuations. Further studies are needed to evaluate the risk of BMI fluctuation and current high BMI to find the optimal balance to reduce associated disease risk.
There are several limitations to this study. First, all measures were based on self-report and therefore may be subject to recall bias. Inclusion of relatives was based on willingness of twin to provide contact information for relatives in conjunction with relatives' willingness to participate. Questions were “yes”, “no” questions and we do not have in depth information on symptoms of disorders, such as edema, which may have influenced weight. We do not know if participants engaged in weight-cycling nor do we know the reasons for weight change (e.g., disease, such as cancer which has weight loss as a common symptom and anorexia nervosa which has low BMI as a required symptom, or deliberate weight loss), amount of time or number of times spent at the high and low BMIs. The HLS questionnaire only asked about current height. It is possible that individuals were still growing or osteopenic bone loss may have occurred. Therefore height at highest or lowest weight might have been different. However this would likely have affected only a small number of individuals and thus unlikely to influence our results substantially. Second, the presence of dominance in this design is confounded with age-specific genetic effects or gene by age interaction(s) and interactions between the causes of intergenerational resemblance and secular trends. Methodological limitations prevented age moderation of variance components, however when the sample was divided into twins who were 55 years and above and below 55 years results were consistent with those from the full sample.
Conclusion
Since there are substantial health risks associated with BMI fluctuation and environmental components of BMI fluctuation account for over 60% of variance in males and over 50% of variance in females, environmental risk factors may be appropriate targets to reduce BMI fluctuation.
Acknowledgements
Dr. Dellava was supported by T32MH20030 (PI: Michael C. Neale) and 5R37DA018673 (PI: Michael C. Neale). Data collection and model development was supported by Grants GM-30250, AG-04954, AA-06781, MH-40828, and HL-48148 from the National Institutes of Health and a gift from RJR Nabisco. We would like to thank all the participants who made this research possible.
References
- Field AE, Coakley EH, Must A, Spadano JL, Laird N, Dietz WH, Rimm E, Colditz GA. Impact of overweight on the risk of developing common chronic diseases during a 10-year period. Arch Intern Med. 2001;161(13):1581–1586. doi: 10.1001/archinte.161.13.1581. [DOI] [PubMed] [Google Scholar]
- Seidell JC, Hautvast JG, Deurenberg P. Overweight: fat distribution and health risks. Epidemiological observations. A review. Infusionstherapie. 1989;16(6):276–281. doi: 10.1159/000222401. [DOI] [PubMed] [Google Scholar]
- Reis JP, Macera CA, Araneta MR, Lindsay SP, Marshall SJ, Wingard DL. Comparison of Overall Obesity and Body Fat Distribution in Predicting Risk of Mortality. Obesity (Silver Spring) 2009 doi: 10.1038/oby.2008.664. [DOI] [PubMed] [Google Scholar]
- Freedman DM, Ron E, Ballard-Barbash R, Doody MM, Linet MS. Body mass index and all-cause mortality in a nationwide US cohort. Int J Obes (Lond) 2006;30(5):822–829. doi: 10.1038/sj.ijo.0803193. [DOI] [PubMed] [Google Scholar]
- Freedman DM, Ron E, Ballard-Barbash R, Doody MM, Linet MS. Body mass index and all-cause mortality in a nationwide US cohort. Int J Obes (Lond) 2006 doi: 10.1038/sj.ijo.0803193. [DOI] [PubMed] [Google Scholar]
- Neovius M, Sundstrom J, Rasmussen F. Combined effects of overweight and smoking in late adolescence on subsequent mortality: nationwide cohort study. BMJ. 2009;338(feb24_2):b496. doi: 10.1136/bmj.b496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarnell JW, Patterson CC, Thomas HF, Sweetnam PM. Comparison of weight in middle age, weight at 18 years, and weight change between, in predicting subsequent 14 year mortality and coronary events: Caerphilly Prospective Study. J Epidemiol Community Health. 2000;54(5):344–348. doi: 10.1136/jech.54.5.344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein EA, DiBonaventura M, Burgess SM, Hale BC. The costs of obesity in the workplace. J Occup Environ Med. 2010;52(10):971–976. doi: 10.1097/JOM.0b013e3181f274d2. [DOI] [PubMed] [Google Scholar]
- Lightwood J, Bibbins-Domingo K, Coxson P, Wang YC, Williams L, Goldman L. Forecasting the future economic burden of current adolescent overweight: an estimate of the coronary heart disease policy model. Am J Public Health. 2009;99(12):2230–2237. doi: 10.2105/AJPH.2008.152595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwimmer JB, Burwinkle TM, Varni JW. Health-related quality of life of severely obese children and adolescents. Jama. 2003;289(14):1813–1819. doi: 10.1001/jama.289.14.1813. [DOI] [PubMed] [Google Scholar]
- Jeffery RW, Drewnowski A, Epstein LH, Stunkard AJ, Wilson GT, Wing RR, Hill DR. Long-term maintenance of weight loss: current status. Health Psychol. 2000;19(1 Suppl):5–16. doi: 10.1037/0278-6133.19.suppl1.5. [DOI] [PubMed] [Google Scholar]
- Wing RR, Phelan S. Long-term weight loss maintenance. Am J Clin Nutr. 2005;82(1 Suppl):222S–225S. doi: 10.1093/ajcn/82.1.222S. [DOI] [PubMed] [Google Scholar]
- Lissner L, Odell PM, D'Agostino RB, Stokes J, 3rd, Kreger BE, Belanger AJ, Brownell KD. Variability of body weight and health outcomes in the Framingham population. N Engl J Med. 1991;324(26):1839–1844. doi: 10.1056/NEJM199106273242602. [DOI] [PubMed] [Google Scholar]
- Blair SN, Shaten J, Brownell K, Collins G, Lissner L. Body weight change, all-cause mortality, and cause-specific mortality in the Multiple Risk Factor Intervention Trial. Ann Intern Med. 1993;119(7 Pt 2):749–757. doi: 10.7326/0003-4819-119-7_part_2-199310011-00024. [DOI] [PubMed] [Google Scholar]
- Lee IM, Paffenbarger RS., Jr. Change in body weight and longevity. Jama. 1992;268(15):2045–2049. [PubMed] [Google Scholar]
- Diaz VA, Mainous AG, 3rd, Everett CJ. The association between weight fluctuation and mortality: results from a population-based cohort study. J Community Health. 2005;30(3):153–165. doi: 10.1007/s10900-004-1955-1. [DOI] [PubMed] [Google Scholar]
- Zhang H, Tamakoshi K, Yatsuya H, Murata C, Wada K, Otsuka R, Nagasawa N, Ishikawa M, Sugiura K, Matsushita K, Hori Y, Kondo T, Toyoshima H. Long-term body weight fluctuation is associated with metabolic syndrome independent of current body mass index among Japanese men. Circ J. 2005;69(1):13–18. doi: 10.1253/circj.69.13. [DOI] [PubMed] [Google Scholar]
- Truett K, Eaves L, Walters E, Heath A, Hewitt J, Meyer J, Silberg J, Neale M, Martin N, Kendler K. A model system for analysis of family resemblance in extended kinships of twins. Behav Genet. 1994:2435–49. doi: 10.1007/BF01067927. [DOI] [PubMed] [Google Scholar]
- Maes HH, Neale MC, Kendler KS, Martin NG, Heath AC, Eaves LJ. Genetic and cultural transmission of smoking initiation: an extended twin kinship model. Behav Genet. 2006;36(6):795–808. doi: 10.1007/s10519-006-9085-4. [DOI] [PubMed] [Google Scholar]
- Eaves LJ, Eysenck HJ, Martin NG. Genes, Culture and Personality: Am Empirical Approach. Oxford University Press; London: 1989. [Google Scholar]
- SAS Institute Inc . SAS/STAT® Software: Version 9. SAS Institute, Inc; Cary, NC: 2004. [Google Scholar]
- Keller MC, Medland SE, Duncan LE, Hatemi PK, Neale MC, Maes HH, Eaves LJ. Modeling extended twin family data I: description of the Cascade model. Twin Res Hum Genet. 2009;12(1):8–18. doi: 10.1375/twin.12.1.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maes HH, Neale MC, Medland SE, Keller MC, Martin NG, Heath AC, Eaves LJ. Flexible Mx specification of various extended twin kinship designs. Twin Res Hum Genet. 2009;12(1):26–34. doi: 10.1375/twin.12.1.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale M, Cardon L. Methodology for Genetic Studies of Twins and Families. Kluwer Academic Publishers. B.V.; Dordrecht, The Netherlands: 1992. [Google Scholar]
- Neale M, Maes H. Methodology for Genetic Studies of Twins and Families. Kluwer Academic Publishers. B.V.; Dordrecht, The Netherlands: 1998. [Google Scholar]
- R Development Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2010. [Google Scholar]
- Boker S, Neale MC, Maes HH, Wilde M, Spiegel M, Brick T, Spies J, Estabrook R, Kenny S, Bates T, Mehta P, Fox J. OpenMx: An Open Source Extended Structural Equation Modeling Framework. Psychometrika. 2011;76(2):306–317. doi: 10.1007/s11336-010-9200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock G, Lewington S, Sherliker P, Clarke R, Emberson J, Halsey J, Qizilbash N, Collins R, Peto R. Body-mass index and cause-specific mortality in 900 000 adults: collaborative analyses of 57 prospective studies. Lancet. 2009;373(9669):1083–1096. doi: 10.1016/S0140-6736(09)60318-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontaine KR, Redden DT, Wang C, Westfall AO, Allison DB. Years of life lost due to obesity. Jama. 2003;289(2):187–193. doi: 10.1001/jama.289.2.187. [DOI] [PubMed] [Google Scholar]
- Stunkard AJ, Foch TT, Hrubec Z. A twin study of human obesity. Jama. 1986;256(1):51–54. [PubMed] [Google Scholar]
- Allison DB, Kaprio J, Korkeila M, Koskenvuo M, Neale MC, Hayakawa K. The heritability of body mass index among an international sample of monozygotic twins reared apart. Int J Obes Relat Metab Disord. 1996;20(6):501–506. [PubMed] [Google Scholar]
- Maes HH, Neale MC, Eaves LJ. Genetic and environmental factors in relative body weight and human adiposity. Behav Genet. 1997;27(4):325–351. doi: 10.1023/a:1025635913927. [DOI] [PubMed] [Google Scholar]