Structure and Dynamics of the Aβ_21–30 Peptide from the Interplay of NMR Experiments and Molecular Simulations

Abstract

We combine molecular dynamics simulations and new high-field NMR experiments to describe the solution structure of the Aβ_21–30 peptide fragment that may be relevant for understanding structural mechanisms related to Alzheimer’s disease. By using two different empirical force-field combinations, we provide predictions of the three-bond scalar coupling constants (³J_H^NH^α), chemical-shift values, ¹³C relaxation parameters, and rotating-frame nuclear Overhauser effect spectroscopy (ROESY) crosspeaks that can then be compared directly to the same observables measured in the corresponding NMR experiment of Aβ_21–30. We find robust prediction of the ¹³C relaxation parameters and medium-range ROESY crosspeaks by using new generation TIP4P-Ew water and Amber ff99SB protein force fields, in which the NMR validates that the simulation yields both a structurally and dynamically correct ensemble over the entire Aβ_21–30 peptide. Analysis of the simulated ensemble shows that all medium-range ROE restraints are not satisfied simultaneously and demonstrates the structural diversity of the Aβ_21–30 conformations more completely than when determined from the experimental medium-range ROE restraints alone. We find that the structural ensemble of the Aβ_21–30 peptide involves a majority population (~60%) of unstructured conformers, lacking any secondary structure or persistent hydrogen-bonding networks. However, the remaining minority population contains a substantial percentage of conformers with a β-turn centered at Val24 and Gly25, as well as evidence of the Asp23 to Lys28 salt bridge important to the fibril structure. This study sets the stage for robust theoretical work on Aβ_1–40 and Aβ_1–42, for which collection of detailed NMR data on the monomer will be more challenging because of aggregation and fibril formation on experimental timescales at physiological conditions. In addition, we believe that the interplay of modern molecular simulation and high-quality NMR experiments has reached a fruitful stage for characterizing structural ensembles of disordered peptides and proteins in general.

Introduction

The amyloid β (Aβ) peptide, comprised of a family of 39–42 residue long fragments cleaved by proteolysis of the APP protein, is the major species in amyloid fibril plaque found in the brain of patients with Alzheimer’s disease (AD).^1,2 However, recent evidence suggests that it may be the prefibrillar monomer and oligomeric states of the Aβ peptides, as opposed to the actual fibril plaque,³ that give rise to the cytotoxicity of the Alzheimer’s disease state.^4–9 Therefore, knowledge of the structural ensembles of the Aβ peptide on the aggregation pathways from monomer to fibril is critical for understanding aggregation outcomes in vitro, with the hope of potentially changing the course of the disease in vivo.

Although significant progress has been made in the characterization of highly ordered amyloid fibril structures of Aβ peptides under physiological conditions,^3,10–14 the aqueous monomeric form is difficult to study by standard structural biology techniques because of its propensity to sequester into these ordered fibril assemblies. Although recent studies by NMR spectroscopy have found some regular structure in the Aβ_1–40 and Aβ_1–42 monomer peptides in high concentrations of non-aqueous solvents (hexafluoroisopropanol, trifluroethanol, and SDS micelles),^15–18 these may or may not be relevant to the correct physiological conditions. Other studies have calculated simple population averaged quantities, such as scalar coupling constants¹⁹ and spin relaxation constants^20,21 for aqueous solution ensembles of the peptide, but these data measure only local rather than tertiary structure and hence provide an incomplete description of the structural ensemble.

In an attempt to probe for any significant structure in the monomeric state by an alternative technique, Lazo et al. subjected the Aβ_1–40 and Aβ_1–42 peptides to digestion by multiple proteases.²² Despite containing a large number of potential proteolytic sites throughout the sequence, the peptide fragment spanning residues 21–30 (AEDVGSNKGA) was found to be a significant product for each enzyme, indicating relative resistance to cleavage. Furthermore, little digestion was seen when the synthetic Aβ_21–30 fragment itself was subjected to the same protease conditions. These results were interpreted to mean that some structure in the 21–30 region protects Aβ_1–40 and Aβ_1–42 from protease degradation, and that this structure is retained in the Aβ_21–30 fragment.²²

One of the primary benefits of studying this small zwitterionic peptide fragment is that it is readily soluble in its monomeric form at concentrations in which the longer and more hydrophobic Aβ_1–40 and Aβ_1–42 sequences aggregate. In addition, many of the amino acids thought to be important for understanding the AD state are part of the Aβ_21–30 fragment. The Aβ_21–30 sequence consists mainly of a hydrophilic region that, in the context of the fibril structure of the full-length Aβ_1–40, comprises a turn connecting the two flanking hydrophobic β-strand regions that is necessary for generating the observed cross-β structure down the fibril axis.¹¹ Additionally, the buried salt bridge between Asp23 and Lys28 in the fibrillar form, determined by solid-state NMR,^11,13,23 is also encompassed by this peptide. It has been shown that mutating either residue dramatically affects fibril formation.^23,24 It is also noteworthy that many of the familial associated disease (FAD) mutants of the APP protein are located between residues 21 and 23, each of which leads to dramatically different in vitro fibril formation properties²⁵ and in vivo clinical outcomes.^24,26–34

A number of experimental and computational studies have attempted to determine what stable structure in the Aβ_21–30 monomer accounts for its protease resistance. Teplow and co-workers studied the wild-type²² as well as five FAD mutants³⁵ of the Aβ_21–30 peptide by using rotating-frame nuclear Overhauser effect spectroscopy (ROESY) NMR experiments. They proposed that WT Aβ_21–30 folds into a single conformer corresponding to a unique bend structure, identified through long-range (i,i+8) crosspeaks for Glu22 H_α to Ala30 HN, and (i,i+6) side chain–side chain crosspeaks for Glu22 to Lys28 in the ROESY spectrum of WT Aβ_21–30; these crosspeaks were found to be absent in many of the FAD mutants.³⁵ Replica exchange molecular dynamics simulations by Baumketner et al. by using the OPLS and TIP3P all-atom models for peptide and water,³⁶ showed that 40% of the peptide ensemble is folded into two distinct bend structures stabilized primarily by Asp23 side-chain interactions with the Ser26 side chain and backbone. Borreguero and co-workers studied the peptide by a coarse-grained model in which they find collapsed structures stabilized by hydrophobic interactions between Val24 and Lys28, as well as electrostatic interactions between Asp23 and Lys28.³⁷ They also simulated five ~100 ns molecular dynamics trajectories by using CHARMM-27 and TIP3P for the peptide and water model, without using any accelerated sampling technique, each with a different combination of density, starting structure, and salt concentration.³⁸ Though the authors acknowledge that their simulations are far too short to converge to the equilibrium ensemble, they report contacts between hydrophobic regions of Val24 and Lys28 that are more stable on the nanosecond time scale than charged interactions between Lys28 and Glu22 or Asp23. Finally, Mousseau, Derreumaux and co-workers used an activation–relaxation sampling technique combined with the OPEP coarse-grained model of Aβ_21–30 and found several clusters of structures, all sharing a turn formed by stabilizing interactions between Val24 and Lys28 of many different side-chain contact combinations.³⁹ In summary, simulations found little evidence of the long-range interactions observed in the NMR experiment but provided little consensus on the solution structure of the Aβ_21–30 peptide.

In this study, we present new NMR experimental measurements on the aqueous Aβ_21–30 peptide fragment, including three-bond scalar coupling constants (³J_H^NH^α), chemical-shift values, ¹³C relaxation parameters, and ROESY spectra measured at 800 and 900 MHz. We determine that although there are a handful of medium-range ROEs, no long-range (i,i + 8) or (i,i + 6) crosspeaks are present, nor are there patterns of α-helical or β-sheet contacts, indicating that the structural ensemble for the Aβ_21–30 fragment is highly diverse. We quantify this structural diversity of Aβ_21–30 by molecular dynamics simulations by using two different water models, which are validated by calculating the same NMR observables from demonstrably converged equilibrium structural and dynamical ensembles. We find that the Amber ff99SB⁴⁰ protein and TIP4P-Ew⁴¹ water models provide robust prediction of the measured ¹³C relaxation parameters and ROESY crosspeaks in particular, indicating that they yield both a structurally and dynamically correct ensemble over the entire Aβ_21–30 peptide.

The interplay of the high-quality NMR experiments and the validated theoretical model allows us to analyze the simulated structural ensemble and show that the medium-range ROE interactions are not satisfied simultaneously. In fact, they arise from separate structural populations of local turn structure in regions 23–27 and 27–30 that together comprise only ~40% of the total equilibrium ensemble and thus provide a qualitatively different result from the single structural model reported by Lazo and co-workers.^22,35 The very good quality of results of this validation study on Aβ_21–30 paves the way for simulating the structural ensemble of the Aβ_1–40 and Aβ_1–42 systems, because solution NMR experiments on these peptides are inherently more difficult because of peptide aggregation. Furthermore, we believe that this study shows that the interplay of modern molecular simulation and high-quality NMR experiments has reached a fruitful stage for characterizing structural ensembles of disordered peptides and proteins in general.

Methods

NMR Experiments

The Aβ_21–30 peptide (AEDVGSNKGA) was synthesized (Anaspec, San Jose, CA) and purified to 98% purity by reverse-phase HPLC. NMR samples contained 10 mM Aβ_21–30 and 25 mM ammonium d₄-acetate in 90% H₂O/10% ²H₂O or 100% ²H₂O. The solution pH was adjusted to 6.0 with 20 µL 1 M NaOH. NMR data were collected at 283 K on a Bruker Avance 500 MHz and Bruker Avance II 800 or 900 MHz spectrometers. All data were processed with NMRPipe⁴² and analyzed with NMRView⁴³ and CARA.⁴⁴> All spectra were recorded at 10 °C to facilitate comparison with previous NMR studies on this peptide.

Chemical shift assignments were obtained with a 2D ¹H–¹H TOCSY. Distance restraints were obtained from two 2D ¹H–¹H ROESY experiments in both 90% H₂O/10% ²H₂O and 100% ²H₂O with a composite pulse spinlock⁴⁵ applied during the 300 ms mixing time. Additional H₂O ROESY spectra were also collected with 200 and 400 ms mixing times but were not used to generate distance restraints. A total of 4096 and 1400 points (States-TPPI) was collected in t₂ and t₁, respectively. Spectral widths in both dimensions were 7184 and 8503 Hz on the 800 and 900 MHz spectrometers, respectively.

To build a single structural model fitting all of the data simultaneously by using a standard NMR structure determination approach, ROESY crosspeaks were classified as strong, medium, weak, and very weak on the basis of peak intensity and converted to 2.9, 3.3, 5.0, and 6.0 Å upper distance restraints, respectively. The set of 155 manually assigned distant restraints was used to calculate 1000 structures with the program CYANA.⁴⁶ The 50 lowest-energy structures of the minimized ensemble were analyzed with the program Pymol.⁴⁷ Structural statistics and hydrogen bonds present in the structure ensemble, detected with the Amber suite⁴⁸ program ptraj, are presented in the Results section.

Spin–lattice (T₁) and spin–spin (T₂) relaxation times for natural abundance ¹³C at the C_α position were measured for all nonglycine amino acids by using the same 100% ²H₂O sample described above. T₁ was measured at 500 MHz by inverse-detected inversion–recovery with delay times 5, 25, 50, 150, 400, 600, 1000, 2000, and 2500 ms.⁴⁹ T₂ was measured at 600 MHz by an inverse-detected CPMG experiment with delay times 0, 20.48, 40.96, 61.44, 82.92, 122.88, 143.36, 163.84, and 204.8 ms.⁴⁹ Relaxation parameters were fit from the data as described previously.⁴⁹

Three-bond scalar coupling constants ³J_H^NH^α were measured from the multiplet structure in a 2D double-quantum filtered COSY measured at 500 MHz with a spectral width of 6127 Hz in both dimensions. To ensure that the experimental line shape was not adversely affected by limited digital resolution, 4096 points were collected in both t₁ and t₂. Quadrature detection in t₁ was obtained according to the States-TPPI method, and the digital resolution was matched to t₂ with linear prediction.

Simulation Protocol

We represent the zwitterionic Aβ_21–30 peptide by using the Amber ff99SB fixed-charge empirical force field.⁴⁰ Amber ff99SB is a recent reparameterization of the backbone dihedral angles of proteins by Simmerling and co-workers to correct previous problems with secondary structure propensities of the original ff99 parameters. Amber ff99SB quantitatively captures the distribution of backbone ϕ/ψ angles compared with quantum mechanical calculations and validation on model peptide and protein systems. We have chosen to run two separate sets of simulations, where we solvate the peptide with TIP3P⁵⁰ and TIP4P-Ew⁴¹ water models, respectively. TIP3P is an older water model that is popularly used in aqueous protein simulations, whereas TIP4P-Ew is a newer reparameterized version of the standard TIP4P water model for use with Ewald summation techniques. We chose TIP4P-Ew as the alternate water model because it reproduces many salient thermodynamic and dynamic features of bulk water properties when compared with experiment,⁴¹ and its excellent performance for temperature trends of these properties is especially relevant for this experimental study which is conducted at 10 °C.

In this work, we use the AMBER9 molecular dynamics simulation package⁴⁸ to generate the structural and dynamical ensembles of Aβ_21–30 peptide fragment in water. The system is prepared by solvating the Aβ_21–30 structure with 1578 TIP3P or 1579 TIP4P-Ew water molecules. A single sodium (Na⁺) ion is included in the system to balance the peptide net charge. Each system is briefly equilibrated by using Andersen thermostats⁵¹ to bring the system up to 300 K, then equilibrated for 125 ps at constant pressure with Berendsen (weak) coupling at 1 bar (default parameters) and 300K temperature to determine the density. The average density of the last 100 ps of the constant pressure simulation is then calculated, and a snapshot containing position and velocity information with that density (within 0.001 g/cm³) is selected as the starting structure for further equilibration in the NVT ensemble. In all simulations, the equations of motion are integrated with 1 fs time steps, the long-range electrostatic interactions are calculated by using Particle Mesh Ewald method,⁵² and a cutoff of 9.0 Å is used for real space electrostatics and Lennard-Jones interactions.

We use replica exchange^53,54 through the sander module of Amber9 to improve convergence at the lower temperatures, by using 64 temperature replicas exponentially spaced between 270 and 507 K with exchange attempts every 1 ps. We ran two independent replica exchange simulations for a time between 45 and 50 ns per replica, of which the first 20 ns of each replica is treated as equilibration. The second replica exchange simulation was started from configurations acquired after 20 ns equilibration in the first replica exchange simulation but by using a new set of randomized velocities. We measure convergence to equilibrium of the two independent simulations by whether they both reach the same linear average of the pair distances over their structural ensembles. We find that the equilibrium populations of the two independent runs differ by no more than 7% in this quantity. We comment later on the challenge of converging these averages and their effect on the predictions of NMR observables in the Results section.

We also ran microcanonical ensemble (NVE) trajectories to measure dynamical quantities because coupling to a thermal bath, especially by the Andersen or Langevin thermostats provided in the AMBER codes, can perturb system dynamics. For each peptide–water model combination, we ran 30 NVE trajectories of 20 ns in length. Starting structures for these trajectories were selected from the 284 K replica of each water model, separated by 1 ns of replica exchange simulation to ensure structural decorrelation. Because only coordinate information (not velocity) was saved for the structural ensemble, structures were equilibrated at 284 K for 100 ps prior to the 20 ns constant energy runs.

We use the ptraj module of AMBER to analyze the DSSP defined secondary structure,⁵⁵ hydrogen bonds, and electrostatic/saltbridge interactions over the generated structural ensembles. We specify all possible donors and acceptors for the hydrogen bonds in our analysis. Default parameters are used for both hydrogen bond detection and DSSP in ptraj.

Simulation of NMR Experimental Observables

By using the SHIFTS^56–58 and SHIFTX⁵⁹ programs, we predict the chemical shifts for all protons and C_α and C_β carbon atoms by averaging these quantities over the members of the Boltzmann weighted simulation ensemble. The chemical shifts were also calculated on a population of unstructured conformations, defined as such if DSSP⁵⁵ did not identify any secondary structure category for any of the 10 residues.

We also calculate the predicted scalar coupling constants ³J_H^NH^α by evaluating the ϕ dihedral angle for each member of the ensemble, calculating the instantaneous scalar coupling constant using the Karplus equation⁶⁰

$$J(\phi )=A{\text{cos}}^2(\phi -60)+B\text{cos}(\phi -60)+C$$ (1)

and collecting the average and standard deviation for ³J_H^NH^α for each residue. We used two types of parameter sets for A, B, and C in eq 1. The first type corresponds to fits of the Karplus equation by using experimentally measured scalar coupling constants and a known reference protein structure; we explore the parameter set for ³J_H^NH^α given by Vuister and Bax where A = 6.51, B = −1.76, and C = 1.60,⁶¹ although other choices are possible.^62–64 In fact, it has been shown that variations between different Karplus parametrizations of eq 1 likely reflect differences in the average dihedral fluctuations about the reference equilibrium folded structure.^62,64 Thus, it is possible that if such parameters are used to generate 〈J〉 over the simulated ensembles, there will be a double counting of such motions. We thus also considered a second parameter set in which a harmonic approximation to this dynamical motion has been removed, where A = 9.5, B = −1.4, and C = 0.30.⁶²

To calculate the spectral density functions for ¹H–¹H spin pairs to predict ROESY data and for ¹³C–¹H pairs to predict the relaxation parameters (T₁ and T₂), we follow the method of Peter et al.⁶⁵ in evaluating the following normalized time correlation function

$$C(\tau )={\langle \frac{1}{r^6(t)}\rangle }^{-1}\langle \frac{P_2(\text{cos}{\chi }_{t,t+\tau })}{r^3(t)r^3(t+\tau )}\rangle$$ (2)

where P₂ is the second-order Legendre polynomial, χ is the angle between the interspin vector in the laboratory reference frame connecting each of the ~1800 pairs of protons as well as the bonded C_α–H_α pairs at time t and t + dτ, r(t) is the instantaneous pair distance, and the angle brackets denote a thermal average. We averaged over 30 independent constant energy (NVE) trajectories at 284 K in evaluation of eq 2, for correlation times τ up to 5 ns. We believe that using many trajectories run in parallel and launched with different representative members of the Boltzmann distribution of peptide conformations, is preferable to a single long trajectory in the NVE ensemble, because it will not exhibit a canonical structural ensemble. Averaging multiple trajectories, each with a slightly different total energy, also has the minor added benefit of sampling the energy distribution of the canonical ensemble despite using constant energy trajectories. It is important to note that we unnormalized eq 2 by the 1/r⁶ average spin–spin distance in each trajectory in order to compute the average over trajectories.

Each resulting average numerical correlation function for a given atom pair is then fit to a triple-exponential form by using a shell script invoking the fit routine in Gnuplot. A triple-exponential form was selected because multiple relaxation modes with different time scales invariably exist for a peptide. In our case, a very fast (<1 ps) mode due to vibration and libration exists, as well as several reorientational modes arising from anisotropic tumbling due to the nonspherical shape of the peptide. Using a four-exponential form did not show substantially different fits for a test group of data and hence was not used. In some pair cases, only two exponentials were required, although three-exponential fits were typical.

The fitted time correlation function is then Fourier-transformed to define the spectral density functions

$$J(\omega )={\displaystyle \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}}C(\tau ){\mathrm{e}}^{i\omega \tau }\mathrm{d}\tau$$ (3)

where we use the following convention for the Fourier transform of an exponential

$${\displaystyle \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}}{\mathrm{e}}^{-\tau /b}{\mathrm{e}}^{i\omega \tau }\mathrm{d}\tau =\frac{2b}{1+{\omega }^2{b}^2}$$ (3a)

and the appropriately chosen constant factors in eqs 3d–4c. We note that the peptide tumbles and locally reorients rapidly enough for all relevant spin–spin vector time correlation functions to approach zero within the time of our 20 ns dynamics simulations.

The quantities in eqs 2 and 3 allow us to define the T₁ and T₂ relaxations at the relevant ¹H and ¹³C Larmor frequencies.⁴⁹ T₁ is defined as the inverse of the spin–lattice relaxation rate

$$R_1=\frac{1}{T_1}={R_1}^{\text{DD}}+{R_1}^{\text{CSA}}$$ (3b)

where R₁^DD and R₁^CSA are the dipolar and chemical shift anisotropy (CSA) components of the spin–lattice relaxation-rate constants, respectively. T₂ is defined as the inverse of the spin–spin relaxation rate

$$R_2=\frac{1}{T_2}={R_2}^{\text{DD}}+{R_2}^{\text{CSA}}+R_{\mathrm{a}}$$ (3c)

where R₂^DD and R₂^CSA are the dipolar and CSA components of the spin–spin relaxation-rate constants, respectively, and R_a is the sum of the relaxation-rate constants for pseudofirst-order processes, such as chemical exchange and diffusion, which we ignore for this analysis. The dipolar relaxation rates

$${R_1}^{\text{DD}}=(1/20)K^2[J({\omega }_{\mathrm{H}}-{\omega }_{\mathrm{C}})+3J({\omega }_{\mathrm{C}})+6J({\omega }_{\mathrm{H}}+{\omega }_{\mathrm{C}})]$$ (3d)

$${R_2}^{\text{DD}}=(1/40)K^2[4J(0)+J({\omega }_{\mathrm{H}}-{\omega }_{\mathrm{C}})+3J({\omega }_{\mathrm{C}})+3J({\omega }_{\mathrm{H}})+6J({\omega }_{\mathrm{H}}+{\omega }_{\mathrm{C}})]$$ (3e)

are the main contributors to the overall relaxation. The constant factor K is defined as

$$K=\frac{{\mu }_0}{4\pi r_{\text{eff}}}\hslash {\gamma }_{\mathrm{a}}{\gamma }_{\mathrm{b}}$$ (3f)

where μ₀ is the permeability of free space, ℏ is Planck’s constant, and γ_a and γ_b are the gyromagnetic ratios for the nuclei of interest, for which the ¹³C relaxation experiment are carbon and hydrogen, and r_eff

$$r_{\text{eff}}={\langle \frac{1}{r^6(t)}\rangle }^{-1/6}$$ (3g)

is the appropriately averaged internuclear distance between atoms.

The chemical-shift anisotropy contributions to the spin–lattice and spin–spin relaxation rates are incorporated in our T₁ and T₂ predictions by assuming an axially symmetric chemical-shift tensor with chemical-shift tensor parallel and perpendicular component difference, Δδ, equal to 25 ppm.⁴⁹

$${R_1}^{\text{CSA}}=(1/5)\mathrm{\Delta }{\delta }^2{\omega }_{\mathrm{C}}^{2}J({\omega }_{\mathrm{C}})$$ (3h)

$${R_2}^{\text{CSA}}=(1/5)(\mathrm{\Delta }{\delta }^2{\omega }_{\mathrm{C}}^2/6)[4J(0)+3J({\omega }_{\mathrm{C}})]$$ (3i)

We can explicitly calculate the full time correlation functions and analytically Fourier transform these fits and, hence, do not need to fit our spectral density functions through a Lipari-Szabo model-free analysis,^66,67 which has limited applicability when the system of interest lacks the separation of internal and external motion timescales, as is the case for Aβ_21–30. In order to compare our simulated T₁ and T₂ relaxation times to the experiment performed in ²H₂O, we scale our time correlation functions by a factor of 1.2 as a simple approximation for the larger viscosity of ²H₂O compared to H₂O at 10 °C.

We also predict the ROESY spectra from our structural ensemble and dynamical trajectories by calculating the intensity

$$I(t_{\text{mix}})=X{\mathrm{e}}^{-\mathrm{\Lambda }{t}_{\text{mix}}}{X}^{-1}I(0)$$ (4a)

where X and Λ are the eigenvectors and eigenvalues of the full relaxation matrix, R, composed of the diagonal elements

$${\rho }_{\mathit{\text{ii}}}={\displaystyle \sum _{j=1,\ne i}^n}\frac{1}{10}{K}^2\left[\frac{3}{2}{J}_{\mathit{\text{ij}}}(2{\omega }_0)+\frac{9}{4}{J}_{\mathit{\text{ij}}}({\omega }_0)+\frac{5}{4}{J}_{\mathit{\text{ij}}}(0)\right]$$ (4b)

and off-diagonal elements

$${\sigma }_{\mathit{\text{ij}}}=\frac{1}{10}{K}^2\left[\frac{3}{2}{J}_{\mathit{\text{ij}}}({\omega }_0)+J_{\mathit{\text{ij}}}(0)\right]$$ (4c)

where ρ is the direct dipolar relaxation rate and σ is the cross-relaxation rate for all proton pairs as described by van Gunsteren and co-workers.^65,68 K is defined as above, with γ_aγ_b equal to γ_H². Unlike the extended atom model (no aliphatic hydrogens) of these previous studies, we simulate all hydrogen atoms explicitly for each methyl group and hence calculate all pair correlation functions, including neighboring methylene and methyl group protons. We ignore water proton coordinates as is the standard assumption in NMR experiments.

We solve this coupled system of differential equations for the magnetization matrix at the mixing time used by the NMR experiments for both H₂O and ²H₂O. We simulate the experimental conditions of heavy water solvation on the relaxation matrix by removing the exchangeable hydrogens including backbone amides (HN), hydrogens in basic NH₃⁺ groups, and hydroxyl hydrogens (HO) from the spin matrix which we accomplished by setting all pair distances with these protons to 30 Å. In order to generate peak predictions, we sum the peak volume contributions (including positive contributions from crosspeaks dominated by spin diffusion) for degenerate spins (methyl groups) as well as those from spins within the same residue that are indistinguishable at the resolution of our NMR experiments. We note that this method explicitly accounts for peak intensity effects caused by methyl group rotation because spectral density functions are calculated for each proton in a methyl group, and the individual intensities from indistinguishable peaks are summed to compare to experimental spectra. Amine peak volumes in the H₂O spectra are scaled by a factor of 0.9 to approximately account for the presence of 10% deuterium exchanged amide protons from the 10% ²H₂O used for NMR lock. Predicted crosspeaks to basic amine and hydroxyl groups are filtered from the predictions because these crosspeaks would be significantly broadened by exchange with solvent protons on the NMR time scale.

In order to directly compare simulations to experiment, we must determine the constant relating the arbitrary experimental crosspeak intensity scale to the simulated intensities for diagonal magnetization of unity at mixing time of 0 ms. This is especially important because the experimental noise level must be determined to evaluate the ability of the predictions to separate observed and unobserved peaks. The constant relating the simulation and experimental scales is calculated by determining the slope of least-squares fit line (constrained to pass through the origin)⁶⁹ for the experimental intensities versus simulated crosspeak volumes of all crosspeaks for all distinguishable pairs separated by four or more bonds, including all long-range, medium-range, and sequential peaks, as well as distant intraresidue pairs. We eliminate crosspeaks between pairs separated by fewer bonds because they are subject to significant TOCSY intensity contributions, evident from line shape distortion. All remaining experimental crosspeak intensities (peak height) are assumed to be proportional to the volume, which assumes no significant line shape distortion. This procedure was repeated for the two water model simulations and for the two experimental solvation conditions (H₂O and ²H₂O). The derived constant, multiplied by the weakest experimentally assigned peak intensity for the appropriate H₂O and ²H₂O experiment, then provides an estimate of the noise level in the simulation. In the Results section, the simulated and experimental intensities are now comparable as a multiplicative factor of the noise.

Results

Chemical Shifts

A robust chemical-shift calculation must describe the anisotropic shielding of the applied magnetic field for the given atom, a quantity that depends sensitively on the local electronic-structure environment. Even for folded proteins with a dominant native conformer, each atom type can exist in many different local environments, making an accurate calculation of chemical shifts for a protein quite a challenge. This problem is exacerbated in the case of disordered proteins that have a far greater diversity of conformations and hence environments; hence, empirical chemical-shift packages that perform well for globular proteins such as SHIFTS^56–58 and SHIFTX⁵⁹ may inadequately predict chemical shifts of disordered proteins.

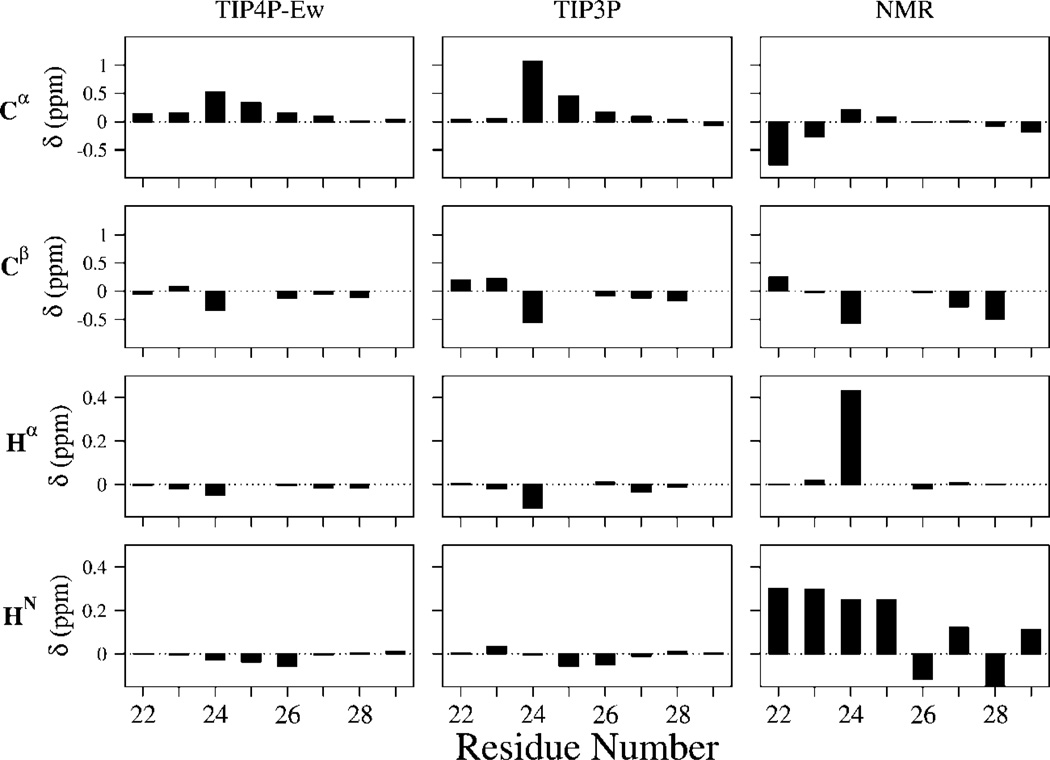
In Figure 1, we show the C_α, C_β, H_α, and H_N experimental chemical shifts for Aβ_21–30 as compared to the calculated chemical shifts over our simulated ensemble for different force fields. For the experimental chemical-shift values, we subtracted the reference value of the chemical shift of a random coil at 25 °C from the average shift for each amino acid;⁷⁰ as the carbon shifts show a very weak dependence on temperature, the 25 °C random coil reference shift is used. The amide proton random coil shift reference for each amino acid, however, is adjusted to a value appropriate for 10 °C.⁷¹ Together, the chemical-shift data emphasize that the peptide is largely unstructured.

Figure 1.

¹³C and ¹H chemical shifts from experiment and simulation for Aβ_21–30. Experimental NMR shifts are calculated as difference between measured shifts and tabulated random coil values. For ¹³C, which is insensitive to temperature changes, we used the tabulated 25 °C random coil shifts, whereas for the amide proton shifts, we used the random coil values of 10 °C to account for the temperature used in this study. The predicted chemical shifts are SHIFTS calculations averaged over the full ensemble after subtracting SHIFTS calculations averaged over the unstructured subpopulations (as defined by lack of DSSP secondary structure for all residues to represent our calculated random coil population).

In order to take into account any anticipated limitations of the calculations of the chemical-shift theory, we calculate the average chemical shifts of our unstructured population, which comprises ~60% of the TIP4P-Ew and ~40% of the TIP3P ensemble. We then use these values as a random coil reference state that is subtracted from the total simulated ensemble with the hope of some cancelation of errors. Figure 1 shows that the resulting ensemble averaged chemical shifts calculated with SHIFTS show at best qualitative agreement with experiment for only the C_β shifts. The same calculation performed with SHIFTX shows similar results. The fact that the calculated carbon and proton shift values deviate significantly from the NMR values may be due to the inability of the theory to capture all of the chemically relevant contributions to these chemical shifts, a notorious problem,⁵⁶ as opposed to inadequacy of the structural ensemble, which we judge later from the calculation of other NMR observables.

Scalar Coupling Measurements

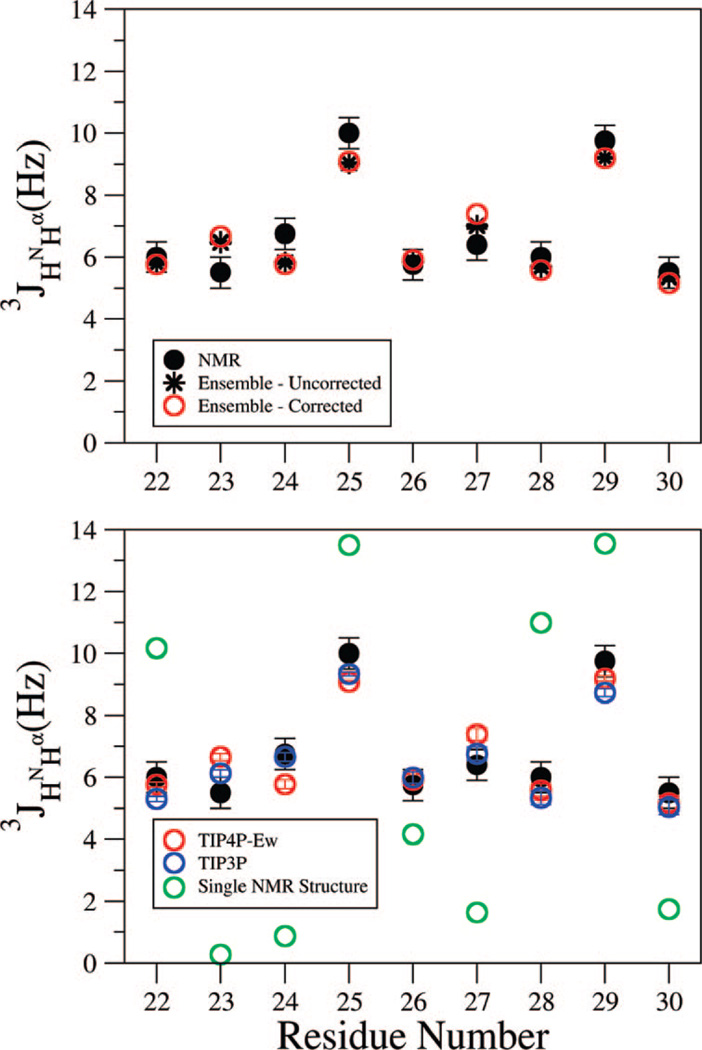
In Figure 2, we compare the ³J_H^NH^α scalar coupling constants, measured from a high-resolution COSY spectrum, to the simulations by using the dynamically uncorrected and harmonically corrected Karplus parameters (see Methods section). It is apparent that the dynamically uncorrected and harmonically corrected Karplus parameter sets work equally well on this disordered system (Figure 2, upper panel). This is because disordered systems, with the greater likelihood that all dihedral angles sample a much larger range of ϕ values, more closely approach the uniform sampling limit of J = A/2 + C. This limit is very similar between very different Karplus parameter sets and, for the sets examined here, are 4.9 and 5.05 Hz for the corrected and uncorrected sets, respectively.

Figure 2.

Comparison of experimental scalar coupling constant ³J_H^NH^α and that calculated from the simulated ensembles. Error bars are experimental uncertainty for NMR values as well as simulated standard deviations calculated for trajectories split into three sections. The coupling constants for the H_α protons of glycine are added to compare to experiment in which they are indistinguishable. (upper panel) Two parametrizations of the Karplus equation averaged over a single replica exchange ensemble by using the TIP4P-Ew model. It is apparent that the dynamically uncorrected and harmonically corrected Karplus parameter sets work equally well on this disordered system. (lower panel) Average over the two independent replica exchange ensembles for different empirical force fields and compared to experimentally determined coupling constants. It is evident that an ensemble measurement gives far better agreement with the experimental ³J_H^NH^α values than that calculated from a single structure based on incorporating all of the ROESY restraints (shown in Figure 6).

However, the use of dynamical corrections to the Karplus equation appears to be more theoretically sound,^62,64 and we apply this in Figure 2, lower panel. This figure shows that the TIP3P and TIP4P-Ew simulations have well-converged average scalar coupling values between their two trajectories, and the two different water models show only small differences, less than 1 Hz. The overall agreement between simulation and experiment is quite good, making clear that both are consistent with an ensemble that is largely random coil, consistent with the chemical-shift data. This is especially clear when we compare the experimental ³J_H^NH^α values to that calculated from a single structure based on incorporating all of the ROESY restraints (shown in Figure 6 and developed further below). However, the simulations are close but nonetheless outside of the experimental error bars for residues 23–25 and may suggest problems with the underlying structural ensembles. However, this may also be due to limitations of the parametrization of eq 1, because the simulated structures come from an unrestrained thermodynamic ensemble incorporating motion for a disordered peptide system, categorically different from the minimized X-ray and NMR structures created from restraints that are used to derive parametrizations of the Karplus equation for proteins.

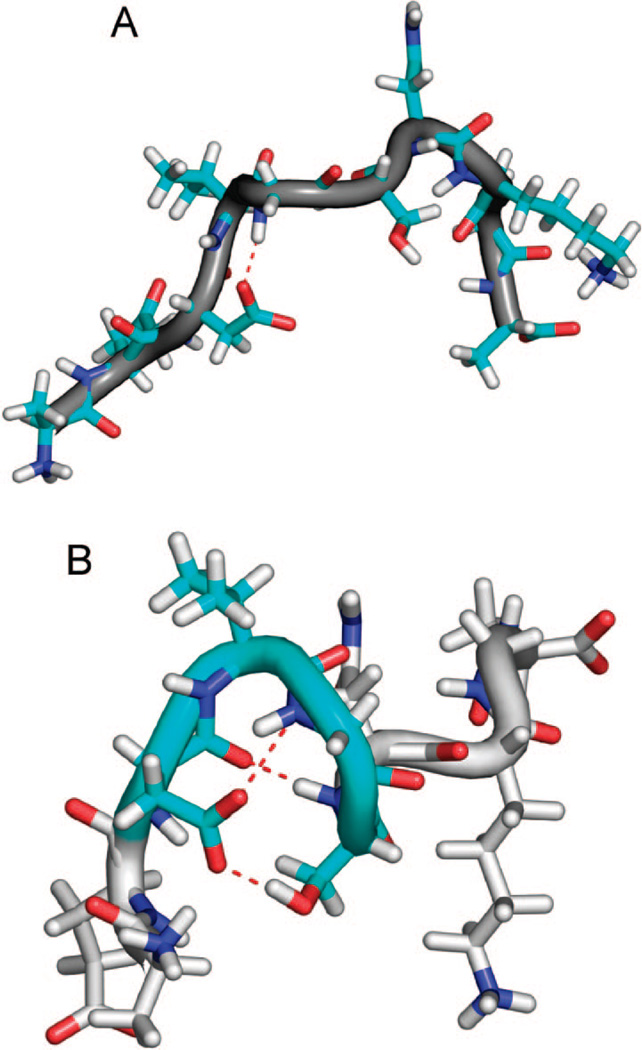
Figure 6.

Representative conformations of the ~30% population with structure for the TIP4P-Ew/ff99SB. (A) The most populated N-terminal hydrogen bond (dotted red) and (B) the hydrogen bonds and electrostatic interactions (dotted red) stabilizing the type-I β-turn (cyan) centered at Val24 and Gly25.

NMR Spin Relaxation

The experimental C_α spin–lattice and spin–spin relaxation times measured for the nonglycine positions of Aβ_21–30 are presented in Table 1. Because the chemical shifts for ¹³C–¹H pairs for Glu22 and Lys28 overlap, T₁ and T₂ at these positions cannot be distinguished, and the parameters are treated as an average of relaxation times at the two positions. Because the combined data for these positions fit well to a single-exponential form, T₁ and T₂ relaxation times are similar for these positions. The experimentally determined relaxation parameters vary by a maximum of 25% for nonterminal residues positions, indicating that the peptide does not contain significantly stiffer and/or slower moving regions on average.

Table 1.

¹³C NMR Spin Relaxation Times T₁ and T₂ for Nonglycine C_α Positions from Experiment and TIP4P-Ew, TIP3P, and Time-Scaled TIP4P-Ew, in Milliseconds^a

	A21	E22	D23	V24	S26	N27	K28	A30
			T1 at 500 MHz
experiment	415	298*	244	291	285	274	298*	475
TIP4P-Ew	492	292	268	272	274	273	287	530
TIP4P-EW, scaled	457	276	253	260	262	261	275	485
TIP3P	853	469	398	389	386	396	413	907
			T2 at 600 MHz
experiment	403	265*	269	230	235	241	265*	372
TIP4P-Ew	445	262	248	236	245	239	242	475
TIP4P-EW, scaled	398	238	225	215	224	218	220	425
TIP3P	860	474	403	386	386	393	402	858

^aGlu22 and Lys28 resonances overlapped; therefore, T₁ and T₂ could not be independently measured.

The relaxation times calculated from the overlapped peaks are indicated with an asterisk.

T₁ and T₂ calculated from simulations of the peptide solvated with TIP4P-Ew model water show excellent agreement with the experimental values (Table 1). Nonterminal amino acid relaxation times are within ±10% for both T₁ and T₂. Consistent with experiment, the terminal amino acids show significantly longer relaxation times (indicating faster motion) than nonterminal ones, although the simulated relaxation times are larger than the experimental values. The discrepancy is greatest for the C-terminal alanine, which may indicate that the simulations predict less structure in this region than in the experiment, although viscosity differences at lower temperature in ²H₂O may influence the dynamics. To test this hypothesis, a time-scaled correlation function was used for all proton pairs to account for the larger solvent viscosity (see Methods section). We find that the C-terminal T₁ and T₂ are now within 15% of the experimental values, whereas the nonterminal relaxation parameters change by only a few percents (Table 1).

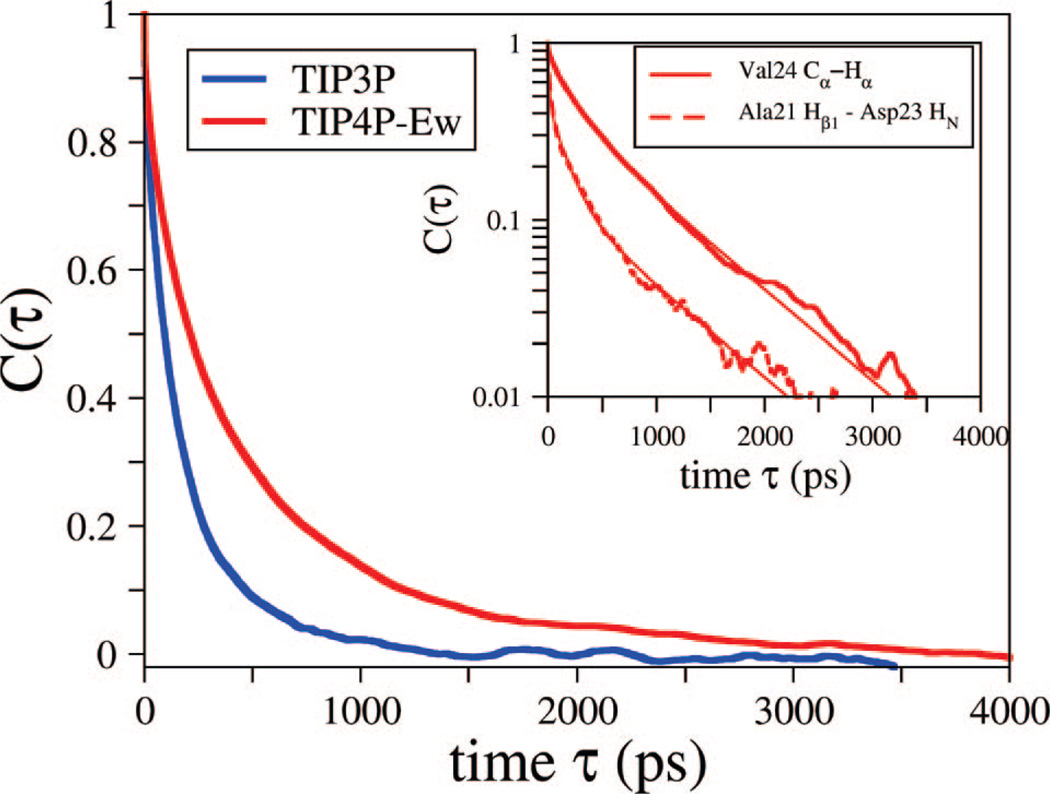
T₁ and T₂ relaxation times calculated from the TIP3P simulations result are ~1.8 times larger than those experimentally observed, for both terminal and nonterminal positions. This overestimate of relaxation time is a result of the faster dynamics of peptide motion in the TIP3P solvent. To demonstrate this difference, the averaged vector autocorrelation function for the ¹³C_α and H_α pair at the Val24 position for both the TIP3P and TIP4P-Ew simulations is presented in Figure 3. The TIP3P simulations result in time correlation functions with fitted decay parameters more than twice as fast as those of the TIP4P-Ew simulations. The faster peptide motion in TIP3P is likely a result of the unrealistically low viscosity (faster self-diffusion) properties of the TIP3P model, speeding up the peptide dynamics. In addition to our observation here for a disordered peptide system, the realistic viscosity of models such as TIP4P-Ew has also most recently been shown to be critical for direct calculation of NMR relaxation times of in globular proteins.⁷²

Figure 3.

Normalized average vector time correlation function for Val24 C_α to H_α position for constant energy trajectories solvated with TIP4P-Ew and TIP3P. The TIP3P model (blue) shows a dramatically faster decay for all vector time correlation functions relative to TIP4P-Ew (red), and we present this as an example. The inset presents example time correlation functions along with the triple exponential fits used in this study on a logarithmic y-axis to evaluate convergence. Presented are Val24 C_α to H_α, and Ala21 H_β1 to Asp23 H_N as an example of a pair used for the relaxation experiment predictions and the ROESY peak predictions, respectively.

Experimental and Simulated ROESY Crosspeaks

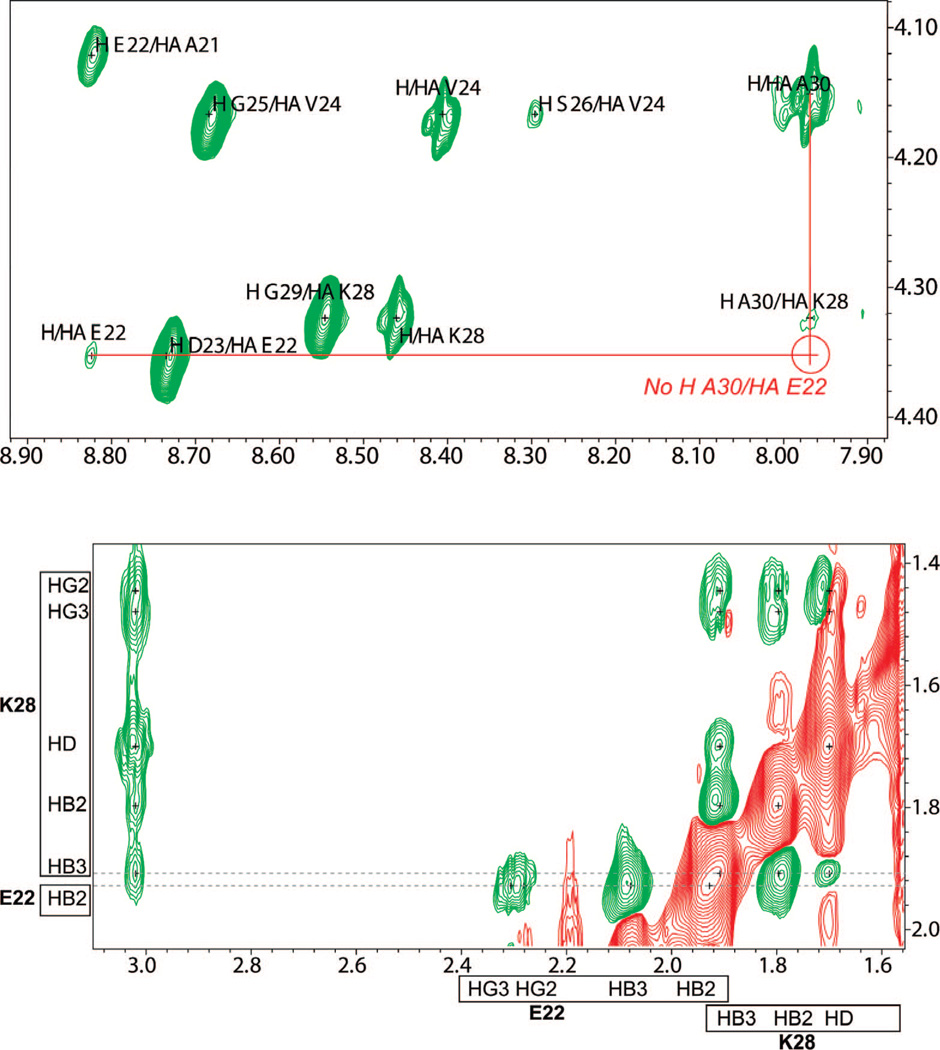
The 2D ROESY experiments in 90% H₂O:10% ²H₂O and 100% ²H₂O yielded a set of 155 assigned ROESY crosspeaks. Although the majority of the crosspeaks were for intraresidue (83) and sequential (44) pairs, 28 weak medium-range ROE interactions were also detected. These medium-range ROE crosspeaks comprise several i,i + 2 and i,i + 3 interactions and two extremely weak i,i + 4 interactions; no longer-range ROE crosspeaks are observed, and no strong patterns of α-helical or β-sheet contacts are evident. Lazo et al. report a long-range i,i + 8 Glu22 H_α to Ala30 HN crosspeak,²² and more recent work from the same group assigns the peak to an overlap of the original Glu22 H_α to Ala30 HN interaction and i,i + 2 Lys28 H_α to Ala30 HN in spectra collected at 500 MHz.³⁵ The observation of the long-range ROE is critical to their proposed NMR model, which is significantly collapsed. However, because of the higher resolution of the spectrum we have collected at 900 MHz, we interpret the crosspeak to be solely attributed to the i,i + 2 contact between Lys28 H_α and Ala30 HN, as shown in Figure 4, upper panel.

Figure 4.

Fingerprint region of ROESY spectrum in H₂O of Aβ_21–30. (upper panel) The crosspeak interpreted by Lazo et al. and Grant et al. as Hα Glu22 with HN Ala30 in their 500 MHz experiments is clearly resolved as only Hα Lys28 to HN Ala30 in our 900 MHz experiment. (lower panel) HB3 Lys28 has a nearly overlapping chemical shift with HB2 Glu22, potentially leading to crosspeak misassignment in previous studies at lower field.²²

An additional set of long-range interactions between the Glu22 and Lys28 side chains is reported by Lazo et al. In our higher-field spectra, we are able to distinguish the small chemical-shift difference between HB3 Lys28 and HB2 Glu22 (Figure 4, lower panel). At lower field, these resonances would overlap very close to the limit of the resolution of the experiment and hence be difficult to distinguish. We thus see no evidence of true Glu22 to Lys28 ROE interactions and believe that the previously reported long-range crosspeaks between these residues are due to misassignment of peaks too close to distinguish at lower field.

The new spectra show that a majority of the medium-range crosspeaks suggest turn or partial collapse structure for residues 22–27, although medium-range interactions are also seen from Ala21 to Asp23 and Val24, indicating that the peptide backbone is not simply extended in the N-terminal region. Two additional pairs of interactions are found in the C-terminal region between the side chain and H_α of Lys28 with the backbone of Ala30, as well as the methyl group (HB) of Ala30 with both HB methylene atoms of Asn27.

Predicted ROESY crosspeaks from simulation were calculated for a 300 ms mixing time and compared to the crosspeaks observed in the H₂O and ²H₂O experimental spectra in Tables 2 and 3. Because medium- and long-range ROE interactions contain the most information about peptide structure, we focus only on these interactions and ignore intra residue and sequential interactions in our comparisons of simulations to experiment. The top-ranked intensities for the ROE crosspeaks predicted to be above the noise level are tabulated along with the experimentally measured value; a dash indicates no crosspeak was seen experimentally, and <1.0 indicates a potential experimental crosspeak so weak that it cannot reliably be definitely assigned. Because we have two independent replica exchange calculations for each water model, we can explicitly evaluate the convergence of the ROESY crosspeaks. Although the r¹ (linear) pair distance averages vary less than a few percents between the simulations and suggest good convergence, a small number of r⁻⁶ averaged pair distance vary by >30% and translate into noticeable changes in the corresponding peak volumes and thus peak ranking. We therefore specifically highlight below the few crosspeaks where the combined ensemble crosspeak predictions do not make evident the significantly different predictions from the independent simulations for both TIP4P-Ew and TIP3P.

Table 2.

Proton Crosspeak Predictions for TIP3P and TIP4P-Ew for the 900 MHz Spectra in H₂O^a

Isim	Iexp	proton 1	proton 2	Isim	Iexp	proton 1	proton 2
TIP3P				TIP4P-Ew
5.4	< 1.0	HA VAL24	HB3 ASN27	4.1	15.7	HB ALA21	HG VAL24
4.4	# 1.8	HB3 ASP23	HB2 SER26	2.8	2.6	HG VAL24	H SER26
4.0	–	HA ASP23	H GLY25	2.6	2.9	HB ALA21	H ASP23
3.0	2.6	HG VAL24	H SER26	1.9	4.9	HG3 GLU22	HG VAL24
2.8	15.7	HB ALA21	HG VAL24	1.9	1.3	HB3 ASP23	H GLY25
2.7	< 1.0	HG3 GLU22	H VAL24	1.7	< 1.0	HG3 GLU22	H VAL24
2.7	–	HB3 ASP23	H SER26	1.6	–	2HD2 ASN27	H GLY29
2.7	–	HA GLU22	HA ASN27	1.3	–	HB3 GLU22	H VAL24
2.6	2.9	HB ALA21	H ASP23	1.3	# 2.4	HB2 GLU22	HG VAL24
2.6	–	HA VAL24	H ASN27	1.3	–	HA GLU22	HA ASN27
2.6	1.3	HB3 ASP23	H GLY25	1.3	1.2	HA GLY25	H ASN27
2.4	4.9	HG3 GLU22	HG VAL24	1.3	# 1.4	HA VAL24	HB2 ASN27
2.3	# 1.4	HA VAL24	HB2 ASN27	1.2	< 1.0	HA VAL24	HB3 ASN27
2.0	2.6	HA VAL24	H SER26	1.2	# 1.8	HB3 ASP23	HB2 SER26
2.0	1.2	HA GLY25	H ASN27	1.2	2.6	HA VAL24	H SER26
1.6	–	HA ASN27	H GLY29	1.1	–	HG VAL24	H ASN27
1.4	# 3.8	HB3 GLU22	HG VAL24	1.1	–	2HD2 ASN27	HA GLY29
1.4	7.2	HG2 GLU22	HG VAL24	1.1	# 3.8	HB3 GLU22	HG VAL24
1.4	2.8	HG VAL24	HB3 ASN27	1.1	7.2	HG2 GLU22	HG VAL24
1.4	–	1HD2 ASN27	H GLY29	1.0	–	HB VAL24	H SER26
1.4	–	HB3 GLU22	H VAL24	1.0	–	HB3 ASP23	H SER26
1.3	–	HA ASP23	HA LYS28	False Negatives
1.3	–	HB3 ASP23	HE2 LYS28	0.9	1.1	HB2 ASN27	H GLY29
1.2	–	HG VAL24	H ASN27	0.7	2.8	HG VAL24	HB3 ASN27
1.2	2.6	HG VAL24	HB2 ASN27	0.6	2.6	HG VAL24	HB2 ASN27
1.2	–	H VAL24	H SER26	0.5	3.3	HB2 ASN27	HB ALA30
1.2	# 2.4	HB2 GLU22	HG VAL24	0.4	1.7	HA LYS28	H ALA30
1.2	–	1HD2 ASN27	HA GLY29	0.4	3.8	HA GLY25	HD2 LYS28
1.2	–	H ASP23	HB2 SER26	0.2	2.5	HB3 LYS28	H ALA30
1.2	–	HG2 GLU22	HA ASN27	0.0	1.1	HA SER26	H LYS28
1.1	–	HG3 LYS28	H ALA30	0.0	3.8	HB3 ASN27	HB ALA30
1.1	–	HB3 ASN27	H GLY29
1.1	–	HB ALA21	HA ASN27
1.0	–	HA GLU22	H LYS28
1.0	–	H ASP23	H SER26
1.0	–	H GLY25	H ASN27
1.0	–	HB ALA21	HB2 SER26
1.0	–	HA ASP23	H SER26
1.0	–	HG VAL24	HA GLY29
False Negatives
0.9	1.1	HA SER26	H LYS28
0.6	3.8	HA GLY25	H D2LYS28
0.6	3.8	HB3 ASN27	HB ALA30
0.5	1.7	HA LYS28	H ALA30
0.3	2.5	HB3 LYS28	H ALA30
0.3	1.1	HB2 ASN27	H GLY29
0.0	3.3	HB2 ASN27	HB ALA30

^aExperimental intensities (Iexp) are normalized to the intensity of the weakest assigned peak. Simulation intensities (Isim) are normalized to experimental intensity as described in the Methods section. Experimental intensities are labeled as a dash if the peak is absent or <1.0 if some evidence of a peak is present but is too weak to be assigned. Simulated intensities are marked with a # if the H₂O prediction is found in the ²H₂O experiment.

Table 3.

Proton Crosspeak Predictions for TIP3P and TIP4P-Ew for the 800 MHz Spectra in ²H₂O^a

Isim	Iexp	proton 1	proton 2	Isim	Iexp	proton 1	proton 2
TIP3P				TIP4P-Ew
11.7	< 1.0	HA VAL24	HB3 ASN27	8.0	7.4	HB ALA21	HG VAL24
10.0	1.8	HB3 ASP23	HB2 SER26	3.9	5.1	HG3 GLU22	HG VAL24
6.1	–	HA GLU22	HA ASN27	3.1	–	HA GLU22	HA ASN27
5.8	7.4	HB ALA21	HG VAL24	3.0	1.4	HA VAL24	HB2 ASN27
5.0	5.1	HG3 GLU22	HG VAL24	2.8	1.8	HB3 ASP23	HB2 SER26
5.0	1.4	HA VAL24	HB2 ASN27	2.7	< 1.0	HA VAL24	HB3 ASN27
3.0	3.8	HB3 GLU22	HG VAL24	2.7	2.4	HB2 GLU22	HG VAL24
3.0	1.8	HG VAL24	HB3 ASN27	2.3	3.8	HB3 GLU22	HG VAL24
3.0	4.3	HG2 GLU22	HG VAL24	2.2	4.3	HG2 GLU22	HG VAL24
2.9	–	HA ASP23	HA LYS28	2.2	0.8	HA GLU22	HG VAL24
2.7	–	HB3 ASP23	HE2 LYS28	1.8	–	HB VAL24	HB2 ASN27
2.5	–	HG2 GLU22	HA ASN27	1.6	1.3	HG VAL24	HB2 SER26
2.5	1.6	HG VAL24	HB2 ASN27	1.5	1.8	HG VAL24	HB3 ASN27
2.5	2.4	HB2 GLU22	HG VAL24	1.5	3.1	HG VAL24	HE2 LYS28
2.4	–	HB ALA21	HA ASN27	1.5	–	HB3 ASP23	HA LYS28
2.3	–	HA VAL24	HA ASN27	1.4	–	HG VAL24	HA SER26
2.2	–	HB ALA21	HB2 SER26	1.4	1.6	HG VAL24	HB2 ASN27
2.1	–	HG VAL24	HA GLY29	1.4	–	HA VAL24	HB2 LYS28
2.0	–	HA GLY25	HA GLY29	1.4	–	HG2 GLU22	HA ASN27
2.0	3.1	HG VAL24	HE2 LYS28	1.3	–	HB ALA21	HB2 SER26
1.9	–	HB3 ASP23	HG3 LYS28	1.3	–	HA SER26	HE2 LYS28
1.8	–	HA GLU22	HA GLY29	1.3	–	HB ALA21	HB3 ASP23
1.8	1.3	HG VAL24	HB2 SER26	1.3	–	HB ALA21	HA ASP23
1.8	–	HG3 GLU22	HB2 SER26	1.2	–	HG VAL24	HA ASN27
1.8	–	HG3 LYS28	HB ALA30	1.2	–	HA GLY25	HE2 LYS28
1.6	–	HG2 GLU22	HB2 ASN27	1.1	0.9	HG VAL24	HA LYS28
1.6	–	HG VAL24	HD2 LYS28	1.1	–	HB2 SER26	HE2 LYS28
1.6	0.8	HA GLU22	HG VAL24	1.0	–	HA ASP23	HB2 SER26
1.6	–	HG3 GLU22	HA ASN27	1.0	–	HB ALA21	HA SER26
1.5	–	HG VAL24	HB3 SER26	1.0	2.5	HB2 ASN27	HB ALA30
1.5	–	HB ALA21	HB ALA30	1.0	–	HG VAL24	HB3 SER26
1.5	–	HB2 SER26	HE2 LYS28	False Negatives
1.5	–	HA GLY25	HE2 LYS28	0.9	1.8	HA GLY25	HD2 LYS28
1.4	–	HB2 GLU22	HA GLY29	0.4	1.0	HB3 SER26	HG3 LYS28
1.3	–	HA ASP23	HB2 SER26	0.1	2.2	HB3 ASP23	HB3 SER26
1.3	1.8	HA GLY25	HD2 LYS28	−0.1	0.8	HB2 ASP23	HB3 SER26
1.3	–	HB3 ASP23	HB2 LYS28	−0.1	3.9	HB3 ASN27	HB ALA30
1.3	–	HB VAL24	HB3 ASN27	−0.3	1.7	HB2 ASP23	HB2 SER26
1.2	–	HB ALA21	HB2 ASN27
1.2	–	HA SER26	HE2 LYS28
1.2	–	HG VAL24	HA ASN27
1.2	–	HA GLU22	HA LYS28
1.2	3.9	HB3 ASN27	HB ALA30
1.2	–	HB ALA21	HB3 ASP23
1.2	2.2	HB3 ASP23	HB3 SER26
1.2	–	HB3 ASP23	HD2 LYS28
1.2	–	HB2 SER26	HG3 LYS28
1.1	–	HB3 ASP23	HA GLY25
1.1	–	HE2 LYS28	HB ALA30
1.1	–	HB ALA21	HB2 LYS28
1.1	–	HB3 GLU22	HA ASN27
1.1	–	HB3 ASP23	HG2 LYS28
1.1	–	HG VAL24	HA SER26
1.0	–	HA VAL24	HE2 LYS28
1.0	–	HB ALA21	HA ASP23
1.0	–	HG3 GLU22	HB2 ASN27
1.0	–	HB ALA21	HA ALA30
1.0	–	HB3 GLU22	HB2 ASN27
1.0	–	HB ALA21	HA VAL24
1.0	–	HG2 GLU22	HA GLY29
False Negatives
0.9	1.0	HG VAL24	HA LYS28
0.3	1.0	HB3 SER26	HG3 LYS28
0.1	2.5	HB2 ASN27	HB ALA30
0.0	0.8	HB2 ASP23	HB3 SER26
−0.7	1.7	HB2 ASP23	HB2 SER26

^aExperimental intensities (Iexp) are normalized to the intensity of the weakest assigned peak. Simulation intensities (Isim) are normalized to experimental intensity as described in the Methods section. Experimental intensities are labeled as a dash if the peak is absent or < 1.0 if some evidence of a peak is present but is too weak to be assigned.

Tables 2 and 3 show that the TIP4P-Ew and TIP3P ensembles predict 12 and 14 of the experimentally assigned crosspeaks, respectively, from the 900 MHz H₂O spectra, and 14 and 15 of the assigned crosspeaks, respectively, from the 800 MHz ²H₂O experiment (note that there is redundancy of crosspeaks between the two experiments so that there are only 28 distinct crosspeaks in total). The true positive crosspeaks encompass i,i + 2, i,i + 3, and i,i + 4 medium-range crosspeaks from across the entire peptide. Thus, both TIP3P and TIP4P-Ew ensembles pick out the majority of the 28 experimentally observed medium-range ROE interactions from the 600 possible distinguishable medium- and long-range interactions.

The predictions also show a number of false-positive crosspeaks, that is, crosspeaks predicted above the estimated noise level in the simulations that are not experimentally observed. In the TIP4P-Ew predictions, all of the false-positive crosspeaks, except one from the H₂O spectrum and four additional from the ²H₂O spectrum, are i,i + 2 or i,i + 3 assignments that involve residues and regions of the chain that have other observed ROE interactions. This suggests that the simulations are bringing together the correct regions of the peptide and that these false positives are due to small differences in the detailed structural distances. In fact, the r⁻⁶ distance averaging to estimate peak volumes is extremely sensitive to distance, such that changes of 2^1/6 (~1.12) in distance can translate to a doubling of the calculated peak volume. In other words, false-positive crosspeaks predicted to be weak but still above the noise by our simulations may be just below the background noise in the experiment if the simulated distances are closer than in the experiment by only a factor of 1.12.

We therefore focus on false positives predicted more than a factor of 2 above the noise. In this case, the differences in quality of the water models are revealed in that the TIP3P simulations have far too many false positives as strongly predicted crosspeaks, suggesting a structural ensemble that is far more collapsed than observed experimentally. Furthermore, the TIP3P model shows poor ranking for what are the strongest experimentally observed peaks. By contrast, TIP4P-Ew has fewer false positives and gets the intensity rankings right for the most prominent experimental peaks. In fact, the TIP4P-Ew simulations of the crosspeak with the strongest intensity between the HB methyl group of Ala21 and the HG methyl groups of Val24 led to the assignment of this peak in the experimental spectra which was initially hidden beneath an experimental artifact. Therefore, we focus on the TIP4P-Ew results in the remainder of this section.

The more significant discrepancies between the experiments and simulation involve false negatives, experimentally observed crosspeaks that are not predicted to be observable by simulation. Because the noise in the experiment is not uniform over the spectra, if we dip just below the estimate for noise by a factor of 2, the TIP4P-Ew simulation predictions show an additional four H₂O and two ²H₂O experimentally assigned crosspeaks. On the basis of the highly sensitive crosspeak intensity discussed above, we could thus classify these as true positives as well. However, five additional missing crosspeaks are a factor of 10 below the noise level and hence are genuine false negatives. One such set of false negatives is the interactions between β methylene protons of Asp 23 and Ser 26, which involve four crosspeaks seen experimentally. Because one of the possible four crosspeaks of methylene pair interactions for these two residues is predicted among the top 10 of the ²H₂O crosspeaks predicted by the TIP4P-Ew simulations, it is apparent that the simulation is bringing together the correct areas of the side chains but not the correct detailed geometry in this region. Apparently, the structure of the turn that is stabilized by the Asp23–Ser26 side-chain contacts favors the proximity of a single proton in a β-methylene pair instead of the four possible contacts between pairs seen experimentally.

The experimental crosspeaks, however, may imply more equivalent distances than are actually present in the underlying structural ensemble. Magnetization selectively ROE transferred through space to a single hydrogen in a methylene pair would subsequently be more evenly redistributed between the pair because of TOCSY-type (through bond) transfer. TOCSY transfer is created by the rotating frame pulse during ROESY mixing, is difficult to remove completely,⁴⁵ and is an effect that is not accounted for by the predicted ROESY spectra. These same arguments apply to the β-methylene protons of Asn 27 and Ala 30, which involve four crosspeaks seen experimentally, whereas the simulations find one of the crosspeaks above the noise and two crosspeaks just below the noise. In summary, a missing crosspeak between protons too spatially distant in the simulated ensemble suggests either that the simulations have imperfect local geometry or that selectively ROE transferred magnetization has been redistributed through TOCSY-type transfer among methylene protons.

Peptide Structure from Experiments and Simulations

Determining a single structure from multiple weak, medium-range ROE experimental crosspeaks for disordered peptides can be misleading because it is also possible that ROE crosspeaks arise from multiple distinct populations or perhaps a fully heterogeneous structural ensemble. Typical structure calculations on structured proteins assume that weak NOE or ROE crosspeaks correspond to large (~4.5–6.0Å) upper distance restraints on a single well-defined structural population, and hence, all the restraints should be applied simultaneously. Although we will show that the peptide ensemble involves significant disorder, and hence, it is inappropriate to use the standard structure determination methods,^73–75 we calculate a single best-fit structure for purposes of comparison.

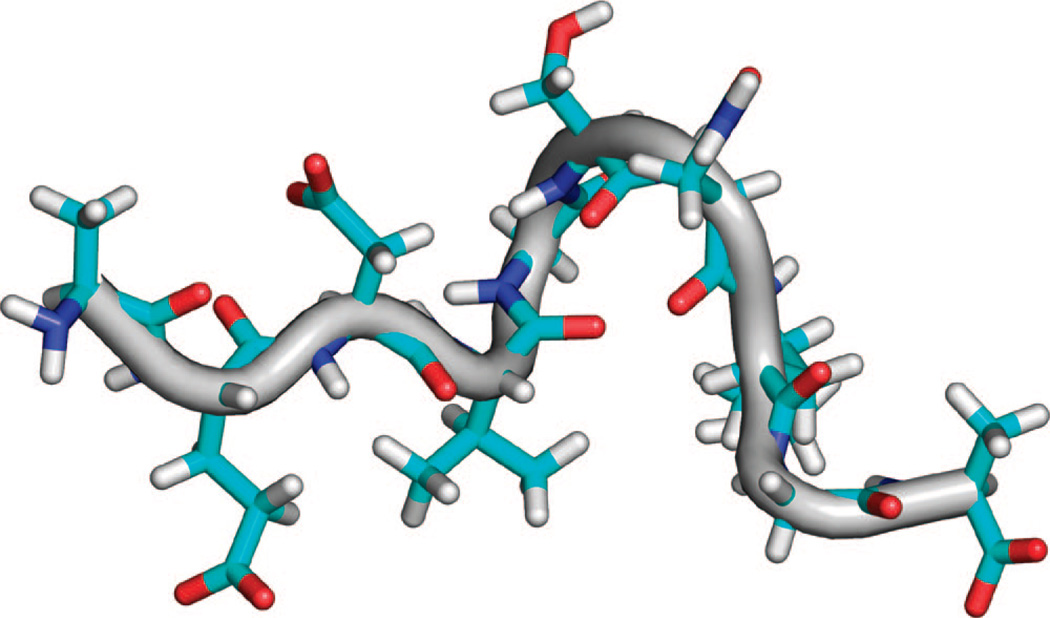
The set of restraints was used to calculate 1000 structures of Aβ_21–30, and the 50 lowest-energy structures were aligned. For the entire peptide, the superposition of the final 50 structures has an rmsd of 0.81 ± 0.42 Å for the backbone atoms and 1.15 ± 0.61 Å for all heavy atoms. A total of 16 of the 20 structures are within 1.0 Å rmsd for all heavy atoms, forming the dominant cluster the lowest-energy structure of which has three major bends, pinching together Asp23 to the Ser26, Gly25 to Lys28, and Asn27 to Ala30 (Figure 5). These bends are created by 12 unique i, i + 3 and i,i + 4 ROE interactions between residues Asp23–Ser26, Val24–Asn27, Val24–Lys28, Asp23–Ser26, Val24–Asn27, Val24–Lys28, Gly25–Lys28, and Asn27–Ala30.

Figure 5.

Representative structure from restraint energy minimized ensemble, simultaneously applying all observed ROE interactions. Peptide N-terminus is on the left side of all molecular drawings in this work.

Many of the crosspeaks for these interactions are very weak and detectable in the ROESY spectrum only when the peptide is dissolved in 100% ²H₂O, and there is only one crosspeak between Gly25 HAs and Lys28 HDs detected. As a result, one of the three bends in the minimized structure backbone is stabilized by one backbone hydrogen bond and a second by a single Lys28 NH₃⁺ interaction, though the great majority of pair distance restraints for observed ROE interactions result in structure not stablized by any favorable intermolecular interactions. This lack of stabilizing interactions was also evident for the minimized structures for the Aβ_21–30 peptide model proposed previously by Lazo et al.²²

Given the good quality of the TIP4P-Ew simulated experimental observables presented above, we can refine the experimental picture by analyzing the underlying simulated ensemble for structural populations. Standard clustering by rmsd is not informative because of the lack of order in much of the ensemble. The two first principal components in a PCA analysis yielded only a single large population, giving little information about the underlying structure. Because hydrophobic collapse is unlikely to be the dominant structuring force in a peptide that has only a single large aliphatic and no aromatic residues, hydrogen-bond interactions are hypothesized to stabilize the structure that gives rise to the ROE interactions. Thus, the most useful tool for partitioning the structures is the patterning of the hydrogen bonding and electrostatic interactions that may persist in subpopulations. It is important to emphasize that 60–65% of the TIP4P-Ew population is unstructured by these metrics; however, the remaining 35–40% of the population does explain the presence of the medium-range restraints observed in the experimental ROESY crosspeaks with a large degree of success.

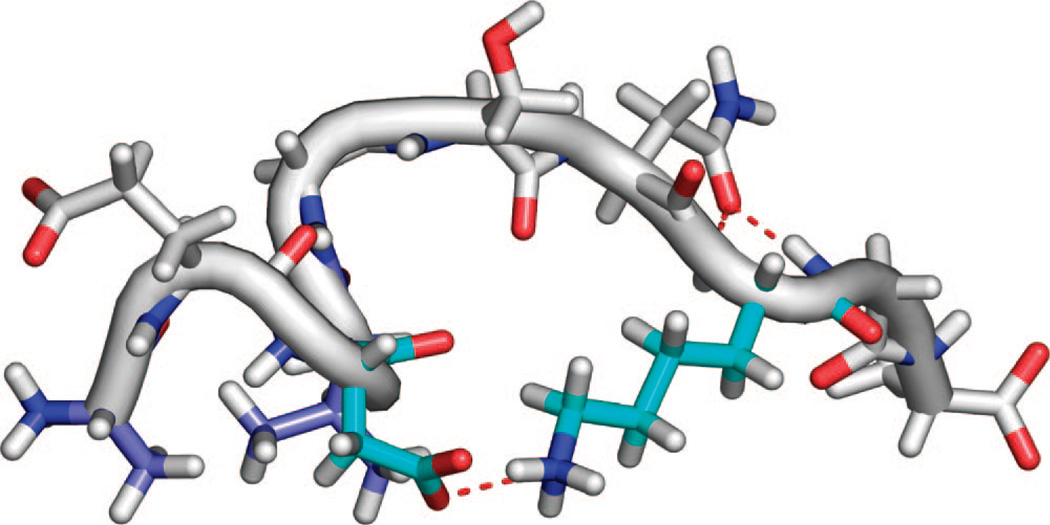
In the TIP4P-Ew simulations, the most populated hydrogen bond is between the side-chain carboxyl oxygens of Asp23 and the backbone amide of G25 (Figure 6A). This interaction is found in 17% of the ensemble and stabilizes the backbone dihedral angles near those of a type-I β-turn for residues Asp23 to Ser26. A true type-I β-turn, which is found in 5% of the population (Figure 6XB), is defined by backbone hydrogen bonding between the backbone carbonyl oxygen of residue i (Asp23) with the backbone amide hydrogen of residue i+3 (Ser26), resulting in the amide hydrogen of i+2 (Gly25) pointing toward the side chain of i, precisely the most populated hydrogen bond we found.

The peptide maintains a conformation near a type-I β-turn if interactions between the carboxyl oxygens of Asp23 to the side-chain hydroxyl of Ser26 are found, consistent with the observed ROEs which brings together the side-chain hydrogens of Asp23 and Ser26. If structures with at least one of these Asp23 to Ser26 interactions are also considered, the type-I β-turn population increases from 5 to 14% of the ensemble, which is much higher than any other turn region in the peptide. Although the TIP3P structural ensemble shows this turn in approximately 35% of the ensemble, its overrepresentation in the structured population most likely contributes to the poor agreement of ROE crosspeak volumes when compared to experiment.

Despite the prevalence of structures with type-I β-turn structure, the β-turn does not nucleate a β-sheet, which would be characterized by backbone contacts between Glu22 and Asn27. Instead, in the structures observed, the backbone amide of Asn27 hydrogen bonds to the backbone carbonyl oxygen of Asp23, precluding the formation of β-sheet structure. Furthermore, this interaction brings the Val24 methyl hydrogens near the Asn27 side-chain hydrogens, accounting for those observed ROE interactions. Other smaller groups of covarying hydrogen bonds are observed, including simultaneous interactions between the backbone carbonyl of Val24 and the backbone amide of both Asn27 and Lys28, bringing in proximity the Val24 side chain with Asn27 side chain as observed in the ROESY spectra.

Salt-bridge formation between Asp23 and Lys28, observed in the solid-state NMR structure of the Aβ_1–40 fibril, is found in 7% of the ensemble (Figure 7), whereas the competing salt bridge between Glu22 and Lys28 is found 1.5% of the time. Together, these salt-bridge structures are observed with comparable frequency to the turn populations, but the salt-bridge contacts do not stabilize either hydrogen bonding structure nor close proximity of other protons in the intervening region. In principle, a close contact involving the basic lysine amine hydrogens may be observed in a ROESY spectrum, but salt bridges, unless stable enough to prevent proton exchange at neutral pH of the basic amine on the NMR experiment time scale as in folded proteins, do not typically bring together NMR visible protons.

Figure 7.

Representative conformation of the salt-bridge structure relevant for the protofibrils. Asp23 to Lys28 salt-bridge (shown by red dotted line between aqua amino acids) found in 7% of the TIP4P-Ew ensemble and Ala21 HB to Val24 HG (both in light blue) van der Waals contacts which give rise to the strongest observed ROE interaction.

Discussion

According to the high-field NMR experiments, Aβ_21–30 shows no long-range and only weak medium-range ROE interactions, demonstrating none of the features of a protein with a single native state. We therefore conclude that the presence of a singly populated collapsed structure incorporating a unique bend due to an i,i + 8 Glu22 H_α to Ala30 HN crosspeak and i,i + 6 Glu22 side chain to Lys28 side chain crosspeak reported by Lazo et al. and Grant et al. is incorrect on two levels. The first is a problem of misassignment in their lower resolution ROESY spectra in which they propose a i,i + 8 interaction that is instead revealed to be a weak i,i + 2 interaction and an i,i + 6 interaction where intraresidue peaks are overlapping, both of which we were able to distinguish by the higher resolution 800 and 900 MHz spectra used here.

More significantly, peptides and disordered protein systems should not conform to a single dominant structure and should only be described by appropriate ensembles. The poor quality of a single structure becomes evident when simultaneously applying all ROE interactions as distance restraints to give a minimized structure with surprisingly few favorable inter-residue interactions. Because there are only a few restraints that are all weak and hence provide only a loose upper bound on the distance, all of the restraints are satisfied by pair distances near this bound. This loose bounding results in a dominant structure with no consensus stabilizing contacts, hydrogen bonds, regular secondary structures, or reverse turns.

We determined a good match between the TIP4P-Ew/ff99SB simulated and experimentally observed structure and dynamics, as measured by ROE crosspeaks and ¹³C relaxation, indicating that these simulations faithfully approximate the ensemble of structures interrogated by the experiments, allowing them to be used to describe the full structural ensemble diversity. We find that the structural ensemble of the Aβ_21–30 involves a majority (~60%) of unstructured population according to lack of any DSSP secondary structure assignment or hydrogen-bonding patterns. However, the remaining minority population involves ~14% population of β-turn structure centered at Val24 and G25, bringing together Asp23 and S26. The simulations also indicate that the Asp23 to Lys28 salt bridge, important to the fibril structure, is formed in ~7% of the ensemble. Finally, a separate set of structures populated only by a few percents brings together the Val24 and Asn27 regions. We emphasize however that the Aβ_21–30 system is highly disordered, and that the ~5–15% of distinct structural populations we measure have been overrepresented in all previous experimental and most simulation studies on this same system. Experimental and simulation data suggest that the structural populations may increase upon lengthening of the Aβ peptide to larger fragments.^85–88

Conclusion

Although significant progress has been made recently in the interpretation of NMR observables for disordered peptide and protein systems,^76–79 combining multiple and independent structural constraints for a system with significant disorder often leads to an inadequate description of the ensemble diversity.⁷⁷ By contrast, molecular dynamics simulations of disordered systems have the opposite challenge where the simulated ensemble is directly observable with good statistical confidence, but the accuracy is difficult to assess because of incomplete convergence and uncertainties of the underlying empirical force fields.^80,81 Although simulations of folded proteins in their native state have been shown to quantitatively reproduce NMR observables (model-free order parameters, relaxation times T₁ and T₂),^40,82,83 partially structured peptides and natively unfolded proteins present a new challenge for simulations in which small energetic biases or inaccuracies can dramatically affect the populations of structures in the equilibrium ensemble. Stock, Schwalbe, and co-workers have recently shown that many earlier generation peptide–water empirical force-field combinations simply do not reproduce the average structural ensemble for a simple disordered system such as polyalanine.⁸⁴

The recent advent of improved empirical force fields, enhanced sampling techniques, and NMR relaxation matrix calculations has allowed us to predict well the high-quality NMR experimental observables generated here. The Amber ff99SB/TIP4P-Ew simulations do not overpredict contacts between regions where there are no experimentally observed ROEs, and thus, there are few false-positive peaks, and false negatives are weak but often just buried in the noise. By contrast, the TIP3P simulations involve structural ensembles that are too collapsed, resulting in far too strong and far too many (false positive) ROE crosspeaks. Additionally, the solution dynamics are much too fast to correctly reproduce the observed ¹³C relaxation times. It would be instructive to see whether the previous calculations on polyalanine might improve with the newer water force field.

At the same time, the experimental and predicted observables do not match perfectly for ff99SB/TIP4P-EW, and the reasons for the discrepancy vary. We used two different chemical-shift programs, SHIFTS^56–58 and SHIFTX⁵⁹ (parameters derived from a physical versus a statistical approach), and largely found the same level of disagreement with the experimental chemical shifts. We believe that the poor agreement of the calculated chemical shifts is inherent in the underlying chemical-shift parametrizations that are optimized for folded states, as opposed to gross deficiencies of the underlying structural ensembles of the disordered peptide studied here. Although comparisons to scalar coupling constants ³J_H^NH^α are overall very good, there are some discrepancies between simulation and experiment for residues 23–25. Although the simulated ensembles may be imperfect, it also seems likely that use of Karplus parameters derived from minimized X-ray and NMR structures created from restraints may in fact be nonoptimal when applied to an unrestrained thermodynamic ensemble for a disordered peptide or protein system. For ROESY spectra, the severity of r⁻⁶ averaging means that slight average-distance changes can have greater than 2-fold effects on the peak volume; therefore, regions of the chain correctly brought together in close proximity may emphasize local geometric rotomers that are imperfectly captured by the empirical force fields. Potential experimental artifacts, such as through-bond TOCSY transfer mechanisms which are not taken into account in the back calculation of ROESY crosspeaks, may additionally contribute to prediction and experiment discrepancies. All of these issues are worthy of consideration for future improvements in next-generation force fields and simulation of NMR observables. Even so, these structural and dynamical predictions match better than any previous predictions for peptides of this length range, a success that we attribute in particular to the advent of new-generation force fields and careful verification that ensembles are adequately converged.

Faithfully predicting NOESY or ROESY crosspeaks is challenging because the nature of the Overhauser effect singles out the minority populations of close-range interactions (if they exist) through a steep power dependence on distance, making them both more structurally informative but much harder to converge in the simulated equilibrium ensemble. By contrast, each member of the structural ensemble contributes equally to averaged quantities such as chemical shift and scalar coupling observables, making prediction of these quantities from simulations much easier to converge but far less structurally informative. If we were only to have examined the chemical-shift and scalar coupling (³J_H^NH^α) measures, we would have found that either the TIP3P or the TIP4P-Ew solvated ff99SB peptide would have equivalently reproduced the experimental data. For a small and disordered peptide that exchanges conformations on time scales faster than the experimental time scale, the scalar coupling and chemical-shift values provide direct Boltzmann-weighted information dominated by the significant percentage of random-coil structure. Conversely, predicted ROE interactions are sensitive to minor populations of close contacts that distinguish a true partially structured ensemble from other partially structured, or even completely unstructured, ensembles. Predicting the ROE interactions is therefore a more stringent test for simulations which must distinguish a smaller population of heterogeneous structure from a high-percentage background of unstructured or random-coil-like structure in the ensemble.

We believe that the interplay of molecular simulation in reproducing a variety of NMR observables such as chemical shifts, scalar couplings, NOE or ROE crosspeaks, and ¹³C relaxations provides the correct tools for characterizing the structural ensemble for disordered systems. We note that proteolysis experiments, which implied well-protected structure for the Aβ_21–30 fragment and the full length Aβ_1–40 and Aβ_1–42 sequences, appear to be an insensitive tool to distinguish a largely disordered ensemble from a highly folded population, at least in this case. As such, this work serves as a validation study for ROESY characterization of Aβ_1–40 and Aβ_1–42 by molecular simulation, where collection of detailed NMR data will be more challenging because of aggregation and fibril formation on experimental time scales at physiological conditions.