Minimal sufficient balance—a new strategy to balance baseline covariates and preserve randomness of treatment allocation

Abstract

In many clinical trials, baseline covariates could affect the primary outcome. Commonly used strategies to balance baseline covariates include stratified constrained randomization and minimization. Stratification is limited to few categorical covariates. Minimization lacks the randomness of treatment allocation. Both apply only to categorical covariates. As a result, serious imbalances could occur in important baseline covariates not included in the randomization algorithm. Furthermore, randomness of treatment allocation could be significantly compromised because of the high proportion of deterministic assignments associated with stratified block randomization and minimization, potentially resulting in selection bias. Serious baseline covariate imbalances and selection biases often contribute to controversial interpretation of the trial results. The National Institute of Neurological Disorders and Stroke recombinant tissue plasminogen activator Stroke Trial and the Captopril Prevention Project are two examples. In this article, we propose a new randomization strategy, termed the minimal sufficient balance randomization, which will dually prevent serious imbalances in all important baseline covariates, including both categorical and continuous types, and preserve the randomness of treatment allocation. Computer simulations are conducted using the data from the National Institute of Neurological Disorders and Stroke recombinant tissue plasminogen activator Stroke Trial. Serious imbalances in four continuous and one categorical covariate are prevented with a small cost in treatment allocation randomness. A scenario of simultaneously balancing 11 baseline covariates is explored with similar promising results. The proposed minimal sufficient balance randomization algorithm can be easily implemented in computerized central randomization systems for large multicenter trials.

Introduction

Confidence in the findings of randomized clinical trials is directly related to the quality of randomization and blinding.¹ Serious baseline imbalances often lead to suspicion of selection bias and unconvincing interpretations of trial results. Berger discussed this in his book in which he provided evidences of such selection biases in 30 trials.² Serious and consistent imbalances in multiple baseline covariates are considered to be the manifestation of selection bias. Among the 30 trials cited in Berger, 13 used pre-generated randomization code lists stratified by clinical center, a method vulnerable to malpractice in randomization. The suspicion of selection bias has resulted in controversial interpretation and acceptance of results of these trials. The National Institute of Neurological Disorders and Stroke recombinant tissue plasminogen activator (NINDS rt-PA) Stroke Study 0 and the Captopril Prevention Project (CAPPP) trial 0 are two such examples discussed by Berger. The NINDS rt-PA Stroke Study claimed an improvement in clinical outcome at three months among subjects treated with intravenous rt-PA compared to the placebo group within 3 h of onset of acute ischemic stroke.³ At first glance, one of the key prognostic factors, stroke severity, as measured by the baseline National Institutes of Health Stroke Scale (NIHSS) score, was similar between the two treatment groups (rt-PA group:14.4±7.5; placebo group:15.2±6.8; p=0.14).^5–10 However, reanalysis of the trial data conducted by an independent committee found that when patients were grouped into five strata (approximate quintiles [Q]) according to baseline NIHSS (Q1, 0–5; Q2, 6–10; Q3, 11–15; Q4, 16–20; and Q5 > 20), there was a statistically significant difference in the distribution of patients between the t-PA and placebo treatment groups.¹⁰ The Food and Drug Administration (FDA) clinical review of the NINDS rt-PA Stroke Study revealed that 13 subjects were randomized out of sequence. All these 13 subjects received placebo, where only two should have. In addition, 18 subjects were randomized in the wrong stratum (time from stroke onset to treatment: 0–90 min versus 91 to 180 min) and changed the assignments for 11 subjects, 10 had been changed from rt-PA to placebo, and only 1 from placebo to rt-PA. Among the 22 subjects whose treatment assignments were switched, the proportion of subjects switched from rt-PA to placebo was over 95%,¹¹ which leads to suspicion of selection bias.² The CAPPP trial compares the effects of angiotensin-converting-enzyme inhibitor (captopril) and conventional therapy on cardiovascular morbidity and mortality in patients with hypertension. Sealed and sequentially numbered envelopes with pre-generated randomization codes were used for randomization. A total of 10,985 subjects were enrolled from 536 health centers in Sweden and Finland. The primary endpoint was a composite of fatal and nonfatal myocardial infarctions, stroke, and other cardiovascular deaths. The primary endpoint events occurred in 363 patients in the captopril group and 335 in the conventional-treatment group with relative risk (RR) of 1.05 (95% CI: 0.90–1.22; p=0.52). Stroke (both fatal and non-fatal were significantly more common with captopril with RR of 1.25 (95% CI: 1.01–1.55; p=0.044). The investigators speculated that the difference in stroke risk is probably due to the lower levels of blood pressure obtained initially in previously treated patients randomized to conventional therapy.⁴ Although no significant test results were reported in Table 1 of the original study article for the comparison of the 19 baseline covariates, subsequent correspondence pointed out that small but highly significant differences between the two treatment groups exist in baseline height, weight, systolic and diastolic blood pressure (with respective p-values of 10⁻⁴, 10⁻³, 10⁻⁸, and 10⁻¹⁸).¹⁰ Frequent violations of the process of randomization by sealed numbered envelopes were blamed for the significant imbalances. A reanalysis based only on “those centers where randomization can be trusted” was recommended but was rejected by the original study team for practical reasons.¹² Researchers suggested that the result of the CAPPP trial be interpreted cautiously.¹

Table 1.

Baseline covariates and their original distribution in the NINDS rt-PA Stroke Study.^a

Baseline covariate	Type	rt-PA arm	Placebo arm	Test statisticsb	p-Value
Clinical center (1, 2, …, 8)	Categorical	(20, 29, 36, 74, 74, 8, 19, 52)	(19, 33, 36, 72, 76, 6, 18, 52)	0.6505	0.9987
NIHSS	Continuous	14.36 ± 7.46	15.21 ± 6.82	−1.4784	0.1398
Age (years)	Continuous	67.96 ± 11.33	65.92 ± 11.92	2.1898	0.0289
OTT (min)	Continuous	119.45 ± 37.38	119.95 ± 35.98	−0.1685	0.8662
Glucose (mg/dL)	Continuous	148.94 ± 70.68	150.60 ± 77.94	−0.2789	0.7804
Stroke subtypec	Categorical	(51, 136, 117, 8)	(30, 137, 135, 10)	6.9560	0.0733
Sex (M, F)	Categorical	(134, 178)	(128, 184)	0.2369	0.6265
Fibrinogen (mg/dL)	Continuous	320.72 ± 98.56	331.72 ± 97.39	−1.3397	0.1808
Weight (kg)	Continuous	76.72 ± 14.99	80.04 ± 17.46	−2.5481	0.0111
Systolic BP (mmHg)	Continuous	153.58 ± 21.91	152.67 ± 20.65	0.5292	0.5968
Diastolic BP (mmHg)	Continuous	84.85 ± 13.10	86.01 ± 13.25	−1.0790	0.2810

Note:

^aPlus–minus values are means ± SD.

^bTwo-sample t-test is used for all continuous baseline covariate, and chi-squared test is used for all categorical baseline covariates.

^cStroke subtype categories are small-vessel occlusive, cardioembolic, large-vessel occlusive, and other.

OTT: onset to treatment time; BP: blood pressure; NIHSS: National Institutes of Health Stroke Scale.

Both NINDS rt-PA Stroke Study and CAPPP trial used randomization code lists pre-generated with permuted block stratified by clinical centers.^3,4 Permuted block stratified by center is the most commonly used method in multicenter clinical trials, and has been recommended in the literature¹³ and in regulatory guidelines.¹⁴ Permuted block randomization provides a consistent balanced treatment allocation. When stratified by a baseline covariate, it attempts to balance the distribution of that covariate between treatment groups. Most multicenter trials are stratified by center either for practical reasons and/or because center is expected to be confounded with other known or unknown prognostic factors. However, in spite of its many documented advantages, permuted block randomization stratified by center has its limitations. First, stratification can only accommodate relatively few categorical baseline covariates, because the number of strata increases exponentially with the number of covariates included in the stratification. As a consequence, some well-known important prognostic covariates, such as baseline NIHSS score and age in the NINDS rt-PA Stroke Study and baseline blood pressure in the CAPPP trial, are left uncontrolled. Second, the permuted block randomization may yield a high proportion of deterministic assignments which could lead to selection bias when perfect blinding of treatment assignment is not possible. When a block size of two, four, or six is used, the proportion of deterministic assignment is 50%, 33%, or 25%, respectively.¹⁵ Contrary to common expectations, varying block size actually increases the proportion of deterministic assignment under the same maximal imbalance level.¹⁵ In multicenter trials, site investigators generally are limited to access study information for their own center only. Without stratification by center, deterministic assignments may not necessarily lead to selection bias. However, when the randomization is stratified by center, deterministic assignments create a threat of selection bias and could adversely affect the validity of the trial results, as shown in the 13 trials discussed in Berger.² In spite of these disadvantages, the stratified permuted block randomization remains the most popular method in clinical trials.

It is widely believed that the distribution of any known or unknown confounding factor tends to be balanced when the sample size is large, because the variance of the mean value of a random variable decreases as the sample size increases. However, at the end of the trial, if a test is conducted for the balance of a baseline covariate that is not included in the randomization algorithm, one in 20 such tests will show significant imbalance (p<0.05) purely by chance no matter how large the sample size; such is the meaning of type I error.¹⁶ This phenomenon has been reported in several journal articles. Altman and Dore¹⁷ found that among the 600 covariate balance tests from 80 trials published in the British Medical Journal, the Journal of the American Medical Association, the a, and the New England Journal of Medicine in 1987, 24 (4%) were significant at 0.05 level. Pocock and Assmann¹⁸ reviewed 50 trials published in these four journals during July to September 1997 and found 18 (6%) of the 299 baseline covariate balance tests reached p<0.05. In other words, every confounding factor has the same chance of having a significant imbalance distribution if its imbalance is not controlled by the randomization algorithm. If a trial has 10 such covariates and assume they are all independent to each other, the chance that at least one covariate has a significant imbalance at 0.05 level is greater than 40%. These imbalances could be attributable to chance, but in terms of the trial data, the empirical imbalances that are observed may complicate clinical interpretation of the data. This is what occurred in the NINDS rt-PA Stroke Study. The only way to prevent serious imbalances in the distribution of prognostically important baseline covariates is to include them in the randomization algorithm. Stratification can achieve balances, but limited to a few categorical covariates.

The minimization method independently proposed by Taves¹⁹ and Pocock and Simon²⁰ controls the treatment allocation imbalances in each of the baseline covariate margins in order to simultaneously achieve balances in the distribution of several covariates between treatment groups. Replacing covariate strata with covariate margins as the imbalance control unit, the minimization method allows more baseline covariates to be controlled by the randomization algorithm. However, the deterministic assignment dilutes the randomness of treatment allocation, leading to resistance of its use in clinical trials.^21,22

Atkinson^23,24 proposed an optimal biased coin algorithm aimed to minimize the variance of the estimate of the treatment for linear models. In general, using Atkinson’s algorithm leads to a high efficiency of the trial when compared to minimization.²⁵ The cross-product matrix calculation involved in the implementation of Atkinson’s algorithm can be simplified for implementation. In theory, Atkinson’s algorithm applies to both continuous and categorical covariates. The use of Atkinson’s algorithm in clinical trial practices is rarely reported, possibly because of the limitation on the linear model.

For clinical trials, most researchers agree that randomization is the best method for achieving comparability and the basis for statistical inference.¹³ Therefore, protection of treatment allocation randomness and prevention of serious baseline covariate imbalances are the primary goals of randomization. In this article, we propose a new randomization strategy, called minimal sufficient balance (MSB), to prevent serious imbalances in clinically justified important baseline covariates, with minimal but sufficient constraint on the simple randomization in order to preserve the randomness of the treatment allocation. This new randomization method is applied to the NINDS rt-PA Stroke Study data by computer simulation. Results show that serious imbalances can be prevented for five baseline covariates with minimal cost in treatment allocation randomness.

Methods

With random treatment assignments in sequentially enrolling clinical trials, baseline covariate imbalances are never entirely avoidable. Perfect balance on every important covariate is neither possible nor necessary. Baseline covariate imbalances should not be minimized without the consideration of the randomness of treatment allocation. The objective of the proposed new randomization strategy is to preserve treatment allocation randomness while preventing serious imbalance from all a priori specified important baseline covariates. The scheme has the following features.

1. Important baseline covariates identified based on clinical practices and previous clinical trials can be included in the randomization algorithm in order to prevent serious imbalances in any of them, thereby enhancing the comparability of the treatment groups with respect to these covariates.

2. Baseline covariates will be treated on the same data scale as they were collected. No categorization or dichotomization is needed for continuous covariates for randomization. Keeping the original data scale will increase the efficiency of covariate imbalance control.

3. Covariate imbalances are measured descriptively. One approach is with the p-value of the t-test for equality of the means of the two treatment groups for continuous covariates and the chi-squared test for categorical covariates. For multicenter clinical trials with a large number of centers, a one-sample binomial test can be used to evaluate the treatment imbalance within each clinical center. We recognize that testing for the homogeneity of baseline covariates at the end of randomized controlled clinical trials is strongly discouraged^26–29 because of the concerns for the invalid interpretation and misuse of the results of such tests. We use the p-values of these tests during the trial in the randomization algorithm as a quantitative measure for covariate imbalances only. If preferred, other measures for imbalances can also be considered.

4. In order to preserve the randomness of the treatment allocation, a biased coin assignment will be used only if: (1) some covariate imbalances exceed their pre-specified limits; and (2) these imbalances could be effectively reduced by a biased coin assignment for the current subject. Otherwise, a simple randomization will be used. The first condition has been used by several randomization designs, such as the Big Stick Design proposed by Soares and Wu,³⁰ and the Maximal Procedure proposed by Berger et al.³¹ that aims to balance the treatment allocation. We introduce the second condition in order to avoid the use of biased coin assignments in circumstances where placing the current subject in either treatment arm will have little or no difference in the imbalance of covariates or reduce the imbalance in some covariates and raise similar amount of imbalance in some other covariates.

The implementation of the MSB randomization strategy is illustrated with an example. Consider a two-arm balanced trial with m baseline covariates to be balanced in the randomization process. When a subject is ready for randomization, distributions of each baseline covariate between the two groups are evaluated based on the p-values of the imbalance tests (i.e., t-test for continuous and chi-squared test for categorical covariates).

For a continuous baseline covariate k, let n_a and n_b be the total number of subjects previously allocated to treatments A and B, respectively. Let x̄_ka, s_ka, x̄_kb, and s_kb be the mean and SD of covariate k for the two patient treatment groups. Let t_k, p_k, $t_k^{\ast }$, and $p_k^{\ast }$ represent the observed test statistic, the corresponding p-value, and their control limits, respectively. The test statistic of the t-test for the equality of the two means is: $t_k=({\overline{x}}_{ka}-{\overline{x}}_{kb})/\sqrt{s_{ka}^2/n_a+s_{kb}^2/n_b}$. For the current subject to be randomized, the choice between a biased coin and simple random assignment will be based on the test results and the current subject’s baseline covariate value x_k

$$\{\begin{array}{ll}\text{Vote}\text{for}A,\hfill & \text{if}[(t_k<-t_k^{\ast })\text{and}(x_k>{\overline{x}}_{kb})]\text{or}[(t_k>t_k^{\ast })\text{and}(x_k<{\overline{x}}_{kb})]\hfill \\ \text{Vote}\text{for}B,\hfill & \text{if}[(t_k<-t_k^{\ast })\text{and}(x_k<{\overline{x}}_{ka})]\text{or}[(t_k>t_k^{\ast })\text{and}(x_k>{\overline{x}}_{ka})]\hfill \\ \text{Neutral}\hfill & \text{otherwise}.\hfill \end{array}$$ (1)

Based on rule (1), if the current subject has a covariate value between the two treatment groups’ average values, neither treatment is favored because the two possible allocations, A or B, for the current subject yield little difference in the imbalance of the covariate.

For categorical covariate k with a small number of categories, such as gender (two categories) and stroke subtype (four categories), a chi-squared test can be used to descriptively assess the imbalance between the two treatment arms. Assume the covariate has g categories. Let n_kja, n_kjb represents the observed number of subjects in the category j of covariate k previously randomized to treatments A and B, respectively. Let E_kja, E_kjb be the expected number of subjects in the j category being allocated to treatments A and B

$$E_{\mathit{kjh}}=\frac{(n_{\mathit{kja}}+n_{\mathit{kjb}}){\sum }_{i=1}^g{n}_{\mathit{kih}}}{{\sum }_{i=1}^g(n_{\mathit{kia}}+n_{\mathit{kib}})},(h=a,b)$$ (2)

$${\chi }_k^2={\sum }_{i=1}^g{\sum }_{h=a,b}[{(n_{\mathit{kih}}-E_{\mathit{kih}})}^2/E_{\mathit{kih}}]$$ (3)

Based on the chi-squared distribution with (g − 1) degrees of freedom, if the corresponding p-value, p_k, is less than its control limit, $p_k^{\ast }$, the following rule is invoked

$$\{\begin{array}{ll}\text{Vote}\text{for}A,\hfill & \text{if}(p_k<p_k^{\ast })\text{and}(E_{\mathit{kja}}>n_{\mathit{kja}})\hfill \\ \text{Vote}\text{for}B,\hfill & \text{if}(p_k<p_k^{\ast })\text{and}(E_{\mathit{kjb}}>n_{\mathit{kjb}})\hfill \\ \text{Neutral}\hfill & \text{otherwise}.\hfill \end{array}$$ (4)

For multicenter clinical trials, randomization is often stratified by clinical center. With the MSB method, clinical center is considered as a categorical baseline covariate, and its marginal imbalance will be controlled in the same way as for other categorical covariates. However, for multicenter trials with many centers (say more than 10), the imbalance within a center can be measured by the difference between the observed allocation ratio within the center and the observed overall or target allocation ratio. In this case, a one-sample test for a binomial proportion can be used. Assume the current subject is in center j. Let n_ja, n_jb be the number of subjects in the center j previously randomized to treatments A and B, respectively. Let n_a, n_b be the total number of subjects previously randomized in the two treatment arms. When n_j = (n_ja + n_jb) ≥ 20, the normal-theory method can be used for the test. The test statistic is

$$z=\left(\frac{n_{ja}}{n_j}-\frac{n_a}{n}\right)/\sqrt{\frac{n_a}{n}\times \frac{n_b}{n}\times \frac{1}{n_j}}$$ (5)

Here, n is the total number of previously randomized subjects. When n_j = (n_ja + n_jb) < 20, the exact method will be used. The p-value for the exact method test is

$$p=\{\begin{array}{ll}2{\sum }_{i=0}^{n_{ja}}\left(\begin{array}{c}{n}_j\\ i\end{array}\right)\times {\left(\frac{n_a}{n}\right)}^i\times {\left(\frac{n_b}{n}\right)}^{n_{ja}-i}\hfill & \text{if}\frac{n_{ja}}{n_j}<\frac{n_a}{n}\hfill \\ 2{\sum }_{i=n_{ja}}^{n_j}\left(\begin{array}{c}{n}_j\\ i\end{array}\right)\times {\left(\frac{n_a}{n}\right)}^i\times {\left(\frac{n_b}{n}\right)}^{n_{ja}-i}\hfill & \text{if}\frac{n_{ja}}{n_j}>\frac{n_a}{n}\hfill \end{array}$$ (6)

For both the normal-theory and the exact methods, if the p-value of the one-sample binomial test, p, is less than its control limit, p^*, a vote is registered based on the following rule

$$\{\begin{array}{ll}\text{Vote}\text{for}A,\hfill & \text{if}(p<p^{\ast })\text{and}(n_{ja}/n_j)<(n_a/n)\hfill \\ \text{Vote}\text{for}B,\hfill & \text{if}(p<p^{\ast })\text{and}(n_{ja}/n_j)>(n_a/n)\hfill \\ \text{Neutral}\hfill & \text{otherwise}.\hfill \end{array}$$ (7)

After all baseline covariate imbalances are checked, the probability for assigning the current subject to treatment A is determined by rule (8)

$$Pr\{\text{Assign}\text{current}\text{patient}\text{to}A\}=\{\begin{array}{ll}\xi \hfill & \text{if}\text{Treatment}A\text{received}\text{more}\text{votes}.\hfill \\ 1-\xi ,\hfill & \text{if}\text{Treatment}B\text{received}\text{more}\text{votes}.\hfill \\ 0.5\hfill & \text{otherwise}.\hfill \end{array}$$ (8)

Here, ξ is the biased coin probability. The value of the biased coin probability can be selected based on the background of the trial. For two-arm balanced trials, ξ=0.65–0.70 is suggested. In practice, one can enforce a balanced allocation for the initial proportion of the trial with the random allocation rule³² within each clinical center in order to balance the risk of operation glitches that often occur in the early phase of the trial. A proper size of this initial proportion can be selected based on the total sample size and the number of clinical centers.

Results

The proposed MSB randomization strategy is applied with computer simulation to the NINDS rt-PA Stroke Study data obtained from the National Technical Information Service (http://www.ntis.gov). All 624 subjects are included in the computer simulation with their data on 11 baseline covariates, including eight continuous covariates and three categorical covariates (Table 1). In the original study, only imbalances in clinical center and dichotomized (0–90 min and 91–180 min) stroke symptom onset to treatment time (OTT) were controlled by a stratified permuted block randomization.

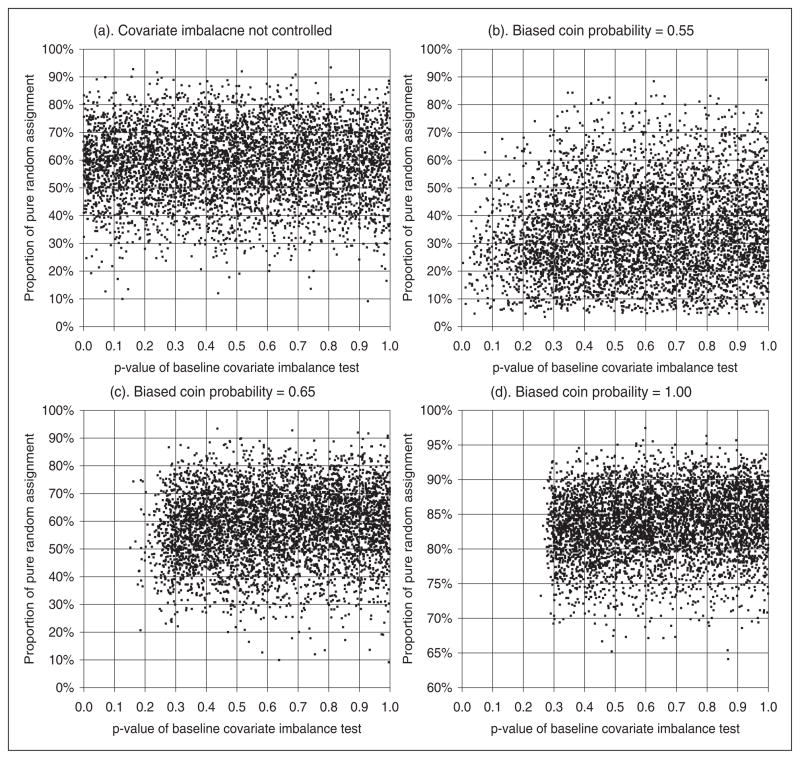
In this simulation study, five baseline covariates (clinical center, NIHSS score, age, OTT, and glucose), are included in the randomization algorithm. A random subject enrollment sequence is generated for each simulation run. The first 20 subjects in each simulation run are assigned with the random allocation rule. Subsequently, the MSB algorithm is applied with imbalance control limit set to p-value ≥ 0.3 for the five covariates. The biased coin probability varies from 0.55 to 1.0. At the end of each simulation run, tests for imbalances between the two treatment groups are conducted for all 11 baseline covariates, including those not balanced by the randomization algorithm. The p-values of these tests are recorded, together with the proportion of biased coin assignments. At the end of 5000 simulation replicates, the performance of the randomization algorithm is evaluated based on the covariate imbalance as measured by the p-values of imbalance tests, and the allocation randomness as measured by the proportion of biased coin assignments. Figure 1 shows the distribution of p-values of imbalance tests based on the computer simulation results.

Figure 1.

Baseline covariate balancing with MSB randomization. NINDS rt-PA stroke study data. Imbalance control limit p-value >0.3, number of controlled covariate=5, simulations=5000. Covariates included in randomization algorithm: clinical center, NIHSS, age, OTT, glucose. Imbalance control limit: p-value ≥0.3. NIHSS: National Institutes of Health Stroke Scale.

As shown in Figure 1(a), for those baseline covariates not included in the randomization algorithm, the p-value for imbalance test is uniformly distributed on [0, 1]. As the biased coin probability increases, the distribution of the p-values of baseline covariate imbalance tests is pushed to the right, as shown in Figure 1(b) and 1(c). When deterministic assignment (ξ = 1.0) is used, the chance that an imbalance test having a p-value less than the control limit 0.3 is trivial, as shown in Figure 1(d). In practice, a biased coin probability of 0.65 is sufficient to prevent serious imbalances. The results shown in Figure 1 demonstrate the effectiveness of the MSB algorithm in the control of baseline covariate imbalance. When a biased coin probability ξ ≥ 0.65 is used, serious imbalances, defined as p<0.05, can be completely prevented for the distribution of NIHSS, age, OTT, glucose, and clinical center between the two treatment groups. On the other hand, all baseline covariates not included in the randomization algorithm have a p-value with a uniform distribution on [0,1], as shown in Figure 1(a). The chance of having a p<0.05 for the imbalance test for any of these covariates is always 5%. Table 2 lists the cumulative probability distribution of p-values for the imbalance tests for all 11 baseline covariates obtained from computer simulations.

Table 2.

Distribution of p-values for baseline covariate imbalance tests with five covariates controlled.^a NINDS rt-PA Stroke Study data, imbalance control limit p-value ≥0.3. Biased coin probability=0.65, simulations=5000

p-Value	Covariates Included in the randomization algorithm					Covariates not included in the randomization algorithm
	Clinical center	NIHSS	Age	OTT	Glucose	Stroke subtype	Sex	Fibrinogen	Weight	Systolic BP	Diastolic BP
Low 2.5% boundary	0.3029	0.3054	0.3057	0.3076	0.3027	0.0315	0.0317	0.0259	0.0272	0.0267	0.0290
Low 5% boundary	0.3205	0.3236	0.3250	0.3266	0.3175	0.0619	0.0567	0.0514	0.0605	0.0491	0.0562
Low 10% boundary	0.3571	0.3593	0.3610	0.3650	0.3532	0.1095	0.1124	0.0985	0.1110	0.1024	0.1080
Median	0.6461	0.6402	0.6461	0.6523	0.6425	0.5041	0.5070	0.4912	0.5116	0.4946	0.4979
Observed in the original Study	0.9987	0.1398	0.0289	0.8662	0.7804	0.0733	0.6265	0.1808	0.0111	0.5968	0.2810

Note:

^at-Tests for the equality of means between the two treatment groups are used for continuous covariates. Chi-squared tests for the relationship between treatment allocation and covariate value are used for categorical covariates.

OTT: onset to treatment time; BP: blood pressure; NIHSS: National Institutes of Health Stroke Scale.

In this simulation, a biased coin assignment (ξ = 0.65) could be used when some of the five baseline covariates have imbalance test p-value greater than 0.3. Computer simulation results show that there is a 97.5% chance that the p-value of imbalance test for a baseline covariate included in the randomization is greater than 0.30. This result addresses the concerns about the comparability of the treatment groups, and to prevent controversial interpretation of trial results.

The cost of baseline covariate balance is the randomness of treatment allocation. With the proposed MSB randomization algorithm, the treatment allocation randomness can be evaluated by the proportion of pure random assignments and the correct guess probability of the treatment allocation. A higher biased coin probability is associated with a higher proportion of pure random assignments. However, this does not mean that a high biased coin probability leads to an overall high randomness of treatment allocation. In the MSB randomization process, treatment allocations are either done purely randomly or using the biased coin probability. The correct guess probability for the purely random proportion is always 50%. The correct guess probability for the other equals the biased coin probability. Table 3 shows the relationship between the biased coin probability used in the MSB randomization and the overall randomness of treatment allocation.

Table 3.

Relationship between the biased coin probability and the treatment allocation randomness. NINDS rt-PA Stroke Study data, imbalance control limit p-Value ≥0.3 for five covariates. 1000 simulation/scenario

Biased coin probability	ξ	0.5	0.525	0.55	0.575	0.6	0.65	0.7	0.8	0.9	1.0
Median proportion of pure random assignments	Mr	100%	24.8%	32.4%	40.2%	46.8%	58.8%	66.2%	75.3%	80.9%	83.8%
Overall correct guess probabilitya	CG	50.0%	51.9%	53.4%	54.5%	55.3%	56.2%	56.8%	57.4%	57.6%	58.1%

Note:

^aCG= ξ × (1 − M_r) + 0.5 × M_r.

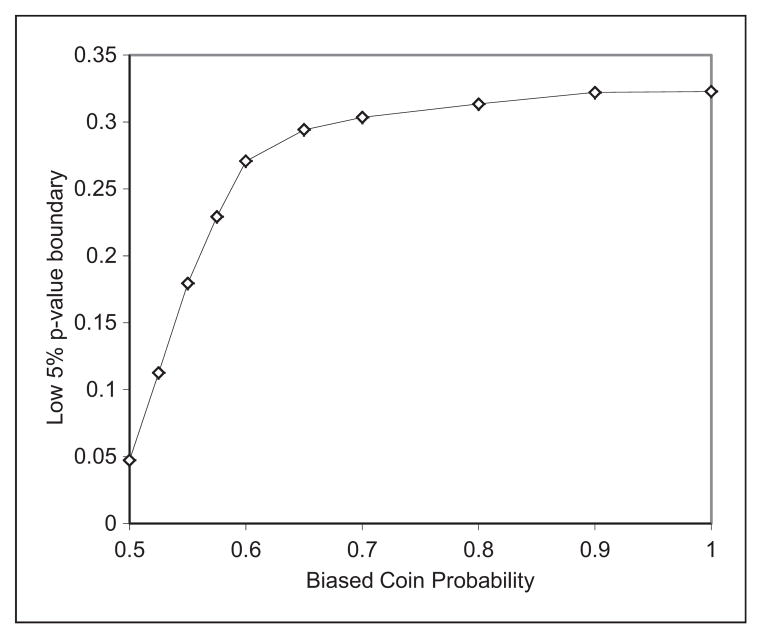
As a comparison, the commonly used permuted block randomization has a proportion of deterministic assignment of 20%, 25%, 33%, and 50%, and a correct guess probability of 66%, 68%, 71%, and 75% when the block size is 8, 6, 4, and 2, respectively.¹⁵ Data in Table 3 show that the MSB randomization has much higher treatment allocation randomness than the permuted block design. The value of the biased coin probability affects the effectiveness of covariate imbalance control. Although the imbalance control limit is set to p-value > 0.3 in the simulations, when an imbalance exceeds this limit, the chance the imbalance being reduced equals the biased coin probability. Figure 2 shows the impact of the biased coin probability on the low 5% boundary of the p-values of imbalance tests for baseline covariates controlled by the MSB randomization algorithm. For example, when ξ = 0.6, the chance a covariate controlled by the randomization algorithm having a p-value of imbalance test less than 0.27 is 5%. In other words, there is a 95% chance the p-value of imbalance test is greater than 0.27. Based on computer simulation results shown in Figure 2, as the biased coin probability increases, a better covariate balancing is expected. However, the benefit of large biased coin probability gradually decreases when the biased coin probability is greater than 0.6. In practice, we recommend that a biased coin probability be selected between 0.6 and 0.7.

Figure 2.

Impact of bias-coin probability on imbalance control. NINDS rt-PA: National Institute of Neurological Disorders and Stroke recombinant tissue plasminogen activator.

To further evaluate the baseline covariate balancing capacity of the MSB randomization algorithm, computer simulation was conducted to balance all 11 baseline covariates listed in Table 1. In clinical trial practice, a need to balance this number of baseline covariates would be rare. The purpose of this simulation is to examine the potential capacity of the proposed MSB method. Results of this simulation are shown in Table 4. For any of the 11 baseline covariates, the chance of having a p-value less than 0.2 in the imbalance test is smaller than 2.5%. There is a 95% chance the p-value of such test will be greater than 0.27. The cost of maintaining balance on 11 baseline covariates is a median of 40% biased coin assignments at ξ = 0.65.

Table 4.

Distribution of p-values for baseline covariate imbalance tests with 11 covariates controlled.^a NINDS rt-PA Stroke Study data, imbalance control limit p-value ≥0.3. ξ =0.65, simulation=1000/scenario

p-Value	Clinical Center	NIHSS	Age	OTT	Glucose	Stroke subtype	Sex	Fibrinogen	Weight	Systolic BP	Diastolic BP
Low 2.5% boundary	0.226	0.259	0.237	0.262	0.244	0.262	0.214	0.245	0.239	0.252	0.246
Low 5% boundary	0.276	0.295	0.279	0.288	0.280	0.292	0.277	0.288	0.278	0.281	0.287
Low 10% boundary	0.309	0.341	0.316	0.323	0.315	0.326	0.309	0.322	0.319	0.322	0.330
Median	0.605	0.631	0.626	0.624	0.624	0.638	0.609	0.634	0.626	0.638	0.610
Observed in the Original study	0.9987	0.1398	0.0289	0.8662	0.7804	0.0733	0.6265	0.1808	0.0111	0.5968	0.2810

Note:

^at-Tests for the equality of means between the two treatment groups are used for continuous covariates. Chi-squared tests for the relationship between treatment allocation and covariate value are used for categorical covariates.

OTT: onset to treatment time; BP: blood pressure; NIHSS: National Institutes of Health Stroke Scale.

Discussion

Baseline covariates could have strong prognostic value on the primary outcome in many clinical trials. Sometimes the baseline disease severity measured by NIHSS, age, time from stroke onset to treatment, and glucose could explain more on the variation in the outcome of an acute stroke trial than the study treatment. In a randomized study, the objective is to equalize the distribution of such factors within each treatment groups so as to minimize biases due to covariate imbalances.³² Having a balanced distribution of these important baseline covariates between the treatment arms can facilitate acceptance of trial results and minimize potential for controversial interpretations. Currently available randomization methods are limited to balance few categorical baseline covariates and at a cost in treatment allocation randomness. The proposed MSB randomization strategy provides a practical solution to this problem.

Interim analyses are commonly used in clinical trials. Balanced baseline covariates are expected at interim analyses in order to reduce the potential confounding effects from baseline covariates. Using the MSB, serious imbalances are prevented throughout the entire study for continuous as well as categorical covariates. Although the computer simulation results presented in the previous section refer to the end of the trial with 624 subjects, similar results have been obtained at the time points when 100, 200, or 300 subjects were randomized. This should allow a data safety and monitoring board to make decisions on futility or overwhelming efficacy with the knowledge that their decision is maximally protected against undue influence by random imbalance on a critical covariate or combination of covariates.

Implementation of the proposed MSB method requires the support of a computerized real-time central randomization system, such as a web-based system or an interactive voice response system. As the availability of modern information technology increases in trial data management and coordinating centers, this requirement should not hinder implementation of the MSB method. With the central randomization system, randomization problems associated with sealed envelopes can be fully eliminated. As the entire randomization algorithm is programmed in to the computer system, no human involvement is necessary to perform imbalance checks. Therefore, there is no concern for unblinding. The proposed MSB has a much higher level of allocation randomness than commonly used randomization designs, such as permuted block and minimization. For example, when the MSB design is implemented with three covariates, pure random assignments will be used for a median of about 90% of subjects, compared to 42% in permuted block design with a block size of 4, and almost zero in minimization. In practice, even if information on baseline covariates and treatment assignments is available for all previously randomized subjects within a specific clinical center, such as the case of open-label trials, site investigators will have no basis to incur selection bias if the treatment allocation is actually purely random, and the randomization is performed in real-time. Therefore, the risk of selection bias for the proposed MSB design is practically negligible.

In comparative clinical trials, the type I error (false positive), the type II error (false negative), and the variance of the estimator of the treatment effect can be affected by baseline covariates if these covariates affect both the primary outcome and the treatment allocation. A balanced baseline, achieved with MSB or other constrained randomization designs, reduces the variability of the difference in the outcomes between treatment groups, and therefore helps to reduce both type I and type II errors.³³ The actual amount of benefit varies based on the type of the outcome and the data analysis model. Rosenkranz studied the impact of randomization method on the analysis of clinical trials with computer simulation, and elaborated that the impact can be substantial. We noticed that this conclusion was made based on a special scenario which in our mind is unlikely in large phase III trials. Further works are needed to quantify the impact of randomization methods, including the MSB, on the type I, type II errors, and the variance of the estimators under specific trial conditions.

In the proposed approach, one of the inherent assumptions is that the covariates are independent. It is not uncommon in clinical trials that some covariates are strongly correlated to each other. To accommodate the correlations, a multivariate extension could be considered. One could also consider data reduction methods such as principle components to combine the correlated covariates using optimal linear combinations. Subsequently, proposed method could be applied to the imbalance observed in this linear combination. This approach would be especially appealing when clinical interpretations of these linear combinations are available.

In addition to balancing the distribution of baseline covariates in the randomization process, other efforts have been made to address the challenges from baseline covariates, including covariate adjusted analysis and subgroup analyses.^34–38 Unless pre-specified before the trial initiation, the value of these post hoc analyses are limited. Most recently, a matching algorithm has been proposed to obtain pairs of subjects with close baseline profiles and eliminate unmatched “outliers” from the efficacy analysis.⁹ Such an approach violates the intent-to-treat (ITT) principle. Analysis results from such a matched dataset do not have the merit of randomized controlled clinical trials.

Although the proposed randomization method can technically prevent serious imbalances in a large number of baseline covariates, we do not advocate the balancing of a large number of baseline covariates. It is important to point out that, when a covariate in included in the randomization algorithm, one should include that covariate in the primary analysis and to interpret the trial results accordingly. The European statistical guideline requires that all factors used in the stratification and minimization be included in the primary analysis. It also recommends that “no more than a few” covariates should be included in the primary analysis.¹⁴

The cost of clinical trial is rising rapidly.³⁹ Although US FDA generally requires two well-controlled clinical trials for New Drug Applications, it is difficult to replicate large trials in practice with limited resources. Hence, it would behoove the investigators to insure that the trial results raise a few, if any, controversial issues by applying randomization procedure that prevents serious baseline covariates yet maintaining randomness of treatment allocation, like the proposed MSB method.