Early Stages of the HIV-1 Capsid Protein Lattice Formation

Abstract

The early stages in the formation of the HIV-1 capsid (CA) protein lattice are investigated. The underlying coarse-grained (CG) model is parameterized directly from experimental data and examined under various native contact interaction strengths, CA dimer interfacial configurations, and local surface curvatures. The mechanism of early contiguous mature-style CA p6 lattice formation is explored, and a trimer-of-dimers structure is found to be crucial for CA lattice production. Quasi-equivalent generation of both the pentamer and hexamer components of the HIV-1 viral CA is also demonstrated, and the formation of pentamers is shown to be highly sensitive to local curvature, supporting the view that such inclusions in high-curvature regions allow closure of the viral CA surface. The complicated behavior of CA lattice self-assembly is shown to be reducible to a relatively simple function of the trimer-of-dimers behavior.

Introduction

The lifecycle of type 1 human immunodeficiency virus (HIV-1) depends on the budding of a spherical, membrane-bound, and initially noninfectious, immature virion from the surface of an infected cell (1–3). A major structural component of the immature virion is the Gag polyprotein, which features a number of protein domains (MA, CA, SP1, NC, and SP2) that are later released under enzymatic cleavage as the virion matures. The intact Gag molecule forms an incomplete hexagonal lattice across the surface of the immature virion (2,4), with the hexameric bundles of Gag stabilized by interactions between the SP1 domains (intrahexamer) and the C-terminal region of the capsid protein (CA) domain (interhexamer) (1,3).

Crucial for the production of a mature and infectious HIV-1 virion is the oligomerization of CA protein dimers into a distinctive cone-shaped capsid structure encapsulating the viral RNA subsequent to Gag cleavage (4–10). The walls of the capsid are formed from a characteristic lattice of CA dimers that features hexameric or pentameric rings of adjacent N-terminal domains (NTDs) interconnected via an outer ring of C-terminal domains (CTDs) (10). The mature CA lattice is quite distinct from the incomplete hexagonal Gag assemblies observed on the surface of the immature virion. For example, the mature CA lattice shows different lattice spacing compared with that of Gag (9.6 nm (6) vs. 8 nm (1–3)), and the SP1 domain of the Gag polypeptide (which is crucial for the formation of the immature Gag lattice (1,3)) is entirely absent from the mature CA lattice. The mature CA lattice also presents a closed surface via the inclusion of a small number of CA pentamers in addition to the ∼250 CA hexamers, according to Euler’s theorem (5). Despite the relative abundance of experimental data describing both immature and mature HIV-1 virion structures, little is known about the early-to-intermediate stages of viral maturation during which enzymatically cleaved CA protein assembles into the mature viral capsid.

Mature CA is known to dimerize readily in solution (11), to the extent that monomer concentrations may be effectively undetectable (12). The fundamental unit of mature lattice formation would therefore appear to be the CA dimer, and mutation studies (7,9) and structural measurements (8) have demonstrated that the dimer interface is located at the CTD of the CA protein. Recent NMR studies (8) suggested that the solution-state dimer interface is also a likely candidate to connect adjacent hexamers in the viral capsid; however, the pentameric arrangements of the CA protein require a distinct dimer interfacial structure for connection to the surrounding hexamers (10), and hence some flexibility must be present in the dimer interface to accommodate such variation. In addition to limited dimer interfacial flexibility, it has been proposed that pivoting motions of CA CTDs relative to the NTDs provide a mechanism to enable the continuous curvature observed in viral capsids (10,13).

CA protein can spontaneously assemble into various naturally curved surfaces in vivo and in vitro, and both cylindrical (5,8,14,15) and conical (5,6) morphologies have been observed in experiments. Nonetheless, the presence of sheets of mature-style p6 lattice seem ubiquitous to such assemblies, and sheet-like organizations of CA with natural curvature are therefore an appealing theoretical model for studies of self-assembly in the mature CA lattice. Here we present a, to our knowledge, novel coarse-grained (CG) computational study of CA lattice self-assembly and dynamics, with particular attention paid to the specifics of the assembly process under the influence of CA dimer flexibility, local surface curvature, and protein concentration to elucidate the early and intermediate stages of HIV-1 CA lattice formation. The large number of CA dimers present in any significant p6 lattice region, and the relatively long timescales required for self-assembly processes make the use of detailed all-atom models of the CA dimer lattice problematic, although all-atom simulations of an intact tobacco mosaic viral capsid have been reported previously (16). Instead, in this work we parameterized the CG model of CA directly from experimental constraints (10) and eliminated many of the explicit molecular degrees of freedom to generate a simpler and less computationally expensive representation of the CA protein. Previous CG studies of viral capsids typically used models of the intact hexamer or pentamer subunits via direction-dependent bond-vector type interactions (17–19) or shape-based approximations (19–23), although more detailed CG models of viral capsids in general are emerging (12,24,25).

Materials and Methods

Model generation

Experimental hexamer (9,26,27) and pentamer (10) structures for HIV-1 CA were examined, and the monomer α-helical structures were found to be conserved (Fig. S1 in the Supporting Material). Chain F of the 3H4E structure (9) was used as a template for CG model generation due to the essentially complete atomic coordinates, with a CG bead inserted for each full turn of the 11 CA α-helices to reproduce the monomer shape and implicitly model outward-facing residues of each α-helix as a single CG bead interaction. Because the CTD of the template structure, and particularly the important helix 9 of the CTD (7), appeared to be deformed, this region was replaced with the CTD of the 2KOD structure (8), which is believed to be the major dimer interfacial motif in the mature CA (26). The final CG monomer was considered as a rigid body. A comparison of the CG model with an all-atom CA monomer is presented in Fig. 1, A and B.

Figure 1.

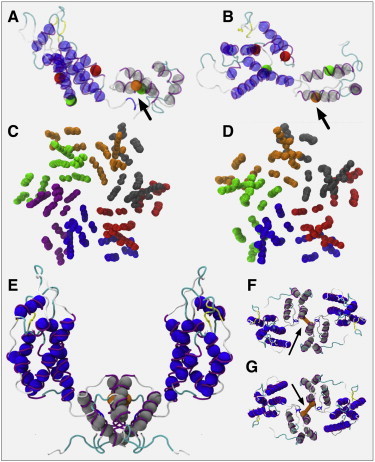
(A) Side and (B) top views of the CG CA monomer structure (spheres) alongside the all-atom template structure backbone (transparent ribbons). NTD of CA are represented as darker gray spheres (blue online), CTD as lighter gray; location of harmonic restraint on helix 9 for the flexible dimer model indicated with arrows. (C and D) Superpositions of the CG CA monomer onto the various experimental hexamer and pentamer structures, with monomer colors varied for clarity. (E–G) Also shown are a side view of (E) and views from above (F) and below (G) the HIV-1 CA dimer model structure, with flexible dimer restraint indicated with arrows.

The default CG bead interaction is a repulsive Morse potential to approximate an impenetrable sphere, with the onset of the excluded volume radius set to ∼12 Å, approximately the diameter of the underlying α-helix, to prevent unphysical helix overlaps. CG monomers were superposed onto experimental hexamer and pentamer structures (Fig. 1, C and D), and any CG bead separations of <12 Å between adjacent CG monomers were reparameterized to the smallest distance in either pentamer or hexamer structures to avoid a priori bias against pentamer or hexamer formation via excluded volume. A Lennard-Jones 12-6 potential energy well replaced the Morse repulsion for two specific CG bead pairs to reproduce conserved experimental close contacts between CA monomers (Fig. 1, A–D), with bead locations corresponding to known important NTD-NTD (helices 2 and 3) and NTD-CTD interactions (helices 4 and 8) (7). The NTD-CTD interaction, for example, is located at a helix-capping interaction that is believed to act as a molecular pivot between adjacent CA proteins in the mature p6 lattice (10). The choice of a Lennard-Jones 12-6 potential allows for a computationally convenient and efficient attractive energy at defined bead separations, while retaining a strong repulsive energy at close ranges to avoid unphysical overlaps between interacting α-helices.

Dimer interfacial structures with PDB accession codes 1A43 (28) and 2KOD (8) were examined by superposing the template all-atom CTD onto the CTDs of the dimer interfaces, with separations across the dimer interface of the C_β atoms on residue 185 (which is important in HIV-1 infectivity (29)) found to be conserved (9.18 Å (1A43) and 9.17 Å (2KOD)). The CG beads were placed at the C_β centers of mass and then linked by a harmonic bond of equilibrium length 9.18 Å to form a flexible dimer model (see Fig. 1, E–G). A rigid dimer model was created by superposing CG monomers onto the CTDs of the 2KOD structure, with the entire dimer structure considered as a rigid body. The final Hamiltonian of the system is calculated as:

$$V=\sum _{i,j\in excl}{D}_0\left[e^{-2\alpha \left(r_{ij}-r_0\right)}-2e^{-\alpha \left(r_{ij}-r_0\right)}\right]+\sum _{i,j\in NN}4{\epsilon }_{NN}\left[{\left(\frac{{\sigma }_{NN}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{NN}}{r_{ij}}\right)}^6\right]+\sum _{i,j\in NC}4{\epsilon }_{NC}\left[{\left(\frac{{\sigma }_{NC}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{NC}}{r_{ij}}\right)}^6\right]+\sum _{i,j\in bound}{K}_{bond}{\left(r_{ij}-r_{bond}\right)}^2+\sum _{i\in restr}{K}_{restr}{\left(r_i-r_{i,restr}\right)}^2$$ (1)

Here excl denotes purely repulsive Morse potentials (D₀ = 0.001 kcal mol⁻¹, α = 4.5 Å⁻¹, r₀ = 12 Å with cutoff 12 Å), and NN and NC are the pairs of sites involved in the LJ 12-6 NTD-NTD and NTD-CTD interactions (σ_NN = 7 Å, σ_NC = 7.5 Å with a cutoff of 25 Å). The harmonic bond restraint (K_bond = 0.1 kcal mol⁻¹ Å⁻², r_bond = 9.17 Å) is only considered for the bound sites in the flexible dimer model. The final harmonic restraint term in the Hamiltonian is applied only where dimers are restrained to a planar or spherical surface, with a weak spring constant K_restr of 0.05 kcal mol⁻¹ Å⁻², to allow limited out-of-surface motions.

All simulations were performed in the canonical ensemble (constant NVT) using the LAMMPS molecular-dynamics (MD) code (30) and a Nose-Hoover thermostat (31), with production data generated from 2 × 10⁷ simulation time steps of 4 fs and trajectory snapshots saved every 10⁴ time steps. CG models blur the connection to real-world time measurements, and therefore the CG MD times reported should not be considered to directly represent any experimental timescale. To ensure increased computational efficiency due to fewer interacting sites and the absence of solvent friction, no explicit solvent was used. Initial planar configurations of p6 lattice were generated from crystal cell expansion of the 3H4E PDB structure (9) containing 112 monomers. Planar systems were initially heated to 10⁴ K for a minimum of 5 × 10⁴ time steps of 5 fs for disordered starting positions, and random velocity distributions were then assigned. Planar simulations used periodic boundary conditions and the minimum image convention. Initial spherical configurations were generated by random insertion of CG dimers onto a spherical surface of radius, producing the desired surface density. Periodic boundary conditions were unnecessary in the spherical simulations.

Protein surface coverage values, ρ, are the proportion of the total simulation surface area covered by a hexameric lattice of spacing 8 nm (as in the immature Gag lattice (3)), broadly corresponding to experimental measurements for convenience (4). Although ρ is calculated according to the immature lattice, the stabilizing CA and SP1 domain interactions of the Gag lattice are also present in the CA-SP1 intermediate (32), which could stabilize regions of immature lattice after CA-SP1 release, and thus the formation of mature p6 lattice may begin in regions of CA density comparable to the immature Gag lattice.

Structures of interest were identified by recursive searches of adjacent monomers of separation ≤ 15 Å for the native NTD-NTD and NTD-CTD contacts. Varying the cutoff distance was found to have only minor qualitative effects on the results presented.

Results and Discussion

The CG model reproduces known CA lattice structures

CG CA dimer models were generated based on conserved structures and distances from experimental measurements (see Materials and Methods). To ensure that the resultant CG model could adequately reproduce a model HIV-1 viral capsid (an important test in justifying the choices made in the model generation), CG dimers with a flexible dimer interface were superposed onto the putative capsid structure of Pornillos et al. (10), and a series of CG MD simulations were performed to determine the important native-contact NTD-NTD and NTD-CTD interaction strengths (denoted by ε_NN and ε_NC) that are required to stabilize the mature capsid morphology. The flexible dimers feature a conserved intermonomer distance that is common to the dimer interfaces that are thought to link adjacent hexamers and hexamers to pentamers in the mature viral capsid (10) (see Materials and Methods), and also approximates the NTD-CTD pivoting that is believed to be necessary for continuous curvature in viral capsids (10,13). The dimer interface was allowed complete flexibility to avoid a priori bias toward either of the dimer interfacial configurations. Starting with the large values of ε_NN/k_BT = ε_NC/k_BT = 42.0, ε_NN and ε_NC were reduced in tandem every 1 × 10⁷ steps to determine the minimum attractive strength required to stabilize the mature capsid structure at 310 K (Fig. 2).

Figure 2.

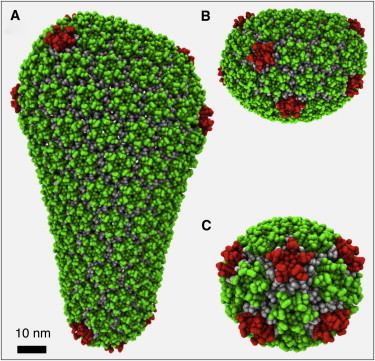
(A) Simulation snapshot of the CG model of the equilibrated mature conical capsid model of Pornillos et al. (10). (B and C) Details of the top (B) and bottom (C) of the mature conical capsid model are also shown. NTDs of hexamer- and pentamer-associated proteins are in lighter and darker gray respectively (green and red online).

Instabilities appeared in the pentameric capsid inclusions for ε_NN/k_BT = ε_NC/k_BT < 9.74 as one or more pentamer-associated monomers broke loose from the CA lattice surface, although the conjugate monomers of the respective dimers remained associated with the surrounding lattice. This value is likely an overestimate of the attractive interactions required to stabilize the capsid in the presence of greater dimer structural rigidity. The similarity of the dimer interface recorded via solution-state NMR to that linking adjacent hexamers in the mature capsid structure (8,10) suggests that the CA dimer interface is naturally somewhat inflexible, and this restricted flexibility would hinder the ability of pentamer-associated monomers to dissociate in the manner observed. The precise flexibility of the dimer interface may be influenced by the loop region connecting helices 8 and 9 of a CA CTD with adjacent NTDs in the mature lattice (9), and hence is potentially sensitive to the local environment. For generality, we therefore constrained the dimer interface only with a conserved experimental intradimer distance to avoid biasing the dimer interfacial structure (see Materials and Methods). The natural stability of this CG model in a mature capsid morphology demonstrates a significant improvement over our previous, more highly CG models of the HIV-1 CA protein, which required the imposition of additional three- and four-body potentials to generate native-style p6 lattice organizations (25), and thus supports the choices made in the CG model generation.

To investigate the ability of the CG model to self-assemble into mature p6 CA lattice (rather than simply remaining stable when placed into existing CA lattice configurations), we performed further simulations using disordered systems of 56 CG dimers weakly restrained to a quasi-2D planar surface to encourage CA lattice formation. The structure of the mature CA lattice is not a simple isotropic aggregate of protein dimers, because the lateral association of adjacent CA proteins is enforced by the shape of the molecules and the nature of the native NTD-NTD and NTD-CTD contacts, and hence these quasi-2D systems are not expected to significantly alter the mechanisms of lattice formation.

To examine the effects of dimer interfacial rigidity on CA lattice self-assembly, we considered two different CA dimer models. The first model featured the same flexible dimer interface as used in the mature capsid simulations described above, and the second dimer model was a completely rigid unit based on the 2KOD PDB structure that is believed to link the adjacent hexamers that form the bulk of the mature viral capsid (8,10). For both types of dimer interface, the interaction strengths of the native NTD-NTD and NTD-CTD contacts were varied independently for surface coverage values of ρ = 0.38 to 0.6 in steps of Δρ = 0.02 (see Materials and Methods) to determine their influence on the lattice self-assembly process.

Visual inspection of the quasi-2D simulation trajectories revealed the formation of distinctive trimer of dimers structures in addition to the familiar pentameric and hexameric CA assemblies (Fig. 3 A), and this arrangement was particularly prominent for completely rigid dimer interfaces (Fig. 3 B). Also apparent was the propensity of all three structural motifs to form at significantly lower attractive strengths for the completely rigid dimer model (Fig. S2, Fig. S3, and Fig. S4). The ability of the same CG model to self-assemble into both pentamers and hexamers lends further support to the suitability of our model for studying CA lattice self-assembly, because it is compatible with the well-established quasi-equivalence theory for HIV-1 CA subunits (9,10,27), which explains the presence of both pentameric and hexameric inclusions on the basis of these structures being stabilized by essentially the same interactions, as is the case in our model. Because the positions were saved every 10⁴ MD integration steps, the temporal resolution of these data is somewhat limited; nonetheless, there was a clear trend for the maximum trimer-of-dimers content being higher than the hexameric content, which was in turn higher than the pentameric content for the range of interaction strengths and surface densities studied. The lack of pronounced asymmetry in the data as a function of the NTD-NTD and NTD-CTD interaction strengths ε_NN and ε_NC (except possibly in the case of trimer-of-dimers content for rigid dimer interfaces at high ρ; see Fig. S3 B and Fig. S4 B) suggested that separate ε_NN and ε_NC could be replaced by one single effective interaction strength, ε, for simplicity.

Figure 3.

CG simulation snapshots of planar self-assembly for the model HIV-1 CA dimer lattice. NTDs are colored by association with hexamers (light gray, green online), pentamers (medium gray, red online), and trimer-of-dimers (dark gray, blue online); when the NTDs are part of both a trimer-of-dimers and a pentamer or hexamer, the color is that of a pentamer or hexamer. Monomers that are not associated with the three structure types are omitted for clarity. (A) Early stage of a flexible dimer simulation with the three major structural motifs present (left) and later stage of same simulation, with the onset of mature p6 lattice formation visible (right). (B) Rigid dimer interface simulations showing enhanced trimer-of-dimers presence and the manner in which such structures may combine via native NTD-NTD and NTD-CTD contacts to form mature lattice precursors. (C) All-atom representation of the trimer-of-dimers structure, with CTD dimer interfaces indicated with lines and the location of NTD hexamer rings indicated with hexagons. Also shown is the CG representation of the trimer-of-dimers structure, with the location in a region of mature-style p6 lattice indicated by the triangle (same color scheme as in A and B). All simulations at ρ = 0.5, with A and B showing two periodic images.

The trimer-of-dimers structure highlighted here is not without precedent. In CG Monte Carlo studies of HIV-1 CA assembly, Chen and Tycko (12) also noted the appearance of similar structures, albeit using a rigid dimer model parameterized from planar CA crystal data (9). The ability of triangular components to generate mature-style viral capsid morphologies was also demonstrated in the simulations of Levandovsky and Zandi (33), in which capsid formation was modeled phenomenologically by the permanent addition of triangular elements to the expanding edge of a connected surface, indicating that such structures can indeed combine to form contiguous regions of hexagonal lattice, as suggested by the nature of the trimer-of-dimers aggregation in Fig. 3, B and C. Tsiang et al. (34) recently released a mathematical model of CA protein cylinder formation, parameterized from the kinetics of experimental polymerization assays, that supports a trimer-of-dimers structure as an important intermediate assembly component. The trimer-of-dimers structure is stabilized by the same native NTD-NTD and NTD-CTD contacts found in both pentamers and hexamers, and hence it would be expected that compounds that are experimentally known to disrupt, such as the NTD-CTD interactions between adjacent CA proteins (e.g., CA-I (35,36) and CAP-1 (37,38)), would likewise adversely affect a trimer-of-dimers formation and hence impede mature capsid formation.

The attractive interaction strength that is sufficient to stabilize the mature capsid in a 3D system, ε/k_BT = 9.74, is likely a significant overestimate of the energy required to stabilize p6 lattice regions in these quasi-2D systems, because the entropy available to the CA dimers in the unrestrained 3D simulation is by definition larger than the conjugate projected entropy of the quasi-2D system, given the additional restrictions on dimer positions and orientations. Greater attractive energies were therefore required to balance the more entropically favorable dissociation of the lattice structure at equilibrium in 3D, according to the free-energy change of moving from the ordered lattice structure to a disordered arrangement of CA dimers.

Mature HIV-1 CA lattice formation is nucleated by triangular arrangements of three CA dimers

The mature CA p6 lattice typically displays an innate curvature, as demonstrated by the morphology of not only the mature conical capsid but also the cylindrical arrangements of CA protein observed in experiment (5,6,8,14,15). To investigate the effects of curvature on CA lattice self-assembly, an aspect essentially absent from the planar simulations described above, we performed larger CG MD simulations featuring 1225 CA dimers weakly restrained to move on a quasi-2D spherical surface (see Materials and Methods). Such a model avoids potential biases from the imposition of lattice continuity across the periodic boundaries of the planar simulations. Moreover, it provides a greater number of events relevant to lattice assembly for statistical analysis relative to a much more challenging fully 3D assembly simulation. The previous surface coverage values of ρ = 0.38–0.6 were reproduced by varying the diameter of the spherical restraint surface. The value of ε, the joint NTD-NTD and NTD-CTD interaction strength suggested by the general symmetry of the planar simulation results in ε_NN and ε_NC, was selected as that which produced mature lattice components over all surface coverage values examined for both flexible and rigid dimers, ε/k_BT = 6.71 (Fig. S2, Fig. S3, and Fig. S4). Five repeat CG MD simulations of 2 × 10⁷ time steps, with separate disordered starting coordinates, were performed for each ρ, and the results were combined.

The average numbers of trimer-of-dimers, pentamers, and hexamers present in the quasi-2D spherical simulations as a function of time are shown in Fig. 4. The results for the flexible and rigid dimer systems differ both qualitatively and quantitatively. Flexible dimer interfaces effectively produce a correlated, monotonic increase in trimer-of-dimer and hexamer composition as a function of time and surface coverage, which is explained by the trimer-of-dimers structures being almost exclusively present as components of mature-style p6 hexagonal lattice regions (Fig. 5, A–C). Dimers with completely rigid interfaces lose this connection, however, with a pronounced decrease in the hexameric content of the system beyond a surface coverage of ρ = ∼0.5, even though the trimer-of-dimers content remains relatively high (see Fig. 4 B). Trimer-of-dimers and hexamer structural motifs are markedly more numerous in simulations using a flexible dimer interface (Fig. 4 A) compared with the rigid dimer interface (Fig. 4 B).

Figure 4.

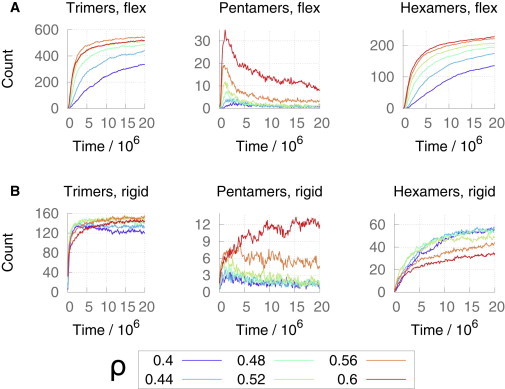
Average number of trimer-of-dimers, pentamers, and hexamers present as a function of CG MD simulation time for ε/k_BT = 6.71 on the quasi-2D spherical surface (color online). (A) Top row: flexible dimer model. (B) Bottom row: rigid dimer model. Error bars are omitted for clarity.

Figure 5.

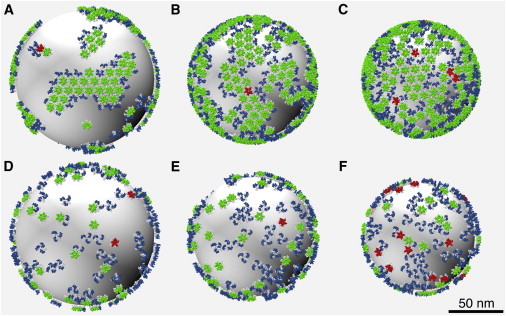
Snapshots from final configurations of quasi-2D spherically restrained CG MD simulations of CA lattice assembly for ε_NN/k_BT = 6.71 (color online). Top row: Flexible dimer model, ρ = 0.38 (A), 0.5 (B), and 0.6 (C). Bottom row: Rigid dimer model, ρ = 0.38 (D), 0.5 (E), and 0.6 (F). Color scheme as in Fig. 2.

The number of pentamers present after the 2 × 10⁷ simulation steps is similar for both flexible and rigid dimer interfaces, and both systems display an early peak and subsequent decrease in pentameric content over time (with this peak being larger for flexible dimer interfaces at higher ρ), but the sharp decay in average pentamer content as a function of time is suppressed at higher values of ρ for the completely rigid dimer interface, to the extent that for ρ = 0.6 the rigid dimer interface effectively displays an increase in pentamer content as a function of time. Because the CA protein monomers in the CG MD simulations are labeled with a unique identifier, it is possible to track the formation of unique structures because of their specific monomer content (Fig. S5). Surprisingly, the number of unique pentamers detected over the course of the simulations is actually greater than the number of unique hexamers (Fig. S5), despite the significantly higher average hexameric content, which suggests that pentamer formation is not a rare event despite the relative paucity of such inclusions in the mature conical capsid. However, this also suggests that the pentamers are rather unstable, as suggested by the mature capsid structure and simulations described above.

We note that the data presented in Fig. 4 indicate that all three structural motifs have not yet reached steady-state levels. The images presented in Fig. 5 are therefore kinetically controlled intermediates as opposed to equilibrium structures (e.g., the mature capsid in Fig. 2). Given sufficiently long simulation times, we expect that the separate regions of expanding p6 lattice (Fig. 5 A) and the presence of defects and frustrations in the lattice structure (Fig. 5, B and C) will be replaced at equilibrium by contiguous regions of p6 lattice with fewer lattice defects and frustrations. Because this study is concerned with the early stages of CA lattice self-assembly, as opposed to the final equilibrium lattice arrangements, the lack of final steady-state structures is not a significant omission.

The use of a spherical surface naturally raises the question as to whether any surface-density-dependent effects are due to increasing ρ itself, or to increasing local surface curvature as the sphere diameter is reduced. Ten repeat simulations of the small planar systems for each ρ were therefore performed at ε = 6.71, and the qualitative behaviors of the trimer-of-dimer and hexamer structural motifs were found to be very similar to those of the spherical surfaces (Fig. S6), suggesting that these effects are largely a function of surface density. The pentameric structures, however, occur less frequently in the planar simulations, both as an average count and from the number of unique pentamer structures identified in proportion to the total number of unique hexamers detected. This finding supports the idea that pentamers exist preferentially under higher local surface curvatures (10), and thus the final pentameric content after 2 × 10⁷ CG MD simulation steps increases as a function of ρ for the spherical surfaces, and therefore as a function of increasing surface curvature.

The behavior in Fig. 4 is complicated, with the number of hexamers present in the system showing different trends as a function of ρ according to the dimer rigidity, and with the strong correlation between trimer-of-dimers and hexamer counts in the presence of a flexible dimer interface being absent for the model with a completely rigid dimer interface. An explanation for this complicated behavior is indicated in Fig. 6 (solid circles and lines), where the probability P_iso of a hexamer forming in isolation is shown along with the probability P_tri of formation sharing one or more monomers with a trimer-of-dimers structure and the probability P_cyc of formation connected to an adjacent cyclic oligomer (specifically, a pentamer or hexamer). The dependence of hexamer formation on sharing monomers with one or more trimer-of-dimer structures, P_tri(hexamer), is striking. P_tri(hexamer) is uniformly high, regardless of ρ or the dimer rigidity, with a commensurately low probability of hexamers forming in isolation, P_iso(hexamer). Note that this is not simply because the trimer-of-dimers structures themselves form a component of the mature p6 lattice, as P_tri(hexamer) and P_cyc(hexamer) are different. The dominant effect appears to be the presence of a trimer-of-dimers template structure in all cases. This model of p6 lattice nucleation and growth is very different from a naïve description of hexameric and pentameric building blocks assembling in isolation before coming together to form the mature CA lattice structure. Although hexamers and pentamers provide a convenient structural description of the mature capsid, our results suggest that the fundamental unit for CA lattice self-assembly is actually a trimer-of-dimers.

Figure 6.

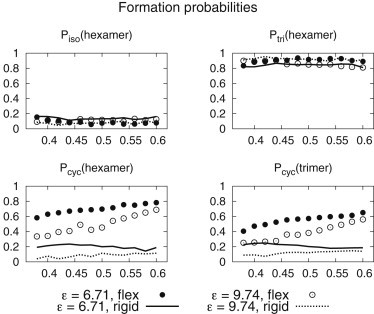
Probability of a hexamer formation unconnected to any other structure (P_iso), sharing a monomer with an existing trimer-of-dimers (P_tri), and connected to an adjacent cyclic pentamer or hexamer structure (P_cyc) for ε/k_BT = 6.71 and 9.74. Also shown is the probability P_cyc(trimer) of a trimer-of-dimers forming attached to an existing cyclic pentamer or hexamer. Error bars are too small to be shown clearly. Data for flexible dimer interfaces and completely rigid dimer interfaces are depicted with circles and lines, respectively. See also Fig. S7.

Thus, to a significant degree, the nature of mature CA protein p6 lattice formation reduces to a function of the trimer-of-dimers behavior, with this structure acting as a template for the formation of hexamers. However, these trimer-of-dimers structures are also highly important for the formation of pentamers in the presence of a flexible dimer interface (Fig. S7), which explains the early peaks in pentameric content shown in Fig. 4 A. Indeed, early-simulation pentamers template onto trimer-of-dimers structures that spontaneously form in isolation, and these conjunctions subsequently dissociate or expand to contain hexamers. Connections to neighboring hexamers impose an implicit hexameric spacing onto the adjacent pentamer structures, a situation that is unfavorable for pentameric integrity, and hence their average count reduces over time from this initial peak as the lattice regions grow.

The rigid CA dimer interface model explicitly includes a measure of this hexameric order in the trimer-of-dimers structures via imposition of the 2KOD dimer interface that is thought to link adjacent hexamers in the mature capsid (10), so this initial peak in pentameric content is rather suppressed. The completely rigid dimer interface also cannot adjust effectively to different lattice curvatures, whereas the flexible dimer model can approximate the CTD pivoting that is believed to be necessary for adapting p6 lattice regions to different local curvatures (10,13), and hence can produce connected hexameric p6 lattice regions across all values of ρ studied. Thus, although the imposition of a completely rigid dimer interface significantly increases P_iso(trimer) (Fig. S7), and is therefore in principle a more effective nucleator of multiple regions of p6 lattice, the ability of these nucleation sites to subsequently generate contiguous p6 lattice is significantly reduced. Instead, isolated pentamers and hexamers form, along with poorly ordered arrangements of dimers with native-style NTD-NTD and NTD-CTD contacts that can act to kinetically jam the system at higher surface concentrations (Fig. S8). These effects can be seen in Fig. 5, D–F, where the presence of isolated trimer-of-dimers, pentamers, and hexamers is clear, whereas the flexible dimer model displays exposed trimer-of-dimers elements mainly at the expanding edges of existing p6 lattice regions, as expected from P_iso(trimer), P_tri(trimer), and P_cyc(trimer) for the flexible dimer model. This important behavior promotes the formation of contiguous regions of mature p6 lattice.

The values of P_iso, P_tri, and P_cyc for pentamers are similar to those of the hexamers for a flexible dimer model (Fig. S7), indicating that pentamers form by the same mechanism as hexamers at the expanding edge of existing lattice regions. This supports the quasi-equivalence theory for CA pentamers and hexamers (10), and suggests that the pentameric inclusions of the mature capsid are formed when the edges of existing lattice regions merge. The imposition of a completely rigid dimer interface produces a significant change in this behavior: whereas P_iso and P_tri for the hexamers appears relatively insensitive to dimer interfacial rigidity, the pentamers display a markedly increased probability of forming in isolation under the influence of a completely rigid dimer interface, with a commensurate reduction in P_tri and P_cyc (Fig. S7).

The average numbers of trimer-of-dimers, pentamer, and hexamer structures present in the CG MD simulations as a function of simulation time do not necessarily reflect the total number of such structures that appeared, because some proportion of these structures may quickly dissociate after formation. This situation (which is analogous in some ways to treadmilling in the cytoskeleton) can lead to a comparatively low instantaneous structure count versus the number of distinct structures actually formed over the course of the simulation, and is the source of the fluctuations of the data presented in Figs. 4 and 7. Whereas the number of unique structures detected over the entire simulation is high in comparison with the instantaneous structure counts as a function of time (e.g., the pentamer counts in Fig. 4 B with reference to Fig. S5), we observe relatively large fluctuations in the structure counts that reflect the transient and unstable nature of the structures formed. The number of unique trimer-of-dimers structures detected at low surface coverage values (Fig. S5) versus the comparatively low instantaneous count of such structures in the simulations for the same low surface coverages suggests a simple method to test our description of the key process in mature-style p6 lattice assembly. It is expected that with an increase in the attractive strength of the CA monomer interactions, these transient, isolated trimer-of-dimer structures would become overstabilized, leading to a commensurate degradation of contiguous p6 lattice as the hexamers template onto these isolated structures, with an associated reduction in the total number of unique trimer-of-dimers structures detected. Therefore, we ran identical spherically restrained simulations with ε/k_BT = 9.74, the interactive strength at which the mature conical capsid was stabilized in 3D. The average compositions of the three structural motifs as a function of time are shown in Fig. 7 (for the total number of unique structures detected and snapshots of the final system configurations, see Fig. S9 and Fig. S10, respectively). For the flexible dimer model at these higher interaction strengths, as with the flexible dimer model at ε/k_BT = 6.71, the overall increase in hexamer content with increasing ρ and simulation time remains, albeit with more rapid increases in hexameric content at low ρ. This increased rate also appears in the trimer-of-dimers count as a function of system time, indicating that the overstabilization of transient isolated trimer-of-dimers structures does indeed lead to enhanced isolated hexamer formation. For the completely rigid CA dimer interface model at the higher interaction strengths, the hexameric content of the system is significantly reduced, despite enhanced trimer-of-dimers presence compared with the rigid dimer model using ε/k_BT = 6.71. This behavior is due to the increased interaction strength overstabilizing disordered native-contact aggregates of CA and preventing hexamer formation (Fig. S8).

Figure 7.

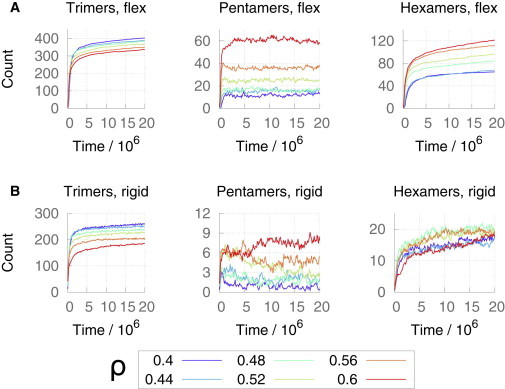
Average numbers of trimer-of-dimers, pentamers, and hexamers present as a function of simulation time for ε/k_BT = 9.74 (color online). (A) Top row: flexible dimer model. (B) Bottom row: rigid dimer model. Error bars are omitted for clarity.

For both flexible and rigid dimer interfaces at ε/k_BT = 9.74, hexamer formation is again dependent on trimer-of-dimer templates (P_tri(hexamer) (see Fig. 6, open circles and dashed lines), and hence these effects can be reduced to a description of the behavior of the trimer-of-dimers structure. Indeed, the probability of a trimer-of-dimers structure forming attached to existing cyclic oligomers (and therefore as part of an expanding region of mature-style CA lattice, P_cyc(trimer); Fig. 6) appears to be a dependable proxy for the otherwise very complicated trends observed in the final hexameric content of the simulations (see Figs. 4 and 7 after 20 × 10⁶ time steps), indicating that the description of the mechanism of p6 lattice growth presented here is robust. Further evidence to support the quasi-equivalent mechanism of pentamer and hexamer formation is given by the enhanced interaction strength producing higher pentameric content for flexible dimer interfaces (Fig. 7 A) as the otherwise transient pentamers are stabilized, whereas P_cyc(pentamer) remains similar to P_cyc(hexamer) (Fig. S7).

The mechanism of lattice growth described here explains the somewhat counterintuitive findings of Chen and Tycko (12), who suggested that the placement of an initial hexamer structure could act to nucleate lattice growth despite the dissociation of the initial hexamer. The mechanism presented here suggests that this initial hexamer induces lattice growth indirectly, via the local generation of trimer-of-dimers structures. The putative CA heptamer structures observed by Chen and Tycko (12) are also occasionally (and transiently) present in the simulations presented here, supporting the intriguing possibility that CA quasi-equivalence can produce structures other than pentamers and hexamers under certain conditions.

Conclusions

The results presented here for the early-to-intermediate stages of HIV-1 CA protein mature lattice formation cover a wide range of conditions. The flexible and completely rigid CA dimer interfaces represent two limiting cases of dimer interfacial behavior over a range of CA densities and native contact interaction strengths. Our CG HIV-1 CA model suggests that formation of the mature HIV-1 p6 CA lattice is highly dependent on the templating of hexamers onto a trimer-of-dimers structure, and complicated trends in the final hexameric content of the model CA lattice self-assembly simulations can be predicted from a simple probability that the trimer-of-dimers structures will form attached to existing CA lattice structures. These simulations also demonstrate the importance of structural flexibility in allowing p6 lattice formation to adapt to different local curvatures, such as the CA dimer CTD pivot motions thought to be necessary for continuous curvature in viral capsids (10,13). However, the simulations also demonstrate that the presence of some limited rigidity in the dimer structure can enhance the spontaneous formation of the important trimer-of-dimers structures at relatively low concentrations and attractive strengths for the native-style CA NTD-NTD and NTD-CTD contacts to help nucleate mature p6 lattice growth.