Differential Dynamic Microscopy: A High-Throughput Method for Characterizing the Motility of Microorganisms

Abstract

We present a fast, high-throughput method for characterizing the motility of microorganisms in three dimensions based on standard imaging microscopy. Instead of tracking individual cells, we analyze the spatiotemporal fluctuations of the intensity in the sample from time-lapse images and obtain the intermediate scattering function of the system. We demonstrate our method on two different types of microorganisms: the bacterium Escherichia coli (both smooth swimming and wild type) and the biflagellate alga Chlamydomonas reinhardtii. We validate the methodology using computer simulations and particle tracking. From the intermediate scattering function, we are able to extract the swimming speed distribution, fraction of motile cells, and diffusivity for E. coli, and the swimming speed distribution, and amplitude and frequency of the oscillatory dynamics for C. reinhardtii. In both cases, the motility parameters were averaged over $\sim {10}^4$ cells and obtained in a few minutes.

Introduction

The motility of single-celled prokaryotes and eukaryotes is important in biology and medicine. The virulence of Helicobacter pylori depends on migration through host epithelial mucosa (1), and the phototaxis of Chlamydomonas reinhardtii and similar photosynthetic algae is predicated on motility (2). Animal reproduction relies on motile sperms. In all cases, organisms with typical linear dimension R in the range of $0.5\mu \text{m}\lesssim R\lesssim 10\mu \text{m}$ swim with speeds of $v\sim 10-100\mu \text{m}/\text{s}$, and thus the Reynolds numbers, Re $=\rho vR/\eta$ (ρ and η are the liquid’s density and viscosity) are vanishingly small ($\lesssim {10}^{-3}$ in water). Microorganisms use a variety of strategies to generate the nonreciprocating motion necessary for low-Re propulsion, e.g., by rotating or beating one or more flagella.

The motility of Escherichia coli bacteria is well understood (3). A wild-type (WT) cell ($\sim 1\mu \text{m}\times 2\mu \text{m}$ spherocylinder) bears six to ten $6-10\mu \text{m}$ helical flagella. When these flagella rotate counterclockwise (CCW, viewed from flagella to cell body), they bundle and propel the cell forward in a straight run. Every $\sim 1$ s, one or more flagella rotate clockwise (CW) briefly and then unbundle, and the cell tumbles. Rebundling leads to a new run in an essentially random direction. This run and tumble gives rise to a random walk.

Such detailed information can only be obtained by single-cell tracking. However, in some situations, only a few parameters may be required, such as the average speed and the motile fraction. Moreover, tracking is laborious and typically averages over $\sim {10}^2$ cells, limiting the statistical accuracy. Lastly, because three-dimensional (3D) tracking requires specialized equipment (4–6), tracking is usually performed on two-dimensional (2D) projections, which further limits statistical accuracy because of cells moving out of the imaging plane.

We recently demonstrated the use of differential dynamic microscopy (DDM) for characterizing the motility of WT E. coli in 3D (7). The method complements rather than replaces tracking; indeed, it relies on fitting data using a parametrized swimming model that was obtained from tracking in the first place. The advantage of DDM is that it delivers a limited number of motility parameters with high throughput by averaging over $\sim {10}^4$ cells in a few minutes using standard microscopy. In this work, we explain the full details and limitations of DDM, and justify in depth the approximations made using simulations and tracking. We apply the method to a smooth swimming (run only) mutant of E. coli, investigate its use on the WT in more detail, and extend it to study the biflagellate WT alga C. reinhardtii, which is a completely different microorganism in terms of timescales, length scales, and swimming dynamics. Our results provide the basis for generalizing DDM to many other biomedically important microswimmers, including spermatozoa.

DDM

The key idea of DDM (7,8) is to characterize the motility of a population of particles (colloids or microorganisms) by studying the temporal fluctuations of the local number density of particles over different length scales via image analysis. This method yields the same quantity accessed by dynamic light scattering (DLS), the intermediate scattering function (ISF), but can access the relevant length scales for microorganism motility more readily than DLS (9).

DDM utilizes time-lapse images of particles, described by the intensity $I\left(\overrightarrow{r},t\right)$ in the image plane, where $\overrightarrow{r}$ is pixel position and t is time. As the particles move, $I\left(\overrightarrow{r},t\right)$ fluctuates with time. DDM analyzes the statistics of $I\left(\overrightarrow{r},t\right)$ to provide information about the particle motions by measuring the differential image correlation function (DICF), $g\left(\overrightarrow{q},\tau \right)$, i.e., the square modulus of the Fourier transform of the difference of two images separated by τ in time:

$$g\left(\overrightarrow{q},\tau \right)={\langle {\left|I\left(\overrightarrow{q},t+\tau \right)-I\left(\overrightarrow{q},t\right)\right|}^2\rangle }_t.$$ (1)

Here, ${\langle \dots \rangle }_t$ means the average over the initial time t, and $I\left(\overrightarrow{q},t\right)$ is the Fourier transform of $I\left(\overrightarrow{r},t\right)$, which picks out the component in the image $I\left(\overrightarrow{r},t\right)$ that varies sinusoidally with wavelength $2\pi /q$ in the direction $\overrightarrow{q}$. With no preferred direction of motion, the relevant variable is the magnitude q of $\overrightarrow{q}$. It can be shown that $g\left(q,\tau \right)$ is related to the ISF, $f\left(q,\tau \right)$, by (7,8,10)

$$g\left(q,\tau \right)=A\left(q\right)\left[1-f\left(q,\tau \right)\right]+B\left(q\right).$$ (2)

where $A\left(q\right)$ depends on the optics, particle shape, and mutual arrangement, and $B\left(q\right)$ represents the camera noise. For independent particles (11),

$$f\left(q,\tau \right)={\langle e^{i\overrightarrow{q}\cdot \Delta {\overrightarrow{r}}_j\left(\tau \right)}\rangle }_j,$$ (3)

where $\Delta {\overrightarrow{r}}_j\left(\tau \right)$ is the jth-particle displacement and ${\langle \dots \rangle }_j$ is an average over all particles.

Equation 3 shows that $f\left(q,0\right)=1$ and $f\left(q,\tau \to \infty \right)=0$. This decay of the ISF from unity to zero reflects the fact that particle configurations (and hence images) separated by a progressively longer delay time, τ, become more decorrelated due to particle motion. The precise form of $f\left(q,\tau \right)$ encodes information on these motions on the length scale $2\pi /q$. The analytic form of the ISF is known in a number of cases (11). Thus, for identical diffusing spheres with diffusion coefficient D, $f\left(q,\tau \right)=e^{-D{q}^2\tau }$. For an isotropic population of straight swimmers in 3D with speed v, $f\left(q,\tau \right)=\text{sin}\left(qv\tau \right)/qv\tau$.

Fig. 1 shows the calculated $f\left(q,\tau \right)$ for 1), diffusing spheres with approximately the same volume as a typical E. coli cell; 2), isotropic swimmers with a speed distribution $P\left(v\right)$ typical of E. coli; and 3), a mixture of these (12) at $q=1\mu$m⁻¹ (see Eq. 4). Note that in the third case, plotting the ISF against $\text{log}\tau$ makes it obvious that there are two processes: a fast one due to swimming that decorrelates density (or, equivalently, intensity) fluctuations over $\sim {10}^{-1}$ s, and a slower diffusive process that decorrelates over $\sim 1$ s (at this q), with fractional contributions $\approx 7:3$.

Figure 1.

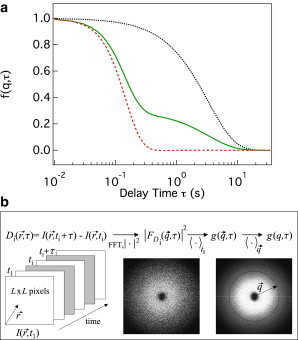
(a) Theoretical ISF, $f\left(q,\tau \right)$, versus τ at $q=1\mu {\text{m}}^{-1}$, for (black dotted line) a population of diffusing spheres with $D=0.3\mu {\text{m}}^2/\text{s}$, (red dashed line) a population of equivalent-size spheres swimming isotropically in 3D with a Schulz speed distribution $P\left(v\right)$ (see Eq. 5) with average speed $\overline{v}=15\mu \text{m}/\text{s}$ and width $\sigma =7.5\mu \text{m}/\text{s}$, and (green line) a 30:70 mixture of diffusers and swimmers. (b) Schematic of the image processing to obtain the DICFs, $g\left(q,\tau \right)$, from the videos (left) collected in an experiment. (middle) nonaveraged image, ${\left|F_{D\text{i}}\left(\overrightarrow{q},\tau \right)\right|}^2$ and (right) averaged image, $g\left(\overrightarrow{q},\tau \right)$, over initial times $t_i$ at $\tau =0.52s$.

We note that any bias due to, e.g., chemotaxis, leads to anisotropy in the measured $g\left(\overrightarrow{q},\tau \right)$, and therefore the method that was recently demonstrated for anisotropic colloids, where $g\left(\overrightarrow{q},\tau \right)$ was analyzed sector by sector (13) rather than azimuthally averaged over $\overrightarrow{q}$, needs to be used. The isotropy assumption seems reasonable for E. coli in the absence of gradients. However, C. reinhardtii is known to be gravitactic (14). Below, we disregard these small but persistent anisotropic effects as a first approximation, and postpone a full exploration to future work. We find that azimuthally averaging over $\overrightarrow{q}$ still allows us to extract useful information that is substantially validated by tracking.

Materials and Methods

Samples

E. coli AB1157 (WT and ΔcheY strains; see Supporting Material) were grown in Luria-Bertani broth (LB) at 30°C and shaken at 200 rpm, harvested in the exponential phase, washed three times by careful filtration (0.45-micron filter) with, and resuspended in, motility buffer (6.2 mM K₂HPO₄, 3.8 mM KH₂PO₄, 67 mM NaCl, 0.1 mM EDTA, pH = 7.0) to optical density 0.3 (at 600 nm), corresponding to $\approx 5\times {10}^8$ cells/ml, and $\approx 0.06$ % by cell volume. Care was taken throughout to minimize damage to flagella. A $\approx 400\mu$m deep flat glass cell was filled with $\approx 150\mu$l of cell suspension, sealed, and observed at $22\pm 1°$C. Swimming behavior was constant over $\approx 10$ min.

Batch cultures of WT C. reinhardtii (CCAP 11/32B) were grown on 3N Bold’s medium (2) and concentrated in cotton by gravitaxis (15). Concentrated cell stock was diluted in growth media to an optical density of 0.175 (at 590 nm), corresponding to $1.4\times {10}^6$ cells/ml, and $\approx 0.002$% by volume of cells. Cells were observed at $22\pm 1°$C in the same glass cells used for E. coli under a 600 nm long-pass filter (Cokin) to avoid a phototactic response (16). The sample dimensions were sufficiently large to avoid boundary effects and small enough to avoid bioconvection or thermal convection (6). Algal motility was constant for 20 min. In all cases, we waited at least 1min before capturing images to avoid drift due to mixing flows.

DDM

We used a Nikon Eclipse Ti inverted microscope and a PC-controlled high-speed camera (Mikrotron MC 1362) with a frame grabber card with 1 GB of onboard memory. The CMOS pixel size $\left(14\times 14\mu {\text{m}}^2\right)$ and magnification determine the inverse pixel size k (in pixel/μm) in the image plane, which together with the image size L (in pixels) define the spatial sampling frequency $\left(q_{\text{min}}=2\pi k/L\right)$. For bacteria, $10\times$ phase-contrast movies (Nikon Plan Fluor with numerical aperture = 0.3) were acquired at $L=500$, giving $k=0.712\mu {\text{m}}^{-1}$ and $0.01⪅q⪅2.2\mu {\text{m}}^{-1}$. This allowed the imaging of $\sim {10}^4$ cells at a bulk density of $5\times {10}^8$ cells/ml in a $0.49{\text{mm}}^2$ field of view with a depth of field $\delta \approx 40\mu \text{m}$, over 38 s at a frame rate of 100 fps. For algae, $4\times$ bright-field movies (Nikon Plan Apo with numerical aperture = 0.2) were acquired at $L=500$, giving $k=0.285\mu {\text{m}}^{-1}$ and $0.004⪅q⪅0.9\mu {\text{m}}^{-1}$, which allowed the imaging of $\sim {10}^4$ cells at a bulk density of $1.4\times {10}^6$ cells/ml in a $3.2{\text{mm}}^2$ field of view with $\delta \approx 200\mu \text{m}$, over 3.8 s at 1000 fps. Imaging at $\approx 200\mu \text{m}$ from the bottom of a $400\mu \text{m}$ thick glass capillary minimized wall effects.

Data reduction and fitting

The image processing and fitting are easily automated (see below; all relevant software is available on request). Fig. 1 b illustrates how we obtain the DICF from the movies. For a given τ, the difference images $D_{\text{i}}\left(\overrightarrow{r},\tau \right)=I\left(\overrightarrow{r},t_{\text{i}}+\tau \right)-I\left(\overrightarrow{r},t_{\text{i}}\right)$ are calculated for a set of N different initial times $t_{\text{i}}$ (typically $\text{i}=1,4,7,\dots ,313$). After computing the fast Fourier transform, $F_{D\text{i}}\left(\overrightarrow{q},\tau \right)$, of each $D_{\text{i}}\left(\overrightarrow{r},\tau \right)$ and calculating ${\left|F_{D\text{i}}\left(\overrightarrow{q},\tau \right)\right|}^2$, we average over the initial times $t_{\text{i}}$, giving $g\left(\overrightarrow{q},\tau \right)={\langle {\left|F_{D\text{i}}\left(\overrightarrow{q},\tau \right)\right|}^2\rangle }_i$, to improve the signal/noise ratio (the averaged image appears less grainy; Fig. 1 b).

For isotropic swimmers, $g\left(\overrightarrow{q},\tau \right)$ is azimuthally symmetric and can be azimuthally averaged to give $g\left(q,\tau \right)={\langle g\left(\overrightarrow{q},\tau \right)\rangle }_{\overrightarrow{q}}$. We linearly interpolate between four adjacent points in discrete $\overrightarrow{q}$ -space to find values for $g\left(\overrightarrow{q},\tau \right)$ along a circle with radius q. The finite image size causes numerical artifacts (18) mainly along the horizontal and vertical center lines of $g\left(\overrightarrow{q},\tau \right)$, which are reduced by omitting the values for $q_x=0$ and $q_y=0$ during the azimuthal averaging. This is repeated for different τ-values to obtain the full time evolution of $g\left(q,\tau \right)$. Calculations were done in LabView (National Instruments) on a four-core PC (3 GHz quad core, 3 GB RAM). Processing $\lesssim 4000$ frames with $L=500$ and averaging over $\approx 100$ initial times $t_i$ take ≈ 5 min.

We fitted each $g\left(q,\tau \right)$ independently to Eq. 2 using the appropriate parametrized model for $f\left(q,\tau \right)$. At each q, nonlinear least-squares fitting based on ${\chi }^2$ minimization using the Levenberg-Marquardt algorithm and the all-at-once fitting procedure in IGOR Pro (WaveMetrics) returns $A\left(q\right)$, $B\left(q\right)$, and motility parameters.

Simulation

We carried out Brownian dynamics simulations in 3D of noninteracting point particles (bacteria) at a concentration and in a sample chamber geometry directly comparable to our experiments, using periodic boundary conditions to keep the bulk density of swimmers constant. Each particle has a drift velocity whose direction and magnitude were chosen from uniform and Schulz distributions, respectively. At each tumble, a WT swimmer undergoes Brownian diffusion and a new swimming direction is chosen uniformly at random after each tumble. The swimming speed is constant for each bacterium.

From these simulations, we constructed 2D pixelated images. Particles in a slice of thickness d, centered at $z=0$, contribute to the image. A particle at $\left(x,y,z\right)$ is smeared into an image covering the pixel containing $\left(x,y\right)$ and the eight neighboring pixels. To define the image contrast of a bacterium, which depends on z, we used the experimentally measured z-contrast function $c\left(z\right)$. This mimics the finite depth of field in a microscope.

Tracking

Both experimental and simulated data were tracked (19) to obtain 2D trajectories, $r_{2D}\left(t\right)$. We used inverted $20\times$ videos of E. coli with bright cells of $\approx 3$ pixels on a dark background and a running average of three frames to improve the signal/noise ratio. In the simulations, equivalent $10\times$ videos could be tracked due to the absence of noise. In all cases, 400 plus features were identified per frame, using only high brightness features near the focal plane. Tracking of simulated movies of nonmotile (NM) or motile cells reproduced the input diffusion coefficient D and swimming speed distribution $P\left(v\right)$. Tracking experimental data for purely NM E. coli yields the same D as obtained by DDM.

The analysis of mixed populations of motile and NM cells is more challenging. We generalized a recently proposed method (21) to analyze such data. Each trajectory is split into short elementary segments of duration $\Delta t$ over which an average swimmer moves $\approx 1$ pixel. First, the mean angle $\langle \left|\theta \right|\rangle$ between successive segments is calculated ($\langle \left|\theta \right|\rangle =\pi /2$ for a random walk and $\langle \left|\theta \right|\rangle =0$ for a straight swimmer). Then, using the trajectory’s start-to-end distance L, duration T, and the mean elementary segment length $\Delta r_{2D}\left(\Delta t\right)$, we calculate the parameter $N_c=\left(L/\Delta r_{2D}\right)/\left(T/\Delta t\right)$. Thus, $N_c=0$ for a random walk with $T\to \infty$ and $N_c=1$ for a straight swimmer. Previous tracking of mixed swimmers and diffusing particles in 2D (at a wall) (21) returned two well-separated clusters in the $\left(N_c,\langle \left|\theta \right|\rangle \right)$ plane, from which motile and NM populations could be separated and the respective $P\left(v\right)$ and D could be extracted via fitting of the mean-squared displacement (MSD), $\langle \Delta r_{2D,NM}^2\left(\tau \right)\rangle =4D\tau$.

However, our 3D data (see below) show a much less well-defined separation, in contrast to the clear distinction in the study by Miño et al. (21) between motile and NM populations in 2D. Therefore, we studied the dependence of motility parameters with the population selection criteria $\left(N_c,\langle \left|\theta \right|\rangle \right)$. In addition, we used another estimate for the diffusion coefficient, $D_g$, obtained by fitting the distribution of 1D displacements, $P\left(\Delta x_{NM}\left(\tau \right)\right)$, to a Gaussian and using the linear increase of the variance of the fitted distribution with τ to obtain $D_g$. Computerized tracking of 200 cells over 200 frames to give the data presented in “Tracking results” took 5 min.

Finally, we tracked the C. reinhardtii videos, identifying $\approx 300$ algae per frame with $\approx 5$ pixels per cell, and applied the above diagnostic (using $\Delta t$ such that $\Delta r\left(\Delta t\right)\approx 1$ pixel on average) to separate straight tracks in the imaging plane from other tracks. Further details are given below.

2D tracking measures $P\left(v\text{cos}\left(\beta \right)\right)$ (where β is the angle with the image plane) rather than $P\left(v\right)$, but this has only a small effect on the results. Tracking only the brightest features within z of the focal plane ensures that only tracks with $\tau v\text{sin}\left(\beta \right)<z$ contribute, which suppresses projection effects. Moreover, the diagnostic method to select straight swimmers further excludes large β tracks from the motile population, because these tracks exhibit a stronger diffusive (E. coli) or circular (algae) component as a result of the projection.

Smooth Swimming E. coli

We previously demonstrated DDM using a WT run-and-tumble E. coli (7). Although many features of the data can be fitted by ignoring the effect of tumbling, some details, such as a small q dependence in the fitted swimming velocity, probably can only be understood by taking tumbling into account. Here, we present measurements for a smooth swimming (SW) mutant. The simplicity of the motion compared with the WT makes this mutant the ideal organism for presenting the details of DDM. We return to the WT further below.

Model of ISF

An SW cell is propelled somewhat off-center by a flagellar bundle rotating CCW at $\sim 100$ Hz, causing the cell body to wobble as it rotates at $\sim 10$ Hz CW. To extract motility parameters from the ISF, it is important to work in the appropriate q range. An upper bound exists because at $q\gtrsim 2\pi /R\sim 6\mu {\text{m}}^{-1}$, where $R\sim 1\mu$m is a typical cell size, both swimming and body wobble contribute to the decay of $f\left(q,\tau \right)$, making impractical to extract swimming parameters cleanly in this regime. A lower bound for q is set by deviations from straight-line swimming due to Brownian orientational fluctuations and/or tumbling. For E. coli, cells run for $\approx 20\mu$m between tumbles, which is also the persistence length of the trajectory of SW cells due to orientational fluctuations.

Thus, within the optimized range of $0.5\lesssim q\lesssim 6\mu {\text{m}}^{-1}$, it is possible to model a population of swimming E. coli as straight swimmers with a speed distribution $P\left(v\right)$ and isotropic directions. Each particle also undergoes Brownian motion, with diffusivity D. To model a natural population, which inevitably contains NM cells, we specify that only a fraction α of the particles are swimming. The resulting ISF is known (12):

$$f\left(q,\tau \right)=\left(1-\alpha \right)e^{-q^{2}D\tau }+\alpha e^{-q^{2}D\tau }\underset{0}{\overset{\infty }{\int }}P\left(v\right)\frac{\text{sin}\left(qv\tau \right)}{qv\tau }dv.$$ (4)

Limited previous data (12,22) suggest that $P\left(v\right)$ is peaked. Using a Schulz (or generalized exponential) distribution,

$$P\left(v\right)=\frac{v^Z}{Z!}{\left(\frac{Z+1}{\overline{v}}\right)}^{Z+1}\text{exp}\left[-\frac{v}{\overline{v}}\left(Z+1\right)\right],$$ (5)

where Z is related to the variance ${\sigma }^2$ of $P\left(v\right)$ via $\sigma =\overline{v}{\left(Z+1\right)}^{-1/2}$, gives (23)

$$\underset{0}{\overset{\infty }{\int }}P\left(v\right)\frac{\text{sin}\left(qv\tau \right)}{qv\tau }dv=\left(\frac{Z+1}{Zq\overline{v}\tau }\right)\frac{\text{sin}\left(Z{\text{tan}}^{-1}\Lambda \right)}{{\left(1+{\Lambda }^2\right)}^{Z/2}},$$ (6)

where $\Lambda =\left(q\overline{v}\tau \right)/\left(Z+1\right)$.

Fig. 1 (green curve) shows an example ISF calculated at $q=1\mu {\text{m}}^{-1}$ using typical E. coli motility parameters in Eqs. 4–6. It shows a characteristic two-stage decay. The integral in Eq. 4 due to the straight swimmers dominates the first, faster process, whereas the purely diffusive first term due to the Brownian motion of nonswimmers dominates the second, slower process.

Much can be learned from visual inspection of this $f\left(q,\tau \right)$. The relative amplitudes of the fast and slow processes can easily be estimated to be $\approx 7:3$, which gives an estimated $\alpha \approx 0.7$. The length scale probed at this q is $\ell \sim 2\pi /q\approx 6\mu$m. By extrapolating the green curve or by reference to the red curve for pure swimmers, we can estimate that the fast process decays completely in ${\tau }_{\text{swim}}\approx 0.5$ s. An order-of-magnitude estimate of the swimming speed is therefore $v\sim \ell /{\tau }_{\text{swim}}\approx 12\mu \text{m}/\text{s}$. The slower, diffusive process decays completely in ${\tau }_{\text{diff}}\approx 20$ s, and thus an estimate of the diffusion coefficient of the nonswimmers can be obtained from $6D{\tau }_{\text{diff}}\sim {\ell }^2$, giving $D\approx 0.35\mu {\text{m}}^2/\text{s}$. These are credible estimates of the parameters used to generate this ISF: $v=15\mu \text{m}/\text{s}$, $D=0.3\mu {\text{m}}^2/\text{s}$, and $\alpha =0.7$.

DDM results

Fig. 2 a shows typical DICFs, $g\left(q,\tau \right)$, measured using DDM in the range of $0.45\le q\le 2.22\mu {\text{m}}^{-1}$ for a suspension of SW E.coli. The measured $g\left(q,\tau \right)$ have a characteristic shape reminiscent of the calculated $f\left(q,\tau \right)$ shown in Fig. 1 a (note the log-scale for the y axis in Fig. 2 a); indeed, Eq. 2 shows that $g\left(q,\tau \right)$ should take the shape of an (unnormalized) upside-down $f\left(q,\tau \right)$. Moreover, the value of $g\left(q,\tau \right)$ at small τ gives a measure of the camera noise $B\left(q\right)$, which is therefore seen to be more or less q independent. The total amplitude of $g\left(q,\tau \right)$ measures $A\left(q\right)$, which evidently increases rapidly as q decreases. This reflects the strong q dependence of both the form factor of a single bacterium and the contrast function of the microscope objective.

Figure 2.

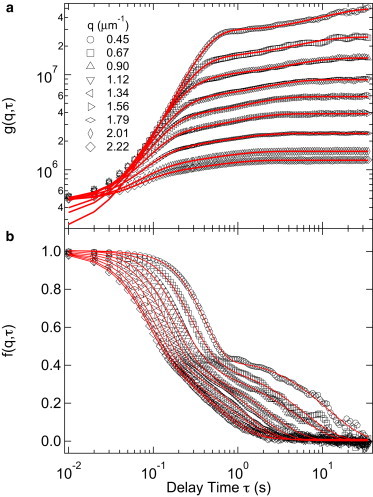
DDM for SW E. coli. (a) Measured (symbols) and fitted (lines) DICFs, $g\left(q,\tau \right)$. (b) ISFs, $f\left(q,\tau \right)$, reconstructed from $g\left(q,\tau \right)$ using Eqs. 2, 4, and 6.

The above qualitative remarks can be quantified by fitting the measured $g\left(q,\tau \right)$ using Eqs. 2, 4, and 6. From the fit, we extract six parameters: $\overline{v}$, σ, D, α, A, and B. The fitted functions $A\left(q\right)$ and $B\left(q\right)$ allow us to calculate $f\left(q,\tau \right)$ from the measured $g\left(q,\tau \right)$ via Eq. 2 (Fig. 2 b). The determination of $A\left(q\right)$ and $B\left(q\right)$ does not necessarily require fitting of $g\left(q,\tau \right)$ and consequently a model for $f\left(q,\tau \right)$. They can simply be determined from the short and long time limits of $g\left(q,\tau \right)$, such as $B\left(q\right)=g\left(q,\tau \to 0\right)$ and $A\left(q\right)=g\left(q,\tau \to \infty \right)-B\left(q\right)$. However, the latter requires well-defined plateaus at both short and long time regimes, which are not always observed depending on the value of q, and the experimental time window restrictions (at short times by the frame rate and at long times by the duration of the movie).

The ISFs calculated from experimental data (especially those for $q\approx 1\mu {\text{m}}^{-1}$) show the characteristic shape already encountered in the theoretical ISF shown in Fig. 1 a, i.e., a fast decay due to swimming, followed by a slow decay due to diffusion. The identity of these two processes is confirmed by the different scaling of the time axis required to collapse the data at different q values: the fast (swimming, or ballistic) decay scales as qτ (Fig. 3 a), and the slow (diffusive) decay scales as q²τ (Fig. 3 b).

Figure 3.

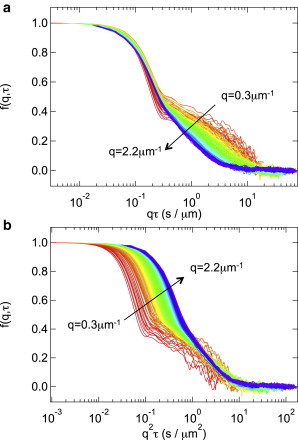
Reconstructed ISFs, $f\left(q,\tau \right)$, shown in Fig. 2 plotted against (a) $q\tau$ and (b) $q^2\tau$. The data collapse for the fast process in a and the slow process in b. The q-value increases by step of ≈ 0.009 μm⁻¹ from the red to the blue end of the spectrum in the range of $0.3\le q\le 2.2\mu {\text{m}}^{-1}$.

A clear separation of the swimming and diffusive decays is important for robust fitting of the ISF using Eq. 4. Such separation of timescales will be achieved if a cell takes much less time to swim the characteristic distance probed, $\ell =2\pi /q$, than to diffuse over the same distance (in the image plane), i.e., ${\tau }_{\text{swim}}\sim \ell /v\ll {\tau }_{\text{diff}}\sim {\ell }^2/4D$, which requires $q\ll q_c\sim v/D\sim 20-50\mu {\text{m}}^{-1}$ for typical E. coli values of v and D. All of the data shown in Fig. 2 b fit comfortably into this regime. (In the regime of $q\gg q_c$, the ISF separates into a fast diffusive process followed by a slower swimming process.)

Fig. 4 shows the fit parameters $\left(\overline{v},\sigma ,\alpha ,D,A,B\right)$ from Eqs. 4–6 as functions of q. A common feature, most evident in $D\left(q\right)$, is the enhanced noise at low q. This is because at low q, the long-time, diffusive part of $f\left(q,\tau \right)$ has not fully decayed in our time window, rendering it harder to determine D accurately. This can be improved by probing $g\left(q,\tau \right)$ over long times. To within experimental uncertainties, the motility parameters $\left(\overline{v},\sigma ,\alpha ,D\right)$ are all q independent for $q\gtrsim 1\mu m^{-1}$, which suggests that our model (Eq. 4) is indeed able to capture essential aspects of the dynamics of a dilute mixture of NM and SW E. coli. A fit using fixed D, over the full q range, results in q-independent motility parameters only when the value used for D is within $10\%$ of the value found in free fitting (data not shown). Averaging over q in the range of $0.5⪅q⪅2.2\mu {\text{m}}^{-1}$ yields $\overline{v}=10.9\pm 0.3\mu \text{m}/\text{s}$, $\sigma =6.43\pm 0.04\mu \text{m}/\text{s}$, $\alpha =0.585\pm 0.002$ and $D=0.348\pm 0.003\mu {\text{m}}^2/\text{s}$ (where error bars are the standard deviation of the mean in all cases except for $\overline{v}$, where they reflect the residual q dependence). Note that the fitting of D is dominated by the diffusion of NM organisms: changing our model from Eq. 4 to one in which the motile cells do not diffuse does not change the results (data not shown). Our $D\approx 0.35\mu {\text{m}}^2/\text{s}$ is slightly higher than the $D\approx 0.30\mu {\text{m}}^2/\text{s}$ obtained for NM E. coli mutants with paralyzed flagella (motA) (7), possibly because of collisional encounters with the motile cells.

Figure 4.

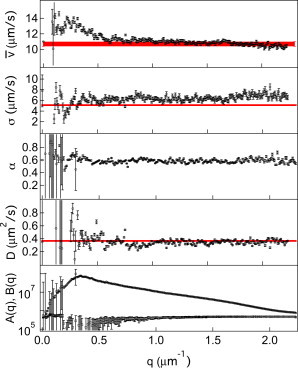
SW E. coli. Fitting parameters versus q using Eqs. 2, 4, and 6. From top to bottom: $\overline{v}$ and σ of the Schulz distribution, motile fraction α, diffusivity D, and $A\left(q\right)$ (○) and $B\left(q\right)$$(\square )$. Horizontal lines are results from tracking, with thickness corresponding to the error bars. No reliable value for α could be obtained from tracking.

We used a Schulz distribution for $P\left(v\right)$ in Eq. 4 for analytic convenience. In Fig. S1 in the Supporting Material we show the fitting parameters obtained by fitting with three different probability distributions. The results for the Schulz and log-normal distributions agree closely (Fig. S2 b), but using a Gaussian form produced noisier data and a significantly lower $\overline{v}$. The latter is because $P\left(v=0\right)\ne 0$ for the Gaussian distribution, strongly overestimating the number of slow swimmers. These spurious slow swimmers in turn cause noisier data for the other parameters. One can draw the same conclusion by fitting (using the same three distributions) the simulated data generated using a Schulz $P\left(v\right)$ with experimental parameters from Fig. 4 (Fig. S2b). Significantly, the calculated $f\left(q,\tau \right)$ from fitting the simulated data generated using a Schulz distribution agree closely with the ISFs obtained from fitting the experimental data using a Schulz distribution (Fig. S2 a).

Figure 5.

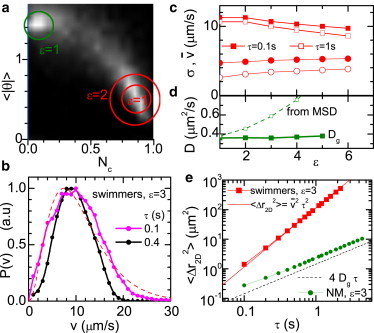
Tracking of SW E. coli. (a) Probability $P\left(N_c,\langle \left|\theta \right|\rangle \right)$ ($\Delta t=0.1$ s) for all tracks. White denotes large values of P. Circles (radius ε, see text) are selection criteria for motile (red, lower right) or NM (green, upper left) cells. (b) $P\left(v\right)$ for $\varepsilon =3$ ($\Delta t=0.1$ s) for two time lags τ. Dashed line: Schulz distribution from DDM. (c) $\overline{v}$$(■)$ and σ (●) of $P\left(v\right)$ versus ε for $\tau =0.1$ s (solid symbols) and $\tau =1$ s (open symbols). (d) Diffusion coefficient of NM cells versus ε, from Gaussian fits to $P\left(\Delta x_{NM}\left(\tau \right)\right)$$(■)$ and linear fits to the MSD $(\square )$. (e) MSD versus τ for motile $(■)$ and NM cells (●) for $\varepsilon =3$, $\Delta t=0.1$ s. Solid line: Motile MSD calculated using ${\overline{v}}_{\varepsilon =3}$ from panel c. Dashed line: NM MSD calculated using $D_{g,\varepsilon =3}$ from panel d.

Figure 6.

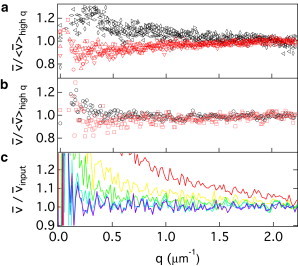
Swimming speed versus q from DDM. (a) Effect of tumbling (experiments): four data sets from the SW (black, top) and four data sets from the WT (red, bottom). (b) Effect of tumbling (simulations): SW (○) and WT $(\square )$. (c) Effect of depth of field δ for straight swimmers (simulations): $\delta =$ 5, 10, 20, 40, 75 and 100 $\mu \text{m}$ from top to bottom. To enable comparison and highlight the difference in q dependence, the swimming speed has been normalized to (a and b) ${\langle v\rangle }_{\text{high}\text{q}}$ or (c) the input mean swimming speed, ${\overline{v}}_{input}=15\mu m/s$, used to generate the simulated data.

Figure 7.

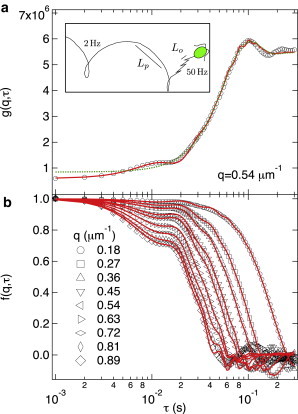
DDM for WT C. reinhardtii. (a) Measured $g\left(q,\tau \right)$ values (symbols). The solid line and dashed line are fits obtained with the oscillatory model (Eqs. 2 and 9) and the linear model (Eqs. 2, 4, and 6), respectively. Inset: Sketch of a helical C. reinhardtii trajectory. The progressive, $L_p$, and (zoomed-in) oscillatory, $L_0$, length scales probed by DDM are shown, with the frequencies of the helical precession (2 Hz) and oscillatory swimming (50 Hz). (b) ISFs, $f\left(q,\tau \right)$, obtained using Eqs. 2 and 9.

Figure 8.

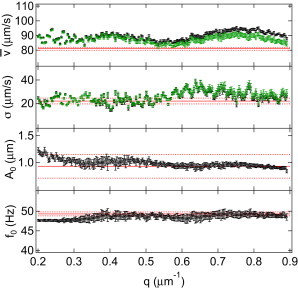
Fitting parameters obtained using the oscillatory model (○, black) or linear model (□, green) as a function of q for C. reinhardtii. From top to bottom: $\overline{v}$ and σ of the Schulz distribution, amplitude $A_0$, and frequency $f_0$. Lines are results from tracking, with dashed lines corresponding to error bars.

Figure 9.

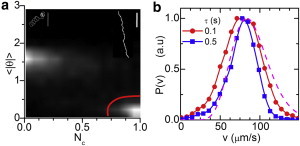
Tracking of C. reinhardtii. (a) Probability $P\left(N_c,\langle \left|\theta \right|\rangle \right)$ of all tracks ($\Delta t=0.05$ s). Tracks within the (red, lower right) bordered region (example in top-right inset, 7 s, scale bar = $150\mu$m) are used to measure $P\left(v\right)$; top-left inset: an excluded track with $N_c<0.4$, 30 s, scale bar = $30\mu$m). (b) Normalized $P\left(v\right)$ from tracks selected in panel a, for two values of τ. Dashed line: $P\left(v\right)$ from DDM analysis.

We fitted the data satisfactorily irrespective of whether bright-field, phase-contrast, or fluorescence imaging was used. However, phase-contrast imaging shows a better signal/noise ratio, $A\left(q\right)/B\left(q\right)$. Changing $A\left(q\right)$ and $B\left(q\right)$ by using a $20\times$ phase-contrast objective (which is suboptimal for our experiment) produced the same results in the relevant q range (data not shown).

Tracking results

Fig. 5 a shows the probability density of the track diagnostics $\left(N_c,\langle \left|\theta \right|\rangle \right)$ (see above). Recall that $\left(N_c,\langle \left|\theta \right|\rangle \right)=\left(1,0\right)$ for straight swimming and $\left(0,\pi /2\right)$ for Brownian diffusion. Although two clear maxima corresponding to diffusion and (nearly straight) swimming are observed, there is a substantial statistical weight of tracks with intermediate $\left(N_c,\langle \left|\theta \right|\rangle \right)$ values. The actual distribution obtained depends on $\Delta t$, the elementary time interval into which we segment trajectories. Our optimal choice, $\Delta t=0.1$ s, over which the average swimming distance is $\approx 1$ pixel, gave the most sharply separated peaks. However, the motile and NM populations are still not cleanly separated in our $\left(N_c,\langle \left|\theta \right|\rangle \right)$ data (Fig. 5 a). We therefore select various populations of motile and NM cells by including tracks with $\left(N_c,\langle \left|\theta \right|\rangle \right)$ values within progressively larger circles centered on their respective peaks in the $\left(N_c,\langle \left|\theta \right|\rangle \right)$ space. The radius of the circle (ε) is measured in units such that the $\left(0\le N_c\le 1,0\le \langle \left|\theta \right|\rangle \le \pi /2\right)$ space in Fig. 5 a is a $10\times 10$ rectangle.

For motile cells, we determined $P\left(v\right)$ at each ε by calculating the speed, $v={\langle \Delta r_{2D}\left(\tau \right)/\tau \rangle }_T$, for each trajectory, averaged over the trajectory duration, T, for various τ. The limit $\tau \to 0$ gives the instantaneous linear speed. In practice, the lowest reasonable τ is set by $\Delta t=0.1$ s. Fig. 5 b shows $P\left(v\right)$ at $\mathit{\epsilon }=3$ for $\tau =0.1$ s and 0.4 s, and Fig. 5 c shows $\overline{v}$ and σ of $P\left(v\right)$ for $\tau =0.1$ s and $\tau =1$ s. Unsurprisingly, $\overline{v}$ decreases with ε as progressively more nonideal swimming tracks are included (first more curved trajectories and then, at larger ε, some diffusive ones). Thus, certain ambiguities in the motility characterization arise with the use of tracking. It was also not possible to extract a value for α reliably, due to the strong dependence on ε.

However, the results for the other motility parameters show reasonable agreement with DDM (Fig. 4). In particular, using $\left(\Delta t,\tau \right)=\left(0.1\text{s},0.1\text{s}\right)$ (Fig. 5 c), and averaging over all ε, $\overline{v}=10.7\pm 0.3\mu \text{m}/\text{s}$ and $\sigma =5.1\pm 0.1\mu \text{m}/\text{s}$. The mean speed ${\overline{v}}_{\epsilon }$ for each ε is also consistent with the MSD of the swimmers (Fig. 5 e). The measured $P\left(v\right)$ depends on τ; for example, some fast swimmers will not be tracked for large τ unless they are perfectly aligned with the image plane, whereas for very short τ the 2D projection will contribute to $P\left(v\right)$ at small v (see above). Yet, for $\tau \sim 0.1-0.2$ s, our measured $P\left(v\right)$ shows broad agreement with the Schulz distribution inferred from DDM (Fig. 5 b). Residual differences between the tracking and DDM $P\left(v\right)$ are within experimental uncertainties, especially because we cannot readily distinguish between fitting the DDM data with Schulz and log-normal distributions (Fig. S2 b). Thus, the exact form of $P\left(v\right)$ is likely the least certain of the output from fitting, although its mean and variance are probably well estimated.

For NM cells, we determined D by fitting the MSDs for selected tracks at several ε. We again found a dependence on $\left(\Delta t,\tau \right)$ and ε. The MSD for $\mathit{\epsilon }>1$ showed deviations from purely diffusive behavior, and/or the resulting values of D depend significantly on ε (Fig. 5 d, open squares). Both effects are due to (likely artificial) non-Gaussian tails in $P\left(\Delta x_{NM}\left(\tau \right)\right)$ (not shown). Another estimate of the diffusion coefficient is $D_g$ (based on Gaussian fits to $P\left(\Delta x_{NM}\left(\tau \right)\right)$; see above), shown as a function of ε in Fig. 5 d. The average value $D_g=0.36\mu {\text{m}}^2/\text{s}$ agrees with the DDM value of $0.35\mu {\text{m}}^2/\text{s}$ and to the one from the MSD for $\varepsilon =1$. Fig. 5 e shows both the incorrect MSD of the diffusers obtained for $\varepsilon =3$ and the appropriate MSD based on $D_g$.

Vertical motion and depth of field

Our derivation of Eq. 2 assumes that the image contrast of a bacterium does not vary with its position along the vertical (optical) z axis, i.e., it assumes an infinite depth of field (δ). The validity of this assumption depends on how fast cells move relative to the finite δ in reality. Giavazzi et al. (18) presented a complex theoretical model, based on the coherence theory, to take this effect into account. Here, we suggest a simple model and use simulations to investigate this effect and its importance over the accessible q-range. Our simple model captures the essential features and reproduces qualitatively and quantitatively the experimental results.

Experimentally, the intensity profile of a bacterium along the z-axis can be described by the contrast function (7):

$$C\left(z\right)=C_B-C_0\left(1-\frac{4z^2}{{\delta }^2}\right)$$ (7)

where $C_B$ and $C_0$ are the background and the amplitude of an object in the focal plane $\left(z=0\right)$, respectively. We determined $C_B$ and $C_0$ experimentally, and then used this function to smear the previously presented simulated data (7) and obtain simulated images at a range of δ. At each δ-value except the lowest, the input values $\left\{\overline{v},\sigma ,\alpha ,D\right\}$ are recovered from DDM analysis of these images at $q\gtrsim 2\pi /\delta$ (the case of $\overline{v}$ is shown in Fig. 6 c). However, for $q\lesssim 2\pi /\delta$, the analysis returns $\overline{v}$ and D values that are too high: disappearance of cells along the z axis due to the rapid fading of $C\left(z\right)$ is mistaken as swimming and diffusion. A comparison of the experimental data (Figs. 4 and 6 a) and the simulated data (Fig. 6 b) shows that the effect of finite depth of field, δ, is negligible for $q>0.5\mu {\text{m}}^{-1}$ using 10× phase-contrast imaging, and that our experimental depth of field $\delta \gtrsim 20\mu$m.

WT E. coli

The motility pattern of WT E. coli in the absence of chemical gradients is well known (5). A cell alternates between running for $t_{\text{run}}\approx$ 1 s and tumbling for $t_{\text{tum}}\approx$ 0.1 s. During the latter, they change direction abruptly. After many tumbling events, the bacterium effectively performs a 3D random walk.

Modeling the ISF using Eq. 4 assumes that swimmers swim straight and do not tumble. We previously applied our method to WT E. coli (7). Here we study the effect of tumbling by comparing systematically the q dependence of the average speed obtained from DDM for WT (run and tumble) and SW (run only) swimmers. Because several experimental data sets were obtained from different batches of cells, we report the speed normalized to ${\langle \overline{v}\rangle }_{\text{high}\text{q}}$, the average in the range $\left(2.0<q<2.2\mu {\text{m}}^{-1}\right)$.

The simulations and experiments show a qualitative difference in $\overline{v}\left(q\right)$ of SW and WT cells (Fig. 6). All of the data for WT cells show a slight decrease in $\overline{v}\left(q\right)$ toward low q, whereas the data for SW cells show the opposite trend. The increase toward low q in the $\overline{v}\left(q\right)$ of the SW is presumably largely due to depth of field effects (see above). The opposite trend in the behavior of $\overline{v}\left(q\right)$ for the WT can be understood as follows: The mean speed, $\overline{v}\left(q\right)$, measured by DDM at a certain q is estimated by $\overline{v}\left(q\right)\sim (2\pi /q)/{\tau }_q$, i.e., the time $\left({\tau }_q\right)$ taken to advect density between two points spatially separated by distance $2\pi /q$. For a straight swimmer, the track length s will be equal to the distance between the two points, i.e., $s=2\pi /q$, so that $\overline{v}\left(q\right)=\overline{v}$. Any deviation from a straight track, e.g., due to changes in direction from tumbling, renders $s>2\pi /q$. Because ${\tau }_q=s/\overline{v}$, we now have $\overline{v}\left(q\right)<\overline{v}$. This effect becomes progressively more pronounced at low q, as observed.

Finally, note that collisions with diffusers (and indeed other swimmers) will likely affect the trajectory of the swimmers in a qualitatively similar way to occasional tumbling. Thus, the largely q-independent motility parameters we obtained suggest that in the space-time window we probe, collisions are at most perturbative; indeed, they should appear as q dependence at low q, as in the case of tumbling. Of course, in more strongly interacting suspensions, the nonswimmer dynamics may be so strongly coupled to those of the swimmers that the motion of the former is no longer diffusive in any sense. New models of the ISF will then be needed to fit the DDM data.

Swimming algae: WT C. reinhardtii

As a final example, we apply DDM to the biflagellate freshwater alga C. reinhardtii, a model for eukaryotic flagellar motility (2). C. reinhardtii has a prolate spheroidal cell body ∼$10\mu$m across with two flagella roughly 10–$12\mu$m long (2). Beating of the latter at $\approx 50$ Hz in an alternation of effective (forward moving) and recovery (backward moving) strokes propels the cell body forward on average, and the cell body oscillates as it advances. The flagellar beat is not perfectly planar, so cells precess around their long axis at $\approx 2$ Hz. This rotation, which is critical for phototaxis (16), results in helical swimming trajectories. For length scales $\sim 100\mu m$ the direction of the axis of the helical tracks is approximately straight, but on larger scales the stochastic nature of the flagellar beat causes directional changes resulting in random walk (6,14,26).

Racey et al. (27) carried out the first high-speed microscopic tracking study of C. reinhardtii, obtaining a $P\left(v\right)$ with mean $\overline{v}=84\mu$m/s, as well as an average amplitude $\overline{A}=1.53\mu$m and frequency $\overline{f}=49$ Hz of the beat. More recent tracking provided a 2D $P\left(v\right)$ with $\overline{v}\approx 100\mu$m/s (28). The swimming of C. reinhardtii has also been studied by DLS (27,29); however, the q limitation of conventional DLS is even greater here than in the case of bacteria because algae swim on larger length scales, requiring smaller values of q. Here, we present the first characterization (to our knowledge) of the swimming motility of C. reinhardtii using DDM.

Model of ISF

The swimming dynamics of C. reinhardtii are on larger length scales and shorter timescales (i.e., the algae swim faster) and of a different nature compared with those of E. coli. The decay of the ISF, $f\left(q,\tau \right)$, will reflect will reflect the swimming stroke of the alga. Cells oscillate at length scales $<10\mu m$, translate in the range of $10\mu m<L<30\mu m$, spiral over $30\mu m<L<100\mu m$, and diffuse for $L>100\mu m$. A schematic representation of a helical trajectory, highlighting the small-scale oscillatory motion, is shown in the inset of Fig. 7 (diffusive length scales are not shown).

At length scales $L\lesssim 30\mu \text{m}$, the time-dependent displacement of a C. reinhardtii cell, $\Delta r\left(\tau \right)$, can be approximated as a sinusoidal oscillation superimposed on a linear progression (29):

$$\Delta r\left(\tau \right)=v\tau +A_0\left[\text{sin}\left(2\pi f_0\tau +\varphi \right)-\text{sin}\left(\varphi \right)\right],$$ (8)

where $A_0$ and $f_0$ are the amplitude and frequency of the swimming oscillation, respectively, and ϕ is a random phase to desynchronize the beating of different cells. Substituting this into Eq. 3, averaging over ϕ, and assuming a Schulz distribution for $P\left(v\right)$ (Eq. 5) gives

$$f_{\text{algae}}\left(q,\tau \right)=\frac{1}{2}\underset{-1}{\overset{1}{\int }}\frac{\text{cos}\left[\left(Z+1\right){\text{tan}}^{-1}\left(\Lambda \chi \right)\right]}{{\left[1+{\left(\Lambda \chi \right)}^2\right]}^{\left(Z+1\right)/2}}{J}_0\left[2q{A}_0\chi \text{sin}\left(\pi f_0\tau \right)\right]d\chi ,$$ (9)

where $\Lambda =q\overline{v}\tau /(Z+1)$, $\chi =\text{cos}\psi$, ψ is the angle between $\overrightarrow{q}$ and $\overrightarrow{r}$, and $J_0$ is the zeroth-order Bessel function. All other terms are as previously defined. The first and second terms describe the contribution from straight swimming and oscillatory beat, respectively. In the limit $q{A}_0\ll 1$ $\left(J_0\to 1\right)$, Eq. 9 reduces to Eq. 6, the same expression as for the progressive model used for E. coli.

The derivation of Eq. 9 assumes that the distributions $P\left(A\right)$ and $P\left(f\right)$ for swimming amplitude and frequency, respectively, are narrowly centered around the values $A_0$ and $f_0$. Moreover, it neglects the diffusion of NM algae, any bias in the swimming direction caused by gravitaxis (30), and the helical nature of the swimming.

DDM results

Fig. 7 a shows a typical DICF, $g\left(q,\tau \right)$, at $q=0.54\mu {\text{m}}^{-1}$ $\left(l\approx 12\mu \text{m}\right)$, for a suspension of WT C. reinhardtii measured by DDM. The reconstructed ISFs are shown in Fig. 7 b for $0.2⪅q⪅0.9\mu {\text{m}}^{-1}$, corresponding to a length scale range of $7⪅l⪅30\mu {\text{m}}^{-1}$. $f\left(q,\tau \right)$ shows a characteristic shape for all q-values, i.e., a fast decay at $\tau \le 0.02$ s due to the oscillatory beat and a slower decay at $\tau \ge 0.02$ s due to swimming. The identity of these two processes is confirmed by their difference in τ and q dependencies. The characteristic time of the fast process is q independent, whereas its amplitude decreases with q. Both observations fully agree with the term $\left(J_0\right)$ due to the oscillatory contribution in Eq. 9. Moreover, 0.02 s corresponds to the period of a 50 Hz oscillatory beat. Finally, the slow process scales perfectly with $q\tau$ (Fig. S3), confirming the ballistic nature (swimming) of this process.

Fig. 8 shows the fitting parameters $\left(\overline{v},\sigma ,A_0,f_0\right)$ from Eq. 2 using the oscillatory model (Eq. 9) as a function of q. All parameters display a small q dependence. This is likely due to effects that are not captured by the simple oscillatory model (e.g., body precession and helical swimming) and will be discussed elsewhere. Averaging over q yields $\overline{v}=89.6\pm 2.8\mu$m/s, $\sigma =24.9\pm 4.6\mu$m/s, $A_0=0.98\pm 0.06\mu$m and $f_0=48.6\pm 0.6$ Hz, with estimated error bars reflecting the residual q dependence. Fitting the experimental data using Eq. 9 requires numerical integration. Using the linear model (Eq. 6) instead, thus ignoring the oscillatory beat, yields similar results for ($\overline{v}$,σ) (Fig. 8). This is because the fast process is mainly ignored when a fit such as that shown in Fig. 7 a is performed. Moreover, using the linear model and a movie for which the lowest $\tau ⪆1/f_0$ (e.g., 100 fps) so that the oscillatory beat does not contribute to the ISF, we obtain the same $\left(\overline{v},\sigma \right)$, thus allowing high-throughput economical measurements of the mean speed of biflagellate algae.

Tracking results

Tracking resulted in two well-separated groups of $\left(N_c,\langle \left|\theta \right|\rangle \right)$ values (see above) that were independent of $\Delta t$, provided $\Delta t>1/f_0$ (Fig. 9 a). We used tracks with $\left(N_c\ge 0.7,\langle \left|\theta \right|\rangle <0.5\right)$, reflecting nearly straight swimmers aligned with the image plane, to obtain $P\left(v\right)$. Misaligned tracks are excluded in the following way: motion perpendicular to the helical axis enhances the circular contribution in the 2D projection, thus reducing $N_c$ and increasing $\langle \left|\theta \right|\rangle$ (insets in Fig. 9 a).

We measured $P\left(v\right)$ for several τ-values and found a slight τ dependency, e.g., due to undetected fast swimmers for large τ (Fig. 9 b). Note that our $P\left(v\right)$ is smaller at small v than in a previous study (28) in which all projected trajectories were considered. Our small-v data are likely closer to the true distribution, due to our exclusion of misaligned tracks. Moreover, our $P\left(v\right)$ values are in reasonable agreement with the result inferred from DDM (Fig. 9 b). We find $\overline{v}=81\pm 1\mu$m/s and $\sigma =22\pm 3\mu$m/s (averaged over different τ), which agree well with the DDM values (Fig. 8). Extending the selected trajectories to ($N_c\ge$ 0.55, $\langle \left|\theta \right|\rangle <0.7$) changes $P\left(v\right)$ and $\overline{v}$ by <$5\%$. We analyzed the oscillating component of the displacement, $r_{os}\left(t\right)$, for straight tracks, defined as $r_{os}\left(t\right)=\left(x_{os},y_{os}\right)\left(t\right)=r_{2D}\left(t\right)-{\langle r_{2D}\left(t\right)\rangle }_{dt}$, with $dt=2/f_0$. $r_{os}\left(t\right)$ is well resolved due to subpixel accuracy $\sim 0.2\mu$m of the coordinates. Fourier analysis of $r_{os}\left(t\right)$ gave $f_0=49.3\pm 0.5$ Hz. We identified an additional modulation frequency of $\sim 10$ Hz (i.e., an extra peak at $f-f_0\simeq 10$ Hz in the power spectrum of $r_{os}\left(t\right)$; to be discussed elsewhere). From the root mean-square value of $r_{os}\left(t\right)$, we determined the average oscillation amplitude $A_0=\sqrt{2\langle x_{os}^2+y_{os}^2\rangle }=0.93\pm 0.22\mu$m. These values are in agreement with a previous study (27) and the DDM results.

Thus, our results simultaneously validate DDM and the simple model (Eqs. 8 and 9) for swimming C. reinhardtii. Our method can therefore be used to characterize the motility of large ensembles of this organism (and potentially of other algae) rapidly and accurately.

Conclusions

DDM is a powerful, high-throughput technique to characterize the 3D swimming dynamics of microorganisms over a range of timescales and length scales ($\sim 3$ and $\sim 1$ order of magnitude, respectively) simultaneously in a few minutes, based on standard imaging microscopy. The timescales and length scales of interest depend on the swimming dynamics of the microorganism, and are easily tuned by changing the frame rate or optical magnification, respectively.

We studied in detail the use of DDM to characterize the motility of SW (run only) and WT (run and tumble) E. coli, as well as WT alga C. reinhardtii. We validated the methodology using tracking and simulations. The latter were also used to investigate the effect of a finite depth of field and tumbling in case of E.coli. Using DDM, we were able to extract 1), the swimming speed distribution, fraction of motile cells, and diffusivity for E. coli; and 2), the swimming speed distribution, and amplitude and frequency of the oscillatory dynamics for C. reinhardtii. In both cases, we obtained these parameters by averaging over many thousands of cells in a few minutes without specialized equipment.

Further developments are possible. For E. coli, analytic expressions for $\overline{v}\left(q\right)$ that take into account the trajectory curvature due to rotational Brownian motion (SW) or directional changes due to tumbling (WT) can be derived. Fitting these expressions to data should yield information about the respective features. For C. reinhardtii, the helical motion, the asymmetric nature of the swimming stroke, and the higher harmonics in the body oscillations observed by tracking could be explored theoretically and with the use of DDM. This will allow us to test simulations that use the method of regularized stokeslets to reproduce the fine details of swimming biflagellate algae (32).

DDM is based on the measurement of the spatiotemporal fluctuations in intensity, and therefore does not require high optical resolution of the motile objects. Thus, DDM can probe a large field of view and yield good statistics even under relatively poor imaging conditions. Moreover, DDM could also be used to probe the anisotropic or asymmetric dynamics (13) of microorganisms, e.g., due to chemotaxis. Finally, DDM is not restricted to dilute suspensions, and can be used to investigate the collective dynamical behavior of concentrated populations (33), although new models of the ISF will be needed. This is analogous to the use of DLS to study concentrated passive colloids (34–36), which also involves the development of new theories for the ISF.

With the availability of DDM, quantitative characterization of motility can become a routine laboratory method, provided that suitable theoretical models are available for fitting of the ISF. We emphasize again that such models can only come from direct microscopic observation or tracking, which therefore remains an indispensable technique, especially if detailed information beyond a few motility parameters is required. On the other hand, even without analytical models, the qualitative features of the measured ISF may still allow conclusions to be drawn and trends to be studied (e.g., the speeding up of the decay of the ISF almost invariably corresponds to faster motion). Thus, DDM has the potential to become a powerful tool for studying microorganism locomotion alongside established techniques of tracking.