STICCS Reveals Matrix-Dependent Adhesion Slipping and Gripping in Migrating Cells

Abstract

Two-color spatio-temporal image cross-correlation spectroscopy (STICCS) is a new, to our knowledge, image analysis method that calculates space-time autocorrelation and cross-correlation functions from fluorescence intensity fluctuations. STICCS generates cellular flow and diffusion maps that reveal interactions and cotransport of two distinct molecular species labeled with different fluorophores. Here we use computer simulations to map the capabilities and limitations of STICCS for measurements in complex heterogeneous environments containing micro- and macrostructures. We then use STICCS to analyze the co-flux of adhesion components in migrating cells imaged using total internal reflection fluorescence microscopy. The data reveal a robust, time-dependent co-fluxing of certain integrins and paxillin in adhesions in protrusions when they pause, and in adhesions that are sliding and disassembling, demonstrating that the molecules in these adhesions move as a complex. In these regions, both α6β1- or αLβ2-integrins, expressed in CHO.B2 cells, co-flux with paxillin; an analogous cotransport was seen for α6β1-integrin and α-actinin in U2OS. This contrasts with the behavior of the α5β1-integrin and paxillin, which do not co-flux. Our results clearly show that integrins can move in complexes with adhesion proteins in protrusions that are retracting.

Introduction

Fluctuation spectroscopy techniques have been used for over a century, notably by Jean Perrin to validate Einstein’s theory of Brownian motion and diffusion using an ultramicroscope (1) . This approach experienced a renaissance with the development in the early 1970s of fluorescence correlation spectroscopy (FCS), which probes the dynamics and binding kinetics of diffusing macromolecules (2–4). The central idea is to measure the fluctuations of fluorescently labeled molecules as they move in and out of a small laser illuminated focal volume as a function of time. These fluctuations provide information on the molecular dynamics (characteristic residency time within the focal volume) and the concentration (from the normalized variance in the fluctuation magnitudes). The fluctuation time series is analyzed by calculating a time autocorrelation function, which is fit with an appropriate decay model to measure the corresponding molecular properties.

An extension of FCS for two fluorescent species was first hypothesized by Eigen and Rigler (5) and later achieved experimentally by Schwille et al. (6) where fluctuations of two different fluorescent markers are cross-correlated with each other, which reveals molecular interactions within a common focal volume. Since then, many other variations of FCS have been successfully implemented (reviewed in Haustein and Schwille (7) and Weidemann and Schwille (8)).

Whereas FCS is a time-domain technique, image correlation spectroscopy (ICS) extends fluorescence fluctuation analysis to the spatial domain. Initially introduced as a method to measure receptor distributions and clustering from spatial autocorrelation analysis of single images (9,10), ICS has been expanded to include measurement of slow transport (temporal ICS) (11,12)), fast transport (raster-scan ICS) (13,14)), and molecular interactions (image cross-correlation spectroscopy (ICCS) (11)). Other related applications have made use of electron-multiplying charge-coupled device cameras in combination with correlation analysis to perform spatially resolved FCS studies (15) as well as pixel-by-pixel correlations within a single image series for biological applications (the software ImFCS or imaging total internal reflection-FCS (16–18)). A novel, to our knowledge, method combining ICCS and single-particle tracking has been recently implemented to determine correlation fractions and lengths (19). Temporal ordering cross-correlation asymmetry is also closely related to both FCCS and ICCS (20); it determines the binding event order in time for complexes composed of multiple types of biomolecules.

An extension of ICS combining space and time correlation analysis of images was called spatio-temporal ICS (STICS (21)). STICS analysis enabled measurement of both velocity vectors and diffusion coefficients and generated transport maps across the entire cell. Two studies, one based on STICS (22), and another based on fluorescence speckle microscopy (23), determined the flow properties of adhesion proteins and cytoskeletal components in cells. Both approaches yielded similar results, revealing that integrins are largely immobile, whereas other adhesion proteins have different levels of flow in the retrograde direction of flowing actin. Several adhesion proteins, e.g., talin and paxillin, flow slowly compared to actin, whereas α-actinin flux is highly coupled both in direction and speed to that of actin (22,23).

These data confirm the existence of an intracellular molecular clutch that regulates the degree of engagement of adhesions to the actin cytoskeleton, and reveal its dynamic nature. A recent study has expanded this model, suggesting the existence of a force-sensitive extracellular clutch that stabilizes adhesions upon application of myosin II-generated force (24). Together, these studies suggest the existence of a multitiered molecular clutch with several potential points of engagement or slippage, including the ECM-integrin interaction and the molecular linkage that connects integrins with actin. However, although these studies made inferences about the interactions between different components of the clutch based on the relative flow rates and directions, they did not reveal whether two molecules are interacting within a common complex, or reside in closely separated (subdiffraction limit) but kinetically similar complexes. Another outstanding question is how this functions generally among different integrins and pliability conditions.

In this study, we demonstrate the feasibility of spatio-temporal image cross-correlation spectroscopy (STICCS) for revealing dynamic associations among fluxing adhesion components, by first testing the method with simulations that realistically capture key aspects of the heterogeneous cell environment and by probing the flux of adhesion proteins in migrating cells using different ECM-integrin pairs. To begin, we generated computer-simulated images to establish different contributions to the auto- and cross-correlation functions from a heterogeneous environment containing both point source particles and macroscopic objects, with variable set transport properties, densities, and signal/noise ratios.

In addition, we validated the method with control measurements on cells expressing a protein labeled with two different colored fluorescent tags. We then applied two-color STICCS to investigate the dynamics of paxillin and either α5β1 (in cells adhered on fibronectin), α6β1 (in cells on laminin), or αLβ2 (in cells adhered to recombinant human intracellular adhesion molecule 1 protein (ICAM-1)) to study their molecular interactions and cotransport in living cells. Previous studies had shown that integrins co-flux with actin in cells expressing α6β1 or αLβ2 but not α5β1 (25). The data reveal a co-fluxing in all cases, except for α5β1, suggesting that the adhesions flux as a complex.

Theory

The image time series from two fluorescence microscope detection channels, a and b, are denoted i_a(x,y,t) and i_b(x,y,t) (see Fig. 1, A and B), with the unnormalized intensity fluctuation correlation function (covariance) in real space and time,

$$r_{ab}\left(\xi ,\eta ,\tau \right)={\langle {\langle \delta i_a\left(x,y,t\right)\delta i_b\left(x+\xi ,y+\eta ,t+\tau \right)\rangle }_{x,y}\rangle }_t,$$ (1)

where $\delta i_a\left(x,y,t\right)=i_a\left(x,y,t\right)-\langle i_a\left(x,y,t\right)\rangle$. An equivalent representation in Fourier (k-) space is (30)

$$r_{ab}\left(\overrightarrow{k},\tau \right)=\langle i_a\left(\overrightarrow{k},t\right)i_b^{\ast }\left(\overrightarrow{k},t+\tau \right)\rangle .$$ (2)

Figure 1.

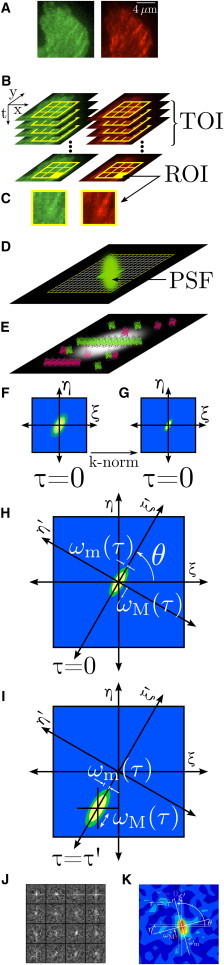
STICCS overview. (A) Fluorescence microscopy images in two channels, red and green, of a cell edge with visible adhesions, which are part of an image time series (B). The time subset of interest (TOI) is the subset of frames analyzed and the ROIs (shown as yellow squares in panels B–D) are the analyzed subregions. (D) The emission point spread function (PSF) represents the general focal volume and is oversampled by the pixels in the imaging charge-coupled device camera to have spatial correlations between adjacent pixels. The pixilated image maps fluorescence intensities integrated from a distribution of fluorophores with a spatial resolution set by the PSF; however, macroscopic fluorescent objects will be larger than the PSF, such as a focal adhesion made up of many fluorescent proteins (E in profile (26–29)). (F and G) General schematics of the spatio-temporal correlation functions (CF: r_aa, r_bb, r_ab, or r_ba) at one ROI before and after k-space normalization, which effectively removes the PSF. Bivariate Gaussian functions are fit for each time lag (H and I), with the axes rotated by an angle θ to align with the major axis of the evolving CF (if present), yielding time-dependent radii of the major (ω_M(τ)) and minor (ω_M(τ)) axes. The CFs are fit for all ROIs (J) and all time lags. (K) Shows one time lag of a typical CF for a 16 × 16 pixel ROI from a cell. Velocity vectors are obtained by fitting the translating CF peaks (I) that are above defined thresholds.

The intensity is summed over all point particles, N_a, in the entire image region of interest (ROI),

$$i_a\left(\overrightarrow{k},t\right)={\Lambda }_a{\mathit{\varrho }}_a\left(\overrightarrow{k}\right)\sum _{j=1}^{N_a}\text{exp}\left(-i\overrightarrow{k}·{\overrightarrow{r}}_j\left(t\right)\right),$$ (3)

where ${\mathit{\varrho }}_a\left(\overrightarrow{k}\right)=\text{exp}\left(-{\varpi }_a^2{\left|\overrightarrow{k}\right|}^2/8\right)$ is the Fourier transform of the point spread function (PSF) and ${\Lambda }_a=q_a{I}_a{\varpi }_a^2\pi /2$ includes the quantum yield; q, the peak laser intensity at focus I; and ϖ is the e⁻² beam radius. We have assumed there is no bleaching or blinking. The point particles can form composite, large (relative to the PSF) macro objects of equal size and shape composed of variable numbers of particle subunits. We assume the particles and macro objects can have different transport properties.

Substituting Eq. 3 into Eq. 2 and separating the matrix into diagonal terms (colocalized particles in both channels) and off-diagonal (cross-) terms (particles in only one channel) gives

$$r_{ab}\left(\overrightarrow{k},\tau \right)={\Lambda }_a{\Lambda }_b{\mathit{\varrho }}_a\left(\overrightarrow{k}\right){\mathit{\varrho }}_b\left(\overrightarrow{k}\right)\left\{\langle \sum _{j=1}^N{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j\left(t\right)-{\overrightarrow{r}}_j\left(t+\tau \right)\right)}\rangle +\langle \sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j\left(t\right)-{\overrightarrow{r}}_m\left(t+\tau \right)\right)}\rangle \right\},$$ (4)

where N = N_a ∩ N_b is the intersection or the number of colocalized particles between each channel in the ROI.

Assuming only flow transport, we separate the first term in Eq. 4 into one of three different particle populations:

• 1.N–F–G, the number of particles outside of the macro objects,
• 2.F, the number of particles that make up macro objects, or
• 3.G, the number of particles superimposed with, but not physically part of the macro objects.

This gives

$$\langle \sum _{j=1}^N{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j\left(t\right)-{\overrightarrow{r}}_j\left(t+\tau \right)\right)}\rangle =\langle \sum _{j=1}^{N-F-G}{e}^{-i\overrightarrow{k}·\overrightarrow{v}\tau }\rangle +\langle \sum _{j=1}^F\phi \left({\overrightarrow{k}}^{\prime },\tau \right)e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau }\rangle +\langle \sum _{j=1}^G{e}^{-i\overrightarrow{k}·\overrightarrow{v}\tau }\rangle ,$$ (5)

$$=\left(N-F-G\right)e^{-i\overrightarrow{k}·\overrightarrow{v}\tau }+F\phi \left({\overrightarrow{k}}^{\prime },\tau \right)e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau }+G{e}^{-i\overrightarrow{k}·\overrightarrow{v}\tau },$$ (6)

$$=\left(N-F\right)e^{-i\overrightarrow{k}·\overrightarrow{v}\tau }+F\phi \left({\overrightarrow{k}}^{\prime },\tau \right)e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau },$$ (7)

where $\overrightarrow{v}$ is the particle velocity, ${\overrightarrow{v}}_{adh}$ is the velocity of the macro objects, and $\phi \left({\overrightarrow{k}}^{\prime },\tau \right)$ is the dynamic form factor (31).

We separate the second term in Eq. 4 (representing the distinct terms) into one of four possibilities:

• 1.j and m are both part of the same macro object,
• 2.j and m are part of different macro objects,
• 3.either j or m are part of a large macro object, or
• 4.neither j nor m are part of a large macro object.

Assuming no contribution from particles that are not part of macro objects, the last two cases will not correlate, and we obtain

$$\langle \sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j\left(t\right)-{\overrightarrow{r}}_m\left(t+\tau \right)\right)}\rangle =L\langle e^{i\overrightarrow{k}·\left(\overrightarrow{R}\left(t\right)-\overrightarrow{R}\left(t+\tau \right)\right)}\sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j^{\prime }\left(t\right)-{\overrightarrow{r}}_m^{\prime }\left(t+\tau \right)\right)}\rangle +\langle \sum _{\ell =1,\ell \ne {\ell }^{\prime }}^L{e}^{i\overrightarrow{k}·\left({\overrightarrow{R}}_{\ell }\left(t\right)-{\overrightarrow{R}}_{{\ell }^{\prime }}\left(t+\tau \right)\right)}\sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j^{\prime }\left(t\right)-{\overrightarrow{r}}_m^{\prime }\left(t+\tau \right)\right)}\rangle ,$$ (8)

where L is the number of macro objects within the ROI and where we redefined the spatial coordinates to incorporate the center of mass of each object (R_L),

$${\overrightarrow{r}}_j^{\prime }\left(t\right)={\overrightarrow{R}}_L\left(t\right)-{\overrightarrow{r}}_j\left(t\right).$$

Putting it back together, we have

$$r_{ab}\left(\overrightarrow{k},\tau \right)={\Lambda }_a{\Lambda }_b{\mathit{\varrho }}_a\left(\overrightarrow{k}\right){\mathit{\varrho }}_b\left(\overrightarrow{k}\right)[\left(N-F\right)e^{-i\overrightarrow{k}·\overrightarrow{v}\tau }+F\phi \left({\overrightarrow{k}}^{\prime },\tau \right)e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau }+L{e}^{i\overrightarrow{k}·\Delta R_0\left(\tau \right)}\langle \sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j^{\prime }\left(t\right)-{\overrightarrow{r}}_m^{\prime }\left(t+\tau \right)\right)}\rangle +\left(L-1\right)e^{i\overrightarrow{k}·\Delta R_1\left(\tau \right)}\langle \sum \sum _{j\ne m}{e}^{-i\overrightarrow{k}·\left({\overrightarrow{r}}_j^{\prime }\left(t\right)-{\overrightarrow{r}}_m^{\prime }\left(t+\tau \right)\right)}\rangle ],$$ (9)

where $\overrightarrow{R}\left(t\right)-\overrightarrow{R}\left(t+\tau \right)\equiv \Delta R_0\left(\tau \right)$ is the separation length at time lag τ between particles within the same macro object and ${\overrightarrow{R}}_{\ell }\left(t\right)-{\overrightarrow{R}}_{{\ell }^{\prime }}\left(t+\tau \right)\equiv \Delta R_1\left(\tau \right)$ is the spatially averaged separation distance between each macro object and its nearest neighbor with the contribution from remaining neighbors assumed negligible.

In k-space, we can normalize and remove the PSF and static object contributions with the τ = 0 amplitude, $r_{ab}\left(\overrightarrow{k},0\right)=N{\Lambda }_a{\Lambda }_b{\mathit{\varrho }}_a\left(\overrightarrow{k}\right){\mathit{\varrho }}_b\left(\overrightarrow{k}\right)$ :

$$\frac{r_{ab}\left(\overrightarrow{k},\tau \right)}{r_{ab}\left(\overrightarrow{k},0\right)}=\frac{N-F}{N}{e}^{-i\overrightarrow{k}·\overrightarrow{v}\tau }+\frac{F}{N}\left[e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau }+L{e}^{i\overrightarrow{k}·\Delta R_0\left(\tau \right)}+\left(L-1\right)e^{i\overrightarrow{k}·\Delta R_1\left(\tau \right)}\right]\phi \left({\overrightarrow{k}}^{\prime },\tau \right).$$ (10)

If we assume all macro objects in a ROI move at the same constant velocity ($\Delta R_0\left(\tau \right)={\overrightarrow{v}}_0\tau ,$ $\Delta R_1\left(\tau \right)={\overrightarrow{v}}_1\tau ,$ and ${\overrightarrow{v}}_0={\overrightarrow{v}}_1={\overrightarrow{v}}_{adh}$), we have

$$\frac{r_{ab}\left(\overrightarrow{k},\tau \right)}{r_{ab}\left(\overrightarrow{k},0\right)}=\frac{N-F}{N}{e}^{-i\overrightarrow{k}·\overrightarrow{v}\tau }+\frac{F}{N}\left(2L-1\right)\phi \left({\overrightarrow{k}}^{\prime },\tau \right)e^{-i\overrightarrow{k}·{\overrightarrow{v}}_{adh}\tau }.$$ (11)

By assuming that a subset of particles assemble into identical large structures moving at the same velocity, where each macrostructure only correlates with itself and its closest neighbor, we are able to obtain an expression of the correlation function (CF) that results in two peaks that are due to particle motion and macro object motions. This assumption is based on the fact that we experimentally detected correlations above background for active assembled adhesions in specific regions of interest, and over time periods during which the fluxing appeared constant by visual examination of Movie S1 and Movie S2 in the Supporting Material (and refer to Cellular Experiments, below).

A low density of particles populating the macro objects results in a dominant particle peak (30,32) whereas a high density of particles results in a dominant macro object peak. Other limits have been explored in detail in Wu et al. (31) and Kurniawan and Rajagopalan (33).

The Supporting Material contains detailed derivations of all cases treated in the simulations (Fig. 2).

Figure 2.

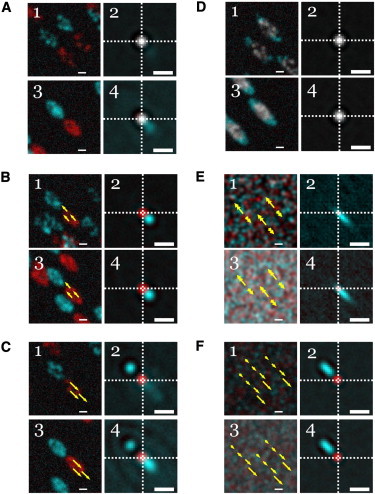
Simulation results and their resulting ACFs obtained via STICCS analysis for the following particle/macroscopic adhesion models: (A) Treadmilling, where adhesions flow due to particle addition/removal at the ends but particles inside the adhesion masks are static. (B) Sliding, where particles and adhesion masks flow together. (C) Antisliding, with particles flowing in the opposite direction of the adhesion masks (so peak separation can be visualized). (D) Spreading of immobile adhesion masks with immobile particles. (E) Particles undergoing anisotropic diffusion and flow in free space. (F) Dispersed flow of four particle populations with different but narrowly distributed velocities. Each model was analyzed for lower and higher particle densities (5 particles/μm², top panels in each square; and 50 particles/μm², bottom panels in each square). Each odd-numbered panel shows the superposition of the first and 100th frames (t = 1 and 100 s) from a single image series while each even-numbered panel shows the superposition of the corresponding ACFs at two time lags (τ = 2 and 15 s). Each of these panels have markers (yellow) superimposed to symbolize the motion of the particles, indicating: (A and D) static motion (solitary yellow rings), (B and C) constant velocity (identical arrows), (E) anisotropic diffusion and flow (double arrows with the longer arrows indicating flow direction along the adhesion mask’s semimajor axis), and (F) dispersed velocities (arrows of variable length representing a distribution of particle speeds). For each panel, data (in red and cyan) represent initial and final configurations, respectively. (White) Areas of overlap between features in the superposition. Scale bars are 5 μm for the image series and 1 μm for the CFs.

We apply the Sparrow resolution criterion to estimate the average interparticle distance that will cross the threshold for detection of a peak due to macro objects: $\Delta x\doteq 0.47\lambda /N_A,$, where λ = 500 nm and N_A = 1.4 is the numerical aperture. We find that $\Delta x\doteq 0.17$ μm or a density of 11 particles/μm². When this limit is exceeded, and $\overrightarrow{v}\ne {\overrightarrow{v}}_{adh}$, we will see two separate peaks. However, when $\overrightarrow{v}\sim {\overrightarrow{v}}_{adh},$ there is only one CF peak, due to collective motion, which contains spatial shoulders due to the shape of the macro objects.

Transforming back to real space results in a narrower peak(s) that evolves according to the dynamics of the particles and macro objects (Fig. 1, F and G), and is analyzed by an extension of STICS where we fit to a bivariate Gaussian to account for anisotropic transport along a direction set by extended adhesion structures. We extract the time-dependent CF peak width from the semimajor and semiminor axes (ω_M(τ),ω_m(τ)), its translation, and also the orientation of the peak, θ(τ) (Fig. 1, H–K).

Materials and Methods

See the Supporting Material.

STICCS analysis

We set 16 × 16 pixel ROIs (Fig. 1, B and C) with adjacent ROIs shifted by four pixels to map areas across each cell. We select a time subset of interest (TOI), t₁ < t < t₂, from the full time series (t₀ to t_final) (Fig. 1 B), with durations ranging from 20 to 100 s (N_f = 10–20 frames) for the real cell image data. The time interval between images is δt and the pixel size along both axes is p_x,y.

Computer simulations

We used computer simulations of microscopy image series of particles and objects to test k-space-normalized STICCS under controlled conditions that modeled the essentially heterogeneous distribution of proteins and adhesions in cells. We tested the ability of STICCS to resolve contributions to autocorrelation and cross-correlation functions (ACFs and CCFs) from multiparticle macrostructures larger than the PSF (e.g., adhesions) and from those of the particles (e.g., labeled proteins) that compose these structures (Fig. 1 E). We detect interactions as cross-correlations from species that are cotransported in a common complex but are not necessarily directly touching.

In an effort to better understand the spatio-temporal CFs calculated from real cellular data, we use the simulations to explore how heterogeneous dynamics, densities, and composite intensities of macro objects and particles all contribute to the CFs.

We explored a range of flow transport conditions and densities for particles and macroscopic objects (simulating adhesions as elliptical image masks). The distinction we make between particles and large objects is that the particles are point emitters that are smaller than the PSF, whereas the macro objects (elliptical masks) are larger than the PSF, but are filled with the same point particles with a predetermined density. The flow parameters of the particles and the adhesion masks are independently set.

Fig. 2 describes the results obtained by simulating one of the following specific transport models:

• Fig. 2 A. Treadmilling (the adhesion mask flows but the particles are stationary).

• Fig. 2 B. Sliding (both adhesions and particles translate in tandem).

• Fig. 2 C. Antisliding (an artificial case to illustrate particle/macro object CF peak separation when adhesions and particles flow in opposite directions).

• Fig. 2 D. Spreading (adhesion mask elongates while the particles and adhesions remain stationary).

• Fig. 2 E. Anisotropic diffusion and flow.

• Fig. 2 F. Dispersive flow (several different particle populations are set flowing with different, but narrowly distributed, velocities).

Fig. 2 shows that these models all produce CFs that fall into one of three general categories:

• 1.the presence of a stationary peak,
• 2.one moving peak, or
• 3.the presence of two peaks, at least one of which is moving.

For the first category, the models yielding stationary and symmetric CFs are seen in both treadmilling (A2) and spreading (D). The common link between these systems is they are all composed of stationary particles regardless of the transformation of the adhesion masks.

For the second category, a single translating CF peak was observed which was symmetric (ω_M(τ) = ω_m(τ) = ω(0)) or asymmetric (ω_M(τ) > ω_m(τ)) with spreading along the semimajor axis. We observe a single Gaussian CF peak with ω_M = ω_M = ω(0) for the sliding model (B). However, we observe anisotropic spreading of the CF along the semimajor axis when a system of particles anisotropically diffuses and flows in free space (E) or undergoes dispersive flow (F). In this latter case, a single ellipsoidal CF peak evolves in time when the populations of particles were moving in free space (not bound within adhesions) but with a distribution of velocities. This is in contrast to the symmetric ω_M = ω_M Gaussian CF peak, which is only observed when the particles collectively move together with adhesions (B). We also observed that in the case of dispersive particle flow, ω²_M increased quadratically in time, which yielded the rate of velocity dispersion.

For the third category, we observed two distinct CF peaks emerge for antisliding (C); one peak is due to the adhesion mask macro objects and the second peak is due to particles. To contrast with this, two peaks were not separately resolved in the sliding cases because the particles and adhesions move at a similar rate in the same direction, resulting in superposition of the overlapping peaks.

The density dependence is most readily observed in the antisliding cases, where the high particle density results in greater amplitude for the macro object CF (as in C4), in contrast to the low density regime where the particle peak was dominant (as in C2). This is consistent with Eq. 11 in a limit where the majority of particles occupy and fill the adhesion masks. A higher particle density can yield an adhesion CF peak of detectable amplitude but still smaller than the particle CF peak.

A faint secondary peak begins to appear for high density treadmilling (as in A4). This ellipsoidal peak is due to the positive correlations of the treadmilling adhesions with themselves because more particles make up the adhesion population, as opposed to the low density regime where the particles are largely detected as individuals, consistent with Eq. 11.

In addition, it may be possible to definitively determine whether adhesions undergo sliding or treadmilling, which appear identical through imaging, but can be potentially distinguished by a single translating peak (sliding) or a stationary particle peak (treadmilling) that may have a secondary adhesion peak at high particle density limits.

For more details on these and other simulations, refer to the Supporting Material.

Fig. 3 presents two image channel simulations with green and red particle populations where we again controlled separate adhesion masks and particles for dynamics and densities. These simulations explored the sensitivity of STICCS to the ratio of colocalized species, N/N_tot, where N_tot = N_a ∪ N_b. When N/N_tot = 20%, both adhesion and particle peaks are present, but the adhesion peak dominates at later temporal lags (red arrow, Fig. 3 H); and when N/N_tot = 80%, the particle cross-correlation peak dominates in amplitude for all temporal lags (blue arrow, Fig. 3 P).

Figure 3.

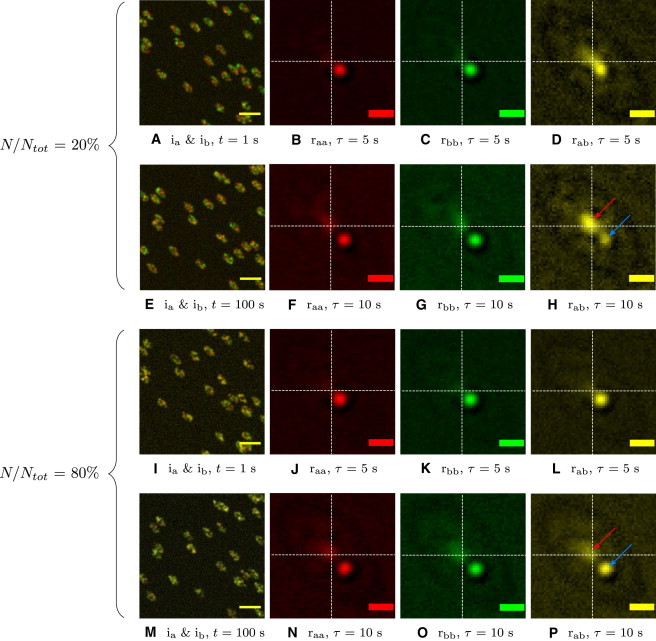
Results from STICCS analysis of simulations of the antisliding model with two particle populations that are fractionally colocalized and imaged in two detection channels. The model was analyzed for lower and higher colocalization of particles (top two rows, 20%; bottom two rows, 80%), with the odd and even rows representing early versus later times (τ = 1 and 100 s) and time lags (τ = 5 and 10 s). The particle density was 10/μm². (First column) Composite images of the channels (red and green), with scale bar 5 μm. (Second, third, and fourth columns) r_aa, r_bb, and r_ab CFs, respectively, where r_ab = r_ba in this scenario with scale bar 1 μm. (H and P, red arrow) Adhesion peak; (blue arrow) particle peak.

A key conclusion that we could immediately draw from these simulations was that the STICCS method, after removing the PSF and static object contributions, usually detects the peak due to particle correlations for the range of conditions simulated. In the context of cellular adhesions, it is important to remember that the adhesions are made up of many identical fluorescent particles that are optically correlated by the PSF and contribute as particles as well as large objects in the image (Fig. 1 E). This is different than the contribution of a single brighter particle or object to the CF, as we explore below.

Cellular experiments

We applied our analysis to the transport and cotransport of integrin receptors with α-actinin and paxillin, all of which are present in adhesions. We first imaged CHO.B2 cells expressing α5-GFP and paxillin-mKusabiraOrange (mKO) and plated on fibronectin and analyzed their dynamics using STICCS. The α5β1-integrin appears largely immobile when compared with the movement of paxillin and α-actinin, although short periods of translation could be seen in some adhesions in a small subset of cells. This agrees with previous studies, which report both little α5 flux and coincident flow directions with other adhesion proteins (22,23,25).

We next investigated fluxing in adhesions in two different cell types migrating on laminin. One is U2OS, an osteosarcoma cell line that endogenously expresses two laminin receptors α3β1 and α6β1, as well as a fibronectin receptor, α5β1 (34), and the other is the CHO.B2 line (which has little endogenous integrin α-subunit) expressing the α6 integrin, which binds to laminin. Figs. 4 and 5 show a protrusion in a U2OS and a CHO.B2 cell, expressing both ectopic α6β1-integrin and α-actinin, and migrating on laminin. In both, the protrusion advances similarly; the cell front moves forward as its sides retract inward. We see strong cross-correlation in the retracting sides as well as in adhesions in protrusions, when the protrusion pauses, but not in the other areas. The right column of Fig. 4 represents the CF radii and angle information for the first time lag (τ = 5 s), corresponding to the same ROI as shown in the left column, where the radii along the major and minor axes of the peak are shown relative to one another, oriented in the direction of flow.

Figure 4.

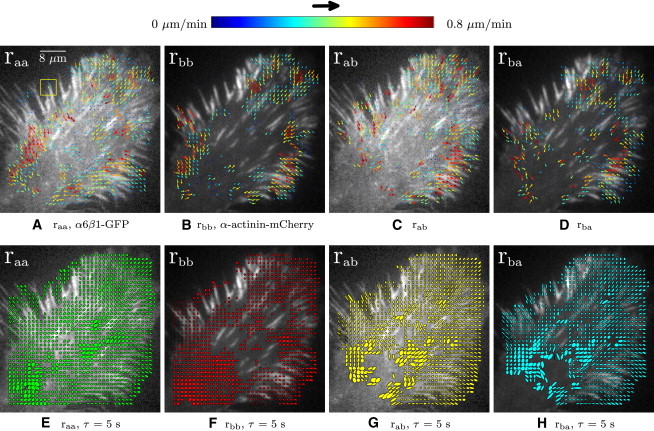
U2OS with α6β1-GFP and paxillin-mKO on laminin. The lamellipodium is protruding toward the northeast, with its sides retracting inward. Vector and elliptical maps are shown in the first and second rows. The elliptical maps represent the radii and orientation of each CF for τ = 5 s. N_f = 20, frames 101–120, δt = 5 s, p_x,y = 0.105 μm, and 16 × 16 pixels (1.7 × 1.7 μm) ROI (yellow square). Representative of three adhesions measured in three cells.

Figure 5.

ACF- and CCF-calculated velocity maps of CHO.B2 α6β1-GFP and α-actinin-mCherry, superimposed on the first image of the TOI. N_f = 10, frames 21–30, δt = 5 s, p_x,y = 0.105 μm, and 16 × 16 pixels (1.7 × 1.7 μm) ROI (yellow square). The bulk of the movement is a protrusion moving in the southwest direction with a retraction of the cell boundary in the northwest corner moving southeast. Representative of four adhesions measured in four cells.

With the STICCS approach using the bivariate correlation function fits, we can generate these maps as a function of lag time to follow the evolution of isotropic or anisotropic diffusive transport in different regions of the cell if desired. The ability to resolve direction permits us to detect and measure molecular transport in aligned or scaffold-tracked systems such as the aligned adhesions in this study. This is illustrated for the same cell shown in Fig. 4, and is presented as correlation maps, individual correlation functions, and a diffusion map in Fig. S7, Fig. S8, and Fig. S9 in the Supporting Material. Every fourth ROI was used to generate Fig. S7 and Fig. S9 to have the same dimensions as the image series (the first frame of both channels is shown in Fig. S7, A and B) and not to oversample the data. This ensures that each ROI map is independent of its neighbors. ACFs (Fig. S7, C and D) and CCFs (Fig. S7, E and F) are the raw correlation functions at τ = 1.

The colored squares seen in Fig. S7, A, B, and E, correspond to the location of the cross-correlation functions presented in Fig. S9 with the coordinates shown as (row, column) with (1,1) in the top-left corner and (1,9) in the top-right. The red square, found on the lamellipodium, shows a symmetric peak illustrating slow isotropic diffusion. The blue square, also found near the cell edge, is a region without any visible adhesions but the CF is broadening along the major axis, indicating anisotropic diffusion and flowing. The green square is a region with a visible cell edge composed of filopodia, which yields one peak representing the motion of the fluorophores (white arrow) and the other due to the translating cell boundary (red arrow), each of which are separately detectable (the second peak velocity matches edge boundary velocity tracking, data not shown). The purple square is in a region with visible adhesions and has a flowing peak that is symmetric at τ = 0, but spreads over time along the direction of flow (major axis), which we interpret as a diffusive flow of the particles based on the simulation results and the fact that ω_M²(τ) increases linearly.

Finally, the yellow square produces a flowing peak that is ellipsoidal at τ = 0 and a plot of ω_M²(τ) as a function of τ is linear, which would be consistent with adhesion sliding whereby particles are undergoing diffusive flow along the track or scaffold where the particles can be found at different points along the track. Fig. S9 shows a diffusion map with a red color-scale indicating magnitude ranges of the extrapolated diffusion coefficient, illustrating “hot” or “cold” regions of diffusion. We would not detect diffusion of cytoplasmic species at the slow imaging rates used. These results show the range of transport phenomena that we can measure in the heterogeneous cell environment for adhesion-related proteins in adherent cells.

To determine whether the coupling of integrin and paxillin depends on the type of integrin heterodimer, we transfected CHO.B2 cells with αLβ2-mCherry, a leukocyte integrin that binds to its cellular ligand ICAM-1, an Ig-like protein expressed in endothelial cells (35), and paxillin-mGFP (Fig. 6 and see Movie S1 and Movie S2). Previous studies show that both integrins can flux in adhesions (25). When plated on ICAM-1, we observed strong coupling (cross-correlation) in adhesions in retracting (right side) regions; however, termination of retraction was accompanied by a decoupling of the integrin and paxillin, with the latter fluxing alone (Fig. 6). In addition, we also detected robust cross-correlation in most adhesions toward the front of protrusions, once the protrusion had paused. The robust co-fluxing suggests slippage at the level of the αLβ2-integrin and its extracellular ligand in these regions (25). It also demonstrates that, by using STICCS, we can detect transient interactions via cross-correlation to measure the onset or termination of cotransport and map where and when this occurs (within ROI and TOI resolution and sampling limits) in the cell. However, cotransport between two species detected by cross-correlation does not necessarily imply direct interaction. Instead, it shows that the two species reside in a common complex that moves together. Such a complex may be as large as the PSF; in this case it could be a macromolecular complex like a mature adhesion or smaller complexes made up of a few molecules that might comprise the substructure of adhesions.

Figure 6.

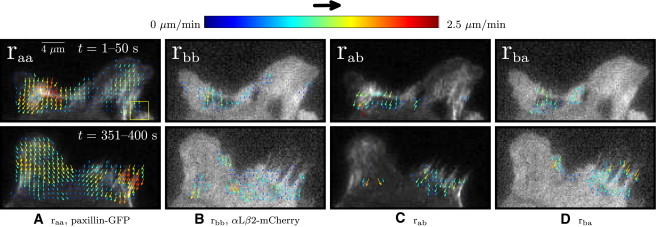
(A and B) ACF- and (C and D) CCF-calculated velocity maps of paxillin-GFP and αLβ2-integrin-mCherry (superimposed on the first image from the TOI). The analyses were performed at two different TOIs, each over N_f = 10 and δt = 5 s. (Top row) Frames 1–10 (t = 1–50 s). (Bottom row) Frames 71–80 (t = 351–400 s). Cross-correlation maps in panels C and D show transient interactions occurring at different times in regions where the adhesions become active. p_x,y = 0.21 μm and 16 × 16 pixels (3.4 × 3.4 μm) ROI (yellow square). Representative of two adhesions measured in four cells.

We also investigated the linkage between α6 and laminin CHO.B2 cells coexpressing α6β1-GFP and paxillin-mKO. Ectopically expressed α6 promotes adhesion and migration on laminin (25). Fig. 7 and Fig. S10 show the ACF- and CCF-generated velocity maps for α6β1-integrin-GFP and paxillin-mKO. We also see co-fluxing in retracting regions as well as in adhesions at the front of protrusions but these were more robust when compared to αLβ2. We detected a very strong cross-correlation while the cell protrusion edge remained stationary during the imaged time interval.

Figure 7.

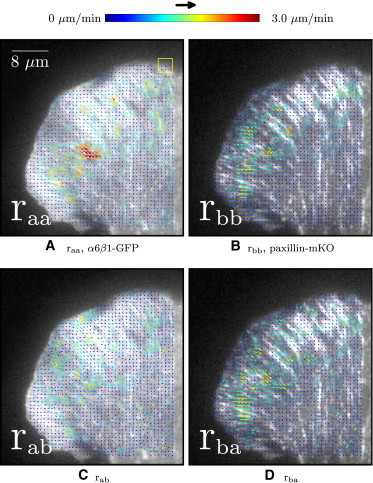
ACF- and CCF-calculated velocity maps of CHO.B2 α6β1-GFP and paxillin-mKO superimposed on the first image from the TOI. N_f = 10, frames 71–80, δt = 5 s, p_x,y = 0.105 μm, and 16 × 16 pixels (1.7 × 1.7 μm) ROI (yellow square). Representative of six adhesions measured in six cells.

Discussion

STICCS measurements reveal transient, modulable interactions between integrins and adhesion proteins as they flux in migrating cells. The interactions and dynamics depend on the integrin/ECM pair as well as the subcellular location. Whereas STICCS does reveal that they are part of the same multimolecular complex, it does not indicate whether the molecules are in direct contact. As there are no reports of direct binding between paxillin and integrins (36), we infer cotransport in a common complex with the exception of α5β1-integrin, for which little cotransport is observed. In addition, by simply shifting the TOI across different portions of a conventional image series, it is possible to map transient interactions between fluorescently tagged macromolecules that turn on and off at different moments in time and in different locations in the cell.

STICCS provides a powerful new, to our knowledge, way to study the formation and time evolution of multimolecular complexes in cells. Single-molecule tracking (37) provides full trajectory information on each molecule tracked; but this method is only valid for labeled proteins at low concentrations. In contrast, STICCS permits accurate quantitative measurements from samples with much higher concentrations of fluorophores but maps average ensemble behavior within the ROI. The data also show that α6β1- and αLβ2-integrins differ from α5β1-integrin. Both α6β1 and αLβ2 co-flux with paxillin in protruding and retracting regions, with the co-fluxing of α6β1 more robust. We observed that αLβ2 could decouple from paxillin in both retracting and protruding regions. In protruding regions, α5β1 is static in general; however, α6β1 and αLβ2 co-flux with paxillin in a retrograde direction (from the cell edge) most of the time. In retracting regions, α6β1 and αLβ2 also co-flux robustly with paxillin, whereas α5β1 is generally static and paxillin fluxes in protruding regions of cells expressing α5β1 and migrating on fibronectin.

For most of the protein pairs and cells we examined in this study, the cross-correlation functions r_ab and r_ba were symmetric and yielded flow vectors that were similar within expected error. However, for the αLβ2 paxillin system, we did observe some asymmetry between the cross-correlation functions, and interestingly this was coupled with initiation or termination of fluxing at the adhesions and was localized in space. As has been shown for time-ordering analysis with FCCS (20), this suggests that there is a lag between the αLβ2-integrin and paxillin during this event, something we plan to study in more detail in both protruding and retracting regions because the ordering could differ during assembly and disassembly.

The cellular adhesion system we studied is just one of many potential application for STICCS. Other possible applications include investigating the transcription dynamics of specific genes in fluorescent RNA (38) or using Fucci-expressed cells to look for cross-correlation between different phases of the cell cycle (39,40). Any system with directional-motor protein-driven transport would be amenable to study using the extended aspect of STICCS that we have introduced, e.g., vesicle trafficking that has already been studied by STICS (41). The cell division spindle and the movement of cargo vesicles along microtubules or actin filaments would be possible candidates. The ability to measure directional or anisotropic diffusion would also be advantageous to measure transport in materials with defined channels that restrict the directional degrees of freedom (42). STICCS is not limited to just fluorescence applications, but would be practical with nearly any linear signal that can be imaged by optical microscopy, and hence be correlated as has been shown recently for STICS (43).

Interactions within a common structure or complex as detected by STICCS could be further studied by Förster resonance-energy transfer (44,45) methods to test for direct interactions. In this way the two methods are complementary and provide different information. However, for large multicomponent adhesions, the protein separation distances are often greater than the Förster radii, so STICCS is useful to map such interactions.

Conclusions

STICCS is an extension of STICS to the realm of cross-correlation so it reveals transient interactions in specific regions of cells over defined time windows that correlate to biological activity. In particular, we detected a turning on-and-off of macromolecular interactions that directly corresponded with dynamic changes in the adhesions. Moreover, by using k-space normalization before STICS analysis, we could usually clearly detect and measure the contribution of the fluorescent proteins within the macroscopic adhesions and follow their dynamics in the heterogeneous cell environment. By applying a bivariate fit to the correlation functions, we could further resolve diffusive and nondiffusive transport along directions set by the adhesion long axis.

Migrating cells undergo retraction in two instances: at the trailing edge, to enable forward movement of the cell; or during protrusion, as part of periodic cycles of protrusion/contraction seen in many migratory cell types (46). Our data have revealed robust cofluctuation of integrin and paxillin in the retracting regions of cells expressing αLβ2 migrating on ICAM-1 and cells expressing α6β1 as they migrate on laminin. In contrast, α5β1 (and αvβ3) are generally uncoupled from the fluxing of other proteins (22,23), revealing an interesting dependence on integrin-ligand pair. Thus, it is now apparent that the linkage between the ECM and actin can slip at the level of either cytoplasmic or extracellular interactions (25).