Dynamical quorum-sensing in oscillators coupled through an external medium

Abstract

Many biological and physical systems exhibit population-density dependent transitions to synchronized oscillations in a process often termed “dynamical quorum sensing”. Synchronization frequently arises through chemical communication via signaling molecules distributed through an external medium. We study a simple theoretical model for dynamical quorum sensing: a heterogenous population of limit-cycle oscillators diffusively coupled through a common medium. We show that this model exhibits a rich phase diagram with four qualitatively distinct physical mechanisms that can lead to a loss of coherent population-level oscillations, including a novel mechanism arising from effective time-delays introduced by the external medium. We derive a single pair of analytic equations that allow us to calculate phase boundaries as a function of population density and show that the model reproduces many of the qualitative features of recent experiments on BZ catalytic particles as well as synthetically engineered bacteria.

1. Introduction

Unicellular organisms often undertake complex collective behaviors in response to environmental and population cues. A beautiful example of this phenomenon is the population-density dependent transition to synchronized oscillations observed in communicating cell populations recently termed dynamical quorum sensing [1, 2]. Density-dependent synchronization has been observed in a wide variety of biological systems including suspensions of yeast in nutrient solutions [1], starving cellular colonies of the social amoeba Dictyostelium [3], and synthetically engineered bacteria [4]. Such transitions have also been observed in experimental studies of electrochemical oscillators and Belousov-Zhabotinsky (BZ) catalytic particles [5, 6].

Previous theoretical work has shown that oscillators coupled through quorum sensing can display synchronized oscillations [7, 8, 9]. Recently, a dynamic quorum sensing transition was found [1] in a simple model of coupled identical limit-cycle oscillators introduced to study synchronization in yeast populations. Additionally, experimental and numerical studies of BZ catalytic particles indicate that heterogeneity in oscillator populations leads to interesting new phenomenon [5, 10, 6]. Nonetheless, the study of density-dependent synchronization in heterogeneous populations of oscillators remains largely unexplored, in stark contrast to oscillators with direct coupling where many analytic results are available [11, 10, 12].

In this paper, we consider a large population of limit-cycle oscillators with a distribution of natural frequencies, coupled diffusively through a common external medium. Our work generalizes earlier models [1] and exhibits extremely rich dynamics as the coupling strength, population density, and frequency distribution are varied. We derive several analytic results and find that model exhibits a rich phase diagram. As with directly coupled oscillators, we find that there are three distinct phases: a synchronized phase with coherent population-level oscillations, an amplitude death phase where individual oscillators cease oscillating, and an incoherent phase where there are no population-level oscillations but individual oscillators still oscillate. We find two types of denisty-dependent phase transitions, a Kuramoto-like incoherence to coherence transition between the synchronized and incoherent phase, and a transition from the synchronized phase to the amplitude death phase. The latter transition can occur due to three distinct physical mechanism: (1) oscillator heterogeneity, (2) degradation of the external medium, and (3) a novel mechanism where at low-population densities the external medium dynamics are not fast enough to support global oscillations. The diversity of physical mechanisms giving rise to the same transition is unique to our system. We show that the model reproduces many qualitative features observed in recent experiments on heterogeneous populations of BZ catalytic particles [5] as well as synthetically engineered bacteria [4].

To illustrate this diverse set of phenomena, we introduce a simple model of N 𢚫 1 coupled limit-cycle oscillators where the amplitude and phase of individual oscillators are represented by a complex number z_j, (j = 1 …N), with natural frequency ω_j. The oscillators are diffusively coupled to an external medium, represented by a complex number Z, through a coupling D. The external medium Z represents particle species that can freely diffuse in the environment and allows individual oscillators to communicate with each other. The specific realizations of Z depends on the context. In metabolic oscillations, it represents common metabolites that diffuse between cells. In the BZ reaction, it represents chemical species that diffuse between autocatalytic beads. In synthetic bacteria, it is the concentration of the autoinducer signaling molecules in the medium. When chemicals leave the oscillators and enter the medium, they are diluted by a factor α = V_int/V_ext ≪ 1, which is the ratio of the volume of the entire system to the that of an individual oscillator. The external medium Z is also degraded at a rate J.

The dynamics of the system are captured by the equation

$$\frac{d{z}_j}{dt}=({\lambda }_0+i{\omega }_j-{\left|z_j\right|}^2)z_j-D(z_j-Z)$$

$$\frac{dZ}{dt}=\alpha D{\displaystyle \sum _j(z_j-Z)-JZ}$$

where the ω_j are drawn from a distribution h(ω) which we assume to be an even function about a mean frequency ω₀. By introducing a dimensionless density, ρ = αN, and shifting to a frame rotating with frequency ω₀, we can rewrite the equations above as

$$\frac{d{z}_j}{dt}=({\lambda }_0+i{\omega }_j-{\left|z_j\right|}^2)z_j-D(z_j-Z)$$

$$\frac{dZ}{dt}=\frac{\rho D}{N}{\displaystyle \sum _j(z_j-Z)-(J+i{\omega }_0)Z,}$$ (1)

where the frequencies ω_j are now drawn from an even distribution g(ω) with mean zero.

2. Linear-stability analysis for homogenous populations

Before analyzing a heterogeneous population, we first consider the special case of uniform frequencies, where g(ω) = δ(ω) in (1), and find surprising results. This model was used previously [1] to model dynamical quorum sensing in yeast suspensions. For homogenous populations, the equations for all the z_j are identical and there are two possible behaviors. The individual oscillators are quiescent with Z = z_j = 0 (amplitude death) or there are synchronized oscillations. We can compute the stability of the amplitude death state by linearizing the system around z_j = Z = 0 and computing the eigenvalues, μ, of the corresponding linearized system. Since all of the oscillators are identical, the dynamics are completely specified by two differential equations, one for the mean-field parameter $z=\frac{1}{N}{\displaystyle {\sum }_j{z}_j=z_j}$ and one for Z. In terms of μ, oscillator death is stable when Re(μ) < 0 for all eigenvalues. The corresponding requirement that the trace be negative implies D > λ₀ in the oscillator death phase. Furthermore, the characteristic equation for the eigenvalues takes the form (μ + A)(μ + B + iω₀) = ρD², with B = Dρ + J and A = D − λ₀. To find the phase boundary, we plug in μ = a + ib and separate the characteristic equation into real and imaginary parts,

$$a+B=\frac{\rho D^2(a+A)}{{\left(a+A\right)}^2+b^2}$$ (2)

$$b+{\omega }_0=\frac{-\rho D^{2}b}{{\left(a+A\right)}^2+b^2}.$$ (3)

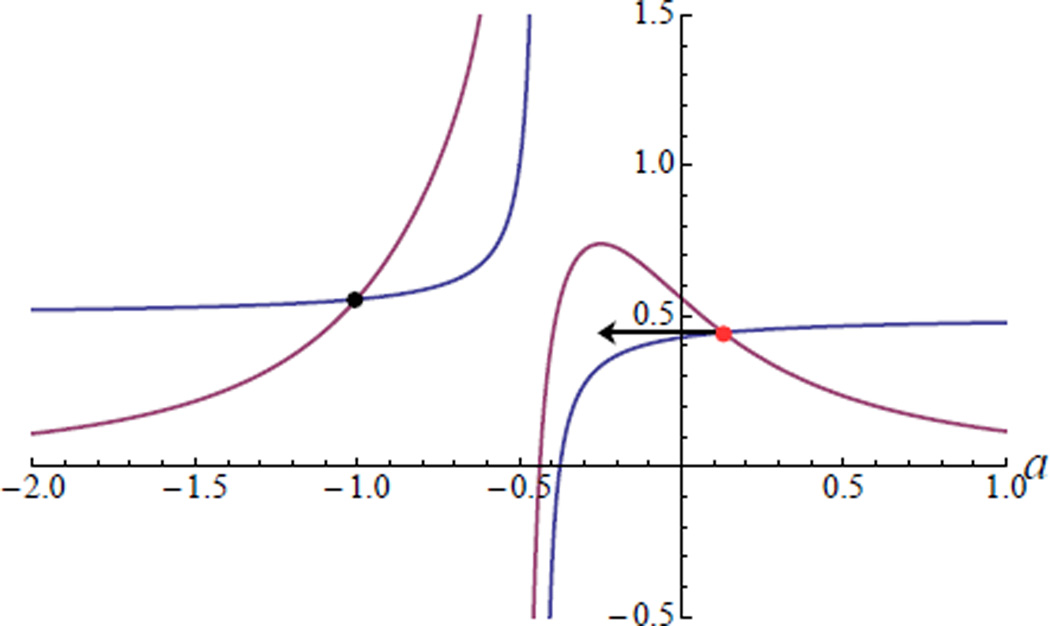
This allows us to solve for b as a function of $a,b(a)=-\frac{{\omega }_0(a+A)}{2a+B+A}$ and plug this into (2). The resulting equation can be analyzed graphically plotting the left and right sides of (2) as a function of a (see Figure 1). Since the characteristic equation is quadratic, there are two solutions, a solution with negative a which guarantees the stability of the external medium, and a second solution which can change sign depending on parameters. As shown in Figure 1, it is clear that if the left-hand side of (2) is greater than the right-hand side at a = 0, then the second solution must also be negative. Thus, the amplitude death phase is stable when

$$\frac{(D\rho +J)(D-{\lambda }_0)}{\rho D^2}\ge \frac{{\left(\rho D+J+D-{\lambda }_0\right)}^2}{{\left(\rho D+J+D-{\lambda }_0\right)}^2+{\omega }_0^2},$$ (4)

where we have rewritten A and B in terms of the original parameters of the model.

Figure 1.

Graphical analysis of the structure of the solutions to eq. (2) and (3). There always exists a solution with a < 0, shown as a black dot. A second solution, shown as a red dot, can have positive or negative a, and thus solving for a = 0 properly identifies the phase boundary.

Interestingly, this equation demonstrates that there are two qualitatively different ways to reach the amplitude death phase. First, when J ≫ 1, the left side is much larger than the right, indicating that oscillations are lost due to degradation of the external medium. More surprisingly, amplitude death may occur even when J = 0 if the natural frequency ω0 of the oscillators is large relative to the squared terms in (4). This can be understood by first recalling that since D − λ0 > 0, isolated oscillators are silent and synchronization can only occur by transmitting information through the external medium. The medium, however, has an effective time scale given by (ρD)⁻¹ on which it can respond to drive from the oscillators. Thus, for small population densities if ω₀ is large, the medium cannot track the fast dynamics of the individual oscillators and amplitude death is stablized. We term this mechanism for the loss of population-level oscillations “dynamic death” to indicate that the underlying cause for the dynamical quorum sensing transition from the synchronized phase to the amplitude death phase is the slow dynamics of the external medium at low density and moderate diffusion coupling and not degradation of the medium. We stress, however, that these two mechanisms give rise to the same phase boundary and do not generate distinct phases. Fig. 2 shows the homogeneous phase boundaries as a function of J, ρ, and D. We have also confirmed the existence of the “dynamic death” mechanism with numerical simulations for the case when J = 0 (see Fig.2B).

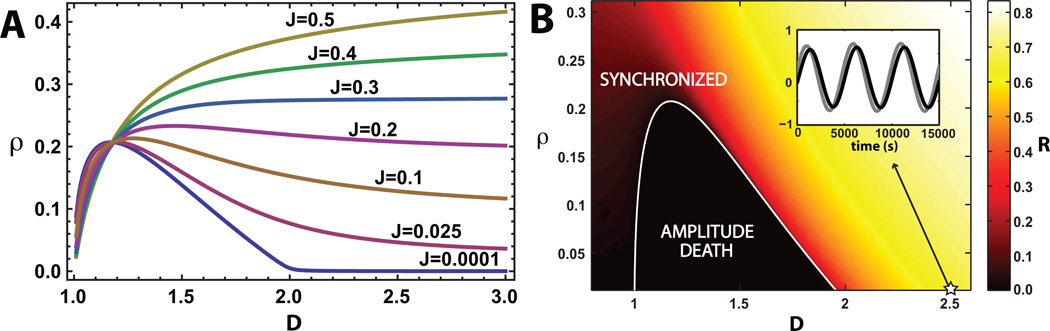
Figure 2.

(A) Phase boundaries for homogeneous oscillators. Phase boundary between the amplitude death phase and the synchronized phase in the ρ vs. D plane for various values of J, with ω₀ = 1 and λ₀ = 1. The synchronized phase occurs above the phase boundary and the amplitude death phase occurs below the boundary. (B) Numerical simulations for J = 0 with N = 40 identical oscillators with random initial conditions. Heat map of the steady-state amplitude of collective oscillations, R = |Z|, showing the transition from the amplitude phase to synchronized oscillations for D > 1. The white curve is the analytic phase boundary. Since J = 0, the phase transition occurs because of slow dynamics of the external medium at low-densities. Inset: Real part of z and Z during low density oscillations showing ~ 1000-fold slowing of oscillations relative to the uncoupled frequency ω₀ = 1s⁻¹ at the starred point (D = 2.5, ρ = 0.001, J = 0).

3. Linear stability analysis for heterogeneous oscillators

We now analyze (1) for the case where the natural frequencies ω_j are drawn from an even distribution g(ω) with zero mean. In this case, the system has three phases: an amplitude death phase where all oscillators are quiet; global, synchronized oscillations; and an incoherent phase where individual elements are oscillating but the oscillations are unsynchronized. The stability boundary of the amplitude death phase can again be calculated as in the homogenous case by linearizing (1) around the death state z_j = 0, Z = 0. This yields the equations,

$$\frac{d\delta z_j}{dt}=({\lambda }_0+i{\omega }_j-D)\delta z_j-D\delta Z$$ (5)

$$\frac{d\delta Z}{dt}={\displaystyle \sum _j\frac{\rho D}{N}\delta z_j-(\rho D+J+i{\omega }_0)\delta Z.}$$ (6)

These equations can be written in matrix form as

$$\left(\begin{array}{c}\stackrel{·}{\delta z_1}\\ \stackrel{·}{\delta z_2}\\ ·\\ ·\\ \stackrel{·}{\delta z_N}\\ \stackrel{·}{\delta Z}\end{array}\right)=M\left(\begin{array}{c}\delta z_1\\ \delta z_2\\ ·\\ ·\\ \delta z_N\\ \delta Z\end{array}\right)$$ (7)

where

$$M=\left(\begin{array}{cccccc}\epsilon +i{\omega }_1& 0& ·& ·& 0& -D\\ 0& \epsilon +i{\omega }_2& ·& ·& 0& -D\\ ·& ·& ·& ·& ·& ·\\ ·& ·& ·& ·& ·& ·\\ 0& 0& ·& ·& \epsilon +i{\omega }_N& -D\\ \frac{\rho D}{N}& \frac{\rho D}{N}& ·& ·& \frac{\rho D}{N}& -(\rho D+J+i{\omega }_0)\end{array}\right)$$ (8)

Stability requires the eigenvalues, μ, of M to satisfy Re[μ] < 0. First notice that stability requires Re[Tr(M)] < 0. This gives the condition

$$\left({\lambda }_0-D\right)-\frac{(\rho D+J)}{N}>0.$$ (9)

We can also calculate the eigenvalues using the characteristic equation of the matrix, Det(μI − M) = 0. A straightforward calculation yields

$$(\mu +(\rho D+J+i{\omega }_0)){\displaystyle \prod _{j=1}^N(\mu -({\lambda }_0-D+i{\omega }_j)}$$ (10)

$$-\frac{\rho D^2}{N}{\displaystyle \sum _{s=1}^N{\displaystyle \prod _{j=1,j\ne s}^N(\mu -({\lambda }_0-D+i{\omega }_j)=0}}$$

In order to take the thermodynamic limit, we rewrite this equation as

$$(\mu +(\rho D+J+i{\omega }_0))=\frac{\rho D^2}{N}{\displaystyle \sum _{s=1}^N\frac{1}{\mu -({\lambda }_0-D+i{\omega }_j)}}$$ (11)

In the thermodynamic limit N → ∞ but with ρ held fixed, (9) and (11) become, respectively,

$$({\lambda }_0-D)<0$$ (12)

and

$$\mu +(\rho D+J+i{\omega }_0))=\rho D^2{\displaystyle \int d\omega \frac{g(\omega )}{\mu -({\lambda }_0-D+i\omega )},}$$ (13)

where we have replaced the sum by an integral over the distribution function g(ω) for the oscillator frequencies. In practice, it is often helpful to write this as two real equations. Substituting μ = a + ib yields two coupled integral equations

$$\frac{a+\rho D+J}{\rho D^2}={\displaystyle \int d\omega g(\omega )\frac{a+D-{\lambda }_0}{{\left(a+D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2}}$$

$$\frac{b+{\omega }_0}{\rho D^2}=-{\displaystyle \int d\omega g(\omega )\frac{b-\omega }{{\left(a+D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2}}$$ (14)

Stability requires that all solutions of these equations obey a ≤ 0. By considering the mean-field equations derived below, it is clear that the stability boundary can be found by putting a = 0 in the above equations, i.e. there exists at most one solution with positive real part.

Putting a = 0 in (14) results in a pair of coupled integral equations that determine the boundary of stability of the death phase:

$$\frac{\rho D+J}{\rho D^2}={\displaystyle \int d\omega g(\omega )\frac{D-{\lambda }_0}{{\left(D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2}}$$ (15)

$$\frac{b+{\omega }_0}{\rho D^2}=-{\displaystyle \int d\omega g(\omega )\frac{b-\omega }{{\left(D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2},}$$ (16)

with D − λ₀ > 0. It is useful to consider various limits of these equations. Notice that when g(ω) = δ(ω), these equations reduce to (2) with a = 0 as expected. Alternatively, consider the case ρ → ∞. In this limit, the left hand side of (16) is zero implying that b = 0, since g(ω) in an even function. Substituting this into (15) yields a single equation for stability of the death state,

$$\frac{\rho D+J}{\rho D^2}={\displaystyle \int d\omega g(\omega )\frac{D-{\lambda }_0}{{\left(D-{\lambda }_0\right)}^2+{\omega }^2}.}$$ (17)

This result was derived in [11, 10] for the stability boundary of the death phase in a system of directly coupled limit-cycle oscillators. This follows naturally by noting that in the limit ρ → ∞, the external medium can respond infinitely quickly. Thus, Z_ext is equal to the order parameter of the system, $Z_{\mathit{\text{ext}}}=\frac{1}{N}{\displaystyle {\sum }_j{z}_j}$, and the model reduces to the one studied in [11, 10, 12]. In this limit, the loss of oscillations is due to the heterogeneity of individual oscillator frequencies. These two limits show that a single set of equations (15)–(16), capture three qualitatively distinct physical mechanisms that can lead to a transition between the synchronized and amplitude death phases: degradation, oscillator heterogeneity, and the dynamics of the external medium.

4. Mean Field equations for frequency locking

To gain further insight into the system, it is useful to consider the mean-field equations for the system. To do so, we put z_j = r_je^iθ_j and Z = Re^iθ into (1) and equate real and imaginary parts:

$$\frac{d{r}_j}{dt}=({\lambda }_0-D-r_j^2)r_j+DR\text{ cos }(\varphi -{\theta }_j)$$

$$\frac{d{\theta }_j}{dt}={\omega }_j+\frac{DR}{r_j}\text{ sin }(\varphi -{\theta }_j)$$ (18)

and

$$\frac{dR}{dt}=\frac{\rho D}{N}{\displaystyle \sum _{j=1}^N{r}_j\text{ cos }(\varphi -{\theta }_j)-(\rho D+J)R}$$

$$\frac{d\varphi }{dt}=-{\omega }_0+\frac{\rho D}{N}{\displaystyle \sum _{j=1}^N\frac{r_j}{R}\text{ sin }(\varphi -{\theta }_j).}$$ (19)

We look for uniform rotating solutions whose angular frequency in the lab frame is ω₀+b by requiring $\frac{dR}{dt}=\frac{d{r}_j}{dt}=0$ and $\frac{d\varphi }{dt}=\frac{d{\theta }_j}{dt}=b$ in (18) and (19). In this case, the position of each oscillator is determined purely by its frequency, so we can regard each oscillator as a function of ω. Substituting in the desired functional form of the solutions into (19) and taking the thermodynamic limit gives

$$R(\rho D+J)=\rho D{\displaystyle \int d\omega g(\omega )r(\omega )\text{ cos }(\varphi -\theta (\omega ))}$$ (20)

$$b+{\omega }_0=\rho D{\displaystyle \int d\omega g(\omega )\frac{r(\omega )}{R}\text{ sin }(\varphi -\theta (\omega )),}$$ (21)

where we have written r(ω) and θ(ω) to emphasize that the amplitude and phase of each oscillator is a function of only the frequency. Using equation (18) and $\frac{d{\theta }_j}{dt}=b$ yields

$$r=\frac{DR\text{ sin }(\theta (\omega )-\varphi )}{(\omega -b)}.$$ (22)

Substituting this into (20) and (21) gives the equations

$$\frac{\rho D+J}{\rho D^2}={\displaystyle \int d\omega g(\omega )\frac{\text{sin }(\theta (\omega )-\varphi )\text{ cos }(\theta (\omega )-\varphi )}{\omega -b}}$$ (23)

$$\frac{b+{\omega }_0}{\rho D^2}=-{\displaystyle \int d\omega g(\omega )\frac{\text{sin }(\theta (\omega )-\varphi )\text{ sin }(\theta (\omega )-\varphi )}{\omega -b}}$$ (24)

Furthermore, substituting $\frac{d{r}_j}{dt}=0$ and $\frac{d{\theta }_j}{dt}=b$ in into (18) one can easily show

$$((\omega -b)\text{ cot }(\theta -\varphi )+{\lambda }_0-D)(1+{\text{ cot}}^2(\theta -\varphi ))=D^2{R}^2/{\left(\omega -b\right)}^2$$ (25)

Combined (23), (24), and (26) define the mean-field equations for the system for frequency locking with amplitude R.

It is clear that in general, solutions to (26) exhibit an emergent frequency amplitude coupling that is not present in the Hopf normal form of the individual oscillators. We cannot, however, solve this analytically because (26) is a cubic equation in cot(θ − ϕ). Nonetheless, for the special case R = 0 (amplitude death), we have the unique solution to (26) that

$$\text{tan }(\theta (\omega )-\varphi )=\frac{\omega -b}{{\lambda }_0-D}.$$ (26)

Substituting this into the equations (20) and (21) yields the stability boundary

$$\frac{\rho D+J}{\rho D^2}={\displaystyle \int d\omega g(\omega )\frac{D-{\lambda }_0}{{\left(D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2}}$$

$$\frac{b+{\omega }_0}{\rho D^2}=-{\displaystyle \int d\omega g(\omega )\frac{(b-\omega )}{{\left(D-{\lambda }_0\right)}^2+{\left(b-\omega \right)}^2}}$$ (27)

Notice that for R = 0, the mean field equations have reduced to (16). Finally, it is also useful to calculate where the boundary given by (27) intersects the stability boundary D = λ₀. To do so, we take the limit (D − λ) → 0 in the equations above. A straightforward calculation shows that the equations reduce to

$$\frac{\rho D+J}{\rho D^2}=\pi g(b)$$

$$\frac{b+{\omega }_0}{\rho D^2}=P\left[{\displaystyle {\int }_{-\infty }^{\infty }d\omega \frac{g(\omega )}{\omega -b}}\right],$$ (28)

where the P denotes the principal value.

Recall that when oscillators are directly coupled to each other (i.e. ρ → ∞), they lock at the mean frequency ω₀ and b = 0. In contrast, when oscillators are coupled through the external medium, there is an effective “viscosity” which slows down the oscillations so they rotate with an angular frequency ω₀ + b, with b < 0. It is clear that b can be made arbitrarily close to −ω₀ at low density, a limit that is frequently encountered in biology, as shown in the inset to Figure 2. The effect of time delays on synchronization of directly coupled oscillators was studied previously and the equations governing the stability of amplitude death bear some similarity to those found in this work [13, 14].

Another interesting phenomena is that increasing J decreases the absolute value of b and hence increases the angular frequency. Thus, somewhat surprisingly, the system exhibits positive period-amplitude coupling despite the fact that there is no explicit coupling between period and amplitude at the level of individual oscillators. Similar behavior was observed in a population of synthetically engineered bacteria in recent experiments [4], though interestingly, in contrast with our phenomenon the period increased as degradation was decreased. The difference between our model and the experiments likely is due to the explicit amplitude-period coupling already present at the single-cell level in the degrade-and-fire mechanism underlying oscillations in individual bacterial oscillators [15].

5. Mean Field equations for incoherence

When D < λ₀, the system can be incoherent, where individual oscillators are rotating in an unsynchronized fashion. The stability equations for the incoherent phase were calculated by generalizing the calculations in [10]. Briefly, we looked for solutions of (19) of the form R = 0, $r_j^2=\lambda {}_0-D$, and θ_j = ω_jt. For such solutions, individual oscillators oscillate at their natural frequencies but there are no coherent oscillations. We calculated the stability boundary for incoherence by checking the stability of the state to small perturbations.

Define a density function ρ(r, θ, ω, t) so that the fraction of oscillators of frequency ω between r and r + dr and between θ and θ + dθ is ρrdθdr. The evolution for ρ is given by the continuity equation

$$\frac{\partial \rho }{\partial t}+\overrightarrow{\nabla }·(\rho \overrightarrow{\nu })=0$$ (29)

where ν⃗ is the velocity of oscillators given by ν⃗ = (ṙ rθ⃗). Substituting (18) and (19) gives

$$\frac{\partial \rho }{dt}+\frac{1}{r}\frac{\partial }{\partial r}(\rho [r^2(a^2-r^2)+KRr\text{cos}(\theta -\varphi )])+\frac{1}{r}\frac{\partial }{\partial \theta }(\rho [r\omega -KR\text{sin}(\theta -\varphi )])=0,$$ (30)

where a² = (λ₀ − D). In the incoherent state

$$\rho =\frac{\delta (r-a)}{2\pi r}.$$ (31)

We now consider a small perturbation in the radial and angular directions and check when the density is stable to these perturbations. In particular, consider

$$\rho =\delta (r-a-\epsilon r_1(\theta ,\omega ,t))\left(\frac{1}{2\pi r}+\epsilon f_1(\theta ,\omega ,t)\right).$$ (32)

For such a perturbation, by the chain rule we have

$$\dot{r}=\epsilon \frac{\partial r_1}{\partial \theta }·\theta +\epsilon \frac{\partial r_1}{\partial t}.$$ (33)

Writing R = εR₁, substituting in (18) and (19), and keeping terms first order in ε yields

$$-2a^2{r}_1+D{R}_1\text{ cos}(\theta -\varphi )=\omega \frac{\partial r_1}{\partial \theta }+\frac{\partial r_1}{\partial t}.$$ (34)

We seek solutions in which R₁ and r₁ are proportional to e^(λ+ib)t and we find that r₁ must obey the equation

$$\omega \frac{\partial r_1}{\partial \theta }+(\lambda +ib+2a^2)r_1=D{R}_1\text{ cos}(\theta -\varphi ).$$ (35)

The solution for r₁ which is periodic in θ is of the form

$$r_1=A\text{ cos}(\theta -\varphi )+B\text{ sin}(\theta -\varphi ),$$ (36)

where

$$A=\frac{D{R}_1(\lambda +ib+a^2)}{{\omega }^2+{\left(\lambda +ib+2a^2\right)}^2}$$ (37)

$$B=\frac{D{R}_1\omega }{{\omega }^2+{\left(\lambda +ib+2a^2\right)}^2}$$ (38)

We now consider the small angular perturbations. We can substitute ρ = δ(r − a)[1/2πr + εf₁] into the continuity equation and keep terms linear in ε to get

$$\frac{\partial f_1}{\partial t}+\omega \frac{\partial f_1}{\partial \theta }-\frac{K{R}_1\text{ cos}(\theta -\varphi )}{2\pi a^2}=0$$ (39)

Assuming the periodic solution is proportional to e^(λ+ib)t as above, one finds

$$f_1=C\text{ cos}(\theta -\varphi )+D\text{ sin}(\theta -\varphi )$$ (40)

with

$$C=\frac{D{R}_1(\lambda +ib)}{2\pi a^2\left({\omega }^2+{\left(\lambda +ib\right)}^2\right)}$$ (41)

$$D=\frac{D{R}_1\omega }{2\pi a^2\left({\omega }^2+{\left(\lambda +ib\right)}^2\right)}$$ (42)

We can now rewrite the steady-state equations stemming from (18) and (19) in terms of the density to get

$$\frac{\rho D+J}{\rho D}R={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{2\pi }r\text{ cos }(\theta -\varphi )\rho rd\theta drg(\omega )d\omega }}}$$

$$\frac{b+\omega }{\rho D}={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{2\pi }r\text{sin}(\theta -\varphi )\rho rd\theta drg(\omega )d\omega },}}$$ (43)

where we have used that the order parameter for the solutions is chosen so that $\frac{d{\theta }_j}{dt}=b$. Substituting in (32), (36), and (40), and keeping terms first order in ε,

$$\frac{2(\rho D+J)}{\rho D}={\displaystyle {\int }_{-\infty }^{\infty }\frac{\lambda +ib}{{\left(\lambda +ib\right)}^2+{\omega }^2}g(\omega )d\omega +}{\displaystyle {\int }_{-\infty }^{\infty }\frac{\lambda +ib+2a^2}{{\left(\lambda +ib+2a^2\right)}^2+{\omega }^2}g(\omega )d\omega }$$ (44)

$$\frac{2(b+{\omega }_0)}{\rho D^2}={\displaystyle {\int }_{-\infty }^{\infty }\frac{\omega }{{\left(\lambda +ib\right)}^2+{\omega }^2}g(\omega )d\omega +}{\displaystyle {\int }_{-\infty }^{\infty }\frac{\omega }{{\left(\lambda +ib+2a^2\right)}^2+{\omega }^2}g(\omega )d\omega }$$ (45)

The bifurcation condition requires that λ = 0. So the stability boundary is given by setting λ = 0 in the equation above. This gives (using usual relationships for principal values of integrals in the limit λ = 0⁺)

$$\frac{2(\rho D+J)}{\rho D}=\pi g(b)+{\displaystyle {\int }_{-\infty }^{\infty }\frac{ib+2a^2}{{\left(0^{+}+ib+2a^2\right)}^2+{\omega }^2}g(\omega )d\omega }$$ (46)

$$\frac{2(b+{\omega }_0)}{\rho D^2}=P\left[{\displaystyle {\int }_{-\infty }^{\infty }d\omega \frac{g(\omega )}{\omega -b}}\right]+{\displaystyle {\int }_{-\infty }^{\infty }\frac{\omega }{{\left(0^{+}+ib+2a^2\right)}^2+{\omega }^2}g(\omega )d\omega }$$ (47)

where P denotes the principal value. Notice that for the line D = λ₀ (i.e. a = 0⁺) these equations reduce to (28) showing that incoherence joins the corner of the death state. Thus, there is a tri-critical point on the line D = λ₀ where the incoherent phase, the synchronized oscillation phase, and the death phase meet. This point is analogous to the tri-critical point discovered in the directly-coupled case [10], except that we have not observed regions exhibiting transient unsteady behavior at low densities (ρ < 1). We emphasize that although unsteady behavior was not observed in our simulations, we have not proven its nonexistence.

6. Explicit equations for Rectangular and Lorentzian Distributions

The derivation presented above is for arbitrary g(ω). When g(ω) is either a rectangular or Lorentzian distribution, we can perform the integrations in (16) explicitly. For a Lorentzian distribution,

$$g(\omega )=\frac{1}{\pi }\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}^2+{\omega }^2}$$ (48)

the equations are particularly simple because the Fourier transform is a simple exponential:

$$\widehat{g}(p)=e^{-\left|p\right|\mathrm{\Gamma }}.$$ (49)

We now plug this into the equations for the stability of amplitude death (15) and use the fact that these equations are in the form of a convolution for b. A straightforward calculation then shows that the resulting equations for the stability boundary are identical to the case where g(ω) = δ(ω), except with D 2212 λ₀ → D − λ0 + Γ,

$$\frac{\rho D+J}{\rho D^2}=\frac{D-{\lambda }_0+\mathrm{\Gamma }}{{\left(D-{\lambda }_0+\mathrm{\Gamma }\right)}^2+b^2}$$

$$\frac{b+i{\omega }_0}{\rho D^2}=-\frac{b}{{\left(D-{\lambda }_0+\mathrm{\Gamma }\right)}^2+b^2}.$$ (50)

Thus Γ has the intriguing effect of decreasing the effective λ₀, thereby pulling the individual oscillators closer to their supercritical Hopf bifurcation.

An analogous set of equations, albeit more unwieldy, can also be derived for a rectangular frequency distribution:

$$\begin{array}{lll}g(\omega )\hfill & =1/\mathrm{\Gamma }\hfill & \text{if}-\mathrm{\Gamma }/2<\omega <\mathrm{\Gamma }/2\hfill \\ \hfill & =0\hfill & \text{otherwise}\hfill \end{array}$$ (51)

In this case, the integrals in (15) and (16) can be performed and yield the equations

$$\frac{a+A}{\rho D^2}=\frac{1}{2\mathrm{\Gamma }}(\text{arctan}[(b+\mathrm{\Gamma })/(a+B)]-\text{arctan}[(b-\mathrm{\Gamma })/(a+B)])$$ (52)

$$\frac{b+{\omega }_0}{\rho D^2}=\frac{1}{2\mathrm{\Gamma }}\text{log }\left[\frac{{\left(b+\mathrm{\Gamma }\right)}^2+{\left(a+B\right)}^2}{{\left(b-\mathrm{\Gamma }\right)}^2+{\left(a+B\right)}^2}\right]$$ (53)

Figure 3 shows the phase boundaries for this case as a function of ρ, D, and J. As expected, for D > λ₀, the death phase and synchronized oscillations are both possible. For large D, as density is increased across the transition, the amplitude of the synchronized oscillations rises sharply with density. For smaller D, this rise in amplitude is less pronounced. When D < λ₀, one also sees a Kuramoto-like transition from incoherent to synchronized oscillations. The same crossover behavior was observed in recent experiments on BZ catalytic particles with a distribution of natural frequencies [5, 6].

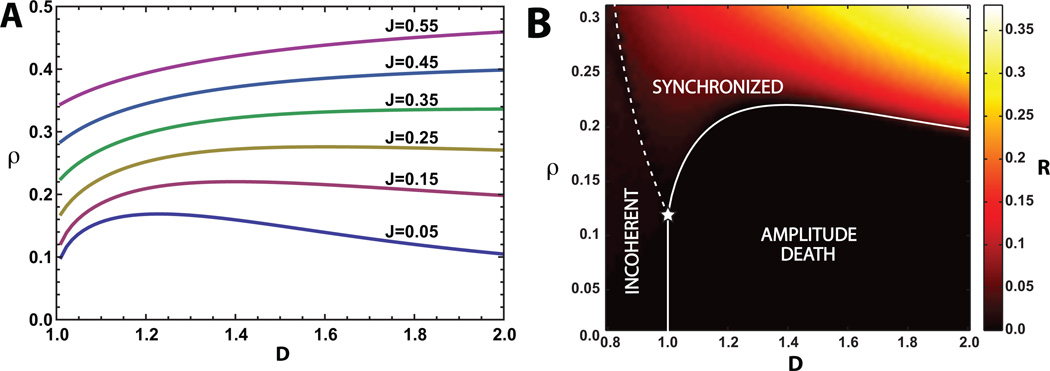
Figure 3.

(A) Phase boundaries in ρ vs D plane for heterogeneous oscillators drawn from a rectangular distribution (Γ = 0.5) for J = .05–0.55 (bottom to top). The synchronized phase occurs above the phase boundary and the amplitude death phase occurs below the boundary. Parameters are as in Fig.2 with ω₀ = 1, and λ₀ = 1. Comparing with the corresponding phase boundaries in Fig. 2 for homogenous oscillators, we see that oscillator heterogeneity increases the density, ρ, at which the transition from amplitude death to synchrony occurs for a fixed D. (B) Numerical simulations for J = 0.15. Heat map of the amplitude of collective oscillation, R = |Z|, from simulations of N = 100 oscillators drawn from a rectangular frequency distribution with parameters as in (A). The dotted line indicates the Kuramoto-like transition from an incoherent phase with D < 1 to synchronized oscillations and the solid line indicates the transition from the amplitude death phase to the synchronized phase. The star marks the point along the line D = λ₀ = 1 at which all three phases meet. This is similar to the experimental results for catalytic BZ particles [5]

7. Discussion

In this paper, we considered the physics of dynamical quorum sensing by studying limit-cycle oscillators diffusively coupled through an external medium. We find that there are three distinct phases: a synchronized phase exhibiting coherent population-level oscillations, an amplitude death phase where individual oscillators cease to oscillate, and an incoherent phase where there are no global oscillations but individual oscillators still oscillate. In addition to a density-dependent Kuramoto-like incoherence to coherence transition between the synchronized and incoherent phase, there is a density-dependent transition from the synchronized phase to an amplitude death phase where all oscillators are quiet. This latter transition can occur due to three distinct physical mechanism: (1) oscillator heterogeneity, (2) degradation of the external medium, and (3) a new mechanism we term “dynamic death” where at low population densities and moderate diffusion constants the external medium dynamics are not fast enough to support global oscillations. It is worth emphasizing that these three mechanisms give rise to the same phase boundary and do not generate distinct phases. Our model reproduces many qualitative features observed in recent experiments on heterogeneous populations of BZ catalytic particles [5] as well as synthetically engineered bacteria [4].

This simple model captures many qualitative features seen in a variety of experiments on oscillators coupled diffusively through an external medium. For example, it was previously argued that when all oscillators are identical, the model is a good description of glycolitic oscillations in suspensions of yeast cells. The model also shows how large amplitude oscillations can emerge as one varies the density and how this behavior crosses-over into a Kuramoto-like transition as D is decreased (see Fig. 3). These qualitative features are in good agreement with experiments on BZ particles [5, 6]. Finally, the model also captures many of the mean-field properties of coupled synthetically-engineered bacteria, including the sudden emergence of oscillations and scaling of amplitude and period of oscillations as one changes the external degradation rate J. However, in contrast to [4], in our model the period and amplitude of the oscillations decrease not increase with increasing J. This discrepancy likely arises from the highly non-linear nature of the “degrade-and-fire” oscillations characterizing the synthetic bacteria [15].

Our results suggest that properly constructed simple models may be able to capture interesting, qualitative behaviors of coupled oscillators. They also suggest that many of the phenomena observed in oscillators coupled through a common external medium may be universal and independent of the particular biological, physical, or chemical realization. Universality has played a key role in expanding our understanding of collective behavior in physical systems. Our work suggests universality may also be useful biology [2]. In the future, it will be interesting to directly relate this simple model to more detailed models [15], extend the simple mean-field model of dynamical quorum sensing explored here to include spatial effects, and to consider the related model of phase-only oscillators coupled by an external medium.

• A simple model of dynamical quorum sensing (DQS) is introduced.

• We find four distinct physical mechanisms that give rise to DQS transitions.

• Our model reproduces the qualitative features of recent experiments.