Estimating the optimal dynamic antipsychotic treatment regime: Evidence from the sequential multiple assignment randomized CATIE Schizophrenia Study

Summary

Treatment of schizophrenia is notoriously difficult and typically requires personalized adaption of treatment due to lack of efficacy of treatment, poor adherence, or intolerable side effects. The Clinical Antipsychotic Trials in Intervention Effectiveness (CATIE) Schizophrenia Study is a sequential multiple assignment randomized trial comparing the typical antipsychotic medication, perphenazine, to several newer atypical antipsychotics. This paper describes the marginal structural modeling method for estimating optimal dynamic treatment regimes and applies the approach to the CATIE Schizophrenia Study. Missing data and valid estimation of confidence intervals are also addressed.

1. Introduction

Schizophrenia is a chronic disease characterized by abnormalities in a person’s perception of reality. Symptoms include hallucinations, delusions, and confused speech and thought processes. The illness places a high level of burden on individuals afflicted with the disease as well as those who care for them. For several reasons schizophrenia can be difficult to manage with a single treatment and is instead managed by continuously monitoring patients and adjusting medication according to how a patient responds to treatment. Individual patients’ response to antipsychotics is often very heterogeneous over the population; additionally, a patient’s response to a medication can vary greatly over time, with the possibility of drug resistances developing. Many of the antipsychotics that are helpful in reducing the symptoms of schizophrenia have very troublesome, and sometimes life threatening, side effects. For these reasons it is better to investigate the long term effects of sequences of treatments for managing schizophrenia, rather than simply comparing the short term effects of one drug against another.

A wide range of analytic techniques have been developed to estimate the optimal adaptive treatment strategy, also called a dynamic treatment regime. Semi-parametric approaches have found the most favor in the statistical community, with techniques such as iterative minimization of regrets (Murphy, 2003), G-estimation (Robins, 2004), Q-learning (Murphy, 2005), machine-learning methods (Pineau et al., 2007), and regret-regression (Henderson et al., 2010; Almirall et al., 2010). Traditionally, more parametric approaches were considered (Bellman, 1957; Bertsekas and Tsitsiklis, 1996) and these may again be gaining attention as Bayesian researchers turn their attention to the area (Thall et al., 2009; Arjas and Saarela, 2010).

Although initially proposed to estimate static treatment regimes (Robins et al., 2000; Hernán et al., 2000) – i.e., treatment regimens that are not tailored to evolving patient characteristics – marginal structural models (MSM) are increasingly being applied to the problem of selecting or indeed estimating the optimal dynamic treatment regime (Lunceford et al., 2002; Wahed and Tsiatis, 2004; Hernán et al., 2006; van der Laan and Petersen, 2007; Robins et al., 2008; Orellana et al., 2010a,b; Cotton and Heagerty, 2011). The approach is particularly appealing because of the relative ease with which the models may be estimated, although considerable data-processing must first be undertaken. We employ this approach to evaluate the optimal antipsychotic therapy regime for schizophrenia.

The paper is organized as follows: In Section 2, we introduce the CATIE Schizophrenia Study, focusing on the objective of our analysis and the key variables that will be considered. This is followed by a detailed description of the marginal structural modeling approach to dynamic treatment regimes and other statistical challenges, such as the treatment of missing information and the construction of valid confidence intervals. Section 4 presents the results of our primary analysis, with a brief discussion of several sensitivity analyses which appear in full in an appendix, and Section 5 discusses the findings and their implications.

2. Background: Setting and Data

2.1. The CATIE Schizophrenia Study

The Clinical Antipsychotic Trials of Intervention and Effectiveness (CATIE) study was an 18 month multi-stage randomized trial of 1460 patients. The details of the design and protocol of the CATIE study have been described in detail elsewhere (Swartz et al., 2003; Stroup et al., 2003; Lieberman et al., 2005; McEvoy et al., 2006; Stroup et al., 2006); thus, here we give a brief review of the CATIE study as it pertains to the scientific question of interest of this paper. The CATIE study was initiated by the National Institute of Mental Health as a practical clinical trial designed to compare the efficacy and tolerability of antipsychotic medications already in use for the treatment of the symptoms of schizophrenia in order to inform clinical practice. In order to meet this goal, a broad entry criterion was established and the trial was designed to mimic real life treatment of schizophrenia as closely as possible. A specific way in which this was done was that the CATIE protocol allowed patients to request to switch to another randomized treatment if they were no longer satisfied with their current treatment.

One of the primary scientific questions of interest of the CATIE study was to compare the long-term effectiveness of newer atypical antipsychotics to perphenazine, a mid-potency first generation antipsychotic (Stroup et al., 2003). At entry into CATIE, patients were randomized to either perphenazine or to one of four possible atypical medications: olanzapine, risperidone, quetiapine or ziprasidone. Ziprasidone was the newest medication included in CATIE to be approved for market use by the U.S. Food and Drug Administration and actually became available after CATIE had already begun enrollment. Five hundred and seventy one patients in CATIE were randomized to treatment before ziprasidone was an eligible treatment option, and thus, could not be randomized to receive ziprasidone in the first stage of treatment. For this reason we restrict our comparison of perphenazine to olanzapine, risperidone, quetiapine and do not include patients randomized to ziprasidone in the atypical comparison arm.

Patients randomized to perphenazine at entry into CATIE and who decided to discontinue treatment with perphenazine were subsequently randomized to either olanzapine, risperidone, or quetiapine. Any patients randomized to an atypical medication (either initially, or subsequent to being assigned to perphenazine) who decided to discontinue their current assigned atypical medication were then offered a choice of two randomization arms: in one arm, patients were randomized to ziprasidone, olanzapine, risperidone, or quetiapine, excluding their previous atypical treatment, while in the other arm patients were randomized to either clozapine, olanzapine, risperidone, or quetiapine, again excluding their previous atypical treatment. Clozapine is known to be a very effective atypical antipsychotic medication, but can dangerously lower a patient’s white blood cell count (Jose et al., 1993), requiring patients taking clozapine to undergo regular blood testing. For this reason, clozapine is the only drug randomly assigned to patients in CATIE that was not double blinded, because of this we do not include clozapine in the atypical comparison arm. Patients dissatisfied with their second atypical medication could opt to switch treatment again; patients then entered a stage of the study in which treatment was neither randomized nor blinded and patients along with their doctors chose from all CATIE medications for treatment. Patients could change among those medications as frequently as they wished.

Tardive dyskinesia (TD) is a rare, but burdensome, side-effect of some antipsychotic medications that causes a person to have involuntary, repetitive body movements, such as facial twitching, grimacing and rapid eye blinking. TD can be irreversible and worsen with continued exposure to a first generation antipsychotic (Sachdev, 2000; Buchanan et al., 2010). There is much evidence linking first generation antipsychotic medications, such as perphenazine, to incidences of TD. There is some evidence that TD may also be a side effect of newer atypical medications, but it is clear that perphenazine has a significantly higher risk of causing TD (Margolese et al., 2005; Buchanan et al., 2010). For this reason patients who had TD at entry into the CATIE study (231, 15.8%) were not eligible to be randomized to perphenazine. As the primary question of interest in this paper is to compare perphenazine to second generation atypical antipsychotics, we remove all patients who had TD at entry into CATIE, as clinical practice would very rarely provide such patients with perphenazine. After excluding patients who were initially randomized to ziprasidone and patients who had TD at entry into CATIE, we are left with a sample size of 1076 individuals.

2.2. Variables of interest

Demographic variables collected at baseline include age, sex, race, marital status, education, and employment status. Further information was collected on the clinical setting from which the patient was recruited (“site type”, e.g. Veterans Affairs (VA) clinic or university hospital), the years on prescription medication prior to study entry, and whether randomized treatment assignment upon study entry resulted in the participant being newly treated, changing medication, or remaining on current medication.

At baseline, the first monthly visit, and at quarterly visits throughout the remainder of the CATIE study, a large number of clinical covariates were recorded, including the Positive and Negative Syndrome Scale (PANSS) score, the Clinical Global Impression Scale, and the Calgary depression score. Side effects were assessed on the same schedule by measuring body-mass index (BMI) and the presence and severity of the symptoms of a movement disorder as measured by three standard scales: the Simpson-Angus EPS mean Scale, Barnes Akathisia Scale, and the Abnormal Involuntary Movement scale. Information on alcohol and illegal drug use was also captured at these visits. At semi-annual clinical visits additional information on participants was collected including mental and physical functioning assessed via SF-12 Health Survey and quality of life (QOL). Furthermore, a measure of medication adherence was collected monthly throughout the study. Additionally, PANSS was collected at any visit at which a CATIE participant changed treatment.

For this analysis, we focus on 12-month PANSS score and 12-month QOL score as the primary outcomes of interest, using a time-varying measure of disease severity, the PANSS score, in order to individualize treatment. The PANSS score is the standard medical scale for measuring symptom severity in patients with schizophrenia (Kay et al., 1987). A low PANSS score indicates few psychotic symptoms; as an individual’s psychotic symptoms increase, so does their PANSS score. The PANSS score is a composite score measured in an interview with the patient and measures the severity and frequency of various symptoms such as delusions, anxiety, and poor attention. The scale of the PANSS score ranges from 30 to 210; the minimum PANSS score observed in the CATIE data is 30 and the maximum observed score is 154. The QOL scale collected in the CATIE study is the Heinrichs-Carpenter Quality of Life Scale, designed to measure deficit symptoms for patients with schizophrenia (Heinrichs et al., 1984). As with the PANSS score, the QOL score is a composite scale that takes into account many aspects of life and is measured in a interview with a trained practitioner. A high QOL score is associated with high functionality. The range of the QOL scale used in the CATIE study is 0 to 6, with the smallest and largest observed QOL scores in the CATIE study being 0.095 and 6 respectively.

2.3. Objective

TD is a potentially irreversible side effect that can greatly affect a patient’s life, leading to an inclination to minimize the life-long risk of a patient developing TD. TD symptoms are experienced in varying levels and often develop slowly. An official diagnosis of TD is made only after observing and evaluating the emerging movement disorder symptoms over an extended period of time. TD is a rare condition, and one would not expect to diagnose a new TD case in an 18 month trial like CATIE. Additionally, since TD is a result of prolonged exposure to antipsychotics (most notably first-generation antipsychotics like perphenazine) it would be difficult to attribute a new diagnosis of TD to a recent change in treatment. For this same reason, one would not expect to notice differences in acute movement score measures between treatment groups over such a relatively short period of time. It has been shown, and is widely accepted, that the longer a patient is on perphenazine (or other first generation antipsychotics) the higher their risk of developing TD (Margolese et al., 2005; Buchanan et al., 2010). Consequently, it is reasonable for individuals and doctors to try to limit the time a person is exposed to perphenazine, unless the symptom reduction that perphenazine provides for the patient outweighs the risk of TD.

Our objective is to identify the optimal therapeutic strategy to minimize schizophrenic symptoms. We compare two regimes. The first regime under consideration is always atypical: treatment with an atypical antipsychotic for 12 months; any of olanzapine, quetiapine, or risperidone may be taken, and switches between these medications are permitted as part of the regime should the patient and physician find the treatment ineffective or the side effects intolerable. The second regime is a perphenazine and atypical regime. In this dynamic regime, indexed by threshold θ, any patient whose PANSS score is at or above θ at treatment baseline will receive the first generation antipsychotic perphenazine, while those with PANSS scores below θ will receive an atypical antipsychotic medication. As part of this regime, during the follow-up period, those patients who begin on perphenazine will be switched to an atypical antipsychotic when symptom severity, as measured by the PANSS score, decreases beyond the threshold θ. Thus, this regime assigns perphenazine to patients with high symptom severity in order to reduce symptoms as measured by the PANSS score; once the symptoms are under control, i.e. under the specified threshold, the patient’s treatment is then switched to an atypical medication in order to reduce the patient’s long term risk of incurring the debilitating side effect of TD. Once a patient initiates treatment with an atypical antipsychotic, changes between different antipsychotics are permitted under the perphenazine and atypical regime.

3. Statistical Methods

3.1. Notation

Time 0 is taken to be the start of the study, and the window of follow-up considered for this analysis is 12 months. We denote the two treatment regimes of interest as AA for the always atypical regime and PA(θ) for the perphenazine and atypical regime, where θ is the PANSS threshold used to determine whether initial treatment is with perphenazine and when to change treatment to an atypical antipsychotic. As noted above, the AA regime that we have defined permits an individual to switch the specific atypical medication taken over the course of their therapy among those being considered (olanzapine, risperidone, and quetiapine). Many CATIE participants who are initially randomized to an atypical antipsychotic discontinue use of this first assigned medication prior to month 12 and are subsequently randomized to a different atypical medication in the next treatment stage. The second regime, PA(θ), that we have defined also allows for individuals to switch between atypical medications once treatment with atypical medication has begun (either from the outset for those patients whose baseline PANSS score was below θ or after switching off perphenazine for those whose baseline PANSS score was at or above θ). Thus, the two regimes under consideration are 𝒜= {AA, PA(θ)} for θ ∈ Θ.

Let Y be the observed PANSS (or QOL) score at month 12. We denote by V a vector of baseline covariates such as participant age and sex, and let L_m denote a vector of time-varying covariates such as treatment adherence and the variables listed in Section 2.2, measured at months m = 0, 1, …,12. Note, that many time-varying variables are not collected at all months; for those months that a variable was not schedule to be collected, we use the last scheduled measurement.

Within the counterfactual framework for causal inference (Neyman, 1923; Rubin, 1978; Robins, 1986), we view the observed data structure as a partially observed version of the full data structure that contains the counterfactual outcome Y_d, d ∈ 𝒜, that would be observed were it possible to assign each participant to regime d for the collection of all possible regimes under consideration, 𝒜. Using this notation, we may define the estimation target of interest to be the (marginal) mean counterfactual outcome E[Y_d], or the mean counterfactual outcome conditional on a subset of baseline covariates E[Y_d|V], specified in some model as E[Y_d|V] = m(d, V|β), V ⊂ L₀.

3.2. A Marginal Structural Modeling Approach to Optimal Dynamic Treatment Regime Estimation for CATIE

3.2.1. Marginal Structural Models for Dynamic Treatment Regimes

Comparing multiple dynamic treatment regimes in a marginal structural modeling framework requires first the realization that an individual’s observed treatment history may be compatible with several treatment regimes, at least for some part of the observation period. From a practical perspective, this implies an augmentation of the original data set to create multiple copies of the same individual for each regime for which their observed history is consistent; we refer to these copies as replicates. For example, if an individual’s data are consistent with regime PA(θ*) through to time j, we say that the replicate follows that regime through to time j; at the point where the individual’s observed history is no longer compatible with regime PA(θ*) – for instance, the individual switches to an atypical medication while their PANSS score is still higher than threshold θ* – then the replicate corresponding to that individual and threshold θ* is artificially censored. Under the assumptions, which are detailed in Section 3.4, a weighted analysis of this augmented data set with artificial censoring mimics an analysis of a trial in which individuals are randomized to follow one of the treatment regimes of interest.

Estimation of the optimal dynamic treatment regime requires finding the regime d that maximizes the population average outcome E[Y_d|V]. Then

$$D_i^{\mathit{\text{I PW}}}(Y_d,L,V|w,\beta )=w_i(A_i|L_i,V_i)\frac{\partial }{\partial \beta }m(d,V_i|\beta )[Y_i-m(d,V_i|\beta )],$$

is the estimating function for the marginal structural model, where w_i = w_i(A_i|L_i, V_i) is a weight for replicate i in the augmented data set. Thus, i corresponds to an individual-regime pair in the augmented data set. The weight, w_i is constructed by estimating the probability of continued observation, i.e. of not being censored for any reason, of a replicate in the augmented data set under the assigned treatment regime. Given a replicate’s current PANSS score and a regime threshold θ, the probability of continued observation at any month is equivalent to the time-dependent probability of being observed and treated, much as in the analysis of HIV treatment initiation by Cain et al. (2010). That is, censoring is a deterministic function of the history of treatment and the history of covariates in addition to the threshold θ.

Letting A_j = 1 denote treatment with an atypical antipsychotic at time j, C_j = 1 indicate artificial censoring at time j, X̄_j denote covariates (including PANSS score) measured up to time j, and Ā_j−1 treatment up to time j − 1. The ‘usual’ inverse of the weight in a MSM is the probability of being treated and observed at any point, given history:

$$P(A_j=1,C_j=0|{\overline{X}}_j,{\overline{A}}_{j-1}\theta )=P(A_j=1|C_j=0,{\overline{X}}_j,{\overline{A}}_{j-1},\theta )\times P(C_j=0|{\overline{X}}_j,{\overline{A}}_{j-1},\theta ).$$

However, if A_j−1 = 1 and C_j = 0, then P(A_j = 1|C_j = 0, X̄_j, Ā_j−1 = 1, θ) = 1. On the other hand, if A_j−1 = 0, C_j = 0, and the covariates are such that the PANSS score measured at month m is below θ, then it must be the case that P(A_j = 1|C_j = 0, X̄_j, Ā_j−1 = 0, θ) = 1. Similarly if A_j−1 = 0 and C_j = 0 and the PANSS score at month m is above θ then P(A_j = 0|C_j = 0, X̄_j, Ā_j−1 = 0, θ) = 1. Thus, for our analysis, unlike a traditional MSM aimed at estimating a static treatment regime, we refer only to censorship weights, rather than treatment weights.

Typically these weights are unknown; even when such probabilities are known, the probabilities are often estimated to improve efficiency of the estimators of β of the marginal model (van der Laan and Robins, 2003). Provided the weights are estimated using consistent estimators of the true treatment and censoring models, solving

$${\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{d\in 𝒜}^{}}{D}_i^{\mathit{\text{I PW}}}(Y_d,L,V|w,\beta )=0$$ (1)

yields consistent estimators of the parameters β.

As in MSMs for static treatment regimes, stabilization of weights is preferable to the use of unstabilized weights (Robins et al., 2000), especially when weight variability is high, although better efficiency is not guaranteed (Cain et al., 2010). Additionally, truncation of the weights can decrease the chance that a small number of replicates will have undue influence on the results of the analysis. We implement stabilized weights and, following convention, we truncate all weights at 10 to avoid excess variability (Cain et al., 2010; van der Laan and Petersen, 2007). The weights for censoring are estimated using

$$w_{\mathit{\text{ci}}}(m)=\frac{P(C_{\mathit{\text{im}}}=0|V_i,C_{\mathit{\text{im}}-1}=0,\theta )}{P(C_{\mathit{\text{im}}}=0|V_i,L_{\mathit{\text{im}}},C_{\mathit{\text{im}}-1}=0,\theta )},$$ (2)

where here C_im = 1 denotes that a replicate was censored at month m for any reason. Note that C_m = 0 implies C₁ = C₂ = … = C_m−1 = 0. These models are typically fit via logistic regression, a strategy that we employ here. Note that it is the models for the denominators of the weights that must be correctly specified for consistent estimation of the parameters of the MSM (Robins, 1999). Furthermore, unlike in the stabilization of weights for marginal structural model estimation of static treatment regimes, the probabilities in the numerators cannot condition on treatment history (Cain et al., 2010).

3.2.2. Application of the MSM approach for Dynamic Treatment Regimes to CATIE

Here we outline the steps of estimating the dynamic treatment regime described in Section 2.3 using the data collected in the CATIE study. We take as the possible thresholds for initiating an atypical antipsychotic at baseline or switching off of perphenazine the set Θ= {30, 35, 40, 45, 50, 55, 60, 65, 70}, with θ = 30 representing the regime always treat with perphenazine as no PANSS scores lie below 30. The estimation procedure for a complete data set proceeds as follows:

1. Create the augmented CATIE data set, by replicating individuals enrolled in the CATIE study. We use the term individual to refer to a participant enrolled in the CATIE study. We use the term to replicate to refer to a row in this augmented data set; a replicate is defined by a CATIE participant and their assigned treatment regime in the augmented data set. Replicates can correspond to the regime AA (always treat with an atypical), as well as each of the dynamic regimes under consideration indexed by threshold θ, PA(θ). Each CATIE participant is replicated according to the number of regimes, as listed below (i)–(iii), that they follow for any length of time over the 12 months under consideration in this analysis.

   1. AA: treat with an atypical antipsychotic, regardless of PANSS score;
   2. PA(30): always treat with perphenazine;
   3. PA(θ), θ ∈ (Θ\30): treat with perphenazine at baseline if PANSS score is at or above θ, then switch to an atypical antipsychotic when PANSS scores falls below θ; if the PANSS score is below θ at baseline, treat with an atypical antipsychotic for the entire 12 months.
      Note that if a replicate’s baseline PANSS score is less than the threshold θ* and the individual was assigned perphenazine at enrollment in the CATIE trial this replicate is not deemed consistent with the regime PA(θ*). Any replicate with a baseline PANSS score below the threshold θ* is considered to follow the regime PA(θ*) only if their initial assigned treatment in the CATIE study was an atypical medication.
2. Censor CATIE replicates. CATIE replicates are censored in the augmented data set, created in the previous step, at the month that any of four following events occur:

   1. An individual, and thus all corresponding replicates, is randomized to clozapine. We censor individuals randomized to clozapine, because assignment to clozapine was not blinded. Clozapine can have severe side effects and requires patients to undergo constant monitoring.
   2. An individual, and thus all corresponding replicates, is randomized to ziprasidone in a subsequent treatment stage.
      We censor individuals assigned to ziprasidone in the later treatment stage of CATIE because ziprasidone was not included in the atypical arm (static treatment regime) in our analysis. This is because of its late approval by the FDA relative to the start of CATIE. Thus, all patients initially randomized to ziprasidone were excluded from the analysis, and all patients who were subsequently randomized to ziprasidone were censored.
   3. An individual, and thus all corresponding replicates, progresses to the unrandomized, unblinded stage of the trial prior to month 12.
      We censor individuals who enter this follow-up stage of the CATIE study because participants were allowed to choose their treatment with their doctors, meaning the treatment is neither randomized nor blinded, and participants could switch treatment as frequently as they wished.
   4. A replicate, for which the corresponding individual is initially assigned perphenazine, is censored for no longer following their assigned dynamic treatment regime. That is, given a PANSS threshold θ, replicates may stop following the regime for one of two reasons:

      1. Before choosing to switch off perphenazine, a replicate’s PANSS score falls below the threshold θ of their assigned regime.
      2. At the visit that treatment is switched from perphenazine, the PANSS score is equal to or greater than θ.

   Note that artificially censoring individuals (and the corresponding replicates) for reasons (i)–(iii) might occur in any analysis of the CATIE data (depending, of course, on the scientific question pursued by the analyst); we refer to this as off-study censoring. Censoring for reason (iv) is specific to the data augmented dynamic treatment regimes analysis, and we refer to this type as simply artificial censoring.

3. Estimate censoring models to ensure parameter estimates are not biased by any covariates that may be predictive of both censoring and 12-month outcome. Estimate stabilized censorship weights using the variables listed below and a spline on month of observation with knots at months 1, 2, …, 11 fit to ensure continuity at the knots. Specifically, we use the baseline variables years on prescription antipsychotic medication, a binary indicator of hospitalization in the three months prior to CATIE entry, factors of the categorical variables site type, sex, race, marital status, education, employment, as well as baseline values of a replicate’s PANSS score, BMI, alcohol and drug use, Calgary depression score, presence and severity of movement disorders, quality of life, physical and mental functioning, and the threshold in the numerator weights. We include these covariates as linear terms in the final mean model which is estimated using the weighted augmented data set. In addition to these variables, we include in the denominator of the weights baseline treatment, current (time-varying) values of BMI, alcohol and drug use, PANSS score, Calgary depression score, presence and severity of movement disorders, quality of life, physical and mental functioning, medication adherence, date of observation, and previous month’s treatment assignment.

4. Construct the final weight for each replicate i by including the estimated randomization probability, giving

   $$w_i={\displaystyle \prod _{m=1}^{12}}{w}_{\mathit{\text{ci}}}(m),$$ (3)

   where w_ci(m), as defined in Eq. (2), denotes the stabilized artificial censoring weight for a replicate in the augmented data set corresponding to an individual-regime pair. The stabilized censorship weight is estimated for months m = 1, 2, …, 12. We estimate censorship models at each month, as individuals may switch treatment at any month in the CATIE study. Since not all variables were collected at every month, we use the last scheduled value for those covariates that were not collected at a particular monthly visit.
5. Perform a weighted linear regression with the weights as above to obtain the coefficient estimates of the model

   $$Y_d=m(d,V|\beta )={\beta }_1\mathrm{𝟙}[d=\mathit{\text{AA}}]+\mathrm{𝟙}[d=\mathit{\text{PA}}(\theta )]({\beta }_2+{\beta }_3\theta )+{\displaystyle \sum _{k=1}^{40}{\beta }_{3+k}{V}_k}$$ (4)

   using Equation (1) where V denotes the baseline variables used in the numerator of the stabilized censorship weights.

3.3. Missing Data

Dropout in studies of antipsychotics in patients with schizophrenia is often high, between 30 and 60% (Adams, 2002). Of the 1076 patients included in our analysis 429 (40%) dropped out of CATIE before month 12. In addition to this missing data due to study attrition, there is some item missingness in the CATIE data arising from individuals missing a visit (but coming back to later visits) or not providing all information at a particular visit. Addressing in detail the subtleties of complex missing data structures in sequential multiple assignment randomized trials such as CATIE is not a trivial task. We briefly describe the methods we use for overcoming the missing data in this analysis and direct the interested reader elsewhere for a complete description (Shortreed et al., 2010).

Our primary analysis uses multiple imputation to overcome missing data due to both drop out and item missingness. Additionally, we perform a sensitivity analysis that uses multiple imputation to overcome item missingness and inverse probability weighting to overcome missing data due to study attrition. We use Bayesian regression methods and the observed CATIE data to estimate the predictive distribution for the missing values at scheduled visits given the observed data from scheduled visits. We use samples from the posterior predictive distribution in order to fill in missing values and produce completed, unaugmented CATIE data sets. After this imputation process has replaced all of the missing values, we proceed with the analysis as described in Section 3.2.2 on each completed data set.

We use nested fully conditional specification (FCS) (van Buuren, 2007; Van Buuren et al., 2006; Nevalainen et al., 2009) to impute all time-varying variables except PANSS at each scheduled month of observation. Note, not all variables were scheduled to be collected at every monthly visit; thus, we only impute scheduled covariate values at the monthly visits in which they should have been collected. FCS allows great flexibility in fitting the predictive distribution and scales well with the number of variables, which is important as there were many variables collected during the CATIE study. Each conditional predictive regression model for missing observation includes as predictors all variables measured at previous months. Specifying the conditional models in this fashion ensures that a joint predictive distribution that is consistent with all the conditional models exists (van Buuren, 2007). In order to enforce smoothness over time in the mean symptom measurement, we use a Bayesian mixed effects model (Schafer, 1997; Schafer and Yucel, 2002) to impute missing time-varying PANSS scores. In the predictive model for missing PANSS observations, we include as predictors variables collected at the same visit as the PANSS score and those collected at earlier visits. We imputed missing information at all scheduled visits, including baseline as well as monthly visits that correspond to an end of treatment stage for the individual.

We begin the CATIE imputation process at baseline, sampling from the posterior predictive distributions for variables containing missing data conditioned on the collection of variables that have no missing values (there are approximately 20 such variables). Once all baseline variables are imputed, we build rich independent conditional imputation models for all variables (except PANSS) collected at month 1. After all month 1 variables (other than PANSS) have been imputed, we use variables measured at baseline and month 1 to build a longitudinal mixed effects Bayesian regression model for PANSS. We replace missing month 1 PANSS values with samples from this posterior predictive distribution. Once this process is complete, conditional models are built for the next collection of variables in time with this process continuing until all variables collected over the course of trial are imputed. This imputation process results in a complete unaugmented CATIE data set and is repeated 25 times.

We use the same imputation process to overcome item missingness in the sensitivity analysis, but estimate inverse probability weights to overcome missing data due to study attrition. In this sensitivity analysis, we estimate additional monthly stabilized weight models for continued involvement in the study using the same predictors as for the censorship models described in Section 3.2.1. Once the multiple imputation is implemented and censorship models for con- tinued involvement are estimated, the augmented data set as described in Sections 3.2.1 and 3.2.2 is created for each of the imputed CATIE data sets.

3.4. Assumptions for the MSM analysis of the CATIE Data to Estimate Optimal Dynamic Treatment Regimes

Our analysis is predicated on five critical assumptions. The first three assumptions are necessary for applying MSM methodology to estimate dynamic treatment regimes, and the final assumptions are needed for overcoming missing data in any analysis.

The first assumption we make is that there are no unmeasured confounders of continued observation in the augmented data set. That is, we assume that L contains all variables that are required to control confounding between censorship for any reason – either artificial or off-study censorship – and the outcome. This assumption is also known as conditional exchangeability or sequential randomization.

Second, we must assume that the model for continued observation in the augmented data set (i.e. not being artificially censored for any reason) is specified correctly. Recall, as noted in Section 3.2.1, we need only model the denominator of the weights correctly. The third assumption is the experimental treatment assignment (ETA) assumption, also referred to as positivity. This assumption requires that there is no combination of confounding variables L for which censoring is guaranteed, and indeed problems arise even if the probability of continued observation is very near zero. In this analysis, this assumption corresponds to ensuring that there is no combination of confounding variables for the weight is undefined (i.e. w_ci(m) = 0⁻¹ for some i or m).

Lastly, we must assume that the models we use for overcoming missing data in the CATIE study are valid. Specifically, we assume that the data are missing at random, which means that missing observations can depend on collected information, but cannot depend on missing values. This assumption allows us to estimate predictive models for the missing data given the observed and use these predicted values to replace missing observations in the imputed data set. This also relies on the assumption that we have correctly specified these imputation models. For the sensitivity analysis that include inverse probability weights to overcome missing data due to study attrition, additionally, we must assume that we correctly model the probability of a participant remaining in follow-up.

Although medications are randomized, for those individuals whose first treatment is perphenazine, the timing (in terms of PANSS) of the switch to an atypical medication is not randomized and hence the censoring of the individual from the different dynamic regimes indexed by θ may be influenced by covariates that also affect the outcome. That L contains all variables required to correct selection bias due to attrition or artificial censoring is not verifiable empirically (see section 3.2.2 for all possible reasons for censoring in the CATIE analysis), however, a very rich collection of variables was measured in CATIE, and it is unlikely that any very important covariate was omitted. Correct specification of the models for censoring is also assumed; a sensitivity analysis to different model choices is also undertaken. A univariate summary of the weights in the CATIE analysis indicates that there are no extreme values, indicating no serious violation of the ETA assumption.

3.5. Bootstrap Confidence Interval Construction

The estimation procedure for dynamic treatment regimes via inverse probability weighting outlined in Section 3.2.1 complicates the calculation of confidence intervals and/or standard errors for two reasons: (i) the estimating equation (1) requires a plug-in estimate of the weights, and (ii) most individuals’ observed treatment history is compatible with multiple treatment regimes, so that they appear in the augmented data set several times (up to nine, in the case of CATIE). Additionally, in the not uncommon case of missing information, the handling of that aspect of the analysis must also be taken into account in estimating confidence intervals.

To appropriately account for the complete estimation procedure (data augmentation, plug-in estimates of weights, and multiple imputation), a non-parametric bootstrap procedure was employed. Following convention we first bootstrap the data then perform the same imputation procedure on the bootstrap re-sampled data as is performed on the full data to ensure correct estimation of standard errors (Shao and Sitter, 1996). Thus, to compute non-parametric confidence intervals for our marginal structural model coefficients, we proceeded as follows:

1. Re-sample with replacement the original (non-imputed) data set B = 1000 times.

2. For the b^th bootstrap data set (b = 1, …,B), perform multiple imputation K = 25 times to find estimates β̂*(b, k) for k = 1, …,K.

3. For the b^th bootstrap data set (b = 1, …, B), average over the imputed data sets’ estimates to compute the final estimate for the b^th bootstrap data set as

   $${\widehat{\beta }}^{*}(b)=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\widehat{\beta }}^{*}(b,k).$$

4. Use percentiles of β̂(b), b = 1, …, B to estimate the confidence interval of the original point estimate β̂, also estimated using K = 25 multiple imputations. Alternatively, the variance of the distribution of β̂*(b) may be used to estimate the standard error of the original point estimate β̂.

We have thus outlined a complete, valid, and practical framework for the estimation of the optimal dynamic treatment regime using the marginal structural modeling framework, including missing data corrections and appropriate confidence interval calculations.

4. Results

Baseline comparisons between the two CATIE randomized groups are presented in Tables 1 and 2. These indicate that randomization resulted in comparable treatment groups at baseline. The only difference of note between the treatment groups occurs in the baseline variable treatment status prior to CATIE: most individuals randomized to perphenazine were on a different drug at entry into the study. We performed the same analysis described in this paper both with this variable included in the weight models and with this variable excluded. As the results were similar, we present only those for the model that includes this variable in the weight models.

Table 1.

Summary of baseline demographic and disease-status covariates in CATIE. Percentage reported for categorical variables. Mean (standard deviation) reported for continuous variables.

Baseline covariates	Perphenazine (n=261)	Atypical (n=815)
Age	40.0 (11.12)	39.1 (10.85)
Male	76.2	73.0
Race
Black	35.6	35.5
White	58.2	60.1
Other	6.1	4.4
Marital status: married	16.5	10.8
Patient education
College graduate	9.6	8.1
Community college or technical school degree	6.5	6.7
Some college, did not graduate	23.0	24.8
GED/High school diploma	33.0	35.2
Did not complete high school	28.0	25.2
Employment status
Did not work	84.6	83.3
Full time	5.8	7.6
Part time	9.7	9.2
Site type
Private practice	12.6	13.1
State mental health	21.1	20.2
University clinic	22.2	23.1
VA	10.7	10.4
Combination	33.3	33.1
Hospitalized in 3 mos. prior to enrollment in CATIE	26.1	29.1
Treatment upon CATIE entry
Newly treated	28.0	27.9
Same medication as that taken prior to enrollment	1.5	20.2
Switched medication from that taken prior to enrollment	70.5	51.9
Years on prescription medication prior to CATIE	13.8 (10.99)	12.9 (9.80)
Months in CATIE spent on first assigned treatment	8.1 (6.98)	8.4 (7.08)

Table 2.

Summary of baseline clinical (functioning and symptom) covariates in CATIE. Percentage reported for categorical variables. Mean (standard deviation) reported for continuous variables.

Baseline covariates	Perphenazine (n=261)	Atypical (n=815)
PANSS (total score)	74.3 (18.12)	76.0 (17.2)
Mental health short form score	41.4 (12.26)	40.2 (11.59)
Physical health short form score	48.7 (10.3)	48.5 (9.99)
BMI	29.7 (6.89)	29.8 (7.14)
Quality of life (total score)	2.8 (1.11)	2.8 (1.05)
Calgary depression score	4.6 (4.58)	4.7 (4.37)
Clinical Global Impression Score
Not ill or minimally ill	6.69	6.3
Mildly ill	21.9	21.1
Moderately ill	47.7	45.8
Markedly ill	17.7	22.2
Severely or very severely ill	5.8	4.6
Illicit drug use (hair test)
No Drugs	61.8	60.0
At least 1 illicit drug found	38.2	40.0
Illegal drug use (clinician-reported)
Abstinent	75.0	75.0
Use without impairment	16.9	14.6
Abuse	6.5	7.6
Dependence	1.5	2.9
Alcohol use (clinician-reported)
Abstinent	61.5	63.8
Use without impairment	30.4	28.7
Abuse	5.8	4.8
Dependence	2.3	2.6
† Simpson-Angus EPS Scale - Presence of symptoms	44.1	44.5
† Simpson-Angus EPS Scale - Symptom severity score*	0.4 (0.36)	0.4 (0.28)
† Barnes Akathisia Scale - Presence of symptoms	33.8	37.7
† Barnes Akathisia Scale - Symptom severity score*	2.3 (1.37)	2.6 (1.57)
† Abnormal Involuntary Movement scale - Presence of symptoms	26.4	28.6
† Abnormal Involuntary Movement scale - Symptom severity score*	2.7 (2.18)	2.7 (2.19)

^*Mean (SD) of movement disorder symptoms calculated only among those individuals who reported presence of symptoms.

^†As noted in Section 2.3, TD is diagnosed over a long period of observation. Movement disorder symptoms recorded at only one clinical visit would not likely lead to a diagnoses of TD. For these reasons some individuals present some movement disorder symptoms at baseline, even after excluding those CATIE participants with an official TD diagnoses.

Table 3 summarizes the model for the probability of continued observation, i.e. of not being censored for any reason, used to construct the censoring weights, averaged over 25 imputations. The standard errors are corrected for the correlation between individuals used to estimate the censorship model and for the multiple imputations. Variables associated with censorship are baseline and time-varying PANSS score, baseline and previous months treatment, the clinical setting from which the patient was recruited (site type), the clinical global impression of illness severity as judge by the clinician, drug use as judge by the clinician, the presence of involuntary movement as measured by the Simpson-Angus EPS Scale, the presence of involuntary movement as measured by the Abnormal Involuntary Movement scale, adherence, and the month of observation, where we define association as a 90% confidence interval that does not contain zero.

Table 3.

Summary of the model for the probability of being censored. Estimates are averaged over 25 imputations and standard errors are corrected for the correlation between individuals in the censorship model and for the multiple imputations. Reference categories for categorical variables are given in parentheses. Also included in the model was a spline on time in months.

Covariates	Avg MI Est.	Std. Error
Race (refer.: Black alone)
White alone	−0.06	0.12
Neither white nor black alone	−0.25	0.24
Marital status - married	0.18	0.16
Patient education (refer.:College Grad)
Community college or technical school degree	−0.21	0.25
Some college, did not graduate	−0.08	0.21
GED/High school diploma	−0.04	0.22
Did not complete high school	−0.16	0.21
Employment Status (refer.: Did not work)
Full Time	0.17	0.20
Part Time	−0.12	0.22
Site type (refer.: Combination)
Private Practice	0.21	0.18
State Mental Health	0.50	0.15
University Clinic	0.21	0.14
VA	0.03	0.21
Hospitalized in 3 mos. prior to enrollment in CATIE	0.23	0.12
Treatment upon CATIE entry (refer.: Newly treated)
Same medication	−0.22	0.20
Switched medication	−0.05	0.12
Years on prescription medication prior to CATIE	−0.002	0.006
Baseline Antipsychotic - Atypical	−1.10	0.22
Baseline PANSS (total score)	−0.009	0.006
Threshold	0.003	0.001
Time varying covariates
Previous Month’s treatment - Atypical	0.34	0.235
PANSS (total score)	0.017	0.007
Mental health short form score	−0.001	0.011
Physical health short form score	−0.003	0.014
BMI	0.018	0.045
Quality of life (total score)	−0.007	0.129
Calgary depression score	−0.006	0.020
Clinical Global Impression) (refer.: Minimally ill)
Mildly ill	0.0360	0.238
Moderately ill	0.499	0.262
Markedly ill	0.785	0.300
Severely or very severely ill	1.058	0.398
Illegal drug use (clinician reported)) (refer.: No use)
Use without impairment	−0.06	0.11
Abuse	−0.33	0.19
Dependence	−0.42	0.42
Alcohol use (clinician reported) (refer.: No use)
Use without impairment	−0.096	0.235
Abuse	−0.097	0.357
Dependence	−0.432	0.632
Simpson-Angus EPS Scale - Presence of symptoms	−0.309	0.184
Simpson-Angus EPS Scale - Symptom severity score	−0.288	0.317
Barnes Akathisia Scale - Presence of symptoms	−0.039	0.223
Barnes Akathisia Scale - Symptom severity score	0.014	0.072
Abnormal Involuntary Movement scale - Presence of symptoms	−0.309	0.184
Abnormal Involuntary Movement scale - Symptom severity score	0.042	0.052
Adherence	−0.013	0.003

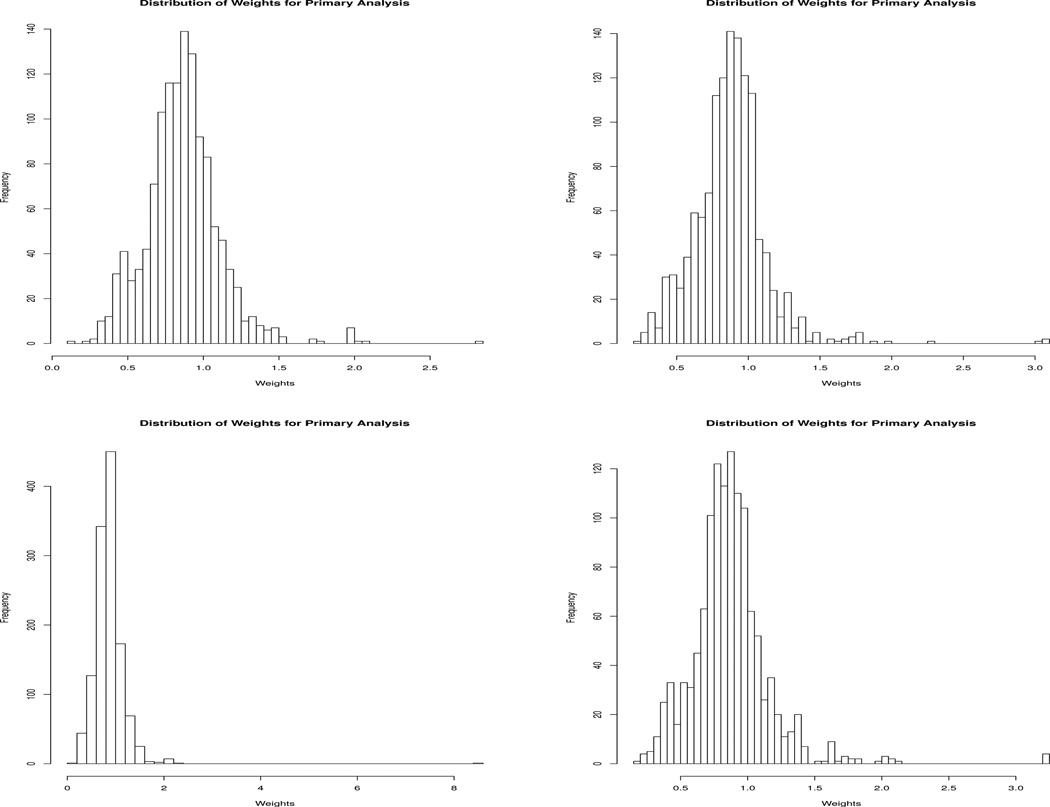
Table 4 presents the number of uncensored individuals who contribute to the MSM, averaged over the 25 imputations on the original data. We include the number of individuals who were eligible to follow each of the regimes at baseline, the number of replicates who were not artificially censored for going off their assigned regime, and the number of replicates who were not censored for any reason in the analysis. Note, that the counts listed here are of the replicates in the augmented data set; thus, many individuals contribute information to several different dynamic treatment regimes. Histograms for the weights used in fitting the dynamic MSM as defined in Eq. (3) for four randomly selected imputations are shown in Figure 1. The minimum weight used for fitting the dynamic MSM over all imputations on the original data was 0.1 and the maximum weight was 15.47 (before truncation), with the 95^th-percentile of all weights being 1.30 (99^th-percentile was 1.78). The distribution of weights is highly concentrated in a small range, indicating that our estimates are unlikely to have been influenced by highly variable weights.

Table 4.

Average number of individuals in the augmented data set who follow the static regime, AA, always treat with an atypical antipsychotic and the each of the perphenazine and atypical regimes, PA(θ), for the entire 12 months. Recall, the regime PA(30) corresponds to a static regime of always treat with perphenazine. Note all numbers in this table are averaged over the 25 imputations used to overcome missing data in the original, non bootstrapped data set, where missing data arose from both item missingness and study attrition. Additionally, we present each data summary by baseline treatment assignment, perphenazine or an atypical, as well as the total number. The first three columns correspond to the individuals who can contribute information for each regime, i.e. the number of replicates who start following each regime; this includes individuals who may be artificially censored for subsequent assignment to clozapine, ziprasidone or for entering into the unrandomized, unblinded phase of CATIE. The second three columns are the number of replicates who were not censored for going off their assigned treatment regime; these individuals could have been censored for subsequent assignment to clozapine, ziprasidone or for entering into the unrandomized, unblinded phase of CATIE. The last three columns are the number of replicates included in the final analysis, this excludes all individuals artificially censored for no longer following their assigned treatment regime, as well as all replicated who were censored because their corresponding individuals were subsequently assigned to clozapine, ziprasidone or entered into the unrandomized, unblinded phase of CATIE.

Treatment regime	N who started on each regime			N who were not artificially censored			N included in final analysis
	Baseline Trt		Total	Baseline Trt		Total	Baseline Trt		Total
	Perp	Atypical	All	Perp	Atypical	All	Perp	Atypical	All
AA	NA	815.0	815.0	NA	815.0	815.0	NA	380.4	380.4
PA(θ = 30)	261.0	NA	261.0	81.0	NA	81.0	81.0	NA	81.0
PA(θ = 35)	259.0	3.0	262.0	76.5	3.0	79.5	73.5	1.0	74.5
PA(θ = 40)	255.0	8.0	263.0	79.3	8.0	87.3	71.1	5.0	76.2
PA(θ = 45)	247.9	24.2	272.1	86.6	24.2	90.8	61.9	14.6	76.5
PA(θ = 50)	240.9	46.4	287.3	94.6	46.4	101.0	47.2	27.6	74.9
PA(θ = 55)	224.8	83.8	308.6	123.6	83.8	207.4	38.8	49.2	88.1
PA(θ = 60)	207.8	132.4	340.1	163.2	132.4	295.5	30.1	72.3	102.4
PA(θ = 65)	183.6	208.0	391.7	234.8	208.0	442.8	25.4	105.4	130.7
PA(θ = 70)	156.6	290.5	447.1	311.3	290.5	601.8	19.4	145.5	164.9

Fig. 1.

Histogram of the complete case weights for the dynamic MSM for four randomly selected imputations of the original (non-bootstrapped) CATIE data set.

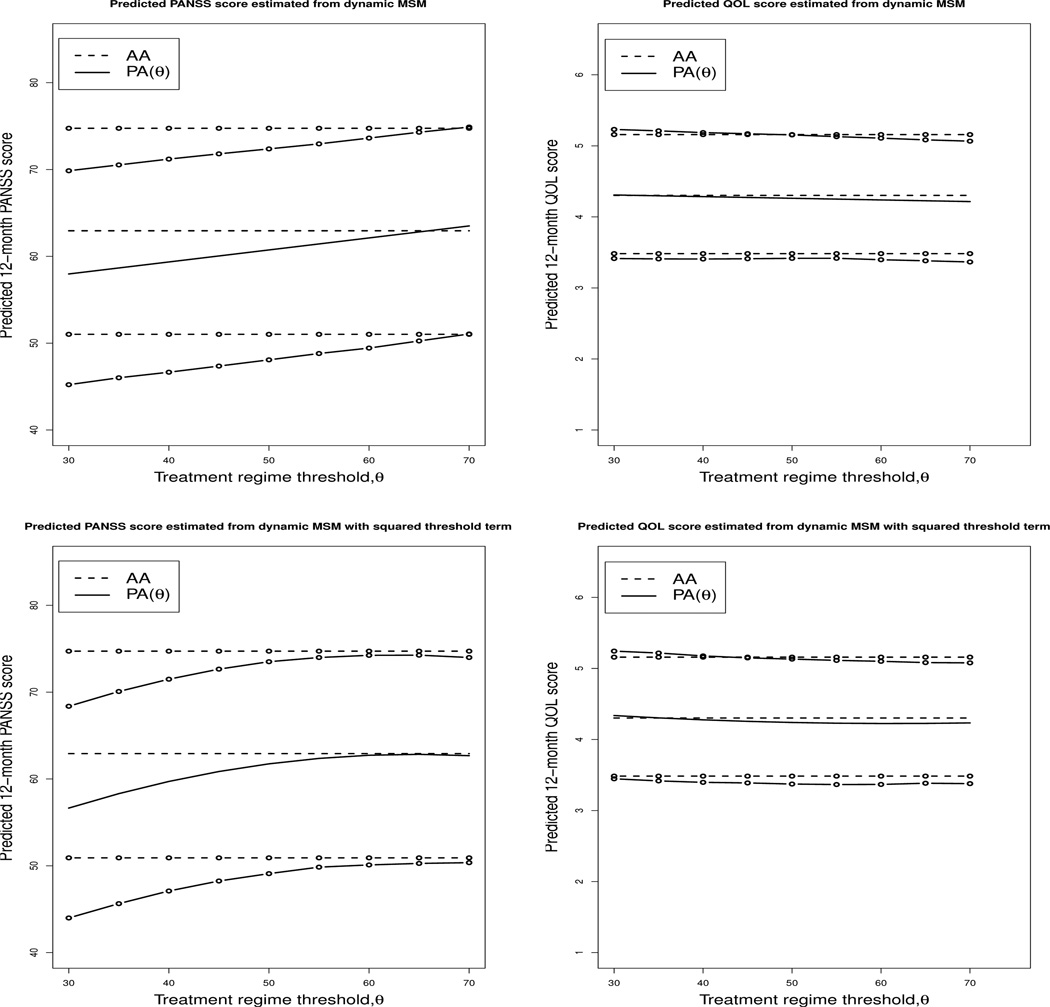
Table 5 presents the results of the marginal structural model analysis comparing the treatment regimes including a linear threshold term. Table 6 presents the results of the same analysis allowing for a squared threshold term in the outcome mean model. In each table we present two estimates for the coefficients: first, the average over 25 imputations on the original data and second, the mean of the bootstrap estimates constructed as described in Section 3.5. We also include the upper and lower bounds for the 95% bootstrap confidence intervals. Figure 2 presents the results of the PANSS and QOL models graphically and contains a plot of the fitted 12-month PANSS and QOL scores against the PANSS thresholds investigated in this analysis. The mean estimates in the tables as well as the predicted mean 12-month PANSS (or QOL) scores depicted in Figure 2 represent an individual who is Caucasian and unmarried, who graduated from college, had not been hospitalized in the 3 months prior to CATIE, was not employed at entry into the CATIE study, had spent 13 years on prescription anti-psychotic medications prior to CATIE, was recruited from a university clinic, had an average baseline PANSS score (75.58), was classified as moderately ill by the clinician global impression of illness severity index, had no drug or alcohol use as judge by the clinician, had no movement disorder symptoms at baseline as measure by any of the three movement disorder scales, and had average baseline values of BMI (29.8), Calgary Depression score (4.7), QOL score (2.8), and mental and physical function as measured by the SF-12.

Table 5.

Estimates of the dynamic treatment regime marginal structural model and corresponding 95% bootstrap confidence intervals, comparing the always atypical (AA) regime with the perphenazine and atypical (PA) regime. The outcome model additionally adjusted for baseline covariates (estimates provided in the Appendix). The parameter PA(θ = 30) corresponds to the expected 12-month outcome for the always treat with perphenazine regime, thus, is equal to β̂₂ + β̂₃30 from Eq. (4).

	12-month PANSS score			12-month QOL score
Covariates	MI est.	Avg Boot est.	95% Boot CI	MI est	Avg Boot est.	95% Boot CI
AA	71.9	62.9	(51.0, 74.8)	4.7	4.3	(3.5, 5.2)
PA(θ = 30)	66.4	58.0	(45.2, 69.9)	3.6	4.3	(3.4, 5.2)
Threshold, θ	1.6×10−1	1.4×10−1	(7.0×10−2, 2.1×10−1)	−3.6×10−3	−2.3×10−3	(−7.0, 3.0)×10−3

Table 6.

Estimates of the dynamic treatment regime marginal structural model and corresponding 95% bootstrap confidence intervals allowing for a squared threshold term, comparing the always atypical (AA) regime with the perphenazine and atypical (PA) regime. The outcome model additionally adjusted for baseline covariates (estimates provided in the Appendix). The parameter PA(θ = 30) corresponds to the expected 12-month outcome for the always treat with perphenazine regime, thus, is equal to β̂₂ + β̂₃30 from Eq. (4).

	12-month PANSS score			12-month QOL score
Covariates	MI est.	Avg Boot est.	95% Boot CI	MI est	Avg Boot est.	95% Boot CI
AA	62.9	62.9	(50.9, 74.7)	4.3	4.2	(3.5, 5.2)
PA(θ = 30)	60.8	61.3	(58.2, 73.0)	4.2	4.2	(3.3, 5.2)
Threshold, θ	7.7×10−1	6.7×10−1	(3.3×10−1, 1.02)	−2.5×10−2	−1.4×10−2	(−4.0, 1.0)×10−2
Threshold2, θ2	−6.0×10−3	−5.2×10−3	(−8.6, −2.0)×10−3	−2.0×10−4	1.0×10−4	(−1.4, 3.0)×10−4

Fig. 2.

Predicted 12-month PANSS and QOL scores from dynamic MSM for the two regimes AA: always treat with an atypical and (2) PA(θ): the perphenazine and atypical regime. In the perphenazine and atypical regime, individuals with a baseline PANSS score greater than or equal to the threshold θ start with perphenazine and switch to an atypical medication when their PANSS score drops below the threshold. Individuals with a baseline PANSS score less than the threshold θ start on an atypical and continue on an atypical medication for the entire 12 months of follow-up considered in this study. The horizontal axis indicated the threshold values for the PA(θ) regime. Recall, as discussed in Section 2.2, the minimum possible PANSS score is 30; thus, PA(θ = 30) corresponds to the regime always treat with perphenazine. The plots in the top row present the expected mean for 12-month PANSS and QOL score, including a linear threshold term in the outcome mean model; the plots in the bottom row graphically depict the results when a square threshold term is included in the mean outcome model. The upper and lower bounds of the 95% confidence interval are indicated with ◦ overlaid on the appropriate lines.

Several sensitivity analyses were conducted to assess the robustness of the findings to the handling of the missing data and modeling choices. We performed two sensitivity analyses that estimate censorship weights with separate models. Additionally, rather than using multiple imputation to account for drop-out in the study, we examined the impact of censoring upon attrition and correcting for this via inverse probability weighting. We considered four approaches to modeling the censoring weights:

1. Use multiple imputation to overcome item missingness as well as missingness due to study attrition. Construct censorship weights by multiplying weights estimated from two separate censorship models; the first for off-study censorship and the second for artificial censoring for the dynamic treatment regimes analysis.

2. Use multiple imputation to overcome item missingness as well as missingness due to study attrition. Construct censorship weights by multiplying weights estimated from four separate censorship models for each type of censorship (i)–(iv), listed in Section 3.2.2.

3. Use multiple imputation to overcome item missingness and inverse probability weighting to overcome missing data due to study attrition. Estimate one censorship model for censorship for any reason, including any type of off-study censorship, artificial censorship or censorship due to study attrition.

4. Use multiple imputation to overcome item missingness and inverse probability weighting to overcome missing data due to study attrition. Estimate separate models censoring due to (i) attrition, (ii) randomization to ziprasidone, (iii) randomization to clozapine, (iv) entry to the unblinded, non-randomized phase of CATIE, as well as (v) the artificial censoring for the dynamic treatment regimes analysis. That is, five different models are fit.

Before mentioning the results of the sensitivity analysis, we note here that there was some evidence that the positivity assumption did not hold in many of the sensitivity analysis that used separate models to model each of the possible reasons for censorship with separate models (i.e. analyses (c) and (d)). Remarkable consistency in the estimates was observed: the four different modeling approaches yielded bootstrap estimates of the parameter associated with θ ranging from 0.14 to 0.16, which we compare with an estimate of 0.14 in Table 5 when using PANSS as the outcome of interest. Taking QOL to be the outcome of interest, all approaches to modeling censorship and overcoming missing data returned estimates of −0.03 for the coefficient of θ, compared to −0.002 in Table 5.

We now consider the results of the analyses that included a squared threshold term in outcome mean model. In the analysis that used PANSS as the outcome, the original analysis that used multiple imputation to account for drop-out and included one model to estimate the weights for continued observation estimated θ at 0.67, while the two IPW approaches gave estimates of 0.76. Using a greater number of models to estimate the different types of censorship separately yielded estimates of the parameter associated with θ of 0.74. All five approaches returned estimates of the coefficient of the squared term of −0.01. The addition of the squared term had virtually no impact on the coefficient for the main effect of θ in the QOL analysis in any of the models; as above, all approaches found similar estimates of the coefficient of the squared threshold term to have a magnitude of less than 0.001. We refer the interested reader to the web appendix for full results of the sensitivity analyses.

5. Discussion and Conclusions

The results presented in Table 5 and Table 6 suggest that there is no significant difference between the dynamic treatment regimes examined here on the 12-month QOL score. These results are consistent with other finding as the symptoms measured by the QOL score are often resistant to treatment (Heinrichs et al., 1984). The model for the 12-month PANSS score suggests that the treatment regimes ‘always treat with perphenazine’ and ‘always treat with an atypical’ are both good treatment strategies in order to reduce 12-month symptoms, as once again there is not significant difference between the predicted mean of these two regimes. As the threshold used for switching from perphenazine to an atypical is increased, meaning that more people will switch from their originally assigned perphenazine to an atypical antipsychotic, 12-month PANSS score increases. The statistically significant threshold, θ, indicates that there is merit to tailoring within the PA(θ) regime, and suggests that for most smaller values of θ, reduced PANSS scores are observed at 12 months if initial therapy with perphenazine is continued rather than changing therapy depending on θ. Patients and their clinicians must weigh the risks associated with developing TD due to prolonged perphenazine exposure with its efficacy in reducing symptoms.

The CATIE study was designed as a practical clinical trial with few exclusion criteria; thus, the CATIE population was selected to be very similar in composition to the population of all schizophrenia patients (Stroup et al., 2003). The results we present in this paper are likely highly generalizable to other samples for the same choice of outcomes of interest. For this analysis we took the PANSS and QOL scores measured at month 12 as the primary outcomes of interest. These outcomes were selected as symptom reduction is often a primary outcome of interest in trials of schizophrenic patients. Measuring outcomes at month 12 allows sufficient time for the medications to take effect and for the possibility of medication failure to occur. It should be noted that both the PANSS and QOL scores of a particular individual can naturally fluctuate over time regardless of treatment. Taking a snap shot in time of a symptom measurement as the outcome of interest may not adequately describe the complex relationship between treatments and their effects on schizophrenia symptoms.

The analysis presented in this paper relies on the validity of the assumptions outlined in Section 3.4. We note that while the assumption of no unmeasured confounders is an untestable assumption, the variable set collected during the CATIE study and used in this analysis was very extensive. In addition, the assumption that the censorship models used in the denominator of the weights are correctly specified is important for consistent estimates. In order to increase the possibility of correctly fitting the probability of continued observation we used a very rich model, as seen in Table 3.

Marginal structural models are straight-forward to implement and have become a common analytic tool for longitudinal data analysis among statisticians and epidemiologists. Thus, due to the familiarity of MSMs, the dynamic regime MSM is an appealing approach for estimating dynamic treatment regimes. A variety of different analytical methods are available for constructing dynamic treatment regimes, as mentioned in Section 1. For example, Q-learning is gaining ground as one of the top choices for estimating dynamic treatment regimes for continuous outcomes, as it can be implemented in its most basic form using standard software packages. Q-learning has the additional benefit of not requiring any data-augmentation as is required for dynamic regime MSMs. Q-learning is closely linked to – and in some cases algebraically equivalent to – G-estimation and iterative minimization of regrets (Moodie et al., 2007; Chakraborty et al., 2010). However, proposed improvements to the basic Q-learning algorithm (Chakraborty et al., 2010) require additional programming and the basic framework is likely less familiar to statisticians not actively working in the area of dynamic treatment regimes. To our knowledge, there exists no literature which compares MSM estimation of dynamic regimes with Q-learning.

The analysis undertaken in this paper represents the first comparison of dynamic treatment regimes of antipsychotic therapies in the CATIE Schizophrenia Study using marginal structural models and inverse probability weighting. In addition to presenting a novel analysis, we have detailed a general framework for the implementation of methodology that is valid for both randomized and observational data, including the data augmentation and estimation procedure as well as valid methods of handling missing data and confidence interval construction.