Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Nov 1.
Published in final edited form as: Biomech Model Mechanobiol. 2012 Jul 3;11(8):1219–1225. doi: 10.1007/s10237-012-0413-8

Cardiomyocytes from late embryos and neonates do optimal work and striate best on substrates with tissue-level elasticity: metrics and mathematics

Stephanie F Majkut 1,✉, Dennis E Discher 2
PMCID: PMC3475743  NIHMSID: NIHMS390582  PMID: 22752667

Abstract

In this review, we discuss recent studies on the mechanosensitive morphology and function of cardiomyocytes derived from embryos and neonates. For early cardiomyocytes cultured on substrates of various stiffnesses, contractile function as measured by force production, work output and calcium handling is optimized when the culture substrate stiffness mimics that of the tissue from which the cells were obtained. This optimal contractile function corresponds to changes in sarcomeric protein conformation and organization that promote contractile ability. In light of current models for myofibillogenesis, a recent mathematical model of striation and alignment on elastic substrates helps to illuminate how substrate stiffness modulates early myofibril formation and organization. During embryonic heart formation and maturation, cardiac tissue mechanics change dynamically. Experiments and models highlighted here have important implications for understanding cardiomyocyte differentiation and function in development and perhaps in regeneration processes.

Keywords: Cardiomyocyte, Mechanosensitivity, Substrate stiffness, Myofibrillogenesis, Striation

1 Introduction

The rhythmic beating of cultured cardiomyocytes, like the rhythmic beating of the heart, provides a clear and simple signature of the central function of these cells. Here, we review recent single-cell experiments and a mathematical model that have helped illuminate prominent effects of matrix elasticity on the function and structure of embryonic and neonatal cardiomyocytes. The elasticity of culture substrates has been shown by several groups to impact beating forces and beating velocities as well as the calcium dynamics of isolated heart cells. The effects extend, after many hours and thousands of beating cycles, to the expression and organization of the striated assembly of contractile proteins, even in dense co-cultures with cardiac fibroblasts. This protein assembly occurs dynamically over minutes, and a recent mathematical model for alignment of striations not only exhibits similar dynamics but also a dependence on matrix elasticity. The measurements and modeling have significant implications for understanding differentiation during early heart development and are particularly important to factor into the many efforts to generate mature cardiomyocytes from stem cells.

2 Optimal elasticity for contraction and calcium excitation

Is the heart a pump or an excitatory tissue? It is both and more of course, but the fundamental function of the adult heart is to contract its internal volume in order to pump blood. Moreover, the only way that a solid-walled tissue such as the heart can contract in volume is if the wall of the heart is elastically deformable. What has been less clear is whether the elasticity of the heart wall impacts the function of beating cardiomyocytes at the single-cell level. The issue is both important and timely because there are many groups that aim to generate—from embryonic stem cells, induced pluripotent stem cells, and cardiac stem cells, among others (Sachinidis et al. 2003; Zwi et al. 2009; Segers and Lee 2008)—cardiomyocytes that will repair adult hearts after a heart attack or other injury. Ultimately, heart is a muscle that does repetitive work on a load, and tissue elasticity Etissue at the scale of a cell is a significant part of that load in contributing to remodeling at a basic molecular level.

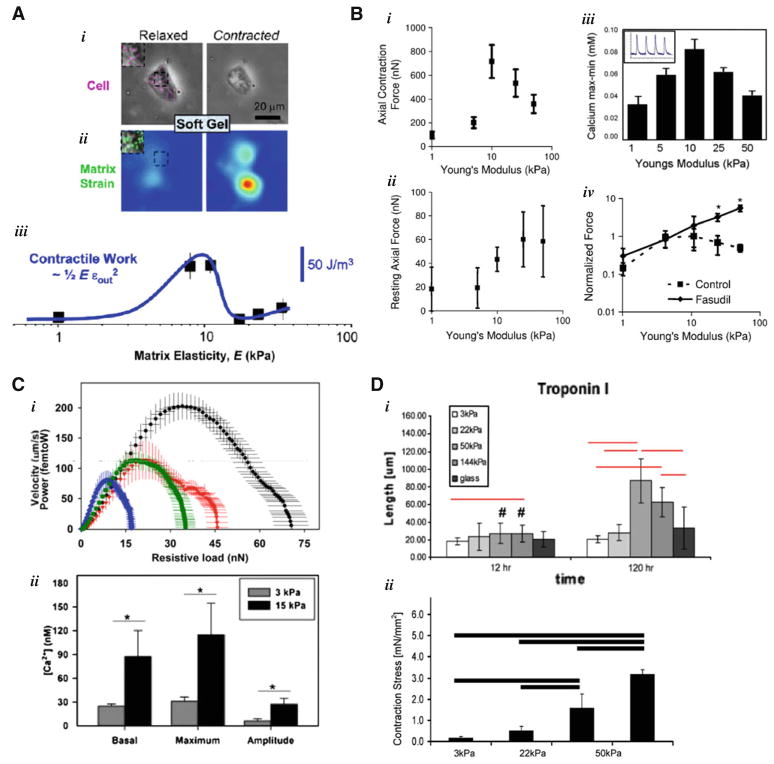
Several recent studies have sought to physically quantify in culture the effects of matrix elasticity Em on late embryonic and neonatal cardiomyocytes. Engler et al. (2008) first made measurements of tissue elasticity Em with atomic force microscopy (AFM) of chick heart at embryonic days 4, 7, 10 (E4,7,10) and then isolated cardiomyocytes from E7 embryos and characterized the morphological and functional effects of substrate stiffness on cells. Collagen-I-coated polyacrylamide gels provide a tunable matrix to which these embryonic cardiomyocytes attach firmly and beat spontaneously (Fig. 1a). Beating of cardiomyocytes, which, as in the human heart, occurs at approximately 1 Hz, applies periodic strains to the matrix that can be estimated from the displacement of beads embedded near the gel surface. The cells thus do an amount of work on the substrates that can be estimated by multiplying the square of the mean matrix strain under the cell, εout, by matrix elasticity, Em. The estimated strains were relatively constant up to about the mean elasticity for heart of ~10 kPa as measured by AFM, and then the strains decrease at higher Em. The latter decrease reflects the fact that there must be some rigidity beyond which the cells simply cannot contract; it turns out that the limiting rigidity is close to the physiological tissue stiffness of ~10 kPa. Work done on the substrate goes as Emεout2 multiplied by a prefactor with units of volume that depends on the geometry of the system (Friedrich and Safran 2012) and can thus be neglected. Engler et al. (2008) estimate this work as 1/2 1/2Emεout2, which exhibits an optimum. Below about 10 kPa, the cells do little work on soft matrix (low Em ), and above about 10 kPa, the cells cannot strain the stiff matrix (low εout). As pointed out, rigid matrix also arises in scarring after a myocardial infarction in adults, which is well known to impede contractile function of the heart. Regardless, the optimal substrate stiffness aligns remarkably well with the micro-elasticity measurements for E7 myocardium.

Fig. 1.

Fig. 1

Open in a new tab

Isolated cardiomyocytes plated on gels of various stiffnesses. a Engler et al. (2008) characterized the morphological and functional effects of substrate stiffness on embryonic cardiomyocytes isolated from E7 chick embryos cultured on collagen-I-coated polyacrylamide (PA) gels. They found that the cells put out the most work on substrates of ~10 kPa. This optimal substrate stiffness matches that of E7 myocardium as they measured by AFM. b Jacot et al. (2008) cultured at NRVM on PA gels of 1, 10, and 50 kPa. They found that 10 kPa optimized NRVM function measured by contractile force-generation and calcium activity (Jacot et al. 2010). Furthermore, inhibition of ROCK and RhoA pathways eliminates the decreased force production of NRVM on stiff gels. c Rodriguez et al. (2011) cultured NRVM on fibronectin-coated microposts with an narrow range of effective moduli ranging from 3 to 20 kPa and found that twitch force, work, and power increased with substrate stiffness. In addition, calcium activity increased in NRVM on stiffer substrates. d Bhana et al. (2009) co-cultured both NRVM and fibroblasts isolated from the same tissue on PA gels for 5 days and monitored not just NRVM morphology and function, but the relative population changes in fibroblasts and cardiomyocytes. They found that cardiomyocyte function and population relative to fibroblasts were optimal at substrate stiffness of 22–50 kPa relative to soft (3 kPa) and stiff (144 kPa)

Using a similar system of gel substrates, Jacot et al. (2008) cultured neonatal rat ventricular myocytes (NRVM) and made careful measurements of both the rhythmic forces in beating as well as the much smaller ‘resting’ forces that are sustainably applied to a substrate due to a basal muscle tone in the cardiomyocytes (Fig. 1b). NRVM do not beat spontaneously and need to be electro-stimulated, whereas the embryonic cardiomyocytes studied by Engler et al. (2008) beat spontaneously. Importantly, calcium spike dynamics measured by Jacot et al. (2008) showed that 10 kPa matrix maximized both contractile force and the amplitude of calcium dynamics. Excitation–contraction coupling (ECC) is a classic phenomenon in muscle physiology (Bers 2001), and these results are consistent with ECC, but highlight the key role of matrix elasticity as a load on cardiomyocytes. The results are clear for individual cells with no confounding impact of cell-to-cell electrical communication, which suggests that one needs to consider Excitation–contraction–Matrix coupling (ECMC) in order to understand heart development and pathophysiology.

Evidence in both studies above showed that the main protein motor in cardiomyocyte contraction, cardiac myosin, maintained a relatively constant level of expression. However, Jacot et al. (2008) used a pharmacological inhibitor of the nonmuscle myosin pathway, namely a drug that blocks Rho-associated kinases (ROCKs), and the results showed that this inhibitor suppresses the decrease in force exerted by NRVM on stiff gels (Fig. 1b). Such findings could lend insight into how and why the same drug protects against heart injury in animal models (Cadete et al. 2010).

Co-cultures of NRVM and matrix-secreting fibroblasts derived from the same hearts were grown on PA gels for 5 days by Bhana et al. (2009), who reported that—in their dense culture systems—cardiomyocyte function and cardiomyocyte numbers relative to fibroblasts appeared optimal at substrate stiffness in the range of Em = 22–50 kPa (Fig. 1d). The higher optimum in substrate stiffness is thought to match the mechanics of adult rat cardiac tissue, which the same group measured by a pipette aspiration method. It should be noted that cardiomyocytes beat synchronously when in direct contact with each other. Synchronously beating cardiomyocyte aggregates produce more force than individual cells (Liu et al. 2012), which may explain why these cells functioned so well on somewhat stiffer substrates than in the other studies and the neonatal tissue from which they were derived.

Bajaj et al. (2010) looked at similar dense co-cultures of E8 chick-derived cardiomyocytes and fibroblasts on PA gels of 1, 18, and 50 kPa and on tissue culture plates for 1–5 days. They found that the cells initially beat with frequencies modulated by substrate stiffness, with the fastest beating on the 18 kPa. However, after 5 days, as the cells proliferated and came into contact with each other, the beat frequencies became more uniform within each culture and across culture conditions, and the fastest beating occurred in the 50 kPa gel cultures. This is likely due to the cells in contact with each other beating in synchrony. Immunofluorescent imaging of focal adhesion (FA) formation and growth in the different culture conditions revealed increased FA area and number on stiff substrates over time and decreased FA area and number on the softest gels over time. Interestingly, this decrease in FA number and size corresponds to a less organized sarcomeric cytoskeleton on soft substrates relative to the well-developed and aligned myofibrils observed on stiff substrates.

Using a very different type of substrate, Rodriguez et al. (2011) cultured NRVM on fibronectin-coated elastic micropilli arrays with effective shear moduli estimated to range from 3 to 20 kPa. The twitch force, work, and power generated by single cells once again increased with substrate stiffness (Fig. 1c). In addition, calcium activity increased in the NRVM on stiffer substrates. The authors also made direct comparisons of forces produced by neonatal myofibrils to adult myofibrils, showing that neonatal myofibrils generate only about one-third the power of adult myofibrils. The results underscore the importance of developmental stage and age of the cells studied.

In addition to functional characterizations of the effects of substrate mechanics on force and work output of cardiomyocytes, several of the studies above also attempted to uncover some of the molecular changes that underlie measurable functional changes. Engler et al. (2008) imaged alpha-actinin and noted that 1 day cultures on ~10 kPa matrix exhibited a maximum fraction of cells with sarcomeric striations. They also applied a novel method of labeling proteins within cells to expose differences in molecular structure or activity (cysteine shotgun mass spectrometry; Johnson et al. 2007), and the analysis indeed identified substrate stiffness–dependent differences in myosin and other cytoskeletal proteins as well as one metabolic protein, the muscle-specific pyruvate kinase M1. The latter is intriguing because the studies of ROCK inhibition of the heart cited above also identified drug-dependent difference in several metabolic proteins (Cadete et al. 2010). On the other hand, such results are very sensible because differential force-generation by muscle places differential demands on metabolism. Moreover, in the drug studies of Jacot et al. (2008), imaging of alpha-actinin in untreated cells revealed a tendency for reorganization of striated sarcomeres into stress fibers, whereas drug treatment blocked this reorganization. As mentioned above, Bajaj et al. (2010) noted that disorganized and unaligned myofibrils in cardiomyocytes grown on soft substrates corresponds to decreased FA area and number relative to the those of cells grown on stiffer substrates, which had well-aligned myofibrils. Rodriguez et al. (2011) quantified the striations of cardiomyocytes on their microposts through measurements of sarcomere spacing and z-disk width. They reported that sarcomere spacing, a sign of myofibril maturity and an indicator of likely force output, fell within accepted values for mature myofibrils on all substrates, and increased with increasing stiffness. Z-disk width, which indicates increased coupling of sarcomeres within a myofibril, also increased with E. Increased sarcomere spacing is associated with increased force production because it allows for a greater number of cross-bridges to form during contraction. Increased z-disk width, in turn, maintains registry of sarcomeres within a myofibril, minimizing myofibril buckling during contraction and maximizing contraction velocity.

3 Matrix elasticity and sarcomere organization

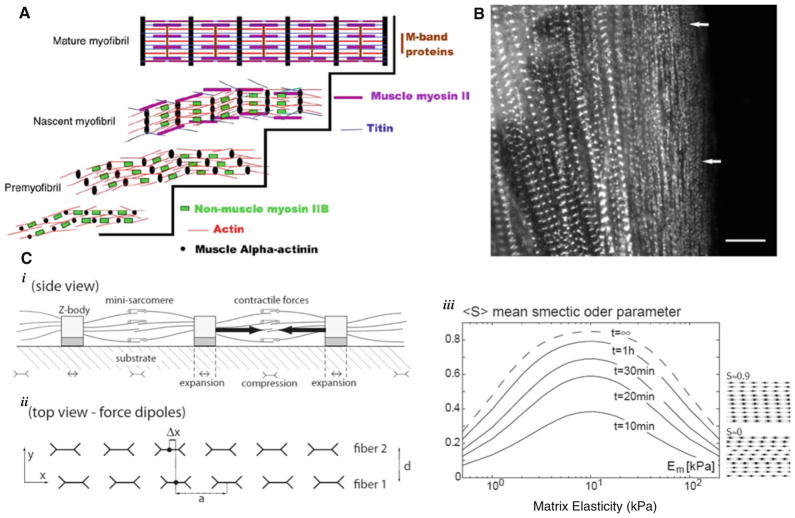
If organizational and structural changes in cytoskeletal structure underlie the functional, mechanical outputs of the cardiomyocytes, how might substrate mechanics modulate this organization? Cardiomyocytes sense and respond to intra- and extracellular mechanical stimuli through a variety of molecular mechanisms; integrins in costameres and focal adhesions transmit loads from the ECM to the cytoskeleton, cadherins connect myofibrils between cells at adherens junctions, and sarcomere-spanning proteins such as titin respond to intracellular stresses (reviewed by McCain and Parker 2011). In considering what types of mechanisms may modulate myofibril organization as observed in the studies above, it is useful to consider how myofibrils form. Sanger et al. (2005) proposed at least one pathway by which myofibillogenesis occurs in striated muscle cells, and the process begins at the cell membrane, adjacent to matrix, with stress-fiber-like periodic premyofibrils. These progressively register with each other and mature into myofibrils through replacement of short filaments of nonmuscle myosin IIB (NMMIIB) by long filaments of muscle myosin II plus incorporation of other sarcomeric proteins (Fig. 2a). Premyofibril formation, registration, and maturation into mature myofibrils have been visualized in live spreading cardiomyocytes in culture (Fig. 2b), in precardiac explants, and also in whole embryonic hearts (Sanger et al. 2010). These studies were performed in a variety of vertebrate organisms; quail, chick, and zebrafish. However, this model is not universally accepted due to possible conflicting evidence from, for example, experiments in which NMMIIB knock-out mice still develop mature myofibrils. Sanger et al. (2010) argue that such evidence does not preclude their model because other NMMII isoforms might be upregulated or otherwise compensate for the loss of NMMIIB. Other mechanisms of myofibrillogenesis have been proposed, such as a self-templating model in which free actin and myosin filaments incorporate into preexisting myofibrils (McKenna et al. 1986; Gregorio and Antin 2000; Sanger et al. 2005). These different mechanisms may occur to different degrees in various circumstances and different species, possibly explaining some of the observations contradicting the Sanger’s premyofibril model. However, it does seem clear the premyofibril pathway to myofibrillogenesis is a prevalent if not a unique pathway.

Fig. 2.

Fig. 2

Open in a new tab

Myofibril formation and registration modulation by substrate stiffness. a Premyofibril model for myofibril formation (Sanger et al. 2005). Striated premyofibrils comprised of alpha-actinin-enriched z-bodies, short actin thin filaments, and nonmuscle myosin IIB filaments mature into mature myofibrils by replacement of nonmuscle myosin II with muscle myosin II and incorporation of other sarcomeric proteins. b Premyofibril formation, registration, and maturation into mature myofibrils have been visualized in live spreading cardiomyocytes, as shown Sanger et al. (2005), in precardiac explants, and in whole embryonic hearts (Sanger et al. 2010). White arrows indicate premoyfibrils deposited near the edge of the spreading cell. c Theoretical model proposed by Friedrich et al. (2011) showing how aligned striated fibers on elastic substrates may come into registry in a substrate stiffness–dependent manner. i Striated fibers apply stresses at the cell–substrate interface that can be modeled as periodic line of force dipoles. ii Adjacent fibers interact through the laterally propagating strain fields they produce. iii These interactions lead fibers to come into registry with each other in a nonmonotonic substrate-elasticity-dependent way. The smectic order S of the resulting arrays of striations is a measure of the level of registration

Since premyofibrils form close to the surface of the cell, this first step of myofibril formation is a likely target of the substrate stiffness modulation that leads to the variation in sarcomeric organization observed in the experiments above. Friedrich et al. (2011) therefore proposed a general physical theory for how striated contractile fibers interactions with an elastic substrate could promote interfiber registry (Fig. 2c). They modeled the force transmitted by a fiber to the substrate as a periodic linear array of force dipoles, and the substrate as an elastic half-space with a matrix elastic modulus, Em, and a Poisson ratio, ν. For two such fibers aligned parallel to each other, the elastic interaction energy between was derived as

Winteraction=Φ(da,ν)ρ12aEmcos(2πΔxa) (1)

Here, a is the sarcomeric periodicity of each fiber, d is the distance between the fibers, and Δx is the phase shift between the two fibers, (Fig. 2c(i)). Φ(da,ν) describes the lateral propagation of the strain field produced by a single fiber. For simplicity, the dipole density was approximated as the first Fourier mode ρ(x)=ρ0+ρ1cos(2πxa), so ρ1 is the amplitude of the dipole density. When ν≈12, as is the case for the polyacrylamide substrates of the experiments discussed previously and da>0.247,Φ(da,12)<0. This indicates that neighboring fibers should be inclined to come into registry such that Δx = 0.

The registration force on one fiber due to this elastic interaction with its neighbor is freg=-∂Winteraction∂Δx. Friedrich et al. (2011) used this relation to model the overdamped sliding of fibers relative to each other, where the net force on the fibers is the sum of the interaction force and a stochastic noise term. They further consider the experimental observations of substrate stiffness strengthening cell-substrate adhesions and active cell contractility. They model these effects as ρ1=ρ1∗EmEm+Em∗. This gives a maximal registration force that is a nonmonotonic function of Em

freg~-ρ12Em~-Em(Em+Em∗)2 (2)

and is modulated by an optimal Em∗. Using this registration force, they simulated the sliding dynamics of an array of n = 10 fibers over a range of Em. To quantify the degree of interfiber registration, they defined the smectic order parameter for the resulting configurations

S=∑i=1n-1cos[2πa(Δxi+1-Δxi)]/(n-1). (3)

The ensemble average of this order parameter, <S>, as a function of matrix elasticity is plotted for various times in Fig. 2c(iii). The resulting curves are fit with the same functional form as the registration force Eq. 2 and exhibit an optimum in matrix elasticity at ~10 kPa. Therefore, elastic coupling between adjacent myofibrils can give rise to organizational trends much like those observed in the studies discussed above. Additionally, organizational dynamics predicted by this model occur on timescales of minutes to hours, which is thousands of cycles of rhythmic beating of cells.

A strong separation of time-scales seems consistent with the slow re-organization of sarcomeres as a function of Em as reported in the experimental studies above of Engler et al. (2008), Jacot et al. (2008), and Rodriguez et al. (2011). Thus, the clearest clock in the cell, its beating frequency, is not strictly coupled to the formation or disruption of the central structure–function relationship in muscle, namely the contractile sarcomere. In materials science, processes such as work-hardening, which improves strength, and cyclic fatigue or failure, which compromise application, seem related to the force-dependent striation processes in muscle. The relation suggests the importance of dislocations, defects, and cracks in heart development and disease, motivating further quantitative measures and mathematical models.

4 Microenvironment of early cardiomyocytes

It is important to note that in the developmental stages of the cardiomyocytes used in the studies above, the heart is a well-differentiated, 4-chambered organ with a substantial extracellular matrix. Although further growth and stiffening of cardiac tissue with development and aging occurs (Bhana et al. 2010; Lahmers et al. 2004), such mature tissue is already much stiffer at ~10 kPa than the earliest beating heart stages that have approximate elastic moduli of ~0.5–2 kPa (Fila et al. 2010; Young and Engler 2011; Zamir et al. 2003). Early embryonic cardiac tissue is very fragile, heterogeneous, and small. It is also only slightly stiffer than early embryonic tissue, which is typically measured to have Etissue in the range of 0.1–1 kPa (von Dassow and Davidson 2009; Young and Engler 2011; Krieg et al. 2008). Since the heart is the first functional organ to develop in the vertebrate embryo, initial myofibril formation, which shortly precedes the first heart beats, occurs much earlier in development than the stages from which the cells in studies cited here are derived. As a result, the impact of mechanical microenvironment on the earliest cardiomyocytes is less well less defined.

5 Conclusion

Given that cardiac mechanics develop progressively in an embryo, an important set of developmental questions emerges from the findings reviewed here that relatively well-developed cardiomyocytes “beat best” on matrices that mimic the mechanics of the original, mature tissues. A first key question is when do cardiomyocytes in the earliest embryo begin to respond to the micro-elasticity of the tissue? Do defects in striation emerge or are they avoided? Do such processes trigger new gene programs in development to promote (or undermine) robustness in structure-function? The experimental analyses and mathematical modeling summarized briefly here offer new tools to apply to such questions, and they are especially relevant to the current work with stem cells that may one day allow repair of adult heart tissue.

Acknowledgments

NIH T32, NIH R01, NIH P01, and NSF are all gratefully acknowledged.

Contributor Information

Stephanie F. Majkut, Email: sfeldm@sas.upenn.edu, Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104-6396, USA

Dennis E. Discher, Email: discher@seas.upenn.edu, Graduate Group of Physics and Astronomy and Biophysical Engineering Lab, University of Pennsylvania, 129 Towne Bldg., Philadelphia, PA 19104-6315, USA

References

  1. Bajaj P, Tang X, Saif TA, Bashir R. Stiffness of the substrate influences the phenotype of embryonic chicken cardiac myocytes. J Biomed Mater Res Part A. 2010;95(4):1261–1269. doi: 10.1002/jbm.a.32951. [DOI] [PubMed] [Google Scholar]
  2. Bers DM. Excitation-contraction coupling and cardiac contractile force. 2. Kluwer; Dordrecht: 2001. [Google Scholar]
  3. Bhana B, Iyer RK, Chen WLK, Zhao R, Sider KL, Likhitpanichkul M, Simmons CA, Radisic M. Influence of substrate stiffness on the phenotype of heart cells. Biotechnol Bioeng. 2009;105(6):2151–2162. doi: 10.1002/bit.22647. [DOI] [PubMed] [Google Scholar]
  4. Cadete VJJ, Sawicka J, Polewicz D, Doroszko A, Wozniak M, Sawicki G. Effects of the Rho kinase inhibitor Y-27632 on the proteome of hearts with ischemia-reperfusion injury. Proteomics. 2010;10(24):4377–4385. doi: 10.1002/pmic.201000393. [DOI] [PubMed] [Google Scholar]
  5. Engler AJ, Carag-Krieger C, Johnson CP, Raab M, Tang H, Spelcher DW, Sanger JW, Sanger JM, Discher DE. Embryonic cardiomyocytes beat best on a matrix with heart-like elasticity: scar-like rigidity inhibits beating. J Cell Sci. 2008;121:3794–3802. doi: 10.1242/jcs.029678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Fila BA, Bayly PV, Taber LA. Mechanical stress as a regulator of cytoskeletal contractility and nuclear shape in embryo epithelia. Ann Biomed Eng. 2010;39(1):443–454. doi: 10.1007/s10439-010-0171-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Friedrich BM, Safran SA. How cells feel their substrate: spontaneous symmetry breaking of active surface stresses. Soft Matter. 2012;8:3223–3230. [Google Scholar]
  8. Friedrich BM, Buxboim A, Discher DE, Safran SA. Striated actomyosin fibers can reorganize and register in response to elastic interactions with the matrix. Biophys J. 2011;100:2706–2715. doi: 10.1016/j.bpj.2011.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gregorio CC, Antin PB. To the heart of myofibril assembly. Trends Cell Biol. 2000;10(9):355–362. doi: 10.1016/s0962-8924(00)01793-1. [DOI] [PubMed] [Google Scholar]
  10. Jacot JG, McCulloch AD, Omens JH. Substrate stiffness affects the functional maturation of neonatal rat ventricular myocytes. Biophys J. 2008;95:3479–3487. doi: 10.1529/biophysj.107.124545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jacot JG, Kita-Matsuo H, Wei KA, Chen HSV, Omens JH, Mercola M, McCulloch AD. Cardiac myocyte force development during differentiation and maturation. Ann N Y Acad Sci. 2010;1188:121–127. doi: 10.1111/j.1749-6632.2009.05091.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Johnson CP, Tang H, Carag C, Speicher DW, Discher DE. Forced unfolding of proteins within cells. Science. 2007;317(5838):663–666. doi: 10.1126/science.1139857. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Krieg M, Arboleda-Estudillo Y, Puech PH, Kafer J, Graner F, Muller DJ, Heisenberg CP. Tensile forces govern germ-layer organization in zebrafish. Nat Cell Biol. 2008;10:429–436. doi: 10.1038/ncb1705. [DOI] [PubMed] [Google Scholar]
  14. Lahmers S, Wu Y, Call DR, Labeit S, Granzier H. Developmental control of titin isoform expression and passive stiffness in fetal and neonatal myocardium. Circ Res. 2004;94:505–513. doi: 10.1161/01.RES.0000115522.52554.86. [DOI] [PubMed] [Google Scholar]
  15. Liu J, Sun N, Bruce MA, Wu JC, Butte MJ. Atomic force mechanobiology of pluripotent stem cell-derived cardiomyocytes. PLoS One. 2012;7(5):e37559. doi: 10.1371/journal.pone.0037559. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. McCain ML, Parker KK. Mechanotransduction: the role of mechanical stress, myocyte shape, and cytoskeletal architecture on cardiac function. Eur J Physiol. 2011;462:89–104. doi: 10.1007/s00424-011-0951-4. [DOI] [PubMed] [Google Scholar]
  17. McKenna NM, Johnson CS, Wang Y. Formation and alignment of Z lines in living chick myotubes microinjected with rhodamine-labeled alpha-actinin. J Cell Biol. 1986;103(6):2163–2171. doi: 10.1083/jcb.103.6.2163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Rodriguez AH, Han SJ, Regnier M, Sniadecki NJ. Substrate stiffness increases twitch power of neonatal cardiomyocytes in correlation with changes in myofibril structure and intracellular calcium. Biophys J. 2011;101:2455–2464. doi: 10.1016/j.bpj.2011.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sachinidis A, Fleischmann BK, Kolossov E, Wartenberg M, Sauer H, Hescheler J. Cardiac specific differentiation of mouse embryonic stem cells. Cardiovasc Res. 2003;58:278–291. doi: 10.1016/s0008-6363(03)00248-7. [DOI] [PubMed] [Google Scholar]
  20. Sanger JW, Kang S, Siebrands CC, Freeman N, Du A, Wang J, Stout AL, Sanger JM. How to build a myofibril. J Muscle Res Cell Motil. 2005;26:343–354. doi: 10.1007/s10974-005-9016-7. [DOI] [PubMed] [Google Scholar]
  21. Sanger JW, Wang J, Fan Y, White J, Sanger JM. Assembly and dynamics of myofibrils. J Biomed Biotechnol. 2010 doi: 10.1155/2010/858606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Segers VFM, Lee RT. Stem-cell therapy for cardiac disease. Nature. 2008;451:937–942. doi: 10.1038/nature06800. [DOI] [PubMed] [Google Scholar]
  23. von Dassow M, Davidson LA. Natural variation in embryo mechanics: gastrulation in Xenopus laevis is highly robust to variation in tissue stiffness. Dev Dyn. 2009;238(1):2–18. doi: 10.1002/dvdy.21809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Young JL, Engler AJ. Hydrogels with time-dependent material properties enhance cardiomyocyte differentiation in vitro. Biomaterials. 2011;32(4):1002–1009. doi: 10.1016/j.biomaterials.2010.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Zamir EA, Srinivasan V, Perucchio R, Taber LA. Mechanical asymmetry in the embryonic chick heart during looping. Ann Biomech Eng. 2003;31:1327–1336. doi: 10.1114/1.1623487. [DOI] [PubMed] [Google Scholar]
  26. Zwi L, Caspi O, Arbel G, Huber I, Gepstein A, Park IH, Gepstein L. Cardiomyocyte differentiation of human induced pluripotent stem cells. Circulation. 2009;120:1513–1523. doi: 10.1161/CIRCULATIONAHA.109.868885. [DOI] [PubMed] [Google Scholar]

RESOURCES