Using Computational and Mechanical Models to Study Animal Locomotion

Abstract

Recent advances in computational methods have made realistic large-scale simulations of animal locomotion possible. This has resulted in numerous mathematical and computational studies of animal movement through fluids and over substrates with the purpose of better understanding organisms’ performance and improving the design of vehicles moving through air and water and on land. This work has also motivated the development of improved numerical methods and modeling techniques for animal locomotion that is characterized by the interactions of fluids, substrates, and structures. Despite the large body of recent work in this area, the application of mathematical and numerical methods to improve our understanding of organisms in the context of their environment and physiology has remained relatively unexplored. Nature has evolved a wide variety of fascinating mechanisms of locomotion that exploit the properties of complex materials and fluids, but only recently are the mathematical, computational, and robotic tools available to rigorously compare the relative advantages and disadvantages of different methods of locomotion in variable environments. Similarly, advances in computational physiology have only recently allowed investigators to explore how changes at the molecular, cellular, and tissue levels might lead to changes in performance at the organismal level. In this article, we highlight recent examples of how computational, mathematical, and experimental tools can be combined to ultimately answer the questions posed in one of the grand challenges in organismal biology: “Integrating living and physical systems.”

Introduction

The case for mathematics in organismal biology

Prior to the 20th century, the biological sciences were primarily focused on the investigation of the entire organism. At the turn of the century, the application of concepts from physics and chemistry to biology and improvements in experimental methods for observing and probing sub-organismal and sub-cellular phenomena led to causal explanations for many biological phenomena. This explosion of knowledge and the high degree of training required to make use of these new techniques led biological investigation down a reductionist path where researchers studied isolated components or subsystems rather than intact organisms (Schaffner 1969; Benson 1989). This reductionist approach led to rapid advancement in many areas of biophysics and neurobiology, as well as in cellular and molecular biology. One of the primary challenges for biology today lies in bringing these disparate areas of research back together to develop multiscale functional models of whole organisms. Animal locomotion offers a prime opportunity to connect several disparate areas of biology as it is the result of interactions between the peripheral and central nervous systems, muscle physiology, and the properties of the environment. Computational and mechanical models are ideally suited to help reveal these interactions.

To bring such disparate areas together, one must connect small-scale dynamics of physiology, including molecular and cellular activity, with the large-scale behaviors of an animal and of groups of animals (Fig. 1). This means that behaviors such as locomotion are inherently multiscale: Dynamics at the level of cells or even single ion channels may influence the behavior of the whole animal (Grillner 2003), and equivalently, changes in the whole animal’s behavior or in its environment may influence cellular activity.

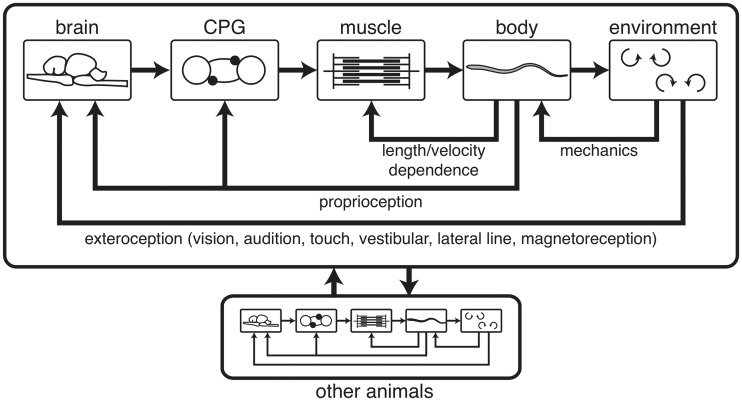
Fig. 1.

A schematic of the nested, multiscale feedback loops present in animal behaviors, such as locomotion. A fish is used as an example, but the schematic holds for most animals. Top: A brain or central ganglion activates and modulates a CPG circuit, which activates muscles that produce force to move the body, which then applies forces to the environment. The environment, however, is mechanically coupled to the body, and applies forces back onto the body. Additionally, the muscles are coupled with the body’s state due to the dependence of force on length and velocity. Finally, both the brain and CPG receive sensory information from the body’s movement (proprioception) and from the environment around it (exteroception). Bottom: Such feedback loops contain another layer of feedback when animals interact with each other.

Figure 1 shows a schematic of the multiscale, nested feedback loops that are present in any locomoting animal, using a fish as an example. In both vertebrates and invertebrates, a brain or head ganglion activates a neural circuit called the central pattern generator (CPG), which is usually distributed through the spinal cord or nerve cord. Once the CPG is activated, it needs no further stimuli to generate a locomotor pattern (Marder and Bucher 2001) that activates the muscles. The muscles produce forces that bend the body, which then interacts with the external environment. The environment may be a fluid, in the case of a fish or a flying insect, or the substrate, in the case of running or crawling animals. Regardless of the type of environment, it produces reaction forces back onto the body (“mechanics” in Fig. 1) that couple with the internal forces to determine the body’s kinematics (Li et al. 2009; Lin and Trimmer 2010; Tytell et al. 2010). Muscle also couples with the body’s kinematics because the force it produces depends upon both its length and shortening velocity (Hill 1938; McMahon 1984). Finally, sensory receptors connect both directly into the CPG and into the brain and influence the ongoing locomotor pattern (Rossignol et al. 2006). Understanding such complex feedback patterns is challenging. Mathematical and physical models provide a way to understand the impact of different components.

Mathematical and physical models allow dissection of the problem

Locomotion can be described as an exchange of momentum between a body and its environment (Dickinson et al. 2000). For example, undulations of a fish’s body can propel the fish forward and the fluid surrounding it backward, on average. The details of the interaction are quite complicated. In particular, the fluid motion around a swimming fish can be very complex, although typical vortical structures have been described for canonical swimming motions (Drucker and Lauder 1999; Triantafyllou et al. 2000; Tytell and Lauder 2004; Dabiri et al. 2005). Mathematical models can provide simplified representations of the flow–body interaction that can be studied more extensively (Lighthill 1970; Wu 1971). The validity of such simplifications can be assessed using asymptotic analyses of the underlying differential equations (Sparenberg 1995).

A synergy exists between modeling, experiments, and simulation for many problems in animal locomotion. Measurements of morphology and motion taken from live animals can be used to set appropriate values of parameters for mathematical models and simulations (e.g., Borazjani et al. 2012). Techniques such as particle image velocimetry can be used to obtain the spatial and temporal information on flow fields generated by organisms (e.g., Drucker and Lauder 1999; Catton et al. 2011; Flammang et al. 2011). This information can then be used to validate simulations of fluid–structure interaction. Once the results of numerical simulations are checked against the real system, the mathematical models can be improved as needed. Based on such a predictive model, numerical simulations can be used to obtain detailed descriptions of phenomena that are difficult to explore experimentally (e.g., Mittal et al. 2006; Borazjani and Sotiropoulos 2010). Numerical simulations may also be used to characterize parameter spaces that extend beyond what is observed in nature (Alben 2008). Mathematical models that combine multiple levels of biological organization may be used to understand how small changes in the physics of tissues can result in large changes in performance at the organismal level (Holmes et al. 2006; Tytell et al. 2010). Study of legged physical models in concert with mathematical models have facilitated progress in understanding the neuromechancial control of terrestrial locomotion (Holmes et al. 2006). The advantage of robotic models is that environmental interaction does not have to be modeled, thereby saving computational cost; in many materials (e.g., granular materials), detailed models at the level of Navier–Stokes equations are unavailable.

Common themes

The unifying theme of the research problems outlined below is that each provides a concrete example of the process of translating biological questions into mathematical models, solving the model’s equations, interpreting the solution, and comparing it with reality through experimentation. All of the examples require the integration of several fields in biology, physics, engineering, or mathematics. For example, mathematical models must be developed that can couple action potentials triggered by noisy pacemakers in jellyfish bells to the generation of tension through appropriate models of muscle and Ca²⁺. Algorithms that connect how organisms use their sensors to detect gradients in the environment can test the rules by which cues guide animals to their desired targets. The nonlinear material properties and geometry of highly deformable insect wings and fish fins must be quantified and accurately modeled to understand how shape and material properties correspond to performance in swimming and flying.

The overview begins with connections between the environment and animal through sensory systems. Specific examples from insects and jellyfish are used to illustrate open questions regarding how environmental stimuli could trigger organisms’ responses. Mathematical models of the nervous system, central pattern generators, and pacemakers are then introduced as tools that can be used to better understand sensory systems. Specific examples from vertebrate and invertebrate locomotion and copepod navigation are discussed.

The next section focuses on neural activation and the resulting movement of an organism through a fluid or over a substrate. The discussion begins with an overview of mathematical models that can be used to describe how neural activation results in muscular contraction and the generation of force. A brief overview of the mathematical models used to describe muscle is given. Specific examples from insect flight are then used to illustrate some of the recent advances and open questions in this area. The forces that result from the contraction of muscle drive the movement of the organism, and mathematical models of fluid–structure and granular–structure interactions are introduced. Examples from fish swimming, insect flight, and sandfish-lizard swimming are used to illustrate several modeling approaches.

Connections are made back to the nervous system by considering the effects of neuromechanical lags of phase in swimming and flying. Specific examples from lamprey and sandfish-lizards are provided. Coupling each of these components requires an understanding of stability and control by the organisms as they navigate through their environments. This motivates a discussion of the identification of closed-loop systems. A specific example of a control algorithm for a yaw turn in flapping insect flight is provided.

Finally, the future directions and challenges for scientific computing, mathematical modeling, experimental biology, and engineering are outlined. This section begins with a discussion on numerical methods for simulating deforming structures in viscous flows. Recent advances made in insect flight through the use of computational fluid dynamics are outlined. When the Reynolds number (Re) is sufficiently high, the flow may be assumed to be inviscid. Techniques for simulating fluid–structure interactions in inviscid flows are discussed with examples taken from fish swimming. When animals move through sand or other substrates, model equations for the environment itself must be developed. Recent methods for simulating sand–structure interaction with applications to the sandfish-lizard are outlined. Challenges in the development of mathematical models for closed-loop sensory-motor interactions are then discussed with examples taken from fish swimming. Finally, the experimental challenges involved with validating mathematical models and providing reasonable parameters are outlined.

Sensory and nervous systems

Sensory feedback

Animals use sensory feedback from proprioceptive sensors, which monitor the current internal state of the animal, and exteroceptive sensors, which gather information from the environment outside the animal (Fig. 1). Both of these broad categories encompass a number of sensory modalities, ranging from the familiar—smell, vision, and taste—to the pressure-sensitive lateral-line systems of fish; electromagnetic field sensing in species including fish, turtles, and birds; and echolocation in bats. From the standpoint of animal locomotion it is more convenient to classify these sensory systems by the information they receive and the processing latency at which they provide it rather than the details of the mechanism used to gather such information. For instance, vision is commonly used in detecting obstacles, predators, or prey at a distance, but requires substantial processing of the information gained from individual photoreceptors before their inputs can be formed into images. Thus, sensing based on vision operates at high latency, potentially leading to locomotor instability in cases in which latencies in sensory feedback exceed the duration of a locomotor cycle.

Potentially in response to these problems, many flying insects, for example, employ two visual systems—a pair of large image-forming compound eyes and a set of ocelli which function as visual horizon detectors, responding to the difference in light intensity between the sky and ground with lower latency than that of the complex compound eyes (e.g., Schuppe and Hengstenberg 1993). Other sensory modes typical of flying animals include use of vision for long-range avoidance of obstacles, inertial sensors such as the halteres of dipteran insects (Pringle 1948), or the vestibular system of birds and bats, and widespread proprioceptive systems such as the wing campaniform sensilla of insects, which likely measure wing deformation during the flapping cycle. See Taylor and Krapp (2007) for an extensive overview of the sensory systems involved in insect flight.

A fundamental question in sensory feedback systems that could be addressed with mathematical modeling would be to test how sensory inputs might be translated into organism’s responses. For example, mathematical modeling could be used to determine how environmental cues regulate the action of the pacemakers and activate central pattern generators. In relatively simple organisms such as jellyfish, models could address how chemical or mechanical cues alter the coordination of the pacemakers, the resulting pulsing kinematics, and the motion of the medusa. Another fundamental question would be to determine how asymmetrical sensory inputs result in asymmetric locomotory responses that move animals towards a stimulus or away from it.

Central pattern generators

In nearly every animal studied to date, rhythmic behaviors are generated by a simple neural circuit, the CPG (Marder and Bucher 2001). Such behaviors include locomotion, which requires rhythmic oscillations of appendages such as the tails of fishes, the limbs of terrestrial animals, and the wings of birds and insects, and also other rhythmic activities such as heartbeat, chewing, scratching, breathing, and possibly even cortical oscillations. In particular, CPGs have been found to be involved in locomotion in every animal studied, including vertebrates and invertebrates that swim (Grillner 1974; Cohen and Wallén 1980; Weeks 1981; Roberts et al. 1998; McLean et al. 2007), walk (Pearson and Rossignol 1991; Kiehn 2006; Borgmann et al. 2009), and fly (Wilson 1961).

The defining characteristic of a CPG is that it can produce a rhythm when artificially isolated (Cohen and Wallén 1980; Marder and Bucher 2001). However, in reality, CPGs receive continual feedback both directly from sensory receptors and from higher processing centers such as a brain or head ganglion (Tytell et al. 2011) (Fig. 1). When isolated preparations are stimulated by sensory stimuli, they can speed up, slow down, or reset the rhythm (Andersson and Grillner 1983; McClellan and Sigvardt 1988; Yu and Friesen 2004).

In a closed-loop situation, when the CPG’s output can alter the sensory inputs, the effects of sensory feedback are hard to predict (Pearson et al. 2006). In particular, the CPG’s frequency when isolated may be quite different from the frequency of the complete coupled system (e.g., Fig. 1). Mathematical models (Williams and DeWeerth 2007; Futakata and Iwasaki 2008) and some experimental data (Hatsopoulos and Warren 1996; Ausborn et al. 2009; Tytell and Cohen 2009) both have suggested that proprioceptive feedback may cause the system to oscillate at the mechanical resonant frequency of the body or limbs, a frequency that may be quite different from the baseline frequency of the CPG on its own.

Pacemaker interactions: Examples from jellyfish

Due in part to their relatively simple design, a significant body of work in comparative biomechanics and neurobiology has focused on understanding jellyfish’s locomotion and feeding. Fluid dynamics of jellyfish have been investigated using mathematical modeling (Daniel 1983, 1984; Dabiri et al. 2007), experiments (Costello and Colin 1994; McHenry and Jed 2003; Dabiri and Gharib 2005; Santhanakrishnan et al. 2012), and numerical simulations (Lipinski and Mohseni 2009; Mohseni and Sahin 2009; Peng and Dabiri 2009; Hamlet and Miller 2011; Herschlag and Miller 2011). Contractions of the bell are generated by pacemakers that activate a ring of coronal swimming muscles and a set of radial muscles (Arai 1997). Expansions of the bell are due solely to muscle relaxation and the bell’s passive elastic properties. The electropotentials of interacting pacemakers used for locomotory control have been mathematically modeled as coupled van der Pol oscillators (van der Pol and van der Mark 1927; Low et al. 2006). Accurate models of the jellyfish’s motor and diffuse nerve nets are in need of development. While propagation of nerve impulses is typically modeled in animals using Hodgkin–Huxley type equations, jellyfish’s motor axons can conduct both rapid Na⁺-dependent action potentials and low-amplitude Ca²⁺ spikes (Mackie and Meech 1985). Ermentrout and Terman propose an interesting tristable model for the propagation of fast-moving Na⁺ action potentials and slow Ca²⁺ spikes in Aglantha digatale that warrants further investigation (Ermentrout and Terman 2010).

Fluid–structure simulations of pulsing jellyfish bells suggest that the timing of the bell’s contraction and expansion have significant implications for swimming and the resulting patterns of fluid mixing. Short, pulsing cycles can increase swimming speed and can sweep fluid rapidly around and past the oral arms. Pulses with long pauses between expansion and the subsequent contraction can create regions of slow of mixing over the oral arms and allow the water brought into the bell to be sampled for longer periods of time (Hamlet and Miller 2011). In the case of the upside-down jellyfish, Cassiopea xamachana, the duration of contraction and expansion times are rather constant (Hamlet et al. 2012). The length of the rest periods between expansion and the subsequent contraction vary greatly from cycle to cycle and can be described as a bimodal distribution of the pause times between cycles. This suggests that a simplifying assumption might be that the lengths of the pauses are described by the Markov Property. The Markov Property is such that given a system that exhibits a particular state i at time t, the probability that the system transitions to state j at time t + 1 is independent of past behavior. Using this assumption, a two-state discrete-time Markov chain (DTMC) can be used to simulate pulsing dynamics of the jellyfish bell. Pause times generated by the DTMC and used as inputs into fluid dynamic simulations suggest that an effective strategy for feeding by Cassiopea might be to alternate between sampling phases and advective phases via long and short pause times.

Guidance mechanisms: Example from copepods

A more complex design is that of the small aquatic crustacean, the copepod. Considered to be the most abundant multicellular organisms on earth, copepods play a key role in the aquatic food chain, transforming primary production into bite-sized pieces for consumption by larval fish, thus promoting recruitment into the fish population and supporting the fisheries industry of humans. However, copepods are much more than fish food. As heterosexual organisms, the male must find his mate. This is not an easy task for individuals that typically are separated by large volumes of water relative to their size. The mechanisms by which copepods locate mates were examined by Doall et al. (1998). The male copepod relies on the interaction of the pheromone emitted by the female copepod and the hydrodynamic wake she creates as she moves through the water in an intermediate Re realm. The female copepod swims generally at a steady speed along either straight or circular paths. The 1-mm multi-oared male copepod is able to randomly intersect the filamentous odor trail left by the 1-mm female copepod within 10 s, before turbulent diffusion erases the trail. It is always the male who detects and pursues mates. As soon as he encounters the female’s trail, the male copepod closely traces the female’s path, suggesting that the male follows detectable chemical and/or hydrodynamic signals left by the female. Using his sensory apparatus, primarily the pair of antennules, the appendages that stretch the farthest from the body in exploring the environment, the male is able to compare the chemical and hydrodynamic gradients in the environment and use these cues as a guide to the signal source, the female copepod. Within 2 s of finding the trail, which averages 10 cm or less in length, yet expands the 1-mm target by up to 100 times the body length, the male is able to accelerate along the trail, stay on track, and catch up with the moving target, the female, and capture her. Using a trail mimic (Yen et al. 2004), this trail-following behavior was visualized in laboratory experiments and displayed a remarkable ability of the male to sense, follow, and stay on the track of the scent mimic (Fig. 2).

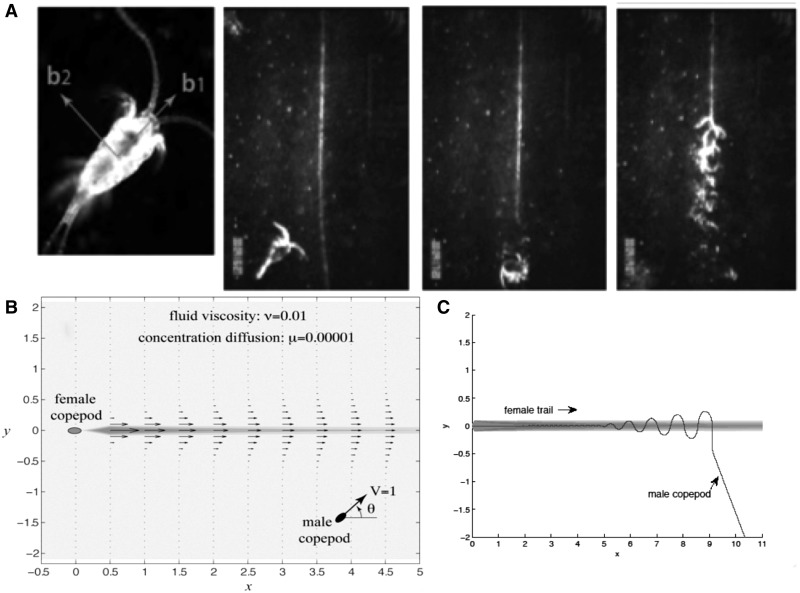
Fig. 2.

(A) The upper left panel shows a picture of the male copepod Temora longicornis (≈1 mm in length). Along its body it is equipped with two arrays of sensors that detect chemical and hydrodynamic signals. The upper three panels on the right are taken from a movie based on Yen’s laboratory experiment. The source of the scent is a slow injection at the top of the tank of a female’s scent, which sinks to the bottom of the tank. Laser optical techniques are used to illuminate the trail of the scent (the white line). The second panel from the left shows the male copepod approaching the female’s trail. It detects the trail and first follows it in the wrong direction, that is, to the bottom away from the source of the scent as shown in the third panel from the left. It then corrects its heading and traces the trail in the direction of increasing chemical and hydrodynamic signals. (B) The female copepod swims to the left in the negative x-direction at a constant velocity U_f. The fluid moves in its trail in the positive x-direction and diffuses in the y-direction, transversely to the trail, with kinematic viscosity ν. The fluid’s velocity field is shown by black arrows. Similarly, the chemical concentration C (x, y, t) (the female’s scent) carried by the trail also diffuses in the y-direction, but at a much weaker diffusivity µ. The chemical concentration is depicted using contour plots. (C) The model tracks the gradient given in B.

In the example in Fig. 2a, the male copepod intersects the female-scented trail (the white line), deforming the signal as he swims up the trail; see Borazjani and Sotiropoulos (2010) for a computational fluid-dynamic analysis of the details of this drag-based swimming, and Catton et al. (2011) for an experimental study of the flow field generated by the female’s swimming motion. The main goal of the work of Kanso and Yen (2011) is to model the mechanisms by which the male follows the female’s trail. As a starting point, we consider an idealized description of the trail in which the fluid moves in the x-direction along the trail and diffuses in the y-direction with kinematic viscosity ν. Similarly, it is assumed that the chemical concentration C(x, y, t) (the female scent) carried by the trail also diffuses in the y-direction but at a much weaker diffusivity µ. An illustration of the hydrodynamic and chemical trail is shown in Fig. 2.

The male copepod may be modeled as a kinematic particle located at (x_m, y_m) equipped with two sets of sensors in the b₁ and b₂ directions as shown in Fig. 2 (left panel). That is, it is able to sense the directional concentration gradients ∇C · b₁ and ∇C · b₂. It can then adjust its orientation, but not speed, based on the chemical gradients it senses. By orientation, we mean the angle θ between the b₁-direction and the x-axis as shown in Fig. 2b. More specifically, the motion of the male is governed by 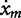= u_x + V cos θ, 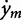= u_y + V sin θ,

= ω(sign(∇C · b₂))H (δ − ∇C · b₁), where u_x and u_y are the components of the fluid’s velocity field evaluated at the copepod’s location (x_m, y_m). When V = 0, the model behaves as a passive tracer in a background flow. When V = 1, the copepod actively tries to turn in the direction of increasing concentration gradient. The rapid response and efficient error-correction performed by the male to remain on track suggests a finely integrated sensory-motor system for the copepod. The constant parameters ω and δ determine the magnitude and duration of this turning motion and H is the Heaviside function. It is important to distinguish the control law proposed here from the source-seeking algorithms of Cochran et al. (2009), which rely on very fast oscillations that continuously probe the environment. Preliminary results show that the model is able to track both rectilinear and circular trails without any information on the trail’s global or relative position. The next set of questions will address the role of the fluid flow field in enhancing or hindering this trail-following ability, and the interplay between the chemical signals and hydrodynamics in achieving such trajectory pursuit.

Muscular activation and movement

Mathematical models of muscles

Mathematical modeling can provide a powerful tool for connecting neural activation to generation of force. One of the earliest mathematical models of the macroscopic behavior of muscles was developed by Hill (1938) to describe the velocity of contraction as a function of the force generated by muscle. This force–velocity curve may be obtained empirically by measuring the velocity of contraction for a given load in a muscle that is in a constant contractile state. The curve may be approximated using the function; V = b(P₀–P)/(P+a), where b and a are constants that arconstants that are determined empirically, V is the contraction velocity, and P is the load. When P = 0, the muscle shortens at its maximum velocity, V_max, and when V = 0, the muscle’s the maximum isometric force, P₀, is reached. Mathematical models of crossbridge dynamics may also be used to derive this empirical force-velocity curve. Such models allow one to relate the microscopic properties of crossbridge models to the macroscopic constants of the muscle (Hoppensteadt and Peskin 2002).

Since Hill’s original paper, numerous mathematical models of muscle have been derived. One of the more famous is the Huxley muscle model, which describes the release and dynamics of intracellular Ca²⁺ as a function of the electropotential and the conversion of free Ca²⁺ to muscular tension (Huxley 1957). There are simpler phenomenological models that have also been used to simulate the dynamics of Ca²⁺ release and the production of muscular tension. One such model is based on a FitzHugh–Nagumo type of system developed for cardiac tissue by Cherubini et al. (2008).

More recently, integrative mathematical models have been used to simulate (1) the generation and propagation of action potentials, (2) the release and dynamics of free Ca²⁺ in the muscular fibers as a function of the electropotential and time, (3) the conversion of free Ca²⁺ to tension generated by the muscular fibers, (4) the deformation of tissues due to the contraction of the muscles, and (5) the movement of fluid due to the resulting motion of the organ or organism. Griffith et al. (2009) and Hand and Griffith (2010) have used an immersed boundary formulation of the bidomain equations to study cardiac electrophysiology and fluid dynamics of an adult heart. The local membrane potential is used to trigger the contraction of the cardiac muscle which drives the motion of the fluid. Chen et al. (2011, 2012) have developed a complete model of a swimming leech, including muscle activation, passive body tension, and fluid dynamics. Tytell et al. (2010) performed similar immersed boundary simulations in which the activation of muscle fibers is used to propel a virtual lamprey through a fluid (discussed below). The muscle fibers themselves are modeled as one-dimensional elastic fibers that produce force according to a Hill-type model of muscular force (Williams 2010).

Timing and activation of patterns: Examples from flight

The muscles of flying animals are typically categorized as providing either the power necessary to produce lift and thrust to keep the animal aloft or control inputs to help the animal maneuver and recover from perturbations in flight. Examples of power muscles include the pectoralis and supracoracoideus in birds and the dorsolongitudinal (DLM) and dorsoventral (DVM) muscles of flying insects. Control muscles include the intrinsic wing muscles of birds, for example, the bicPNG and wrist extensors and a suite of small muscles in flying insects that attach to the wing’s sclerites or to the thorax along with the DLM and DVM. In birds, control muscles actively both influence the trajectory of the wing stroke and change the properties of the airfoil itself (Hedrick and Biewener 2007). In insects, control muscles are also known to absorb energy from the power muscles (Tu and Dickinson 1994). However, these distinctions between power and control are not absolute, and the power muscles of birds and insects are asymmetrically modulated during flight maneuvers (Wang et al. 2008; Warrick and Dial 1998).

The power muscles of flight in vertebrates and insects are typically stimulated prior to each half stroke, that is, in advance of each downstroke and upstroke, although neuromuscular latency may push the actual neural activation of muscle far out of phase with the apparent wing movements in animals with high wingbeat frequencies such as hummingbirds (Altshuler et al. 2010; Tobalske et al. 2010). Additionally, the flight power muscles of some insect groups are asynchronous and self-stimulate following contraction, reducing the frequency at which neural control inputs to the flight motor may be provided (Pringle 1957). Modulation of muscles for flight control differs substantially among vertebrates and insects. Vertebrates’ flight muscles are modulated by changes in the timing and duration of stimuli, along with the magnitude or number of muscle motor units recruited; modulation along all these axes may be common in maneuvering birds (Warrick and Dial 1998; Hedrick and Biewener 2007). Unlike vertebrate flight muscle for which neural inputs may vary in intensity, insect flight muscles are primarily modulated via the presence (or absence) of a neural activation and its phase with respect to the wing-beat cycle (e.g., Kammer 1967). Phase of activation during the stretch-shorten cycle imposed on a muscle, dramatically influences the output of mechanical power (e.g., Josephson 1997) and is sufficient to shift a muscle from net release of energy to net absorption of energy (Ahn and Full 2002).

Interaction of body and environment

Fluid–structure interaction

The natural world is replete with interesting examples of fluid–structure interactions such as the pumping of blood by the heart, swimming in fluids from the scale of bacteria to whales, flying on scales from the tiniest parasitoid wasps to large birds, and the flapping of fins. Efforts to understand the dynamics of these types of problems through mathematical analysis, laboratory experiments, and numerical modeling are a rapidly expanding area in integrative and mathematical biology. The above examples vary over a large range of spatial and temporal scales and involve many different types of geometries. Quite often, direct measurement of the biological flows is not practical or possible and laboratory experiments can provide only limited data. Hence, numerical simulations are a valuable means of gaining insight into the detailed dynamics of the fluid–structure system.

Study of swimming by fish swimming: Vortex sheet methods

Swimming by fish is relatively well studied among locomotory systems, and is the subject of multiple review papers (Lighthill 1969; Sfakiotakis et al. 1999; Triantafyllou et al. 2000; Fish and Lauder 2006) and books (Aleev 1977; Childress 1981; Blake 1983; Webb and Weihs 1983; Videler 1993; Sparenberg 1995; Shadwick and Lauder 2006). The kinematics and mechanical systems of fish have led to bio-inspired designs for man-made vehicles, but have not always led to propulsive advantages (Sagong et al. 2008; Choi 2009).

Direct numerical simulation of swimming has been successfully performed using a variety of Navier–Stokes solvers for deforming bodies. Some of the methods can be classified as immersed-boundary methods (Fauci and Peskin 1988; Peskin 2002; Akhtar et al. 2007; Miller and Peskin 2009; Borazjani and Sotiropoulos 2010; Tytell et al. 2010), or Lagrangian approaches using regularized fluid or vortex particles (Cottet and Koumoutsakos 2000; Eldredge 2006; Hieber and Koumoutsakos 2008). An alternative method, which is less expensive computationally, proceeds from an assumption about the flow structure. At high Reynolds number, the flow past a solid body typically consists of thin layers of strong fluid shear (and vorticity) which occur in a layer along the body’s surface, and in “free” shear layers that have flowed away from the body’s surface into the surrounding fluid. For thin undulating bodies, or bodies with appendages such as fins, separation at the trailing edge or distal edge can be particularly important (Tytell and Lauder 2004; Lauder et al. 2006). Therefore, a natural assumption about the flow structure, used since the early days of airfoil theory (Thwaites 1987), is that the boundary layer only separates at the sharp edge. This assumption does not apply in all cases, particularly for a nonstreamlined or completely smooth body (such as a sphere) (Stewartson 1975; Smith 1986; Haller 2004). However, separation at the edges is a good assumption for many slender flexible bodies, such as undulating fish or flapping filaments (Akhtar et al. 2007; Lauder et al. 2007; Shelley and Zhang 2011). Passive flexibility can play a role in causing separation to occur at the edges only (Dong and Lu 2005). Anderson et al. found no separation of the boundary layer on swimming fish upstream of the trailing edge (Anderson et al. 2001). When separation occurs at a sharp edge, the flux of vorticity from the boundary layer into the surrounding fluid has been determined by the “Kutta condition” in various forms (Crighton 1985). Typically, applying the Kutta condition at an edge corresponds to imposing the unique value of vorticity flux there which removes a singularity in flow velocity.

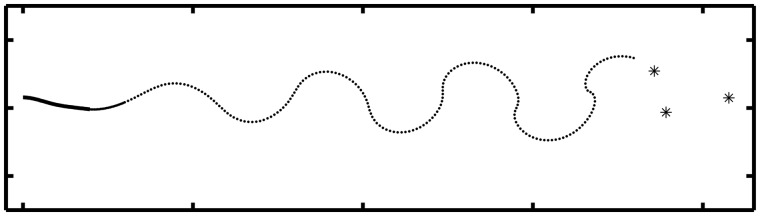
Methods have been developed to solve for the inviscid flows past sharp-edged bodies including plates, tubes, and deforming and flexible filaments, using the Kutta condition (Krasny 1991; Nitsche and Krasny 1994; Jones 2003; Shukla and Eldredge 2007; Alben 2009). Using the methods of Alben (2009) and Alben et al. (2012), we simulated 2D flows past freely swimming flexible foils. In Fig. 3 we show a snapshot of a “swimming” flexible foil (thick solid line) and its vortex sheet wake (dotted line). The foil is oscillated vertically at the leading edge, sinusoidally in time. It bends under fluid pressure forces and moves horizontally to the left with a velocity at which the period-averaged thrust and drag forces cancel. Thrust forces are due to the difference in pressure across the foil acting in the leftward direction. Viscous drag forces act on the surface of the foil. In Fig. 3, the dotted line representing the vortex sheet wake is meshed adaptively to save computing time, while preserving the large-scale roll-up of the wake in agreement with simulations at high Reynolds numbers (Krasny 1986; Cottet and Koumoutsakos 2000). If leading edge separation does not occur, a leading-edge suction force is naturally included in this model (Thwaites 1987; Saffman 1992; Eloy and Schouveiler 2011).

Fig. 3.

Instantaneous position of a flexible foil (thick solid line at left) and vortex-sheet wake (dotted line) shed from the foil’s trailing edge, computed by the methods of (Alben 2009; Alben et al. 2012). Asterisks at the right denote the locations of point vortices used to approximate far-field portions of the vortex sheet.

In a quiescent flow, a generic vortex sheet rapidly develops many complex spiral structures, and is quite expensive to evolve for long times (Jones 2003). However, if the shed vortex sheet is advected away from the body (Alben 2008; Alben and Shelley 2008), or, as in Fig. 3, the body swims with a non-zero average speed, portions of the shed vortex sheet far from the body can be approximated by a small number of point vortices, shown by the asterisks in Fig. 3. Details are given by Alben (2009). In this case, the fluid–structure interaction can be reduced to solving a small number of equations discretized on the body, and evolving a modest number of discrete vortex elements in the fluid.

Aerodynamics of insect flight

To stay aloft, insects must flap their wings and generate sufficient force to overcome gravity. To search for food and avoid prey, they must perform maneuvers with agility. Insects’ aerial acrobatics result from a concerted effort of the insect’s brain, flight muscles, and flapping wings. One promising approach to understanding this complex interactive system is to start from the exterior, analyzing the physical interaction between a flapping wing and the flow. The unsteady aerodynamics of the flapping wing then provides an input into the modeling of the 3D flight of the coupled body and wing system. By analyzing the stability and the dynamics of such a system, we can begin to gain insights into the different strategies employed by insects to execute maneuvers. Together, the analyses of these inter-connected building blocks offer a route for obtaining mechanistic understanding of complex flight behaviors.

One of the many pieces of the puzzle in understanding insect flight dynamics is the aerodynamics of a flapping wing (Weis-Fogh and Jensen 1956; Childress 1981; Ellington 1984; Spedding 1992; Dudley 1998; Dickinson et al. 1999; Wang 2005). Although much is known about classical airfoil theory, an insect’s wing is much smaller than an airfoil and it creates unsteady flows. Consider a dragonfly, for example: its chord (c) is ∼1 cm, wing length (l) ∼4 cm, and wing frequency (f) is ∼40 Hz. The tip speed (u) is about 1 m/s, and the corresponding Reynolds number, Re = (uc/η), where η is kinematic viscosity, is about 10³. A smaller insect, the chalcid wasp, has a wing length of about 0.5–0.7 mm and beats its wing at about 400 Hz. Its Reynolds number is about 25. The range of Reynolds numbers in insect flight is about 10 to 10⁴, which lies in between the two limits that are convenient for theories: inviscid flows around an airfoil and Stokes flows experienced by micro-organisms.

The flow around a flapping wing is governed by the Navier–Stokes equation, subject to the wing’s movement. The movement of the wing is affected, in turn, by the movement of the flow. A mathematical challenge is to determine the solution to the coupled equations of the flow and the wing’s movement. There is no simple analytic solution to such a coupled system, even in the case of flow past a flat plate. Therefore, one either has to make simpler but relevant theoretical models or construct sensible numerical algorithms for simulating these flows.

The aerodynamic models fall roughly into two categories. One is the quasi-steady model of aerodynamic forces, which relates the instantaneous force to the kinematics of the wing directly. This provides a practical tool for quick estimates (Weis-Fogh and Jensen 1956; Weis-Fog 1973; Ellington 1984). Recent experiments and computations have made significant progress in taking into account some of the key unsteady effects, such as dynamic stall, in revising the traditional models based on thin airfoil theory (Dickinson et al. 1999; Sane 2003; Andersen et al. 2005; Wang et al. 2004). The other kinds of models treat the flow as a collection of vortices or vortex sheets in an otherwise inviscid flow (Wagner 1925; von Karman and Burgers 1963; Pullin and Wang 2004). The rules for generating vortices is based on variants of the Kutta condition, which was first introduced in the analysis of airfoil theory. These models provide a tractable system for computing and analyzing the unsteady effects and the coupling between the flow and the wing and is appealing for its computational efficiency (Alben 2008; Jones and Shelley 2005; Alben 2008).

Neuromechanical phase lags

Fluid–structure interaction seems to be particularly critical for the development of a “neuromechanical phase lag”: a lag between muscle activation and muscle shortening that gets increasingly longer at points closer to the tail (Wardle et al. 1995). Fishes, swimming amphibians and snakes, and lizards that move through sand all develop a phase lag.

Fishes

Near the tail tip in fishes, the neuromechanical lag can be so long that muscles near the tail are electrically active even as they are forcibly stretched by external fluid forces. Muscles produce the highest forces when they are stretched while active (McMahon 1984), and thus the increasing phase lag has been hypothesized to stiffen the flexible tail so that it transfers force more effectively to the fluid (Blight 1977).

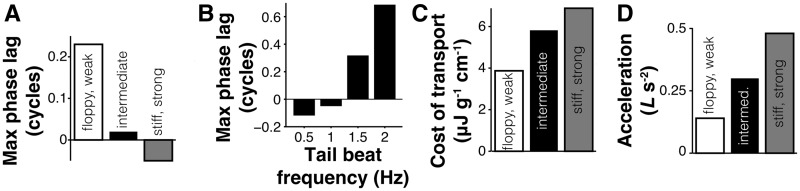
Recent computational results support the hypothesis that the phase lag may increase swimming efficiency. Tytell et al. (2010) simulated a flexible swimming animal for which the body forces and fluid forces were fully coupled together, but with no sensory feedback (i.e., the right three boxes in Fig. 1). Certain combinations of body stiffness and muscle strength resulted in a phase lag (Fig. 4A), similar to that seen in fishes (Williams et al. 1989). Those swimmers that had large phase lags also used relatively little energy for locomotion (Fig. 4C), but also accelerated slowly (Fig. 4D). Unlike the condition in fishes (Wardle et al. 1995), the phase lag in the computational swimmer was highly sensitive to tail beat frequency (Fig. 4B), suggesting that sensory feedback may be important for maintaining an appropriate phase lag over a range of frequencies.

Fig. 4.

In a computational swimmer with no sensory feedback, the neuromechanical phase lag changes with mechanical parameters (A) and frequency of tailbeat (B) and has an impact on swimming performance (C and D). (A) Change in maximum phase lag between muscle activation and the beginning of muscle shortening for a swimmer with a relatively floppy body (flexural stiffness EI = 0.64 MPa) and weak muscles (open bar), for an intermediate body (EI = 0.76 MPa; filled bar), and for a stiff body (EI = 0.98 MPa) with relatively strong muscles (filled gray bar). (B) Change in maximum phase lag for an intermediate swimmer as frequency of tailbeat changes. (C, D) Trade-off between cost of transport (C) and initial acceleration from rest (D) for the three swimmers shown in panel (A). Data from Tytell et al. (2010).

Fig. 5.

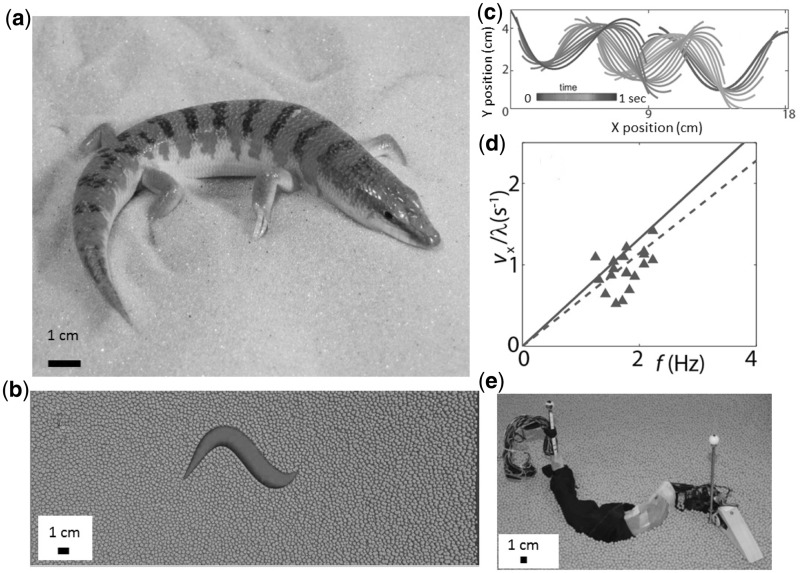
The sandfish lizard (Scincus scincus) (a) at rest on the 0.3-mm diameter glass particles. (b) Multiparticle discrete element method (DEM) simulation of the sandfish swimming subsurface in a simulated box of glass particles, 3 mm in diameter. (c) Midline trajectories of the simulated sandfish during swimming. (d) Forward swimming speed versus frequency of undulation in a biological experiment (points), DEM simulation (dashed lines) and resistive force theory (solid lines) in a loosely packed granular medium (58% by volume) (Maladen et al. 2011). (e) Physical robot model of the sandfish at rest on a granular medium of plastic particles, 6 mm in diameter. The robot swims with performance comparable with that of the live organism.

Sandfish Lizard

A diversity of small organisms, including lizards (Mosauer 1932), snakes (Norris and Kavanau 1966), scorpions, and beetles inhabit dry deserts (Brown 1974; Ezcurra 2006) composed of sand, a granular material (Jaeger et al. 1996b). Many of these organisms move effectively on and within a substrate that displays both solid and fluid-like characteristics in response to stress. Little is known about the behaviors and neuromechanical control strategies used by animals when they are subsurface. Recent studies (Maladen et al. 2009, 2011) of the locomotion of a small (∼8 cm long, snout-vent length) desert-dwelling lizard, the sandfish (Scincus scincus) (Fig. 5), which inhabits the Saharan Desert of Africa, observed that when challenged with a granular medium of 0.3-mm glass particles (with properties similar to desert sand) the animal walked on the surface using its limbs to propel itself. High speed x-ray imaging revealed that once subsurface the animal no longer used limbs for propulsion. Instead it placed the limbs against its sides and executed an undulatory motion of the body with large amplitude axial oscillation, using the body to “swim” within the granular medium at speeds up to ∼2 bl/s. Subsurface swimming kinematics were well characterized by a single-period sinusoidal traveling wave propagating along the body from head to tail; the ratio of amplitude to wavelength was approximately 0.2. The animal increased its forward speed by increasing its frequency of undulation. The ratio of the average forward swimming speed, η = v_x/v_w was approximately 0.5, independent of both initial conditions of the granular bed and particle size. To investigate the neuromechanical strategy of the sandfish during walking, burial, and swimming, we (Sharpe et al., in review) used high speed x-ray and visible light imaging with synchronized electromyogram (EMG) recordings of the activity of epaxial muscle (the iliocostalis muscle group) activity. While moving on the surface, undulation of the body was not observed and EMG showed no activation. During subsurface sand-swimming, EMG revealed an anterior-to-posterior traveling wave of muscle activation that traveled faster than the kinematic wave, similar to organisms swimming in Newtonian fluids (Wardle et al. 1995; Tytell et al. 2010; Chen et al. 2012). This ratio was independent of the volume fraction of the granular bed.

Sand–structure interaction

The study of locomotion on and within granular media (GM) like desert sand presents challenges to modeling, in part because the physics of interaction—that of localized forcing, for example, the penetration and movement of feet, limbs, heads, or bodies (Li et al. 2009; Maladen et al. 2009; Mazouchova et al. 2010)—is presently poorly understood, relative to progress made in rapid granular flows (Jenkins and Richman 1985; Goldhirsch 1999), or slowly deforming flows described by soil mechanics (Terzaghi 1943; Nedderman 1992). GM exhibit complex rheology (Jaeger et al. 1996a) affected by both the properties of the particles (e.g., coefficient of friction, polydispersity, particle shape) and the compaction state of the medium. The frictional nature of GM produces a yield force, a threshold below which grains do not flow in response to forcing (Nedderman 1992). Above the yield force GM flow and, for low intrusion speeds, the force on the intruder is independent of speed (Wieghardt 1975), unlike the case for fluids. Like the hydrostatic force in fluids, the average stress within GM increases approximately linearly with depth.

Studies of localized forcing with horizontally and vertically translating intruders in initially homogeneous GM have been conducted (Albert et al. 2001; Geng et al. 2001; Goldman and Umbanhowar 2008; Umbanhowar and Goldman 2010). Vertical intrusion of objects into GM results in a penetration force linear in depth and linear in projected intruder surface area. The resistance of GM to penetration α is a function of the material properties and packing state. Much like the case of fluids, intruders moving horizontally through GM experience forces of drag and lift. In GM however, these forces arise from normal and frictional forces on the intruder’s surface, which are supported by force chains between particles in the bulk (Geng et al. 2001). For arbitrary shapes of intruders, we have discovered that both drag and lift can be well approximated by decomposing the leading surface into flat plates and summing the normal and tangential (frictional) forces on the plates. Since part of the grains can also be pushed upward or downward by the leading surface, the intruder may experience a net positive or negative lift depending on its shape (Ding et al. 2011).

Closed-loop control of locomotion

In addition to the body–environment interactions described above, such as fluid–structure interactions, which lead to changes in shape in flapping wings of insects and consequently to changes in aerodynamic performance, animals also interact with the environment at a whole-organism scale (Hedrick et al. 2009). These interactions come in the form of changes in the state of the environment such as the arrival of a gust of wind, or changes in the state of the animal such as a maneuver that initiates a left turn, or even continued forward acceleration changing the velocity of the organism with respect to its environment. The ability of animals to manage these environmental interactions lies at the heart of their apparent locomotor stability and allows them to move through spatially and temporally varying environments.

Studies of locomotor stability and interactions of animals and environments often begin with a perturbation applied to a freely behaving or freely moving animal. Permitting free movement of the animal is critical in these cases because the response of an animal to a perturbation can arise both from an active, sensory-based change to the locomotor pattern, or through the interaction of the current locomotor pattern with the new environmental condition. Studies such as tethered-flight experiments on insects (e.g., Götz 1968; Robert and Rowell 1992) that do not permit movement of the animal cannot reveal the portion of the response due to environmental interaction, even in cases in which sensory feedback is presented in a closed-loop manner. However, perturbations to freely behaving animals, whether brought about by direct mechanical effects (e.g., Jindrich and Full 2002), sensory manipulations (e.g., Rohrseitz and Fry 2011), or resulting from maneuvers performed by the animal (Cheng et al. 2011), result in a closed-loop response incorporating both animal–environment feedback and sensory feedback. These different modes of response can be separated and quantified by combining whole-animal perturbation or maneuvering experiments with physical or computational models capable of revealing the response of the locomotor system to a new environmental state in the absence of sensory feedback, that is, the open-loop response of the system. Once the open-loop response is quantified, the closed-loop sensory feedback portion of the response is revealed as the difference between the observed experimental response and the model open-loop response (Cowan and Fortune 2007; De 2010). Depending on the nature of the system in question, the open-loop response may need to incorporate one or more internal feedback loops. For example, muscle-driven locomotion is subject to intrinsic limits on force or power set by the properties of the actuator and may not be able to adopt the same kinematic pattern in a new environment, given a constant neural input. Additionally, the effects of multiple levels of neural feedback may also be included. For instance, proprioceptive feedback to the CPG may enhance (or reduce) stability, requiring less (or more) compensation in the outer sensory feedback loops.

Cheng et al. (2011) provide a recent, illustrative example of the power of this combined approach of modeling and whole-animal perturbation applied to free-flight pitch maneuvers in hawkmoths. First, the equations of motion for a rigid body with six degrees of freedom were reduced to the set of equations governing the observed motion of the animal. Coefficients for the coupling terms relating the equations to one another were determined from a physical model incorporating the wing kinematics of steady hovering by the animal. Next, the values for the coupling terms observed in the natural behavior of the animal were extracted from the kinematics via nonlinear regression fits to the equations of motion; the differences between the coefficients from the model and the animal reveal the effects (or absence) of sensory feedback relating to the different degrees of freedom in the model.

Control algorithm for a yaw turn in flapping flight

An exciting recent advance in the study of insect flight is the integration of a kinematic tracking algorithm, aerodynamic modeling, and dynamic analysis with high-precision experimental measurements of free flight (Ristroph et al. 2009b, 2010; Bergou et al. 2010). We illustrate this approach with a recent analysis of a yaw maneuver (Bergou et al. 2010) (see Fig. 6). To generate the vertical force necessary to sustain flight, small insects must beat their wings hundreds of times per second. Under the constraint of rapid wingbeats, how can insects manipulate these wingbeats to induce flight maneuvers?

Fig. 6.

Computer-reconstructed 3D motion of a fruit fly executing a sharp yaw turn (figure from Bergou et al. 2010). The shadows are from high-speed measurements fon images from a video camera. In this case, the fly makes a 120° turn in about 80 ms. The asymmetry between left and right wings is generated with the bias in the rest angle of the effective torsional spring at the wing’s hinge.

During the yaw turn, asymmetries appear in all three wing–angle kinematics. However, not all of these are involved in inducing the turn. For example, the most apparent asymmetry—the shift in the mean stroke angles of the wings—simply reorients the aerodynamic forces about the yaw axis of the fly and does not affect the torque that causes the turn. To gauge the importance of the wing–motion asymmetries for inducing the turn, one can use a quasi-steady aerodynamic model to determine the average yaw torque generated by the wingbeats. The torque turns out to act as if it were generated by a torsional spring with an adjustable equilibrium position. The time series of this torque further shows that a fruit fly modulates its wing pitch by shifting the rest angle of this torsional spring. In one instance, the insect modulates left and right wing pitch by about 15° over a period of five strokes. This bias leads to a sharp 120° turn in 80 ms, or 18 wing beats. By changing the strength and duration of the asymmetry in the wing’s rest angles, flies can control their angle of turn. The model predicts a linear relation between the yaw angle and the bias of the equilibrium position in the torsional spring.

For fruit flies, the mechanical properties of the wing hinge appear to be finely tuned in ways that enable modulation of wing pitch through only slight active actuation. The spring-like behavior of the wing hinge also connects the time scale of a turning maneuver with the time scale of the wing’s actuation. This supports the notion that animals can take advantage of mechanical properties of their bodies to simplify the complex actuation necessary to move (Dickinson et al. 2000).

Free maneuvering flight and insects’ behaviors for recovering from external perturbations have offered a window into the controls used to make turns and to make the transition between different flight modes. It will be interesting to understand the myriad active and passive recovery strategies employed during these different maneuvers. The integration of theory, experiments, and computations has become a necessity in the studies of animal locomotion and is likely to bring new quantitative insights to important biological questions.

Future directions and challenges

Computational methods

Deforming structures in viscous flows

The fundamental computational challenge associated with problems of fluid–structure interaction is the accurate simulation of a moving, flexible structure in a surrounding fluid. A number of methods for solving such problems have been developed and include the immersed boundary method (Peskin 2002), the immersed interface method (Li and Lai 2001; Lee and LeVeque 2003; Xu and Wang 2006), distributed Lagrange multiplier methods (Shi and Phan-Thien 2005; Shirgaonkara et al. 2009), the blob projection method (Cortez and Minion 2000), and other variations inspired by Peskins immersed boundary method (Mittal and Iaccarino 2005). Although these methods have significantly advanced our understanding of fluid–structure interactions in the biological world, most studies have been limited by severe computational demands ubiquitous with these types of problems (Newren et al. 2007; Hou and Shi 2008). If one can make either the inviscid or Stokes flow assumption, then the computational time can be greatly improved using methods such as vortex sheets (Krasny 1986) for the former case and the Method of Regularized Stokeslets (Cortez et al. 2005) for the latter.

In the Stokes setting, when inertia can be neglected, the fluid equations become linear and allow the construction of a numerical method without grids in the fluid domain. Structures may be represented by a collection of Lagrangian markers. For the case of the Method of Regularized Stokeslets, these markers correspond to the location of regularized fundamental solutions to the Stokes equations. This numerical method allows a simple representation of very thin structures like cilia and flagella that operate at very low Reynolds numbers. The linearity of the Stokes equations translates into a linear relationship between velocity and force, with the advantage that only an efficient method for solving a linear system is needed to tackle very complicated fluid–structure interactions.

Intermediate Reynolds numbers and insect flight

When both viscous and inertial forces are significant, the full Navier–Stokes equations may be used to provide an in-depth look at the physics of flows around organisms. Direct numerical simulations have been used to enhance our understanding of a wide range of problems in biological fluid dynamics at intermediate scales, including jellyfish propulsion (Lipinski and Mohseni 2009; Herschlag and Miller 2011), fish swimming (Fauci and Peskin 1988; Mittal et al. 2006), ctenophore propulsion by comb plates (Dauptain et al. 2006), multi-oared copepod propulsion (Borazjani and Sotiropoulos 2010), and insect flight (Sun and Lan 2004; Andersen et al. 2005; Miller and Peskin 2009; Nakata and Liu 2012).

To quantify the unsteady aerodynamics of insect flight, for example, recent efforts have brought a suite of computational fluid-dynamics techniques to obtain detailed descriptions of the flow around the wings. Although there are commercial software packages for simulations of flow, there is not a one-size-fits-all computational algorithm to answer any given question. For flapping flight, the interesting flow behaviors tend to originate at the moving interface. On the other hand, computational schemes typically encounter the greatest difficulty in resolving flows near the interface. There have been continued efforts to develop improved algorithms for addressing sharp-interface problems (Griffith and Peskin 2005; Mittal and Iaccarino 2005; Xu and Wang 2006).

Often, it is beneficial to develop a method tailored to the question. For example, in the case of a single rigid flapping wing, one can resort to high-order numerical schemes and take advantage of the coordinate transformations and conformal mapping to resolve the sharp wing tips so as to avoid grid-regeneration (Wang 2000b; Alben and Shelley 2005; Spagnolie and Shelley 2009). In the case of multiple wings, the immersed boundary method and the immersed interface method are versatile tools for simulating both rigid and flexible wings (Mittal and Iaccarino 2005; Xu and Wang 2006; Miller and Peskin 2009). One advantage of these Cartesian-grid-based methods is their relative ease in handling the moving interface without grid-regeneration (Peskin 1972). The immersed boundary and immersed interface methods, along with other types of computational methods, have brought quantitative understanding to hovering flight (Wang 2000a), transition to forward flight (Alben and Shelley 2005), the role of clap-and-fling at small Reynolds numbers (Miller and Peskin 2005), the 3Ddimensional effects of flow (Sun and Lan 2004), and the role of wing flexibility (Miller and Peskin 2009; Vanella et al. 2009).

In addition to experiments, 3D simulation of flight will allow us to disentangle the feed-back loops,for example, visual and mechanical feedbacks, which are simultaneously present in insects (Pringle 1948; Sherman and Dickinson 2003; Dickinson 2005; Taylor and Krapp 2007). A systematic dynamical analysis of the intrinsic instabilities and the feedback controls of 3D flapping flight can further inform us about the physical constraints on the time scale of sensory feedback loops. The solutions provide ideas for constructing simpler models such as the ones described previously. They may also reveal subtler effects that are critical for our understanding of the efficiency of flapping flight (Pesavento and Wang 2009).

Vortex sheet methods for inviscid flows

Many aspects of vortex sheet models of high Reynolds number (inviscid) flows remain to be understood in detail. When is the Kutta condition valid, and how does it arise from viscous fluid mechanics? When is vortex sheet separation delayed to the trailing edge for a flexible body? How does the Kutta condition relate to dissipation of energy? How is conservation of momentum affected in numerical implementations? Regularization is a robust approach to simulating free vortex sheets with a smooth representation (Krasny 1986). Regularization can be tapered to zero near the body to limit its effect on the process of vortex shedding (Alben 2010). How can the total momentum of the fluid–structure system be preserved in the presence of regularization? How can we use vortex sheets to model separation from the leading edge of a sharp body, even when the tangential component of the local flow velocity is directed onto the edge? Resolving these questions will help to understand the limits of vortex sheet methods in representing flows of high Reynolds number.

Locomotion in granular media

Unlike aerial and aquatic environments, common terrestrial environments like dirt, leaf litter, rubble, and sand are not yet adequately described by models at a level comparable with those that describe the flow of fluids (e.g., the Navier–Stokes equations). Prediction of ground reaction force is therefore a challenge, and consequently, quantitative discovery of locomotor principles and construction of devices (like robots) that operate effectively in such environments remains elusive. As noted earlier, GM provides an excellent test-bed for studies of terrestrial locomotion in flowing environments. However, the physics of the flow of GM is least developed in the regime relevant to that of locomotor-interaction, that of localized forcing. Challenged by the lack of constitutive equations for GM, we have modeled interaction with granular environments in two ways: Detailed simulations utilizing the multi-particle Discrete Element Methods (DEM) (Rapaport 2004; Poschel 2005) and empirical models of interaction using a Resistive Force Theory (RFT) inspired by theory developed to explain swimming at low Reynolds number (Gray and Hancock 1955).

In the DEM approach (Fig. 5b), The GM is modeled as ensembles of particles that undergo collisions among themselves and with intruders. Particle–particle and particle–intruder interactions include repulsive and viscous forces in the normal direction, and a frictional force in the tangential direction. Once validated against experiment, the DEM simulation can provide a predictive model over a wide range of experimental conditions. Multibody software can be coupled with the DEM simulation to create models of organisms. In the case of sand–swimming, analyzing particle flow around the virtual sandfish demonstrates that movement can be thought of as occurring within a “frictional” fluid in which force is dominated by frictional contacts within the material locally flowing around the body. The DEM model quantitatively reproduces kinematic features of the locomotion (e.g. speed versus frequency, Fig. 5). In the cases of walking and running on granular media, the DEM model accurately reproduces the locomotion of a small robot (F. Qian et al., submitted for publication).

Although DEM allows for detailed interrogation of fields of force and flow developed during locomotion, it is computationally costly and does not allow for analytic understanding of locomotion. Further, DEM is limited to relatively large particles or small volumes. Simulations of realistically large environmental substrates composed of 10⁹ − 10¹² particles are at the limits of present computational power. To remedy this, we have developed an empirical approach for swimming and walking organisms and robots inspired by the RFT (Maladen et al. 2009). RFT (Gray and Hancock 1955) was originally developed for swimming at low Reynolds number to gain insight into swimming in the granular medium. In the RFT, the body or limb of the organism is partitioned into infinitesimal elements along its length. When moving relative to the medium, each element experiences resistive thrust and drag. During swimming, resolving these forces into perpendicular and parallel components and balancing them by integrating forces over the length of the body (and head) predicts forward swimming speed at a given frequency. Because at biologically relevant swimming speeds (0–0.4 m/s) force is independent of speed (Wieghardt 1975; Maladen et al. 2009), the force on an element can be characterized as a function of only the direction of the velocity relative to its orientation.

Because resistive force laws in GM are not available, we measured the forces on rods with comparable cross sections to the animal body as the rods were dragged through GM at a fixed depth. With these force laws, the RFT agrees well with the DEM model (Fig. 5d). The angular dependence of the force laws in GM resembles the forces generated in a Newtonian fluid at low Reynolds number: The perpendicular force increases and the parallel decreases with the angle between the velocity of the rod and its longitudinal axis. However, while the functional forms of the forces in low Reynolds number (Re) can be approximated as sines and cosines, in GM, they do not have these simple functional forms. Further, the ratio of the average magnitude of the perpendicular forces to the parallel forces is larger in GM (>3:1) than in fluid (≈2:1). Consequently, thrust is relatively larger in GM compared with that in a fluid at low Reynolds number. The difference in force laws explains the higher η observed for sandfish (≈0.5) compared with non-inertial low-Re swimmers in fluids (≈0.2). The RFT also suggests that the packing state (volume fraction) does not affect η (or net torque) because, both thrust and drag scale similarly with changes in packing. Recently, we have extended the RFT laws to vertical intrusion and find excellent predictive ability for performance of a legged robot walking on a granular medium of poppy seeds (C. Li et al., manuscript in review). Finally, RFT and DEM approaches have been tested against a physical robot model, a seven-segment robotic sandfish, and compare well, predicting performance as parameters like amplitude and wavelength of undulation are varied (Maladen et al. 2011) (Fig. 5e).

Closed-loop sensory-motor interactions

As described above, many challenges remain in understanding the complex physics of the interactions between muscles, body, and environment (the right side of Fig. 1). A further challenge is to understand the closed-loop effects of such interactions on an animal’s nervous system (the left side of Fig. 1). Sensory-motor feedback in active, behaving animals is highly challenging to approach experimentally because of the difficulties of performing neurophysiological recordings in behaving animals. However, such experiments are critical, because the state of the nervous system can change qualitatively during a behavior, as compared with the same cells at rest or in an isolated preparation. For example, a class of visual interneurons in fruit flies double their gain during flight, compared with their state at rest (Maimon et al. 2010).

Mathematical models, even relatively simple ones, can be critical for understanding the role of sensory-motor interactions in a closed-loop system. For example, Cowan and Fortune (2007) used simple linear models of the locomotor dynamics of a swimming fish to analyze the tuning of sensory systems. They examined how fish maintain position in a slowly moving refuge. Even though the refuge moves slowly, for stable closed-loop dynamics, the simple model predicts that sensory systems should respond to high frequencies, which was indeed what was found experimentally. More complex models, such as that of Tytell et al. (2010), predict that the nervous system must change its activation properties as swimming frequency changes to maintain an effective neuromechanical phase lag (Fig. 4). Understanding how an animal responds to perturbations will be critical, and may require development of new techniques for analyzing data from rhythmic neuromechanical systems (see e.g., Revzen and Guckenheimer 2008, 2012).

Experimental challenges

Interactions of running, crawling, and climbing organisms (Alexander 2003) on natural terrestrial substrates generate many fascinating limb/body–ground interactions. For example, organisms can encounter surfaces with different orientations and these can require adhesive contact forces to climb (Cartmill 1985). Organisms can encounter substrates with gaps that are large compared with the size of the foot or body and which can require either careful foot placement or rapid movements to bridge gaps. Surfaces like sand or leaf litter can also flow beneath footsteps or upon intrusion of the body. Since natural terrestrial substrates are so complex, we desire laboratory versions that encapsulate features found in natural environments. To that end, experiments have been developed to create surfaces for which adhesion and incline can be varied (Goldman et al. 2006). Surfaces with gaps and obstacles (Bläsing and Cruse 2004; Daley and Biewener 2006; Spagna et al. 2007) have been used to study stability and control. Techniques like fluidized beds (Maladen et al. 2009; Li et al. 2009) have been used to control state of homogeneous granular media. However it is still a challenge to prepare states of different wetness or of particle size and shape; novel techniques are required.

As models of animal locomotion become more sophisticated and include effects such as surface deformation in response to applied forces, or encompass a closed-loop perturbation response extending over many locomotor cycles, recording methods for acquiring comparable measurements from freely behaving animals must keep pace. Many current experimental configurations use stereo videography followed by semi-automated landmark tracking to provide kinematics that are the link between experiment and model. This has the great advantage of not requiring any manipulation of the animal or attachment of any apparatus, but also imposes substantial limitations. However, current videography practices scale poorly to recording complete surfaces rather than landmarks or extended locomotor sequences. For example, a model of a deforming fin of a fish used up to 300 individually tracked landmarks per video frame to reconstruct the deforming locomotor surface (Mittal et al. 2006). Application of computer vision techniques to acquisition of kinematics can greatly enhance their throughput for simple measurements (Fontaine et al. 2009; Ristroph et al. 2009a) and can also, under appropriate experimental conditions, allow automated reconstruction of wing surfaces by using image–pattern recognition algorithms to automatically match many landmarks, building up a surface that can then be matched to an existing model of a deforming wing (Walker et al. 2010; Guo and Hedrick 2012). Several variants of this overall procedure exist, including some that use markers applied by the researcher—necessary in the case of animals with transparent locomotor surfaces (Walker et al. 2009; Koehler et al. 2011).

Techniques for recording from the nervous system of awake, behaving animals are also becoming critical. Current techniques involve tethering an animal in a virtual reality chamber that relays visual stimuli (e.g., Page and Duffy 2008; Dombeck et al. 2010; Maimon et al. 2010). Techniques for performing such recordings as animals move and respond to perturbations will be important.

For tiny intermediate-Re organisms, mapping out the 3D flow field along with collecting data on the kinematics of the locomotory appendages and direction of high-speed motion of the body is especially difficult for aquatic organisms like plankton. Recent developments in 3D particle image velocimetry (PIV) incorporate multiple high-speed, high-resolution cameras focused on a small volume illuminated at wavelengths undetected by the organism to obtain nonintrusive observations of flow fields of escaping aquatic copepods that are 1–2 mm long. Asymmetry in the flow due to motion of the body and action of the multiple swimming legs does not match that predicted in computational fluid dynamics (CFD) or analytical models (Kiorboe et al. 2010; Jiang and Kiorboe 2011a,b). Improvement of our understanding of how copepods have adapted to life at intermediate Re is expected from empirical analyses using tomographic PIV.

Conclusions

The above examples illustrate how theoretical frameworks can help biologists pose and answer fundamental questions in biological design. Moreover, modeling mathematically unexplored biological systems will generate new mathematical models that are likely to identify new problems in analysis and computation. For example, complex 3D fluid–structure interaction in animal locomotion have motivated the development of new or improved numerical methods such as a Lattice–Boltzman formulation of the immersed boundary method (Zhu et al. 2011), adaptive versions of the immersed boundary and interface methods (Griffith et al. 2009), hybrid vortex sheet methods, and the application of spectral deferred corrections to the method of regularized Stokeslets (L. A. Miller et al., manuscript in preparation). The neuromechanical and control models are expected to lead to similar innovations in modeling and numerical methods. For example, the stochasticity of pacemakers appears to be an integral component of propulsion by jellyfish and will require the development of efficient numerical methods for stochastic neuromechanical models. The active and passive mechanical properties of muscle fibers and the elastic properties of animal tissues have complex geometries and behaviors that will motivate the development of new methods and models for muscular dynamics.

Beyond basic science, the application of physics and mathematics to organismal biology can lead to innovations in industry, medicine, and athletics. For example, research on insect flight has led to the improved design of micro-air vehicles that exhibit the stability and maneuverability of flying animals (Ellington 1999; Rudolph et al. 2002). New numerical methods for studying fully-coupled fluid–structure interactions could be used to model passive and active fin deformations and inform the design of highly maneuverable micro underwater-vehicles (MUVs). Research on swimming at small scales could translate into novel designs for nanoparticles used in drug delivery. Beyond locomotion, similar computational methods could be applied to the study of muscular hydrostats such as octopus arms, earthworm bodies, and elephant trunks. Insights from these studies could be used to improve the design of manipulators with large degrees of freedom.

Comparisons between performances of animals and humans and biomechanics using the tools of mathematics could also lead to advancements in biologically inspired devices and materials. Some examples include hiking shoes with soles modeled after mountain-goat hooves, prosthetic limbs that store elastic energy (Czerniecki et al. 1991), and materials that can self-heal, inspired from abalone shells (Greenwald 2005). Quantitative analyses of these systems can also be an extremely powerful tool for understanding animal design and human biomechanics. A striking example of this was the redesign of the running tracks at Madison Square Garden and the Meadowlands Arena by the late Professor Thomas McMahon based on a simple mechanical model of human runners (McMahon 1990).

Funding

The authors would like to thank the Society for Integrative and Comparative Biology, Divisions of Comparative Biomechanics, Invertebrate Zoology, Vertebrate Morphology, Ecology and Evolution, and Neurobiology for funding and support; travel support for the associated symposium and workshop was also provided by NSF IOS #1132986. The Burroughs Wellcome Fund (to D.I.G. and L.A.M.); NSF Physics of Living Systems, Army Research Lab MAST CTA, Army Research Office, and the Blanchard Milliken fund (to D.I.G.); NSF IOS-0920358 (to T.L.H.) and AFOSR grant FA9550-10-1-006 monitored by Dr Douglas Smith (to T.L.H. and Rajat Mittal); NIH CRCNS R01 NS054271 (to E.T. and Avis H. Cohen) and ARO Grant 111 234 (Sam Stanton, program officer); NSF DMS 1022802 and NSF FRG 0854961 (to L.A.M.); NSF OCE-0928491 (to J.Y.); NSF DMS 1022619 (to S.A.); and NSF (to Z.J.W.).