Linear and nonlinear measures of fetal heart rate patterns evaluated on very short fetal magnetocardiograms

Abstract

We analyzed the effectiveness of linear short- and long-term variability time domain parameters, an index of sympatho-vagal balance (SDNN/RMSSD) and entropy in differentiating fetal heart rate patterns (fHRPs) on the fetal heart rate (fHR) series of 5, 3 and 2 min duration reconstructed from 46 fetal magnetocardiograms. Gestational age (GA) varied from 21 to 38 weeks. FHRPs were classified based on the fHR standard deviation. In sleep states, we observed that vagal influence increased with GA, and entropy significantly increased (decreased) with GA (SDNN/RMSSD), demonstrating that a prevalence of vagal activity with autonomous nervous system maturation may be associated with increased sleep state complexity. In active wakefulness, we observed a significant negative (positive) correlation of short-term (long-term) variability parameters with SDNN/RMSSD. ANOVA statistics demonstrated that long-term irregularity and standard deviation of normal-to-normal beat intervals (SDNN) best differentiated among fHRPs. Our results confirm that short- and long-term variability parameters are useful to differentiate between quiet and active states, and that entropy improves the characterization of sleep states. All measures differentiated fHRPs more effectively on very short HR series, as a result of the fMCG high temporal resolution and of the intrinsic timescales of the events that originate the different fHRPs.

1. Introduction

The different behavioral states observed in the fetus are the functional expression of the intrauterine development of the human central nervous system (CNS). The recognition of normal and abnormal fetal neurological function in utero may lead to a better antenatal prediction of risk for adverse neurological outcomes, irrespective of intrapartum management. Since the assessment of neonatal behavior has been shown to be a better predictor of neurodevelopmental disability than neurological examination (Seme-Ciglenecki 2003, Kurjak et al 2004, 2005), the same approach has been adopted for fetal well-being assessment. Therefore, the characterization of fetal behavioral states evaluated on antenatal functional recordings has become increasingly important in an attempt to assess fetal neurodevelopment.

Since the fetal cardiac rhythm is controlled by the autonomic nervous system (ANS), the analysis of fetal heart rate variability (fHRV) is a simple way to acquire valuable information on fetal behavioral states and, indirectly, on the ANS development. In 1997, the National Institute of Child Health and Human Development Research (NICHHDR) on fetal monitoring developed standardized and unambiguous definitions for fetal heart rate (fHR) tracings, and identified the non-stress test (NST), a cardiotocographic (CTG) recording performed in normal conditions, as an accurate method for identifying healthy fetuses in an intrapartum setting (NICHHDR 1997).

Although recent studies have demonstrated that the NST is affected by poor reproducibility and effectiveness in both ante- and intrapartum FHR recordings (Ayres-de-Campos et al 1999, Bernardes and Ayres-de-Campos 2010), during the last decade the NST has been routinely used in clinical practice to monitor the fHR and uterine contractions and to assess fetal well being (Park et al 2009). Consequently, much attention has been devoted to identifying fHRV parameters that can be evaluated on NST. Since recent studies (Lange et al 2005, 2009, Schneider et al 2008, 2009) have demonstrated that the recommended standards for HRV evaluation in adults (Task Force 1996) cannot be directly applied to fetal studies, new linear and nonlinear parameters started to be tested as potentially better estimators of the fetal state.

Short-term variability (STV) is a linear method based on the difference of beat-to-beat HR variation averages that is widely used to analyze fHRV. An interesting feature of STV is that it does not require very long fHR series to be evaluated. Studies performed on large populations (Dawes et al 1992, Pardey et al 2002) showed that STV is able to discriminate between fetuses with and without severe risk factors. Concurrently, also nonlinear parameters have been employed in the analysis of fHRV, such as entropy, a typical nonlinear quantity used to estimate the regularity of a time series and the presence of nonlinearities (Pincus 1991) that may be suitable to capture the complex behavior of the developing ANS.

In 2003, Signorini et al digitalized CTG recordings of 35 healthy and high-risk fetuses, and calculated the values of linear and nonlinear parameters for periods of quiet and active fetal states previously identified by visual inspection (Signorini et al 2003). They demonstrated that entropy can differentiate between normal and high-risk fetuses in both quiet and active states, with lower values for healthy fetuses. These results were in agreement with those obtained using the linear parameters calculated in the frequency domain.

Later, Magenes et al (2004) investigated the linear and nonlinear features of fHRV extracted from CTG recordings during quiescence periods and after vibroacoustic stimulation, and observed a significant increase in fHRV after vibroacoustic stimulation that was correlated with changes in both entropy and the time domain parameters. In particular, short- and long-term variability parameters increased after stimulation, while entropy was higher during the quiet period before stimulation. In agreement with Signorini et al (2003), Magenes and colleagues suggested that the prevalence of quiet periods in suffering fetuses might produce higher entropy values than in healthy fetuses. These findings were recently corroborated by Annunziata et al (2012), who confirmed the increase of STV and the decrease of entropy after fetal vibroacoustic stimulation, and further observed that these changes were significantly associated with favorable perinatal outcomes.

In 2006, Ferrario et al analyzed CTG recordings grouped by gestational age (GA) at delivery and further classified on the basis of fetal conditions at birth: normal (N), recognized suffering (RS) and not recognized suffering (NRS) (Ferrario et al 2006). They calculated linear HRV parameters and three entropy estimators, and found that the long-term irregularity (LTI, defined in section 2.3.2) was the only linear parameter able to detect significant differences between N and RS fetuses, although only in fetuses near term. On the other hand, they observed that, at earlier gestation (30–35 weeks), the entropy estimators significantly differentiated between RS and NRS fetuses. The higher entropy values found in suffering fetuses were interpreted as a consequence of the prevalence of quiet periods as compared to healthy fetuses.

In 2006, Frank et al analyzed fHR series extracted from fetal magnetocardiographic recordings (fMCG), which offer the advantage over CTG that HR series are calculated on a beat-to-beat basis with a time resolution of 1 ms (Frank et al 2006). Frank and colleagues demonstrated that, when fHR is estimated on fMCG, the combined use of one linear quantity (low-frequency power) and an entropy estimator (Kullback–Leibler entropy) can improve the classification of quiet and active fetal states from 80% to 94% success rate.

A similar approach was adopted by Schneider et al (2008), who analyzed the fMCG of 103 normal fetuses between 24 and 41 gestational weeks. FMCG were grouped on the basis of GA and fetal behavioral patterns classified according to the criteria defined by Nijhuis et al (1982) for fetuses from 32 weeks of gestation onwards, i.e. visual inspection of HRV patterns and detection of acceleration/deceleration occurrence and intensity. Schneider and colleagues identified three fHR patterns (fHRPs) (quiet sleep (fHRP I), active sleep (fHRP II) and active wakefulness (fHRP III)), and observed active wakefulness only in fetuses older than 32 gestational weeks. In addition to standard HRV indices, they calculated the mean permutation entropy (PE_mean) as a complexity measure, and the ratio between SDNN and RMSSD (SDNN/RMSSD) as a potential marker for sympatho-vagal balance in the fetus, given that SDNN provides information on the overall HRV and sympathetic and vagal oscillations (Task Force 1996) while RMSSD reflects vagal control (Elghozi and Julien 2007, Buch et al 2002). In agreement with Frank et al (2006), they found that the combined use of linear (SDNN/RMSSD) and nonlinear (PE_mean) parameters could more effectively classify fHR patterns and assess ANS maturation. This approach was very recently corroborated by the findings of another study on fetal ECG recordings (Signorini et al 2011).

In 2009, Schneider and colleagues further verified that the SDNN/RMSSD ratio is successful in detecting the differential development of the two branches of the fetal ANS that occur before and after 32 weeks of gestation and give origin to the different fHRP.

Other authors have explored the possibility of describing the maturation of the ANS through the quantification of nonlinear features of fHR series derived from fMCG (van Leeuwen et al 1999, 2003, Hoyer et al 2009). Lange et al (2009) verified that fHR and its overall variance were sufficient to classify different fetal behavioral states during late gestation (GA ≥ 36 weeks), and that nonlinear and symbolic dynamics measures, calculated on fHR series obtained from 5 min of high-resolution fMCG, may help elucidate new aspects of these states. They also underlined the value of fMCG in the assessment of short-term fHR changes that may have some relevance to fetal behavioral states.

This study aimed to contribute to (1) the assessment of the effectiveness of linear and nonlinear fHRV measures in differentiating among fetal behavioral states, and (2) to explore the relevance of short-term variability measures in the definition of these states. FHR series were reconstructed from high-resolution fMCG recordings of variable duration, decreasing from 5 to 2 min. FMCGs were recorded during the second half of gestation in singleton pregnancies with no risk factors. Since no acceleration/deceleration patterns can be observed on very short fHR series, fetal behavioral states were identified with fHRPs defined on the basis of the overall fHR variability, measured with the standard deviation of the fHR series, as proposed by Lange et al (2009) for late gestation. FHR series of different durations were then grouped by fHRP, and the obtained fHRV measures were compared with those found by other authors (Magenes et al 2004, Frank et al 2006, Ferrario et al 2006, Schneider et al 2008, Hoyer et al 2009, Annunziata et al 2012). For each fHRP and for each fHR series duration, several quantities were calculated: time domain parameters to estimate short- and long-tem fHRV (Task Force 1996, Magenes et al 2004), the SDNN/RMSSD ratio to evaluate the sympatho-vagal balance and two entropy measures to assess fHRP complexity. Finally, the effectiveness of each parameter in differentiating among fHRP as a function of the fHR series duration was verified.

2. Material and methods

2.1. Acquisition systems and fMCG recordings

A total of 46 fMCG (GA range: 21–38 weeks; average: 27 ± 4 weeks) were recorded in healthy pregnancies. Acquisitions were performed at ITAB, University Foundation `G d'Annunzio', `G d'Annunzio' University, Chieti (Italy) and at the Department of Medical Physics, University of Wisconsin at Madison (USA). All participants provided written informed consent. Before fMCG acquisitions, which had an average duration of 5 to 10 min, the position of the fetal heart was determined by means of an ultrasound scan.

2.1.1. fMCG acquisitions in Chieti (Italy)

Twenty women with singleton uncomplicated pregnancy participated in the study; two of them underwent repeated fMCG acquisitions, for a total of 22 fMCG datasets (GA range: 21–37 weeks). FMCG was acquired with a 55-channel low-temperature dc-SQUID (superconducting quantum interference device) integrated magnetometers system (Argos 200, AtB SrL, Pescara, Italy) operating in a shielded room for environmental magnetic noise reduction. Sampling frequency was 1 kHz, and the analog band-pass filter was 0.016–250 Hz.

2.1.2. fMCG acquisitions in Madison (USA)

Twenty-four fMCG data sets were collected in multiple sessions in six non-symptomatic fetuses (GA range: 24–38 weeks). FMCG was recorded with a 37-channel biomagnetometer (Magnes, 4D Neuroimaging, Inc., San Diego, CA, USA) housed within a high-magnetic permeability room. The signal was digitized at 520 Hz and the analog band-pass filter was 0.1–200 Hz.

2.2. FMCG signal pre-processing

All acquisitions provided data sets of multiple simultaneous recordings in which the fetal cardiac signal was mixed with the maternal cardiac signal and environmental noise. Before extraction of the fetal magnetocardiograms, a digital filter was applied to further band-limit the signals to 1.0–100 Hz (Chieti data) and to 1.0–80 Hz (Madison data). These band-pass filters have very similar performance and do not compromise the quality of the fetal traces (Wakai et al 2003, Comani et al 2005).

Two different methods were used to separate the fetal cardiac signals from the fMCG data sets: an independent component analysis (ICA) algorithm (the fixed-point ICA—FastICA) for the fMCG data sets recorded in Chieti, and the matched filtering method for the fMCG data sets recorded in Madison. FastICA separates signals that originate from statistically independent sources by minimizing their mutual information (Hyvarinen 1999). The fetal and maternal cardiac signals, as well as other physiological and interference signals embedded in the fMCG recordings, are considered statistically independent, and FastICA was demonstrated to have the best performance in fMCG applications (Comani et al 2004, Hild et al 2007). Matched filtering is a temporal filtering technique in which a template of the interfering signal is subtracted from the recording whenever the interfering heartbeat is detected. A template of the maternal QRS complexes is scaled to adapt to beat-to-beat amplitude changes, and then subtracted from the recordings (Wakai and Lutter 2002). The separated fetal magnetocardiograms were then used to reconstruct the fHR series.

2.3. Fetal HR series preparation

2.3.1. Reconstruction of fHR series

For each fetal magnetocardiogram, the R peaks were automatically detected using dedicated software, and the R–R time interval series were calculated (Hamilton and Tompkins 1986). For each fetal magnetocardiogram, an fHR series was then reconstructed from the corresponding R–R time interval series.

2.3.2. Reconstruction of fetal HR sub-series

In order to verify the effectiveness of the linear and nonlinear parameters in typifying the different behavioral patterns on short epochs, three HR sub-series of different durations (5, 3 and 2 min) were reconstructed from each fHR series. The 5 min sub-series was selected at the beginning of the original fHR series, whereas two 3 (2) min sub-series were selected at both the beginning and the end of the original fHR series. Therefore, for each fMCG recording, we had one HR sub-series of 5 min duration, two HR sub-series of 3 min duration and two HR sub-series of 2 min duration.

2.4. Definition of groups (fetal heart rate patterns—fHRPs)

Since the fHR sub-series considered in this study were too short to identify acceleration/deceleration events or other events classically used to define fetal states (Nijhuis et al 1982), we categorized the fHR sub-series into three groups (fHRPs) solely on the basis of the overall fHR variability, measured by the standard deviation of fHR (HRSD). This criterion is compatible with the definition of fHRPs given by Nijhuis et al (1982), as well as by Schneider et al (2008, 2009) and by Lange et al (2009) in previous studies based on fMCG recordings. The groups are defined as follows.

• (1)Group I (quiet sleep, corresponding to fHRP I): HRSD < 5 cycles per minute (cpm).
• (2)Group II (active sleep, corresponding to fHRP II): 5 cpm < HRSD <10 cpm.
• (3)Group III (active wakefulness, corresponding to fHRP III): 10 cpm < HRSD.

2.5. Fetal HRV measures

To extract relevant information about fHRV from each HR sub-series, we computed a set of ten parameters, eight linear parameters in the time domain and two regularity indices or nonlinear measures.

2.5.1. Linear fHRV parameters

The linear time domain parameters include a sub-set of the parameters usually computed in HRV studies in adults (Task Force 1996). Spectral analysis of the fHR series was not included because the representation of the frequency spectrum in the human fetus is currently under discussion, and the low- and high-frequency bands defined for adults seem inappropriate for fetal studies (Hartmann et al 1997, Van Leeuwen et al 2003, David et al 2007). Therefore, since the normal to normal beat intervals (SDNN) and the root mean square of successive differences of the normal beats (RMSSD) reflect the overall variability of sympathetic and vagal oscillations and the vagal control, respectively, their ratio was considered suitable to represent the balance between overall and short-term fHRV, as the LF/HF ratio in adult studies (Schneider et al 2008).

Therefore, the following linear parameters were calculated.

• (1)mHR—the mean fHR during the selected epoch, in cpm.
• (2)HRSD—heart rate standard deviation, in cpm, used to define the behavioral groups.
• (3)SDNN—defined as the standard deviation of normal-to-normal beat intervals in ms. This parameter expresses the overall variability of sympathetic and vagal oscillations in short data windows.
• (4)RMSSD—the root mean square of successive differences in ms. This parameter reflects vagal control.
• (5)SDNN/RMSSD—the ratio between SDNN and RMSSD, introduced by Schneider et al (2008) as a new marker of the sympatho-vagal balance. This parameter substitutes for the LF/HF ratio, which is a frequency domain measure that expresses the ratio between the spectral power in the low- (0.04–0.15 Hz) and in the high-frequency (0.15–0.4 Hz) bands (Task Force 1996).
• (6)
  Delta—a raw measure of the short-term RR time interval variability in a given time window. This parameter, given in ms, is calculated on a per minute basis and is a raw measure of fHRV. It is defined as (Magenes et al 2004)

  $$\text{Delta}=\frac{\sum _{i=1}^m[\text{max}\left(T_{24}\left(i\right)\right)-\text{min}\left(T_{24}\left(i\right)\right)]}{m},$$

  where m is an index identifying each minute of the RR interval series, and T₂₄ is the mean RR time interval (in ms) calculated every 2.5 s. The maximum and minimum T₂₄(i) are calculated for each minute.
• (7)
  STV (short-term variability)—an indirect beat-to-beat measure of fHRV estimated in 1 min intervals (given in ms). It is defined as (Magenes et al 2004)

  $$\text{STV}=\frac{\sum _{i=1}^{24}{T}_{24}(i+1)-T_{24}\left(i\right)}{24},$$

  where T₂₄(i) is defined as for Delta. This algorithm will produce 24 STV values for each minute.
• (8)
  LTI (long-term irregularity)—a long-term measure of fHRV. This parameter (given in ms) is defined as the inter-quartile range (1/4–3/4) of the distribution l₂₄(j), calculated over 3 min (Magenes et al 2004); l is calculated as follows:

  $$l_{24}\left(j\right)=\sqrt{{T_{24}}^2\left(j\right)+{T_{24}}^2(j+1)},$$

  for j ∈ [a; b – 1], b – a = 72 (3 min).

When LTI was calculated on the 2 min HR sub-series, the algorithm was adapted to the shorter timescale.

2.5.2. Nonlinear fHRV parameters

The calculated regularity indices are as follows

• (9)ApEn (approximated entropy)—a measure of signal regularity (Pincus 1991, Pincus et al 1991). ApEn expresses the logarithmic frequency with which blocks of m consecutive signal values will remain close to each other within a tolerance of r. Therefore, small values of ApEn indicate strong repeatability in a sequence, whereas large ApEn values entail large fluctuations and reduced predictability of the signal. ApEn is the most widely used class of entropy, and, despite its strong dependence on record length (Pincus et al 1991), it generally provides reliable information on the regularity of a signal.
• (10)SampEn (sample entropy)—another measure of signal regularity (Richman and Moorman 2000) developed to overcome the limitations of ApEn related to recording length and to the possible lack of consistency in the quantification of the signal's regularity on short recordings.

2.6. Statistical analysis

For each group (Groups I, II and III), we estimated the dependence of the linear and nonlinear parameters on fetal maturation and on the sympatho-vagal balance by calculating their correlation with GA and SDNN/RMSSD, respectively. The Pearson product-moment correlation coefficient r was calculated to measure the strength of the linear dependence between two variables. It calculates the covariance of the two variables divided by the product of their standard deviations. Three levels of statistical significance were considered: p < 0.001, p < 0.01 and p < 0.05.

In order to verify the effectiveness of the linear and nonlinear parameters in differentiating across the different behavioral states (Groups I, II and III), we performed a one-way analysis of variance (ANOVA) across groups for all parameters except HRSD, since it was used to define the groups.

The ANOVA statistics generalizes the t-test to more than two groups. Performing multiple two-sample t-tests would increase the chance of committing a type I error. For this reason, ANOVA produces an F-statistic, the ratio of the variance calculated among the means to the variance within the groups. If the group means are drawn from the same population, the variance between them should be lower than the variance of the samples, following the central limit theorem. A higher ratio therefore implies that the samples were drawn from different populations. We used the one-way ANOVA because we wanted to examine the significant effect of one independent variable at a time (each of our fetal FHR measures) on the three defined groups.

Both Pearson correlation and ANOVA statistics were separately performed for the different HR sub-series (5, 3 and 2 min duration).

3. Results

3.1. General statistics

The numbers of HR sub-series available for the entire study population and for the defined groups (I, II and III) as well as the related GA range are given in table 1. The upper limit of the GA range for Groups II and III exceeds 32 weeks because of two fetuses only, at 35 and 38 weeks, respectively. The small number of HR series included in Group III is due to the fact that fHRPs of higher variability generally occur during the second half of the third trimester, i.e. for GA > 32 weeks (Schneider et al 2008). For these reasons, the results of our analysis essentially refer to fetuses younger than 32 weeks GA. Furthermore, the results obtained for Group III should be considered with caution, given the small number of cases.

Table 1.

Number of HR sub-series available for the entire population of fMCG recordings and for the defined groups (Groups I, II and III). For each group and for each HR sub-series, the gestational age (GA) range (minimum GA–maximum GA) is given in weeks.

			Group I		Group II		Group III
	Entire population		Quiet sleep		Active sleep		Active wakefulness
HR series duration	Number of HR series	GA range	Number of HR series	GA range	Number of HR series	GA range	Number of HR series	GA range
5 min	46	21–38	19	22–31	20	21–38	7	25–35
3 min	92	21–38	41	21–31	42	21–38	9	21–35
2 min	92	21–38	49	21–31	34	21–38	9	25–35

The distribution characteristics of the linear and nonlinear parameters calculated for each group and for each HR sub-series are given in table 2. In agreement with previous results (Schneider et al 2008), we found an increase of the SDNN/RMSSD ratio and a decrease of entropy (both ApEn and SampEn) from quiet to active state. By comparing the results obtained for the different HR sub-series, we can see how these trends are more marked on the shorter HR sub-series. In particular, SampEn seems to have the maximum variation from quiet to active state on the shortest HR sub-series (2 min duration).

Table 2.

Distribution characteristics (median; 25th, 75th percentile in parentheses) of the linear and nonlinear fHRV measures obtained for the different groups (entire population, Groups I, II and III). The parameters were calculated for the different HR sub-series (5, 3 and 2 min duration) separately. The number of total HR sub-series analyzed for each group is given in parentheses. The number of 3 and 2 min HR sub-series included in Groups I, II and III differ because the groups were defined separately for these HR sub-series.

5 min HR sub-series
	Entire population (46)	Group I (19)	Group II (20)	Group III (7)
mHR (cpm)	143 (140;147)	142 (140;145)	143 (138;147)	152 (147;154)
SDNN (ms)	17.6 (12.0;22.7)	11.6 (9.6;12.7)	21.1 (19.1;22.7)	32.9 (27.9;35.6)
RMSSD (ms)	5.1 (4.4;6.0)	4.0 (2.7;5.0)	5.9 (5.2;8.9)	5.1 (4.7;8.2)
SDNN/RMSSD	2.9 (2.6;4.0)	2.8 (2.4;3.6)	2.9 (2.6;3.8)	5.5 (4.3;5.9)
Delta (ms)	41.6 (31.6;62.5)	31.6 (26.2;37.7)	54.5 (37.4;65.7)	75.7 (67.8;91.5)
STV (ms)	6.0 (4.7;8.2)	4.6 (3.9;5.3)	7.3 (6.2;8.8)	9.2 (7.8;10.4)
LTI (ms)	23.8 (17.6;40.8)	17.6 (15.0;19.9)	30.9 (23.7;40.5)	63.2 (57.1;67.1)
ApEn	0.64 (0.56;0.84)	0.79 (0.62;1.00)	0.64 (0.55;0.80)	0.51 (0.46;0.56)
SampEn	0.54 (0.41;0.67)	0.66 (0.50;0.95)	0.55 (0.40;0.63)	0.39 (0.35;0.44)

3 min HR sub-series
	Entire population (92)	Group I (41)	Group II (42)	Group III (9)
mHR (cpm)	143 (139;147)	143 (141;146)	142 (138;146)	150 (141;153)
SDNN (ms)	15.9 (10.0;22.5)	9.7 (8.1;11.3)	20.3 (17.6;23.8)	31.7 (31.0;33.3)
RMSSD (ms)	4.8 (3.8;6.2)	3.9 (2.8;4.6)	5.7 (4.7;6.9)	7.3 (5.4;8.2)
SDNN/RMSSD	3.0 (2.3;3.8)	2.4 (2.1;3.2)	3.2 (2.7;4.1)	4.9 (3.7;5.8)
Delta (ms)	44.7 (30.7;66.9)	29.8 (26.1;35.6)	61.1 (50.1;71.6)	87.3 (78.5;91.9)
STV (ms)	6.0 (4.6;8.5)	4.5 (3.8;4.8)	7.6 (6.1;9.5)	10.3 (7.7;14.5)
LTI (ms)	23.5 (15.6;35.4)	14.8 (12.7;18.8)	30.4 (26.0;37.7)	68.0 (55.4;73.7)
ApEn	0.70 (0.55;0.87)	0.84 (0.67;1.01)	0.64 (0.52;0.78)	0.52 (0.38;0.62)
SampEn	0.59 (0.43;0.79)	0.75 (0.57;1.34)	0.52 (0.39;0.67)	0.37 (0.25;0.54)

2 min HR sub-series
	Entire population (92)	Group I (49)	Group II (34)	Group III (9)
mHR (cpm)	143 (139;147)	143 (140;146)	142 (138;148)	146 (141;151)
SDNN (ms)	14.5 (9.5;20.4)	9.8 (8.2;12.4)	19.1 (16.3;22.4)	34.3 (31.4;38.2)
RMSSD (ms)	4.8 (3.6;6.2)	4.1 (3.2;5.0)	5.1 (4.1;6.7)	7.4 (6.4;15.3)
SDNN/RMSSD	2.6 (2.2;4.0)	2.2 (1.8;3.1)	3.6 (2.6;4.7)	4.6 (2.6;5.5)
Delta (ms)	44.0 (30.3;61.2)	30.8 (25.1;36.8)	59.9 (50.4;68.3)	94.2 (82.5;144.0)
STV (ms)	5.7 (4.5;8.5)	4.7 (3.5;5.4)	7.5 (6.7;10.1)	12.4 (11.2;14.0)
LTI (ms)	23.5 (15.8;35.8)	16.4 (12.7;19.8)	34.0 (27.2;42.2)	63.7 (51.9;73.7)
ApEn	0.71 (0.56;0.87)	0.85 (0.65; 0.93)	0.64 (0.52;0.72)	0.42 (0.38;0.48)
SampEn	0.66 (0.43;1.13)	1.02 (0.58;1.55)	0.52 (0.42;0.68)	0.32 (0.27;0.36)

Also other parameters increased from quiet to active state, namely SDNN, RMSSD, Delta, STV and LTI. Similar variations of Delta, STV and LTI were observed by other authors (Magenes et al 2004, Hoyer et al 2009, Annunziata et al 2012). Slight differences can be observed in the values of these parameters across groups as a function of the HR sub-series duration. Furthermore, a remarkable change in mHR could be observed only between sleep and wakefulness (Groups I and II versus Group III).

3.2. Pearson correlation tests

The results of the Pearson correlation test between the calculated parameters and GA are summarized in table 3, where only significant correlations are reported. The Pearson correlation test did not highlight any significant dependence of the linear and nonlinear parameters on GA when the entire population was considered (not reported).

Table 3.

Pearson correlation between the variability measures and gestational age (GA) for the three HR sub-series and as a function of the defined groups (Groups I, II and III). The number of total HR sub-series analyzed for each group is given in parentheses. As for table 2, the number of 3 and 2 min HR sub-series included in Groups I, II and III differ because the groups were defined separately for these HR sub-series. Only significant correlations are reported.

5 min HR sub-series
	Group I (19)	Group II (20)	Group III (7)
SDNN	−0.49*	−0.45*
RMSSD		−0.51*
SDNN/RMSSD	−0.61**
LTI	−0.59**
SampEn		0.44*

3 min HR sub-series
	Group I (41)	Group II (42)	Group III (9)
STV	0.33*
SDNN/RMSSD	−0.33*

2 min HR sub-series
	Group I (49)	Group II (34)	Group III (9)
SDNN	−0.43**		−0.74*
RMSSD		−0.36*
SDNN/RMSSD	−0.29*
LTI	−0.47***
ApEn	0.36**
SampEn	0.38**

^***p < 0.001,

^**p < 0.01,

^*p < 0.05.

When the two fHRPs related to sleep were considered (Groups I and II, i.e. quiet and active sleep), only a few parameters showed a significant correlation with GA. In agreement with Schneider et al (2008), we found a significant negative dependence of SDNN/RMSSD on GA for Group I on all HR sub-series (p ranging from 0.05 to 0.01), although the correlation became weaker as the duration of the HR sub-series decreased (r ranging from −0.61 to −0.29). We also observed a significant negative correlation between LTI and GA for Group I on the 5 and 2 min HR sub-series, and a weak positive correlation between STV and GA for Group I on the 3 min HR sub-series. Positive correlations between entropy measures and GA were obtained for Group II on the longest HR sub-series (SampEn) and for group I on the shortest HR sub-series (ApEn and SampEn). This result is in contrast with the findings by Schneider et al (2008), who observed no correlation between entropy and GA for quiet and active sleep states and a negative correlation between entropy and GA for active wakefulness.

When the active wakefulness group was considered (Group III), a significant correlation was observed only between SDNN and GA on the 2 min HR sub-series (r −0.74, p < 0.05), in contrast with the finding by Hoyer et al (2009), who observed an increase of SDNN with GA for active wakefulness. However, this inconsistency between Hoyer's results and ours may be due to several factors, such as the length of the HR series (Hoyer analyzed series of at least 30 min duration) and/or, most probably, the small number of cases included in our Group III. For these reasons this result might not be reliable and we will not consider it in the discussion.

The Pearson correlation test between the linear and nonlinear parameters and SDNN/RMSSD aimed at assessing any significant correlation between these parameters and the sympatho-vagal balance in the fetus. The results are summarized in table 4, where only significant correlations are reported.

Table 4.

Pearson correlation between the variability parameters and SDNN/RMSSD for the three HR sub-series and the defined groups. The number of total HR sub-series analyzed for each group is given in parentheses. Only significant correlations are reported.

5 min HR sub-series
	Entire population (46)	Group I (19)	Group II (20)	Group III (7)
SDNN	0.42**
RMSSD	−0.33*	−0.64**	−0.74***	−0.91**
STV		−0.48*
LTI	0.54***
ApEn	−0.60***	−0.77***
SampEn	−0.51***	−0.66**

3 min HR sub-series
	Entire population (92)	Group I (41)	Group II (42)	Group III (9)
SDNN	0.41***
RMSSD	−0.28**	−0.66***	−0.68***	−0.89**
Delta	0.29**
STV		−0.46**		−0.86**
LTI	0.60***	0.44**	0.33*	0.87**
ApEn	−0.69***	−0.74***	−0.51***
SampEn	−0.58***	−0.65***	−0.36*

2 min HR sub-series
	Entire population (92)	Group I (49)	Group II (42)	Group III (9)
SDNN	0.37***
RMSSD	−0.32**	−0.55***	−0.75***	−0.94***
Delta			−0.48**
STV		−0.30*	−0.45**
LTI	0.54***	0.42**		0.88**
ApEn	−0.69***	−0.74***	−0.55***
SampEn	−0.65***	−0.68***	−0.48**

^***p < 0.001,

^**p < 0.01,

^*p < 0.05.

First, we observed an obvious correlation between SDNN/RMSSD and SDNN (positive correlation, entire population, all HR sub-series, p varying from <0.01 to <0.001) and between SDNN/RMSSD and RMSSD (negative correlation, all groups, all HR sub-series, p varying from <0.05 to <0.001, increasing correlation coefficient from quiet to active states).

In agreement with Schneider et al (2008), we also observed a highly significant negative correlation between SDNN/RMSSD and the entropy measures (ApEn and SampEn) for the entire population and for Group I on all HR sub-series (p < 0.001; in one case p < 0.01), as well as for Group II on the two shorter HR sub-series (p varying from <0.05 to <0.001).

With regard to the short-term variability measures, Delta showed fairly weak although significant correlations with SDNN/RMSSD: a positive correlation for the entire population on the 3 min HR sub-series (r = 0.29, p < 0.01), and a negative correlation for Group II on the 2 min HR sub-series (r = −0.48, p < 0.01). Conversely, STV always negatively correlated with SDNN/RMSSD: a weak correlation for Group I on all HR sub-series (r ranging from −0.30 to −0.48, p varying from <0.05 to <0.01), a weak correlation for Group II on the 2 min HR sub-series (r = −0.45, p < 0.01), and a strong correlation for Group III on the 3 min HR sub-series (r = −0.86, p < 0.01).

On the other hand, LTI showed a highly significant positive correlation with SDNN/RMSSD for the entire population on all HR sub-series (p < 0.001), and for all groups on the two shorter HR sub-series (p varying from <0.05 to <0.01). It is noteworthy that the values of the correlation coefficient for active wakefulness were much higher than those for sleep states (r = 0.87 and 0.88).

3.3. ANOVA statistics

The one-way ANOVA statistics across groups was performed to verify the effectiveness of the linear and nonlinear parameters in differentiating among fHRPs (Groups I, II and III). The results of the analysis performed for the three HR sub-series are summarized in figure 1 (5 min HR sub-series), figure 2 (3 min HR sub-series) and figure 3 (2 min HR sub-series).

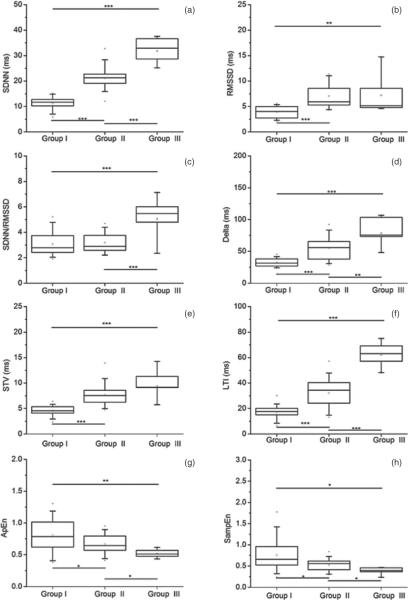
Figure 1.

ANOVA statistics for each variability parameter across groups, as calculated on the 5 min HR sub-series. *** p ≤ 0.001, ** p ≤ 0.01 and * p ≤ 0.05. The panels refer to: (a) SDNN; (b) RMSSD; (c) SDNN/RMSSD; (d) Delta; (e) STV; (f) LTI; (g) ApEn; (h) SampEn.

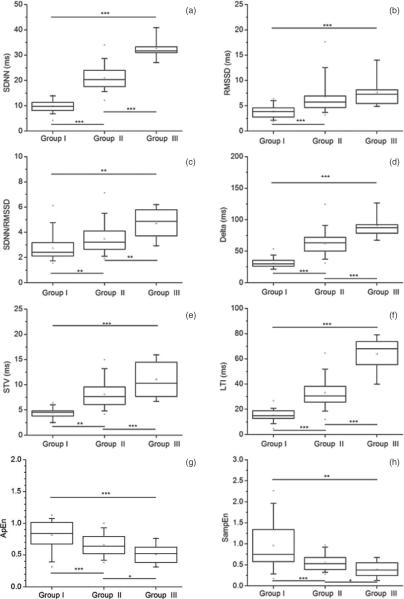
Figure 2.

ANOVA statistics for each variability parameter across groups, as calculated on the 3 min HR sub-series. *** p ≤ 0.001, ** p ≤ 0.01 and * p ≤ 0.05. The panels refer to (a) SDNN; (b) RMSSD; (c) SDNN/RMSSD; (d) Delta; (e) STV; (f) LTI; (g) ApEn; (h) SampEn.

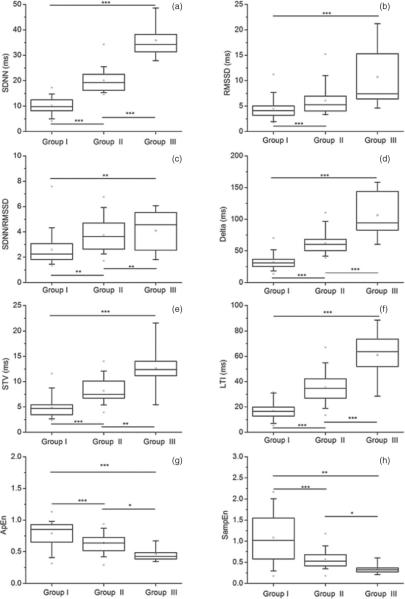
Figure 3.

ANOVA statistics for each variability parameter across groups, as calculated on the 2 min HR sub-series. *** p ≤ 0.001, ** p ≤ 0.01 and * p ≤ 0.05. The panels refer to (a) SDNN; (b) RMSSD; (c) SDNN/RMSSD; (d) Delta; (e) STV; (f) LTI; (g) ApEn; (h) SampEn.

We can see that most of the variability measures differentiated among groups. Among them, LTI and SDNN showed the best performance, since they were the only parameters able to differentiate among all groups on all HR sub-series at a very high significance level (p < 0.001). RMSSD differentiated between quiet and active states (Group I versus Group II, and Group I versus Group III) on all HR sub-series (p < 0.001).

Although we observed an increasing SDNN/RMSSD value from Groups I to III on all HR sub-series (see table 2), the ANOVA statistics showed that SDNN/RMSSD differentiated across all groups only on the shorter HR sub-series (3 and 2 min duration, p < 0.01), and only between Groups I and III and between Groups II and III when the longer HR sub-series was used (p < 0.001).

With regard to short-term variability measures, Delta differentiated among all groups on all HR sub-series at a very high significance level (p < 0.001), with a small drop in significance (p < 0.01) for the comparison between Groups II and III on the longer HR sub-series. STV also performed very well on the 3 and 2 min HR sub-series, differentiating among all groups (p varying from <0.01 to <0.001). However, STV failed to differentiate between Groups II and III on the 5 min HR sub-series.

Finally, both ApEn and SampEn differentiated among all groups on all HR sub-series, but with variable significance levels (p varying from <0.05 to <0.001). These results are in line with those obtained by Schneider et al (2008), who showed that the mean permutation entropy was able to differentiate between fHRPs I and II and between fHRPs II and III, although only on a subgroup of GA ranging approximately from 35 to 41 weeks. Our findings on ApEn and SampEn are as well in agreement with Frank et al (2006), who demonstrated an improved differentiation between quiet and active states using entropy estimators.

4. Discussion

The purpose of this study was to contribute to the assessment of the effectiveness of linear and nonlinear fHRV measures in differentiating among fetal states defined exclusively on the basis of the overall fHR variability, and to explore the relevance of linear and nonlinear fHRV measures in the definition of these states, especially when very short fMCG recordings were used to reconstruct fHR series. The linear and nonlinear fHRV measures calculated for the different fHRPs from the 21st gestational week onward were largely in agreement with previous findings by other authors, although we could not evaluate the influence of fetal gender on the fHRV measures, observed by some authors in both normal and growth-restricted fetuses (Van Leeuwen et al 2006, Gonçalves et al 2007, Bernardes et al 2009, Aziz et al 2012). Unfortunately, we had no information on the sex of the fetuses included in our study population, which we can only hypothesize to be evenly distributed between males and females. We achieved also some new results, especially related to the use of short time series, as we will discuss in detail below.

FMCG allows for a beat-to-beat reconstruction of the R–R intervals, and also for a more precise quantification of the R–R interval durations, with a resolution of ±ms. The high temporal resolution of fMCG is undoubtedly crucial for the detection of short-term features of the fHR behavior, which, on the contrary, could be overlooked when techniques with lower time resolution such as cardiotocography are used. If we consider the higher frequencies associated with vagal modulation (up to 1.7 Hz), cardiotocography does not appear an optimal system to analyze autonomic rhythms, whereas the high temporal resolution of fMCG can improve our understanding of the developing ANS. For the same reasons, we expect that the more precise quantification of the overall fHR variability, measured as the standard deviation of the HR series (HRSD) reconstructed from MCG recordings, can be reliably used to classify the groups, or fetal states. Our results on the variations of linear and nonlinear fHRV measures among groups confirm the reliability of this approach, in agreement with other authors (Schneider et al 2008, 2009, Lange et al 2009). We adopted a very simple criterion to classify the groups also because we wanted to test the relevance of linear and nonlinear fHRV measures to define the fetal states on very short fHR series, and therefore we could not base the definition of the fetal states on the observation of events such as accelerations/decelerations, which can be detected only on longer timescales. The lower accuracy of cardiotocography with respect to fMCG and the different gestational period considered can explain the differences between our results and those obtained by other authors, who observed an overlapping of intra- and inter-fetal fHR variations occurring across the fHRP in the antepartum period (Gonçalves et al 2007).

In agreement with Schneider et al (2008), we found an increase of the SDNN/RMSSD ratio from quiet (Group I) to active (Group II) states, which is considered a sign of increasing HRV and fetal activity, and demonstrates the prevalence of sympathetic activity during active states. Interestingly, we could clearly detect this trend also on very short HR sub-series (2 min duration). Consistent with this result and in agreement with another author (Hoyer et al 2009), we also observed a predominance of sympathetic activity during active wakefulness. The other linear parameters measuring fHRV also increased from quiet to active states, as previously observed by other authors (Magenes et al 2004, Annunziata et al 2012), but we further demonstrated that their changes were more evident on the shorter HR sub-series. We also detected a decrease of both entropy estimators from quiet to active states on all HR sub-series, which shows how active states are characterized by less complex patterns. This result is in agreement with previous observations that entropy decreased after vibroacoustic stimulation (Magenes et al 2004, Annunziata et al 2012) and was higher in suffering fetuses because of a prevalence of quiet periods (Signorini et al 2003, Ferrario et al 2006, Gonçalves et al 2007, Bernardes et al 2008). Again, we observed that the changes in the entropy values among the fHRPs were more marked on shorter HR sub-series. In particular, SampEn underwent the largest changes from quiet to active states on the 2 min HR sub-series.

However, it should be kept in mind that contradictory results have been obtained so far with regard to the value of entropy measures in differentiating behavioral states in healthy fetuses and in fetuses affected by severe pathologies such as intrauterine growth restriction (IUGR) or acidemia (Ferrario et al 2009, Gonçalves et al 2006, Yum et al 2001). Indeed, Ferrario et al (2009) used multiscale entropy (MSE) and the algorithmic complexity of a time series proposed by Lempel and Ziv (1976) to separate severe IUGR fetuses from not so severe IUGR and normal fetuses during the last weeks before delivery, and found that severe IUGR fetuses showed higher entropy values than normal and not severe IUGR fetuses. This result, which seems incongruent with their previous findings on normal, recognized suffering and not recognized suffering fetuses (Ferrario et al 2006), is in agreement with the outcome of other studies on compromised laboratory animals (Gonçalves et al 2008, 2010) or human fetuses affected by cardiac failure or acidemia (Yum et al 2001, Gonçalves et al 2006).

Since these studies were based on cardiotocographic recordings, we may hypothesize that the inconsistencies derive, even partly, from the use of cardiotocography, which has a very low time resolution as compared to fMCG and is affected by a number of pitfalls affecting its reliability (Ayres-de-Campos et al 1999, Bernardes and Ayres-de-Campos 2010). It may well be that the higher entropy values observed by these authors in sick fetuses at term (Ferrario et al 2009, Gonçalves et al 2006, Yum et al 2001) are a sign of more complex fHR patterns with very rapid fHR variations, in agreement with our results on increased vagal control toward the end of pregnancy, as detailed below. However, this panorama suggests that further studies are needed to test the role of entropy measures in differentiating fetal states in severely suffering fetuses and in separating healthy fetuses from IUGR fetuses or fetuses affected by acidemia. We believe that these studies should be performed using fMCG, because this technique has a higher time resolution than cardiotocography and allows for a more precise definition of the R–R intervals.

With regard to the dependence of the linear and nonlinear parameters on GA, we could confirm the result by Schneider et al (2008) that a significant decrease of SDNN/RMSSD with GA occurred during quiet sleep states (Group I), indicating an increased level of vagal influence toward the end of pregnancy. Given that vagal impulses occur on short timescales, this assumption implies an increase of short-term activity with increasing GA during quiet sleep. Consistent with this assumption, we observed that in quiet sleep states long- and short-term variability (measured by LTV and STV, respectively), decreased and increased as gestation progressed.

When we analyzed the correlation between entropy and GA, we found a significant increase in entropy with GA in sleep states, which is in contrast with the findings by Schneider et al (2008), who observed no correlation between entropy and GA for quiet and active sleep states, and a negative correlation between entropy and GA for active wakefulness. Since the values of mHR for all groups in our population are comparable on all HR sub-series, and given that the correlation coefficients for entropy and GA are quite low (between 0.36 and 0.44), we might interpret this outcome as an indication that sleep states tend to be characterized by fHRPs with a higher level of complexity as gestation advances. This interpretation is corroborated by the already mentioned concurrent decrease/increase of long-/short-term variability (measured by LTI and STV) with GA during quiet sleep. Since the positive correlation between entropy and GA in our data is more evident for quiet sleep states and for short HR series, it might be possible that the apparent incongruence with the results by Schneider et al (2008) be ascribed to the duration of the HR series. In this case, shorter series could be more suitable to detect possibly transient although significant entropy variations that might be smoothed out when averaging on longer HR series. An increase of entropy with GA in quiet sleep is also consistent with the increase of short-term activity, measured by STV, and of vagal influence observed toward late gestation for the same state, as discussed earlier.

When we assessed whether any significant correlation occurred between the linear and nonlinear parameters and the sympatho-vagal balance in the fetus, quantified by the SDNN/RMSSD ratio, we observed a highly significant negative correlation between entropy and SDNN/RMSSD during sleep states. This correlation was stronger on the shorter HR sub-series. The fact that lower values of ApEn and SampEn were associated with increased values of the SDNN/RMSSD ratio during sleep states is in agreement with the remark by Schneider et al (2008) that increased SDNN/RMSSD values were correlated with decreased mean permutation entropy. This further demonstrates that increased overall ANS activity (SDNN) occurring at the cost of reduced parasympathetic activity (RMSSD) is associated with low complexity. Considering that SDNN/RMSSD decreases with GA during quiet states and that higher levels of complexity tend to characterize sleep states as GA advances, we interpret the negative correlation between entropy and SDNN/RMSSD as a demonstration that the prevalence of vagal influence with ANS maturation, indicated by several authors (Ohta et al 1999, Zhuravlev et al 2002, Schneider et al 2008), might be associated with an increase in complexity of the fHRPs during sleep states.

We further observed a significant negative correlation of STV and a concurrent significant positive correlation of LTI with SDNN/RMSSD. Both correlations were stronger for active wakefulness states, and more evident on the two shorter HR sub-series. The other short-term variability measure, Delta, did not show a consistent correlation with SDNN/RMSSD, except for a significant negative correlation during active sleep detected on very short HR sub-series. These results can be explained in relation to the typical timescales of parasympathetic and sympathetic activities, with vagal impulses being more rapid than sympathetic stimulation. From this perspective, the short-term variations of the fHR series, quantified by STV (and ultimately also by Delta), would reflect vagal control, whereas longer term variations, quantified by LTI, would reflect sympathetic activity or, more generally, the overall ANS activity. Since vagal control prevails under resting conditions, the strong negative (positive) correlation of STV (LTI) with SDNN/RMSSD during active wakefulness could convey augmented parasympathetic activity during active wakefulness tending to return the body functions to normal after they have been altered by sympathetic stimulation. This interpretation is also supported by the fact that the relations between short- and long-term variability measures and the SDNN/RMSSD ratio are more evident on shorter HR series. Similarly to what is observed earlier with regard to the relation of LTI, STV and entropy with GA during quiet sleep, very short HR sub-series seem to be more appropriate for the characterization of rapid events on the basis of the sympathetic/parasympathetic balance. Nonetheless, our results on active wakefulness should be taken with caution, because Group III includes only a small number of cases. In order to verify the consistency of our findings, it would be interesting to reproduce our study on a larger population of fetuses near term, when active wakefulness states are more frequent.

Another purpose of our study was to assess the performance of the linear and nonlinear parameters in the differentiation among groups (fHRPs) on very short time series, which might provide us with a simple tool for the identification of fetuses with abnormal behavior.

Our results show that almost all variability measures differentiated among groups. However, the best results were achieved with LTI and SDNN, both able to differentiate among all groups on all HR sub-series at a very high significance level (p < 0.001). It was demonstrated that both LTI and SDNN are an expression of fHRP long-term variability related to the overall ANS activity with a prevalence of sympathetic activation, which is at the origin of fetal activity. The observation that LTI is able to differentiate among fetal states complements the findings by Ferrario et al (2006), who demonstrated, for fetuses at term, that LTI was the only linear fHRV parameter able to discriminate between normal and suffering fetal conditions. From these results, it is evident that measures of the overall ANS activity (SDNN) or of the associated long-term variability (LTI) can be effectively used to distinguish different fetal states, even on very short HR series. Conversely, RMSSD differentiated very well between quiet and active states, but not between sleep and wakefulness, confirming that RMSSD is strongly modulated by vagal activation and is not representative of the entire system.

On the other hand, when we consider the results of the ANOVA statistics on SDNN/RMSSD, we can see how this parameter differentiated across all groups, but more effectively when shorter time series were used. This finding confirms our comments on the relationship between short- and long-term variability measures and the SDNN/RMSSD ratio: SDNN and RMSSD are sensitive to differential changes in the sympathetic and vagal activities, which are characterized by longer and shorter timescales, respectively. Our results suggest that the actual balance between sympathetic and parasympathetic activation, which causes the different fHRPs, could be more efficiently detected on shorter HR series.

Coherently with this hypothesis that short HR series were more suitable to detect the rapid changes occurring in the sympathetic/parasympathetic balance, we observed that also the two short-term variability measures (Delta and STV) differentiated among all groups (fHRPs) at a very high significance level, especially when the two shorter HR series were used.

Finally, both ApEn and SampEn differentiated among all groups on all HR sub-series, again with higher significance levels on shorter HR series. These results complement those obtained by Schneider et al (2008), who showed that the mean permutation entropy was able to differentiate between quiet sleep and active sleep, and between active sleep and active wakefulness on a group of fetuses with GA ranging from 35 to 41 weeks. Our findings are also compatible with the observation by Frank et al (2006) that the differentiation between quiet and active states was improved when entropy estimators were used together with a linear measure of the overall ANS activity.

As a concluding remark, we may say that our results confirm a number of previous findings on the meaning and effectiveness of the linear and nonlinear parameters used to evaluate and distinguish the fHRPs. Short- and long-term variability parameters can provide useful information for the evaluation of the changes in the sympatho-vagal balance occurring during the transition from quiet to active states and vice versa. In particular, LTI and SDNN seem to be the most effective parameters to separate among fetal states. On the other hand, our results showed that entropy estimators may improve the characterization of sleep states and their differentiation from active wakefulness. Consequently, a conjoint use of linear time-domain fHRV parameters and of entropy estimators should be recommended, in agreement with other authors who demonstrated that this approach improves the characterization of fetal states in all their variants (Schneider et al 2008, Frank et al 2006).

Another interesting result of our study regards the effect of very short HR series on the estimate of the linear and nonlinear parameters used to assess the fHRPs. In particular, short-term variability measures and entropy estimators seemed to become more effective in separating fetal states when the 2 min HR series were used. As already discussed, this may be related to the intrinsic timescales of the events causing the onset or the disruption of the different fHRPs. We are convinced that the effectiveness of such short HR series and of short-term variability parameters is also related to the high time resolution of fMCG recordings. Further investigation on a larger population of fetuses with GA spanning from mid-pregnancy to term would be useful to better understand the behavior of the linear and nonlinear parameters as a function of the different fetal behavioral states along gestation.