Abstract
Motivation: A common practice in biomarker discovery is to decide whether a large laboratory experiment should be carried out based on the results of a preliminary study on a small set of specimens. Consideration of the efficacy of this approach motivates the introduction of a probabilistic measure, for whether a classifier showing promising results in a small-sample preliminary study will perform similarly on a large independent sample. Given the error estimate from the preliminary study, if the probability of reproducible error is low, then there is really no purpose in substantially allocating more resources to a large follow-on study. Indeed, if the probability of the preliminary study providing likely reproducible results is small, then why even perform the preliminary study?
Results: This article introduces a reproducibility index for classification, measuring the probability that a sufficiently small error estimate on a small sample will motivate a large follow-on study. We provide a simulation study based on synthetic distribution models that possess known intrinsic classification difficulties and emulate real-world scenarios. We also set up similar simulations on four real datasets to show the consistency of results. The reproducibility indices for different distributional models, real datasets and classification schemes are empirically calculated. The effects of reporting and multiple-rule biases on the reproducibility index are also analyzed.
Availability: We have implemented in C code the synthetic data distribution model, classification rules, feature selection routine and error estimation methods. The source code is available at http://gsp.tamu.edu/Publications/supplementary/yousefi12a/. Supplementary simulation results are also included.
Contact: edward@ece.tamu.edu
Supplementary Information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Perhaps no problem in translational genomics has received more attention than the discovery of biomarkers for phenotypic discrimination. To date, there has been little success in developing clinically useful biomarkers and much has been said concerning the lack of reproducibility in biomarker discovery (Boulesteix and Slawski, 2009; Ioannidis, 2005; Sabel et al., 2011; Zhang et al., 2008). In particular, recently a report concerning comments made by US Food and Drug Administration (FDA) drug division head Janet Woodcock stated:
Janet Woodcock, drug division head at the FDA, this week expressed cautious optimism for the future of personalized drug development, noting that ‘we may be out of the general skepticism phase, but we’re in the long slog phase…’. The ‘major barrier’ to personalized medicine, as Woodcock sees it is ‘coming up with the right diagnostics’. The reason for this problem is the dearth of valid biomarkers linked to disease prognosis and drug response. Based on conversations Woodcock has had with genomics researchers, she estimated that as much as 75% of published biomarker associations are not replicable. ‘This poses a huge challenge for industry in biomarker identification and diagnostics development’, she said (Ray, 2011).
Evaluating the consistency of biomarker discoveries across different platforms, experiments and datasets has attracted the attention of researchers. The studies addressing this issue mainly revolve around the reproducibility of signals (for example, lists of differentially expressed genes), their significance scores and rankings in a prepared list. They try to answer the following question: Do the same genes appear differentially expressed when the experiment is re-run? Boulesteix and Slawski (2009), Li et al. (2011), Zhang et al. (2009) and the references therein suggest several solutions to this and related questions. Our interest is different.
A prototypical reproducibility paradigm arises when a classifier is designed on a preliminary study based on a small sample, and, based on promising reported results, a follow-on study is performed using a large independent data sample to check whether the classifier performs well as reported in the preliminary study. Many issues affect reproducibility, including the measurement platform, specimen handling, data normalization and sample compatibility between the original and subsequent studies. These may be categorized as laboratory issues; note that here we are not talking about the issue of providing access to data and software for follow-up studies on published results (Hothorn and Leisch, 2011). One can conjecture mitigation of these issues as laboratory technique improves; however, there is a more fundamental methodological issue, namely, error estimation. In particular, inaccurate error estimation can lead to ‘overoptimism’ in reported results (Boulesteix, 2010; Castaldi et al., 2011).
Consider a protocol in which the expressions of 30 000 genes are measured from 50 patients, each suffering from a different stage of breast cancer—30,000 features and a sample size of 50. The typical analysis proceeds in the following fashion: (i) based on the data, a feature set is chosen from the 30 000; (ii) a classifier is designed, with feature selection perhaps being performed in conjunction with classifier design and (iii) the classification error is measured by some procedure using the same sample data upon which feature selection and classifier design have been performed. Given no lack of reproducibility owing to laboratory issues, if the error estimate is sufficiently deemed small and a follow-on study with 1000 independent data specimens is carried out, can we expect the preliminary error estimate on a sample of 50 to be reproduced on a test sample of size 1000? Since the root-mean-square (RMS) error between the true and estimated errors for independent-test-data error estimation is bounded by 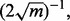 where m is the size of the test sample (Devroye et al., 1996), a test sample of 1000 insures
where m is the size of the test sample (Devroye et al., 1996), a test sample of 1000 insures 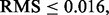 so that the test-sample estimate can be taken as the true error.
so that the test-sample estimate can be taken as the true error.
There are two fundamental related questions (Dougherty, 2012): (i) Given the reported estimate from the preliminary study, is it prudent to commit large resources to the follow-on study in the hope that a new biomarker diagnostic will result? (ii) Prior to that, is it possible that the preliminary study can obtain an error estimate that would warrant a decision to perform a follow-on study? A large follow-on study requires substantially more resources than those required for a preliminary study. If the preliminary study has a very low probability of producing reproducible results, then there is really no purpose in doing it. We propose a reproducibility index that simultaneously addresses both questions posed earlier. Our focal point is not that independent validation data should be used—this has been well argued, for instance, in the context of bioinformatics to avoid overoptimism (Jelizarow et al., 2010); rather, the issue addressed by the reproducibility index is the efficacy of small-sample preliminary studies to determine whether a large validating study should be performed. We set up a simulation study on synthetic models that emulate real-world scenarios and on some real datasets. We calculate the reproducibility index for different distributional models (and real datasets) and classification schemes.
We consider two other scenarios: (i) multiple independent preliminary studies with small samples are carried out and only the best results (minimum errors) reported and (ii) multiple classification schemes are applied to the preliminary study with small samples and only the results (minimum errors) of the best classfier are reported. A decision is made for a large follow-on study because the reported errors show very good performance. Yousefi et al. (2010, 2011) show that there is a poor statistical relationship between the reported results and true classifier performance in these scenarios, namely, there is a potential for significant optimistic ‘reporting bias’ or ‘multiple-rule bias’. These two biases can substantially impact the reproducibility index.
2 SYSTEMS AND METHODS
We define a classifier rule model as a pair 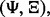 where
where 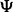 is a classification rule, possibly including feature selection, and
is a classification rule, possibly including feature selection, and  is a training-data error estimation rule on a feature-label distribution F. Given a random sample
is a training-data error estimation rule on a feature-label distribution F. Given a random sample 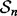 of size n drawn from F, the designed classifier is
of size n drawn from F, the designed classifier is 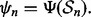 The true error of
The true error of 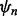 is given by
is given by 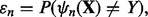 where
where 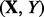 is a feature-label pair. The error estimation rule
is a feature-label pair. The error estimation rule  provides an error estimate,
provides an error estimate, 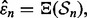 for
for 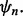 To characterize reproducibility, we postulate a preliminary study in which a classifier,
To characterize reproducibility, we postulate a preliminary study in which a classifier, 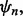 is designed from a sample of size n and its error is estimated. We say that the original study is reproducible with accuracy
is designed from a sample of size n and its error is estimated. We say that the original study is reproducible with accuracy
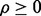 if
if 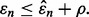 One could require that the true error lies in an interval about the estimated error, but our interest is in whether the proposed classifier is as good as claimed in the original study, which means that we only care whether its true performance is below some tolerable bound of the small-sample estimated error.
One could require that the true error lies in an interval about the estimated error, but our interest is in whether the proposed classifier is as good as claimed in the original study, which means that we only care whether its true performance is below some tolerable bound of the small-sample estimated error.
Given a preliminary study, not any error estimate will lead to a follow-on study: the estimate has to be sufficiently small to motivate the follow-on. This means there is a threshold, 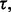 such that the second study occurs if and only if
such that the second study occurs if and only if 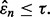 We define the reproducibility index by
We define the reproducibility index by
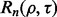 depends on the classification rule,
depends on the classification rule, 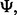 the error estimation rule,
the error estimation rule, 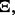 and the feature-label distribution F. Clearly,
and the feature-label distribution F. Clearly, 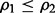 implies
implies 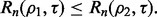 If
If 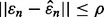 almost surely, meaning
almost surely, meaning 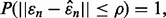 then
then 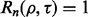 for all
for all 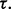 This means that, if the true and estimated errors are sufficiently close, then, no matter the decision threshold, the reproducibility index is 1. In practice, this ideal situation does not occur. Often, the true error greatly exceeds the estimated error when the latter is small, thereby driving down
This means that, if the true and estimated errors are sufficiently close, then, no matter the decision threshold, the reproducibility index is 1. In practice, this ideal situation does not occur. Often, the true error greatly exceeds the estimated error when the latter is small, thereby driving down 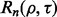 for small
for small 
We are interested in the relationship between reproducibility and classification difficulty. Fixing  and
and  makes
makes 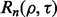 dependent on F. If we parameterize F, and call it
dependent on F. If we parameterize F, and call it 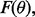 then we can write the reproducibility index as
then we can write the reproducibility index as 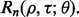 If we select
If we select 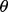 so there is a 1-1 monotonic relation between
so there is a 1-1 monotonic relation between  and the Bayes error,
and the Bayes error, 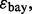 then there is a direct relationship between reproducibility and intrinsic classification difficulty,
then there is a direct relationship between reproducibility and intrinsic classification difficulty, 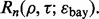
If we know the joint distribution between the true and estimated errors, then the entire analysis can be done analytically, for instance, in the case of the 1D Gaussian model with linear discriminant analysis (LDA) classification and leave-one-out (LOO) error estimation (Zollanvari et al., 2010). Fixing the variances and letting the means be zero and 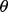 gives the desired scenario. We can now analytically derive the reproducibility index
gives the desired scenario. We can now analytically derive the reproducibility index 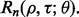 Unfortunately, there are very few distributions for which the joint distribution between the true and estimated errors is known. If not, then we use simulation to compute
Unfortunately, there are very few distributions for which the joint distribution between the true and estimated errors is known. If not, then we use simulation to compute 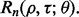
2.1 Analysis
To analyze the reproducibility index as a function of  and tie this to the joint distribution of the true and estimated errors, we expand
and tie this to the joint distribution of the true and estimated errors, we expand 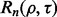 to obtain
to obtain
Consider the special case in which 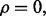 and let
and let 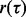 denote the probability fraction in the denominator. Then we have the upper bound
denote the probability fraction in the denominator. Then we have the upper bound 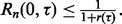 To gain insight into this bound, we postulate a geometrically simple model whose assumptions are not unrealistic. First, we assume that the linear regression of
To gain insight into this bound, we postulate a geometrically simple model whose assumptions are not unrealistic. First, we assume that the linear regression of 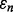 on
on 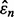 is a horizontal line, which has been observed approximately in many situations (Hanczar et al., 2007, 2010). This means that
is a horizontal line, which has been observed approximately in many situations (Hanczar et al., 2007, 2010). This means that 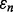 and
and 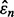 are uncorrelated, which have also been observed for many cases. Then, let us approximate the resulting joint distribution by a Gaussian distribution with common mean
are uncorrelated, which have also been observed for many cases. Then, let us approximate the resulting joint distribution by a Gaussian distribution with common mean 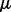 (unbiased estimation) and
(unbiased estimation) and 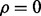 (according to our assumptions). Finally, let us assume that the standard deviation of
(according to our assumptions). Finally, let us assume that the standard deviation of 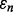 is less than the standard deviation of
is less than the standard deviation of 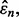 as is typically the case for cross-validation. Letting
as is typically the case for cross-validation. Letting 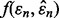 denote the joint Gaussian density,
denote the joint Gaussian density,
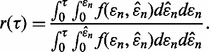 |
Figure 1 shows a pictorial of a single-level cut of the joint distribution, along with the horizontal regression line and the 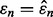 axis. Relative to the level cut, the dark gray and light gray regions correspond to the regions of integration for the numerator and denominator, respectively, of
axis. Relative to the level cut, the dark gray and light gray regions correspond to the regions of integration for the numerator and denominator, respectively, of  It is clear that for small
It is clear that for small  becomes large, thereby making
becomes large, thereby making  small.
small.
Fig. 1.
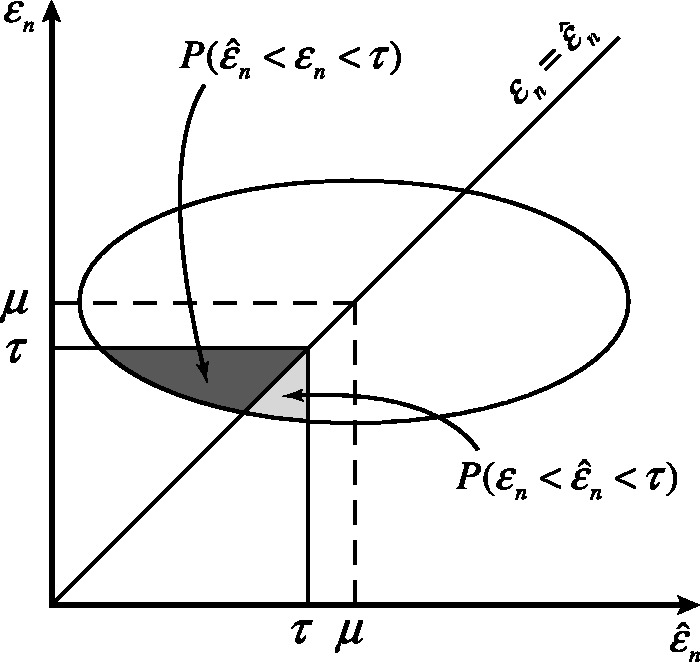
A single-level cut of the joint distribution and corresponding probabilities
2.2 Synthetic model
A model is adopted for generating synthetic data, which is built upon parameterized multivariate distributions, each representing a class of observations (phenotype, prognosis condition, etc.). The model is designed to reflect a scenario in which there are subnetworks (pathways) for which genes within a given subnetwork are correlated but there is no (negligible) correlation between genes in different subnetworks. The situation is modeled by assuming a block covariance matrix (Hanczar et al., 2010; Hua et al., 2005; Yousefi et al., 2010, 2011).
Sample points are generated from two equally likely classes, Y = 0 and Y = 1 with d features. Therefore, each sample point is specified by a feature vector 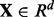 and a label
and a label 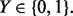 The class conditional densities are multivariate Gaussian with
The class conditional densities are multivariate Gaussian with 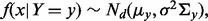 for y = 0, 1, where
for y = 0, 1, where 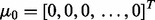 and
and 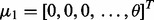 are
are 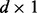 column vectors (for d = 1, we have
column vectors (for d = 1, we have 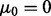 and
and 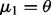 ), and
), and 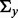 is a
is a 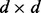 block matrix with off-diagonal block matrices equal to 0 and
block matrix with off-diagonal block matrices equal to 0 and 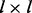 on-diagonal block matrices
on-diagonal block matrices 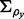 being 1 on the diagonal and
being 1 on the diagonal and 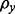 off the diagonal.
off the diagonal.
Three classes of Bayes optimal classifiers can be defined depending on 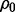 and
and 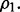 If the features are uncorrelated, i.e.
If the features are uncorrelated, i.e. 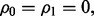 the Bayes classifier takes its simplest form: a future point is assigned to the class to which it has the closest Euclidian distance. When
the Bayes classifier takes its simplest form: a future point is assigned to the class to which it has the closest Euclidian distance. When 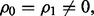 the Bayes classifier is a hyperplane in
the Bayes classifier is a hyperplane in 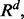 which must pass through the midpoint between the means of two classes. If
which must pass through the midpoint between the means of two classes. If 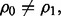 the Bayes classifier takes a quadratic form, and decision surfaces are hyperquadrics.
the Bayes classifier takes a quadratic form, and decision surfaces are hyperquadrics.
2.3 Real data
We consider four microarray real datasets, each having more than 150 arrays: pediatric acute lymphoblastic leukemia (ALL) (Yeoh et al., 2002), multiple myeloma (Zhan et al., 2006), hepatocellular carcinoma (HCC) (Chen et al., 2004), and a dataset for drugs and toxicant response on rats (Natsoulis et al., 2005). We follow the data preparation instructions reported in the cited articles. Table 1 provides a summary of the four real datasets. A detailed description can be found in the Supplementary Materials.
Table 1.
Four microarray real datasets used in this study
| Dataset | Dataset type | Feature—sample size |
|---|---|---|
| Yeoh et al. (2002) | Pediatric ALL | 5077—149/99 |
| Zhan et al. (2006) | Multiple myeloma | 54 613—156/78 |
| Chen et al. (2004) | HCC | 10 237—75/82 |
| Natsoulis et al. (2005) | Drugs response on rats | 8491—120/61 |
2.4 Classifier rule models
Three classification rules, two linear and one non-linear, are considered: LDA, linear support vector machine (L-SVM) and radial basis function SVM (RBF-SVM). Three error estimation methods are considered: 0.632 bootstrap, LOO and 5-fold cross-validation (5F-CV). In total, we have nine classifier rule models.
LDA is a plug-in rule for the optimal classifier in a Gaussian model with common covariance matrix. The sample means and pooled sample covariance matrix obtained from the data are plugged into the discriminant. Assuming equally likely classes, LDA assigns a sample point x to class 1 if and only if 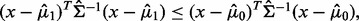 where
where 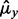 is the sample mean for class
is the sample mean for class 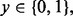 and
and 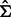 is the pooled sample covariance matrix. LDA usually provides good results even when the assumptions of Gaussianity with common covariances are mildly violated.
is the pooled sample covariance matrix. LDA usually provides good results even when the assumptions of Gaussianity with common covariances are mildly violated.
Given a set of training sample points, the goal of support vector machine classifier is to find a maximal margin hyperplane. When the data are not linearly separable, one can introduce some slack variables in the optimization procedure allowing for mislabeled sample points and solve the dual problem. This classifier is called L-SVM, which is essentially a hyperplane in the feature space. Alternatively, using a transformation the data can be projected into a higher-dimensional space, where it becomes linearly separable. One can avoid using the transformation and work with a kernel function that is expressible as an inner product in a feature space. The equivalent classifier back in the original feature space will generally be non-linear (Boser et al., 1992; Cortes and Vapnik, 1995). When the kernel function is a Gaussian radial basis function, the corresponding classifier is referred to as RBF-SVM.
In general, the 0.632 bootstrap error estimator can be written as,
where 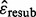 and
and 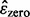 are the resubstitution and bootstrap zero estimators. The resubstitution uses the empirical distribution by putting mass 1/n on each of the n sample points in the original data. A bootstrap sample is made by drawing n equally likely points with replacement from the original data. A classifier is designed on the bootstrap sample, and its error is calculated by counting the misclassified original sample points not in the bootstrap sample. The basic bootstrap zero estimator is the expectation of this error with respect to the bootstrap sampling distribution. This expectation is usually approximated by a Monte-Carlo estimate based on a number of independent bootstrap samples (between 25 and 200 is typical, we use 100).
are the resubstitution and bootstrap zero estimators. The resubstitution uses the empirical distribution by putting mass 1/n on each of the n sample points in the original data. A bootstrap sample is made by drawing n equally likely points with replacement from the original data. A classifier is designed on the bootstrap sample, and its error is calculated by counting the misclassified original sample points not in the bootstrap sample. The basic bootstrap zero estimator is the expectation of this error with respect to the bootstrap sampling distribution. This expectation is usually approximated by a Monte-Carlo estimate based on a number of independent bootstrap samples (between 25 and 200 is typical, we use 100).
In 5F-CV, the sample 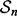 is randomly partitioned into five folds
is randomly partitioned into five folds 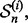 for i = 1, 2,…, 5. Each fold is held out of the classifier design process in turn as the test set, a (surrogate) classifier
for i = 1, 2,…, 5. Each fold is held out of the classifier design process in turn as the test set, a (surrogate) classifier 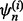 is designed on the remaining sets
is designed on the remaining sets 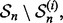 and the error of
and the error of 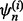 is estimated by counting the misclassified sample points in
is estimated by counting the misclassified sample points in 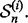 The 5F-CV estimate is the average error counted on all folds. Beside the variance arising from the sampling process, there is ‘internal variance’ resulting from the random selection of the partitions. To reduce this variance, we consider 5F-CV with 10 repetitions, meaning that we also average the cross-validation estimates of 10 randomly generated partitions over
The 5F-CV estimate is the average error counted on all folds. Beside the variance arising from the sampling process, there is ‘internal variance’ resulting from the random selection of the partitions. To reduce this variance, we consider 5F-CV with 10 repetitions, meaning that we also average the cross-validation estimates of 10 randomly generated partitions over 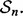 LOO error estimation is a special case of cross-validation with n folds, where each fold consists of a single point. Therefore, LOO has no internal variance since there is only a single way to partition the data into n folds. With small samples, cross-validation tends to be inaccurate owing to high overall variance (Braga-Neto and Dougherty, 2004) and poor correlation with the true error (Hanczar et al., 2007).
LOO error estimation is a special case of cross-validation with n folds, where each fold consists of a single point. Therefore, LOO has no internal variance since there is only a single way to partition the data into n folds. With small samples, cross-validation tends to be inaccurate owing to high overall variance (Braga-Neto and Dougherty, 2004) and poor correlation with the true error (Hanczar et al., 2007).
2.5 Simulation design
For the synthetic data, we assume that the features have multivariate Gaussian distributions as described in Section 2.2. We choose 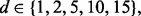 l = d if
l = d if 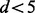 and l = 5 if
and l = 5 if 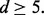 We also assume that
We also assume that 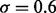 and the pair
and the pair 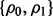 takes three different values: {0, 0}, {0.8, 0.8} and {0.4, 0.8}. For fixed
takes three different values: {0, 0}, {0.8, 0.8} and {0.4, 0.8}. For fixed 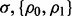 and d, we choose
and d, we choose  so that the Bayes error equals some desired values; specifically, from 0.025 to 0.4 (or the maximum possible value depending on
so that the Bayes error equals some desired values; specifically, from 0.025 to 0.4 (or the maximum possible value depending on 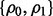 ) with increments of 0.025. This will define a large class of different distribution models in our simulation. From each distribution model, we also generate random samples of size 30, 60 and 120 (half from each class) to emulate real-world problems, where only a small number of sample points are available. Due to the large number of simulations in this study, we have limited the dimension of the cases studied; however, the reproducibility index is not limited by dimension and, owing to the increased estimation variance, one can expect that, with larger dimensions, reproducibility can be expected to be even more problematic in such circumstances.
) with increments of 0.025. This will define a large class of different distribution models in our simulation. From each distribution model, we also generate random samples of size 30, 60 and 120 (half from each class) to emulate real-world problems, where only a small number of sample points are available. Due to the large number of simulations in this study, we have limited the dimension of the cases studied; however, the reproducibility index is not limited by dimension and, owing to the increased estimation variance, one can expect that, with larger dimensions, reproducibility can be expected to be even more problematic in such circumstances.
For each model, we generate 10 000 random samples. For each sample, the true and estimated error pairs of all classifier rule models are calculated. The true errors of the designed classifiers are found exactly if analytical expressions are available. Otherwise, they are calculated via a very large independent sample (10 000 points) generated from the same distribution model. For each 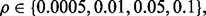
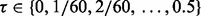 and classifier rule model, we empirically calculate
and classifier rule model, we empirically calculate 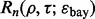 from 10 000 true and estimated error pairs.
from 10 000 true and estimated error pairs.
The real-data simulation is essentially the same as for the synthetic data, except that each real dataset now serves as a high-dimensional distribution model. Thus, there is a need for feature selection, which is part of the classification rule. Another difference is in calculating the true error: at each iteration, n = 60 sample points are randomly picked for training, and a feature-selection step is carried out where d = 5 features with highest t-scores are selected. Then a classifier is designed and its error estimated. The remaining held-out sample points are used to calculate the true error.
3 RESULTS AND DISCUSSION
The complete set of simulation results can be found in the companion website of this article, including graphs for the joint distributions and reproducibility indices for different distribution models, real datasets and classifier rule models. Here, we provide some results that represent the general trends observed in the simulations.
3.1 Joint distribution
The joint distributions between 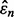 and
and 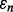 are estimated with a density estimation method that uses bivariate Gaussian kernels. Here we present the results for only two synthetic distribution models with d = 5 features and different sample sizes. For the first model, the class-conditional covariance matrices are equal and the features are uncorrelated. The target Bayes error is set to 0.2, being equivalent to
are estimated with a density estimation method that uses bivariate Gaussian kernels. Here we present the results for only two synthetic distribution models with d = 5 features and different sample sizes. For the first model, the class-conditional covariance matrices are equal and the features are uncorrelated. The target Bayes error is set to 0.2, being equivalent to 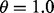 . The results are shown for LDA and 5F-CV in Figure 2(a–c). For the second model, the class-conditional covariance matrices are assumed to be unequal and the features are correlated (
. The results are shown for LDA and 5F-CV in Figure 2(a–c). For the second model, the class-conditional covariance matrices are assumed to be unequal and the features are correlated (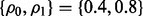 ). The target Bayes error is 0.1, which results in
). The target Bayes error is 0.1, which results in 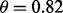 . Figure 2(d–f) shows the corresponding graphs when RBF-SVM and LOO are used. Each plot also includes the regression line (dotted) and a small circle, indicating the sample mean of the joint distribution. Lack of regression and correlation, slightly high-bias and very high-variance for the estimated error are evident for small sample sizes. These graphs, which are consistent with ones in previous studies (Dougherty et al., 2010; Hanczar et al., 2007), show a resemblance to Figure 1, indicating that our analysis in Section 2.1 is suitable for the synthetic model.
. Figure 2(d–f) shows the corresponding graphs when RBF-SVM and LOO are used. Each plot also includes the regression line (dotted) and a small circle, indicating the sample mean of the joint distribution. Lack of regression and correlation, slightly high-bias and very high-variance for the estimated error are evident for small sample sizes. These graphs, which are consistent with ones in previous studies (Dougherty et al., 2010; Hanczar et al., 2007), show a resemblance to Figure 1, indicating that our analysis in Section 2.1 is suitable for the synthetic model.
Fig. 2.
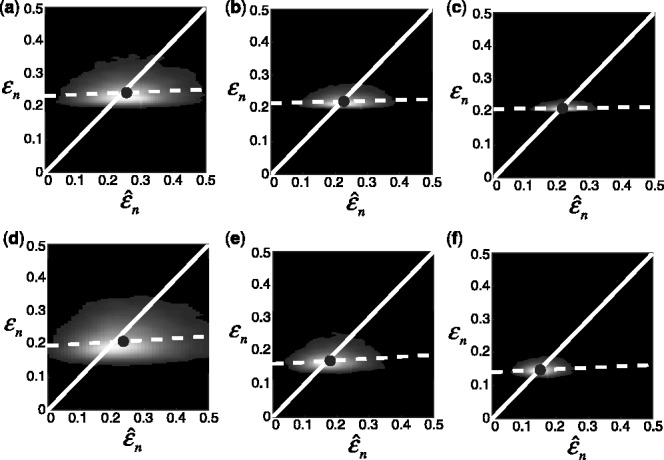
Joint distribution of the true and estimated errors for n = 30, 60, 120, d = 5, two classification rules (LDA and RBF-SVM) and two error estimation methods (5F-CV and LOO). The covariance matrices are equal with features uncorrelated for LDA and unequal with features correlated for RBF-SVM: (a) n = 30, LDA, 5F-CV, 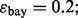 (b) n = 60, LDA, 5F-CV,
(b) n = 60, LDA, 5F-CV, 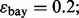 (c) n = 120, LDA, 5F-CV,
(c) n = 120, LDA, 5F-CV, 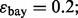 (d) n = 30, RBF-SVM, LOO,
(d) n = 30, RBF-SVM, LOO, 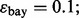 (e) n = 60, RBF-SVM, LOO,
(e) n = 60, RBF-SVM, LOO, 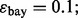 (f) n = 120, RBF-SVM, LOO,
(f) n = 120, RBF-SVM, LOO, 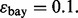 The white line shows the
The white line shows the  axis, the dotted line shows the regression line and the circle indicates the sample mean of the joint distribution
axis, the dotted line shows the regression line and the circle indicates the sample mean of the joint distribution
The expected true errors for different classification rules applied to different real datasets are listed in Table 2. Similar to the synthetic data, the joint distributions for the real data are estimated using a bivariate Gaussian-kernel density estimation method. Here we only present the joint distribution results for the multiple myeloma dataset (Zhan et al., 2006) with LDA as the classification rule in Figure 3(a–c), and for the HCC dataset (Chen et al., 2004), when RBF-SVM is used, in Figure 3(d–f). In all cases, correlation between the true and estimated errors is small in absolute value and negative, the regression line having negative slope, which means that the conditional expectation of the true error decreases as the estimate increases. This behavior is not anomalous (Dougherty et al., 2010); indeed, a negative correlation has been shown analytically for LOO with discrete classification (Braga-Neto and Dougherty, 2010).
Table 2.
Expected true errors of three classification rules used on the real datasets
| Dataset | LDA | L-SVM | RBF-SVM |
|---|---|---|---|
| Yeoh et al. (2002) | 0.080 | 0.083 | 0.080 |
| Zhan et al. (2006) | 0.186 | 0.193 | 0.188 |
| Chen et al. (2004) | 0.154 | 0.151 | 0.140 |
| Natsoulis et al. (2005) | 0.247 | 0.258 | 0.301 |
Fig. 3.
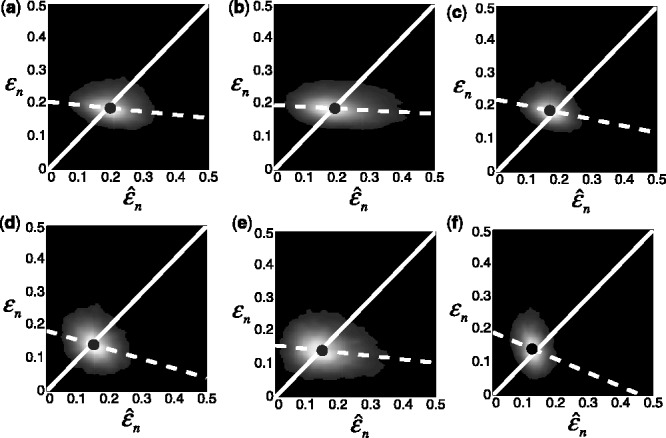
Joint distribution of the true and estimated errors for two real datasets and different classifier rule models. The training size is 60, and d = 5 features are selected using t-test feature selection method: (a) multiple myeloma, LDA and 5F-CV; (b) multiple myeloma, LDA and LOO; (c) multiple myeloma, LDA and 0.632 bootstrap; (d) HCC, RBF-SVM and 5F-CV; (e) HCC, RBF-SVM and LOO; (f) HCC, RBF-SVM and 0.632 bootstrap. The white line shows the 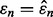 axis, the dotted line shows the regression line and the circle indicates the sample mean of the joint distribution
axis, the dotted line shows the regression line and the circle indicates the sample mean of the joint distribution
3.2 Reproducibility index
Figure 4 shows the reproducibility index as a function of 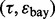 for different sample sizes and
for different sample sizes and 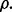 We assume d = 5 uncorrelated features with equal class-conditional covariance matrices. The classification rule is LDA and error estimation is 5F-CV. Note that LDA is a consistent classification rule for this distribution model. As the Bayes error increases, a higher reproducibility index is achieved only for larger
We assume d = 5 uncorrelated features with equal class-conditional covariance matrices. The classification rule is LDA and error estimation is 5F-CV. Note that LDA is a consistent classification rule for this distribution model. As the Bayes error increases, a higher reproducibility index is achieved only for larger 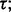 however, for
however, for 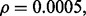 which is close to zero, the upper bound for the reproducibility index is about 0.5, which is consistent with our analysis in Section 2.1. It is also notable that the rate of change in the reproducibility index gets slower for higher Bayes error and smaller sample size. Even though the rate of change in the reproducibility index is faster for sample size 120, the maximum is almost identical to what we have for sample size 60. This phenomenon can be attributed to the difficulty of classification (for higher Bayes error), high-variance of the error estimate, flat regression and lack of correlation between the true and estimated errors due to the small-sample nature of the problem.
which is close to zero, the upper bound for the reproducibility index is about 0.5, which is consistent with our analysis in Section 2.1. It is also notable that the rate of change in the reproducibility index gets slower for higher Bayes error and smaller sample size. Even though the rate of change in the reproducibility index is faster for sample size 120, the maximum is almost identical to what we have for sample size 60. This phenomenon can be attributed to the difficulty of classification (for higher Bayes error), high-variance of the error estimate, flat regression and lack of correlation between the true and estimated errors due to the small-sample nature of the problem.
Fig. 4.
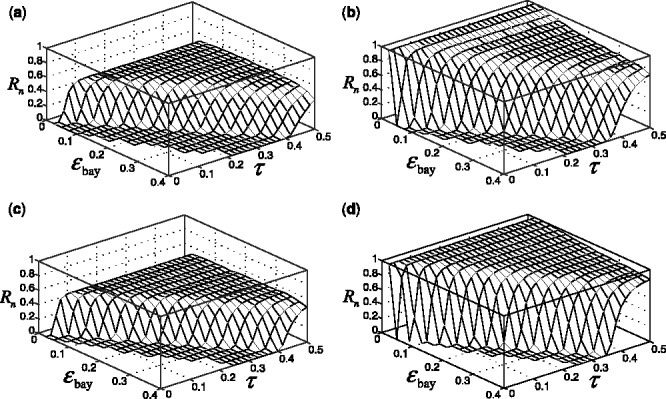
Reproducibility index for n = 60, 120, LDA classification rule and 5F-CV error estimation. d = 5 and the covariance matrices are equal with features uncorrelated. (a) n = 60, 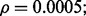 (b) n = 60,
(b) n = 60, 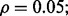 (c) n = 120,
(c) n = 120, 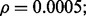 (d) n = 120,
(d) n = 120, 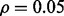
An irony appears in Figure 4 when one tries to be prudent by only doing a large-scale experiment if the estimated error is small in the preliminary study, that is, only proceeding to a follow-on study if 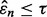 and
and  is small. From the ridges in the figure, we see that the reproducibility index drops off once
is small. From the ridges in the figure, we see that the reproducibility index drops off once  is chosen below a certain point. While small
is chosen below a certain point. While small  decreases the likelihood of a follow-on study, it increases the likelihood that the preliminary results are not reproducible. Seeming prudence is undermined by poor error estimation. For larger
decreases the likelihood of a follow-on study, it increases the likelihood that the preliminary results are not reproducible. Seeming prudence is undermined by poor error estimation. For larger 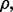 reproducibility improves; however, for
reproducibility improves; however, for 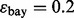 and 60 sample points, which is very typical in real-world classification problems, even for very large
and 60 sample points, which is very typical in real-world classification problems, even for very large 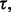 say
say 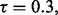 we have
we have 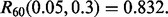
Figure 5 shows the results for the case of a distribution model with correlated features, unequal covariance matrices and 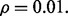 The classification rules are LDA and RBF-SVM. 5F-CV serves as the error estimation rule. LDA is no longer a consistent rule for this model, and we expect RBF-SVM to produce classifiers that, on average, perform better. If so, we would then expect the reproducibility index to be better for RBF-SVM because lower Bayes error usually means more accurate cross-validation error estimation, at least for the Gaussian model (Dougherty et al., 2011). The graphs confirm this: as the reproducibility index for higher Bayes error is uniformly (slightly) better for RBF-SVM. The improvement is notable for RBF-SVM, compared with LDA, for larger sample size: for
The classification rules are LDA and RBF-SVM. 5F-CV serves as the error estimation rule. LDA is no longer a consistent rule for this model, and we expect RBF-SVM to produce classifiers that, on average, perform better. If so, we would then expect the reproducibility index to be better for RBF-SVM because lower Bayes error usually means more accurate cross-validation error estimation, at least for the Gaussian model (Dougherty et al., 2011). The graphs confirm this: as the reproducibility index for higher Bayes error is uniformly (slightly) better for RBF-SVM. The improvement is notable for RBF-SVM, compared with LDA, for larger sample size: for 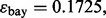 we have
we have 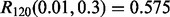 for RBF-SVM while
for RBF-SVM while 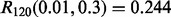 for LDA.
for LDA.
Fig. 5.
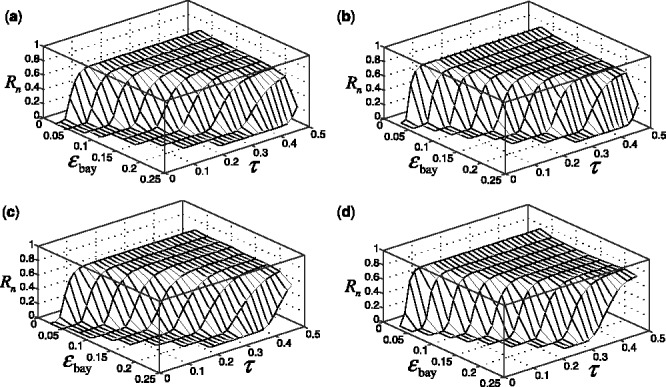
Reproducibility index for 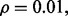 n = 60, 120, two classification rules (LDA and RBF-SVM) and 5F-CV error estimation. d = 5 and the covariance matrices are unequal with features correlated (
n = 60, 120, two classification rules (LDA and RBF-SVM) and 5F-CV error estimation. d = 5 and the covariance matrices are unequal with features correlated (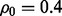 and
and 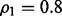 ). (a) n = 60, LDA; (b) n = 120, LDA; (c) n = 60, RBF-SVM; (d) n = 120, RBF-SVM
). (a) n = 60, LDA; (b) n = 120, LDA; (c) n = 60, RBF-SVM; (d) n = 120, RBF-SVM
Figure 6 presents the reproducibility index results for the real data when LDA and RBF-SVM are used, and their errors are estimated with 5F-CV and LOO. The trends are very similar to those in the synthetic data. The reproducibility index for 5F-CV is highly variable among datasets, specifically the datasets with higher expected true error have lower reproducibility index for small- to mid-range values of 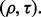 The situation is worse for LOO due to its high variance.
The situation is worse for LOO due to its high variance.
Fig. 6.
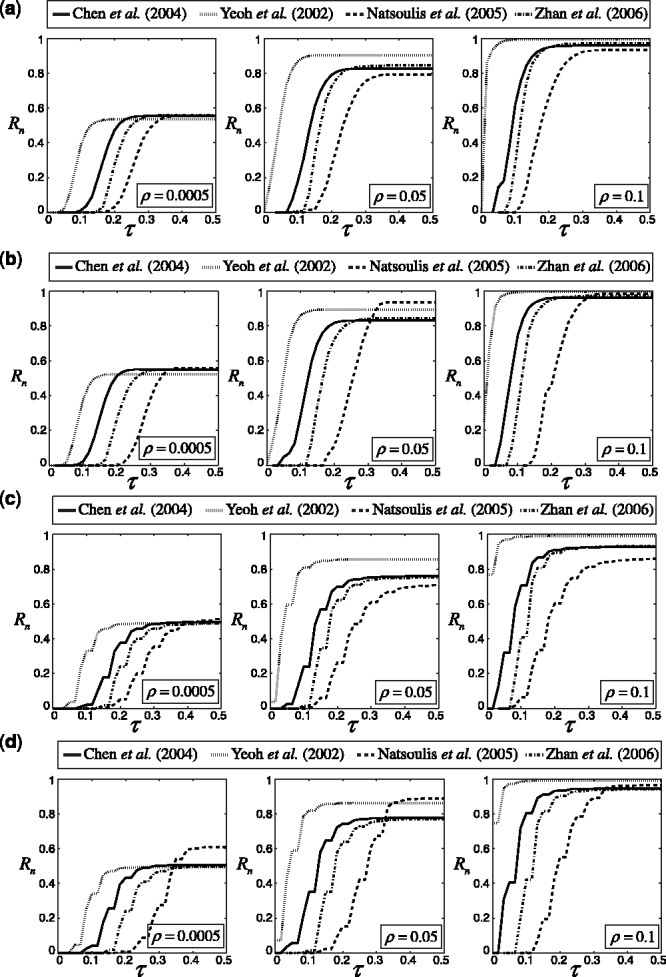
Reproducibility index for the real datasets, two classification rules (LDA and RBF-SVM) and two error estimation methods (5F-CV and LOO). The training sample size is 60, and d = 5 features are selected using t-test feature selection method: (a) LDA, 5F-CV; (b) RBF-SVM, 5F-CV; (c) LDA, LOO; (d) RBF-SVM, LOO
3.3 Reporting bias effect
Suppose that a study has tested a proposed classification rule on several datasets and reported only the best results, i.e. the ones on the datasets with the lowest estimated errors. Yousefi et al. (2010) have shown that, for a very large class of problems, this practice introduces a major source of (reporting) bias to the results.
Let 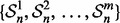 be a family of m i.i.d. samples of size n, randomly drawn from a single distribution. Given a fixed classifier rule model, for each
be a family of m i.i.d. samples of size n, randomly drawn from a single distribution. Given a fixed classifier rule model, for each 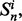 a classifier is designed, its error estimated and the true error of the designed classifier is also calculated. Assume that instead of reporting all the estimated errors, only the minimum estimated error is reported:
a classifier is designed, its error estimated and the true error of the designed classifier is also calculated. Assume that instead of reporting all the estimated errors, only the minimum estimated error is reported: 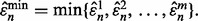 Letting
Letting 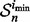 denote the sample on which the minimum error estimate occurs, the corresponding true error is then
denote the sample on which the minimum error estimate occurs, the corresponding true error is then 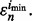 In this case, the reported estimated error is
In this case, the reported estimated error is 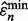 for the dataset
for the dataset 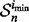 . Hence, the reproducibility index is computed for the pair
. Hence, the reproducibility index is computed for the pair 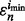 and
and 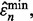 and the reported study is reproducible with accuracy
and the reported study is reproducible with accuracy
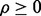 from the m performed studies if
from the m performed studies if 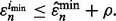 The reproducibility index for m independent datasets takes the form
The reproducibility index for m independent datasets takes the form
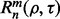 depends on the number of datasets, the classification rule, the error estimation rule and the feature-label distribution, these being
depends on the number of datasets, the classification rule, the error estimation rule and the feature-label distribution, these being 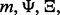 and F, respectively. Quantities such as
and F, respectively. Quantities such as 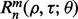 and
and 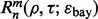 are defined before.
are defined before.
To illustrate the effect of reporting bias, for a fixed 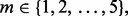 we randomly draw m pairs from the previously generated 10 000 error pairs. The minimum estimated error and its corresponding true error are found and recorded. This process is repeated to generate 10 000 new error pairs. Now similar to
we randomly draw m pairs from the previously generated 10 000 error pairs. The minimum estimated error and its corresponding true error are found and recorded. This process is repeated to generate 10 000 new error pairs. Now similar to 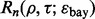 , we calculate
, we calculate 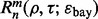 for each m,
for each m, 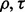 and classifier rule model. Figures 7 and 8 show the effect of reporting bias on the reproducibility index for m = 2, 5, d = 5, LDA and 5F-CV when the covariance matrices are equal and the features are uncorrelated. Compare Figure 8 with Figure 4. Strikingly, but not surprisingly, we do not need more than m = 5 samples to observe a rapid drop (almost half) of reproducibility for
and classifier rule model. Figures 7 and 8 show the effect of reporting bias on the reproducibility index for m = 2, 5, d = 5, LDA and 5F-CV when the covariance matrices are equal and the features are uncorrelated. Compare Figure 8 with Figure 4. Strikingly, but not surprisingly, we do not need more than m = 5 samples to observe a rapid drop (almost half) of reproducibility for 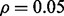 as the Bayes error and
as the Bayes error and  increase. Moreover, for
increase. Moreover, for 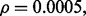 the reproducibility index is almost zero independent of the sample size. As m increases, the reporting bias,
the reproducibility index is almost zero independent of the sample size. As m increases, the reporting bias, 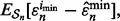 also increases. Pictorially, the wide flat distribution in Figure 1 becomes more circular with smaller variance and gets shifted to the left side of the
also increases. Pictorially, the wide flat distribution in Figure 1 becomes more circular with smaller variance and gets shifted to the left side of the 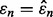 axis. Thus, the probability that
axis. Thus, the probability that 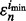 is smaller than
is smaller than 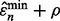 diminishes to 0 even though
diminishes to 0 even though 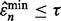 for all
for all 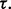
Fig. 7.
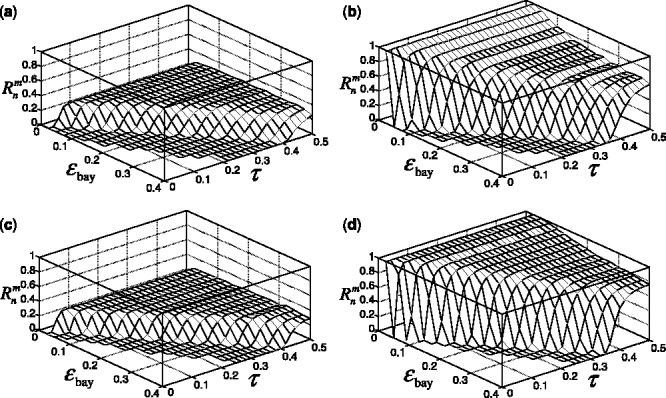
Reporting bias effect on the reproducibility index for m = 2, n = 60, 120, LDA classification rule and 5F-CV error estimation. d = 5 and the covariance matrices are equal with features uncorrelated: (a) n = 60,  (b) n = 60,
(b) n = 60,  (c) n = 120,
(c) n = 120, 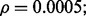 (d) n = 120,
(d) n = 120, 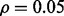
Fig. 8.
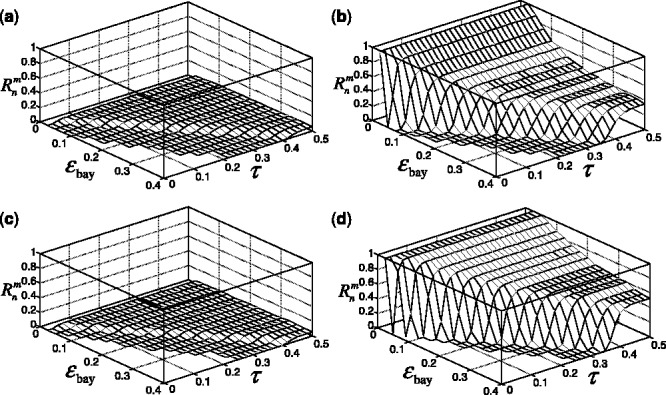
Reporting bias effect on the reproducibility index for m = 5, n = 60, 120, LDA classification rule and 5F-CV error estimation. d = 5 and the covariance matrices are equal with features uncorrelated: (a) n = 60, 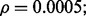 (b) n = 60,
(b) n = 60, 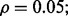 (c) n = 120,
(c) n = 120, 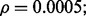 (d) n = 120,
(d) n = 120, 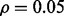
3.4 Multiple-rule bias effect
Suppose r classification rules are considered in the preliminary study and only the results of the best one are considered. In this case, a random small sample is drawn from the feature-label distribution F, and r classifiers are designed. Assuming F is unknown, the errors of the designed classifiers are estimated from sample data using s different error estimation methods, and the classification rule leading to the classifier with minimum estimated error is chosen as ‘best’. This practice has been shown to introduce substantial optimistic bias (Yousefi et al., 2011).
Denote r classification rules by 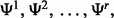 and s error estimation rules by
and s error estimation rules by 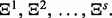 In total, there are m = rs classifier rule models:
In total, there are m = rs classifier rule models: 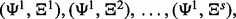
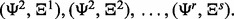 Given a random sample
Given a random sample 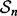 drawn from F, the classification rules yield r designed classifiers:
drawn from F, the classification rules yield r designed classifiers: 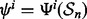 for i = 1, 2,…, r. The true error of
for i = 1, 2,…, r. The true error of 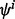 is denoted by
is denoted by 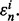 Let
Let 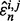 denote the jth estimated error for
denote the jth estimated error for 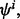 where j = 1, 2,…, s. The minimum estimated error is
where j = 1, 2,…, s. The minimum estimated error is
Letting 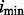 and
and 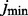 denote the classifier number and error estimator number, respectively, for which the error estimate is minimum, we have
denote the classifier number and error estimator number, respectively, for which the error estimate is minimum, we have 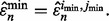 The corresponding true error is then
The corresponding true error is then 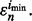
The reproducibility index is now computed for the pair 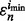 and
and 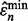 and the reported study is reproducible with accuracy
and the reported study is reproducible with accuracy
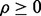 from the m performed studies if
from the m performed studies if 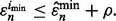 The reproducibility index for m classifier rule models is defined by
The reproducibility index for m classifier rule models is defined by
Quantities such as 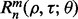 and
and 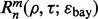 are defined as before.
are defined as before.
We use the original true and estimated error pairs described in Section 2.5 and consider three classification rules (LDA, L-SVM and RBF-SVM) and three error estimation methods (0.632 bootstrap, LOO and 5F-CV). Therefore, we can have r = 1, 2, 3. We generate all 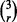 possible collections of classification rules of size r, each associated with three error estimation rules, resulting in
possible collections of classification rules of size r, each associated with three error estimation rules, resulting in 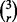 collections of classifier rule models of size m = 3r. For each collection of size m, we find the true and estimated error pairs from the original error pairs and record the minimum estimated error and its corresponding true error. We repeat this process 10 000 times. Now, similar to
collections of classifier rule models of size m = 3r. For each collection of size m, we find the true and estimated error pairs from the original error pairs and record the minimum estimated error and its corresponding true error. We repeat this process 10 000 times. Now, similar to 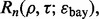 we calculate
we calculate 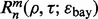 for each m,
for each m, 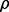 and
and 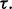 Figure 9 shows the effect of multiple-rule bias on the reproducibility index for m = 3, d = 5, LDA and 5F-CV when the covariance matrices are equal and the features are uncorrelated. The cases for m = 6, 9 are given on the companion website. Similar observations to those of reporting bias can be made here. The reproducibility index decreases for increasing m.
Figure 9 shows the effect of multiple-rule bias on the reproducibility index for m = 3, d = 5, LDA and 5F-CV when the covariance matrices are equal and the features are uncorrelated. The cases for m = 6, 9 are given on the companion website. Similar observations to those of reporting bias can be made here. The reproducibility index decreases for increasing m.
Fig. 9.
Multiple-rule bias effect on the reproducibility index for m = 3, n = 60, 120, LDA classification rule, and 5F-CV error estimation. d = 5 and the covariance matrices are equal with features uncorrelated: (a) n = 60,  (b) n = 60,
(b) n = 60,  (c) n = 120,
(c) n = 120, 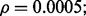 (d) n = 120,
(d) n = 120, 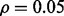
3.5 Application methodology
Application of the reproducibility index in practice requires that the defining probability be computed, or at least approximated, beforehand. This requires prior knowledge regarding the feature-label distribution. If the feature-label distribution was known and the corresponding theory regarding the joint distribution of the true and estimated errors developed, then 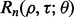 could be directly computed for different values of n,
could be directly computed for different values of n, 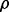 and
and 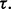 For instance, in the case of LDA in the Gaussian model with known covariance matrix, the joint distribution is known exactly in the univariate case and can be approximated in the multivariate case (Zollanvari et al., 2010). Of course, if the feature-label distribution was known, then there would be no reason to collect any data; just derive the Bayes classifier from the model. Thus, when we speak of prior knowledge, we mean the assumption that the feature-label distribution belongs to an uncertainty class of feature-label distributions. Considering our earlier remarks about parameterizing the feature-label distribution by
For instance, in the case of LDA in the Gaussian model with known covariance matrix, the joint distribution is known exactly in the univariate case and can be approximated in the multivariate case (Zollanvari et al., 2010). Of course, if the feature-label distribution was known, then there would be no reason to collect any data; just derive the Bayes classifier from the model. Thus, when we speak of prior knowledge, we mean the assumption that the feature-label distribution belongs to an uncertainty class of feature-label distributions. Considering our earlier remarks about parameterizing the feature-label distribution by 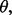 thereby treating it as
thereby treating it as 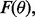 the uncertainty class can be denoted by
the uncertainty class can be denoted by 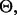 with each
with each 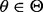 determining a possible feature-label distribution. Furthermore, taking a Bayesian perspective, we can put a prior distribution,
determining a possible feature-label distribution. Furthermore, taking a Bayesian perspective, we can put a prior distribution, 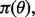 perhaps non-informative, on
perhaps non-informative, on 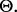
Assuming an uncertainty class in the case of reproducibility is pragmatic because reproducibility concerns error-estimation accuracy and virtually nothing practical can be said concerning error-estimation accuracy in the absence of prior knowledge (Dougherty et al., 2011). For instance, the most common measure of error-estimation accuracy is the RMS between the true and estimated errors, and, without distributional assumptions, the RMS cannot be usefully bounded in the case of training-data-based error estimators unless the sample size is very large, well beyond practical biological circumstances and beyond what is needed to split the data into training and testing data. As noted by Fisher in 1925, ‘Only by systematically tackling small sample problems on their merits does it seem possible to apply accurate tests to practical data’ (Fisher, 1925). Large-sample bounds do not help. Owing to this limitation, optimal error estimation relative to a prior distribution on an uncertainty class of feature-label distributions has been developed (Dalton and Dougherty, 2011a) and applied in gene-expression classification (Dalton and Dougherty, 2011b).
Given an uncertainty class and prior distribution, the problem is to ensure a desired level of reproducibility before experimental design; that is, determine n, 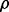 and
and  so that the desired level is achieved. A conservative approach would be to ensure
so that the desired level is achieved. A conservative approach would be to ensure 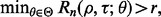 where r is the desired level of reproducibility. If we assume that
where r is the desired level of reproducibility. If we assume that 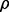 and
and  are given, satisfaction of the inequality would yield a required sample size n. The weakness of this approach is that the minimization requirement is determined by worst-case values of
are given, satisfaction of the inequality would yield a required sample size n. The weakness of this approach is that the minimization requirement is determined by worst-case values of 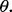 A less conservative approach, and the one we take here, is to require that
A less conservative approach, and the one we take here, is to require that 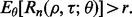 One could apply other (more conservative) criteria, such as
One could apply other (more conservative) criteria, such as 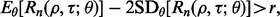 where
where 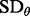 denotes standard deviation with respect to
denotes standard deviation with respect to 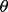 . As noted, for demonstration purposes, we stay with
. As noted, for demonstration purposes, we stay with 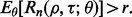
Rarely can this inequality be evaluated analytically. We demonstrate a Monte-Carlo approach to find the minimum sample size yielding a desired reproducibility index for classification rule 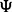 with error estimation rule
with error estimation rule  Assume, from our prior knowledge, that the feature-label distribution generating the experimental samples, after processing the data, can be approximated with the synthetic model introduced in Section 2.2, with d = 2 features,
Assume, from our prior knowledge, that the feature-label distribution generating the experimental samples, after processing the data, can be approximated with the synthetic model introduced in Section 2.2, with d = 2 features, 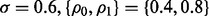 and
and  being normally distributed with mean 1.167 and variance
being normally distributed with mean 1.167 and variance 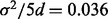 (
(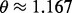 corresponding to
corresponding to 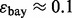 ). For given
). For given 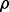 and
and 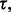 and for fixed n, generate random
and for fixed n, generate random 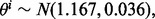
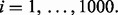 For each
For each 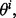 draw random samples
draw random samples 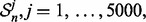 from the distribution model
from the distribution model 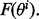 For each sample
For each sample 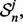 design a classifier
design a classifier 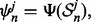 calculate its true error using an independent large sample drawn from the same distribution
calculate its true error using an independent large sample drawn from the same distribution 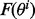 and estimate its error by
and estimate its error by 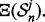 Now calculate
Now calculate 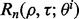 empirically from these 5000 pairs of true and estimated errors and approximate
empirically from these 5000 pairs of true and estimated errors and approximate 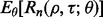 by averaging over
by averaging over 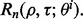 Repeat the procedure for different n until
Repeat the procedure for different n until 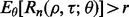 for a given r. Figure 10 shows the expected reproducibility index for LDA, RBF-SVM and 0.632 bootstrap error estimation with respect to different sample size,
for a given r. Figure 10 shows the expected reproducibility index for LDA, RBF-SVM and 0.632 bootstrap error estimation with respect to different sample size, 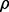 and
and 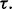 If r = 0.6,
If r = 0.6, 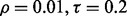 and the classification rule is LDA, Figure 10a shows that n must exceed 82. As another example, the graph in Figure 10d shows that, for r = 0.8,
and the classification rule is LDA, Figure 10a shows that n must exceed 82. As another example, the graph in Figure 10d shows that, for r = 0.8, 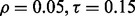 and RBF-SVM,
and RBF-SVM, 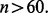
Fig. 10.
Expected reproducibility index for LDA and RBF-SVM classification rules, and 0.632 bootstrap error estimation as a function of n: (a)  LDA; (b)
LDA; (b)  RBF-SVM; (c)
RBF-SVM; (c) 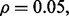 LDA; (d)
LDA; (d) 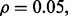 RBF-SVM
RBF-SVM
3.6 Concluding remarks
Performance reproducibility is an epistemological issue: What knowledge is provided by a study? Ultimately, we are led back to the core epistemological issue in biomarker prediction, accuracy of the error estimate. To the extent that the estimated classifier error differs from the true error on the feature-label distribution, there is lack of knowledge at the conclusion of the first study. If there is virtually no reproducibility, then there is virtually no knowledge. Thus, there is no justification for a large study based on the preliminary study. Indeed, why proceed with the preliminary study if there is no reason to believe that its results will be reproducible? The issue of reproducibility should be settled before any study, small or large. The proposed reproducibility index provides the needed determination.
Ultimately, the reproducibility index depends on the accuracy of the error estimator, and if we judge accuracy by the RMS, then the deviation variance of the estimator plays a crucial rule since 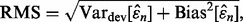 where the bias and deviation variance are defined by
where the bias and deviation variance are defined by 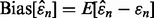 and
and 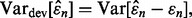 respectively. When the bias is small, as in the case of LOO,
respectively. When the bias is small, as in the case of LOO,
where 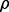 is the correlation coefficient between the true and estimated errors. As we see in Figures 2 and 3,
is the correlation coefficient between the true and estimated errors. As we see in Figures 2 and 3, 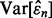 tends to be large and
tends to be large and 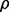 tends to be very small or even negative (Braga-Neto and Dougherty, 2010; Hanczar et al., 2007). This large variance and lack of positive correlation results in lack of reproducibility for small samples.
tends to be very small or even negative (Braga-Neto and Dougherty, 2010; Hanczar et al., 2007). This large variance and lack of positive correlation results in lack of reproducibility for small samples.
Let us conclude with some remarks concerning validation, which, in our particular circumstance, means validation of the classifier error from the original small-sample study. For complex models, such as stochastic dynamical networks, validation of the full network is typically beyond hope, and one must be content with validating some characteristic of the network, such as its steady-state solution, by comparing it to empirical observations (Dougherty, 2011). As for how close the theoretical and the corresponding empirical characteristic must be to warrant acceptance, closeness must be defined by some quantitative criterion understood by all. The intersubjectivity of validation resides in the fact that some group has agreed on the measure of closeness (and the requisite experimental protocol), although they might disagree on the degree of closeness required for acceptance (Dougherty and Bittner, 2011). In the case of classification (as noted in the Introduction), when applying a classifier on an independent test set, the RMS possesses a distribution-free bound of 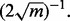 Agreeing to using the RMS as the closeness criterion and using this bound, one can determine a test sample size to achieve a desired degree of accuracy, thereby validating (or not validating) the performance claims made in the original experiment.
Agreeing to using the RMS as the closeness criterion and using this bound, one can determine a test sample size to achieve a desired degree of accuracy, thereby validating (or not validating) the performance claims made in the original experiment.
The situation is much more subtle when using the RMS on the training data. In very few cases are any distribution-free bounds known and, when known, they are useless for small samples. To obtain useful RMS bounds, one must apply prior distributional knowledge. There is no option. Given prior (partial) distributional knowledge, one can determine a sample size to achieve a desired RMS (Zollanvari et al., 2012). Furthermore, given a prior distribution on the uncertainty class, one can find an exact expression for the RMS given the sample, meaning that one can use a censored sampling approach to sample just long enough to achieve the desired RMS (Dalton and Dougherty, 2012a). Prior knowledge can also be used to calibrate ad hoc error estimators such as resubstitution and LOO to gain improved estimation accuracy (Dalton and Dougherty, 2012b). One might argue that assuming prior knowledge carries risk because the knowledge could be erroneous. But if one does not bring sufficient knowledge to an experiment to achieve meaningful results, then he or she is not ready to do the experiment. Pragmatism requires prior knowledge. The prior knowledge is uncertain, and our formulation of it must include a measure of that uncertainty. The more uncertain we are, the less impact the knowledge will have on our conclusions. In the case of the reproducibility index, we have introduced a few criteria by which one can decide whether, in the framework of this uncertainty, a desired level is achieved. A key point regarding uncertainty in the context of reproducibility is that, should the prior distribution on the uncertainty class be optimistic, it may result in carrying out a second study without sufficient justification but it will not lead to an overoptimistic conclusion because the conclusion will be based on the independent larger follow-on study in which the prior knowledge is not employed. This is far better than basing the decision to proceed with a large independent study on a meaningless error estimate.
ACKNOWLEDGEMENT
The authors thank the High-Performance Biocomputing Center of TGen for providing the clustered computing resources used in this study; this includes the Saguaro-2 cluster supercomputer, partially funded by NIH grant 1S10RR025056-01.
Conflict of Interest: none declared.
REFERENCES
- Boser BE, et al. COLT ’92: Proceedings of the Fifth Annual Workshop on Computational Learning Theory. New York: ACM; 1992. A training algorithm for optimal margin classifiers; pp. 144–152. [Google Scholar]
- Boulesteix A-L. Over-optimism in bioinformatics research. Bioinformatics. 2010;26:437–439. doi: 10.1093/bioinformatics/btp648. [DOI] [PubMed] [Google Scholar]
- Boulesteix A-L, Slawski M. Stability and aggregation of ranked gene lists. Brief. Bioinform. 2009;10:556–568. doi: 10.1093/bib/bbp034. [DOI] [PubMed] [Google Scholar]
- Braga-Neto UM, Dougherty ER. Is cross-validation valid for small-sample microarray classification? Bioinformatics. 2004;20:374–380. doi: 10.1093/bioinformatics/btg419. [DOI] [PubMed] [Google Scholar]
- Braga-Neto UM, Dougherty ER. Exact correlation between actual and estimated errors in discrete classification. Pattern Recognit. Lett. 2010;31:407–413. [Google Scholar]
- Castaldi PJ, et al. An empirical assessment of validation practices for molecular classifiers. Brief. Bioinform. 2011;12:189–202. doi: 10.1093/bib/bbq073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, et al. Novel endothelial cell markers in hepatocellular carcinoma. Modern Pathol. 2004;17:1198–1210. doi: 10.1038/modpathol.3800167. [DOI] [PubMed] [Google Scholar]
- Cortes C, Vapnik VN. Support-vector networks. Mach. Learn. 1995;20:273–297. [Google Scholar]
- Dalton LA, Dougherty ER. Bayesian minimum mean-square error estimation for classification error–Part I: Definition and the Bayesian MMSE error estimator for discrete classification. IEEE Trans. Signal Process. 2011a;59:115–129. [Google Scholar]
- Dalton LA, Dougherty ER. Application of the Bayesian MMSE error estimator for classification error to gene-expression microarray data. Bioinformatics. 2011b;27:1822–1831. doi: 10.1093/bioinformatics/btr272. [DOI] [PubMed] [Google Scholar]
- Dalton LA, Dougherty ER. Exact MSE performance of the Bayesian MMSE estimator for classification error–Part II: Consistency and performance analysis. IEEE Trans. Signal Process. 2012a;60:2588–2603. [Google Scholar]
- Dalton LA, Dougherty ER. Optimal MSE calibration of error estimators under Bayesian models. Pattern Recognit. 2012b;45:2308–2320. [Google Scholar]
- Devroye L, et al. A Probabilistic Theory of Pattern Recognition. New York: Springer-Verlag; 1996. [Google Scholar]
- Dougherty ER. Validation of gene regulatory networks: scientific and inferential. Brief. Bioinform. 2011;12:245–252. doi: 10.1093/bib/bbq078. [DOI] [PubMed] [Google Scholar]
- Dougherty ER. Prudence, risk, and reproducibility in biomarker discovery. BioEssays. 2012;34:277–279. doi: 10.1002/bies.201200003. [DOI] [PubMed] [Google Scholar]
- Dougherty ER, Bittner ML. Epistemology of the Cell: A Systems Perspective on Biological Knowledge. New York: John Wiley; 2011. [Google Scholar]
- Dougherty ER, et al. Performance of error estimators for classification. Curr. Bioinform. 2010;5:53–67. [Google Scholar]
- Dougherty ER, et al. The illusion of distribution-free small-sample classification in genomics. Curr. Genomics. 2011;12:333–341. doi: 10.2174/138920211796429763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. Statistical Methods for Research Workers. Edinburg: Oliver and Boyd; 1925. [Google Scholar]
- Hanczar B, et al. Decorrelation of the true and estimated classifier errors in high-dimensional settings. EURASIP J. Bioinform. Syst. Biol. 2007;2007:12. doi: 10.1155/2007/38473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanczar B, et al. Small-sample precision of ROC-related estimates. Bioinformatics. 2010;26:822–830. doi: 10.1093/bioinformatics/btq037. [DOI] [PubMed] [Google Scholar]
- Hua J, et al. Optimal number of features as a function of sample size for various classification rules. Bioinformatics. 2005;21:1509–1515. doi: 10.1093/bioinformatics/bti171. [DOI] [PubMed] [Google Scholar]
- Hothorn T, Leisch F. Case studies in reproducibility. Brief. Bioinform. 2011;12:288–300. doi: 10.1093/bib/bbq084. [DOI] [PubMed] [Google Scholar]
- Ioannidis JPA. Why most published research findings are false. PLoS Med. 2005;2:e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelizarow M, et al. Over-optimism in bioinformatics: an illustration. Bioinformatics. 2010;26:1990–1998. doi: 10.1093/bioinformatics/btq323. [DOI] [PubMed] [Google Scholar]
- Li Q, et al. Measuring reproducibility of high-throughput experiments. Ann. Appl. Stat. 2011;5:1752–1779. [Google Scholar]
- Natsoulis G, et al. Classification of a large microarray data set: algorithm comparison and analysis of drug signatures. Genome Res. 2005;15:724–736. doi: 10.1101/gr.2807605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray T. FDA’s Woodcock says personalized drug development entering ‘long slog’ phase. Pharmacogen. Rep. 2011 http://www.genomeweb.com/mdx/fdas-woodcock-says-personalized-drug-development-entering-long-slog-phase (26 October 2011, date last accessed) [Google Scholar]
- Sabel MS, et al. Proteomics in melanoma biomarker discovery: great potential, many obstacles. Int. J. Proteom. 2011;2011:8. doi: 10.1155/2011/181890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeoh EJ, et al. Classification, subtype discovery, and prediction of outcome in pediatric acute lymphoblastic leukemia by gene expression profiling. Cancer Cell. 2002;1:133–143. doi: 10.1016/s1535-6108(02)00032-6. [DOI] [PubMed] [Google Scholar]
- Yousefi MR, et al. Reporting bias when using real data sets to analyze classification performance. Bioinformatics. 2010;26:68–76. doi: 10.1093/bioinformatics/btp605. [DOI] [PubMed] [Google Scholar]
- Yousefi MR, et al. Multiple-rule bias in the comparison of classification rules. Bioinformatics. 2011;27:1675–1683. doi: 10.1093/bioinformatics/btr262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan F, et al. The molecular classification of multiple myeloma. Blood. 2006;108:2020–2028. doi: 10.1182/blood-2005-11-013458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M, et al. Apparently low reproducibility of true differential expression discoveries in microarray studies. Bioinformatics. 2008;24:2057–2063. doi: 10.1093/bioinformatics/btn365. [DOI] [PubMed] [Google Scholar]
- Zhang M, et al. Evaluating reproducibility of differential expression discoveries in microarray studies by considering correlated molecular changes. Bioinformatics. 2009;25:1662–1668. doi: 10.1093/bioinformatics/btp295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zollanvari A, et al. Joint sampling distribution between actual and estimated classification errors for linear discriminant analysis. IEEE Trans. Inform. Theory. 2010;56:784–804. [Google Scholar]
- Zollanvari A, et al. Exact representation of the second-order moments for resubstitution and leave-one-out error estimation for linear discriminant analysis in the univariate heteroskedastic Gaussian model. Pattern Recognit. 2012;45:908–917. [Google Scholar]


