Gait analysis in patients with idiopathic scoliosis

Abstract

Introduction

The goal of this study was to observe scoliotic subjects during level walking to identify asymmetries—which may be related to a neurological dysfunction or the spinal deformity itself—and to correlate these to the severity of the scoliotic curve.

Methods

We assessed the gait pattern of ten females (median age 14.4) with idiopathic scoliosis characterised by a left-lumbar and a right-thoracic curve component. Gait analysis consisted of 3D kinematic (VICON) and kinetic (Kistler force plates) measurements. The 3D-segment positions of the head, trunk and pelvis, as well as the individual joint angles of the upper and lower extremities, were computed during walking and static standing. Calculation of pertinent kinetic and kinematic parameters allowed statistical comparison.

Results

All subjects walked at a normal velocity (median: 1.22 m/s; range:1.08–1.30 m/s; height-adjusted velocity: 0.75 m/s; range: 0.62–0.88 m/s). The timing of the individual gait phases was normal and symmetrical for the whole group. Sagittal plane hip, knee and ankle motion followed a physiological pattern. Significant asymmetry was observed in the trunk’s rotational behaviour in the transverse plane. During gait, the pelvis and the head rotated symmetrically to the line of progression, whereas trunk rotation was asymmetric, with increased relative forward rotation of the right upper body in relation to the pelvis. This produced a torsional offset to the line of progression. Minimal torsion (at right heel strike) measured: median 1.0° (range: 5.1°–8.3°), and maximal torsion (at left heel strike) measured 11.4° (range 6.9°–17.9°). The magnitude of the torsional offset during gait correlated to the severity of the thoracic deformity and to the standing posture, whereas the range of the rotational movement was not affected by the severity of the deformity. The ground reaction forces revealed a significant asymmetry of [Msz], the free rotational moment around the vertical axis going through the point of equivalent force application. On the right side, the initial endo-rotational moment was lower, followed by a higher exo-rotational moment than on the left. All the other force parameters (vertical, medio–lateral, anterior–posterior), did not show a significant side difference for the whole group. The use of a brace stiffened torsional motion. However the torsional offset and the asymmetry of the free rotational moment remained unchanged.

Conclusion

The most significant and marked asymmetry was seen in the transverse plane, denoted as a torsional offset of the upper trunk in relation to the symmetrically rotating pelvis. This motion pattern was reflected by a ground-reaction-force asymmetry of the free rotational moment. Further studies are needed to investigate whether this behaviour is solely an expression of the structural deformity or whether it could enhance the progression of the torsional deformity.

Introduction

The aetiology of idiopathic scoliosis is still unknown. A cerebral asymmetry [5] or a developmental abnormality in the central nervous system [1] are possible causes. A neurological disorder that affects the locomotor system can be expected to alter the gait pattern. Using the techniques of comprehensive gait analysis, which allow analysing pathomechanisms of the locomotor system, it should be possible to identify asymmetries in scoliotic subjects during level walking. These asymmetries may be related to a neurological dysfunction or to the spinal deformity itself. A pilot study conducted at our hospital [10] of 21 patients (aged 10 to 36) with idiopathic scoliosis revealed no systematic asymmetry of the vertical ground reaction forces in relation to the side of the scoliotic curve. Although an asymmetry of at least one gait parameter was noted in 20 subjects, multiple regression analysis showed that there was no relation between the noted gait asymmetry and the curve direction, curve magnitude or vertebral rotation. However, functional asymmetries of the central nervous system have been described in patients with idiopathic scoliosis [1,5]. More detailed quantitative analysis is necessary to further investigate the possibility of a reproducible effect on gait. Thus, it seems probable that asymmetries may be present in the fore–aft and medio–lateral directions or in the transverse plane, and that these are coupled with asymmetric movements in the peripheral joints, trunk and pelvis and are related to the individuals’ scoliotic curves.

The goal of this study was to identify asymmetries in scoliotic subjects’ forces and movement strategies during level walking, in order to correlate them to the severity of the scoliotic deformity, using three-dimensional gait analysis techniques.

Materials and methods

Ten females with idiopathic scoliosis were included in this study (see Table 1). The subjects—median age, 14.4 years—all had a left-lumbar and a right-thoracic component of their curves, of varying severity. The Cobb angle was determined from longitudinal X-ray films including the cervical, thoracic and lumbar spine. Surgery was planned in the four subjects with the most severe deformities. Three subjects with mild to moderate deformities were treated with a brace, and three had no treatment during the gait study. The subjects who had a brace were tested with and without the brace.

Table 1.

Clinical data: age, Cobb angle of thoracic and lumbar curves, current treatment. Subjects arranged according to increasing thoracic curve

Subject	Age (years)	Cobb angle, thoracic curve (°)	Cobb angle, lumbar curve (°)	Treatment
A	10.3	0	9	Brace
B	11.8	3	27	Brace
C	14.4	29	38	Brace discontinued
D	18.8	40	23	Brace discontinued
E	14.6	41	22	No treatment
F	13.2	46	32	Brace
G	20.0	55	60	Surgery planned
H	14.0	66	36	Surgery planned
I	36.3	67	45	Surgery planned
J	14.4	73	47	Surgery planned

Gait analysis

Each subject’s performance in static standing and gait was assessed at the Laboratory for Biomechanics, ETH Zürich. Kinematic and kinetic data were collected simultaneously during level walking over a 25 m walkway. Each subject was asked to walk barefoot at her most comfortable speed (self-selected free gait velocity).

Kinematic analysis

Data capture

Three-dimensional motion analysis was performed using a five-camera VICON System (Oxford Metrics). Spherical retroreflective markers (Ø 25 mm) were placed bilaterally over the following anatomical landmarks on the trunk and the upper and lower extremities:

• Head: the bilateral jaw joint and median suture on top.

• Trunk: bilateral acromion, Th1.

• Upper extremities: bilateral radial epicondyle and dorsum of the wrist.

• Pelvis: bilateral anterior superior iliac spine, sacrum on the midline of S1.

• Lower extremities: bilateral midline of the thigh, lateral joint line of the knee, lateral shank (fibula), lateral malleolus, posterior aspect of the calcaneus and dorsum of the foot, between the first and second metatarsal head.

The five phase-locked and strategically placed VICON cameras recorded the marker position coordinates bilaterally at a sampling rate of 50 Hz. This technique allowed a simultaneous motion assessment of both lower extremities as well as the trunk and arm positions.

Data processing

Further data processing was performed using the biomechanical analysis package “ANALYZE”, written by D. Meglan [8] and modified by our laboratory. The kinematic analysis was based upon the principles of three-dimensional rigid body mechanics. Segment position and orientation were calculated relative to a global coordinate system, using the recorded marker-based information and anthropometric data. Individual joint angles were then calculated relative to a joint-centred coordinate system (JCS), referenced to the proximal segment.

Data analysis

A parameter analysis was used to statistically compare the joint angles between the two sides at defined phases of the gait cycle. The relative range of rotational motion between the segments of the pelvis, upper trunk (orientation of the shoulders) and head was analysed. A dynamic offset of the rotational trunk–pelvis segment position with respect to the line of progression was calculated:

“Torsional offset”=(minimal trunk–pelvis rotation [°]+maximal trunk–pelvis rotation [°])/2

In the scoliotic subjects, minimal rotation occurred around right heel strike and maximal rotation around left heel strike (see Fig. 1). If the trunk rotates symmetrically in relation to the line of progression, the positive values around left heel strike and the negative values around right heel strike have the same magnitude, leading to a torsional offset of 0°.

Fig. 1.

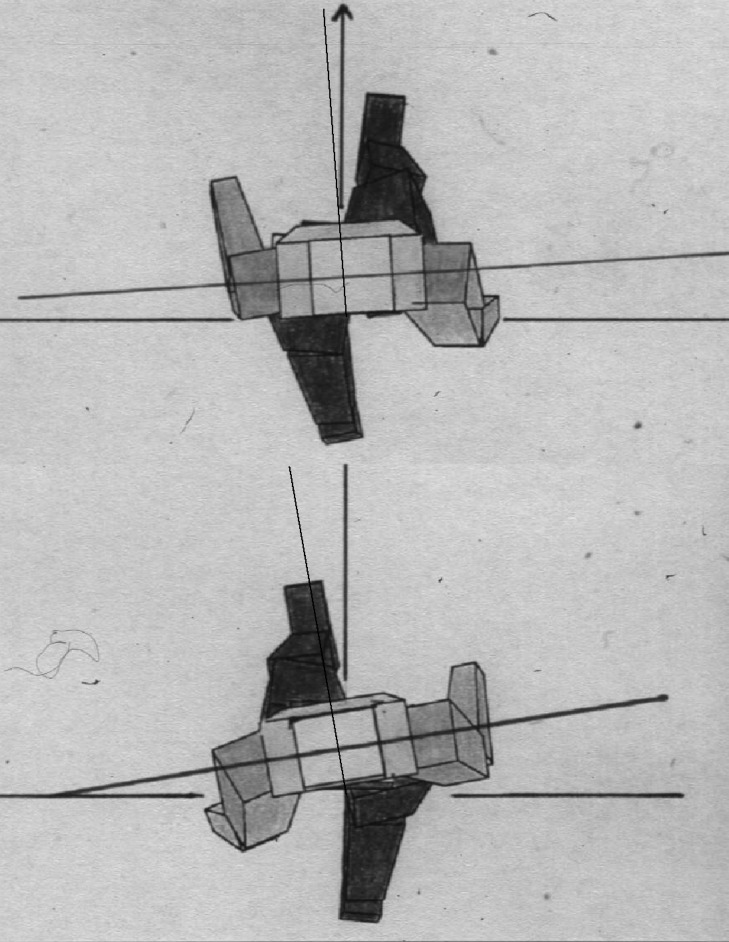
View of the body segments in the transverse plane in relation to the line of progression, for right heel strike (above) and for left heel strike (below) of a scoliotic subject. The difference of the trunk segment orientation between right and left heel strike reflects the torsional offset during gait. If the trunk rotates symmetrically in relation to the line of progression, the torsional offset is 0°

Kinetic analysis

Data capture

The ground reaction forces were recorded by two 3D Kistler force plates (Kistler Instrumente), which were embedded into the floor in the middle of the 25-m walkway. The sampling rate was 1000 Hz.

Data processing and analysis

The vertical, medio–lateral and fore–aft forces were all graphed, normalised to body weight. The force plate recordings were further analysed by a parameter analysis program, developed in the laboratory by Stüssi et al.[12]. Specific parameters—such as the peak values of the ground reaction forces in all three dimensions and the integral (difference of the impulse) of the fore– aft shear forces and the free rotational moments—were used for statistical analysis. The free rotational moment [Msz] results from the distribution of shear forces at the foot-to-ground interface. It is the moment at which the vertical axis passes through the point of force application. The angular momentum is the integral over time of the rotational moment.

Time–distance parameters

The following time–distance parameters were calculated from kinematic and force-plate readings: velocity, cadence, stride length, step length, and the relative and absolute durations of the individual gait phases: total stance time, single-limb stance time and double-limb stance time for each side.

Statistical analysis:

Five trials were analysed for each subject and each testing condition to calculate the mean and standard deviations of the time–distance parameters, as well as the chosen kinematic parameters. Ten trials were analysed for the force plate parameters. The asymmetry index (ASI) described by Herzog et al.[6] was used to quantify the difference between the right and left side. The variable X represents the measured gait parameter of the corresponding side.

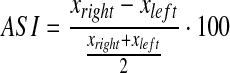An ASI value of zero indicates that there is perfect symmetry for that particular gait variable. In healthy subjects asymmetry limits were found to vary from ±4% to over ±13%, depending on the chosen gait variable [6].

Further side-to-side comparison was performed using a nonparametric test (Wilcoxon signed-rank test). Values were considered significant on a level of p< 0.05.

Results

Time– distance parameters

All subjects walked at a normal velocity (mean: 1.22 m/s, SD: 0.07, range: 1.08–1.30 m/s; height-adjusted velocity: 0.75 m/s, SD: 0.07, range: 0.62–0.88 m/s). While the cadence measured within normal limits compared to published norms, the stride length, normalised to leg length, was slightly reduced in some subjects. The timing of the individual gait phases was normal and symmetrical for the whole group. The mean asymmetry index (ASI) for step length and for the duration of the gait phases was below 2, indicating an asymmetry of less than 2%. The individual asymmetry values ranged between 0 and 7. This corresponds to symmetry values within the physiological variation [6](see Table 2).

Table 2.

Time–distance parameters

	Mean	SD	Range	Published norm
Gait velocity (m/s)	1.22	0.07	1.08–1.30	1.24 [9]
Stride (m)	1.23	0.09	1.09–1.33	1.28 [9]
Stride/leg length	1.45	0.08	1.34–1.54	1.58 [12]
Cadence (steps/min)	118	7	111–133	117 [9]

Kinematic analysis

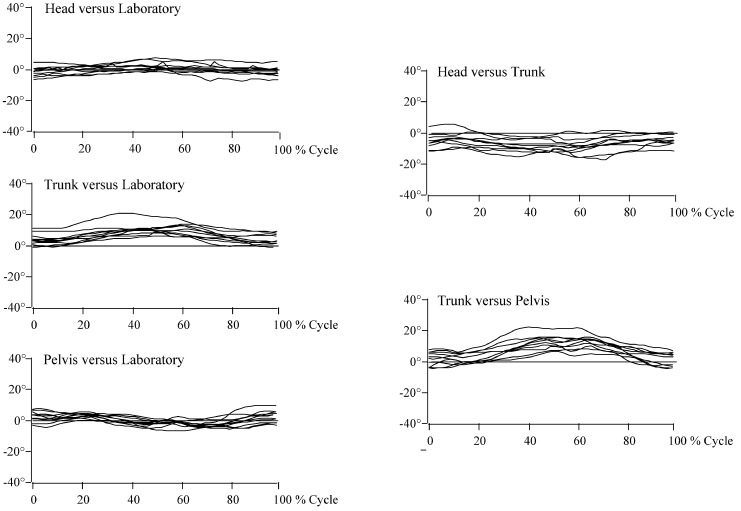
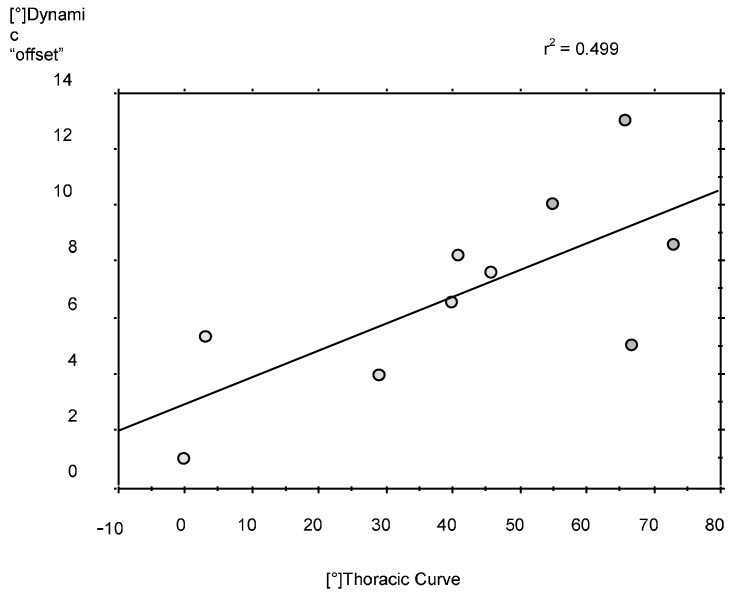
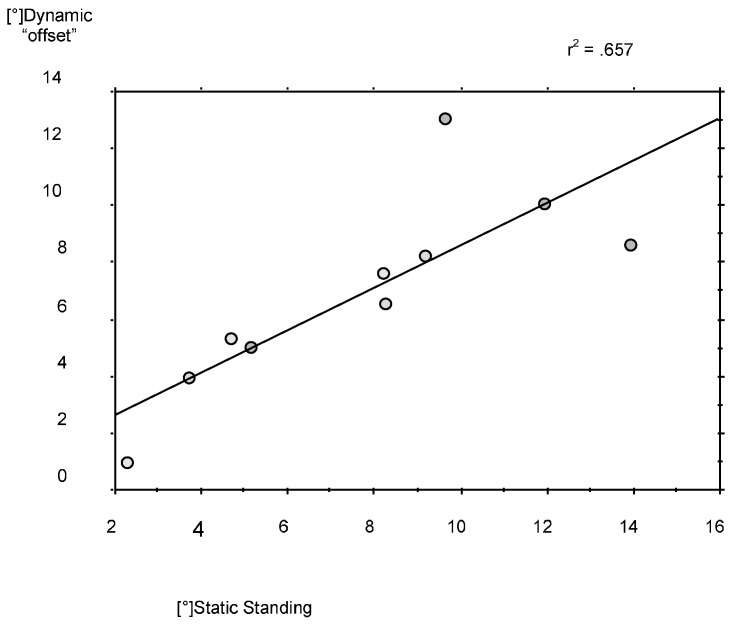
Sagittal plane hip, knee and ankle motion followed a physiological motion pattern, with only minor side-to-side variations within normal limits. Transverse plane motion of the trunk revealed a significant asymmetry (see Fig. 1 and 2). During gait, the pelvis and the head rotated symmetrically to the line of progression, whereas trunk rotation was asymmetric, with increased relative forward rotation of the right upper body in relation to the pelvis, producing a torsional “offset” to the line of progression (see Table 3). At right heel strike, torsion was minimal, with a median of 1.0° (range: 5.1°–8.3°). At left heel strike, torsion measured 11.4° (range: 6.9°–17.9°). The magnitude of the torsional offset during gait correlated to the severity of the thoracic deformity (r²=0.499) and to the standing posture (r²= 0.657). This demonstrated a similar rotational alignment of the trunk in relation to the pelvis. (See Table 3, Fig. 3 and Fig. 4). However, the dynamic range of the rotational movement between pelvis and trunk during gait was not affected by the severity of the deformity. Thus, rotational motion around the offset axis was also measured in the severe curves.

Fig. 2.

Left: Representative motion curves of each subject, for the head, trunk and pelvis, relative to laboratory coordinates. The head and the pelvis display a symmetric motion in relation to the line of progression. Trunk motion is asymmetric; the right shoulder is advanced. Right: Relative motion of the head versus the trunk and the trunk versus the pelvis, reflecting torsional deformity

Table 3.

Static and dynamic rotation of the trunk in relation to the pelvis. Subjects arranged according to increasing thoracic curve

Subject	Standing posture (°)	Gait
		Minimal torsion (at right heel strike) (°)	Maximal torsion (at left heel strike) (°)	Range of torsional motion (°)	Offset (°)
A	2.3	−5.8	7.7	13.5	1.0
B	4.7	−1.1	11.6	12.7	5.3
C	3.8	−1.1	8.8	9.9	3.9
D	8.3	−4.6	17.6	22.2	6.5
E	9.2	3.8	12.6	12.6	8.2
F	8.2	3.3	11.9	8.6	7.6
G	12.0	4.7	15.4	10.7	10.0
H	9.7	6.6	19.4	12.8	13.0
I	5.2	−5.0	15.0	20.0	5.0
J	13.9	1.6	15.7	14.1	8.6

Fig. 3.

Correlation between the dynamic torsional offset of the trunk–pelvis angles (°) and the thoracic curve Cobb angles (°). The more severe curves demonstrate a greater dynamic torsional offset

Fig. 4.

Correlation between the dynamic torsional offset of the trunk–pelvis angles (°) and the static standing trunk–pelvis angle (°). The correlation indicates that the static torsional deformity is carried over to the dynamic situation

Analysis of the torsional offset in relation to the severity of the lumbar curve showed no relevant correlation (r²= 0.266).

Upper extremity motion

Asymmetry of arm swing was seen in most subjects. One side demonstrated a larger range of flexion/extension motion at the shoulder and the elbow, compared to the other side, with no systematic pattern. The magnitude and direction of the asymmetry did not correlate with the severity of the scoliotic curve. Five subjects had more shoulder motion on the right side, and the other five had more on the left, unrelated to their deformity. Mean side difference for the whole group measured 1.2°±10.9° for elbow motion and 9.7°±10.3° for shoulder motion (see Table 4).

Table 4.

Dynamic range of elbow and shoulder flexion during gait. Subjects arranged according to increasing thoracic curve. Difference between left and right in (°) flexion. Note that a negative value of the side difference indicates a higher range of flexion on the right side and a positive value a higher range of flexion on the left side

Subject	Elbow flexion (°)			Shoulder flexion (°)
	Left	Right	Side difference (L−R)	Left	Right	Side difference (L−R)
A	14.2	14.5	−0.3	8.6	10.9	−2.3
B	15.7	18.2	−2.5	13.3	11.0	2.3
C	19.1	45.4	−26.3	15.7	31.7	−16.0
D	23.1	35.9	−12.8	22.2	26.7	−4.5
E	33.2	30.3	2.9	25.3	16.1	9.2
F	13.9	7.3	6.6	16.4	12.2	4.2
G	15.7	22.6	−6.9	13.7	10.8	2.9
H	22.9	10.0	12.9	31.8	8.2	23.6
I	26.9	27.0	−0.1	19.9	24.9	−5.0
J	11.8	9.9	1.9	11.2	11.8	−0.6

Kinetic analysis

The vertical ground reaction forces did not display an asymmetry for the whole group (see Tables 5 and 6). Only two individuals had an asymmetry >5% of the first peak during loading.

Table 5.

Parameters of vertical ground reaction forces, normalised to body weight and anterior–posterior impulse. Individual results for each subject. Subjects arranged according to increasing thoracic curve

Subject	First peak			Through			Second peak			a/p impulse
	Fz2n (N/Bw)			Fz3n (N/Bw)			Fz4n (N/Bw)			(Ns)
	Left	Right	ASI	Left	Right	ASI	Left	Right	ASI	Left	Right	ASI
A	1.23	1.28	−4.0	0.64	0.63	1.6	1.22	1.22	0	17.09	19.09	0
B	1.27	1.18	7.4	0.73	0.76	−4.0	1.04	1.04	0	16.16	15.48	0
C	1.06	1.09	−2.8	0.89	0.89	0	1.11	1.10	0.5	24.84	26.45	0.9
D	1.03	1.13	−9.3	0.74	0.70	5.6	1.20	1.26	−4.9	32.62	35.40	−4.9
E	1.16	1.16	0	0.73	0.74	−1.4	1.14	1.12	1.8	26.94	28.10	1.8
F	1.15	1.14	0.9	0.76	0.77	−1.3	1.14	1.13	0.9	22.17	22.85	0.9
G	0.96	0.97	−1.0	0.82	0.83	−1.2	1.25	1.20	4.1	26.41	24.69	4.1
H	1.06	1.06	0	0.77	0.78	−1.3	1.22	1.19	2.5	31.68	31.73	2.5
I	1.07	1.08	−0.9	0.78	0.80	−2.5	1.10	1.11	−0.9	40.32	40.23	−0.9
J	1.03	1.02	1.0	0.80	0.80	0	1.17	1.14	2.6	30.54	29.57	2.6

Table 6.

Vertical force parameters and anterior–posterior impulse

	Left	Right
T (s)	610, SD 45.8	611, SD 48.4	p=.721
Fz2n (N/Bw)	1.10, SD 0.10	1.11, SD 0.09	p=.374
Fz3n (N/Bw)	0.77, SD 0.07	0.77, SD 0.07	p=.236
Fz4n (N/Bw)	1.16, SD 0.07	1.15, SD 0.07	p=.293
a/p impulse (Ns)	26.9, SD 7.4	27.4, SD 7.4	p=.359

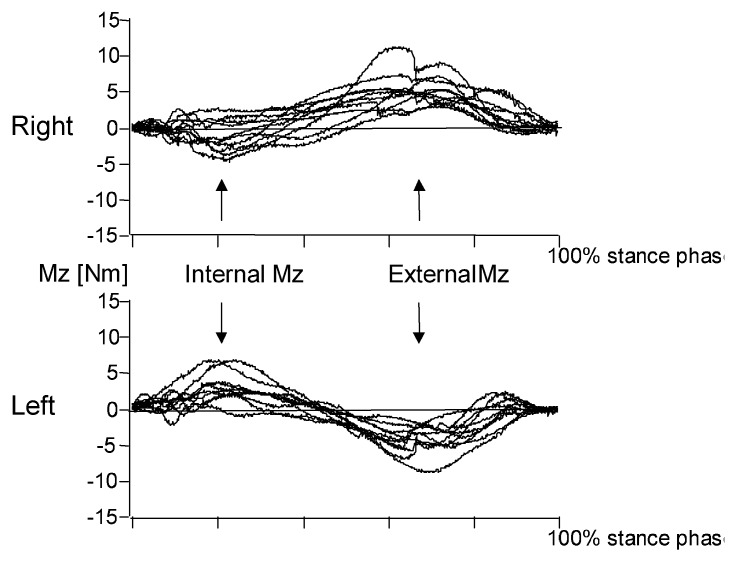
The most striking asymmetry was seen in the free rotational moment Msz [Nm] and the angular momentum [Nms]. The right side had a significantly lower internal (p=0.007) and a significantly higher external (p=0.03) rotational moment peak (see Fig. 5 and Tables 7 and 8).

Fig. 5.

Free rotational moment Msz [Nm]: median curve of each subject

Table 7.

Free rotational moment (Msz, in Nm): individual results for each subject

Sub-ject	Msz internal rotational moment			Msz external rotational moment
	Left	Right	ASI	Left	Right	ASI
A	0.35	0.37	−5.6	−0.54	−0.72	−28.6
B	0.52	0.32	47.6	−0.46	−0.57	−21.4
C	0.25	0.21	15.4	−0.33	−0.52	−44.7
D	0.25	0.08	103.0	−0.34	−0.40	−16.2
E	0.18	0.11	48.2	−0.38	−0.47	−22.5
F	0.40	0.34	16.2	−0.73	−0.61	18.7
G	0.46	0.20	80.0	−0.58	−0.68	−16.7
H	0.34	0.30	11.0	−0.39	−0.67	−52.1
I	0.31	0.13	83.7	−0.27	−0.34	−22.9
J	0.54	0.05	168.9	−0.57	−0.92	−46.9

Table 8.

Free rotational moment and angular momentum

	Right	Left
Msz internal rotational moment	0.21, SD 0.12	0.36, SD 0.12	p=.007
Msz external rotational moment	0.59, SD 0.17	0.46, SD 0.14	p=.03
Change of angular momentum in endo-rotational direction (Nms) = kg m2	0.26, SD 0.21	0.47, SD 0.26	p=.007
Change of angular momentum in exo-rotational direction (Nms) = kg m2	1.13, SD 0.32	0.66, SD 0.22	p=.005

Comparison: un-braced versus braced condition in three subjects tested with and without brace

The force plate data did not show any significant difference between the braced and un-braced conditions. The asymmetry of the ground reaction forces for [Msz] the free rotational moment remained unchanged. The brace’s major influence was seen in the kinematic study, clearly reducing the dynamic range of pelvic and trunk motion. There was less pelvic motion in the frontal plane and less overall rotational movement of the trunk relative to the pelvis in the transverse plane. Using the brace, only 2° to 5.7° torsional motion was measured (see Table 9), whereas, without it, torsional motion ranged 8.6° to 13.5°. However, torsional offset remained unchanged in the un-braced condition. Thus, the brace stiffened the trunk but did not change the torsional alignment offset.

Table 9.

Static and dynamic rotation of the trunk in relation to the pelvis, for the three subjects who had a brace. Comparison of the un-braced and braced conditions

Subject	Standing posture (°)		Gait
			Minimal torsion (at right heel strike) (°)		Maximal torsion (at left heel strike) (°)		Range of torsional motion (°)		Offset (°)
	No brace	Brace	No brace	Brace	No brace	Brace	No brace	Brace	No brace	Brace
A	2.3	2.5	−5.8	0.2	7.7	3.5	13.5	3.3	1.0	1.8
B	4.7	7.7	−1.1	5.3	11.6	11.1	12.7	5.7	5.3	8.2
F	8.2	5.9	3.3	5.0	11.9	7.0	8.6	2.0	7.6	6.0

Discussion

Only limited data exist on the gait pattern of scoliotic subjects. The goal of this study was to detect asymmetries in the gait pattern of young women with an idiopathic scoliosis and to correlate them to the severity of the scoliotic curve. The free gait velocity was normal compared to published norms [9,13], indicating normal functionality with respect to walking speed. Only the stride length showed a tendency to be below the normal range. Most of the traditionally recorded gait parameters—such as time–distance, vertical and anterior–posterior ground reaction forces, as well as the sagittal plane joint angles—did not demonstrate a significant or clinically relevant asymmetry between the two sides in this group of subjects. The asymmetry index of the vertical and anterior–posterior ground reaction force parameters was within the range recorded for healthy subjects by Herzog et al. [6]. No increased asymmetry was noted in the severe scoliotic curves. These findings are consistent with previous studies: Schizas [10] found no relation between noted asymmetries of the vertical ground reaction forces and the curve direction, curve magnitude or vertebral rotation in 21 subjects. In time and frequency domain analyses of ground reaction forces in 20 subjects, Giakas [4] found the only asymmetries in the frequency domain of the medial–lateral forces. Chen [2] reported poor postural stability with a higher sway area for scoliotic subjects. However, their gait patterns were similar to those of normal subjects.

The major asymmetry found in the present kinematic data was the rotational alignment of the trunk. The orientation of the shoulder was asymmetric in relation to the line of progression and to the orientation of the pelvis, the right shoulder being more advanced, whereas the pelvis and the head rotated symmetrically. To describe the rotational trunk alignment, we introduced the formula: torsional offset=(minimal trunk–pelvis rotation [°]+maximal trunk–pelvis rotation [°])/2. If the trunk and the pelvis rotate symmetrically in relation to the line of progression, the torsional offset is 0°.

The magnitude of the torsional offset correlated to the degree of the thoracic component of the scoliotic deformity. It ranged from 1° in the subject with the mildest scoliotic curve to 13° in a subject with a severe deformity. Since the standing posture demonstrated a similar rotational alignment of the trunk in relation to the pelvis, the offset during gait is most likely caused by the structural deformity. However, the dynamic range of torsional motion between pelvis and trunk was not affected by the severity of the deformity. Rotational movements around the offset axis were also measured in the severe curves. Thus, the more severe curves still allowed rotational motion to occur.

Abnormal transverse plane alignment was also found by other investigators [3, 7]. Lenke [7] described a reduction of the acromion–pelvis angle after surgery with long spinal fusion, in 30 subjects with adolescent idiopathic scoliosis. In the present study, the un-braced condition was compared to the braced condition in the three subjects who were treated with a brace at the time of the gait study. The brace stiffened the trunk and pelvic movements but did not change the abnormal trunk–pelvis alignment. The rotational offset remained. Thus, in contrast to the results of Lenke [7] after surgery, our study indicates that a brace only stiffens torsional movements but may not correct the rotational alignment. However, with only three braced subjects, the data are not conclusive and should only be looked at as example.

Another striking finding of our study was the ground reaction force asymmetry of the free rotational moment and the angular momentum during gait. The free rotational moment [Msz] results from the distribution of shear forces at the foot-to-ground interface. This is the moment around the vertical axis through the point of force application. This moment has been described [11] to show a large variability between subsequent trials for the same subject as well as between healthy subjects. However, in general, one can state that, in healthy subjects, an internal moment during the first part of the stance phase and an external moment during the second part of the stance phase can be observed. The magnitudes on the right and left sides are expected to be comparable in a steady state gait. A clearly asymmetric pattern existed in the scoliotic subjects: on the right side a lower internal rotational moment and a higher external rotational moment were measured compared to the left. The asymmetry of the rotational transmission of the ground reaction forces to the floor is likely to be an expression of the torsional deformity. Further studies are needed to investigate the clinical significance of these findings in respect to the magnitude and the scoliotic curve progression.

Conclusion

In our group of young scoliotic subjects, the traditionally recorded gait parameters—such as time–distance, vertical and anterior–posterior ground reaction forces, as well as the sagittal plane joint angles—did not demonstrate significant or clinically relevant asymmetry between left and right sides. However, a significant and marked asymmetry was seen in the transverse plane, with a torsional offset of the upper trunk in relation to the symmetrically rotating pelvis. This motion pattern was reflected by a ground reaction force asymmetry of the free rotational moment and angular momentum. Thus, this study demonstrates that scoliotic patients do reveal gait asymmetries of selected biomechanical parameters in the transverse plane. Further studies are needed to investigate whether this behaviour is solely an expression of the structural deformity or whether it could even enhance the progression of the torsional deformity. If the dynamic behaviour during gait is found to promote curve progression, a gait education program aimed at reversing the torsional trunk–pelvis offset and the torsional ground reaction forces should be implemented.