Abstract
The finite helical-axes method can be used to describe the three-dimensional in vitro kinematics of the spine. However, this method still suffers from large stochastic calculation errors and poorly conceived visualisation techniques. The aim of the present study, therefore, was to improve the currently used finite helical axes description, by use of a less error-prone calculation algorithm and a new visualisation technique, and to apply this improved method to the study of the three-dimensional in vitro kinematics of the spine. Three-dimensional, continuous motion data of spinal motion segments were used to calculate the position and orientation of the finite helical axes (FHAs). The axes were then projected on plane antero-posterior, lateral and axial radiographs in order to depict the relation to the anatomy of each individual specimen. A hinge joint was used to estimate the measurement error of data collection and axes calculation. In an exemplary in vitro experiment, this method was used to demonstrate the ability of a prosthetic disc nucleus to restore the three-dimensional motion pattern of lumbar motion segments. In the validation experiment with the hinge joint, the calculated FHAs were lying within ±2.5 mm of the actual joint axis and were inclined relative to this axis at up to ±1.5°. In the exemplary in vitro experiment, the position and orientation of the FHAs of the intact specimens were subject to large inter-individual differences in all loading directions. Nucleotomy of the lumbar segments caused the axes to spread out, indicating complex coupled motions. The implantation of the prosthetic disc nucleus, for the most part, more than reversed this effect: the axes became oriented almost parallel to each other. The experiments showed that the present improved description of finite helical axes is a valid and useful tool to characterise the three-dimensional in vitro kinematics of the intact, injured and stabilised spine. The main advantage of this new method is the comprehensive visualisation of joint function with respect to the individual anatomy.
Keywords: Spine, Kinematics, Helical axis, Biomechanics, In vitro experiment
Introduction
Kinematical methods are widely used to describe the function of the healthy spine, the effect of degeneration or trauma, or the quality of treatment procedures. For in vitro experiments on the spine, usually three angles are reported, typically Cardanic/Eulerian angles or projection angles. Prerequisite for a description of these is a predefined, anatomical coordinate system. The coordinate system generally used for the study of the spine spans the frontal, sagittal and transverse planes. The three Cardanic/Eulerian or projection angles can therefore be called lateral bending, flexion–extension and axial rotation angles [19, 25]. A description of spinal motion by the use of these angles is readily understood. However, the respective predefined axes mostly do not reflect the actual rotary axes of the joint. Furthermore, variations in the localisation of the axes reduce the reproducibility of results and may lead to an over- or underestimation of angle values, called ‘‘crosstalk effect’’ [1, 17]. Moreover, the Cardanic/Eulerian description is limited, since the three angles are sequence dependent, i.e., for a given rigid-body movement there exist six different values for each of the three Cardanic/Eulerian angles [4]. This problem is most evident in the case of large, coupled vertebral motions. Furthermore, the three translations have to refer to fixed points. Since, for this reason, their calculation is technically more demanding than the calculation of angles, most in vitro studies on the spine concentrate on angles, even if the translations were relevant.
In view of these limitations, the finite helical axis of motion has been proposed as an alternative to describe the three-dimensional rigid-body movement of the spine [15, 16, 19]. At each moment in time, the motion of a rigid body can be broken down into a rotation about, and a translation along, a single axis [23]. This axis, which generally varies in position and orientation from one moment to the next, is called a helical axis of motion, or screw axis. The position and orientation of the helical axis, and the translation along and rotation about it, cover all six degrees of freedom of the three-dimensional rigid-body movement. In contrast to the Cardanic/Eulerian description or the description of projection angles, the helical axes constitute the actual axes of motion of the joint, and their positions and orientation relative to each other do not depend on any predefined coordinate system [23].
The helical axes of motion of the spine have mostly been averaged over large displacements [5, 8, 12, 13, 14, 15, 16, 19, 22, 23]. In these cases, the stochastic calculation error, which is inversely proportional to the displacement magnitude, is small [3, 23], whereas the deterministic error is large. If the helical axes are supposed to reflect a continuous movement, the displacement over which separate axes are averaged should be as small as possible. The helical axes then are called finite helical axes (FHAs). Since their displacements are small, FHAs are characterised by small deterministic errors but large stochastic errors. Due to these large stochastic errors, not much work has been published using the finite helical axis method [11, 24]. In 1994, Woltring et al. applied this approach to the kinematics of the spine [24]. In preliminary experiments, they estimated the FHAs for flexion–extension movements of the cervical spine and were able to demonstrate differences in axis position and orientation between healthy volunteers and patients who suffered from whiplash injury. One year later, Nägerl and co-workers estimated the FHAs for axial-rotation movements of cadaveric lumbar spine specimens in order to depict joint function [11]. This approach was promising, since the movements of the specimens could for the first time directly be explained by their anatomy. Unfortunately, however, the authors only reported points of intersection of the FHAs with predefined anatomical planes.
The aim of the present study, therefore, was to improve the currently used finite helical axes description using a recently published less error-prone calculation algorithm [10], and a new visualisation technique and to apply this improved method to study the three-dimensional in vitro kinematics of the spine.
Materials and methods
Data acquisition and FHA calculation
In the testing of spinal segments Cardanic/Eulerian angles, projection angles or helical axes are generally determined for the superior vertebra relative to the inferior vertebra. Therefore, raw data of the three-dimensional movement of the superior relative to the inferior vertebra were needed. The data were collected using a high-resolution, ultrasound motion-analysis system (WinJaw/WinBiomechanics, Zebris, Isny, Germany; measuring frequency 20 Hz, resolution 0.1 mm). It comprises two lightweight plastic crosses, which have to be fixed as rigidly as possible to the anterior surface of the superior and inferior vertebral body (Fig. 1). The cross fixed to the inferior vertebra is equipped with three ultrasound transmitters for emission of pulsed ultrasound waves, and the cross at the superior vertebra is fitted with three or four ultrasound receivers. The time delay between emission of the pulses from the lower cross and reception by the upper cross was used to calculate the projection angles for flexion-extension, lateral bending and axial rotation and to estimate the finite helical axes using the new and less error-prone algorithm published by Marin et al. 2003 [10].
Fig. 1.
An ultrasound motion-analysis system was used to collect three-dimensional motion data of the upper vertebra, relative to the lower vertebra, during application of pure-moment loads in a specially designed spine tester. Data were used to calculate the finite helical axes of motion and projection angles
Error estimation
The measurement error of the FHA description caused by data collection and axis calculation was estimated using two aluminium bodies, which were connected to each other via a hinge joint. They were mounted in a spine tester [20] and equipped with the two crosses of the motion-analysis system. Then three pure-moment loading cycles were applied with a constant rate of 1°/s until a rotation of ±10° was reached. Position and orientation of the calculated FHAs were then compared to position and orientation of the actual rotary axis of the hinge joint.
Visualisation of the FHAs on plane radiographs (registration)
The visualisation of the position and orientation of the FHAs with respect to the individual anatomy of each single specimen on plane radiographs implies a proper registration technique. Registration is defined as the mathematical process for matching the coordinate system used for data acquisition to the coordinate system used in the radiographs. For this purpose, at least three landmarks had to be defined. Since localisation of external anatomical landmarks is known to be difficult and subjective, artificial landmarks were created: three metallic spheres with a central hole and a diameter of 2.5 mm or 4 mm were implanted into the cortex of both the upper and lower vertebral body, one anteriorly, one at the right side and one at the left. These positions were chosen because they allowed also using the spheres to define the coordinate system needed for calculation of the projection angles. Due to their central cavity, it was easy to reliably and reproducibly digitise the spheres before data collection and to locate them on the radiographs, taken in antero-posterior, lateral and axial direction. An additional fixation device allowed a precise and reproducible positioning of the specimens in the X-ray machine (Faxitron, Hewlett Packard).
Automation of FHA calculation and registration
The evaluation was carried out using a custom-made software tool written in Matlab 6.5 (The Mathworks, MA, USA). Input parameters were the three-dimensional motion data and digitised antero-posterior, lateral and axial radiographs. The output consisted of graphic files showing the finite helical axes superimposed on the radiographs. Basically, this software tool worked in four steps:
The three-dimensional motion data were filtered using a wavelet transform [2]
The helical axes of motion were calculated according to the algorithm published by Marin et al. [10]
The radiographs were scaled. This was necessary since the dimensions of the specimens on the radiographs did not completely correspond to their actual dimensions. For this purpose the actual distance between the spheres was compared to their distance on the radiographs, and a magnification factor was calculated
The calculated finite helical axes were visualised on the scaled radiographs
Exemplary experiment with a lumbar, prosthetic disc nucleus
In an exemplary experiment the new method was used to describe the ability of the PDN prosthetic disc nucleus (Raymedica Inc., Minneapolis, MN, USA, Fig. 2) to restore the three-dimensional motion pattern of lumbar motion segments after nucleotomy.
Fig. 2.
The PDN prosthetic disc nucleus consists of a hydrogel core (upper left corner) encased in a polyethylene jacket (lower right corner). The device is designed to assume the cushioning function of a healthy disc, while restoring/maintaining disc height and allowing normal motion
Eleven fresh-frozen, human cadaveric L4–5 motion segments (mean age 52 years) were thawed at room temperature prior to testing. All soft tissue was removed, leaving the ligaments and joint capsules intact. For fixation purposes, the upper half of the upper vertebra and the lower half of the lower vertebra were embedded in polymethymethacrylate (PMMA). In order to improve the connection between specimen and PMMA, screws were drilled into the vertebral bodies prior to embedding. To allow registration, three metallic spheres were implanted into the cortex of both the upper and lower vertebral bodies as described above, and the specimens were X-rayed in three planes.
After this preparation procedure, the specimens were mounted in the spine-testing apparatus and equipped with the ultrasound motion-analysis system (Fig. 1). The pearls were digitised with a specially designed pointer, which could be attached to the lower cross of the motion-analysis system. Then, the specimens were loaded—quasi-statically, without axial preload—with pure-bending moments in flexion/extension, right/left lateral bending and right/left axial rotation. In each loading direction three loading cycles were applied until ±7.5 Nm were reached. The motion data of all three cycles were used to calculate the FHAs, and the data of the third cycle were used to calculate range of motion (ROM) and neutral zone (NZ) of the projection angles. The same testing procedure was repeated a second time after a lateral nucleotomy of the L4–5 intervertebral disc and a third time after implantation of the PDN device.
Results
Error estimation
The FHAs calculated for the hinge joint were lying within ±2.5 mm around the actual joint axis and were inclined relative to this axis at up to ±1.5°.
Exemplary experiment with a lumbar, prosthetic disc nucleus
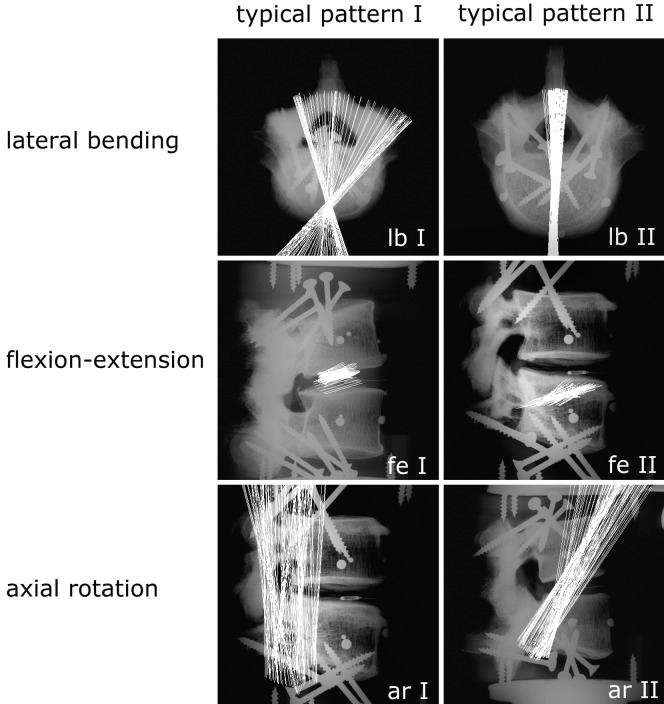
The finite helical axes showed large inter-individual differences in position and orientation in all loading directions (Fig. 3). In lateral bending they were either spread out in the horizontal plane with a central point of intersection within the anterior third of the disc (Fig. 3, lb I), or they were lying parallel to each other and oriented in an antero-posterior direction (Fig. 3, lb II). In flexion-extension, the FHAs were mostly parallel to each other and were either running through the disc (Fig. 3, fe I), or through the inferior vertebra (Fig. 3, fe II). In axial rotation the axes were positioned close to the facet joints. In some cases they were oriented in cranio-caudal direction (Fig. 3, ar I); in others they were tilted slightly anteriorly (Fig. 3, ar II). Nucleotomy generally caused further spreading of the FHAs, indicating large and complex coupled motions. The implantation of the PDN device more than reversed this effect: the FHAs did not spread out, but rather became oriented even more parallel to each other than in the intact state. This behaviour was most obvious in lateral bending (Fig. 4a).
Fig. 3.
Typical position and orientation of the FHAs of intact lumbar L4–5 segments during pure-moment loading in lateral bending (lb I, lb II), flexion-extension (fe I, fe II) and axial rotation (ar I, ar II). Inter-individual differences in position and orientation of the axes were large. However, for each loading direction, two typical patterns could be defined. Note the three pearls implanted into the cortex of both upper and lower vertebral bodies. These were used for registration
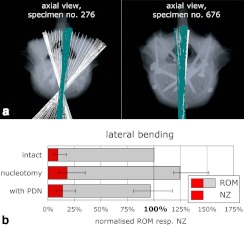
Fig. 4 a.
Under pure-moment, lateral-bending loading, the FHAs of some of the intact L4–5 segments were spread out in the transverse plane (specimen No. 276, light FHAs). In some others (specimen No. 676, light FHAs) as well as after implantation of the PDN-device, they were parallel to each other in an antero-posterior direction (specimen No. 276, dark FHAs; specimen No. 676, dark FHAs). b Range of motion (ROM) and neutral zone (NZ) in lateral bending were almost restored after implantation of the PDN device. Mean and range of 11 specimens after normalisation to the individual intact ROM
In three cases, once in flexion-extension and twice in axial rotation, the FHAs could not be calculated, because the time-displacement curves were not monotonic.
Compared to the intact state (100%), nucleotomy increased the ROM in flexion-extension to: in median, 116%; in lateral bending, 124%; and in axial rotation, 116%. Once the PDN device was implanted, the ROM was reduced to 81%, 96%, and 97%, respectively (Fig. 4b).
Discussion
This paper describes the improvement of the finite helical axes description using a less error-prone calculation algorithm and a new visualisation technique. It also presents a first application of this improved method to the study of the three-dimensional in vitro kinematics of the spine.
Error estimation
The performance of the description of the finite helical axis strongly depends on the measurement error, which is determined by the following factors:
The accuracy in raw data acquisition. This point includes the motion-analysis system itself, as well as errors caused by its fixation to the specimen. As to the motion-analysis system, the resolution specified by the manufacturer was 0.1 mm for the distance between each ultrasound transmitter and receiver. The additional error caused by possible oscillations of the lightweight plastic crosses during motion was minimized by, first, fixing the crosses to the specimens as rigidly as possible and second, filtering the remaining noise using a wavelet transform [2]
The stability in calculating the position and orientation of the finite helical axes. This includes the effect of the position and attitude of the ultrasound markers on the calculation error. On the plastic crosses of the ultrasound motion-analysis system used in the present study, the three markers were placed on the three vertices of an isosceles triangle. The three angles of the triangle were 65°, 65° and 50°. This marker configuration was shown to be associated with smaller errors for the calculation of angular and translational displacements, as compared to a position with angles of up to 160–170° [7]. A further factor shown to influence the calculation error is the distance between the markers and the centre of rotation of the joint. The closer the markers are to the centre of rotation, the smaller the errors are for rotations and translations [7]. This effect also applies to the calculation of helical axes [18, 23]. Thus, in order to minimize the calculation error, the distance between the markers and the specimen should be kept as small as possible. However, if this distance becomes too small, the error caused during data acquisition increases. Therefore, in practice, a compromise is needed between these two competing error sources
The accuracy in registration, i.e., in agreement between the coordinate system used for data acquisition and that used in the radiographs
The measurement error of the first two of these three points, i.e., the accuracy in raw data acquisition and the stability in calculation, was experimentally estimated by the use of a hinge joint. Even though the angular step between two consecutive helical axes was very small (<0.1°), the finite helical axes calculated with the algorithm described by Marin et al. [10] only had a maximum distance to the real hinge-joint axis of 2.5 mm and a maximum tilting relative to the real axis of 1.5°. This validation experiment includes all competing error sources caused by data acquisition and axes calculation during a real experiment. Consequently, it directly depicts the error of the actual test set-up, whereas mathematical error estimations, as proposed by Woltring et al. [23] or Veldpaus et al. [18], would only provide theoretical errors for single error sources.
The measurement error caused by the third of the three points, the registration, depends on many factors, such as the kind of X-ray apparatus or the position of the specimen with respect to film and focus. This additional error, therefore, has to be determined separately for each experiment. If small specimens such as cervical spine specimens are X-rayed in the apparatus used for the present experiments (Faxitron, Hewlett Packard) the image distortion is less than 3%. However, if large lumbar specimens are X-rayed, distortion may exceed 10%. Thus, future improvements of the present finite helical axes description should focus on reducing the image distortion of large specimens.
Interpretation of finite helical axes
Finite helical axes can easily be interpreted if the following basic considerations are taken into account:
If the movement takes place about a fixed centre of rotation, all FHAs pass through this centre of rotation
During motion, the displacement of any anatomical structure increases with increasing distance to the FHA
In an unstable segment, the FHA is assumed to migrate towards the remaining intact structures [9]
The FHA direction in space presents the amount of rotational coupling that occurs during the movement. The helical axes of a pure lateral-bending movement, for example, would be oriented in a strictly antero-posterior direction. However, if a flexion movement was coupled, the axes would, to a certain degree, additionally be tilted in a lateral direction.
Exemplary experiment with a lumbar, prosthetic disc nucleus
The aim of any prosthetic intervertebral disc or disc nucleus is to restore the physiological spinal motion pattern. In the present study, the projection angles and the description of finite helical axes were both used to check whether the PDN prosthetic disc nucleus was capable of meeting these demands. While the ROM of the intact status could almost be restored by implantation of the PDN device (Fig. 4b) [6, 21], the position and orientation of the FHAs in some cases could not. This discrepancy between the motion pattern before and after implantation was most obvious in lateral bending. In this loading direction, the FHAs of several specimens were spread out in the intact condition, but parallel to each other after implantation (Fig. 4a). Thus, the intact specimens were characterised by coupled flexion–extension movements, whereas the movement after implantation was similar to that of a hinge joint with only one degree of freedom. This suppression of the coupled motions could also be shown in an exemplary evaluation of the main and coupled projection angles (Fig. 5). In contrast to these specimens, where the PDN device was not capable of restoring the initial motion pattern, others were characterised by FHAs, which were parallel to each other, not only after implantation but already in the intact state (Fig. 4a). In these cases the PDN-device almost completely restored the initial motion pattern.
Fig. 5 a.
Main projection angle (lateral bending) (dark curves) and coupled flexion–extension projection angle (light curves) of a representative L4–5 segment before implantation of a PDN prosthetic disc nucleus b After implantation. The PDN device hardly affected range of motion in lateral bending but significantly reduced the coupled flexion–extension movement
In this in vitro experiment the main advantage of the FHA description was the visualisation of the three-dimensional motion with respect to the individual radiographic anatomy. Additionally, the position and orientation of the axes covered four degrees of freedom, whereas the description of the main Cardanic/Eulerian or projection angle, which is common for in vitro experiments on the spine, covers only one degree of freedom. On the other hand, the projection angles allowed a quantitative evaluation of the motion data, whereas the FHA description presented here only qualitatively characterised joint function.
Conclusions
The experiments showed that the present, improved description of finite helical axes is a valid and useful tool for characterising the three-dimensional kinematics of the intact, injured and stabilised spine. As compared to the more common description of the main Cardanic/Eulerian angle or the main projection angle, the key advantage of the new description is that the three-dimensional movement is visualised with respect to the individual radiographic anatomy. However, the Cardanic/Eulerian description or the description of projection angles both allow a comprehensive, quantitative evaluation of motion, whereas the FHA description only qualitatively depicts joint function. Therefore, if both, quality and magnitude of motion of spinal segments are of interest, a combination of the presented FHA description and the commonly reported main angles are recommended.
Acknowledgment
The authors would especially like to thank Raymedica Inc. (Minneapolis, MN, USA) for the supply of their implants.
References
- 1.Chao J Biomech. 1980;13:989. doi: 10.1016/0021-9290(80)90044-5. [DOI] [PubMed] [Google Scholar]
- 2.Chau Gait Posture. 2001;13:102. doi: 10.1016/S0966-6362(00)00095-3. [DOI] [PubMed] [Google Scholar]
- 3.Cheze Hum Mov Sci. 1998;17:1. doi: 10.1016/S0167-9457(97)00018-3. [DOI] [PubMed] [Google Scholar]
- 4.Crawford NR (2002) A sequence of two rotations—50 degrees torso flexion followed by +/-120 degrees of head axial rotation—was monitored using (essentially) goniometers and simultaneously measured by Euler XZY an YZX decompositions of marker data from an electromagnetic system (flock of birds). Clin Biomech (Bristol, Avon) 17(2):166–168; author reply, 169 [DOI] [PubMed]
- 5.Cripton J Biomech. 2001;34:1091. doi: 10.1016/S0021-9290(01)00054-9. [DOI] [PubMed] [Google Scholar]
- 6.Eysel Acta. 1999;Neurochir:1083. doi: 10.1007/s007010050486. [DOI] [PubMed] [Google Scholar]
- 7.Goel Spine. 1991;16:1000. doi: 10.1097/00007632-199108000-00029. [DOI] [PubMed] [Google Scholar]
- 8.Grassmann Spine. 1998;23:1155. doi: 10.1097/00007632-199805150-00016. [DOI] [PubMed] [Google Scholar]
- 9.Haher TR, O’Brien M, Felmly WT et al (1992) Instantaneous axis of rotation as a function of the three columns of the spine. Spine [Suppl 6] 17:S149-154 [DOI] [PubMed]
- 10.Marin Hum Mov Sci. 2003;22:285. doi: 10.1016/S0167-9457(03)00036-8. [DOI] [PubMed] [Google Scholar]
- 11.Nagerl Z Orthop Ihre Grenzgeb. 1995;133:481. doi: 10.1055/s-2008-1039927. [DOI] [PubMed] [Google Scholar]
- 12.Osterbauer Erratum. 1992;in:following. [Google Scholar]
- 13.Osterbauer J Manipulative Physiol Ther. 1996;19:231. [PubMed] [Google Scholar]
- 14.Oxland J Spinal Disord. 1994;7:130. doi: 10.1097/00002517-199407020-00006. [DOI] [PubMed] [Google Scholar]
- 15.Panjabi J Biomech. 1971;4:203. doi: 10.1016/0021-9290(71)90005-4. [DOI] [PubMed] [Google Scholar]
- 16.Panjabi J Biomech. 1981;14:447. doi: 10.1016/0021-9290(81)90095-6. [DOI] [PubMed] [Google Scholar]
- 17.Ramsey DK, Wretenberg PF (1999) Biomechanics of the knee: methodological considerations in the in vivo kinematic analysis of the tibiofemoral and patellofemoral joint. Clin Biomech (Bristol, Avon) 14(9):595–611 [DOI] [PubMed]
- 18.Veldpaus J Biomech. 1988;21:45. doi: 10.1016/0021-9290(88)90190-x. [DOI] [PubMed] [Google Scholar]
- 19.White AA, Panjabi MM (1990) Clinical Biomechanics of the Spine, 2nd edn. Lippincott, Philadelphia
- 20.WilkeEur Spine J 19943917874556 [Google Scholar]
- 21.Wilke HJ, Kavanagh S, Neller S, Haid C, Claes LE (2001) Effect of a prosthetic disc nucleus on the mobility and disc height of the L4–5 intervertebral disc postnucleotomy. J Neurosurg [Suppl2] 95:208–214 [DOI] [PubMed]
- 22.Winters Spine. 1993;18:1178. doi: 10.1097/00007632-199307000-00009. [DOI] [PubMed] [Google Scholar]
- 23.Woltring J Biomech. 1985;18:379. doi: 10.1016/0021-9290(85)90293-3. [DOI] [PubMed] [Google Scholar]
- 24.Woltring J Biomech. 1994;27:1415. doi: 10.1016/0021-9290(94)90192-9. [DOI] [PubMed] [Google Scholar]
- 25.Wu J Biomech. 2002;35:543. doi: 10.1016/S0021-9290(01)00222-6. [DOI] [PubMed] [Google Scholar]