Demonstration of vertebral and disc mechanical torsion in adolescent idiopathic scoliosis using three-dimensional MR imaging

Abstract

This study was designed to demonstrate and measure mechanical torsion in patients with adolescent idiopathic scoliosis using three-dimensional magnetic resonance (MR) imaging. Ten patients with adolescent idiopathic scoliosis were imaged with three-dimensional MR imaging, and the data post-processed through multiplanar reconstruction to produce images angled through individual endplates. Transverse rotation was measured at each endplate and these measurements used to calculate the amount of vertebral and disc mechanical torsion present. A test object was imaged in order to validate the measurement technique. Mechanical torsion was demonstrated within the vertebral bodies and discs of the imaged subjects, with vertebral mechanical torsion contributing on average 45% of the overall transverse plane deformity. It is concluded that deformation occurs in the transverse plane within the vertebrae and discs of subjects with idiopathic scoliosis, and a significant proportion of the rotation present in the scoliotic spine occurs as a result of plastic deformation within the vertebrae themselves. We believe that this is the first systematic demonstration of mechanical torsion in idiopathic scoliosis.

Introduction

The rotational element of the spinal deformity in adolescent idiopathic scoliosis has been recognised as a fundamental component of the scoliotic curve for nearly 200 years [2]. The nature of the rotational deformity remains poorly understood, although there have been several recent papers studying the three-dimensional deformity within scoliotic vertebrae and discs [15,16]. It is widely assumed that transverse rotation observed along the vertebral body line (“geometric torsion” [20]) occurs as a result of rotation of each vertebra relative to its neighbours. The extent to which transverse rotational deformity occurs as a result of transverse rotational deformation (or “mechanical torsion” [20]) within the vertebrae and discs themselves has not previously been defined.

The concept of mechanical torsion within discs and vertebrae has remained poorly defined. In a comprehensive review of three-dimensional terminology published by the Scoliosis Research Society in 1994, mechanical torsion was described as “the relative rotation or vertebral deformations between lines joining similar landmarks on vertebrae”, and was further defined as “vertebral deformation due to the relative axial rotation of the endplates” [20]. The report stressed the theoretical nature of this property, and that it remains unknown to what extent it is present within the scoliotic curve. It is stated in the paper that “up to now, no one has defined or used local mechanical torsion”.

It has been proposed by several researchers that the complex intrinsic vertebral and disc deformations occurring in idiopathic scoliosis are defined by the relative three-dimensional orientation of adjacent endplates. Notable among these research groups are Kojima and Kurokawa [12,13], who first described the concept of endplate vectors in 1992, and subsequently by Aubin et al. [6]. Comparison of the relative transverse rotation of successive endplates provides a possible means for the measurement of intrinsic rotational deformation, or mechanical torsion.

A technique for the measurement of the relative inclination of vertebral endplates in the coronal and sagittal planes has been described using three-dimensional reconstructions of stereoradiographs [6]. Analysis of the relative transverse rotation of adjacent endplates, and therefore mechanical torsion, cannot be achieved with this technique, because radiographs do not image vertebral structure in the transverse plane.

We have previously described a technique using three-dimensional MR imaging and multiplanar reconstruction for the imaging of idiopathic scoliosis that allows reconstruction of images in the plane of individual endplates [7], and have defined the intra-observer and inter-observer variation for this process. MR utilises no ionising radiation, unlike computed tomography (CT), and is appropriate for the imaging of the adolescent spine. The aim of this study is to further validate three-dimensional MR as a technique for measuring rotation at individual endplates, and to use it to define the mechanical torsion present within discs and vertebrae in a series of patients with adolescent idiopathic scoliosis. The objectives are to measure the amount of mechanical torsion present in discs and vertebrae, to determine the relative proportion that occurs within vertebrae as opposed to discs, and to examine the relationship between these values and other anatomical parameters.

Materials and methods

Measurement of vertebral and disc mechanical torsion

Ten patients (eight girls, two boys, age range 12–17 years) with adolescent idiopathic scoliosis and right thoracic curve were included in the study. Subjects were selected prospectively and consecutively, following the receiving of fully informed consent from the subjects and the subjects’ guardians. Patient demographics are documented in Table 1.

Table 1.

Patient demographics

Subject	Age (years)	Standing Cobb angle (°)	Curve apex
Girl	14	65	T8
Girl	12	50	T8
Girl	15	70	T7
Girl	17	44	T8
Boy	13	63	T9
Girl	14	47	T10
Girl	14	57	T8
Girl	13	36	T10
Girl	16	53	T7
Boy	15	61	T8

Each patient was imaged on a 1 Tesla Siemens Magnetom Impact scanner using a quadrature surface coil. In each case, the subject was positioned with the thoracic curve cushioned and with the pelvis in a neutrally rotated position. Three-dimensional MR imaging of the juxta-apical 10 vertebrae of the curve was performed using DESS imaging (TR 30 ms; TE 9/45 ms; flip angle 40°). L5 was selected as a neutral, non-rotated vertebra in each case, and was imaged with axial spin echo T1 imaging (TR 884 ms, TE 15 ms).

Using the multiplanar reconstruction software available on the linked workstation, sections were selected through the plane of each individual endplate of the imaged 10 juxta-apical vertebrae on the sagittal and coronal data sets (Fig. 1), in order to produce reconstructed images in the specific three-dimensional plane of each endplate. In this way, representations of the transverse vertebral anatomy in the plane of the superior and inferior endplates were obtained [7]. The upper endplate images were in practice reconstructed a few millimetres below the endplate at the point where posterior elements were first visible. The close proximity of the reconstructed image to the actual plane of the upper endplate means that there is unlikely to be significant error introduced into the estimation of upper endplate rotation. Illustrative examples of superior and inferior endplate anatomy are shown in Figs. 2a, b. These images were then stored for analysis on magneto-optical disc.

Fig. 1.

Coronal image from three-dimensional data set showing selection of plane through an individual vertebral endplate

Fig. 2 a.

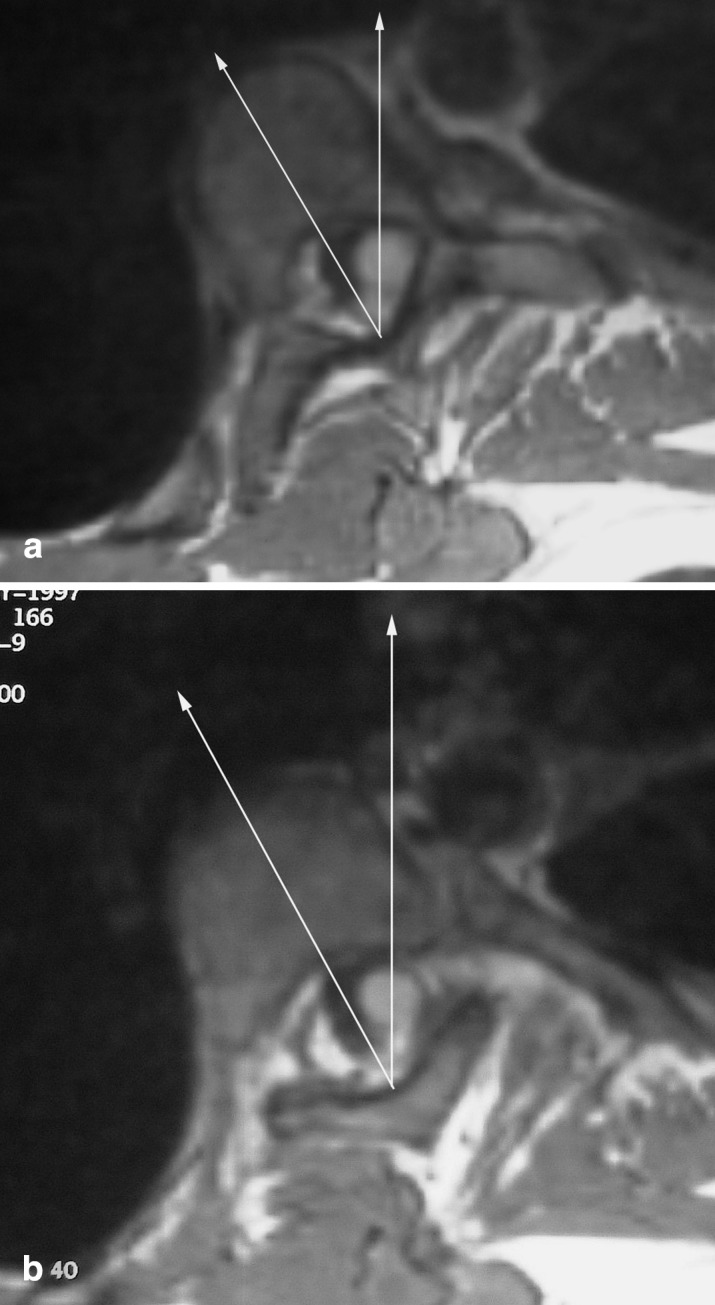
Reconstructed image in the plane of the superior endplate of a scoliotic vertebra, demonstrating the data points used for measurement of transverse plane rotation. b Equivalent reconstructed image and data points in the plane of the inferior endplate of a scoliotic vertebra

The stored endplate images were subsequently analysed to measure the degree of transverse rotation in each case, using the technique described and validated by Ho et al. [10], as follows. Two datum points were identified: one at the junction of the laminae at the base of the spinous process, and the other at the mid-point of the posterior surface of the vertebral body. Endplate rotation was measured by comparing the line between these two points with a sagittal line drawn by the computer on the workstation. The measurement technique is illustrated in Fig. 2. The computer-generated sagittal plane is defined by the direction of the main magnetic field (B₀) of the scanner, and is perpendicular to the scanner table.

The measured endplate transverse rotation was subsequently compared with the rotation of the neutral L5 vertebra in order to correct for any apparent rotation induced by the position of the subject in the scanner. In this way, corrected values of transverse rotation at each endplate were obtained. In each case, 20 readings were obtained, at the superior and inferior endplates of the ten imaged vertebrae at the apex of the scoliotic curve. The measured angles of endplate inclination in the sagittal and coronal planes were also recorded.

The amount of transverse mechanical torsion occurring within the vertebrae was measured by recording the incremental change in transverse plane rotation occurring between the superior and inferior endplates of each vertebral body. In a similar way, the amount of mechanical torsion occurring within the discs was measured by recording the increment in transverse plane rotation occurring between the inferior endplate and the superior endplate of adjacent vertebrae. The total amount of mechanical torsion occurring within the ten imaged vertebrae and nine imaged discs in each case was then measured by simple addition. The percentage of total transverse mechanical torsion occurring within the superior nine vertebral bodies as opposed to the nine imaged discs was subsequently calculated.

Apical rotation was measured by noting the maximal endplate transverse rotation at the apical vertebra. Cobb angle was measured from the coronal T1 data set analysed during the multiplanar reconstruction in an analogous way to measurements obtained from plain radiographs, using the maximally inclined vertebrae to define the Cobb angle. The degree of thoracic kyphosis was assessed from the sagittal T1 data set by measuring the angle subtended by the superior endplate of the uppermost visualised vertebra and by the inferior endplate of the lowermost imaged vertebra. This is in accordance with other recent studies of thoracic hypokyphosis in idiopathic scoliosis [18].

The correlation between the total amount of vertebral and disc mechanical torsion with other curve parameters (Cobb angle, lordosis, and apical transverse rotation) was evaluated, as was the correlation between the relative mechanical torsion within the vertebrae and the discs with these curve parameters. The correlation coefficient was calculated using Pearson’s correlation.

In each case, the progressive change in endplate transverse rotation was analysed using quadratic regression analysis, and a mean quadratic regression curve was calculated.

Validation of diagnostic accuracy of measurement of endplate rotation

A test object was designed and constructed to assess the diagnostic accuracy of three-dimensional MR imaging for the measurement of endplate axial rotation with varying degrees of coronal and sagittal inclination (Fig. 3). The materials used for the construction were chosen for their MR compatibility. The test object, consisting of a single dry mid-thoracic vertebra bathed in vegetable oil, was mounted within a cylindrical plastic holder, designed to allow rotation in the transverse plane and inclination in the coronal and sagittal planes to predefined three-dimensional angulations.

Fig. 3.

Test object used for the validation of the process for measurement of endplate transverse rotation

The test object was scanned on a Siemens Magnetom Impact 1 Tesla MR scanner with three-dimensional MR imaging using DESS (TR 30 ms; TE 9/45 ms; flip angle 40°). The test object was scanned with transverse plane rotations of 0, 5°, 10°, 20°, 30° and 40°, in the absence of coronal and sagittal plane tilt. The test object was subsequently scanned with transverse plane rotations of 10°, 20° and 30°, with additional 10°, 20° and 30° of sagittal or coronal tilt, respectively. Finally, the test object was scanned with 10°, 20°, 30° and 40° transverse plane rotation, sequentially with 10°, 20°, 30° and 40° of combined coronal and sagittal tilt. Images were post-processed using multiplanar reconstruction, and transverse rotation at the superior and inferior endplates measured as described previously, resulting in a total of 30 measurements. The readings were analysed using Altman-Bland plots [3]. The mean and the 95% confidence intervals were calculated for diagnostic accuracy.

>Results

Mechanical torsion

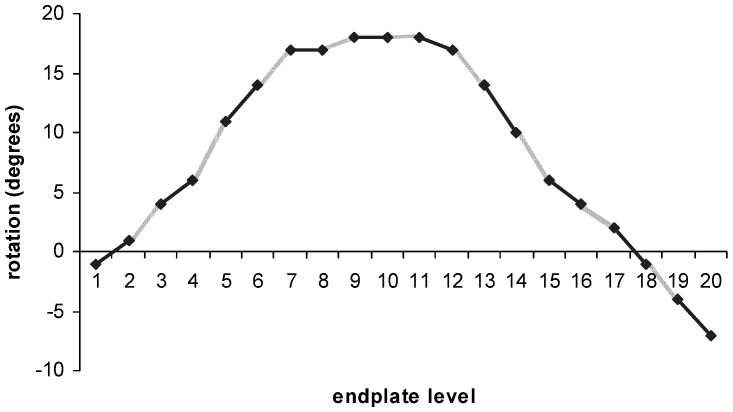
There was a typical progression in endplate rotation towards the apex of each curve, with a subsequent regression. An illustrative example is shown in Fig. 4.

Fig. 4.

Graph showing progression in endplate rotation from most superior endplate (1) to most inferior (20) in a typical patient (patient 9). Continuous line vertebral mechanical torsion; broken line disc mechanical torsion

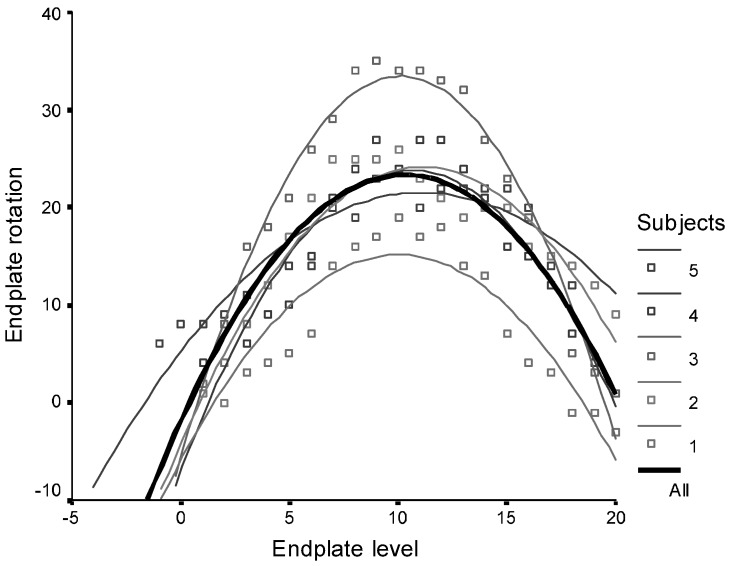
Quadratic regression curves for five typical patients are shown in Fig. 5. The r-squared value for the mean curve was 0.63, with P<0.00005.

Fig. 5.

Quadratic regression curves showing sequential endplate rotation for five selected patients, including a mean plot

The measured values for total mechanical torsion occurring within the upper nine vertebral bodies and the nine intervertebral discs for the ten imaged subjects are shown in Table 2. Nine vertebrae were used to allow relative values of vertebral and disc torsion to be calculated, given that only nine discs were imaged. The upper nine vertebrae were arbitrarily chosen for this purpose. The absolute vertebral mechanical torsion and absolute mechanical torsion as measured with three-dimensional MR imaging fitted a normal distribution. The mean absolute vertebral mechanical torsion (as opposed to disc or total torsion) over nine levels was 21.6°, with a standard deviation of 5.2°. The mean absolute disc mechanical torsion (as opposed to vertebral or total torsion) over nine levels was 27.0°, with a standard deviation of 5.4°.

Table 2.

Total mechanical torsion occurring within vertebrae and intervertebral discs, and percentage of overall mechanical torsion occurring within the vertebral bodies (“relative vertebral torsion”)

Subject No.	Vertebral mechanical torsion (°)	Disc mechanical torsion (°)	Total mechanical torsion (°)	Relative vertebral torsion (%)
1	18	29	47	38
2	19	33	52	36
3	25	39	64	39
4	16	23	39	41
5	23	24	47	49
6	15	12	27	55
7	29	38	67	43
8	25	17	42	59
9	17	24	41	41
10	29	31	60	48

The relative mechanical torsion occurring within the vertebral bodies and within the discs is documented in Table 2. The relative vertebral mechanical torsion as measured with three-dimensional MR imaging fitted a normal distribution. The mean relative vertebral mechanical torsion over nine levels was 44.9%, with a standard deviation of 7.6%.

No significant relationship existed between absolute and relative vertebral mechanical torsion, between absolute vertebral mechanical torsion and Cobb angle, between absolute or relative vertebral mechanical torsion and kyphosis, or between relative vertebral mechanical torsion and apical rotation.

The Pearson correlation coefficient for the relation of relative vertebral mechanical torsion and Cobb angle was –0.552, with a significance of P=0.098.

The Pearson correlation coefficient for the relation of total absolute vertebral mechanical torsion and apical rotation was 0.600, with a significance of P=0.067.

Technique validation

The mean of the difference between the actual and the measured endplate rotation from measurements of the test object was 0.767° (0.300, 1.234). The 95% confidence intervals were ±2.46°.

Discussion

This study has shown that deformation occurs in the transverse plane within the vertebrae of subjects with idiopathic scoliosis. The identification of vertebral and disc mechanical torsion confirms Arkin’s suggestion of nearly 60 years ago that a significant proportion of the rotational deformity occurs as a result of plastic deformation within the vertebrae themselves [4].

Mechanical torsion is demonstrated in all the curves imaged in this study, implying the process that is causing the torsional deformation is universal and common to all scoliotic curves. Quadratic regression analysis of the curve profiles of endplate transverse rotation confirms the consistent nature of this pattern. Intravertebral torsion was maximal within the peri-apical segments, with relatively little torsion occurring within the apical vertebrae and discs.

Mechanical torsion is demonstrated in relatively mild degrees of deformity. Indeed, the greatest proportion of mechanical torsion occurring within the vertebral bodies was observed in the least severe scoliotic curve, as defined by the Cobb angle. An inverse relationship is demonstrated between the relative vertebral mechanical torsion and the severity of the scoliotic curve. This observation suggests that more severe curves (as suggested by higher degrees of coronal plane deformity) are associated with relatively greater amounts of mechanical torsion occurring within the discs than within the vertebrae. This may reflect decreasing ability of bone to undergo plastic deformation with increasing age relative to the discs.

These observations lend support to the theory that torsion is a fundamental part of the early pathomechanical process. In order for mechanical torsion to arise, there must be a consistent, long-term deforming force present that results in a rotational torque being applied to the growing vertebral body, and it would seem likely that this force is fundamental to the pathogenesis of the scoliotic curve.

Whatever the origin of the torsional force in scoliosis [8,17,19,24], the elastic deformations that occur will be subsequently followed by plastic deformations within the vertebrae, in keeping with basic bone remodelling laws [11,23,25]. There is substantial clinical and experimental evidence to indicate that increased pressure parallel to the direction of epiphyseal or apophyseal growth will inhibit growth [5,8,9,21], and that decreased pressure will accelerate growth (the Hueter–Volkmann law). It may be that torsional deformation occurs in scoliotic vertebrae as a result of the oblique deflection of growth caused by torsional forces applied to the apophyseal plate. When extrapolated to the production of vertebral mechanical torsion, it is likely that an initial oblique deflection of the growth plate induced by applied torsional forces will result in a vicious cycle, in which superadded gravitational forces are increasingly applied in an oblique fashion to the growth plate, thereby exacerbating the tendency of the vertebral body to undergo plastic torsional deformation.

The measurement technique is demonstrated to be robust in the evaluation of the rotated test object when varying amounts of coronal and sagittal inclination were superadded. The addition of coronal and sagittal inclination to transverse rotation in other workers’ studies has demonstrated that significant errors are introduced into rotation measurements when using two-dimensional cross-sectional measurement techniques [1,14], and this has been partly explained by the loss of clarity of anatomical landmarks with increasing degrees of coronal and sagittal tilt. In contrast, it has been demonstrated in this experiment that multiplanar reconstruction allows the production of accurate representations of the vertebrae in the plane of the superior and inferior endplates, validating the use of this process for the analysis of relative endplate transverse rotation.

Comment should be made regarding the validity of using measurements of the coronal, sagittal and rotational components of the scoliotic deformity obtained in the supine position as opposed to the standing position. It is well established that the measured Cobb angle is reduced when radiographed in the supine rather than the standing position [18,22]. The reduction in apparent coronal and sagittal deformity in the supine position is considered to be a systematic factor, and is likely to affect each patient to an equivalent degree. In terms of vertebral rotation, a study by Ho et al. demonstrated no statistical difference between measurements of rotation obtained from plain films taken in the supine and standing positions [10]. Despite this, it seems likely that the degree of transverse plane rotation will reduce when measured in the supine position, in a similar fashion to the relaxation observed in the coronal and sagittal plane deformities, and it may be that the relative amount of disc mechanical torsion was underestimated in this study because of this factor. It is noted, therefore, that the observations made in the course of this study reflect the scoliotic deformity when observed in the supine position. It would seem reasonable to extrapolate such observations to the anatomy of the scoliotic spine in the standing position. It should also be noted that the number of patients included in this study is relatively small, and that confirmation of these findings is required in a larger observational study.

In conclusion, we have demonstrated that deformation occurs in the transverse plane within the vertebrae and discs of subjects with idiopathic scoliosis, and that this is a universal process. This observation has been possible because of the application of a three-dimensional cross-sectional imaging technique to the investigation of the scoliotic curve. The demonstration that vertebral mechanical torsion contributes on average 45% of the overall rotational deformity indicates that a significant proportion of the rotation present in the scoliotic spine occurs as a result of plastic deformation within the vertebrae themselves. The identification of vertebral and disc mechanical torsion has important implications with respect to the understanding of the fundamental pathomechanical processes involved in the evolution of the scoliotic deformity. It may be that the existence of vertebral and disc mechanical torsion presents a fundamental barrier to the degree of derotation that can be achieved with current spinal instrumentation.