Anterior thoracic posture increases thoracolumbar disc loading

Abstract

In the absence of external forces, the largest contributor to intervertebral disc (IVD) loads and stresses is trunk muscular activity. The relationship between trunk posture, spine geometry, extensor muscle activity, and the loads and stresses acting on the IVD is not well understood. The objective of this study was to characterize changes in thoracolumbar disc loads and extensor muscle forces following anterior translation of the thoracic spine in the upright posture. Vertebral body geometries (C2 to S1) and the location of the femoral head and acetabulum centroids were obtained by digitizing lateral, full-spine radiographs of 13 men and five women volunteers without previous history of back pain. Two standing, lateral, full-spine radiographic views were obtained for each subject: a neutral-posture lateral radiograph and a radiograph during anterior translation of the thorax relative to the pelvis (while keeping T1 aligned over T12). Extensor muscle loads, and compression and shear stresses acting on the IVDs, were calculated for each posture using a previously validated biomechanical model. Comparing vertebral centroids for the neutral posture to the anterior posture, subjects were able to anterior translate +101.5 mm±33.0 mm (C7–hip axis), +81.5 mm±39.2 mm (C7–S1) (vertebral centroid of C7 compared with a vertical line through the vertebral centroid of S1), and +58.9 mm±19.1 mm (T12–S1). In the anterior translated posture, disc loads and stresses were significantly increased for all levels below T9. Increases in IVD compressive loads and shear loads, and the corresponding stresses, were most marked at the L5–S1 level and L3–L4 level, respectively. The extensor muscle loads required to maintain static equilibrium in the upright posture increased from 147.2 N (mean, neutral posture) to 667.1 N (mean, translated posture) at L5–S1. Compressive loads on the anterior and posterior L5–S1 disc nearly doubled in the anterior translated posture. Anterior translation of the thorax resulted in significantly increased loads and stresses acting on the thoracolumbar spine. This posture is common in lumbar spinal disorders and could contribute to lumbar disc pathologies, progression of L5–S1 spondylolisthesis deformities, and poor outcomes after lumbar spine surgery. In conclusion, anterior trunk translation in the standing subject increases extensor muscle activity and loads and stresses acting on the intervertebral disc in the lower thoracic and lumbar regions.

Introduction

Knowledge of the loads and stresses acting on spinal tissues assists in the understanding of degenerative or abnormal spinal conditions. In many biomechanical studies, functional spinal units (FSUs) have been used in experimental and finite element modeling to evaluate stresses in the vertebral body and discs under different loading conditions [1, 8, 25]. Although forces and moments applied to FSUs give insight as to how loads are distributed and tolerated, experimental studies based on the FSU cannot accurately replicate the complex kinematic and muscular loading behavior of the intact spinal column [13, 22, 32]. Further, FSU experiments cannot be used to predict how postures of the trunk affect muscular loads, intervertebral loads, and intervertebral disc stresses. Since the intervertebral disc (IVD) has been implicated as a source of chronic low back pain [27], the loads and stresses acting on the intervertebral disc are among the most studied topics in spinal biomechanics [1, 8, 25].

In the absence of external forces, the largest contributor to IVD loads comes from trunk muscular activity. Moreover, trunk muscular effort is directly linked to the posture of the trunk and pelvis [6, 8, 14, 20, 29]. Of interest, therefore, is the relationship between spinal posture, trunk-muscle activity, and the resultant stresses in the IVD. Indeed, during the past decade, an increasing number of radiographic studies have reported relationships between spine morphology (geometry, alignment and curvature) and lower back pain [7, 10, 16, 17, 43]. Other radiographic measurements may also have a relationship to lower back pain and disability. For example, recent studies of people afflicted with chronic low back pain [16], flat-back syndrome [3], spondylolisthesis [18], and adjacent segment degeneration following lumbar fusion [26], have identified a forward, displaced, sagittal “plumb-line” as a risk factor associated with prolonged pain, disability, or generalized inferior outcomes after spinal surgery.

An understanding of IVD stresses in displaced trunk postures might aid in the understanding of pain, disability and progression of sagittal plane deformities in back pain populations. Direct evaluation of IVD loads and stresses can be obtained from in vivo, intradiscal pressure measurements [40, 41, 44]. Other methods to estimate IVD loads and stresses include instrumented spinal prostheses [3–39, 45], but such methods are impractical for clinical use. Alternatively, the magnitude of forces acting on the thoracolumbar spine can be estimated with biomechanical models [9, 19, 23, 24, 33]. The objective of this study was to use a postural-loading model to characterize the changes in thoracolumbar disc stresses and extensor muscle forces that follow anterior translation of the thoracic spine. We hypothesized that anterior trunk translation and concomitant, increased extensor muscle activity would increase thoracolumbar IVD loads and stresses.

Materials and methods

Eighteen asymptomatic subjects (13 men, five women, average age 28.0 years, SD 6.94; mean height, 177.2 cm±10.5 cm [values are referred as mean±SD], and weight of 76.5 kg±16.2 kg) were recruited from a local university to participate in this study. In addition to providing basic demographic data, subjects reviewed the Institutional Review Board approved study protocol and provided informed consent for their participation. A numerical rating scale from 0–10 (0=no pain to 10=severe pain, or bed ridden) was administered to confirm the subjects’ asymptomatic status. The subjects had an average visual analog score of 0.58, indicating that they were pain-free on the day of study participation, with no prior history of back pain requiring medical attention.

Two standing, lateral, full-spine radiographic views were obtained for each subject: a neutral-posture lateral radiograph and a radiograph during anterior translation of the thorax relative to the pelvis (while keeping T1 aligned over T12). For the neutral position, subjects were asked to step toward the X-ray grid cabinet and assume a neutral posture by marching in place and nodding their heads briefly, prior to assuming their natural, upright standing posture. For the anterior, translated thorax posture, subjects were asked to fix the pelvis in space, only moving the chest anteriorly, relative to the pelvis, while keeping the shoulders horizontal. In this manner, subjects were asked to anteriorly translate the thorax as much as possible. Subject positioning for the two postures is illustrated in Fig. 1.

Fig. 1.

Radiographic set-up for comparison of spinal loads and stresses during A anterior translation of the thorax; and B the neutral standing posture

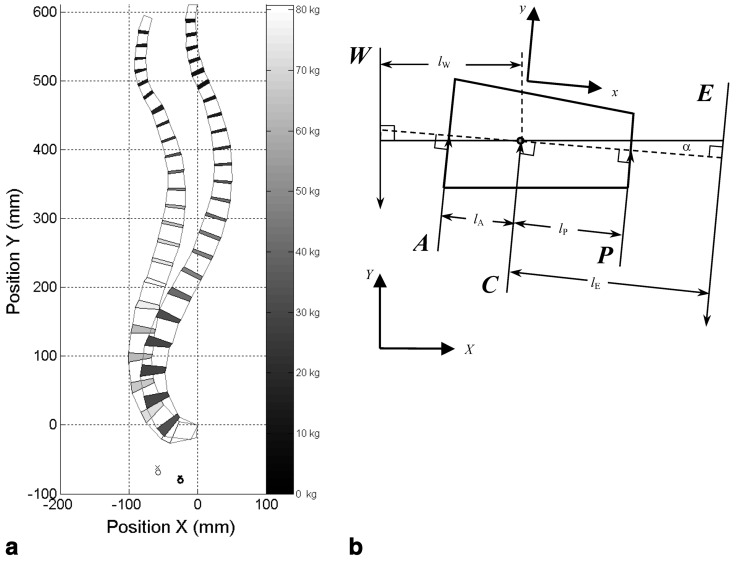
Sagittal alignment and four-point, sagittal plane geometry of the C2-through-S1 vertebrae were obtained from the neutral posture and anteriorly translated thorax radiographs, by digitizing the vertebral body (VB) corners. The digitizing system consisted of a sonic digitizer (GP-9, GTCO CalComp, Columbia, MD, USA) with 0.125 mm resolution and 0.5 mm accuracy, and an IBM-compatible computer. X,Y coordinates of the VB corners were corrected for radiographic magnification. Thus, an anatomically accurate, sagittal plane quadrilateral-element model of the anterior spinal column (C2–S1) was constructed for the neutral and anterior translated postures of each subject (Fig. 2a). The resulting geometry data for VB quadrilateral-element nodes were stored in a text file for processing, using a custom Matlab program (The Mathworks, Natick, MA, USA). Several angles and sagittal-balance parameters of clinical interest were determined from the quadrilateral-element model. Angles were calculated by intersecting the VB posterior tangents at T1 and T12 (thoracic angle), T12 and S1 (lumbar angle), and the angular measurement between horizontal and a line through the superior S1 endplate (Ferguson’s sacral base angle) [11]. Sagittal-balance parameters including C4–L4, T1–T12, C7–hip axis (HA), T4–HA, S1–HA, T12–S1, C7–S1 and T4–S1 were calculated as the distance (along the X-axis) between the respective vertebral-body centroids for each posture.

Fig. 2.

a Representative quadrilateral-element spine model (C2–S1) illustrating neutral and anterior translated postures (subject 008, 68 kg, 173 cm). The global X,Y coordinate system (digitizing tablet origin) represents the posterior-inferior corner of the S1 vertebral body. Acetabulum and femoral-head centers are indicated by the symbols x and ο, respectively (bold symbols correspond to the anterior translated posture). Intervertebral disc-load magnitudes are in gray-scale, with lower load values shown in darker gray. b Detail of the quadrilateral-element model. α is the angle between the horizontal axis X and the anterior-posterior IVD bisector. The local coordinate system used to determine IVD forces and stresses is represented as x-y. Other parameters defined in text

The quadrilateral-element VBs and IVDs were biomechanically modeled using the procedure described by Keller et al. [21] and Keller and Nathan [19]. The procedure consists of computing the location of the VB and IVD centroids from the X,Y coordinates of the quadrilateral element [31]. Compressive forces and shear forces were then determined about each IVD centroid, according to static translational and rotational equilibrium of postural forces. In this simple upright-posture model, static equilibrium is based solely upon the balance of body-weight forces and posterior trunk-muscle forces (erector spinae muscles). Although the effects of trunk-muscle synergism (contribution of anterior muscles), passive spinal tissues (ligament-load sharing) and intra-abdominal pressure are not considered, the compressive stress predictions for the quadrilateral-element model show good agreement with other experimental and analytical studies. Body-weight load (W) above each segment, and values for the body-weight-moment arms, posterior-muscle-moment arms (l_E) and disc cross-sectional areas for each of the C2–S1 segments, were based upon the reference data published by Keller and Nathan [19] and were all varied according to spinal level. The body-weight loads above each segment were computed as a percentage of the subject body weight (BW), ranging from 7.3% BW at C2–C3 to 60% at L5–S1.

For the neutral-posture analysis, the line of gravity, which formed the reference for the body-weight-moment arm, was initially positioned 10 mm anterior to the centroid of the L4 vertebral body [19, 35]. While the line of gravity may not correspond precisely to the center of mass for a given spine segment [35], it is considered a reasonable estimate of the loading conditions experienced by the spine in the upright posture [34]. The average deviation of the center of mass with respect to the center of mass at L4 is only 5.9 mm for levels T1–L5 [35]. For the anteriorly translated thorax model, the line of gravity of the trunk was shifted anteriorly in direct proportion to the mean anterior shift in the location of the C2–S1 VB centroids.

The IVD compressive forces, C=W(l_W/l_E+cosα), and shear forces, S=Wsinα, computed by the static postural analysis, represent the normal forces and tangential forces, respectively, acting on the anterior-posterior bisector of each IVD quadrilateral (Fig. 2b). The angle α is the angle between the horizontal axis and the anterior-posterior bisector of the IVD. Compressive forces (C), acting at the IVD centroid, were also partitioned into anterior force (A) and posterior force (P) components, using the following relationships [21]: P=C/{β[(h_A/h_P)(1+l_A/l_E)]−l_P/l_E+1} and A=βPh_A/h_P, where h_A=anterior IVD height (mm) and h_p=posterior IVD height (mm); l_A=anterior-to-centroid IVD length (mm) and l_P=posterior-to-centroid IVD length (mm); and β=1 is an empirical constant relating the anterior IVD stiffness to the posterior IVD stiffness (assumed to be equal in this analysis).

The posterior muscle vector, E=C−Wcosα=Wl_W/l_E, was assumed to be normal to the IVD bisector (parallel to C). The extensor muscle-moment arm (l_E) was scaled according to the individual subject height as follows: l_E=Dl_E*(HT/DHT). Dl_E is the reference extensor-muscle-moment arm (varied according to vertebral level) and DHT is the height (174.2 cm). HT is the subject-specific body height. IVD compressive stresses and shear stresses for each segment were also computed from the respective compressive force and shear force using the IVD cross-sectional area of each segment (DA), scaled for each subject as follows: DA=DDA*(HT/DHT)², where DDA=reference disc area (varied according to vertebral level). Scaling of the muscle-moment arms and disc areas in this fashion results in values that are consistent with values published for similar height and weight subjects [21].

Descriptive statistics were performed on all variables. Statistical comparisons of the changes in IVD loads and stresses, extensor muscle forces and sagittal alignment following anterior translation of the thorax were performed using a two-tailed, paired-observations t-test.

Results

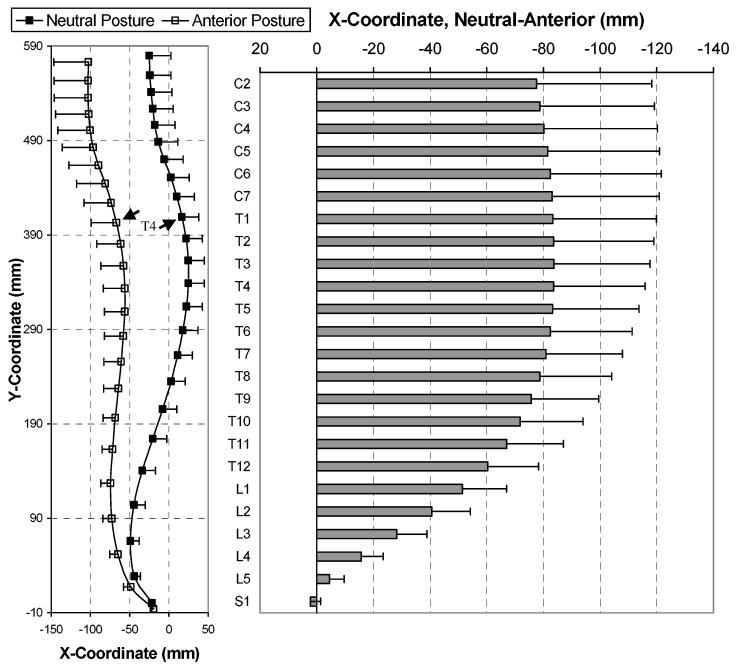
Sagittal balance parameters for the neutral and anterior translated postures are summarized in Table 1. Anterior translated posture (T_z) is considered positive when the centroid of the upper reference site is located posterior to that of the lower reference site. In the neutral posture, the mean, T1–T12 sagittal alignment (+Tz) was +1.8 mm (range, −44.9 mm to 29.7 mm), increasing to a mean sagittal alignment of −21.2 mm (range, −75.5 mm to 24.7 mm) in the anterior translated posture. Differences in T1–T12 alignment for neutral and anterior postures were statistically significant (p=0.007). Comparing the neutral with the anterior posture, subjects were able to translate their thorax forward (+Tz) +101.5 mm±33.0 (vertebral centroid of C7 compared with a vertical line through the hip axis), +81.5 mm±39.2 (vertebral centroid of C7 compared with a vertical line through the centroid of S1) (vertebral centroid of C7 compared with a vertical line through the vertebral centroid of S1), and +58.9 mm±19.1 (centroid of T12 compared with a vertical line through the centroid of S1). The sagittal profiles and average shift in the C2–S1 vertebral body centroids are illustrated in Fig. 3. Overall, the largest absolute, anterior VB shift occurred at T3 (+83.7 mm±33.9 mm). Anterior translation of the thorax resulted in mean changes of −13.1° ±10.3° in the thoracic (T1–T12) angle, +1.7°±12.9° in the lumbar (T12–S1) angle, and +9.5°±6.7° in the pelvic (Ferguson) angle. This compares with initial, neutral posture values of 46.0°±12.0°, −62.3°±11.7°, and 43.4°±6.3°, respectively.

Table 1.

Summary of eight separate measures of mean sagittal balance (SD) and their respective changes from the neutral upright posture to the anterior translated (T_z) posture. T_z is considered positive when the centroid of the upper reference site is posterior to that of the lower reference site. HA hip axis

Centroid–centroid measurement	Tz neutral posture (mm)	Tz anterior posture (mm)	Absolute Δ Tz neutral−anterior change (mm)
C4–L4	+26.4 (23.9)	−38.1 (40.3)	64.5 (38.0)*
T1–T12	+1.75 (20.1)	−21.2 (29.2)	23.0 (25.8)**
C7–HA	+38.6 (20.7)	−62.8 (35.4)	101.5 (33.0)**
T4–HA	+68.9 (19.1)	−33.1 (29.2)	102.0 (27.1)**
S1–HA	+31.2 (12.9)	+11.2 (15.2)	19.9 (15.6)**
T12–S1	+13.1 (16.1)	−45.8 (14.1)	58.9 (19.1)**
C7–S1	+7.43 (24.3)	−74.1 (38.3)	81.5 (39.2)**
T4–S1	+37.7 (20.6)	−44.4 (31.7)	82.1 (33.9)**

*p<.05

**p<.001

Fig. 3.

Overall averaged sagittal profiles (C2–S1) obtained for 18 subjects. Vertebral body centroids (mean, SD) for neutral and anterior postures are illustrated. Graphic on right shows mean (SD) anterior-posterior (X coordinate) shift in vertebral body centroids

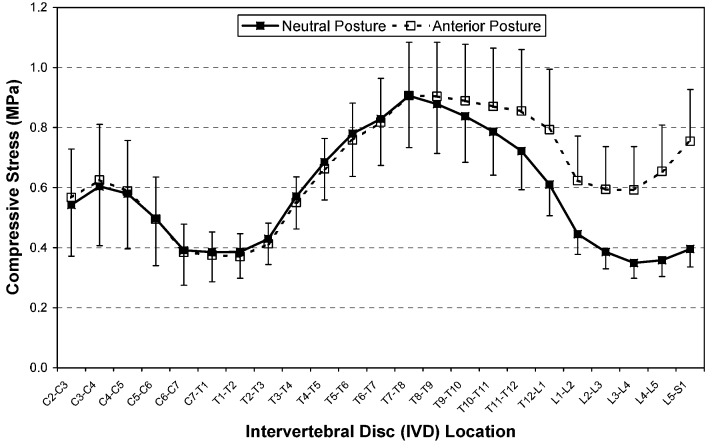
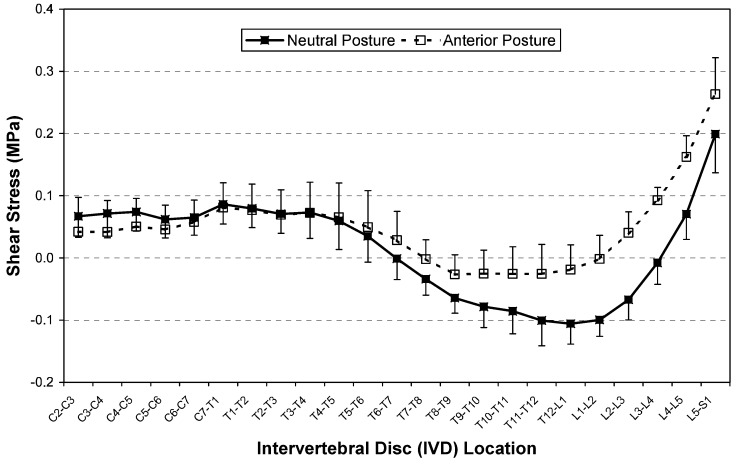
In the neutral posture, IVD shear stresses averaged 14.7%, 10.5% and 22.4% of the compressive stresses for the cervical, thoracic and lumbar regions, respectively. IVD stresses increased for the anterior translated posture in comparison with the neutral posture. Compressive stresses (Fig. 4) and shear stresses (Fig. 5) were significantly (p<0.05) increased in the anterior translated posture for all levels below T8–T9 and T5–T6, respectively. The maximum postural increase was observed in IVD compressive stress (92.2%), at L5–S1, and in shear stress (609%), at L3–L4 (Table 2). Extensor muscle loads also increased significantly to 942%, from 8.2% (p<0.05), in the anterior translated posture for levels below T7–T8.

Fig. 4.

Mean (SD) IVD compressive-stress distribution for C2–S1 segments of 18 subjects. Statistically significant differences (paired-observation t-test, p<0.05) between neutral and anterior postures were observed for T9–T10 to L5–S1 segments

Fig. 5.

Mean (SD) IVD shear-stress distribution for the C2–S1 segments of 18 subjects. Negative values indicate anterior shear. Statistically significant differences (paired-observation t-test, p<0.05) between neutral and anterior postures were observed for T6–T7 to L5–S1 segments

Table 2.

Summary of model-predicted changes in intervertebral disc stresses and extensor muscle force for the anterior-translated thorax posture, compared with neutral posture. Values indicate maximum regional change, with location of maximum change in square brackets. Values in parentheses indicate percent change with respect to neutral posture. The line of gravity shifted anteriorly an average 64.8 mm (SD 24.4 mm) following anterior translation of the thorax

Region	Compressive stress (kPa)	Shear stress (kPa)	Muscle force (N)
Cervical	24.2 (12.4%) [C2–C3]	−29.8 (−101%) [C3–C4]	4.0 (330.6%) [C2–C3]
Thoracic	183.0 (28.7%) [T12–L1]	86.9 (87.1%) [T12–L1]	180.0 (54.6%) [T12–L1]
Lumbar	358.6 (92.2%) [L5–S1]	100.6 (609%) [L3–L4]	438.5 (942%) [L4–L5]

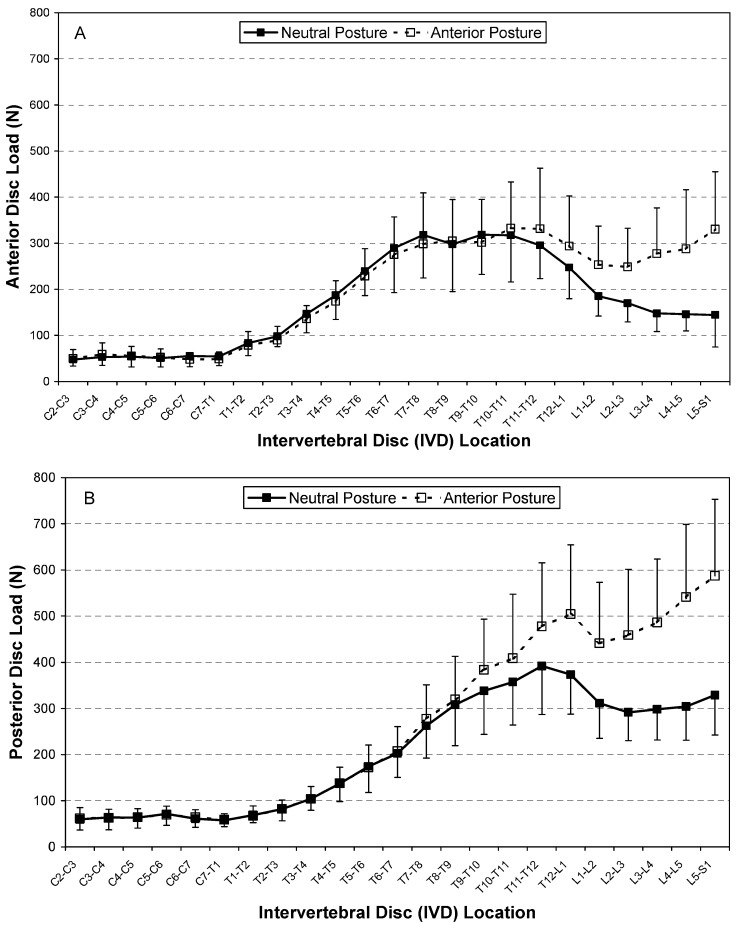
In the neutral posture, the anterior disc loads were highest in the mid-to-lower thoracic region (T6–T12), with the maximum anterior disc load of 319 N±86 N at the T9–T10 level (Fig. 6A). The posterior disc loads were highest at the T9–L1 levels, with a maximum load of 392 N±105 N predicted at the T11–T12 level (Fig. 6B). For the anterior posture, the highest anterior disc loads were predicted in the mid-to-lower thoracic region (T9–L1) and in the lower lumbar discs (L4–S1), with the maximum anterior disc load of 332 N±100 N at the T10–T11 level. In this posture, the posterior disc loads were largest at the T9–L1 level for the thoracic region and largest at the lower discs (L3–S1) in the lumbar region, with the maximum load of 587 N±166 N predicted at the L5–S1 level. The greatest increase in disc loads associated with the neutral-to-anterior translation occurred in the L3–S1 regions, with a maximum at L5–S1 (anterior disc+223%±364%; posterior disc+80.8%±37.8%; centroid+92.2%±42.1%). Changes in anterior and posterior loads were significant (p<0.05) for all disc levels below T11–T12 and T8–T9, respectively.

Fig. 6.

Mean (SD) A Anterior IVD compressive-load and (B) posterior IVD compressive-load distributions for neutral posture and anterior translated posture. Statistically significant differences (paired-observation t-test, p<0.05) between neutral and anterior postures were observed for T8–T9 to L5–S1 segments (posterior load) and T11–T12 to L5–S1 segments (anterior load)

Discussion

The present study was undertaken to compare the loads and stresses acting on the thoracolumbar spinal regions in two different upright spinal postures: neutral alignment and anterior translation of the thorax. The model predictions confirm our hypothesis that increased IVD loads and stresses are associated with anterior translated posture of the thoracic spinal column.

A number of in vivo studies have characterized the disc-load changes associated with anterior translation [30, 41] and flexion of the trunk [31, 42, 44]. In an in vivo study of eight normal subjects and 28 low back pain patients, Sato et al. [41] measured the L4–L5 intradiscal pressure in three sitting and three comparable standing positions (neutral, flexion, extension), while simultaneously exposing a lateral, lumbar radiograph of each subject in each position. The load acting on the L4–L5 disc averaged 800 N in upright stance, 996 N in upright sitting, and reached approximately 2,000 N during upright flexion. Intradiscal pressure was influenced by body posture and found to be linearly dependent on the sagittal plane angle of the L4–L5 motion segment from flexion to the neutral posture [41]. We could locate only one study comparing the anterior trunk posture with the neutral posture for intradiscal pressure, however it was performed in the seated position with some flexion. Wilke et al. [44] found an increase in intradiscal pressure at L4/L5 of 0.18 MPa in the sitting-bent-forward position compared with neutral sitting postures. Taking the increased load in the standing posture into consideration, the finding from Wilke et al. [44] is comparable to the findings of this study (0.3 MPa increase at L4–L5).

In a mathematical modeling study in which S1 was fixed and T1–T12 was considered a rigid body, Kiefer et al. [24] predicted an increased compressive load of 120 N at the L5–S1 disc for 40.0 mm of anterior displacement of the T1 vertebra relative to S1. In the current study, with no constraint of the pelvis or sacrum, we predicted an increased load at the L5–S1 disc of approximately 400 N for an 80.0 mm anterior displacement of T1 centroid, relative to the S1 centroid.

The function of the trunk muscles has been found to be related to lower back disorders [4]. The increase in the extensor muscle load in the anterior translated trunk posture could have several important implications for patients with low back pain and a forward-displaced sagittal alignment. First, in these subjects, the trunk muscles under high loads will also have an increased intramuscular pressure. This increased muscular pressure has been suggested to cause a type of compartment syndrome leading to pain and dysfunction in the muscle [29]. Second, the increased load on extensor muscles contributes to the increased compressive loads and stresses experienced by the IVD.

The biomechanical model provides an approximation of the postural forces and stresses acting on the thoracolumbar spine. However, like most models, it has inherent limitations. Many of these are detailed in previous reports [19, 21], wherein the authors also state that the postural model accurately predicts the compressive stresses acting on the thoracolumbar spine in upright standing postures. Of particular note with respect to the model predictions of shear stresses, however, is our assumption that the C2–S1 extensor muscle moment can be approximated as a force vector acting parallel to the local Y coordinate of each IVD. This is a gross approximation, since the lumbar extensor muscle has force components that act horizontally to the plane of the IVD [2]. Approximating the line of action of the erector spinae muscle groups in this manner has a relatively small effect on compressive force and stress calculations, but more specific implications in the case of the shear-force and stress calculations. Namely, in our model, C2–S1 shear forces and stresses, averaging about 14% of the compressive forces and stresses, oppose the body-weight-induced anterior shear acting on the IVD in the cervicothoracic (~C2–T6) and lower lumbosacral (L5–S1) regions. They also oppose the body-weight-induced posterior shear acting on the IVD in the thoracolumbar region (~T6–L4). However, because of the anterior curvature of the lumbosacral spine (see Fig. 2a), our estimates of shear stresses in this region (L4–S1) are most likely overestimated. More precise information regarding the line of action of lumbar extensor muscles and other trunk muscles can be obtained from anatomical studies or by analyzing serial images of the trunk [9]. In this study the available subject-specific anatomic data was limited to a precise description of the anterior vertebral column obtained from digitizing landmarks on lateral full-spine radiographs.

With the largest concentration of pain fibers, the posterior region is considered to be the most pain-sensitive of the IVD [5, 27]. These high compressive loads, causing increased compressive stress, may at the very least produce pain, and at the worst initiate or contribute to a degenerative remodeling response in the posterior IVD region. Indeed, a relationship between mechanical stress in the IVD and cell metabolism has been previously identified [15]. Recent clinical findings indicate that abnormal sagittal balance (anterior translation of 25 mm or more for C7–S1) is associated with a greater incidence of degenerative disc disease [26]. In the present study, experimentally controlled changes in the anterior sagittal balance (average neutral-anterior posture translation=82 mm for C7–S1) were shown to significantly increase thoracolumbar disc loads and stresses. Our study findings, although theoretical, support the notion that postures that increase disc loads and stresses may initiate or contribute to a degenerative remodeling response.

In normal subjects without history of back injury, pain, treatment or degenerative changes on X-ray, the alignment of T12 relative to S1 has been found to be within close proximity to vertical, i.e., 5 mm±17 mm [17, 43]. Similarly, in full-spine lateral radiographs obtained in the upright neutral position from 80 normal subjects, the vertical alignment of the T1–T12–S1 centroids were within 2.3 mm of each other [12]. In contrast, in chronic lower back pain subjects and flat-back patients, the sagittal balance is generally displaced, well anterior to normal [3, 16]. Whether this is a result of the pain or contributes to the pain remains to be clarified. We speculate that the latter is true in chronic pain syndromes, due to the increased loads and stresses found in the anterior-translated trunk posture.

A forward-displaced, sagittal spinal alignment has been associated with lumbar spondylolisthesis in children and adults [18, 28]. Recently, Kawakami and colleagues [18] identified radiographic risk factors for poor recovery rates in patients with degenerative lumbar spondylolisthesis who were undergoing decompression and posterolateral fusion. Vertical alignment of L1, with respect to S1, of greater than 35 mm anterior was identified as a risk factor associated with reduced recovery and severe, residual lower back pain. Our results of increased shear load and stress on the IVD during anterior translation of the thorax may, in part, explain these poor outcomes, and others, in the Kawakami subjects with large degrees of anterior sagittal balance.

Abnormal sagittal postural and spinal alignment causes increased forces to act upon the spine and IVD. These forces may predispose individuals to problems such as lumbar disc pathologies, spondylolisthesis abnormalities, and poor outcomes in spinal surgery. Increased disc loads and stresses may also contribute to pain and possibly progression of thoracic deformity [21]. Compared to the upright sagittal posture, we observed that an anterior, translated thorax that maintains relative sagittal alignment of T1 through T12 anterior to S1 resulted in large increased loads and stresses on the thoracolumbar junction and lumbar spine. This information is useful to surgeons and clinicians in determining the causative factors of back pain and in the correction of abnormal posture. Further research is needed to determine the effect of other abnormal postures on the tissues that constitute the human frame.

Conclusions

This study has shown that anterior trunk translation (maintaining sagittal alignment of T1–T12 anterior to S1) in the standing subject increases extensor muscle activity and increases loads and stresses acting on the intervertebral disc in the lower thoracic and lumbar regions.