Abstract.
Monitoring of tissue blood volume and local oxygen saturation can inform the assessment of tissue health, healing, and dysfunction. These quantities can be estimated from the contribution of oxyhemoglobin and deoxyhemoglobin to the absorption spectrum of the dermis. However, estimation of blood related absorption in skin can be confounded by the strong absorption of melanin in the epidermis and epidermal thickness and pigmentation varies with anatomic location, race, gender, and degree of disease progression. Therefore, a method is desired that decouples the effect of melanin absorption in the epidermis from blood absorption in the dermis for a large range of skin types and thicknesses. A previously developed inverse method based on a neural network forward model was applied to simulated spatial frequency domain reflectance of skin for multiple wavelengths in the near infrared. It is demonstrated that the optical thickness of the epidermis and absorption and reduced scattering coefficients of the dermis can be determined independently and with minimal coupling. Then, the same inverse method was applied to reflectance measurements from a tissue simulating phantom and in vivo human skin. Oxygen saturation and total hemoglobin concentrations were estimated from the volar forearms of weakly and strongly pigmented subjects using a standard homogeneous model and the present two layer model.
Keywords: radiative transfer, multilayered media, oximetry, tissue optics, artificial neural network, inverse method, multispectral imaging
1. Introduction
Diffuse optical spectroscopy (DOS) can be used to characterize the optical properties of skin by measuring the amount of radiative energy remitted from the skin.1–3 Spatial frequency domain imaging uses patterned illumination to determine the absorption and reduced scattering coefficients of a turbid medium based on the spatial frequency dependent reflectance function. The method has been described in detail in the literature.4–12 Instead of measuring the total reflectance, spatial frequency domain techniques measure the attenuation of specific spatial frequency components of the illuminating pattern as it propagates in a tissue. Typically, a one dimensional sine-wave pattern with controlled spatial frequency is used and set to have sensitivity to a particular physical depth since higher frequencies tend to probe a more superficial volume. Additionally, high spatial frequencies have been shown to be more sensitive to the tissue’s scattering coefficient. On the other hand, lower frequencies (i.e., ) have been shown to be sensitive to the tissue’s absorption coefficient.4,5,7,13–15
Previously, we presented an accurate and efficient model of light transfer through optical media suitable for analyzing spatial frequency domain data for multilayered media. An artificial neural network was trained to map a set of optical properties of two layer media to a spatial frequency domain solution of the radiative transfer equation (RTE). Additionally, we developed an iterative inverse method with the neural network as a forward model that could be used to analyze reflectance of two layer media to determine the optical properties of each layer. In this study, we apply the neural network model to (i) simulated skin phantoms, (ii) two layer polydimethylsiloxane (PDMS) phantoms, and (iii) in vivo measurements from human volar forearms with varying pigmentation. The accuracy, application, and limitations of the present model are discussed in the context of biomedical spatial frequency domain spectroscopy of skin.
2. Background
2.1. Structure of The Skin
The human skin consists of the epidermis and dermis and is supported by a subcutaneous layer of fat. Epidermal thickness ranges between ten to hundreds of micrometer in thickness. The cells in the epidermis include the basal keratinocytes, melanocytes, and Langerhans.16 Melanocytes synthesize melanin, the skin protein mainly responsible for racial and seasonal variation in skin color. Melanin is contained in organelles knows as melanosomes.16,17 Melanosomes concentration in the epidermis varies between 1% and 43% of the epidermal volume corresponding to lightly or darkly pigmented skin, respectively.16–19 However, the degree of pigmentation by melanin associated with genetic and seasonal variation was assessed in this study with the Fitzpatrick skin pigmentation scale which categorizes human skin into one of six categories.20 Skin Type I refers to white skin which burns easily when expose to the sun and never tans while Type VI refers to skin that is very dark, never burns due to solar exposure and tans easily. Melanosomes are concentrated near to the basement membrane.21–23 In normal skin, melanin absorption dominates the total absorption in the epidermis in the visible range and NIR.14,16–19
The dermis, located beneath the epidermis, is responsible for the skin's pliability, mechanical resistance and temperature control. The thickness of the dermis ranges between 450 μm and several millimeters.24–27 The dermis is primarily composed of collagen fibers, nerves, capillaries, and blood vessels but also contains elastin, fibroblasts, and Schwann and endothelial cells.16,17 Collagen fibers make up 70% of the dermis, giving it strength and toughness. Elastin maintains normal elasticity and flexibility. The dermis consists of the papillary and reticular dermal layers. The papillary dermis connects the epidermis to underlying tissue and consists of long, thin randomly oriented collagen fibers. Thicker bundles of collagen run parallel to the skin surface in the deeper reticular layer. The volume of blood in the dermis ranges between 0.2 and 7% and varies with bodily location.19,28 Erythrocytes (red blood cells) occupy approximately half of the blood volume and are responsible for oxygen transfer from the lungs throughout the body. Erythrocytes are composed mainly of hemoglobin molecules which reversibly bind to oxygen molecules in the lungs to form oxyhemoglobin. Hemoglobin is known as deoxyhemoglobin once it has released its oxygen molecules. Hemoglobin absorption dominates the total absorption in the dermis in the visible range and near infrared (NIR).14,16,17
2.2. Depth Sensitivity of Spatial Frequency Domain Reflectance
Spatial frequency domain spectroscopy involves illumination of media with a spatially varying intensity pattern of the form,
| (1) |
where is the spatial frequency expressed in , is the incident optical power at the spatial frequency and measured in mW, and is the spatial coordinate parallel to the medium’s surface and measured in mm. The remitted energy differs from the illumination pattern due to the optical and geometric property characteristics of the sample.4–7 In fact, the spatial frequency dependent reflectance measured from a turbid medium encodes both depth and optical property information, enabling both quantitation and low resolution depth sectioning of the spatially varying optical properties of a medium.5,8–10
Several investigators have established the depth-sensitivity of spatial frequency domain imaging.5,8–10 Cuccia et al.,5 demonstrated that spatially modulated illumination facilitates quantitative wide-field optical property mapping and exhibits sensitivity to buried heterogeneities in turbid media. They performed spatial frequency domain imaging of tissue simulating phantoms with embedded heterogeneities using 42 spatial frequencies between 0 and . They showed that changes in demodulated reflectance at low versus high spatial frequencies are sensitive to the lower versus upper embedded heterogeneities. This work showed that spatial frequency domain spectroscopy can detect contrast between background and heterogeneity, but did not provide a quantitative technique for determining the optical properties of the heterogeneity itself.
Konecky, et al.,8 used spatial frequency domain imaging to detect tube heterogeneities buried in homogeneous tissue simulating phantoms. They measured spatial frequency dependent reflectance from the heterogeneous phantoms at 11 spatial frequencies. They then used an inverse method based on the diffusion approximation to reconstruct tomographic contrast images of the buried tubes. This model, however, may not be applicable if the highly absorbing heterogeneity is close to the surface (i.e., the epidermis of the skin).
2.3. Artificial Neural Networks For Two Layer Spectroscopy
The present study couples the inherent depth sensitivity of spatial frequency domain imaging with an accurate and fast semi-empirical model of light transfer through tissue that does not suffer from the limitations of approximate methods such as the diffusion approximation. We performed multiple Monte Carlo simulations and then fit a machine learning algorithm—an artificial neural network—to the output data. An artificial neural network is a data structure that can accurately approximate a nonlinear relationship between a set of input and output parameters from multiple samples of the input-output pairs.29 Neural network based approaches to determining optical scattering and absorption coefficients of biological tissue and phantom reflectance measurements have been proposed by other investigators.30–38 Wang, Shastri and Pfefer developed a neural network to detect the optical properties of two layer media using spatially resolved reflectance measurements.38 They then used their inverse model to detect the absorption and reduced scattering coefficients of two layer media in the ultra-violet and visible ranges, for which the tissues’ absorption coefficient is typically greater than its reduced scattering coefficient. However, they reported large prediction errors in all their parameters (absorption and scattering coefficients of the top and bottom layer). Additionally, their method required multiple spatially resolved measurements. This study uses a forward and inverse model designed for spatial frequency domain measurements of two layer media from a single detector.
3. Methods
3.1. Digital Skin Simulating Phantom Preparation
We first tested the artificial neural network on digital skin phantom data generated by Monte Carlo simulations. We modeled the skin as two layer system depicted in Fig. 1. The absorption coefficient of the epidermal layer as a function of was defined as
| (2) |
where was the molar extinction coefficient of melanin measured in and was the molarity of melanin in the epidermis measured in µM and was assumed to range between 0.01 and 0.06 µM.19,28 The absorption coefficient of the dermis as a function of was calculated as
| (3) |
where and were the molar extinction coefficients of oxyhemoglobin and deoxyhemoglobin, respectively, was the percent oxygen saturation of hemoglobin, and was the molarity of hemoglobin in the dermis measured in µM and was assumed to range between 20 and 200 µM. Values of lower than 20 µM resulted in an essentially transparent epidermis while the spectral features of the dermal tissue became invisible for larger than 200 µM. The scattering coefficients of the epidermis and dermis were modeled according to a power-law relationship with wavelength,
| (4) |
| (5) |
where and are the so-called scattering amplitude and power, respectively.39
Fig. 1.
Illustration of the two layer geometry, optical properties, and illumination considered.
The spatial frequency dependent reflectance , was determined with Monte Carlo simulations. Monte Carlo simulation software developed by Wang and Jacques40 was used to calculate the radial diffuse reflectance function where was the radial distance from the simulation’s origin. Then, the spatial frequency domain diffuse reflectance function was calculated with the Hankel transform using the method suggested by Cuccia et al.,13
| (6) |
where is the 0’th order Bessel function of the first kind. Each simulation was run with photon packets.
3.2. Two Layer Silicone Phantom Preparation
A two layer skin simulating phantom was prepared by combining two homogeneous phantoms with distinct absorption and scattering characteristics.41,42 Polydimethylsiloxane (PDMS) served as a base for each phantom. Curing agent from a commercially available kit (Kit P-4, Eager Plastics) was added to bulk PDMS at a ratio of 10 parts PDMS to one part curing agent. PDMS is weakly absorbing and non-scattering in the NIR. Scattering was achieved by the addition of rutile powder (Ti-602, Atlantic Equipment Engineers), which has a high index of refraction relative to PDMS, but negligible absorption in the NIR spectrum.43 The epidermis simulating phantom was colored with coffee.42 The absorption spectra of coffee and melanin both lack distinct spectral features and exhibit power law-like decay from the visible into the near infrared. For this reason, coffee has been used a cost-effective and readily available colorant for epidermis simulating phantoms in our study and by other investigators.44,45 India ink (PRO-4100, Pro Art) was added to the dermis simulating layer to achieve a desired level of absorption. Approximately 0.07 g India Ink () was required to generate an absorption of roughly , and approximately 0.2 g () was needed to generate reduced scattering coefficient of roughly at 650 nm. These amounts did not significantly change the volume of the phantom. The thicknesses of the top and bottom layer phantoms were 250 µm and 1 cm, respectively. The refractive index of both phantoms was approximately 1.43, which was a close approximation of tissue. After preparation and cleaning, the thin epidermal phantom was placed upon the dermal phantom. A roller was used to squeeze out any air bubbles that formed between the two phantoms during assembly.
3.3. Spatial Frequency Domain Imaging System
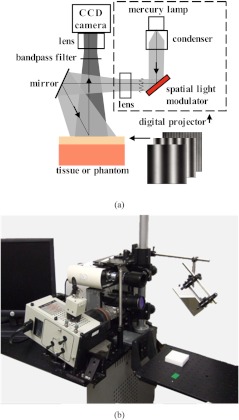
Spatial frequency domain imaging was achieved by illuminating a surface of interest with light having a spatially varying intensity and capturing the reflected image with a charge coupled device (CCD) camera. A schematic and photograph of the instrument used in this study is shown in Fig. 2. Broadband light was generated with a Newport Corporation power source (Newport Corporation, Irvine CA) and a 250 watt tungsten lamp. This light was used to illuminate a DLP Developers Kit 1 digital micro-mirror device (Texas Instrument, Dallas TX), which spatially modulated the light to be projected onto the phantom. Frequency patterns for the spatial modulation were generated using customized software (Modulated Imaging Inc., Irvine CA). The patterned light was projected onto the surface of interest via a 45 deg mirror. Six spatial frequencies spaced evenly between from 0 to were used during the imaging.46 The diffusely reflected light images were acquired with a Nuance Multispectral Imaging System (CRi Inc., Woburn,MA), which consists of a liquid crystal tunable filter capable of acquiring at discrete wavelengths (10 nm bandwidth) between 650 nm and 1100 nm, and a , front illuminated CCD. A field of view was acquired by the CCD using binning in hardware and an exposure time of . Cross-polarizers were placed at the source and detector in order to eliminate specular reflection. Thus, the modeling component of this study only considered the diffuse reflectance because specular reflectance was removed by cross-polarization. Additionally, the modeling did not consider polarization of the diffusely reflected light because multiple scattering events of light in the tissue would effectively randomize the polarization angels of the reflected energy. Illumination by eleven (11) uniformly spaced wavelengths between 650 and 800 nm were used during two layer silicone phantom and in vivo measurements.
Fig. 2.
Schematic (a) and photograph (b) of spatial frequency domain imager used in this study.
3.4. In vivo Skin Measurements
The volar forearms of four subjects were imaged with the spatial frequency domain imaging (SFDI) system under UC Irvine IRB protocol HS# 2008-6307. Each subject of varying skin color was male, between 20 and 30 years of age, and in good health. Subjects were imaged in a comfortable, seated position. Subjects were allowed to rest for 5 min prior to imaging to reduce the effect of systemic vascular changes. Data post-processing and analysis for digital, silicone phantoms, and in vivo measurements were completed in MATLAB (Mathworks, Natick, MA).
For each patient, a resting baseline was measured for 3 min. A Hokanson AG101 Rapid Cuff Inflator was then used to immediately occlude venous blood flow into the volar forearm at a pressure of 200 mm Hg. This was maintained for 3 min before being released for a final 3 min of recovery.
During the entire 9 min period, continuous SFDI measurements were acquired using four equally spaced wavelengths between 650 and 749 nm at five spatial frequencies equally spaced from 0 to .
4. Analysis
4.1. Two Layer Skin Model
Figure 1 shows the two layer geometry, optical properties, and illumination considered in this study. Human skin was approximated by two layers, the epidermis and the dermis. Note that we made the simplifying assumption that melanin and blood were uniformly distributed in the epidermis and dermis, respectively. The epidermis was illuminated by a collimated light source. The spatial frequency of the illumination pattern was considered to range between 0 and .The index of refraction, absorption coefficient, reduced scattering coefficients, and thickness of the epidermis where denoted by , , , and , respectively. The index of refraction was assumed to be 1.40 to represent biological tissue47 and was suitable for both the silicone phantom and human skin. The absorption coefficient was assumed to range between 0.10 and .47–53 The reduced scattering coefficient was assumed to be identically since it was shown previously that large changes in resulted in minimal changes in the reflectance of the two layer medium(see Fig. 2 of Ref. 54). Thus setting to a constant value of sufficiently captured the effect of scattering in the thin superficial layer. Finally, the thickness was assumed to range between 15 and 150 μm.26,55,56 Additionally, it was shown that the individual values of and were not expected to be detectable from spatial frequency dependent reflectance (see Fig. 7 of 54). Hence, this study focused on determining the optical thickness of the epidermis defined as
| (7) |
The index of refraction, absorption coefficient, and reduced scattering coefficients of the dermal layer where denoted by , , and , respectively. For simplicity, a matched index boundary condition was assumed between the epidermis and dermis (i.e., ). The absorption coefficient of dermis, , was assumed to range between 0.01 and while reduced scattering coefficient was assumed to range between 0.50 and .47–53
4.2. Inverse Problem with the Least-Squares Fitting
The forward model defined in Eq. (5) of Ref. 54 was used along with an iterative inverse method to estimate parameters , , and from a spatial frequency dependent reflectance . This was done by choosing , , and to minimize a quadratic cost function,
where was the spatial frequency dependent reflectance at spatial frequency and was the total number of spatial frequencies. In this study, was minimized with the Levenberg-Marquardt algorithm implemented in MATLAB. Six spatial frequencies between 0 and were used ().
5. Results and Discussion
5.1. Digital Skin Phantom Spectroscopy
Figure 3(a) shows estimates of the reduced optical thickness for between 40 and 150 μm, between 0.01 and 0.10 µM, equaling to 75 µM, and equaling to 50%, and both equaling , equaling to 1.30, and equaling to 1.35. Relative percent error between the true and estimated value are shown as a function of wavelength in the upper left corner of each panel. For these biometric parameters and for between 650 and 800 nm, ranged between 0.13 and , ranged between 0.013 and , ranged between 1.77 and , and ranged between 1.35 and . Figure 3(a) illustrates that the reduced optical thickness was well estimated in the NIR by the present inverse method from spatial frequency dependent reflectance with six evenly spaced spatial frequencies between 0.00 and . Furthermore, it was apparent that the estimation error was less for thick and highly pigmented epidermis (i.e., and ) than for thin and weakly pigmented epidermis (i.e., and ). This is due to the diminished sensitivity of the spatial frequency dependent reflectance function to when was small as depicted in Fig. 7 of Ref. 54. Figure 3(b) shows estimates of the reduced optical thickness retrieved from spatial frequency dependent reflectance functions with 2% additive noise. True noise levels depend on the (i) instrumentation used, (ii) integration time, (iii) filtering, and (iv) oversampling. A 2% noise level was added for illustrative purposes. As expected, noise corruption has a larger effect on estimation of optically thin epidermal layers than on optically thick layers.
Fig. 3.
Estimation of for tissue simulating digital phantom (a) without noise and (b) with 2% noise. Relative percent error between the true and estimated value are shown as a function of wavelength in the upper left corner of each panel.
Figure 4(a) depicts estimates of the dermal absorption coefficient for between 40 and 150 μm, between 0.01 and 0.10 µM, equaling to 75 µM, and equaling to 50%, and both equaling , equaling to 1.30, and equaling to 1.35. The melanin concentrations equaling to 0.01and 0.10 µM corresponded to an epidermal absorption coefficient of 0.20 and at 694 nm and were typical of lightly and moderately pigmented subject, respectively. Accurate determination of is essential for transcutaneous tissue oximetry which attempts to determine the dermal blood volume and oxygen saturation by decomposing into absorption contribution by oxyhemoglobin and deoxyhemoglobin according to Eq. (3). It is desired that estimation of be independent of epidermal thickness and pigmentation when, for example, imaging tissue with large changes in epidermal thickness or melanin due to natural or pathological factors. Figure 4(a) illustrates that the present method accurately detects in the NIR for a large range of epidermal thicknesses and melanin concentration. In addition, Fig. 4(b) shows that the method was robust to 2% additive noise. Figure 4 illustrates that analysis of spatial frequency dependent reflectance can probe beneath optically thin and thick superficial layers.
Fig. 4.
Estimation of for tissue simulating digital phantom (a) without noise and (b) with 2% noise. Relative percent error between the true and estimated value are shown as a function of wavelength in the upper left corner of each panel.
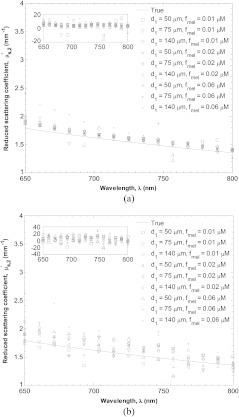
Figure 5(a) illustrates the effectiveness of the present method in estimating the reduced scattering coefficient of the dermal layer for between 40 and 150 μm, between 0.01 and 0.10 µM, equaling to 75 µM, and equaling to 50%, and both equaling , equaling to 1.30, and equaling to 1.35. Relative percent error between the true and estimated value are shown as a function of wavelength in the upper left corner of each panel. Additionally, Fig. 5(b) shows these results in the presence of 2% additive noise. The method performed well in retrieving in the NIR despite large variations in epidermal thickness and pigmentation and which varied with .
Fig. 5.
Estimation of for tissue simulating digital phantom (a) without noise and with (b) 2% noise. Relative percent error between the true and estimated value are shown as a function of wavelength in the upper left corner of each panel.
5.2. Two-Layer Silicone Phantom Spectroscopy
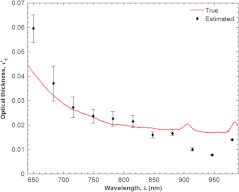
Figure 6 shows the estimated and true optical thickness of the two layer silicone phantom as a function of wavelength between 650 and 980 nm. The standard deviations of the estimates at each wavelength are also shown. The true optical thickness of the simulated epidermal layer was a superposition of the monotonically decreasing absorption coefficient of coffee onto the relatively featureless absorption characteristics of pure PDMS. The small absorption peaks of PDMS were observed at 910 nm. The absorption peak at 980 nm was attributed to coffee. The estimated absorption coefficient of the simulated epidermal layer predicted by the present model was similar in trend and magnitude to its true value.
Fig. 6.
Estimated and true optical product of the top layer thickness and absorption coefficient of the two layer silicone phantom. The standard deviations of the estimates at each wavelength are also shown.
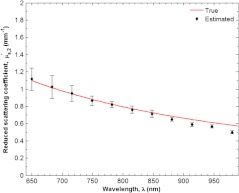
Figure 7 shows estimated and true absorption coefficient of the supporting layer of silicone phantom representing dermis in skin. The true absorption coefficient was close to for nearly the entire wavelength range between 650 and 980 nm. It exhibits a strong peak at 910 nm from PDMS. The estimated absorption coefficient did not deviate from the true absorption coefficient by more than 10% for the entire range displayed. Additionally, the strong absorption peak near 910 nm was well captured by the two layer model. Similarly, Fig. 8 depicts estimated and true reduced scattering coefficient of the bottom layer as a function of wavelength between 650 and 980 nm. The true reduced scattering coefficient exhibits the typical exponential decay with wavelength and monotonically decreases from 1.1 and . The estimated reduced scattering coefficient closely followed the true value of for the entire range shown. In fact, the two values were never deviated from one another by more than 10%.
Fig. 7.
Estimated and true absorption coefficient of the supporting layer of silicone phantom representing dermis in skin. The standard deviations of the estimates at each wavelength are also shown.
Fig. 8.
Estimated and true reduced scattering coefficient of the supporting layer of silicone phantom representing dermis in skin. The standard deviations of the estimates at each wavelength are also shown.
5.3. In vivo Skin Measurements
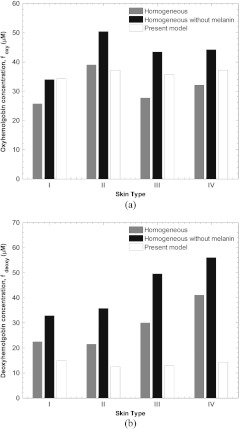
Previous sections established the ability of the present model in analyzing simulated and measured diffuse reflectance phantoms from two layer media. The present section compares results from a previously developed homogeneous model6 and the present two layer model in analysis of spatial frequency domain spectroscopy measurements from human skin on the volar forearm. It aims to justify the complexity of two layer spectroscopy in the context of tissue oximetry. For example, Fig. 9 shows estimates of oxyhemoglobin and deoxyhemoglobin concentrations denoted by and , respectively, for four subjects with increasingly darker skin type predicted by a homogeneous model6 and by the present two layer model. The absorption coefficient estimated by the homogeneous model6 denoted by –was spectrally decomposed to determine the constituent chromophore concentrations. Results are presented for spectral decomposition with and without melanin as a contributing chromophore. Furthermore, Fig. 9 shows the estimation of oxyhemoglobin and deoxyhemoglobin by spectral decomposition of the dermal absorption coefficient determined from analysis of the same data with the present model. We assumed that was completely determined by absorption due to blood and that all melanin absorption was segregated to . The cross-talk between epidermal melanin and dermal chromophore concentrations is most apparent in Fig. 9(b) that shows the apparent deoxyhemoglobin concentration increasing artificially for subjects with darker skin tone. This effect was apparent for both melanin compensated and non-compensated decomposition of . On the other hand, the estimates oxyhemoglobin and deoxyhemoglobin by the present two layer model did not exhibit coupling with melanin. In fact, estimates of deoxyhemoglobin–which were apparently more sensitive to melanin concentration–stay within 5 µM of each other regardless of skin type. Since all subjects were age-matched, healthy males, and rested prior to imaging, similar oxyhemoglobin and deoxyhemoglobin measurements were expected.
Fig. 9.
Estimates of (a) oxyhemoglobin and (b) deoxyhemoglobin concentration for four subjects with increasingly darker skin type predicted by a homogeneous model (with and without melanin compensation) and by the present two layer model.
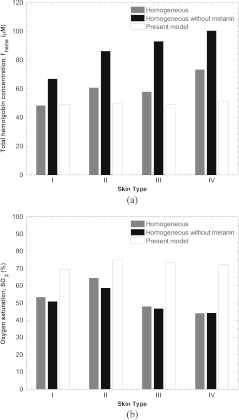
Figure 10 shows the effectiveness of the two layer model in predicting transcutaneous oximetry information in the presence of variable melanin content in the epidermis. It depicts estimates of total hemoglobin concentration and oxygen saturation denoted by and , respectively, for four subjects with increasingly darker skin type from Type I to Type IV on the Fitzpatrick skin pigmentation scale.20 The homogeneous model6 over predicts total hemoglobin concentration for darker subjects because melanin absorption artificially increase . Furthermore, the homogeneous model predicts artificially low oxygen saturations since both melanin and deoxyhemoglobin absorb more strongly in the low NIR. In fact, for the Type IV subject, the predicted oxygen saturation was 44% which was unrealistically low value. The values predicted by the homogeneous model ranged between 44% and 65% and decreased as skin pigmentation increased. On the other hand, the two layer model predicts realistic and similar values of between 69% and 75% for all four subjects regardless of pigmentation. Additionally, the values predicted by the present model shows no coupling to epidermal melanin concentration.
Fig. 10.
Estimates of (a) total hemoglobin and (b) oxygen saturation for four subjects with increasingly darker skin type predicted by a homogeneous model (with and without melanin compensation) and by the present two layer model.
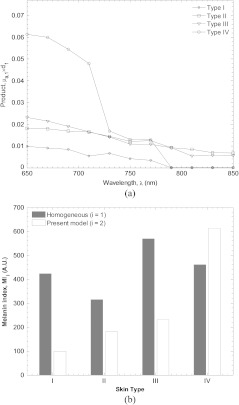
A practical tissue oximetry system would both remove the effects of melanin from the transcutaneous oximetry signal and quantify pigmentation in the epidermis. Figure 11 shows estimates of epidermal melanin content for subjects of varying skin type predicted by spectral decomposition of the homogeneous absorption coefficient and the present two layer model. Figure 11(a) shows the wavelength dependent product of epidermal thickness (assumed to be 70 µm) and calculated epidermal absorption coefficient with the epidermal reduced scattering coefficient assumed to be . The epidermal absorption coefficient exhibits monotonically decreasing behavior with wavelength, typical of melanin absorption. A melanin index can be defined as,
| (8) |
where was estimated by spectral decomposition of . Additionally, we defined a melanin index based on results from the two layer model defined as
| (9) |
Figure 11(b) shows and for four subjects with increasing skin pigmentation. It indicates that the melanin index predicted by the homogeneous model did not correlate with skin type. In fact, Type I and IV subjects—which should represent extremes of –were 423 and 460, respectively. The maximum melanin index of 569 was calculated for the subject with Type III skin. On the other hand, values of for Type I, II, III and IV subjects was 141, 258, 330, and 875, respectively. As expected, the melanin index increased with increasing skin type. In fact, Type IV skin exhibited a melanin index 6.2 times higher than Type I skin.
Fig. 11.
(a) The product of epidermal thickness and absorption coefficient as a function of wavelength estimated by the present model. An epidermal thickness of 70 µm and epidermal scattering coefficient of were assumed. (b) Melanin index predicted by a homogeneous model and the present two layer model.
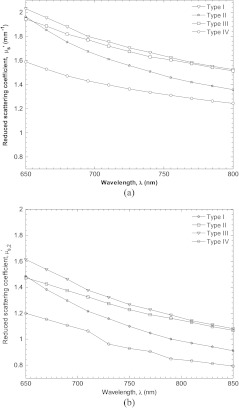
Figure 12 illustrates estimates of the reduced scattering coefficient for four subjects with increasingly darker skin type predicted by a homogeneous model6 and the present two layer model as a function of wavelength. The reduced scattering coefficients predicted by both models have similar shape. However, the reduced scattering coefficient predicted by the two layer model was approximately lower than the prediction by the homogeneous model. This may be due to a coupling between melanin absorption and the tissue’s reduced scattering coefficient which both exhibit an exponential decay with wavelength. When considered homogeneous, the tissue’s bulk absorption coefficient is a combination between melanin and blood absorption. Subsequently, the bulk reduced scattering coefficient may be exaggerated to compensate for the artificially large absorption coefficient. However, the present two layer model segregates melanin absorption to the epidermal absorption coefficient and so reduces coupling between melanin absorption and the dermal reduced scattering coefficient .
Fig. 12.
Estimates of the reduced scattering coefficient for four subjects with increasingly darker skin type predicted by a (a) homogeneous model and (b) the present two layer model.
5.4. In vivo Skin Measurements During Forearm Occlusion
Finally, Fig. 13 shows estimates of the oxygen saturation measured from lightly and strongly pigment subjects during a forearm occlusion experiment predicted by the standard homogeneous model and the present two layer model. Figure 13(a) indicates that estimates of measured from the strongly pigmented subject exhibit a baseline around 52%. On the other hand, the weekly pigmented subject exhibits a baseline of approximately 65%. The reasons for this discrepancy is described above. On the other hand, Fig. 13(b) indicates that the two layer model predicts a baseline value around 70%. Furthermore, both subjects exhibit a drop of approximately 10% during occlusion and a the typical hyperemic response after pressure was released. Figure 13 indicates that the present two layer model can effectively remove the effects of strong pigmentation from the signal during dynamic perfusion events.
Fig. 13.
Oxygen saturation measured from lightly and strongly pigment subjects during a forearm occlusion experiment predicted by a (a) homogeneous model and (b) the present two layer model.
6. Conclusion
This study describes a technique for analyzing spatial frequency dependent reflectance of two layer turbid media. The present model can be used to determine the optical thickness of a strongly absorbing superficial layer and the absorption and reduced scattering coefficient of a supporting semi-infinite supporting layer. An artificial neural network was used to map input optical properties to a spatial frequency dependent reflectance function of two layer media. The accurate and efficient forward method was used in conjunction with a gradient descent method to determine the optical properties of the two layer medium.
The neural network inverse method was applied to (i) simulated spatial frequency dependent reflectance of skin, (ii) a two layer silicone tissue simulating phantom, and (iii) in vivo human skin from subjects of varying skin type. Analysis of the simulated spatial frequency dependent reflectance of skin showed that the optical thickness of the epidermis and absorption and reduced scattering coefficients of the dermis could be determined independently and with minimal coupling. Additionally, the optical properties of the two layer tissue simulated phantom could be determined from spatial frequency dependent reflectance measurements. Finally, in vivo experiments showed that the present two layer model can be used to quantify melanin pigmentation and estimate hemoglobin concentration and saturation in humans of varying skin pigmentation.
Current work involves implementing a neural network approach which directly maps a measured spatial frequency dependent reflectance spectrum to optical properties as described in Eq. (7) of Ref. 54. This would allow for rapid generation of high resolution two dimensional chromophore maps similar to those reported in Ref. 6 but presenting information about two distinct tissue layers. However, present experiments with this approach indicate that the direct method may have been over-trained on sample data and is thus highly sensitive to experimental noise and offset. We are also pursuing human and animal model occlusion studies to show the utility of this approach over the full range of realistic vascular conditions associated with ischemia, hyperemia, inflammation, and, for example, necrosis. Once characterized in a controlled lab setting, the present algorithm can be deployed to analysis of clinical spatial frequency domain imaging data.
Acknowledgments
The authors gratefully acknowledge funding provided by the NIH SBIRs1R43RR030696-01A1, the NIH NIBIB Biomedical Technology Research Center (LAMMP: 5P-41RR01192), the Military Photomedicine Program, AFOSR Grant No. FA9550-08-1-0384, and the Beckman Foundation.
References
- 1.Hirsch J. C., et al. , “Near-infrared spectroscopy: what we know and what we need to know—a systematic review of the congenital heart disease literature,” J. Thorac. Cardiovasc.Surg. 137(1), 154–159 (2009). 10.1016/j.jtcvs.2008.08.005 [DOI] [PubMed] [Google Scholar]
- 2.Erickson S. J., Godavarty A., “Hand-held based near-infrared optical imaging devices: a review,” Med. Eng. Phys. 31(5), 495–509 (2009). 10.1016/j.medengphy.2008.10.004 [DOI] [PubMed] [Google Scholar]
- 3.Matcher S. J., et al. , “Performance comparison of several published tissue near-infrared spectroscopy algorithms,” Anal. Biochem. 227(1), 54–68 (1995). 10.1006/abio.1995.1252 [DOI] [PubMed] [Google Scholar]
- 4.Bevilacqua F., et al. , “Method and apparatus for performing quantitative analysis and imaging surfaces and subsurfaces of turbid media using spatially structured illumination,” U.S. patent 6,958,815 B2 (2003).
- 5.Cuccia D. J., et al. , “Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain,” Opt. Lett. 30(11), 1354–1356 (2005). 10.1364/OL.30.001354 [DOI] [PubMed] [Google Scholar]
- 6.Cuccia D. J., et al. , “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Weber J. R., et al. , “Noncontact imaging of absorption and scattering in layered tissue using spatially modulated structured light,” J. Appl. Phys. 105(10), 102028 (2009). 10.1063/1.3116135 [DOI] [Google Scholar]
- 8.Konecky S. D., et al. , “Quantitative optical tomography of sub-surface heterogeneities using spatially modulated structured light,” Opt. Express 17(17), 14780–14790 (2009). 10.1364/OE.17.014780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weber J. R., Cuccia D. J., Tromberg B. J., “Modulated imaging in layered media,” in Proc. IEEE Engineering in Medicine and Biology Society (EMBS'06), pp. 6674–6676, IEEE, Piscataway, NJ: (2006). [DOI] [PubMed] [Google Scholar]
- 10.Belanger S., et al. , “Real-time diffuse optical tomography based on structured illumination,” J. Biomed. Opt. 15(1), 016006 (2010). 10.1117/1.3290818 [DOI] [PubMed] [Google Scholar]
- 11.Rajaram N., Nguyen T. H., Tunnell J. W., “Lookup table-based inverse model for determining optical properties of turbid media,” J. Biomed. Opt. 13(5), 050501 (2008). 10.1117/1.2981797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bassi A., et al. , “Spatial shift of spatially modulated light projected on turbid media,” J. Opt. Soc. Am. A Opt. Image Sci. Vis. 25(11), 2833–2839 (2008). 10.1364/JOSAA.25.002833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.David J. C., et al. , “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saager R. B., Cuccia D. J., Durkin A. J., “Determination of optical properties of turbid media spanning visible and near-infrared regimes via spatially modulated quantitative spectroscopy,” J. Biomed. Opt. 15(1), 017012 (2010). 10.1117/1.3299322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yafi A., et al. , “Postoperative quantitative assessment of reconstructive tissue status in a cutaneous flap model using spatial frequency domain imaging,” Plast. Reconstruct. Surg. 127(1), 117–130 (2011). 10.1097/PRS.0b013e3181f959cc [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Young A. R., “Chromophores in human skin,” Phys. Med. Biol. 42(5), 789 (1997). 10.1088/0031-9155/42/5/004 [DOI] [PubMed] [Google Scholar]
- 17.Anderson R. R., Parrish J. A., “The optics of human skin,” J. Investigat. Dermatol. 77(1), 13–19 (1981). 10.1111/jid.1981.77.issue-1 [DOI] [PubMed] [Google Scholar]
- 18.Dwyer T., Prota G., Blizzard L., Ashbolt R., Vincensi M. R., “Melanin density and melanin type predict melanocytic naevi in 19–20 year olds of northern European ancestry,” Melanoma Res. 10(4), 387–394 (2000). 10.1097/00008390-200008000-00011 [DOI] [PubMed] [Google Scholar]
- 19.Jacques S. L., “Origins of tissue optical properties in the UVA, visible, and NIR regions,” in OSA TOPS on advances in optical imaging and photon migration 2, Alfano R. R., Fujimoto J. G., Eds., pp. 364–371, Optical Society of America, Washington, DC: (1996). [Google Scholar]
- 20.Fitzpatrick T. B., “The validity and practicality of sun-reactive skin types I through VI,” Arch. Dermatol. 124(6), 869–871 (1988). 10.1001/archderm.1988.01670060015008 [DOI] [PubMed] [Google Scholar]
- 21.Matts P. J., Dykes P. J., Marks R., “The distribution of melanin in skin determined in vivo,” Brit. J. Dermatol. 156(4), 620–628 (2007). 10.1111/bjd.2007.156.issue-4 [DOI] [PubMed] [Google Scholar]
- 22.Nielsen K. P., et al. , “The importance of the depth distribution of melanin in skin for DNA protection and other photobiological processes,” J. Photochem. Photobiol. B: Biol. 82(3), 194–198 (2006). 10.1016/j.jphotobiol.2005.11.008 [DOI] [PubMed] [Google Scholar]
- 23.Tadokoro T., et al. , “UV-induced DNA damage and melanin content in human skin differing in racial/ethnic origin,” FASEB J. 17(9), 1177–1179 (2003). 10.1096/fj.02-0865fje [DOI] [PubMed] [Google Scholar]
- 24.Southwood W. F. W., “The thickness of the skin,” Plastic Reconstruct. Surg. 15, 423 (1955). 10.1097/00006534-195505000-00006 [DOI] [PubMed] [Google Scholar]
- 25.Lee Y., Hwang K., “Skin thickness of Korean adults,” Surgical and Radiologic Anatomy 24(3–4), 183–189 (2002). 10.1007/s00276-002-0034-5 [DOI] [PubMed] [Google Scholar]
- 26.Gambichler T., et al. , “In vivo data of epidermal thickness evaluated by optical coherence tomography: Effects of age, gender, skin type, and anatomic site,” J. Dermatol. Sci. 44(3), 145–152 (2006). 10.1016/j.jdermsci.2006.09.008 [DOI] [PubMed] [Google Scholar]
- 27.Sandby-Moller J., Poulsen T., Wulf H. C., “Epidermal thickness at different body sites: relationship to age, gender, pigmentation, blood content, skin type and smoking habits,” Acta DermatoVenereol. 83(6), 410–413 (2003). 10.1080/00015550310015419 [DOI] [PubMed] [Google Scholar]
- 28.Krishnaswamy A., Baranoski G. V. G., “A Biophysically Based Spectral Model of Light Interaction with Human Skin,” Comput. Graph. Forum 23(3), 331–340 (2004). 10.1111/j.1467-8659.2004.00764.x [DOI] [Google Scholar]
- 29.Duda R. O., et al. , And a Scene Pattern Classification, Wiley, New York, Chichester: (2001). [Google Scholar]
- 30.Warncke D., et al. , “A neural network based approach for determination of optical scattering and absorption coefficients of biological tissue,” J. Phys.: Conf. Ser. 178(1), 012047 (2009). [Google Scholar]
- 31.Pan M. C., et al. , “Artificial neural networks-based diffuse optical tomography,” in Biomedical Optics, OSA Technical Digest (CD), paper BSuD37, Optical Society of America, Washington, DC: (2010) [Google Scholar]
- 32.Zhang L., Wang Z., Zhou M., “Determination of the optical coefficients of biological tissue by neural network,” J. Mod. Opt. 57(13), 1163–1170 (2010). 10.1080/09500340.2010.500106 [DOI] [Google Scholar]
- 33.Farrell T. J., et al. , “A CCD and neural network based instrument for the non-invasive determination of tissue optical properties in-vivo,” Proc. SPIE 2135, 117–128 (1994). 10.1117/12.175987 [DOI] [Google Scholar]
- 34.Farrell T. J., Wilson B. C., Patterson M. S., “The use of a neural network to determine tissue optical properties from spatially resolved diffuse reflectance measurements,” Phys. Med. Biol. 37(12), 2281 (1992). 10.1088/0031-9155/37/12/009 [DOI] [PubMed] [Google Scholar]
- 35.Pfefer T. J., et al. , “Reflectance-based determination of optical properties in highly attenuating tissue,” J. Biomed. Opt. 8(2), 206 (2003). 10.1117/1.1559487 [DOI] [PubMed] [Google Scholar]
- 36.Sharma D., et al. , “Evaluation of a fiberoptic-based system for measurement of optical properties in highly attenuating turbid media,” Biomed. Eng. Online 5, 49 (2006). 10.1186/1475-925X-5-49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bruulsema J. T., et al. , “Correlation between blood glucose concentration in diabetics and noninvasively measured tissue optical scattering coefficient,” Optics letters 22(3), 190–192 (1997). 10.1364/OL.22.000190 [DOI] [PubMed] [Google Scholar]
- 38.Wang Q., Shastri K., Pfefer T. J., “Experimental and theoretical evaluation of a fiber-optic approach for optical property measurement in layered epithelial tissue,” Appl. Opt. 49(28), 5309–5320 (2010). 10.1364/AO.49.005309 [DOI] [PubMed] [Google Scholar]
- 39.Cerussi A., et al. , “In vivo absorption, scattering, and physiologic properties of 58 malignant breast tumors determined by broadband diffuse optical spectroscopy,” J. Biomed. Opt. 11(4), 044005 (2006). 10.1117/1.2337546 [DOI] [PubMed] [Google Scholar]
- 40.Wang L., Jacques S. L., Zheng L., “MCML—Monte Carlo modeling of light transport in multi-layered tissues,” Computer methods and programs in biomedicine 47(2), 131–146 (1995). 10.1016/0169-2607(95)01640-F [DOI] [PubMed] [Google Scholar]
- 41.Ayers F., et al. , “Fabrication and characterization of silicone-based tissue phantoms with tunable optical properties in the visible and near infrared domain,” Proc. SPIE 6870, 687007 (2008). 10.1117/12.764969 [DOI] [Google Scholar]
- 42.Saager R., et al. , “Multilayer silicone phantoms for the evaluation of quantitative optical techniques in skin imaging,” Proc. SPIE 7567, 756706 (2010). 10.1117/12.842249 [DOI] [Google Scholar]
- 43.Firbank M., Oda M., Delpy D. T., “An improved design for a stable and reproducible phantom material for use in near-infrared spectroscopy and imaging,” Phys. Med. Biol. 40(5), 955 (1995). 10.1088/0031-9155/40/5/016 [DOI] [PubMed] [Google Scholar]
- 44.Nishidate I., Aizu Y., Mishina H., “Estimation of melanin and hemoglobin in skin tissue using multiple regression analysis aided by Monte Carlo simulation,” J. Biomed. Opt. 9(4), 700 (2004). 10.1117/1.1756918 [DOI] [PubMed] [Google Scholar]
- 45.Amouroux M., et al. , “Diffuse reflectance spectroscopy’s sensitivity to a melanic layer thickness variations: an in vitro study on skin phantoms,” Proc. SPIE 6628, 66280Y (2007). 10.1117/12.727851 [DOI] [Google Scholar]
- 46.Weber J. R., et al. , “Noncontact imaging of absorption and scattering in layered tissue using spatially modulated structured light,” J. Appl. Phys. 105(10), 102028 (2009). 10.1063/1.3116135 [DOI] [Google Scholar]
- 47.Tuchin V. V., Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis, TT38, SPIE press, Bellingham, WA: (2000). [Google Scholar]
- 48.Meglinski I. V., Matcher S. J., “Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions,” Physiol. Measur. 23(4), 741–753 (2002). 10.1088/0967-3334/23/4/312 [DOI] [PubMed] [Google Scholar]
- 49.Douven L., Lucassen G., “Retrieval of optical properties of skin from measurement and modeling the diffuse reflectance,” Proc. SPIE 3914, 312–323 (2000). 10.1117/12.388058 [DOI] [Google Scholar]
- 50.Ryan T., “Cutaneous circulation,”in Biochemistry and Physiology of the Skin, 2nd ed., Goldsmith L. A., Ed., pp. 817–877, Oxford University Press, New York: (1983). [Google Scholar]
- 51.Stenn K., “The skin,” in Cell Tissue Biology, Weiss L., Ed., pp. 541–572, Urban and Schwarzenberg, Baltimore: (1988). [Google Scholar]
- 52.van Gemert M. J., et al. , “Skin optics,” IEEE Trans. Biomed. Eng. 36(12), 1146–1154 (1989). 10.1109/10.42108 [DOI] [PubMed] [Google Scholar]
- 53.Anderson R. R., Parrish J. A., “The optics of human skin,” J. Invest. Dermatol. 77(1), 13–19 (1981). 10.1111/jid.1981.77.issue-1 [DOI] [PubMed] [Google Scholar]
- 54.Yudovsky D., Durkin A. J., “Spatial frequency domain spectroscopy of two layer media,” J. Biomed. Opt. 16(10), 107005 (2011). 10.1117/1.3640814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sandby-Moller J., Poulsen T., Wulf H. C., “Epidermal thickness at different body sites: relationship to age, gender, pigmentation, blood content, skin type and smoking habits,” ActaDerm-Venereol. 83(6), 410–413 (2003). 10.1080/00015550310015419 [DOI] [PubMed] [Google Scholar]
- 56.Lee Y., Hwang K., “Skin thickness of Korean adults,” Surg. Radiol. Anat. 24(3–4), 183–189 (2002). 10.1007/s00276-002-0034-5 [DOI] [PubMed] [Google Scholar]