Abstract
Volume-based registration (VBR) is the predominant method used in human neuroimaging to compensate for individual variability. However, surface-based registration (SBR) techniques have an inherent advantage over VBR because they respect the topology of the convoluted cortical sheet. There is evidence that existing SBR methods indeed confer a registration advantage over affine VBR. Landmark-SBR constrains registration using explicit landmarks to represent corresponding geographical locations on individual and atlas surfaces. The need for manual landmark identification has been an impediment to the widespread adoption of Landmark-SBR. To circumvent this obstacle, we have implemented and evaluated an automated landmark identification (ALI) algorithm for registration to the human PALS-B12 atlas. We compared ALI performance with that from two trained human raters and one expert anatomical rater (ENR). We employed both quantitative and qualitative quality assurance metrics, including a biologically meaningful analysis of hemispheric asymmetry. ALI performed well across all quality assurance tests, indicating that it yields robust and largely accurate results that require only modest manual correction (<10 min per subject). ALI largely circumvents human error and bias and enables high throughput analysis of large neuroimaging datasets for inter-subject registration to an atlas.
Keywords: Individual variability, PALS-B12, registration, anatomical alignment, cortex, automated
Introduction
A major challenge in functional and structural neuroimaging is to compensate for variability across individuals with respect to their underlying neuroanatomy, especially the highly convoluted cortical mantle (Galaburda et al., 1990; Thompson et al., 1997; Thompson et al., 1998). This variability is informative in its own right for understanding disease states (Csernansky et al., 2008; Van Essen et al., 2006) and normal brain function (Thompson et al., 1998) but presents a serious obstacle when attempting to make inferences about a particular cortical location across individuals. Volume-based registration (VBR) approaches, whether using linear (affine) or nonlinear algorithms, (Anderson et al., 2007a, b; Hellier et al., 2002; Woods et al., 1998a; Woods et al., 1998b) generally result in less accurate alignment of corresponding gyri and sulci (Anticevic et al., 2008; Desai et al., 2005). An alternative approach uses surface-based registration (SBR), which capitalizes on explicit surface representations of cortical convolutions in individual subjects, derived from standard structural MR scans (Fischl et al., 2002; Van Essen et al., 2001).
Several software packages provide rapid and robust generation of individual cortical surface models and offer SBR implementation based on energy minimization approaches [Energy-SBR, e.g. Freesurfer, Brain Voyager (Fischl et al., 1999a; Fischl et al., 1999b; Goebel et al., 2006)] or landmark-based approaches [Landmark-SBR, e.g. Caret (Van Essen et al., 2001)]. Efforts to quantify and compare registration quality of various SBR methods have revealed significant differences across methods but with tradeoffs that indicate advantages and disadvantages of each method (Klein et al., 2010; Pantazis et al., 2010). Along with differences in alignment quality for different SBR methods, another important methodological consideration is the desirability of automation – especially given the increasing emphasis on large datasets in both structural and functional neuroimaging studies (Biswal et al., 2010; Yarkoni et al., 2011).
Previous studies indicate Landmark-SBR outperforms affine VBR based on inter-subject alignment of identified sulci and of functional activations (Anticevic et al., 2008; Argall et al., 2006; Desai et al., 2005; Van Essen, 2005). However, the need for manual delineation of landmarks in each subject (Van Essen et al., 2001) constitutes a processing bottleneck and also a risk of rater bias across individual cases and studies. An automated landmark identification (ALI) algorithm described here greatly reduces the need for human intervention in generating the ‘Core 6’ landmarks used to register individual subjects to the human PALS-B12 atlas (Van Essen, 2005).
To evaluate the accuracy and reliability of the automatically generated landmarks, we compared the ALI results with those obtained by two newly trained human raters plus an expert neuroanatomical rater (ENR) responsible for delineating the original PALS-B12 landmarks (Van Essen, 2005). We evaluated performance differences in terms of: 1) the distance of generated landmarks (i.e. trajectory of landmark contours) relative to those from the expert rater measured in subject-specific (pre-SBR) space; 2) qualitative inspection of the spatial dispersion of landmarks both before and after SBR; 3) the 3D distance between corresponding points of individual cortical surfaces after registration to PALS-B12 atlas using expert rater landmarks versus those generated by ALI and the other two human raters; and 4) hemispheric asymmetries in sulcal depth (Van Essen, 2005; Van Essen et al., 2006) determined after SBR using different landmark sources.
Materials and Methods
Subjects
Twenty healthy right-handed young adults (7 male and 13 female; mean age, 25 years) were recruited from the Washington University Community by the Psychology Department subject coordinator. All subjects gave informed consent as approved by the Washington University IRB and were paid $25/h for their participation.
Scanning
Subjects were scanned on a 3T Allegra scanner at the Washington University Medical School. Subjects underwent both functional and structural neuroimaging data collection (Anticevic et al., 2010a; Anticevic et al., 2010b) but only structural data were analyzed here. All structural images were acquired using a sagittal magnetization-prepared radio-frequency rapid gradient-echo (MP-RAGE) 3D T1-weighted sequence (TR = 2400 ms, TE = 3.16 ms, flip = 8°; voxel size = 1 mm3).
Structural Data Preprocessing
Each T1-weighted structural volume was registered to the 711-2B atlas using a 12-parameter affine transform and re-sampled to 1 mm3 voxels (Buckner et al., 2004; Ojemann et al., 1997). Automated cortical segmentation and surface generation was carried out using FreeSurfer (Fischl et al., 2004). All pial and white matter cortical surfaces were visually inspected for accuracy; no errors were detected. For each subject, pial and white matter cortical surfaces were converted to Caret format and averaged to obtain a cortical midthickness surface (Van Essen, 2005) that was aligned to the individual-subject anatomy in 711-2B space. Surfaces were inflated and mapped to a spherical configuration with distortions reduced by multi-resolution morphing. Maps of cortical geography (gyral versus sulcal cortex) and sulcal depth were generated automatically (Van Essen, 2005).
Automated Landmark Identification (ALI)
Six anatomical landmarks (“Core 6”) originally identified on the basis of high inter-individual consistency (Van Essen, 2005) were generated using an automated algorithm. Fig. 1A illustrates these landmarks on an inflated surface of an individual left hemisphere. This includes landmarks along the fundus of the central (CeS) and calcarine (CaS) sulci and the Sylvian Fissure (SF), along the superior temporal gyrus (STG), and along dorsal and ventral portions of the boundary between cortex and the non-cortical ‘medial wall’ (MW-dors, MW-vent). Fig. 2 illustrates landmark generation framework across raters. The scripts and associated datasets for running ALI are available in Caret versions 5.62 (February 2011) and later and can be used in conjunction with the Freesurfer to Caret pipeline scripts and dataset (http://brainvis.wustl.edu/wiki/index.php/Caret:Download#Download_Freesurfer_to_PALS-B12_Pipeline_Distribution).
Figure 1.
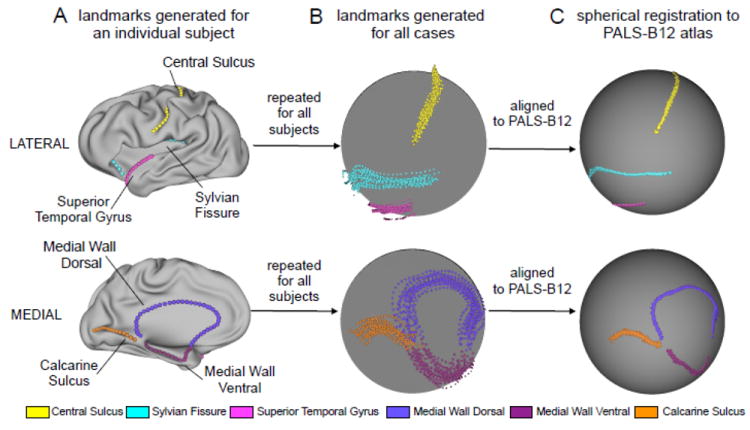
General framework of PALS-B12 registration procedure. Core 6 landmarks are displayed on the lateral (top panel) and medial (bottom panel) surface representations. (A) An individual subject example is shown with all landmarks marked on a moderately inflated surface representation for ease of visual inspection. Here results from the expert neuroanatomical rater (ENR) are shown for a single case. (B) As noted in the main text, landmarks for every subject were generated by: automated landmark identification (ALI), ALI landmark correction (ALI-Corrected), two trained raters (R1 & R2), and ENR. This yielded a total of five landmark sets across each subject (i.e. ALI, ALI-corrected, R1, R2 and ENR). This process was then repeated for all subjects. Results across subjects are shown for all five landmarks on a spherical representation (ENR results are used an exemplar). (C) All individual subject surfaces were then registered using a spherical registration algorithm to the PALS-B12 atlas (Van Essen, 2005). Results following PALS-B12 registration are shown on a standard spherical 73,730-vertex representation (again ENR results are used as an exemplar). This figure is extended to illustrate the SBR procedure across all raters (Fig. 2).
Figure 2.
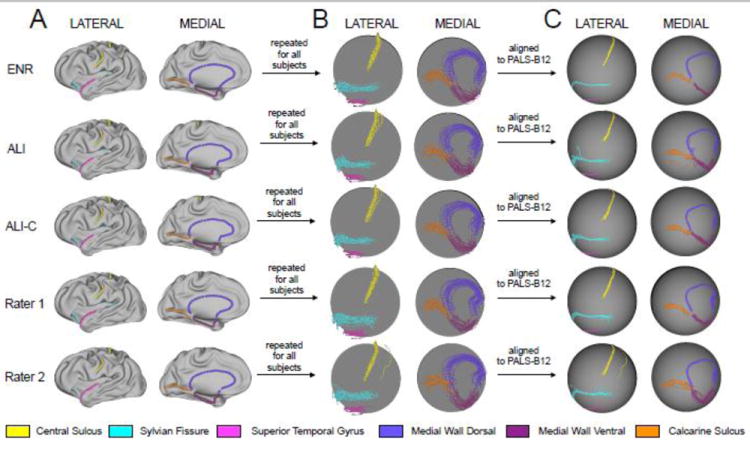
General framework of PALS-B12 registration procedure is shown across all raters. (A) Core 6 landmarks are displayed on the lateral (left panel) and medial (right panel) surface representations. Individual subject example is shown with all landmarks marked on a moderately inflated surface representation for ease of visual inspection. Example landmarks are shown for: automated landmark identification (ALI), ALI following manual correction (ALI-C), two trained human raters (R1 & R2), and an expert neuroanatomical rater (ENR). (B) This process was then repeated for all subjects. Results across subjects are shown for all five landmarks on a spherical representation for both lateral (left panel) and medial (right panel) views. (C) All individual subject surfaces were then registered using a spherical registration algorithm to the PALS-B12 atlas (Van Essen, 2005). Results following PALS-B12 registration are shown on a standard spherical 73,730-node representation for both lateral (left panel) and medial (right panel) views.
The ALI algorithm generates landmark contours using multiple sources of information about cortical shape in the individual subject, including (i) the corpus callosum (CC) segmentation extracted from Freesurfer, (ii) the midthickness and inflated surfaces, (iii) maps of mean curvature (folding) and sulcal depth, and (iv) discrete maps of sulcal vs gyral cortex (Van Essen, 2005). ALI operates on midthickness surfaces in 711-2B stereotaxic space, but automatically transforms surfaces in MNI152/305 or Talairach space to 711-2B space (see http://brainvis.wustl.edu/help/pals_volume_normalization). It also uses population-average volumetric maps of the extent of 40 cortical sulci derived from the 12 subjects contributing to the PALS-B12 atlas (Van Essen, 2005).
Hemisphere-specific Sulcal Identification
The initial step in determining the location of major sulci in each individual hemisphere is to intersect the probabilistic volumes of 40 sulci onto the individual midthickness surface by assigning each vertex the value (0 to 12) of the voxel it intersects. These values are modified by multiplying by the sulcal depth at that location (thereby weighting in favor of deeper folds) and setting the value to zero for vertices not inside the discretized sulcal map. Customized additional steps are carried out for the hippocampal fissure (HF). The resultant probabilistic times depth (PTD) map is thresholded at an empirically determined value for each sulcus. PTD values are summed for each spatially discrete cluster of vertices (with customized additional steps for the postcentral sulcus), and the clusters for each sulcus are sorted based on the summed values (PTDsum). Vertices are assigned a sulcal label if they belong to the cluster with the highest PTDsum value (or, for specified sulci, if they belong to the top two or three clusters and meet other empirically determined criteria). After this initial sulcal labeling, each region is dilated to include all neighboring vertices that are sulcal in the discretized map (but with additional empirically determined spatial constraints for the HF and CaS).
The following landmark-specific sections describe geodesic contours, most often along the midthickness surface, but sometimes on the inflated surface. This method finds the shortest path along the vertices within the region of interest (ROI), from the starting vertex to the end vertex, using Dijkstra’s Algorithm (Dijkstra, 1959). The criteria used to constrain the ROI ensure these vertices lie along the fundus of a sulcus or crown of a gyrus.
Central Sulcus (CeS)
Vertices within the probabilistic atlas mapping of the CeS whose mean curvature on the inflated surface is less than -0.1 are selected, and the most medial and inferior vertices within the ROI are found. A more restricted ROI with curvature -0.16 or less is dilated until these medial and inferior vertices are included, and a geodesic contour is drawn between them. Ends are trimmed to within 19 mm of the insular operculum at the ventral end as well as 18 mm from the medial wall at the superior end. The operculum is identified by finding the most inferior vertex within the CeS ROI, then moving inferiorly along the surface, limiting coronal movement (i.e., find local minimum along Z). A similar strategy is used to find the medial wall (move in medial direction from most superior vertex in CeS ROI, limit coronal movement).
Superior Temporal Gyrus (STG)
Vertices within the probabilistic atlas mapping of the STG are restricted to those anterior to the most inferior point of the CeS landmark. A geodesic contour is drawn between the most posterior and the most inferior (temporal pole) of the remaining vertices. Contour points are adjusted to run along the gyral ridge by displacing them along mesh vertices in a superior (positive-Z) direction while restricting the displacement in X and Y directions. When the point cannot move any further in the superior direction, it has reached the crown of the gyrus.
Sylvian Fissure (SF)
Contiguous vertices within the probabilistic atlas mapping of the SF at least 7 mm deep are intersected with vertices whose curvature on the inflated surface is less than -0.05. The inferior branch of the circular sulcus is found by identifying the most inferior of the selected vertices. For the superior branch, a geodesic contour is drawn between the most posterior vertex and the deepest vertex anterior to the temporal pole. From there, the contour continues inferiorly, to the deepest vertex within 10 mm anterior and 12 mm inferior to the previous point, then inferiorly along the fundus toward the vertex closest to -/+16.0, 12.0, -19.0 (711-2B space). It is then trimmed to 10 mm superior of this vertex. The intersection of the inferior and superior branches is found, and the superior branch’s contour is trimmed to 12 mm posterior of this intersection along the ellipsoid surface. The Sylvian contour uses a modified version of the geodesic method that gives preference to links whose vertices have lower mean curvature (aiming for the fundi of branches of the circular sulcus)
Calcarine Sulcus (CaS)
The anterior and posterior extents of a probabilistic atlas mapping of the CaS whose inflated mean curvature is less than or equal to -0.07 are found. The ROI is further restricted to inflated mean curvature below -0.16 and a geodesic contour is drawn, posterior to anterior, along vertices in the restricted ROI. This contour is extended posteriorly to the most posterior vertex in the hemisphere (i.e., occipital pole), using the less stringent ROI; then, any contour points less than 24 mm anterior to occipital pole are trimmed.
Medial Wall Dorsal
If no CC segmentation was provided, then one is segmented from the anatomical volume. Although no formal comparison was carried out, following our qualitative inspection the Freesurfer-generated aseg.mgz generated a more reliable CC segmentation than that produced by the ALI using the same anatomical volume as input. Any CC segmentation can be used, provided its filename includes “corpus” and “callosum” (case insensitive), which will cause the ALI to bypass CC segmentation and use the input volume directly. The analyses carried out herein extracted the CC from the Freesurfer aseg.mgz. Points (“foci”) are generated along the top of the CC, and then a geodesic contour is drawn on the midthickness surface connecting the vertices between these foci, but weighted toward lateral vertices, in order to draw the contours further laterally into the fundus of the callosal sulcus. Spikes in the contour are detected by finding the points along the contour closest to the foci used to draw the contour and by comparing the directions of the links to the points in the contour before and after that point. If a sharp angle is detected, a new position for that focus is estimated by searching for the closest surface vertex to a point generated by taking the current focus coordinates and moving them in the direction of the bisection of that angle. After repeating this procedure for all foci, if at least one focus changed, the contour is redrawn and the process is iteratively repeated until no better positions are identified for the foci.
Medial Wall Ventral
Vertices that intersect with the mapped probabilistic atlas representation of the hippocampal fissure (HF) on the inflated surface are intersected with vertices having a sulcal depth value of at least 10 mm. The most inferior (IHFV) and superior (SHFV) vertices are identified. The shortest path along the midthickness surface from the temporal pole (local anterior maximum) to the IHFV is found, and a periamygdaloid vertex (PAV) identified 30mm along that path from the temporal pole. A contour is generated that extends from the more superior of the SHFV or ventral splenium marker along a trajectory defining the crease of the HF posteriorly, then 12.5 mm lateral to the medial aspect of the parahippocampal gyrus up to the PAV, then to the anterior endpoint of the medial wall dorsal contour.
The dorsal and ventral contour are merged and intersected with the calcarine contour and a template frontal cut. Points are deleted near the frontal junctions, until the gap between the dorsal and ventral is 19 mm. Points near the calcarine junction are deleted to produce a 16 mm gap between the calcarine, medial wall dorsal, and medial wall ventral contours.
Landmark Evaluation
Landmark contours were resampled so that each landmark contained the same number of points in all subjects as the corresponding source contour. For each landmark point, the normal range of variability in its 3D position in individual midthickness surfaces was determined using the 12 subjects that contributed to the PALS-B12 atlas. Following ALI in any given subject, each landmark contour was evaluated to determine the percentage of contour points that lie within two standard deviations of the corresponding PALS-B12 contour points. An automated script reports the average “overlap percentage” for each landmark contour. It also generates images of landmark trajectories relative to the population average, to facilitate inspection of contours whose overlap percentages are low (less than 95%). All images and metrics were inspected by two trained raters (AA and DD). Manual edits were made when warranted, based on criteria used for manual landmark delineation (see below), resulting in a set of ‘ALI-Corrected’ landmarks. All major ALI errors were reliably flagged by the quality assurance measures (i.e. every instance requiring major manual correction following ALI). The total time needed to perform manual evaluation and editing was less than 2 hours total for all 20 subjects (less than 3 min per hemisphere on average).
Manual Landmark Generation
The trained raters (R1 & R2) were trained concurrently in two 3-hour sessions. All human raters (R1, R2 and ENR) independently generated ‘Core 6’ landmark for each subject using the same criteria (http://brainvis.wustl.edu/help/landmarks_core6/landmarks_core6.html/) (Van Essen, 2005). The two raters (R1, R2) were graduate students who were trained by the ENR in less than two days. ALI corrections were made by a different rater (AA) than those who manually drew the landmarks.
Surface-based Registration (SBR)
Landmark-SBR was carried out by projecting landmarks to the individual’s spherical surface, then deforming the individual sphere so that its landmarks were aligned to the PALS-B12 atlas target landmarks, coupled with distortion reduction in the regions between landmarks (Van Essen, 2005) (Fig. 1). Each subject’s midthickness surface was re-sampled to a standard ‘74k’ mesh containing 73,730 vertices (Saad et al., 2005). An associated ‘deformation map’ file allowed additional datasets (e.g., landmark contours generated by other raters – see below) to be mapped from the individual to the atlas surface. Surface-based registration was carried out separately for all five sets of generated landmarks (i.e. ALI and ALI-Corrected, R1, R2 and ENR).
ALI versus Manual Landmark Comparisons
Five analyses were used to evaluate the quality of cortical landmark delineation for ALI relative to other raters:
Using the resampled landmark contours represented on each individual’s midthickness surface, the Euclidean distance was computed between each ENR landmark point and the corresponding point in the ALI, ALI-corrected, R1, and R2 landmarks. These distances were averaged across all points in each landmark contour, yielding four average distance measures (ENR versus R1, R2, ALI, and ALI-corrected) for each of six landmarks. The larger the average distance, the greater the disparity for that landmark relative to that drawn by the ENR. Differences across raters were analyzed using a factorial ANOVA design (see bellow).
All landmarks were inspected visually for dispersion on the midthickness, inflated and spherical surface configurations prior to Landmark-SBR. This provided a qualitative measure of differences between landmark contour trajectories in pre-SBR format.
After Landmark-SBR of each individual to PALS-B12 using the ENR landmarks, the resultant deformation map was applied to the ALI, ALI-corrected, R1 and R2 landmark contours. This provided a sensitive qualitative measure of residual differences between landmark contour trajectories. If each rater’s landmarks were identical to those of the ENR then the results following SBR would show no dispersion on visual inspection.
Each hemisphere’s midthickness surface was resampled to the PALS 74k standard mesh after registration using all five sets of landmarks (ALI, ALI-corrected, R1, R2, and ENR). A map of 3D coordinate differences was computed between corresponding vertices in the ENR-based midthickness surface and each of the other four midthickness surfaces. These maps were averaged across all 20 individuals, separately for the left and right hemispheres. This provided spatial maps of the impact of landmark trajectory differences on the identification of SBR-based geographic correspondences across the entire hemisphere. This approach is analogous to the approach in step 3, but captures the deviation in terms of 3D distances, across subjects, for each rater relative to the ENR across the entire cortical sheet. That is, we computed the Euclidean distance for a given rater for each cortical vertex relative to ENR for each subject – an approach that afforded inspection of the spatial location along the cortical sheet where a given rater deviated from the ENR.
We analyzed hemisphere asymmetries in sulcal depth for the 20 subjects separately for all five sets of landmarks in order to assess the impact of rater differences on a known structural asymmetry (Van Essen et al., 2006). For surfaces registered by each set of landmarks, a paired t-test of sulcal depth was carried out using surface-based Threshold-Free Cluster Enhancement (TFCE) (Hill et al., 2010) and 5000 iterations using the hemisphere asymmetry as the dependent measure. Surface area measurements of the resulting significant clusters were computed on the PALS-B12 average midthickness surface, then adjusted by the average distortion between individual and population-average midthickness surfaces (Van Essen, 2005). Results across raters were compared both qualitatively (i.e. visual inspection) as well as quantitatively by examining the surface of resulting significant clusters.
Results
Landmark Distance Quantification
Fig. 3 shows the average distance (separation) between ENR landmark points and each rater’s landmarks, grouped by landmark for the left hemisphere (top) and right hemisphere (bottom). For the MW-dors and CeS, average distances were only ~1 mm and showed minimal inter-rater differences. At the other extreme, average differences were larger and more variable for the MW-vent. To test for statistical significance of these differences, we computed repeated-measures ANOVA with Rater (4 levels - ALI, ALI-corrected, R1, R2) × Landmark (6 levels – CeS, CaS, MW-dors, MW-vent, STG, SF) × Hemisphere (left versus right) as factors for distance from ENR as the dependent measures. The ANOVA results (Fig. 3A-B) revealed a significant main effect of Landmark [F(5,95)=86.6, p<0.001], main effect of Rater [F(3,57)=47.5, p<0.001], but no main effect of Hemisphere [F(1,19)= 0.61, p=0.44, NS]. No term involving Hemisphere reached significance, indicating similar results across raters and landmarks irrespective of hemisphere. The ANOVA results also revealed a highly significant Rater × Landmark interaction [F(1,285)=31.5, p<0.001], indicating that performance relative to ENR differed across raters as a function of landmark location. This is partly due to the high degree of variability between raters R1 and R2 (Fig. 3). The ALI and ALI-Corrected results differed minimally from one another and were similar to the average of the R1 and R2 results for most landmarks, but were slightly worse for the STG and SF. For three landmarks (CaS, CeS, and MW-dors), ALI performed as well or nearly as well as raters R1 and R2. For two landmarks (STG and SF), ALI was slightly worse, but the differences were less than 2 mm on average. For the MW-vent landmark, ALI performed worse than R1 by 2 – 3 mm on average, but was better than R2 by 1 – 2 mm on average. The impact of these differences on overall inter-subject alignment quality is addressed below.
Figure 3.
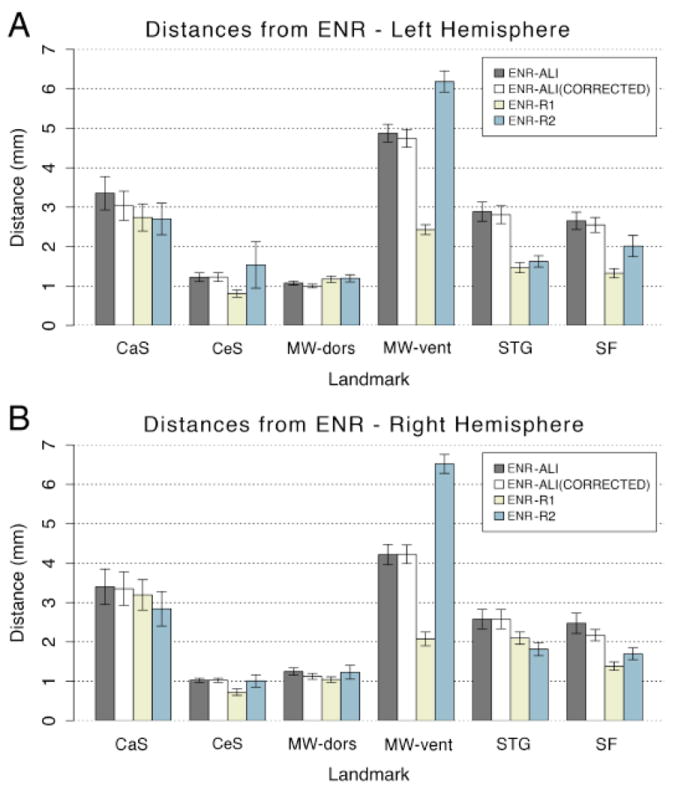
Distances in mm from the expert neuroanatomical rater (ENR) are shown across all raters (ALI – automated landmark identification, R1 – Rater 1, R2 – Rater 2) and all landmarks (central suclus – CeS, calcarine sulcus - CaS, dorsal component of the medial wall – MW-dors, ventral component of the medial wall – MW-vent, superior temporal gyrus - STG, and sylvian fissure – SF). Results are shown for both (A) left and (B) right hemispheres. All distances were computed prior to SBR to avoid potentially obscuring differences post registration to the PALS-B12 atlas.
Landmark Dispersion on Spherical Maps
Fig. 4 shows the spherical landmark trajectories for the left hemisphere of all 20 subjects generated by each of the raters and methods, illustrating the degree of individual variability in landmark trajectories prior to SBR. Fig. 4A shows the landmarks drawn by the ENR. The dispersion for each landmark reflects normal individual variability prior to SBR; it is comparable in magnitude to the landmarks drawn by ENR for the 12 individual subjects contributing to the PALS-B12 atlas [cf. Fig. 2F, I from (Van Essen, 2005)]. Alignment is best for the CeS (yellow), reflecting the fact that the CeS was used for rigid-body rotation of all individual spheres to the ‘spherical standard’ configuration. Figure 4B-E shows results for landmarks generated by ALI, ALI-corrected, and raters R1 and R2. The dispersion of landmark trajectories is in general similar to that for the ENR, but for a few landmark/rater combinations it is modestly greater. Of particular note are occasional outliers, such as an incorrectly drawn CeS (yellow) by Rater 2 for one subject and an incorrect CaS (orange) for one subject in ALI (Fig. 4B) that was corrected in ALI-Corrected (Fig. 4C). This qualitative inspection illustrates that the spatial variability of generated landmarks following ALI and ALI-Corrected closely match those of the ENR. However, as with the quantitative distance measure (Fig. 3), there is considerable variability in the dispersion of landmark trajectories for the two human raters relative to the ENR. Results were similar for the right hemisphere (not shown).
Figure 4.
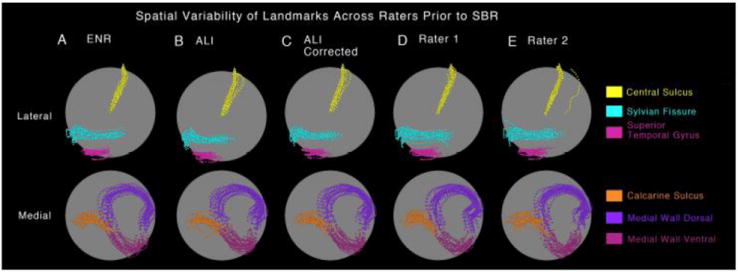
Spatial variability of ‘Core 6’ landmarks prior to SBR is shown on a spherical configuration for the (A) expert neuroanatomical rater (ENR), (B) automated landmark identification (ALI), (C) ALI-Corrected, (D) Rater 1, and (E) Rater 2. The top panel shows the lateral view with central sulcus, sylvian fissure and superior temporal gyrus displayed in yellow, cyan and pink colors respectively. The bottom panel shows the medial view with calcarine sulcus, medial wall dorsal segment and medial wall ventral segment displayed in orange, dark and light purple respectively. The ‘clouds’ of variability allow for qualitative inspection of similarity across raters prior to surface registration to the PALS-B12 atlas.
For the results shown in Fig. 5, each individual hemisphere was registered to the PALS-B12 atlas using the ENR landmarks, resulting in accurate alignment of the ENR landmarks for each subject (Fig. 5A). The four sets of independently generated landmarks (ALI, ALI-Corrected, R1 and R2) were then registered to the atlas sphere using the deformation map generated by the ENR registration (see Methods). As expected, the dispersion of landmark contours is much smaller than the pre-SBR distribution in the preceding figure. The manual editing of the ALI landmarks (~2h total for all cases) not only corrected the rare errors that were large (i.e., the outliner CaS landmark) but also reduced the more modest dispersion in the SF, MW-dors, and MW-vent landmarks (Fig. 5C versus 5B), indicating consistency with the ENR landmarks. Because most corrections involved only minor aspects along part of the landmark, there was little impact on the average distance measures (ALI versus ENR and ALI-Corrected versus ENR in Fig. 3) but these minor corrections nonetheless achieved a better match to the ENR.
Figure 5.
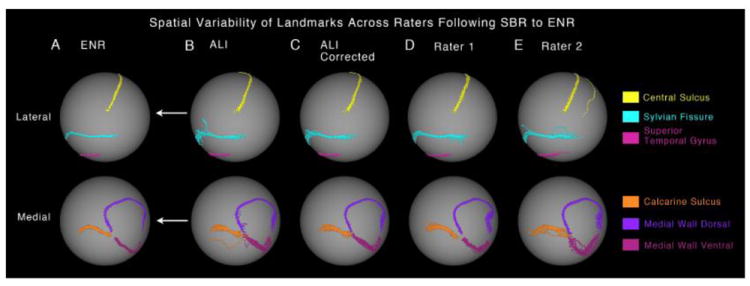
Spatial variability of ‘Core 6’ landmarks following SBR to the PALS-B12 atlas is shown on a spherical configuration for the (A) expert neuroanatomical rater (ENR), (B) automated landmark identification (ALI), (C) ALI-Corrected, (D) Rater 1, and (E) Rater 2. The arrows indicate that all raters were registered to the PALS-B12 atlas using the ENR deformation parameters. The top panel shows the lateral view with central sulcus, sylvian fissure and superior temporal gyrus displayed in yellow, cyan and pink colors respectively. The bottom panel shows the medial view with calcarine sulcus, medial wall dorsal segment and medial wall ventral segment displayed in orange, dark and light purple respectively. The ‘clouds’ of variability allow for qualitative inspection of similarity and differences in landmark drawing between ENR and each of the other raters. If a given rater achieved perfect precision relative to the ENR for a given landmark, then the ‘cloud’ of variability would be minimal for that landmark and would precisely match the ENR results.
3D Displacements for SBR Using Different Landmarks
By carrying out SBR to the PALS-B12 atlas for each subject using all five sets of landmarks (ALI, ALI-corrected, R1, R2, and ENR), we obtained five versions of each individual midthickness surface represented on the 74k mesh (see Fig. 2). We then computed the 3D (Euclidean) distance between each surface vertex on the ENR-registered midthickness surface to the corresponding vertex in each of the other midthickness surfaces. These 3D distances (absolute values) were then averaged across all subjects in order to generate an average coordinate-difference map for each landmark source compared to the ENR based surfaces. Fig. 6 shows the average coordinate-difference across all four raters relative to the ENR. This provided a cortex-wide assessment of the spatial impact of landmark variability relative to the ENR. Consistent with the preceding analyses, the greatest difference was observed between the maps for R1 and R2, particularly in anterior cortical regions for the left hemisphere (Fig. 6C versus 6D) and right hemisphere (not shown). For R1 the average deviation from the ENR exceeded 10 mm in some prefrontal locations, indicating that inconsistencies in human raters can result in substantial variability in SBR even on the same dataset. Indeed, although R1 performs well by most of the other measures, the 3D distance map illustrates the impact of inter-rater biases when comparing the ENR and R1 medial wall dorsal contours near the frontal junction (also see Fig. 3). In contrast, most notable areas of deviation for the ALI and ALI-Corrected results are in medial occipital cortex around the CaS landmark. Inspection of cases where the coordinate difference between ENR and ALI was large revealed that in some cases, where the occipital pole is offset from the posterior CaS contour along the x or z-axis, the ENR extended the CaS contour too far caudally. This was mainly because Euclidean distance was used in lieu of the desired metric of distance only along the y-axis. In contrast, ALI is more reliable in setting the posterior limit of the CaS landmark to 24 mm anterior to the occipital pole. In that respect, the differences between ALI and ENR landmarks in large measure reflect greater fidelity of the ALI method.
Figure 6.
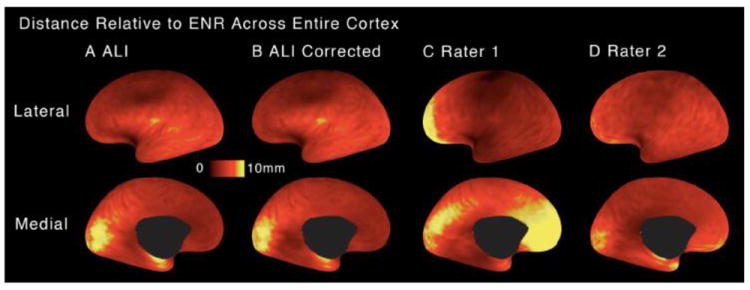
Mean 3D cortical distances following SBR to the PALS-B12 atlas is shown on a flattened surface configuration relative to the expert neuroanatomical rater (ENR) for: (A) automated landmark identification (ALI), (B) ALI-Corrected, (C) Rater 1, (D) Rater 2. Brighter colors mark areas of greater mean 3D distance from the ENR. Critically, results illustrate deviations for each rater from ENR once SBR was carried out separately for landmarks generated by each rater (illustrated in Fig. 2).
Hemispheric Asymmetry
Human cortex has prominent hemispheric asymmetries in the vicinity of the Sylvian Fissure and superior temporal sulcus (STS) that can be quantified using maps of sulcal depth in the two hemispheres (Van Essen et al., 2006). If inter-subject alignment were eroded by biases or inconsistencies in landmark delineation, it would presumably reduce the sensitivity to detect consistent and significant sulcal depth asymmetries in a sample of subjects. To address this issue, a paired t-statistic map for left-versus-right sulcal depth in the 20 subjects was computed for the five sets of landmark delineated in this study (Fig. 7). Significant clusters revealed by the Threshold-Free Cluster Estimate (TFCE) method are outlined in black (see Methods). The total surface area above significance was greater for the ALI and ALI-corrected (3354.35 and 3152.95 mm2) than for any of the other three methods (2262.89, 1508.95, and 1459.60 respectively for ENR, R1, and R2). Overall, the pattern of asymmetry was qualitatively similar across ALI, ALI-Corrected, and ENR. The size of the ALI clusters suggests that the automated process produced results that are at least as sensitive as ENR in inter-subject alignment in this region. The results for R1 and R2 showed smaller asymmetry clusters, suggestive of poorer inter-subject alignment.
Figure 7.
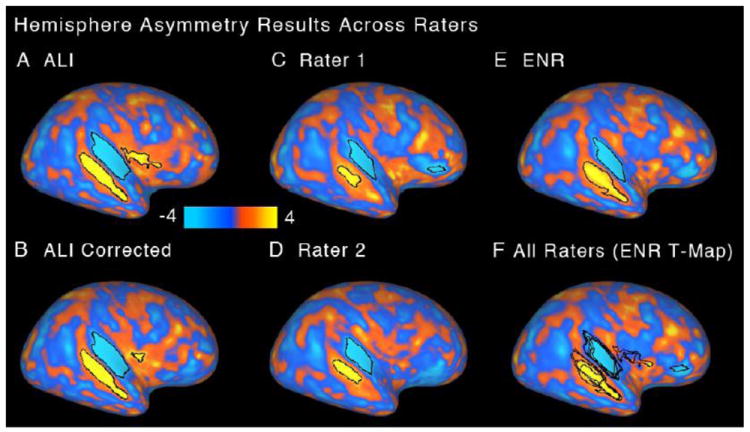
Hemisphere asymmetry results are shown as t-statistic maps for (A) automated landmark identification (ALI), (B) ALI-Corrected, (C) Rater 1, (D) Rater 2, and (E) expert neuroanatomical rater (ENR). Significant asymmetry clusters are highlighted in black borders. (F) Results of all raters are shown overlaid on the ENR-generated t-map. As in Fig. 6, results illustrate hemisphere asymmetry results for each rater once SBR was carried out separately for landmarks generated by each rater (illustrated in Fig. 2).
Discussion
The present study evaluated the consistency of ALI relative to two trained human raters and an expert neuroanatomical rater using multiple estimates of ALI performance. Our results indicate robust performance by ALI, particularly when coupled with manual editing. We also demonstrate significant inconsistencies across human raters in landmark identification.
ALI yielded consistent results in a population of healthy adult subjects, matching ENR results across multiple measures. In the regions where ALI and ENR differ, an important question is which set of landmarks produces better inter-subject alignment for biologically meaningful analyses. Our tests of hemispheric asymmetries in sulcal depth indicate that ALI performed as sensitively as ENR and perhaps even better in some areas, at least for the landmarks on the lateral aspect of the hemisphere (of note, greater significant extent does not guarantee biological significance). In the calcarine sulcus, ALI and ENR landmarks differ significantly. One aspect of delineating the CaS sulcus landmark involves setting its posterior termination 24 mm anterior to the occipital pole, and this appears to be executed more reliably by the ALI method (i.e., find the most posterior node in the hemisphere, subtract 24 mm along the y axis, and trim the contour beyond that point). This probably also resulted in ALI outperforming ALI-corrected in this region: If the ENR and corrections rater chose different reference points on the occipital pole, e.g., with substantial delta along the x or z axes, it would affect distance measurements used to trim contour points. Thus, unless the ALI has deviated from the fundus of the CaS, the corrections rater should not second-guess the ALI in this region.
A reasonable question is how much ALI differs from ALI-corrected (i.e., is it worth the effort to correct the contours, particularly for large sample sizes). We have not carried out a large-scale test comparing ALI versus ALI-corrected, but we have identified cases where a contour is altogether missing (this happens infrequently using Freesurfer-generated CC segmentations). In the event this occurs, the alternatives are to draw the contour manually or to exclude the subject from an analysis. Furthermore, in situations were a contour falls a few mm short of its proper termination it represents less of a problem than if it falls many mm short of it. Hence, we advise that the necessary corrections to the ALI landmarks are carried out, which can be accomplished after a modest training effort. In addition, we would like to acknowledge that in the present study we used a single ENR. That is, there may be subtle but important differences even across ENR, which may produce differences in findings of ALI accuracy. Nevertheless, it is worth noting that ALI compared well relative to more naïve raters.
Some software packages such as FreeSurfer and BrainVoyager support high-throughput processing of surfaces using fully automated segmentation, surface generation, and SBR (Fischl et al., 2002; Fischl et al., 2004; Goebel et al., 2006). While this is advantageous in many respects, there are some shortcomings in these situations. Overt misregistration of sulci and gyri sometimes occurs, even in regions like the central sulcus that are relatively consistently folded (Pantazis et al., 2010). A straightforward process for identifying and correcting misregistration errors is currently lacking in these software packages. In contrast, ALI by design is not fully automated. Instead, ALI provides a manual editing stage, which is designed to be straightforward, quick to carry out and requires only modest neuroanatomical expertise. Our results indicate substantial inconsistency across human raters in primary landmark identification. Therefore, it is more efficient to use human raters for editing rather than primary landmark identification purposes. This can reduce gross landmark identification errors and is likely to produce more consistent results across studies. These issues are increasingly important as neuroimaging datasets rapidly expand, analyses across datasets and centers increasingly become a reality (Biswal et al., 2010), and consistency in longitudinal and multi-center clinical studies is paramount (Potkin et al., 2008).
An important unresolved issue is which type of SBR methodology (e.g. Landmark-SBR versus Energy-SBR) achieves maximal inter-subject alignment, especially in regions of high folding variability. Pantazis et al. (2010) compared FreeSurfer, BrainVoyager, and their 26-landmark registration method applied to the same group of subjects, using sulcal landmarks and geographic regions of interest to assess inter-subject alignment. They found that each method had advantages and disadvantages, depending on the region and the specific measure used; FreeSurfer performed better in some respects, but both FreeSurfer and BrainVoyager were susceptible to crude registration errors. Van Essen and colleagues (Van Essen et al., 2011) compared registration of individual hemispheres to a common target using (i) initial registration to FreeSurfer’s fsaverage atlas (Energy-SBR) vs. (ii) initial registration to PALS-B12 (Landmark-SBR), in both cases followed by inter-atlas registration to the ‘fs_LR’ surface-based atlas (using Landmark-SBR). The differences between registration methods were modest in most regions but were substantial (> 2 cm) in some regions, but do not reveal which SBR method is more effective in reducing inter-subject variability. Additional insights could be gained by comparing SBR methods using data from task-activation fMRI paradigms [e.g., (Anticevic et al., 2008; Sabuncu et al., 2010)], resting-state fMRI analyses, or alternative modalities such as myelin maps (Glasser and Van Essen, 2011). Another issue is that alignment consistency for a given algorithm may differ in the cortex of individuals with brain disease or disorders (Anticevic et al., 2008; Csernansky et al., 2008). For instance, prior work has demonstrated a clear advantage for landmark-based SBR when applied to both anatomical and functional MRI data in patients diagnosed with schizophrenia (Anticevic et al., 2008). However, no study has evaluated whether different SBR methods produce similar degree of improvement in different clinical populations.
In conclusion, our analysis indicates that automated landmark identification coupled with manual editing is recommended over purely manual delineation of landmark contours when registering data to the human PALS-B12 atlas. Additional studies are needed to ascertain the relative strengths and limitations of landmark-based versus energy-based SBR algorithms in compensating for individual variability in neuroanatomy.
Acknowledgments
We would like to acknowledge Andrea Lui, Heather Wilkins and Erin Reid for excellent support with data analyses. This work was supported by NIMH grant R01 MH 60974 to DVE and NIMH grant R01 MH 066031 for DMB.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson JLR, Jenkinson M, Smith SM. Non-linear optimisation. FMRIB technical report TR07JA1 2007a [Google Scholar]
- Anderson JLR, Jenkinson M, Smith SM. Non-linear registration, aka spatial normalisation. FMRIB technical report TR07JA2 2007b [Google Scholar]
- Anticevic A, Dierker DL, Gillespie SK, Repovs G, Csernansky JG, Van Essen DC, Barch DM. Comparing surface-based and volume-based analyses of functional neuroimaging data in patients with schizophrenia. Neuroimage. 2008;41:835–848. doi: 10.1016/j.neuroimage.2008.02.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anticevic A, Repovs G, Barch DM. Resisting Emotional Interference: Brain Regions Facilitating Working Memory Performance During Negative Distraction. Cognitive, Affective, & Behavioral Neuroscience. 2010a;10:159–173. doi: 10.3758/CABN.10.2.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anticevic A, Repovs G, Shulman GL, Barch DM. When less is more: TPJ and default network deactivation during encoding predicts working memory performance. Neuroimage. 2010b;49:2638–2648. doi: 10.1016/j.neuroimage.2009.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Argall BD, Saad ZS, Beauchamp MS. Simplified intersubject averaging on the cortical surface using SUMA. Human brain mapping. 2006;27:14. doi: 10.1002/hbm.20158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal BB, Mennes M, Zuo X-N, Gohel S, Kelly C, Smith SM, Beckmann CF, Adelstein JS, Buckner RL, Colcombe S, Dogonowski A-M, Ernst M, Fair D, Hampson M, Hoptman MJ, Hyde JS, Kiviniemi VJ, Kötter R, Li S-J, Lin C-P, Lowe MJ, Mackay C, Madden DJ, Madsen KH, Margulies DS, Mayberg HS, McMahon K, Monk CS, Mostofsky SH, Nagel BJ, Pekar JJ, Peltier SJ, Petersen SE, Riedl V, Rombouts SARB, Rypma B, Schlaggar BL, Schmidt S, Seidler RD, Siegle GJ, Sorg C, Teng G-J, Veijola J, Villringer A, Walter M, Wang L, Weng X-C, Whitfield-Gabrieli S, Williamson P, Windischberger C, Zang Y-F, Zhang H-Y, Castellanos FX, Milham MP. Toward discovery science of human brain function. Proc Natl Acad Sci USA. 2010;107:4734–4739. doi: 10.1073/pnas.0911855107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Head D, Parker J, Fotenos AF, Marcus D, Morris JC, Snyder AZ. A unified approach for morphometric and functional data analysis in young, old, and demented adults using automated atlas-based head size normalization: reliability and validation against manual measurement of total intracranial volume. Neuroimage. 2004;23:724–738. doi: 10.1016/j.neuroimage.2004.06.018. [DOI] [PubMed] [Google Scholar]
- Csernansky JG, Gillespie SK, Dierker DL, Anticevic A, Wang L, Barch DM, Van Essen DC. Symmetric abnormalities in sulcal patterning in schizophrenia. Neuroimage. 2008;43:440–446. doi: 10.1016/j.neuroimage.2008.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai R, Liebenthal E, Possing ET, Waldron E, Binder JR. Volumetric vs. surface-based alignment for localization of auditory cortex activation. Neuroimage. 2005;26:1019–1029. doi: 10.1016/j.neuroimage.2005.03.024. [DOI] [PubMed] [Google Scholar]
- Dijkstra EW. A note on two problems in connexion with graphs. Numerische Mathematik. 1959;1:269–271. [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M. Whole Brain Segmentation Automated Labeling of Neuroanatomical Structures in the Human Brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJW, Makris N, Ségonne F, Quinn BT, Dale AM. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004;23(Suppl 1):S69–84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999a;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human brain mapping. 1999b;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galaburda AM, Rosen GD, Sherman GF. Individual variability in cortical organization: its relationship to brain laterality and implications to function. Neuropsychologia. 1990;28:529–546. doi: 10.1016/0028-3932(90)90032-j. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Van Essen DC. Mapping Human Cortical Areas In Vivo Based on Myelin Content as Revealed by T1- and T2-Weighted MRI. Journal of Neuroscience. 2011;31:11597–11616. doi: 10.1523/JNEUROSCI.2180-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goebel R, Esposito F, Formisano E. Analysis of functional image analysis contest (FIAC) data with brainvoyager QX: From single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Human brain mapping. 2006;27:392–401. doi: 10.1002/hbm.20249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellier P, Ashburner J, Corouge I, Barillot C, Friston K. Inter subject registration of functional and anatomical data using SPM. Medical Image Computing and Computer-assisted Intervention — MICCAI. 2002;2489:590–597. [Google Scholar]
- Hill J, Dierker D, Neil J, Inder T, Knutsen A, Harwell J, Coalson T, Van Essen DC. A Surface-Based Analysis of Hemispheric Asymmetries and Folding of Cerebral Cortex in Term-Born Human Infants. Journal of Neuroscience. 2010;30:2268–2276. doi: 10.1523/JNEUROSCI.4682-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A, Ghosh SS, Avants B, Yeo BTT, Fischl B, Ardekani B, Gee JC, Mann JJ, Parsey RV. Evaluation of volume-based and surface-based brain image registration methods. Neuroimage. 2010;51:214–220. doi: 10.1016/j.neuroimage.2010.01.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ojemann J, Akbudak E, Snyder A, McKinstry R, Raichle M, Conturo T. Anatomic localization and quantitative analysis of gradient refocused echo-planar fMRI susceptibility artifacts. Neuroimage. 1997;6:156–167. doi: 10.1006/nimg.1997.0289. [DOI] [PubMed] [Google Scholar]
- Pantazis D, Joshi A, Jiang J, Shattuck DW, Bernstein LE, Damasio H, Leah RM. Comparison of landmark-based and automatic methods for cortical surface registration. Neuroimage. 2010;49:2479–2493. doi: 10.1016/j.neuroimage.2009.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potkin SG, Turner JA, Brown GG, McCarthy G, Greve DN, Glover GH, Manoach DS, Belger A, Diaz M, Wible CG, Ford JM, Mathalon DH, Gollub R, Lauriello J, O’Leary D, van Erp TG, Toga AW, Preda A, Lim KO FBIRN. Working memory and DLPFC inefficiency in schizophrenia: The FBIRN study. Schizophrenia bulletin. 2008;35:19–31. doi: 10.1093/schbul/sbn162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Reynolds RC, Argall B, Japee S, Cox RW. SUMA: an interface for surface-based intra- and inter-subject analysis with AFNI. 2005;1512:1510–1513. [Google Scholar]
- Sabuncu MR, Singer BD, Conroy B, Bryan RE, Ramadge PJ, Haxby JV. Function-based Intersubject Alignment of Human Cortical Anatomy. Cereb Cortex. 2010;20:130–140. doi: 10.1093/cercor/bhp085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson PM, MacDonald D, Mega MS, Holmes CJ, Evans AC, Toga AW. Detection and mapping of abnormal brain structure with a probabilistic atlas of cortical surfaces. J Comput Assist Tomogr. 1997;21:567–581. doi: 10.1097/00004728-199707000-00008. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Moussai J, Zohoori S, Goldkorn A, Khan AA, Mega MS, Small GW, Cummings JL, Toga AW. Cortical variability and asymmetry in normal aging and Alzheimer’s disease. Cereb Cortex. 1998;8:492–509. doi: 10.1093/cercor/8.6.492. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. A Population-Average, Landmark- and Surface-based (PALS) atlas of human cerebral cortex. Neuroimage. 2005;28:635–662. doi: 10.1016/j.neuroimage.2005.06.058. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Dierker D, Snyder AZ, Raichle ME, Reiss AL, Korenberg J. Symmetry of cortical folding abnormalities in Williams syndrome revealed by surface-based analyses. Journal of Neuroscience. 2006;26:5470–5483. doi: 10.1523/JNEUROSCI.4154-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analyses of cerebral cortex. Journal of the American Medical Informatics Association. 2001;8:443–459. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Glasser MF, Dierker D, Harwell J, Coalson T. Parcellations and hemispheric asymmetries of human cerebral cortex analyzed on surface-based atlases. Cereb Cortex in revision. 2011 doi: 10.1093/cercor/bhr291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. general methods and intrasubject, intramodality validation. Journal of Computer Assisted Tomography. 1998a;22:139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Watson JDG, Sicotte NL, Mazziotta JC. Automated image registration: II. intersubject validation of linear and nonlinear models. Journal of Computer Assisted Tomography. 1998b;22:153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. Large-scale automated synthesis of human functional neuroimaging data. Nature Methods. 2011;8:665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]


