Genotype–phenotype mapping in a post-GWAS world

Abstract

Understanding how metabolic reactions, cell signaling, and developmental pathways translate the genome of an organism into its phenotype is a grand challenge in biology. Genome-wide association studies (GWAS) statistically connect genotypes to phenotypes, without any recourse to known molecular interactions, whereas a molecular biology approach directly ties gene function to phenotype through gene regulatory networks (GRNs). Using natural variation in allele-specific expression, GWAS and GRN approaches can be merged into a single framework via structural equation modeling (SEM). This approach leverages the myriad of polymorphisms in natural populations to elucidate and quantitate the molecular pathways that underlie phenotypic variation. The SEM framework can be used to quantitate a GRN, evaluate its consistency across environments or sexes, identify the differences in GRNs between species, and annotate GRNs de novo in non-model organisms.

Why build a genotype–phenotype map?

One vision of the future is an era of ‘personal genomics’, wherein ‘-omic’ data (e.g., genome sequence, methylation, histone acetylation, expression, alternative splicing, protein abundances, and metabolites) will predict the disease susceptibility of an individual. This requires a molecular mechanistic description of how genetic variation leads to molecular phenotypes and, ultimately, disease. How to develop such predictive models is an open question, with much work remaining to formulate the basic intellectual framework and statistical/computational methodologies needed to interpret the plethora of data available [1]. Understanding the functional consequences of naturally occurring mutations in model organisms is a fast and cost-effective way of constructing mechanistic models and verifying their predictions.

Disease-associated alleles are increasingly being identified in non-coding regions of the genome, and these alleles likely affect gene regulation [2,3]. A fundamental challenge is to discern why some polymorphisms in regulatory regions lead to altered gene expression whereas others do not. However, even once a regulatory variant has been identified, it is not immediately obvious how it affects the phenotype. Furthermore, functional polymorphisms typically segregate in natural populations at low frequency, and therefore even if the effects of all polymorphisms were annotated it would not be practical to develop separate treatment strategies individually for thousands of polymorphisms. Truly significant translational advances will only take place once the effects of regulatory polymorphisms are understood as components of GRNs. Then approaches to counterbalance GRN malfunctions may be developed that can compensate for numerous regulatory polymorphisms. The past several years have seen tremendous progress in the elucidation of GRNs, including networks that encompass thousands of elements [1]. What remains unclear, however, is how to validate these GRNs, because traditional gene-by-gene molecular studies are not feasible at this scale.

It is our opinion that the way forward is through the annotation and quantitation of GRNs through analysis of allele-specific expression in large panels of heterozygous genotypes. In model organisms, generating heterozygous individuals is simple, for instance by crossing isogenic genotypes derived from natural alleles with a tester genotype (we refer to this as ‘common reference design’). Similar approaches may be developed for naturally heterozygous non-model organisms, including humans, although the statistical models would necessarily become more complex [4–7]. Here we outline this approach using the sex-determination (SD) pathway in flies and the flowering-time (FT) pathway in plants for illustration.

Using allele-specific expression (ASE) to quantitate known GRNs

ASE in first-generation heterozygotes (F1s) can be used to partition cis and trans effects (Figure 1a). Cis effects are due to regulatory polymorphisms occurring between alleles of a gene. They manifest as allele-specific expression within heterozygous individuals. Trans effects arise from the regulatory interactions between genes and are detected through shared expression deviation of both alleles within an F1 genotype from an average allele expression in a whole panel of genotypes [8–13]. Here we consider the common reference design (Figure 1a), and we assume that cis and trans effects are statistically independent of each other (i.e., no cis by trans interactions). Each F1 genotype i (i = 1, …, n) has two alleles per gene: the tester allele t and the varying allele i. Note that the i^th allele is found in the i^th F1 genotype. RNAseq reads that capture one or more polymorphisms can be assigned to the allele of origin. For a given gene, we consider the expression level E_ii of allele i in F1 genotype i. The expression of an allele can be written in terms of deviations C due to cis regulatory mutations at the allele, and T due to trans effects from genes that are upstream in the GRN such that: E_ii = μ + C_i + (T_i + T_t)/2; and that of the tester allele in the same F1 genotype as: E_ti = μ + C_t + (T_t + T_i)/2; where μ is the average expression level for all alleles. For each allele, the cis and trans effects are deviations from the population mean, and these deviations sum to zero: ${\sum }_{i=1}^n{C}_i=0$ and ${\sum }_{i=1}^n{T}_i=0$. The expected difference (E_ti – E_ii) between the expression of alleles within an F1 genotype, over the entire population of n heterozygous genotypes, is ${\sum }_{i=1}^n\frac{E_{ti}-E_{ii}}{n}$, and substituting the equations above, this can be rewritten as ${\sum }_{i=1}^n\frac{C_t-C_i}{n}=C_t$. The cis effect of allele i can now be calculated as ${\widehat{C}}_i=\widehat{E_{ii}}-\widehat{E_{ti}}+\widehat{C_t}$. The expectation for E_t is ${\sum }_{i=1}^n{E}_{ti}=\mu +C_t+T_t/2$. Thus, we can calculate the trans effect in F1 genotype i by subtraction: $\widehat{T_i}=2\left(\widehat{E_t}-\widehat{\mu }-{\widehat{C}}_t-\frac{{\widehat{T}}_t}{2}\right)$. For every gene and every allele in our panel of heterozygous genotypes, we can use RNA-seq data to test the relative contributions to expression variation of cis-regulatory variation at this gene. Note that, when the structure of a GRN (i.e., which upstream genes affect the gene of interest) is unknown, we can still estimate the combined effect of variation in all upstream transacting genes. In conclusion, the numbers of RNAseq reads aligned to varying and tester alleles allow one to calculate cis and trans contributions to the deviation of gene expression in a given genotype from an average ‘normal’ level.

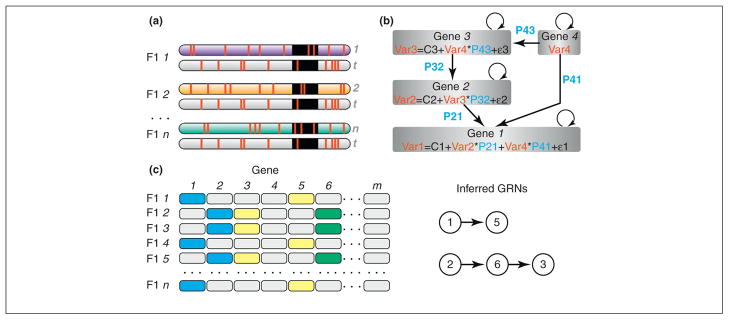
Figure 1.

Genetic approaches to constructing and quantitating GRNs. (a) An experimental crossing design to detect allele-specific expression (ASE). Each isogenic genotype chromosome (colored) is present in a F1 with a common tester chromosome (gray). SNPs are marked in red. A single gene is denoted in black. RNAseq can detect the abundance of allele i = 1, 2,.., n transcripts relative to the tester allele t in each of the n F1 genotypes. (b) A graphical illustration of structural equation modeling (SEM) (Box 1); straight arrows correspond to trans-regulatory effects and curved arrows indicate cis-regulatory effects. (c) ASE data enable the construction of GRN connections de novo. An allele transcript level is perturbed in comparison with the population mean among the n genotypes as a result of cis-regulatory mutations in the gene itself (blue), trans effects from other genes (yellow), or both (green). Note that cis-regulatory mutations in a given gene affect downstream genes in trans (e.g., Gene 1 → Gene 5). Transcriptional covariation analyzed with SEMs (Box 1) can then identify network connections between Genes 1 → 5 and 2 → 6 → 3. SEMs can thus hypothesize the structure of the network and simultaneously quantify the connections; these predictions can then be tested in an independent panel of genotypes.

If the GRN structure is known from prior molecular biological experiments, we can now go a step further and resolve the combined trans effects on the gene of interest by calculating the proportion of trans influence from each of the upstream genes. We propose using structural equation models (SEMs) to achieve this (Box 1). We and others have successfully implemented SEMs to test GRNs [14–18]. Using this framework one can ask, for example for the four genes in the GRN in Figure 1b, does expression variation in Genes 2 and 4 affect the transcription of Gene 1? These trans effects can be modeled as: Gene1 = Gene4 * P₄₁ + Gene2 * P₂₁ + e, where Gene1, Gene4, and Gene2 are the expression levels of these genes within each F1 genotype, and P₄₁ and P₃₁ are the path coefficients (Box 1). The path coefficients correspond to the overall individual trans effect of genes in the GRN on the expression of a focal gene (Gene 1 in our example). Note that e is the expression variation, that is not accounted for by trans effects in the GRN, and contains both effects of cis-regulatory mutations on the gene itself (curved arrows in Figure 1b) and residual variation ε. These terms can be estimated as described above with F1 individuals, and directly incorporated intoSEMs (Box 1). The result is a SEM that incorporates both cis and trans regulatory effects on GRN function.

Box 1. Structural equation models (SEMs).

SEMs were introduced by Wright [38], and are increasingly adopted for modeling causal inference [39,40]. A SEM is envisaged as estimating a graph where a series of equations describe the strength and directions of links between nodes. Suppose one wants to predict the expression level of Gene 1 in a population of genotypes (Figure 1b). A genotype might exhibit stronger or weaker expression of this gene, characterized as a variable Gene1. Gene1 is acted upon by Gene2, which is expected to co-vary with Gene1. A larger or smaller amount of Gene2 is regulated by Gene3 and Gene4. These nodes act on each other through the pathway coefficients P₂₁, P₃₂, and P₄₂, which essentially represent a measure of how the expression of one gene affects the expression of another. The model does not need to include the entire pathway because the upstream effects are captured by covariance terms, for example Cov (Gene3, Gene4). The essential idea is that if Gene1, Gene2, Gene3, and Gene4 are measured simultaneously in multiple genotypes, a covariance matrix can be used to estimate all three pathway coefficients simultaneously. Classic approaches require the number of genotypes to be at least five times the number of model parameters [39]. The SEM is not expected to explain 100% of the variance in Gene1, but instead a fraction V1 of it. Residual unexplained variance is treated as error (E1). The ratio of variance accounted for [Variance (V)] and not accounted for [Variance (E)] is used to test for significance. Pathway coefficients correspond to partial regressions of an output (for example Gene1) onto input (in this example Gene2), estimated for the whole pathway simultaneously. Although linear models can adequately capture effects of small-scale perturbations [17], methods incorporating non-linear effects are also available [41].

Because we are employing a class of models with well-developed statistical theory [38–44] there are also corresponding methods to evaluate the model fit [45–48], and these can be used to compare one species (or condition) to another. If the SEM model does not fit well, for example due to the abundance of cis by trans interactions, then the model can be adjusted. The structure of the refit model can be compared to the original model and information criteria used to determine whether the differences are significant. A search can be made over sets of possible structures to choose the one with the best fit [48], including those with loops as in Figure 1b. SEMs can also deal with whole-organism downstream phenotypes by considering them as the variable that the pathway affects or is affected by (Figure 2b). For example, the state of the SD pathway in [18] predicts fly lifespan.

Quantitating the network and comparing its performance across environments (sexes)

A fundamental question is how GRN function is rewired in different environments. In organisms with two sexes, every cell maintains a male or female identity – which can be considered as a precisely replicated environment. In Drosophila, the SD cascade is a well-understood GRN [19]. The SD pathway is regulated by alternative splicing, which is straightforward to infer from RNAseq data. The splicing cascade has been described as a binary function, where particular isoforms are turned on or off depending on the sex of the cell [19]. In reality, however, the levels of particular isoforms vary quantitatively [20,21], and this has been investigated to explore if the variation in isoform production affects the downstream targets of this GRN in adults [22]. Yolk protein (Yp) genes [23] are terminal expression targets of the SD pathway, and males express low levels of these genes in the fat body whereas females express them at high levels (Figure 2a). The extent of sexual dimorphism in Yp expression was found to differ greatly between natural genotypes, as did the levels of sex-specific isoforms upstream of Yp, providing quantitative measures for the connections within the SD GRN.

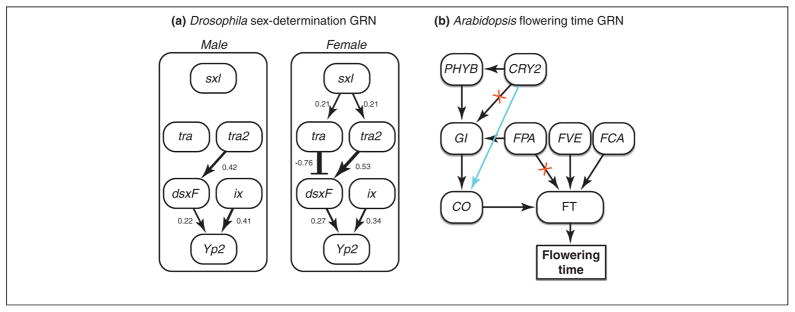
Figure 2.

Quantitating gene regulatory networks using natural genetic variation. (a) A subset of the regulatory interactions in the Yolk protein (Yp) expression network in flies, established through thirty years of empirical research [19]. The presence of two X chromosomes in females causes the transcript from Sex lethal (Sxl) to be functionally spliced. The SXL protein then splices the transcript from the gene transformer (tra) into a functional transcript, and TRA protein interacts with the protein encoded by transformer 2 (tra2) to splice doublesex (dsx) to its female-specific isoform (dsxF). dsxF encodes a transcription factor that affects the majority of structural and behavioral aspects of female differentiation. In males, Sxl is spliced into a non-functional transcript (SxlM), causing tra to be mis-spliced and non-functional. In the absence of tra activity, dsx is spliced to dsxM, which causes most male somatic-cell differentiation. dsx transcripts share a common DNA-binding domain but have different protein-interaction domains. Arrows indicate activation of expression/splicing; bars indicate inhibition. Although most of the connections are logical, some could not have been predicted from major effect mutations (e.g., the tra effect in females). Numbers beside each connection reflect quantitation in males and females using allele-specific RNAseq [17]. In this example, the phenotype predicted by the GRN is the level of expression of Yp2 expression. (b) Selected genes and their connections in a regulatory network for the photoperiod and autonomous flowering-time (FT) pathways in A. thaliana [49]; modified from [28]. The integration of signals from multiple inputs takes place in leaves, substantially through the master regulator constans (CO). This gene encodes a transcription factor that acts as a long-distance signal between leaves and the shoot meristem [50]. The variance–covariance structure in allele-specific RNAseq data from homologs to this pathway in a non-model plant may reveal that some regulatory connections have been lost (red Xs on connections between CRY2 → GI and FPA → FT) whereas others have been gained (blue connection between CRY2 → CO).

Applying SEM techniques (Box 1) to the SD pathway, one can ‘quantitate’ the GRN as a whole in each sex (Figure 2a) [18] instead of analyzing the gene connections in the network individually [22]. Although previous work [18] focused on the trans effect, it is also possible to include the effects of cis-regulatory mutations. Once the cis and trans contributions of regulatory polymorphisms have been estimated within each condition, SEM models can be compared for their structure (i.e., GRN architecture). Furthermore, GRNs can also be compared quantitatively with respect to the magnitude and direction of particular parameters. These comparisons enable the identification of GRN differences between conditions, environments, times, or tissues.

Translating GRNs from model species to relatives

Model organisms, although of fundamental importance to genetics, represent a tiny fraction of the diversity of life. How can we leverage information from genetic models to understand the other 99.99…% of organisms? We illustrate our approach using the well-known GRN for FT in Arabidopsis thaliana (Figure 2b), which has implications for many important crops. Plant breeding has a deep tradition of modeling phenotypes with process-based approaches [24,25]. Although physiological methods have been used traditionally [26,27], a recent trend is to estimate phenotypic outcomes by directly modeling the underlying gene and gene interactions at the expression level [28–33]; this technique can be further extended using our approach.

A neural network model based on information from forward-genetic studies about the FT GRN has been developed to simulate FT in A. thaliana (Figure 2b) [25,28]. Suppose we measure the ASE of A. thaliana homologs in another species. Although elements of this network are likely to be conserved, it will also evolve – as all pathways do. For instance, a study [34] comparing the genomes of A. thaliana and A. lyrata found that FLC and MAF2 – two genes central to regulating FT in A. thaliana – have experienced independent, post-speciation duplications; furthermore, 35 of 60 FT genes have diverged in intron–exon structure. Gene regulatory connections will cause a variance-covariance structure of expression across multiple natural genotypes – this structure will reflect changes in the regulatory network in comparison with the model species. For example, if there is no covariation between the genes involved in the FT signaling cascade, CRY2 and GI, or between FPA and FT in our plant of interest, then the values of these connections would be set to zero (Figure 2b). Similarly, if covariation is observed between cis mutations in CRY2 and trans effects on CO, then one can hypothesize that a new regulatory connection had arisen between these two genes (Figure 2b). Using this approach, a GRN annotated in a model species can be validated and/or adjusted in the non-model species of interest.

It is not necessary to examine the entire pathway – an advantage because it might be fairly complex. Instead, one can focus on a specific module. Consider the pathway module composed of the genes CRY2, PHYB, GI, and CO (Figure 2b). How would one distinguish the direct effect of CRY2 on CO from an indirect effect – where CRY2 polymorphisms affect PHYB then GI, and finally CO, and a direct connection between CRY2 and CO does not exist? In the SEM framework (Box 1), this would manifest as significantly non-zero pathway coefficients between CRY2, PHYB, GI, and CO; whereas the pathway coefficient going directly from CRY2 to CO would be zero. Thus, the cis–trans decomposition approach to inferring GRNs can be applied across species to document how sequence changes alter the regulatory connections either by small alterations of the strength of the GRN connections or through architectural changes.

Modeling the cis effects of regulatory sequence polymorphisms

Although we showed above the principles of cis–trans decomposition from ASE, one also needs to address how to evaluate the significance of effects. To test for a cis effect in the allele-specific data above, the standard linear model Y_ijk = μ + β_j + g_i + βg_ij + ε_ijk can be fit, where Y is the measure of expression of allele j (which can be either the isogenic genotype allele i or the tester allele t,) for F1 genotype (denoted by g) i and replicate k (enabling estimation of residual error ε), and the significance of β can be evaluated [10,11]. In reality, the effect of C_i might be due to multiple regulatory DNA polymorphisms. With a large enough sample size, the contribution of each regulatory polymorphism can be estimated in much the same way as in regular GWAS: let there be m polymorphisms segregating in regulatory regions of one gene, and define Δ_mi to be an indicator variable exhibiting the presence (1) or absence (0) of a regulatory polymorphism m in genotype i. Then, the variances and covariance involving C_i and Δ_mi can be estimated as: Var (E_ti − E_ii) = Var (C_t − C_i) = Var C_t +Var C_i − 2 Cov (C_t, C_i) = Var C_i, because Ct is a constant in this F1 population (thus its variance and covariance are zero), and the contribution of a polymorphism to this variance is Cov (C_i, Δ_mi). Sampling disequilibrium among causal polymorphisms, resulting from population structure, can be accounted for by adding these polymorphisms into the model (Figure 1b).

Annotating GRNs de novo

It has taken decades of dedicated work by molecular and developmental biologists to elucidate the SD and FT GRNs. These pathways have been incredibly useful for understanding the link between genotype and phenotype, but we would also like to discover GRNs de novo for other phenotypes of interest. We can identify transcriptional relationships among genes, including directionality, with eQTL methods similar to those of [35–37]. One limitation is that few, frequently only two, genotypes are used for inferring eQTLs; thus cis-regulatory variation in most of the GRN nodes is absent whenever the two parental alleles are functionally identical. Cis–trans decomposition (Figure 1a) removes this limitation by assaying a large panel of genetically varying individuals, thereby every – or nearly every – gene possesses cis-regulatory polymorphisms in a subset of genotypes (Figure 1c). Downstream genes affected by these mutations in trans are also annotated in every genotype. From similar information, molecular and developmental biologists have been annotating GRNs for over a century: they generated a cis-regulatory mutation (e.g., by underexpressing or overexpressing the gene) and examined which downstream genes showed altered expression (i.e., in trans). With natural variation, there is no need to generate cis-regulatory mutations, they are already abundant. But how to disentangle which cis mutation causes which trans effect? In our opinion, the large number of natural genotypes will help. Every gene may possess cis-regulatory mutations in a large fraction of natural genotypes; in Drosophila, for example, significant cis-expression differences are detected in up to 20% of isogenic genotypes [9,12]. If cis mutations in Gene 1 always cause a trans effect on Gene 5 (Figure 1c), this will be easily detectable as covariance between these terms, provided that the panel of genotypes is sufficiently large for rigorous statistical testing. Coupled with molecular approaches to identify regulatory interactions (e.g., protein interaction networks, ChIP-seq, 3D genome reconstructions), a robust GRN can be built. The cis–trans decomposition approach plays the key role of establishing the directionality of regulatory connections: cis → trans.

Concluding remarks

Once the graphical structure is determined to describe a GRN for the phenotype of interest, we can develop a single comprehensive SEM that includes the GRN structure, the regulatory effects of each segregating polymorphism, and the quantitative regulatory effects of genes on each other. One general way to look at this is that the GRN provides the network structure, that is, the path diagram, whereas the SEM analysis then provides the dynamics by measuring the strength of connections of the network. We emphasize that the framework we have developed above enables us to put into a single model all of the effects of segregating cis-regulatory polymorphisms and trans effects, ultimately allowing the phenotype to be predicted. By ‘quantitating’ a network, this approach enables comparisons of GRN structure and the strengths of regulatory connections between locally adapted populations, environments, and, ultimately, species. In principle, the SEM approach can identify the sub-pathways that permit adaptation to environments and can enable comparisons between the patterns of sequence evolution of these genes. Importantly, these models could be used to predict which genes and regulatory relationships in a GRN can be modified to improve organism performance and health. Clearly, several developments will need to be made for this potential to materialize. First, the effects of natural regulatory polymorphisms are qualitative rather than quantitative. Extensive modeling and simulation will be necessary to establish statistical guidelines for experimental designs. Second, cis and trans influences on expression variation might not be independent, and we will need to work out how to incorporate these potential interactions into our framework. Nevertheless, we believe that a SEM framework that merges the GWAS and GRN approaches is the next logical step to take in the post-GWAS world.

Glossary

Allele-specific expression

the relative gene expression level of each of the two alleles of a given gene in a diploid

Cis effect

the effect of a regulatory mutation, in or close to a gene, on allele-specific expression of that gene

e-QTL

quantitative trait locus that modifies the expression level of a gene

Flowering-time (FT) pathway

a GRN that controls plant flowering time in response to light, temperature, and other pathways

Gene regulatory network (GRN)

a graph in which genes are nodes and regulatory relationships between genes are directed edges connecting nodes; here nodes represent gene transcript levels and edges are the effects, either direct or indirect, on the transcript level of downstream genes

Genome-wide association study (GWAS)

a study in which millions of polymorphisms segregating in natural populations are tested for their effect on a phenotype of interest

Isogenic genotype

a genotype sampled from a natural population in which heterozygosity is eliminated by repeated selfing or brother–sister mating

Sex-determination (SD) pathway

a GRN in insects controlled by the number of X chromosomes whose output determines whether an individual develops as male or female

Structural equation model (SEM)

a method closely tied to multiple regression wherein one assumes a causal pathway of interactions (here, the GRN) and then estimates the strength of the interactions between components. It does so through path coefficients, P(x,y) for the interaction between x and y, which have the simple interpretation as standardized partial regression coefficients, or the amount of change in y given a standard deviation change in x (Box 1)

Trans effect

the effect on expression of a focal gene due to variation in expression of upstream genes, which could vary due to genetic or environmental differences