An Abridged Transition State Model to Derive Structure, Dynamics and Energy Components of DNA Polymerase β Fidelity

Abstract

We show how a restricted reaction surface can be used to facilitate the calculation of biologically important contributions of active site geometries and dynamics to DNA polymerase fidelity. Our analysis, using human DNA polymerase beta (pol β), is performed within the framework of an electrostatic linear free energy response (EFER) model. The structure, dynamics and energetics of pol β-DNA-dNTP interactions are computed between two points on the multidimensional reaction free energy surface. “Point 1” represents a ground state activation intermediate (GSA), which is obtained by deprotonating the terminal 3’OH group of the primer DNA strand. “Point 2” is the transition state (PTS) for the attack of the 3’O^- (O_nuc) on the P_α atom of dNTP substrate, having the electron density of a dianionic phosphorane intermediate. Classical molecular dynamics simulations are used to compute the geometric and dynamic contributions to the formation of right and wrong O_nuc–P chemical bonds. Matched dCTP•G and mismatched dATP•G base pairs are used to illustrate the analysis. Compared to the dCTP•G base pair, the dATP•G mismatch has fewer GSA configurations with short distances between O_nuc and P_α atoms, and between the oxygen in the scissile P-O bond (O_lg) and the nearest structural water. The thumb subdomain conformation of the GSA complex is more open for the mismatch, and the H-bonds in the mispair become more extended during the nucleophilic attack than in the correct pair. The electrostatic contributions of pol β and DNA residues to catalysis of the right and wrong P-O_nuc bond formation are 5.3 and 3.1 kcal/mol, respectively, resulting in an 80-fold contribution to fidelity. The EFER calculations illustrate the considerable importance of Arg183 and an O_lg-proximal water molecule to pol β fidelity.

DNA base-excision repair involving human DNA polymerase β (pol β) is an essential defense mechanism against genetic alterations that may typically result in cancer in humans (1-4). Biochemical (5) and crystallographic (6) studies, including a recent pol β-DNA-dNTP ternary complexes with incorrect dNTP substrates (7) provide insight in determining the role of conformational and structural factors involved in pol β mechanisms and fidelity (1). It has been suggested that the chemical step is rate-limiting in pol β–catalyzed nucleotide insertion based on studies of time-resolved fluorescence in conjunction with rhodium(III) metals and solvent viscosity alterations (8-10), and by the observation of Brønsted linear free-energy relationships (LFER) for dNTP substrates with β–γ bridging oxygen replaced by haloalkanes (11, 12).

Phosphodiester bond hydrolysis in aqueous solution is associated with a broad high-energy transition state region, which allows either distance between the alpha phosphorus of the incoming dNTP and O3’ of the primer nucleotide (P_α-O_nuc) or between P_α and leaving group oxygen of the dNTP (O_lg) to be between 1.7 to 2.4 Å, provided that the sum of these distances is less than 4.0 Å (13, 14). All these substrate geometries need to be stabilized in the active site of enzymes that catalyze this class of reaction, DNA polymerase being a prominent example. Thus, a rigorous study of the protein or substrate modifications on enzyme catalysis requires an accurate evaluation of the complete reaction free energy surface for each protein or substrate variant - a task that is currently far too demanding to be practically useful. However, it has been proposed that it may be possible to effectively reduce this surface substantially by selecting a suitable subset of geometries (15).

Theoretical computational analyses of transition states (TS) for polymerase-catalyzed deoxyribonucleotide insertion have employed several variants of quantum mechanics/molecular mechanics (QM/MM) (11, 13, 16-21). For the chemical reaction in pol β, an ONIOM (a specific type of QM/MM calculation) analysis suggests that the highest activation barrier occurs early on the nucleotidyl transfer reaction coordinate (17, 22). This early transition state featured a longer P_α–O_nuc bond than P_α–O_lg bond. Subsequent empirical valence bond (EVB) calculations suggested a late semi-concerted TS to be rate-limiting, but the free energies of early TS configurations were only marginally lower, thus retaining the early TS as a plausible option for the rate-limiting TS (11, 12, 23). Owing, however, to limited sampling of the TS region of the free energy surface during ONIOM or EVB calculations, dynamical aspects of the active site elements stabilizing the TS were not determined. A far more efficient sampling of the TS region uses molecular dynamics (MD) simulations on the TS model generated using classical MM force fields (24, 25). This type of sampling was applied in recent studies of TS dynamics in RNAse A (26), and to the effects of amino acid substitutions on pol β fidelity (15, 27).

To address enzyme catalysis, it is necessary to compare the simulated TS properties either to the same TS in aqueous solution (15, 27), or to a ground-state of the enzymatic reaction (26). However, because the 3’-terminal deoxyribose of the primer strand carries an extra proton in the reactant state, the primer-dNTP substrate carries a different total charge in the ground- and transition-states of the nucleotidyl transfer reaction. This variation in the overall charge significantly diminishes the utility of computer simulations to provide consistent energetic and structural comparisons. To avoid the inaccuracies inherent in the computational treatment of long-range electrostatic interactions in biomolecular simulations (28), here we employ a ground state model that is activated by deprotonating O_nuc (GSA) as the initial state in an electrostatic linear free energy response (EFER) model. We further postulate a TS structure that geometrically mimics the TS for the nucleophilic attack, but wherein its atomic charges correspond to a fully developed dianionic pentavalent phosphorane intermediate (PTS). The MD simulations on GSA and PTS states are then used to monitor differential interactions of the charges of the probe region of the GSA and PTS states with their respective active site or aqueous solution surroundings. The probe region of the substrate is designed to have its total charge close to zero by including α- and β-phosphates of dNTP, O_nuc, and the catalytic Mg²⁺ ion. The proposed linear-response treatment is reminiscent of the model used in our earlier simulations of relative dNTP binding, in which the probe region represents atoms of the dNTP base in charged and uncharged states, and the DNA-pol β complex with the right or wrong templating bases represents the probe surroundings (29).

The structural aspects of catalysis are described by comparing the dynamics of the contacts of pol β active site residues with the primer-dNTP substrate in the GSA and PTS states. Such a structural analysis effectively extends the reach of X-ray diffraction analysis to elusive short-lived species. Classical MD simulations are capable of generating a detailed dynamical picture of any part of the protein internal architecture, often leading to an overabundance of model-dependent structural data. To focus on pol β catalysis, we emphasize those geometric features that differ significantly between simulations of the PTS and GSA complexes. To expand this analysis to pol β fidelity, we compare the same set of geometric features for pol β bound to a model PTS containing either a right or wrong dNTP substrate.

Methods

Initial Structure Preparation

The simulations were initiated using two crystal structures of the human DNA polymerase β (pol β): a ternary complex including ddCTP bound opposite dG template (30) (PDB code 2FMP; residues 10-335), and a ternary complex containing G:dAMPCPP mismatch in the active site (7) (PDB code 3C2M; residues 10-335). The 3’-terminal dideoxynucleotide of the primer strand and ddCTP in the structure 2FMP were modified by adding the 3’-O- and 3’-OH groups, respectively. GSA complexes were generated from the crystal structures as follows: the dAMPCPP in the crystal structure 3C2M was modified by replacing the -CH₂- group in the P_α – P_β bridge by oxygen; one Na⁺ ion in the active site was replaced by Mg²⁺ in the crystal structure 2FMP; additionally, two Mn²⁺ ions in the active site in the 3C2M structure were replaced by Mg²⁺ ions. These alterations of the original crystal structures were made to carry out our simulations for catalytically competent and biologically relevant pol β complexes in solution. PTS models were prepared from GSA complexes by connecting O3’ to P_α. GSA and PTS models for simulations in water included dNTP, two Mg²⁺ ions and deoxyribose of the primer dC.

The structure and atomic charges of the PTS model were chosen to be similar to those used to model pentavalent intermediate in empirical valence bond (EVB) simulations of the catalytic reaction of T7 DNA polymerase (13) and pol β (11) (Figure 1S and Tables 1S - 5S). In particular, Morse potentials for the P_α-O_nuc and P_α-O_lg bonds were replaced by harmonic potentials with equilibrium bond distance of 1.9 Å for each of these bonds. In addition, charges of two non-bridging oxygen atoms of β-phosphate and of the O_lg atom were chosen to be slightly more negative than in the intermediate or ground valence-bond states, in accordance with the trends observed in ab initio calculations (14, 31), used for CHARMM force field of TS of transphosphorylation reactions (25), or in direct calculations of TS binding in pol β (15, 27) (Table 1S). The use of weak harmonic potentials to model axial PO bonds in the TS is consistent with the existence of a shallow free energy surface near this state in DNA pol β (11) and in ab initio calculation of methanolysis of dimethyl phosphate in aqueous solution (14). The combination of the atomic charges and van der Waals radii of our PTS model, and Mg²⁺ ions (charge +2, R* = 1.3 Å, ε = 0.06 kcal/mol) (13) resulted in average Mg-O(phosphate) bond distances in the 2.01 - 2.07 Å range.

GSA and PTS models were immersed into a 33 Å radius sphere of TIP3P water molecules, generated using the Qprep module of the program Qdyn (32). The origin was centered on the N_H2 atom of Arg283 for the simulations in protein to include the whole C-terminal protein sub-domain (thumb) inside the simulation sphere (Figure 1), and on the P_α atom of dNTP for the simulations in water. MD simulations in the protein were carried out with the following selections of the charged amino acid residues: Asp (190, 192, 256, 263, 276, 314, 318, 321, 332), Glu (203, 232, 288, 295, 309, 316, 329, 335), Lys (27, 41, 48, 206, 230, 234, 262, 280, 289, 317, 326, 331), Arg (40, 149, 152, 182, 183, 254, 258, 283, 299, 328, 333) and the charged nucleotides G (6, 7, 9) and C (8, 10) of the DNA template. This selection resulted in the total charge -0.95 e (e = 1.602 × 10⁻¹⁹ C) inside the simulation sphere for all simulated systems. In general, this selection of the charged residues is consistent with Glu, Asp, Lys and Arg that lie closer than 27 Å from the center of the simulation sphere having charges based on their pKa in water, whereas those that lie further than 27 Å from the center of the simulation sphere being overall electroneutral. The total charge of the simulated systems in water was -0.63 e.

Figure 1.

The overall structure of the simulated system. The primer-template DNA is shown in magenta. The N-terminal lyase domain (green), and fingers (orange), palm (cyan) and thumb (yellow) subdomains of nucleotidyl transferase domain are named according to the original pol β nomenclature (6) in which the protein structure resembles the left hand (1). dNTP substrate is shown in blue sticks.

MD simulations and analysis

Molecular dynamics (MD) trajectories were generated using the AMBER 94 force field (33) implemented in the program Q, version 5.01 and 5.06 (32). The structures of the simulated systems were equilibrated by a gradual heating of the simulated system from 5K to 298K in a series of twelve MD simulations with gradually increasing step size (0.5 to 2 fs) and 190 ps simulation time in total. Subsequent production trajectories were generated at 298 K using 2 fs integration time and the velocity scaling algorithm (34). In calculations of linear-response free energies, electrostatic interaction energies of the ‘probe’ region with the rest of the simulated system were evaluated for all distances. This probe region is comprised of the O3’ atom of the primer nucleotide and seven atoms of the dNTP triphosphate group that differ in their partial charge between GSA and PTS states. To keep the total charge of the probe region near zero (-0.52 e), a Mg²⁺ atom was also included in this region (Figure 1S, Table 1S).

The root-mean square deviation (RMSD) values for the simulated part of the protein obtained from the calculated trajectories (Figure 2S) indicate that the deviation of the simulated protein structure from the X-ray reference geometry stabilized after about 1 ns. The energies and geometries were sampled every 250 steps. The SHAKE algorithm (35) was applied to hydrogen atoms of both solute and solvent molecules. The non-bonded interactions between non-probe atoms were evaluated explicitly for distances shorter than 10 Å. The local reaction field (LRF) method was used to include long-range electrostatic interactions for distances longer than 10 Å (36). The long-range atom-pair list was updated every 10 steps. The TIP3P water molecules were subjected to the surface-constraint all-atom solvent (SCAAS) type boundary conditions (37, 38) implemented in the program Q (32). These boundary conditions were designed to mimic infinite aqueous solution.

The differential analysis of trajectories for the right and wrong GSA and PTS complexes were carried out for RMSD of the thumb sub-domain and DNA. The calculated distances between the following groups or atoms were also analyzed: bases of dNTP and template dG, O3’ of primer and P_α of dNTP, P_α and O_lg, the catalytic Mg_A and the teminal O3’ of the primer strand, the catalytic MgA and oxygen atoms of triphosphate group of dNTP, structural Mg_B and oxygen atoms of triphosphate group of dNTP, 3’-OH and O1B of dNTP, Arg183-NH2 and O1B of dNTP, Asn279-ND2 and O2 of dCTP, Asn279-ND2 and N3 of dATP, hydrogen atoms of selected water molecules and oxygen atoms of the triphosphate group of dNTP, dNTP-PG and Arg149-CZ and O_lg in MD simulations and crystal structures of pol β.

The electrostatic catalytic effect, ΔG^ES_cat was calculated as

$$\Delta G_{\mathit{cat}}^{\mathit{ES}}=\Delta G_p^{\mathit{GSA}\to \mathit{PTS}}-\Delta G_w^{\mathit{GSA}\to \mathit{PTS}}$$ (1)

In this expression, subscripts p and w denote, respectively, free energies obtained by simulations in the protein and water. Free-energy changes accompanying the transition from the GSA to PTS state, ΔG^GSA→PTS, were evaluated from the MD ensemble averages (<>) of electrostatic interaction energies (U) between the probe region and the rest of the simulated system as

$$\Delta G_p^{\mathit{GSA}\to \mathit{PTS}}=\mathit{0.5}\ast \mathit{[}<U(\mathit{PTS})-U(\mathit{GSA}){>}_{\mathit{GSA}}+<U(\mathit{PTS})-U(\mathit{GSA}){>}_{\mathit{PTS}}\mathit{]}$$ (2)

The formula (eq 2) represents a special version of a time-independent linear-response theory (39). This electrostatic linear-response formula can be derived either by approximating the potential energy change along a reaction coordinate by the intersection of two parabolas of equal curvature (29, 40) or by expanding the exponential function in the free energy perturbation formula (41) into a Taylor series (42, 43). We refer to the model characterized by eq. 2 as the “electrostatic free-energy response” (EFER) model because it approximates free energy contributions to enzyme catalysis using the calculated electrostatic energies. The EFER acronym allows us to distinguish this model from the linear-response approximation (LRA) (29, 40), which uses eq.2 to evaluate solvation free energies and free energies of protein-ligand binding.

Dynamics of the atoms in the thumb subdomain in MD simulations was monitored by evaluating their RMSD from the corresponding atoms in 2FMP or 3C2M crystal structures using the program VMD 1.87 (44). Global RMSD of the thumb subdomain was calculated after aligning the C, C_α and N backbone atoms of the residues 153 - 275 in the palm subdomain; the residues 242 - 250 of the palm loop and residues 160, 212 - 214 in palm α-helices are located outside the simulation sphere excluded from this alignment set. Internal thumb RMSD was separately evaluated after aligning the C, C_α and N backbone atoms of the thumb subdomains. Each reported RMSD value was then obtained by subtracting the internal RMSD from the corresponding global RMSD. The magnitude of fluctuations from the mean correspond to two standard deviations, for which 95% of simulated points fall within the fluctuation range. Radial distribution functions (RDF) were generated using VMD program. RDF were calculated using VMD as follows: a histogram of all atom pair distances between O_lg (Figure 1S) and oxygen atoms of all water molecules within 8 Å radius from O_lg was compiled with δr of 0.1 Å and then normalized using the average number density of bulk water. The normalized local density, ng(r), was plotted against δr. Electrostatic potential was calculated by APBS 1.2.1 (45) using APBS Tool plugin in PyMOL by solving nonlinear Poisson-Boltzmann equation with the following settings: temperature, atomic radii and atomic charges were identical to simulation parameters; grid of 65 × 65 × 65 points in 16.016 × 20.079 × 16.725 A³ grid box was centered to the centre of mass of the selected atoms; the remaining parameters were set to default values in the APBS Tool plugin in PyMOL (22): protein dielectric of 2.0, solvent dielectric of 80, solvent radius of 1.4 Å and ionic strength of 0. The resulting electrostatic potential map was visualized using APBS Tool plugin in PyMOL as a solvent accessible surface.

Results

Geometry of the dNTP substrate in its PTS state

The average P_α-O_nuc and P_α-O_lg distances and their distributions are the same for the correct and incorrect dNTP in the PTS complex (Figure 3S). MD trajectories of the PTS complexes yield P_α–O_nuc distances in the 1.7 - 2.1 Å range. This wide range and the corresponding average distance of 1.87 Å are consistent with a weak harmonic force constant and a P_α–O_nuc equilibrium bond length of 1.9 Å that are used in the MM force field for the PTS state (Table 3S). In contrast, the use of the same MM bonding parameters for the distance to the leaving group, P_α–O_lg, results in a P_α–O_lg bond length that fluctuates between 1.4 and 1.8 Å. These distances are similar to those sampled for the P_α–O_lg bond in the GSA complex.

We performed control-simulations of mono- and diphosphate esters in aqueous solution (Table 6S) that indicate that the weak harmonic potential of the P_α–O_lg bond can be significantly perturbed by electrostatic interactions of the negatively charged substrate with its water or protein environment, and the catalytic Mg²⁺ ion. According to Born’s formula for solvation of charged molecules by polar solvents (46), the free energy of these interactions is more favorable for shorter P_α–O_lg bond distances, which make the negative charge of the triphosphate moiety more compact. The P_α–O_nuc bond length is less affected by electrostatic interactions than the P_α-O_lg bond length because the catalytic Mg²⁺ ion and the rest of the substrate environment pull on the P_α–opposite directions, so that the Mg²⁺ ion favors a more elongated P_α–O_nuc bond owing to its strong interaction with O_nuc.

The relaxation of the symmetric to the asymmetric configuration of the axial PO bonds that occurs in this MM model is unlikely to reflect the actual substrate energetics in the pol β active site because a QM rather than MM description of the substrate is required in the TS area of the reaction surface. However the intrinsic substrate energetics is not the subject of this paper; we have focused instead on changes of protein-substrate energetics and dynamics between the two postulated states of the substrate, GSA and PTS. Taking advantage of the deformation of the symmetrical MM bonding potentials of the P_α-O_nuc and P_α-O_lg bonds by the electrostatic interactions with their environment is one possible strategy to achieve stable MD sampling of the desired PTS region of the free energy surface. In this region, the average P_α-O_lg bond length is similar to its value in GSA, while exhibiting an increased amplitude of fluctuations from its equilibrium value. Consequently, the major differences between the dNTP geometries in the GSA and PTS states are limited to the P_α-O_nuc bond length and O-P_α-O bond angles. This geometric similarity allows the postulated differences in the atomic charges in GSA and PTS states to elicit a response from the protein or solution environment that scales linearly with the magnitude of the electrostatic interaction between the probe region of the substrate and its environment, and thus affirms the validity of the approximation of eq. 2.

Linear-response free energy calculations

An approach of the O_nuc atom to α-phosphate is accompanied in the EFER model with a redistribution of the negative charge from deoxyribose to α- and β-phosphate groups. This charge redistribution upon going from GSA to PTS, which is identical for right and wrong dNTP substrates, is the main postulated structural signature of the EFER pol β model. The resulting perturbation of the substrate electrostatic potential (Figure 2) is too subtle to affect the overall conformation of the protein (Figure 4S), but it is sufficient to alter the positions and dynamics of the protein active site residues. Monitoring the resulting geometric changes of the active site and the corresponding free energy changes by MD linear-response simulations may provide better understanding of structure-function relationships than QM/MM methods, in which the active site dynamics is either completely ignored or limited to extremely short trajectories.

Figure 2.

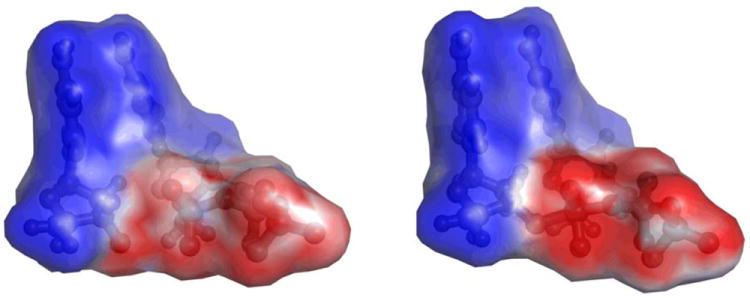
Electrostatic potential generated by the 3’-terminal primer nucleoside fragment and dCTP substrate in GSA and PTS-model complexes of pol β. The calculated potential values fall in the 0 – -18 kcal/mol range, with the high and low values displayed in shades of blue and red, respectively, and the midpoint (white) set at -10.8 kcal/mol.

Electrostatic interactions of the substrate atoms with their environment can either increase or decrease the activation free energy required to form the O_nuc – P_α bond. The MD calculations monitor these interactions for the probe region in its GSA and PTS states in aqueous solution and pol β (eq. 2). Although, the point charge MM model does not rigorously reflect the anisotropy of atomic charge densities (21), the importance of these quantum effects is diminished by the thermal motions of atoms in the active site. Since the negative charge density becomes more localized on the nucleophile + substrate as the O_nuc ⋯. P_α distance is reduced, the PTS is expected to be better solvated by polar solvents than the GSA. The calculated electrostatic energies in aqueous solution show that the corresponding energetic stabilization amounts to 32.7 kcal/mol (Table 7S). Since the identity of the dNTP base should not affect the solvation free energy of the probe region in water (47), this stabilization free energy was obtained by averaging results of simulations of 3’-deoxyribose-dCTP·Mg²⁺ and 3’-deoxyribose-dATP·Mg²⁺ complexes. The relative PTS stabilization by its environment further increases in ternary pol β complexes, where it is larger for the complexes containing the right dNTP (38.0 kcal/mol) than the wrong dNTP (35.8 kcal/mol). These free energies indicate that the protein/DNA environment facilitates the PO bond-formation step by 5.3 kcal/mol, and contributes 2.2 kcal/mol to fidelity of pol β catalyzed formation of the GC base pair versus the GA mispair.

Structural differences of right and wrong pol β complexes in PTS and GSA states

The ‘wrong’ GSA and PTS complexes (i.e., complexes that contain the G·dATP mispair) feature a conformation of the thumb subdomain that is closed to about 90% (Table 8S, Figures 5S - 6S). Thus, the surprising stabilization of the closed pol β conformation by an incorrect bound dNTP and Mn²⁺ metal ions that was established crystallographically (7) is retained after replacing Mn²⁺ by Mg²⁺ and deprotonating O_nuc in the simulated wrong GSA complex. Moreover, the distance of protein backbone atoms of the wrong GSA complex from their crystallographic counterparts, which is measured by the RMSD function, is on average shorter when the reference crystallographic structure contains the WC nascent base pair (i.e., the right complex) than the mispaired one. Nevertheless, the trajectory of the wrong GSA complex still maintains close proximity to the crystallographic coordinates of the wrong complex that were used to initiate this trajectory (Figure 5S). The implied positioning of the simulated wrong GSA complex in between the two crystallographic reference points is most apparent for vertical positions of the nucleotides of the template strand that are located at +1 and +2 positions downstream from the template nucleotide dG (Figure 3, left, and Figure 7S). Since the calculated geometric differences of the right and wrong pol β ternary complexes are smaller than indicated by crystallography, it is important to use computer simulations to identify geometric and dynamic features that are most relevant for catalysis and fidelity. The comparison of the calculated dynamics of GSA and PTS complexes points to three such features, base-pairing, structural water near O_lg, and hydrogen bonding of the β-phosphate with Arg 183.

Figure 3.

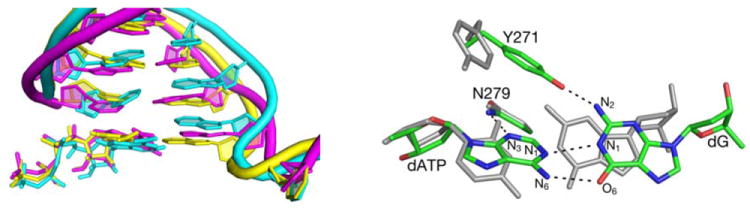
Left: Overlap of the DNA and dNTP structures from a representative snapshot of MD simulation of pol β containing dG•dATP pair (magenta) with the crystal structures of the DNA in ternary pol β complexes containing the dG•dCTP (yellow) and dG•dATP base pairs (cyan). Right: Overlap of the average calculated structures of the dG•dCTP (grey) and dG•dATP (atom-type colors) base pairs in the GSA pol β - DNA-dNTP complex. Hydrogen bonding interactions in the dG•dATP mispair are shown with dashed lines.

A small vertical translocation of the bases in the template DNA strand allows the formation of stable O⋯H-N (1.90 Å) and N-H⋯N (2.02 Å) hydrogen bonds between the template G and incoming dATP mispaired nucleotide (Figure 3, right). In contrast, the mispaired bases are linked by only one hydrogen bond (O⋯H-N) in the crystal structure (7). The calculated length of the N-H…N hydrogen bond in the G•dATP pair is 0.13 Å longer than the average length of the corresponding hydrogen bond in the dG•dCTP pair. The two hydrogen bonds in the simulated mispair structure are retained upon going to PTS (Figure 8S), but both hydrogen bonds are about 0.1 Å longer in PTS than in the GSA complex. In contrast, hydrogen bonds in the correct base pair are lengthened only by 0.02 Å upon going to PTS, indicating larger destabilization of PTS for incorrect dNTP than for the correct dNTP.

The insertion of a larger adenine residue in place of cytosine is accommodated by a large horizontal shift of the G (template) nucleotide, and by the formation of the new hydrogen bond between the amino group of this nucleotide and Tyr 271. During this process, Tyr 271 releases the carbonyl group of the terminal primer nucleotide, with which it interacts when a correct dNTP is bound in the active site. This, and other small structural rearrangements for the G•dATP mispair, e.g., rearrangements that involve the 3’-terminal primer nucleotide, result in a smaller number of prereactive MD configurations (0.6%) with short distance (< 3.3 Å) between the O3’ (O_nuc) atom of the primer nucleotide and P_α atom of dNTP than observed in simulations with dG•dCTP (3.9%). The average O_nuc⋯P_α distances calculated for GSA complexes with correct and incorrect dNTP substrates are, however, similar (3.58±0.19 Å and 3.61±0.12 Å, respectively). The GSA trends that favor the reactivity of the correct dNTP are consistent with the ground-state distances of 3.4 and 3.6 Å calculated previously (48) for the same dG•dCTP and dG•dATP nascent pol β base pairs, respectively. These trends may be common for all neutral nascent base-pairs, as indicated by the O_nuc⋯P_α distaces of 3.4 ± 0.05 and 3.6±0.3 Å obtained as an average over 4 matched and 11 mismatched pairs, respectively, in the pol β ternary complex (48).

Since experiments with kinetic isotope effects (12) indicated that proton transfer may contribute to the rate-limiting chemical step, we assessed possible structural underpinnings of this contribution by tracing the distances of water molecules from the leaving group oxygen (O_lg, Figure 4) during MD simulations of the GSA and PTS complexes (Figure 5). In the GSA for correct dNTP insertion, the number-density of water molecules (represented by their oxygen atoms) reaches its maximum at 3.2 Å from O_lg. This most probable O_wat - O_lg distance is in excellent agreement with the observation of the structural water 3.2 Å from O_lg in the GC-crystal crystal structure (30) (Figure 4). The water density maximum increases and its most probable distance from O_lg shortens to 3.0 Å in the PTS. These structural variations can be rationalized by more negative charge of O_lg and equatorial oxygen atoms postulated for the PTS force field (Table 1S) and by better ability of dNTP in the PTS configuration to accommodate cyclic H-bonding arrangements (Figures 9S and 10S, Tables 9S and 10S). Thus, the nucleotidyl transfer reaction is accompanied by a significant reorganization of the water molecules surrounding O_lg.

Figure 4.

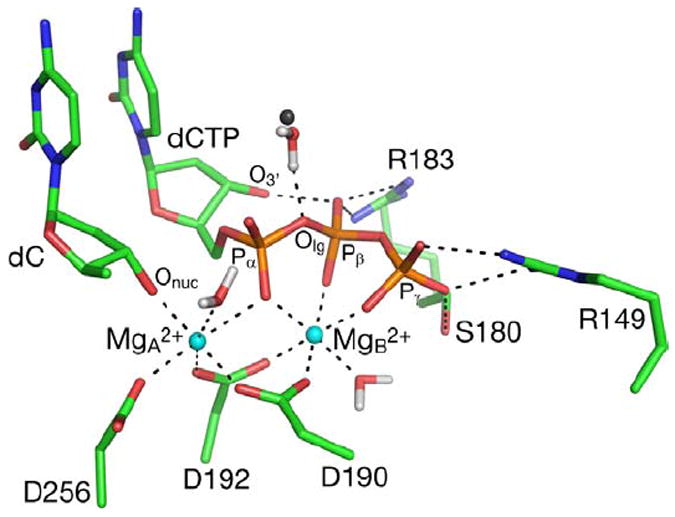
A snapshot from the MD trajectory of GSA with the correct dG•dCTP base pair. A water molecule in the closest distance from the leaving group oxygen, and its counterpart from the the crystal structures of pol β containing the dG•dCTP base pair, are represented by a red/white and grey spheres, respectively. The first coordination sphere of Mg²⁺ ions, and hydrogen bonding interactions of active site residues with the triphosphate moiety of the substrate are shown as dashed lines. Hydrogen atoms on non-water atoms are not shown.

Figure 5.

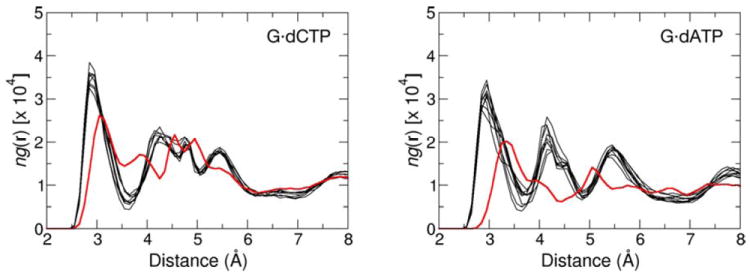
Radial distribution functions (RDF) for the hydration of the O_lg atom in the active site of pol β-DNA-dNTP complex containing the dG•dCTP (left) and dG•dATP (right) nascent base pair. Each graph line represents relative number-density of the oxygen atoms of water molecules as a function of their distance to O_lg in the GSA (red) and PTS (black) complexes. Sensitivity of the RDF to small changes in the simulation conditions is illustrated for PTS by comparing the RDF obtained from eight separate MD trajectories.

A water molecule that diffuses close to O_lg has only a small chance to H-bond with O_lg, and this probability decreases upon going from GSA (4.7%) to the PTS model (0.7%) (Tables 9S and 10S). Thus, this water molecule is unlikely to donate proton to O_lg in concert with the PO bond making/breaking. Perhaps more importantly, because of the large pK_a difference between H₂O and inorganic pyrophosphate, the full or partial proton transfer in a late TS would likely increase rather than decrease the overall activation barrier. This is even more pronounced for the PTS. Nonetheless, water near O_lg can still stabilize the PTS by forming stronger H-bonding interactions to the pyrophosphate moiety (as opposed to transferring its proton) as a part of overall electrostatic stabilization involving the entire protein active site.

The water number-density maximum occurs at 3.5 and 3.1 Å in the simulations of the wrong GSA and PTS complexes (Figure 5). The heights of the relative water density maxima are lowered with respect to their heights in simulations of the complexes containing the dG•dCTP base pair. Thus, the O_lg is surrounded on average by fewer molecules at longer distances in G•dATP-containing complexes than in complexes containing the correct nascent base pair. This decrease in the water occupancy near O_lg appears to contribute to a smaller observed k_cat for insertion of the incorrect dNTP.

The presence of a 3’OH…OP_β H-bond between the deoxyribose and β-phosphate groups of dNTP has been shown to inversely correlate with k_cat in several pol β mutants (i.e., mutants with higher k_cat show weaker intramolecular H-bonding) (49). This intramolecular H-bond is present in 99.9% of the configurations sampled in simulations of the GSA complex containing the correct dCTP, but only in 88% of configurations in the PTS model (using a 2.5 Å threshold for the H…O distance as a definition of H-bond, Figure 6). This pattern is reversed for PTS model complexes with the incorrect dATP, which shows intramolecular H-bonding in 99.5% configurations but GSA in only 93.7% of the configurations.

Figure 6.

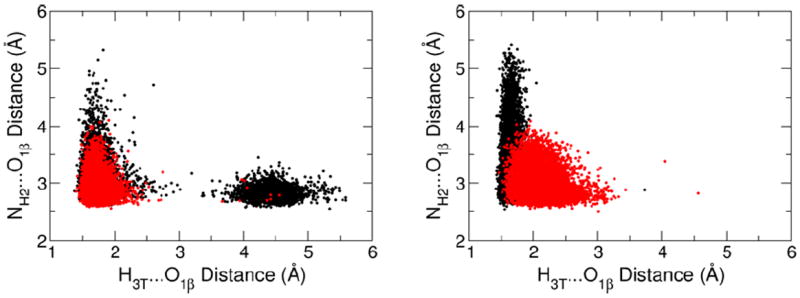
The distribution of the distances characterizing the internal dNTP hydrogen bond between the O3’H group of deoxyribose and a non-bridging oxygen of the β-phosphate, and the hydrogen bond between the same β-phosphate oxygen and Arg183. Each dot corresponds to a single snapshot along a 10 ns MD trajectory for the GSA (red) and PTS model (black) complexes of pol β. The distance distributions from the simulations with the correct and incorrect dNTP substrates are shown in the left and right plots, respectively.

The anticatalytic effect of intramolecular H-bonding could be attributed to the competition of O3’H of the deoxyribose with an NH₂ group of Arg183 for the same H-bond acceptor (Figure 4). The configurations that lack the intramolecular H-bond, i.e., those with an H_3T…O_1β distance larger than 2.5 Å in Figure 6, tend to have shorter distances between Arg183 and β-phosphate (Figure 6, y-axis). Thus, on average, Arg183 is significantly farther from β-phosphate in the PTS for the incorrect dNTP than in the GSA. In contrast, the insertion of the correct dNTP at the end of the primer strand is facilitated by an increased population of PTS configurations forming H-bonds to Arg183, an effect attributable to a reduction in intramolecular H-bonding in this state.

Discussion

Recent calculations of the contribution of the chemical step to pol β fidelity employed two variants of the QM/MM approach. An ab initio QM description of the reaction generating a phosphodiester bond was combined with minimization of the MM energy of nearby protein residues to yield an early TS with P-O_nuc and P-O_lg distances of 2.2 and 1.9 Å (17). These calculations indicated that the main fidelity contribution stems from the reorganization of the coordination sphere of the catalytic Mg²⁺ ion reflecting the pre-chemistry step (17, 22). The EVB QM/MM calculations, which combined the EVB description of the reaction with the dynamical MM description of the protein, resulted in a late TS with PO_nuc and PO_lg distances of 1.68 and 2.15 Å, and the fidelity originating from the corresponding chemical step of the catalytic reaction (11, 12, 23). Large differences between these computational studies reflect differences in the computational methodology, including important differences in the treatment of solvation.

Since ab initio QM/MM calculations usually neglect solvent and protein dynamics they are prone to insufficient stabilization of electronic and geometric structures with large excess electron density, such as oxoanions. To partly alleviate this problem, the γ-phosphate of dNTP needs to be simulated in its protonated (-1) state (17, 22). A reduced stabilization of high substrate charges may help to explain why the dianionic pentavalent intermediate ([-O_nuc–PO₂(OR)–O_lg-]^2-) is absent on the P_αO_nuc/P_αO_lg reaction energy surface in the QM/MM framework. It is also not surprising that ab initio and semiempirical QM/MM methods that explicitly evaluate proton transfer to the reaction coordinate suggest that high negative charges developing on the substrate or nucleophile during the catalytic reaction of nucleotidyl transferases need to be stabilized by a concerted proton transfer via a chain of water molecules (18, 19, 21, 50, 51). Support that these calculations can provide an accurate estimate of catalytic reaction energies might be obtained were one to use the same method to derive realistic barriers for the same reaction in aqueous solution, or to calculate realistic pKa constants of ionizable residues in the active site. However, in the specific case of pol β a proton-transfer rate-limiting step involving nucleophilic oxygen is inconsistent with large measured leaving-group substituent effects (11, 12) and small kinetic isotope effects (11).

Previously, the existence of a high-energy dianionic pentavalent intermediate was postulated in an EVB simulation of a T7 DNA polymerase reaction in aqueous solution, in part because stepwise reactions are easier to model using the EVB Hamiltonian and in part because the protein environment in T7 DNA polymerase was shown to significantly deepen the free energy minimum corresponding to this intermediate (13). This effect was not obtained in pol β simulations, where a quasi-concerted reaction profile was found to be more consistent with experimental Brønsted linear free energy relationships (11). However, the apparent preference for the concerted TS may still be a consequence of an underestimate of solvation effects in EVB simulations. Although these simulations include nanosecond dynamics, they may not encompass a full complement of environmental effects because of the approximations inherent in the description of long-range electrostatic interactions, and the fact that a limited composition of the system and trajectory length does not enable penetration of water molecules and counterions through the protein structure. One indication of such undersolvation is the formation of the ion-pair between the Arg 149 side-chain and the γ-phosphate. This ion-pair was observed in our current and previous (11, 49) simulations as well as in MD simulations (52) that employed other force fields, but not in the high-resolution crystal structures (Table 11S).

There remain challenging difficulties to overcome to improve the reliability of computer simulations in calculating DNA polymerase fidelity. Calculations using structural and kinetic data as initial information for modeling provide potentially important insights into chemical and conformational fidelity mechanisms that reflect individual contributions from DNA template-dNTP substrate interactions, specific amino acid residues, metals and water. One way to harness these contributions is to examine solvation energies for the probe-region of the protein or substrate, and then to determine the extent to which these data reproduce kinetic and fidelity data. The linear-response variants of this approach allowed us to analyze the energetic effects of right vs wrong base pairing, by altering the templating base (29), or by “mutating” charged protein side-chains near the active site (15, 27).

The EFER model, presented in this paper, was designed to maximize the potential of computer simulations to predict meaningful kinetic outcomes of small variations in the substrate chemical structure, or DNA or protein sequence near the active site. Its application revealed the synergy of the geometric/dynamical and linear-response energetic data for an important chemical step of the pol β catalyzed reaction. Our approach, in which the TS is modeled by a simple molecular mechanical force field, can readily be extended to encompass a different rate-limiting chemical TS, for example one for proton transfer (50, 53) or for the rotation of the OH bond on the protonated phosphorane (19). The approach of Warshel et al (15, 27) is the closest to our present linear-response model. The difference between the two approaches is that the two states evaluated by Warshel et al (15, 27), namely the dNTP substrate having the same TS structure in the aqueous solution and in the enzyme, differ significantly in the TS environment.

In contrast, protein structural differences between GSA and PTS states reside mainly near the dNTP substrate. This local character permits a factoring out of the energetic effects of dynamical fluctuations of distant protein residues that tend not to converge on a nanosecond simulation timescale. To eliminate large structural responses, we approximated the ground state of the nucleotidyl transfer reaction, which represents the state with the 3’O_nucH group, by GSA, which is the state with the 3’O_nuc- group. This approximation retains the large energetic difference between GSA and PTS because the energetic cost for deprotonating the 3’O_nucH group in pol β is small (~ 3 kcal/mol) (11, 23). Thus, although the postulated GSA and PTS states do not represent a true ground state and rate-limiting TS, respectively, the calculated free energy response to postulated structural differences between GSA and PTS states is substantial. This response contributes about 50% of the overall polymerase catalytic effect (13), and, after performing simulations on the complex containing a wrong dNTP, it generates an 80-fold contribution to the overall pol β fidelity.

The calculated catalytic and fidelity effects include contributions from all simulated protein and DNA residues, the ‘structural’ Mg²⁺ ion, and the base and γ-phosphate portions of the dNTP substrate. However, since the ‘catalytic’ Mg²⁺ ion was considered as a part of the probe region, its differential interactions with GSA and PTS states were excluded from the calculated free energies. Thus, the missing half of the overall catalytic effect is contributed by the nucleophile deprotonation step and the effect of the ‘catalytic’ Mg²⁺ ion on the nucleophilic attack step. Similarly, the calculated fidelity represents a portion of the overall fidelity of the pol β, which includes additional contributions from dNTP binding and possibly the deprotonation of the 3’O_nucH group.

Previously, considerable attention has been centered on the large conformational rearrangement of the pol β thumb subdomain going from an open to a closed and, presumably, catalytically active state (23). Spectroscopic kinetic data suggest that the rate of transition from open to closed is too rapid to be rate-limiting (8-12) for insertion of either right or wrong dNTP substrates. Even so, the “outcome” of this conformational change, i.e., the structure and relative free energy of the dNTP-DNA-pol β ternary complex, is essential for understanding, conceptualization, and quantification of pol β fidelity. Here, our simulations show that complexes containing incorrect dNTP remain in a closed form.

Many local interactions that were monitored in our MD trajectories, for example coordination distances of Mg²⁺ ions, showed no significant differences between right and wrong dNTP. Remarkably, few structural elements that did show such differences happened to favor the right dNTP. These differences include larger fluctuations of the O_nuc⋯P_α distance in the right GSA complex. These fluctuations tend to bring the nucleophile to the vicinity of P_α more frequently than for the wrong dNTP. We also observed weaker binding of the base of the wrong dNTP, which is consistent with longer calculated H-bonding distances in the G•dATP mispair than in the Watson-Crick pair. The relative binding free energy of 1.6 kcal/mol of the G•dATP mispair in pol β (29) also indicated a significant binding contribution to fidelity, which was attributed to the electrostatic preorganization of the active site (29, 48). Notably, in the absence of DNA polymerase, simulations of correct and incorrect base pairs in DNA in solution using the same MD method showed negligible ‘fidelity’ (54), including its preorganization component (55).

Further weakening of the base-base H-bonding interactions in the G•dATP mispair was observed in the PTS complex. These differences in right and wrong dNTP interactions occurring between PTS and GSA structures were also observed for the Arg 183 side chain. The strength of this interaction was correlated with the absence of intramolecular dNTP hydrogen bonding. That is, since the positively charged Arg183 stabilizes the extra negative charge that develops on the β-phosphate upon going from GSA to PTS, any hindrance of this interaction, be they either steric or electrostatic, should diminish PTS stabilization. An electrostatic hindrance is caused by sharing the non-bridging oxygen on β-phosphate as proton acceptor with the intramolecular dNTP H-bonding. Because this H-bonding interaction involves a 3’OH group of the deoxyribose, it is affected by the puckering mode of the dNTP deoxyribose moiety, which, in turn, may sense base-pairing between the incoming dNTP and templating base, or the presence of -O2’H substituent in a ribonucleotide substrate (56).

In this study we have eliminated most degrees of freedom of the simulated system. We can thereby calculate chemical catalysis and fidelity, which reflect the key properties of pol β. Retention of the huge numbers of degrees of freedom would, in our view, tend to confuse or obscure any rigorous interpretation of QM/MM calculations. Thus, we suggest that the EFER model provides a tractable and rapid QM/MM alternative. Perhaps its principal virtue is to be able to compute both the structural and energetic aspects of pol β fidelity using just two pairs of classical MD calculations on the GSA and PTS states for right and wrong pol-p/t DNA-dNTP complexes. Notably, we have found that dNTP conformation and its coordination by Mg²⁺ ions remain practically identical for the right and wrong dNTP, while the thumb subdomain is only marginally more closed in the right complex. The calculated differences in the active site dynamics of the GSA and PTS states in the right and wrong complexes indicate that pol β fidelity is significantly modulated by the template-dNTP base pairing, structural water in the vicinity of O_lg, and hydrogen bonding to Arg 183. The latter interaction is anticorrelated with the intramolecular dNTP hydrogen bonding. The observed propensity of the differential hydrogen-bonding from several active site groups to favor the right dNTP suggests that the PTS and actual rate-limiting TS for the nucleotidyl transfer reaction are structurally similar. This conclusion is further supported by the results of free energy simulations based on electrostatic linear-response model, which provided both reasonable catalytic and fidelity contributions from the nucleophilic attack reaction step. The EFER model, which combines the electrostatic linear response model with the two-state reaction model based on the GSA and PTS states, offers a straightforward way to make computational predictions of catalytic changes caused by chemical modifications of the pol β catalytic complex.

Abbreviations

pol β

DNA polymerase β

EFER

electrostatic linear free energy response

GSA

ground state activation intermediate

PTS

dianionic pentavalent phosphorane intermediate

O_nuc

3’-oxygen of the primer nucleotide

O_lg

bridging oxygen between α- and β-phosphate

LFER

linear free energy relationship

TS

transition state

QM/MM

quantum mechanics/molecular mechanics

EVB

empirical valence bond

MD

molecular dynamics

RMSD

root-mean square deviation

LFR

local reaction field

SCAAS

surface-constraint all-atom solvent

RDF

radial distribution function