Evaluating the effects of olivocochlear feedback on psychophysical measures of frequency selectivity

Abstract

Frequency selectivity was evaluated under two conditions designed to assess the influence of a “precursor” stimulus on auditory filter bandwidths. The standard condition consisted of a short masker, immediately followed by a short signal. The precursor condition was identical except a 100-ms sinusoid at the signal frequency (i.e., the precursor) was presented before the masker. The standard and precursor conditions were compared for measurements of psychophysical tuning curves (PTCs), and notched noise tuning characteristics. Estimates of frequency selectivity were significantly broader in the precursor condition. In the second experiment, PTCs in the standard and precursor conditions were simulated to evaluate the influence of the precursor on PTC bandwidth. The model was designed to account for the influence of additivity of masking between the masker and precursor. Model simulations were able to qualitatively account for the perceptual data when outer hair cell gain of the model was reduced in the precursor condition. These findings suggest that the precursor may have reduced cochlear gain, in addition to producing additivity of masking. This reduction in gain may be mediated by the medial olivocochlear reflex.

INTRODUCTION

A primary function of the cochlea is to separate the middle ear’s response to sound into individual frequency channels (von Békésy, 1960). This spectral separation results in a tonotopic (or frequency) map across the length of the cochlea. In other words, the cochlear response at a given place along the tonotopic axis is tuned to a narrow bandwidth of frequencies (Rhode, 1971). The range encompassed by this bandwidth has been used to characterize the frequency selectivity of the peripheral auditory system (e.g., Fletcher, 1940; Patterson, 1976; Glasberg and Moore, 1990; Oxenham and Shera, 2003). In terms of signal processing, the cochlea’s response is analogous to a bank of bandpass filters. Given this analogy, responses of the basilar membrane are often discussed in terms of filter properties such as filter best frequency (BF) and filter bandwidth (for a review, see Oxenham and Wojtczak, 2010). Nonlinearities associated with the cochlea’s outer hair cells (OHCs) have been shown to influence cochlear filter properties (e.g., Sellick et al., 1982). Specifically, as the gain of the OHCs is reduced, filters in the base of the cochlea broaden and the filter BF shifts to a lower frequency (Ruggero and Rich, 1991).

One mechanism involved in reducing cochlear gain is the medial olivocochlear (MOC) reflex (Cooper and Guinan, 2006). This reflex reduces the cochlear gain attributed to the OHCs in response to sound and may be responsible for improved detection and discrimination in the presence of background noise (Kawase et al., 1993). Moreover, the MOC reflex may be involved in dynamic range adaptation (Dean et al., 2005), which is hypothesized to improve neural coding over a wide range of sound levels. An interesting byproduct of reducing cochlear gain is that auditory filter bandwidth is also affected (e.g., Cooper and Guinan, 2006). This suggests that the effects of the MOC reflex may be studied through behavioral measures of frequency selectivity. Despite this, simultaneous masking studies on the dynamics of frequency selectivity (i.e., how frequency selectivity adapts over the course of stimulation) have produced mixed results. Some report a decrease in frequency selectivity over time (Strickland, 2001) while others report an increase (Bacon and Viemeister, 1985; Bacon and Moore, 1986; Kimberley et al., 1989; Wright and Dai, 1994; Bacon et al., 2002). The discrepancy between studies is likely related to methodological issues. In cases where the dynamics of frequency selectivity are studied by lengthening the masker (or equivalently delaying the signal from masker onset), frequency selectivity increases (Bacon and Viemeister, 1985; Bacon and Moore, 1986; Kimberley et al., 1989; Bacon et al., 2002). Conversely, when frequency selectivity is studied by preceding the masker with broadband noise at a fixed level (i.e., a “precursor”), frequency selectivity decreases (Strickland, 2001). Strickland (2004) argued that the increase in frequency selectivity over time reported in previous studies (e.g., Wright and Dai, 1994; Bacon et al., 2002) could be accounted for by assuming that cochlear suppression adapts.

In forward masking, where the masker does not suppress the signal, studies comparing estimates of frequency selectivity for short and long maskers have produced similarly mixed results, with one study reporting slightly broader tuning with masker duration (Kidd et al., 1984) and another reporting sharper tuning (Bacon and Jesteadt, 1987). Based on the assumption that the MOC reflex plays a role in the dynamics of frequency selectivity, it may be difficult to observe a large change in tuning between short and long maskers. As discussed by Jennings (2011), gain reduction by the MOC reflex may not be controlled when manipulating masker duration. For example, when measuring psychophysical tuning curves (PTCs) at several signal levels, the amount of gain reduced by a long masker will depend on the signal level. For high signal levels, the masker level at threshold will also be high and thus elicit a greater reduction in gain than at lower signal levels. Conversely, if the same experiment were repeated with a precursor instead of a long masker, the experimenter could fix the precursor level and thereby hold constant the amount of gain reduction across PTCs of different signal level.

Krull and Strickland (2008) described a technique that may allow the experimenter to control the amount of gain reduction elicited by the MOC reflex. This technique takes advantage of the sluggish onset of the reflex (Backus and Guinan, 2006) by presenting the masker and signal before the reflex produces an appreciable response. Masking thresholds for this “standard” condition are compared with a “precursor” condition, where a precursor tone is presented before the masker. This precursor is assumed to “get the reflex going,” so that when the signal is presented, cochlear gain has been reduced. Conversely, in the standard condition, the gain is at or near the maximum amount given that the short masker is expected to have little or no effect on reducing gain. Jennings et al. (2009) measured PTCs and compared estimates of frequency selectivity between standard and precursor conditions. They found that PTCs in the precursor condition were broader for all subjects. Moreover, they found that the difference in masking threshold at the tip and tail of the PTCs were well described by a model that included cochlear compression and gain reduction.

The results from Jennings et al. (2009) were limited to one signal level and one measurement technique (PTCs); therefore, it is unknown whether similar results would be found at other signal levels or with other measurement techniques. Furthermore, the modeling predictions were limited to masker frequencies at the tip (4000 Hz) and tail (2200 Hz) of the PTC, which prevented the model from predicting filter bandwidths. In the present study, the first experiment measured PTCs and notched noise tuning characteristics (NNTCs) in the standard and precursor conditions at several signal levels. The NNTC measurement was included because it is thought to better control for off-frequency listening and it evaluates whether another measurement of frequency selectivity results in broadened tuning in the precursor condition. The second experiment simulated PTCs using a model. Simulations that involved gain reduction, in addition to additivity of masking (Penner et al., 1980), were able to qualitatively account for the PTC data. The behavioral data for PTCs and NNTCs in the standard condition are presented and analyzed in a different way in another paper (Jennings and Strickland, 2012).

EXPERIMENT I: BEHAVIORAL ESTIMATES OF FREQUENCY SELECTIVITY WITH AND WITHOUT A PRECURSOR

Subjects and procedure

Six adults with normal hearing served as subjects in the experiment. Prior to enrollment in the study, subjects were evaluated using a battery of audiometric tests to rule out the presence of a hearing loss. This battery consisted of a case history, otoscopy, pure-tone audiometry, tympanometry, and distortion product otoacoustic emissions. Subjects with normal middle ear function and detection thresholds below 15 dB hearing level (HL) for audiometric frequencies (i.e., 500–8000 Hz) were enrolled in the study. A training period preceded data collection. This period lasted approximately 8–10 h. During the training period, subjects participated in a representative sample of the conditions described in the experiments. Subjects were paid for their participation.

All experiments took place in a sound-attenuated room using Tucker-Davis Technologies (TDT) (Alachua, FL) hardware. Stimuli were generated digitally (sampled at 25 kHz), output to four separate digital-to-analog channels (TDT DA3-4, 16-bit), low pass filtered at 10 kHz (TDT FT5 and FT6-2), mixed (TDT SM3), and sent to an ER-2 insert earphone via a headphone buffer (TDT HB6). These earphones have a flat frequency response at the eardrum for frequencies between 250 and 8000 Hz. Detection thresholds were measured using a three-alternative forced-choice procedure that estimated 70.7% correct on the psychometric function (Levitt, 1971). During a given trial, the subject heard three listening intervals marked visually on the computer screen and separated by 500 ms. Two of these listening intervals contained the masker. In the other interval (chosen randomly) the signal and masker were presented. The subject pressed a button to indicate the interval in which the signal was perceived. Feedback was given to indicate a correct or incorrect response. The masker level was decreased after an incorrect response and increased after two consecutive correct responses. Fifty trials were presented to estimate threshold. The step size was 5 dB until the second reversal, after which it decreased to 2 dB. A reversal was defined as a change in the step direction (i.e., from a high level toward a lower level, or vice versa). To calculate the threshold for a given run, the masker levels for all reversals at the smaller step size were averaged. If the total number of reversals at the smaller step size was an odd number, the first of these reversals was discarded and the remaining were averaged. A threshold search was rejected if the following conditions were met: (i) the standard deviation was greater than 5 dB or (ii) the signal was correctly identified at the maximum output level [95 dB sound pressure level (SPL) in the PTC experiment, and 89 dB SPL in the NNTC experiment] over two consecutive trials. For each condition, at least four thresholds were averaged to obtain the final threshold value.

Estimating frequency selectivity in the standard condition

Psychophysical tuning curves in forward masking were obtained using a 4-kHz sinusoidal signal. The signal was 6 ms (3-ms ${\text{cos}}^2$ rise/fall ramps) in duration and occurred immediately ($\Delta t=0$) after the 20 ms sinusoidal masker (5-ms ${\text{cos}}^2$ rise/fall ramps). Tuning curves were measured for a series of signal levels ranging from 35 to 60 dB SPL in 5 or 10 dB steps. The lowest level of this range (35 dB SPL) corresponds roughly to 10–15 dB sensation level (SL). Masker frequencies ranged from one octave below to a quarter octave above the signal frequency. The dependent variable was masker level at threshold. Off-frequency listening (Johnson-Davies and Patterson, 1979; O’Loughlin and Moore, 1981) was limited by presenting noise simultaneously with the masker and signal. The spectrum level of this noise was 50 dB/Hz below the signal level (Nelson et al., 2001). The spectrum of the off-frequency listening noise varied according to the masker frequency similar to Jennings (2011). For maskers below the signal frequency, the off-frequency listening noise had a high-pass characteristic. Similarly, for maskers above the signal frequency the off-frequency listening noise had a low-pass characteristic. Finally, for maskers at the signal frequency, the off-frequency listening noise had a notched characteristic. This approach assumes that off-frequency listening can occur in cochlear regions basal and apical to the signal place. The cutoff frequencies for the high-pass, low-pass, and notched noises were similar to those used by Oxenham and Plack (1997). Specifically, these cutoff frequencies were $0.9f_s$ for the low-pass noise and $1.2f_s$ for the high-pass noise, where $f_s$ is the signal frequency. For one subject (S1), the high-pass noise was not effective in restricting off-frequency listening when the masker frequency was just below the signal frequency (i.e., when the masker was 3750 Hz). This was evident from the masker level at threshold being much higher than expected, resulting in a “W”-shaped PTC. For this particular subject and condition a notched off-frequency listening noise was used instead of the high-pass noise.

The notched noise method provides an alternate technique for measuring frequency selectivity. The stimulus characteristics of the signal and masker were the same as for the PTC experiment, except the masker was a notched noise instead of a sinusoid. The spectral parameters of the notched noise were set according to Oxenham and Simonson (2006). Specifically, the notched noise was created by independently generating two bands of noise, one above the signal frequency (high-frequency noise band) and the other below the signal frequency (low-frequency noise band). High- and low-frequency noise bands had bandwidths of 1000 Hz. The notch-widths, ($\Delta f$), were normalized to the signal frequency and were 0.0, 0.025, 0.05, 0.1, 0.2, 0.3, and 0.4. Asymmetric notch conditions were also tested in three subjects (S1, S3, and S4) where the $\Delta f$ values for the upper notch (signal frequency to the cutoff of the high-frequency noise band) and lower notch (signal frequency to the cutoff of the low-frequency noise band) were measured in the following pairs, respectively: 0.1 and 0.3, 0.2 and 0.4, 0.3 and 0.1, or 0.4 and 0.2. Thresholds for these conditions (where available) were used to estimate auditory filter shapes (see Sec. 2E); however, many thresholds in the standard condition for high-level signals reached the maximum output of the equipment. Given this observation and the lack of asymmetric-notch conditions for S2 and S5, the discussion of the data will focus on the symmetric-notch conditions (see the Appendix for a table of thresholds in the asymmetric condition). In contrast to the PTC experiments, off-frequency listening was not expected to greatly influence the measured thresholds (Patterson, 1976); therefore, off-frequency listening noise was not presented.

This experiment was designed to estimate frequency selectivity when MOC reflex strength is weak (i.e., gain is maximal). The short masker and short masker-signal interval were chosen to take advantage of the sluggishness of the MOC reflex. In other words, subjects were assumed to detect the signal before the MOC reflex had time to build in strength.

PTCs and NNTCs in the precursor condition

The stimuli used in the precursor condition were similar to the standard condition, except a 100-ms precursor was presented before the masker. There was no delay between the precursor offset and the masker onset ($\Delta t=0$). The frequency of the sinusoidal precursor was the same as the signal (4 kHz) and was set at a constant level throughout the experiment. The level of the precursor was chosen based on the growth of masking experiment (described in Sec. 2D). Preliminary data suggested that precursor levels between 40–60 dB SPL would shift signal threshold in quiet by about 10–15 dB. The precursor levels needed to achieve this shift for each subject are presented in Table TABLE I.. The precursor condition is designed to estimate frequency selectivity when MOC reflex strength had time to reduce gain to near the maximal amount for the elicitor (i.e., the precursor). Estimates of frequency selectivity were compared between the standard and precursor conditions to test the hypothesis that the precursor reduced frequency selectivity.

TABLE I.

Absolute thresholds for the signal (θ) and the precursor levels ($L_{\text{PRE}}$) used in the precursor condition. The precursor levels selected were based on the growth of masking experiment (see text) and resulted in a 10–15 dB shift in quiet threshold.

Subject	θ (dB SPL)	$L_{\text{PRE}}$ (dB SPL)
S1	21.54	50
S2	20.00	50
S3	25.20	50
S4	24.31	40
S5	22.24	30
S6	24.50	40

Growth of forward masking with the precursor

A supplementary growth of masking experiment was used to determine the precursor level needed to shift signal threshold in quiet by 10–15 dB. This experiment served as an attempt to control the magnitude of masking produced by the precursor in the main PTC and NNTC experiments. Previous studies set the precursor at a constant level for all subjects (e.g., Krull and Strickland, 2008; Jennings et al., 2009); however, such an approach may result in the precursor producing a different amount of masking among subjects. In the supplementary experiment, the temporal and spectral properties of the signal and precursor were as described in Sec. 2B. Silence occupied the 20-ms interval previously occupied by the masker. In other words, no masker was presented and a 20-ms delay existed between the precursor’s offset and the signal’s onset. Thresholds were obtained for several signal levels ranging from 5 to 30 dB SL. In this case, threshold was defined as the precursor level needed to just mask the signal. The criteria used to select the precursor level for the PTC and NNTC experiments were as follows: (i) the precursor level resulted in a 10–15 dB shift in the signal’s threshold in quiet and (ii) the precursor level was a multiple of 10. These selection criteria have several advantages. First, if the MOC reflex is elicited by the precursor, the amount of gain reduced by the reflex should be roughly equal to the shift in threshold if it is assumed that no other masking effects are produced by the precursor (see Jennings and Strickland, 2010). Thus, the 10–15 dB threshold shift criterion ensures the amount of gain reduction was similar across subjects. Second, restricting precursor levels to be a multiple of 10 facilitates comparison with previous studies that also used this criterion (e.g., Krull and Strickland, 2008; Jennings et al., 2009; Jennings and Strickland, 2010; Roverud and Strickland, 2010). Quiet threshold and precursor levels for each subject are shown in Table TABLE I..

Estimating filter bandwidths

Filter sharpness was estimated from NNTCs using the power spectrum model of masking (Fletcher, 1940) and assuming rounded exponential (Roex) filter shapes (Patterson et al., 1982) as follows:

$$W(f_l)=(1-w)(1+p_l|g|)e^{-p_l\left|g\right|}+w(1+t_l|g|)e^{-t_l\left|g\right|},$$ (1)

$$W(f_u)=(1+p_u|g|)e^{-p_u\left|g\right|},$$ (2)

where W is the filter weighting function, l and u denote the upper and lower sides of the filter, g is the normalized deviation from the center frequency $|\Delta f|/f_c$, p (“$p_l$” or “$p_u$”), and t (“$t_l$” or “$t_u$”) determined the filter slopes at the tip and tail respectively, and w (“$w_l$” or “$w_u$”) determined the intersection of these two slopes. This method of fitting the NNTCs assumes that the signal is detected at a constant signal-to-noise ratio (SNR) at the output of an auditory filter centered on the signal frequency, whose slopes are defined by Eqs. 1, 2. Filter bandwidths were obtained from the Roexfits and used to calculate filter sharpness using the “quality factor” (Q) metric. Specifically, Q equals the filter’s center frequency divided by its bandwidth. Common Q values include bandwidths at 3 and 10 dB down from the filter peak (denoted $Q_3$ and $Q_{10}$). Initially, PTCs were also fit with Roex filter shapes; however, the fits were poor in the precursor condition. Given this finding, PTC bandwidths and Q values were obtained from data point interpolations rather than from Roex filter shapes.

RESULTS

NNTCs

Notched noise tuning characteristics as a function of signal level are presented in Fig. 1, where each column of panels displays data from a different subject. Within each panel the standard (open symbols) and precursor (closed symbols) NNTCs are compared. At high levels, some NNTCs in the standard condition are absent [e.g., S1 (55 dB), S4 (55 and 60 dB)] due to limits imposed on the maximum output of the headphones (95 dB SPL for tones, 89 dB SPL for noise). When comparing NNTCs of a given signal level across subjects (e.g., comparing filled or open symbols across adjacent columns) the effects of inter-subject variability are apparent. Given this variability, the data will be described for each subject individually, rather than by averaging the data across subjects. Estimates of filter sharpness obtained from the Roex fits are plotted in Fig. 2a. Sharp auditory filters have large Q values while broad filters have small Q values. For all but two comparisons [S2 (55 dB), S3 (60 dB)], the filters estimated in the precursor condition are broader than filters estimated in the standard condition.

Figure 1.

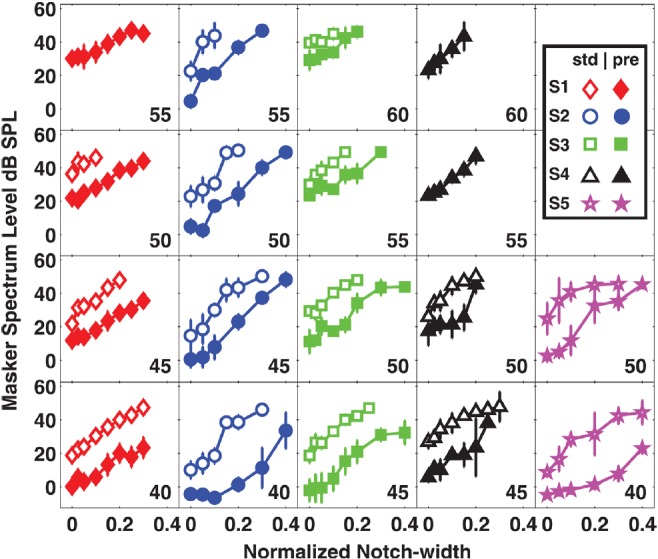
(Color online) NNTCs for standard (open symbols) and precursor (closed symbols) conditions as a function of signal level in five subjects. Signal level in dB SPL is displayed in each panel. Each column of panels represents a different subject as shown by the legend. The data plotted are from normalized notch-widths (x-axis) that were symmetric around the center frequency (4000 Hz). For visual clarity, asymmetric notch-widths are not plotted, however, they were included in fitting the data and are provided in Table TABLE III. in the Appendix. Error bars represent one standard deviation about the mean.

Figure 2.

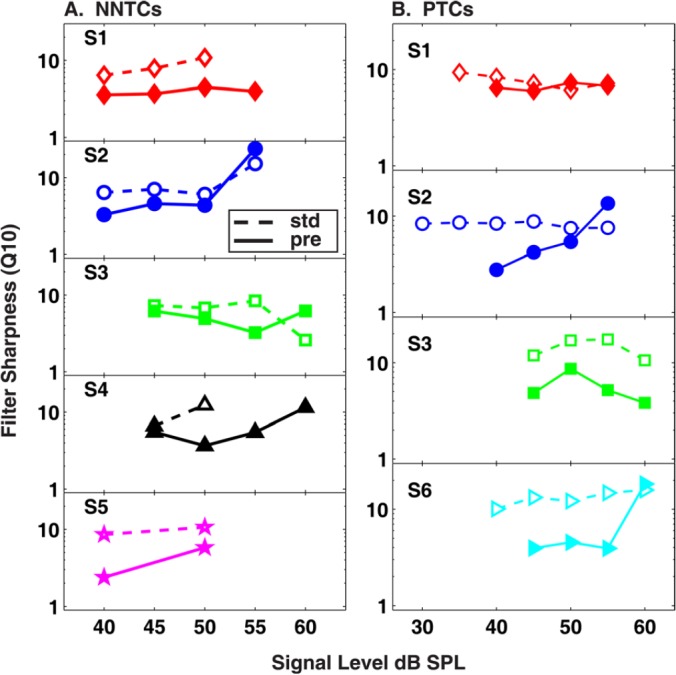
(Color online) Estimates of filter sharpness ($Q_{10}$) for (a) NNTCs and (b) PTCs. The standard (“std”) and precursor (“pre’’) conditions are displayed as open and closed symbols, respectively. Each panel represents a different subject and shows $Q_{10}$ estimates as a function of signal level in dB SPL.

PTCs

Psychophysical tuning curves in the standard (open symbols) and precursor (closed symbols) conditions are presented in Fig. 3. The organization of the figure panels is the same as in Fig. 1, where each column represents a subject and rows represent different signal levels. Similar to the NNTC experiment, appreciable inter-subject variability was observed. Given this variability, the data will be described for each subject individually, rather than by averaging the data across subjects. Estimates of PTC filter sharpness are plotted in Fig. 2b. Similar to the NNTC data the filters estimated in the precursor condition were generally broader than filters estimated in the standard condition.

Figure 3.

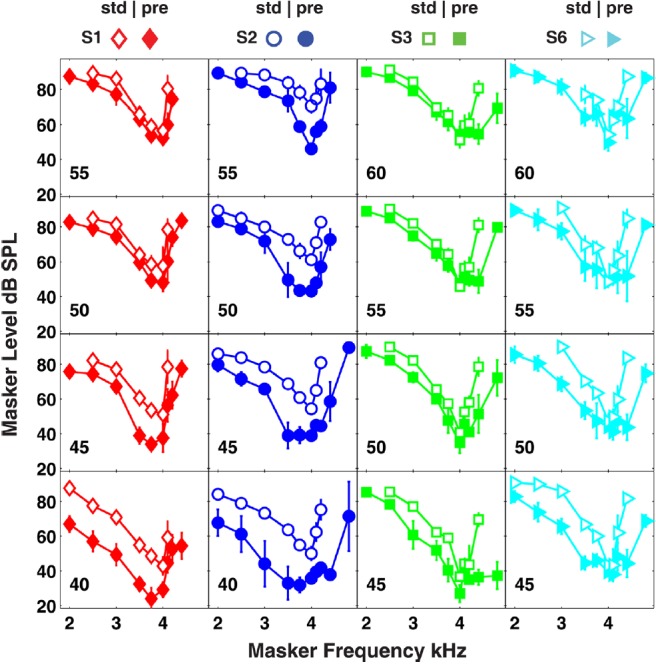
(Color online) PTCs in the standard (open symbols) and precursor (closed symbols) conditions as a function of signal level in four subjects. Each column of panels represents a different subject. Signal level in dB SPL is plotted in each panel. Error bars represent one standard deviation about the mean.

In evaluating the statistical significance of broadened tuning in the precursor conditions, Q values were logarithmically transformed (because Q is a ratio) and submitted to a repeated-measures analysis of variance (ANOVA). For the NNTC data, a one-way ANOVA was run with condition (standard vs precursor) as the factor. Prior to computing the ANOVA, Q values for each listener were averaged for signal levels 50 dB SPL and below (note that the number of values in the average varies slightly across level). The effect of condition was statistically significant for $Q_3$$[F(1,\hspace{0.17em}4)=27.688,p=0.0062]$ and $Q_{10}$$[F(1,\hspace{0.17em}4)=29.131,\hspace{0.17em}p=0.0057]$ suggesting that the precursor broadened filter bandwidths for NNTCs measured at 50 dB SPL and below. A two-way ANOVA was run on the PTC data with signal level and condition as factors. $Q_3$ and $Q_{10}$ were averaged across low (17.50–27.50 dB SL) and high (27.51–37.50 dB SL) signal levels (values for individual subjects are provided in Tables 2, TABLE III. in the Appendix). In other words, the signal-level factor was grouped into low and high categories based on SL. Similar to the NNTC analysis, the effect of condition was statistically significant for $Q_3$$[F(1,\hspace{0.17em}4)=10.70,p=0.0467]$; however, it was not significant for $Q_{10}$$[F(1,\hspace{0.17em}4)=7.245,\hspace{0.17em}p=0.0743]$. Neither the effect of signal level nor the interaction between signal level and condition were significant. These results provide further support for the conclusion that the precursor broadened filter bandwidths.

TABLE II.

Estimates of filter sharpness derived from NNTCs using Roex (pwtp) filter shapes. The level of the signal or “probe” is presented in the column labeled “Lp.” Rows corresponding to the standard and precursor conditions (see Secs. 2B, 2C) are labeled in the left-most column as “std” and “pre,” respectively. Frequency selectivity is quantified in terms of Q₃ and Q₁₀ values and tabulated for each subject (columns).

		S1		S2		S3		S4		S5
std/pre	Lp	Q3	Q10	Q3	Q10	Q3	Q10	Q3	Q10	Q3	Q10
std	40	14.9	6.41	14.7	6.41	—	—	—	—	20	8.55
pre	40	8.26	3.58	7.58	3.29	—	—	—	—	5.49	2.37
std	45	18.5	7.87	16.1	7.04	16.9	7.3	15.4	6.62	—	—
pre	45	8.62	3.7	10.6	4.59	14.3	6.17	12.8	5.52	—	—
std	50	31.3	10.8	13.9	6.06	16.1	6.8	28.6	12.3	24.4	10.6
pre	50	10.4	4.48	10.2	4.39	11.4	4.93	8.47	3.66	13.3	5.78
std	55	—	—	34.5	15.2	20	8.4	—	—	—	—
pre	55	9.26	3.98	55.6	23.8	7.52	3.24	12.7	5.46	—	—
std	60	—	—	—	—	5.32	2.29	—	—	—	—
pre	60	—	—	—	—	15.2	6.21	26.3	11.4	—	—

TABLE III.

Estimates of filter sharpness interpolated from PTCs in the standard (std) and precursor (pre) conditions (left-most column). The level of the signal or “probe” is presented in the column labeled “Lp.” Frequency selectivity is quantified in terms of Q₃ and Q₁₀ values and tabulated for each subject (columns).

		S1		S2		S3		S6
std/pre	Lp	Q3	Q10	Q3	Q10	Q3	Q10	Q3	Q10
std	30	—	—	21.5	8.35	—	—	—	—
std	35	26.3	9.33	16.5	8.55	—	—	—	—
std	40	27.1	8.37	22.4	8.4	—	—	30.6	10.1
pre	40	16	6.47	7.02	2.78	—	—	—	—
std	45	14.1	7.2	27.8	8.79	54	11.9	25	13.3
pre	45	10.3	6.01	6.59	4.21	52	4.84	22.5	3.94
std	50	11.2	7.3	22.5	7.49	56.9	17.1	26.5	12.2
pre	50	12.6	7.33	9.39	5.41	46.8	8.64	10	4.52
std	55	14.4	7.2	23	7.56	58.2	17.5	47.2	14.8
pre	55	12.2	6.77	45.2	13.5	7.95	5.18	10.3	3.92
std	60	—	—	—	—	45.7	10.6	53.2	15.9
pre	60	—	—	—	—	6.83	3.82	61.1	18.3

EXPERIMENT II: MODEL SIMULATIONS OF PTCS WITH AND WITHOUT A PRECURSOR

The results from Experiment (Expt.) I suggest that a precursor may reduce frequency selectivity. Several mechanisms could be responsible for this reduction, two of which are evaluated here by simulating PTCs in forward masking. Detection thresholds were predicted using a modified version of a well-established masking model (Oxenham and Moore, 1994). Data from masking experiments are often interpreted in terms of processes in the auditory periphery. Perhaps the most common interpretation of such experiments assumes that cochlear non-linearities, such as compression, play a large role in shaping masking data (Oxenham and Bacon, 2004). Given the proposed importance of cochlear non-linearities, any attempt to model masking data should ensure that cochlear non-linearities are well accounted for by the model.

The temporal window model and cochlear non-linearities

Oxenham and Moore (1994) demonstrated the importance of including cochlear non-linearities in models of masking. Their model, known as the “temporal window” model, consists of three stages. The first stage accounts for cochlear filtering and compression. The second accounts for “central” processes including squaring, low-pass filtering, and temporal integration. The windowing function (i.e., the “temporal window”) commonly used for temporal integration consists of the sum of two exponentials. The time constants of these exponentials were derived from psychophysical data (Moore et al., 1988; Oxenham and Moore, 1994). The third stage accounts for the processes involved in detecting the signal. A common implementation of this stage assumes that an “interval comparison” strategy is used to detect the signal (e.g., Oxenham and Moore, 1994). In other words, the listener compares two intervals involving: (i) the masker or (ii) the signal and the masker (“signal + masker”). When the ratio of the outputs to the masker and the signal + masker reaches a criterion value, the signal is assumed to be detected.

The temporal window model has been successful at predicting a wide body of masking data. Despite this success, there are certain instances where the model falls short (Oxenham, 2001; Plack et al., 2002). In these instances, this is largely due to the simplicity of its first stage (cochlear filtering and non-linearity). For example, the model lacks the cochlear processes associated with suppression and medial olivocochlear feedback and as such does not predict psychophysical suppression (Houtgast, 1972), overshoot (Zwicker, 1965), and temporal effects in forward masking (e.g., Jennings et al., 2009; Jennings and Strickland, 2010; Roverud and Strickland, 2010). Plack et al. (2002) replaced the first stage of the temporal window model with a robust cochlear model developed by Meddis and colleagues (Meddis et al., 2001; Lopez-Poveda and Meddis, 2001). This approach was effective at predicting an array of psychophysical phenomenon including suppression, growth of on and off-frequency masking, and PTCs in simultaneous and forward masking. A similar approach is taken in this paper, however, with a different cochlear model.

An alternative model of cochlear non-linearity

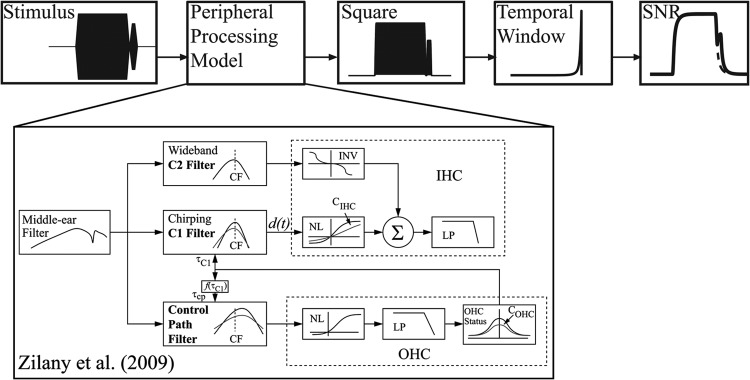
Carney and colleagues (Carney, 1993; Zhang et al., 2001; Bruce et al., 2003; Zilany and Bruce, 2006; Zilany et al., 2009) developed a model of the cat peripheral auditory system and tested this model against a wide array of published physiological data (for a review, see Heinz, 2010). The most recent version of this model (Zilany et al., 2009) has been called the “power-law” model because of its use of power-law dynamics to account for synaptic adaptation. A strength of the power law model is its ability to capture cochlear non-linearities including compression and suppression. In addition, the model’s OHC gain can be adjusted to simulate feedback from the MOC reflex. In the current simulations, part of the power-law model was substituted for the first stage of the temporal window model as shown in Fig. 4. Given this substitution, the composite model will be referred to as the power law-temporal window (PL-TW) model. In the power-law model the stimulus is filtered by the middle ear module and then processed in three parallel filter paths (Zilany and Bruce, 2006). The interaction between the “C1 filter” and control path filter accounts for many cochlear non-linearities including suppression and compression (Zhang et al., 2001; Heinz et al., 2001). The degree of non-linearity is realized via a scaling constant called $C_{\text{OHC}},$ which forms part of the model’s OHC module (box labeled “OHC” in Fig. 4). Conceptually, the $C_{\text{OHC}}$ parameter can be thought of as a gain control for the OHCs. The value of $C_{\text{OHC}}$ ranges from 0 (no gain) to 1 (full gain). Given the relationship between $C_{\text{OHC}}$ and OHC gain, several investigators have used $C_{\text{OHC}}$ to simulate hearing impairment (Zilany and Bruce, 2006, 2007; Heinz and Swaminathan, 2009) and MOC feedback (Jennings et al., 2011; Chintanpalli et al., 2012). In the PL-TW model, the output of the inner hair cell module (box labeled “IHC”) is squared and then fed into a sliding temporal integrator. At the output of the integrator the SNR is calculated. The details of how thresholds are predicted from the PL-TW model are presented in Sec. 4D.

Figure 4.

A block diagram of the temporal window-power law model. This model is similar to Oxenham and Moore (1994) except the nonlinear stage is replaced with a computational model of the auditory periphery (Zilany et al., 2009). The inset is a block diagram of the power-law model for auditory nerve responses. The OHC health can be manipulated by adjusting the model’s $C_{\text{OHC}}$ parameter. (Figure modified slightly from Fig. 2 in Zilany et al. (2009), and used with permission from the Acoustical Society of America.)

Stimuli

The objective of the modeling experiment was to simulate the two sets of PTCs presented in Expt. I; one set with a precursor and the other without. The temporal parameters (duration, rise/fall ramps, etc.) of the precursor, masker, and signal were the same as in the psychophysical experiment presented in Secs. 2B and 2C. Similarly, the range of masker frequencies spanned from one octave below to a quarter octave above the signal frequency. To account for the difference in the cochlear map between cat and human, the signal frequency used in the simulations was 11 kHz. This signal frequency in the cat cochlea corresponds roughly to 4 kHz in the human cochlea according to the Greenwood cochlear map (Greenwood, 1990). Off-frequency listening noise was presented in a manner similar to the psychophysical experiment (see Sec. 2B).

Procedure

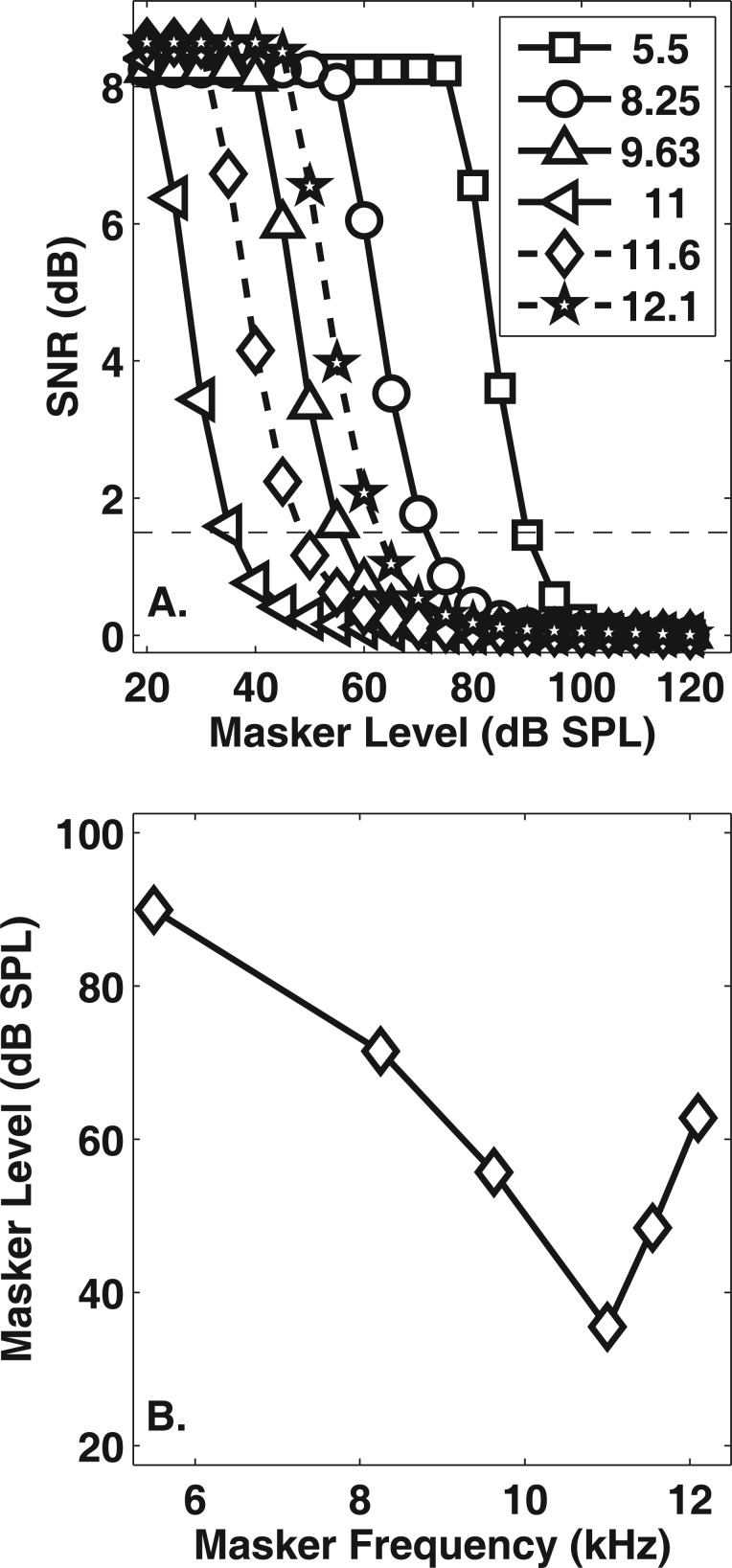
Thresholds for simulated PTCs were obtained by comparing the difference between the model’s response to the masker (masker interval) and its response to the masker plus the signal (target interval). This approach mimics a two-alternative forced-choice task common in psychophysical research. For a given signal level, masker and target interval simulations were collected for masker levels ranging from 0–120 dB SPL. The organization of the model simulations involved first defining the stimulus parameters of the experiment and preparing a list of masker and target intervals needed to predict thresholds. Next, the stimuli were generated based on the information in this list and then presented to the power-law model. After the IHC output was retrieved, the data were down-sampled and saved. Only the response of the characteristic frequency (CF) corresponding to the signal frequency was evaluated. The IHC output for the masker and target intervals, at a given signal level, was loaded, squared, and then passed through the temporal integration window via convolution. The difference in dB between intervals was calculated resulting in a vector of SNR values across time. The maximum SNR value in the vector (i.e., the best time slice) was saved for each signal/masker pair and subsequently used to estimate threshold. After these SNR values were saved for each masker frequency, a PTC was constructed by interpolating masker threshold at each masker frequency for a defined SNR. Figure 5 displays an example of this procedure for an SNR of 1.5 (horizontal dashed line in the top panel).

Figure 5.

An example of how PTCs were predicted from model simulations. (a) SNR plotted as a function of masker level for various masker frequencies (symbols). The dashed horizontal line represents an SNR of 1.5 dB. (b) A PTC resulting from a criterion SNR of 1.5 dB.

Model settings

The PL-TW model had five parameters. Three of these parameters exist in the temporal window, one in the decision device, and one in the gain settings of the OHCs. The forward-masking slopes of the temporal window were defined by a double exponential function

$$W(t)=(1-w)\exp (t/{\tau }_1)+w\hspace{0.17em}\exp (t/{\tau }_2),$$ (3)

where $W(t)$ is the weighted windowing function, ${\tau }_1$ and ${\tau }_2$ are time constants, and w is a weighting factor. In previous psychophysical experiments (Oxenham and Moore, 1994; Plack and Oxenham, 1998), the time constants and weighting factor of the temporal window have been statistically adjusted to best fit the data. During the fitting process, the parameters in stage 1 (i.e., the stage representing cochlear non-linearities) are often fixed, while the temporal window parameters are adjusted. The purpose of the current experiment is not to provide a quantitative comparison with psychophysical data; therefore, it is not necessary to statistically adjust temporal window model parameters to fit the data. Instead, temporal window parameters were set based on previous experiments (e.g., Oxenham and Moore, 1994; Oxenham, 1998, 2001) and were ${\tau }_1$ = 4 ms, ${\tau }_2$ = 29 ms, and $w=0.16$. Several other ${\tau }_1$, ${\tau }_2$, and w parameter values were evaluated and found to have a negligible effect on the results (data not shown). Another parameter in the masking model is the SNR value defining the threshold for the signal in the presence of the masker. It was assumed that this ratio is constant across conditions. Several possible SNR values were used to make predictions and then compared with the behavioral data. The SNR values used ranged from 0.5–7 dB, which is similar to the range of SNR values in published psychophysical data in forward masking (e.g., Plack and Oxenham, 1998; Oxenham, 2001).

The model’s OHC gain was adjusted based on two theories of forward masking. These theories make explicit assumptions about how two consecutive forward maskers are processed in the auditory system. In the context of Expt. I, these theories seek to provide an explanation of the effect of presenting a precursor before the masker. For clarity, a description of each theory is given only for the specific case circumscribed by the stimuli described in Expt. I. In this case, the masker is short, the precursor is relatively long, and the delay between masker offset and signal onset is 0 ms. The first theory assumes that the precursor and masker energies are integrated (or “added”) at the output of the peripheral model. Due to this assumption, this theory is often called the “additivity of masking” theory or simply the “additivity” theory. This theory assumes that OHC gain is constant across standard and precursor conditions. Thus, the gain of the OHCs was not reduced in simulations evaluating the additivity theory. In contrast, the second theory assumes that, in addition to additivity, the precursor reduces the gain applied to the signal and is observed as increased masking. This theory is called the “additivity + gain reduction” theory. In this theory, the amount of gain reduction is a function of the level of the precursor. In the PTC study described in Expt. I, the precursor level was chosen to produce a 10–15 dB shift in threshold. Thus, in simulations evaluating the additivity + gain reduction theory the gain of the OHCs was reduced by 15 dB in the precursor condition relative to the standard condition. This amount of gain reduction was achieved using the model’s $C_{\text{OHC}}$ parameter. Thus, the only difference between simulations evaluating the additivity and the additivity + gain reduction theories was the amount of gain reduction in the model’s OHC module.

Masker thresholds tend to decrease rapidly when the signal level is set near absolute threshold. These “near-threshold effects” are thought to be due to the influence of noise within the subject or “internal noise.” An example of this noise is the heart rate or respiration of the subject. In a masking task, the internal noise is thought to act as a second masker. The effect of the internal noise is well accounted for by assuming energies from the masker and the internal noise add together to produce greater masking (Humes and Jesteadt, 1991; Plack and Skeels, 2007). The average absolute threshold for the signal in Expt. I was 23 dB SPL. For the model simulations, the IHC output to the signal set at this level (${\text{IHC}}_{\theta }$) was measured. To simulate the influence of internal noise, all values of the IHC output less than ${\text{IHC}}_{\theta }$ were replaced with ${\text{IHC}}_{\theta }$.

Modeling results and discussion

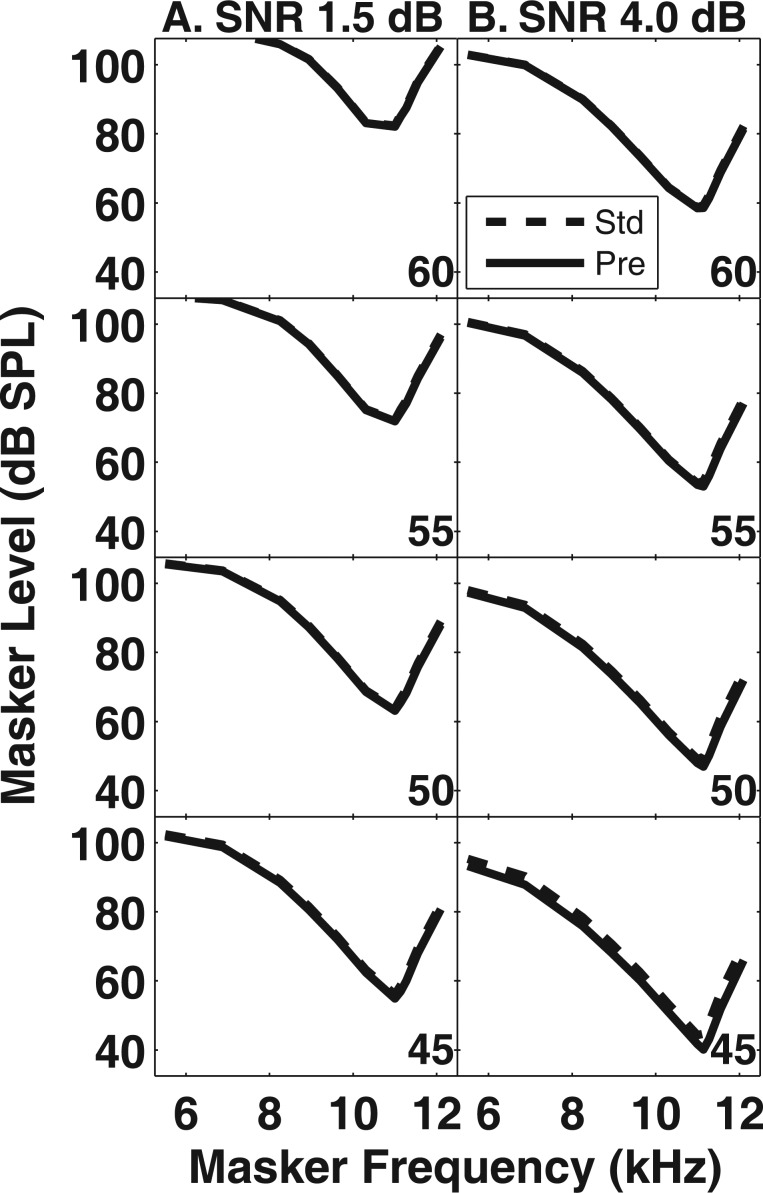
Simulated PTCs evaluating the additivity hypothesis are presented in Fig. 6 for four signal levels (rows) and two SNRs (columns). In each panel, simulated PTCs for the standard (dashed lines) and precursor (solid lines) conditions are displayed, along with the associated signal level in the lower right-hand corner. These signal levels are similar to those used in Expt. I in terms of dB SPL and dB SL. In general, the results of the model simulations evaluating the additivity hypothesis were similar regardless of the condition (i.e., standard vs precursor), the signal level, or the SNR (1.5 and 4.0 dB in the left and right columns, respectively). These simulations suggesting that additivity of masking does not predict that PTC bandwidths broaden when a precursor is presented.

Figure 6.

Simulated PTCs based on the assumptions of the additivity-of-masking hypothesis (see text). Each panel displays simulated PTCs in the standard (dashed lines) and precursor (solid lines) conditions. The signal level associated with each pair of PTCs is indicated in the lower right corner of each panel. (a) Simulated PTCs with a SNR set to 1.5 dB. (b) Simulated PTCs with an SNR set to 4 dB.

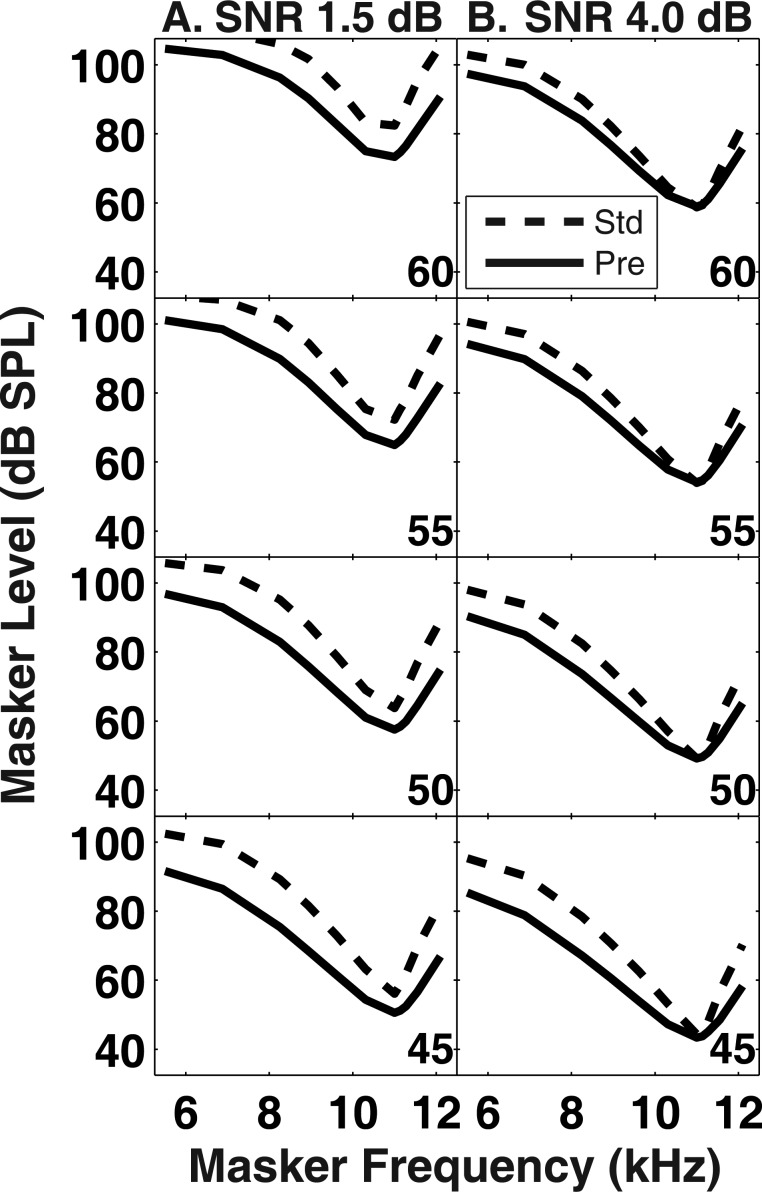
Figure 7 displays simulations evaluating the additivity + gain reduction theory in the same format as Fig. 6. In these simulations, PTCs in the precursor condition were appreciably broader than those in the standard condition. The difference in PTC bandwidth between standard and precursor conditions decreased with increasing signal level. Finally, the vertical offset between PTCs in the standard and precursor conditions depended on the SNR, where the smaller SNR (1.5 dB) produced a larger offset [Fig. 7a]. The magnitude of the vertical offsets observed in the behavioral data (Fig. 3) was variable across subjects, suggesting that different SNRs between subjects may account for this variability.

Figure 7.

Simulated PTCs based on the assumptions of the additivity + gain reduction hypothesis where cochlear gain was reduced by 15 dB (see text). Each panel displays simulated PTCs in the standard (dashed lines) and precursor (solid lines) conditions. The signal level associated with each pair of PTCs is indicated in the lower right corner of each panel. (a) Simulated PTCs with a SNR set to 1.5 dB. (b) Simulated PTCs with an SNR set to 4 dB.

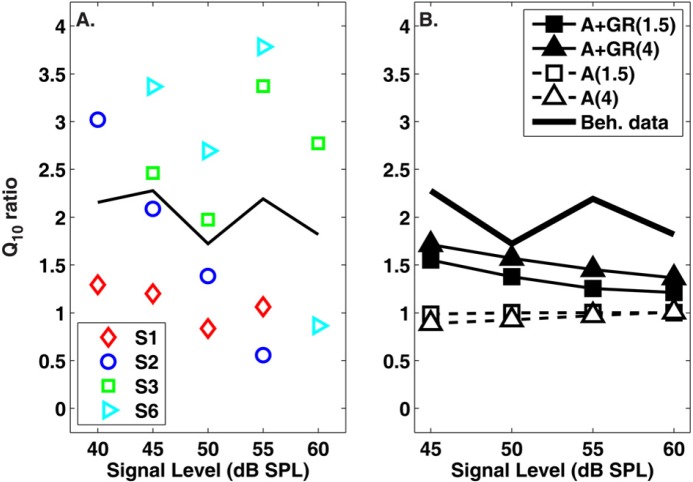
The ratio in $Q_{10}$ between standard and precursor conditions was calculated for the behavioral data, and for the simulations in Figs. 67. This ratio is presented in Fig. 8, where Fig. 8a displays the behavioral data in individual (symbols) or averaged (solid line) form and Fig. 8b compares this average with the model simulations. Although there is appreciable variability in the behavioral data, the additivity + gain reduction model simulations appear to catch the general trend of decreasing ratio in $Q_{10}$ with signal level. In contrast, the additivity simulations predict equal frequency selectivity in standard and precursor conditions, regardless of signal level.

Figure 8.

(Color online) The ratio of $Q_{10}$ values between experimental conditions (standard $Q_{10}$/precursor $Q_{10}$) for psychophysical tuning curves measured empirically (a) or simulated with the model (b). The solid line in (a) and (b) is the mean of the behavioral data presented in (a). Symbols in (b) represent simulations based on the additivity (A) or additivity + gain reduction hypothesis (A + GR). The SNR (in dB) for a given simulation is also provided in the legend in parentheses.

GENERAL DISCUSSION

Estimates of frequency selectivity in the precursor condition were broader than the standard condition except for at the highest signal level in some subjects (S2 and S3 in NNTCs and S2 and S6 in PTCs). These results are consistent with Jennings et al. (2009) who reported broader PTCs in the precursor condition at one signal level. Only three subjects participated in both measurements of frequency selectivity; therefore, it is difficult to determine if the ratio of $Q_{10}$ values (i.e., the standard $Q_{10}$ divided by the precursor $Q_{10}$ for a given level) was correlated between PTCs and NNTCs. As discussed in Jennings (2011), a correlation may not exist due to increased off-frequency listening or mutual suppression of high and low-side noise bands in the NNTC experiment. Furthermore, the effects of cochlear compression are not accounted for by PTC and NNTC techniques and further suggest that a correlation may not exist between PTCs and NNTCs. However, the influence of compression can be accounted for if iso-level filters are inferred by transforming the data by the cochlear input–output (I/O) function at the signal place (Eustaquio-Martin and Lopez-Poveda, 2011). Similarly, as discussed by Eustaquio-Martin and Lopez-Poveda (2011), compression may explain why PTCs and NNTCs do not always show decreasing filter bandwidths with stimulus level as often observed in physiological studies (e.g., Ruggero et al., 1997).

The present results suggest that the largest difference between standard and precursor PTC bandwidths may be for lower signal levels. This finding is consistent with gain reduction being largest at the low input levels (Murugasu and Russell, 1996; Cooper and Guinan, 2006). Moreover, cochlear compression may accentuate this difference. For example, maskers on a compressed I/O function (i.e., those with frequencies near the signal frequency), would experience a relatively larger decrease in masker threshold compared to maskers on a linear I/O function (i.e., those with frequencies at the tails of the PTC). Conversely, the masker at the signal frequency may experience the same magnitude of gain reduction as the signal and result in a small change in threshold. At higher signal levels, the signal is less influenced by gain and may be on the compressive part of the I/O function. This would result in the precursor producing a smaller change in masker threshold. This explanation may also account for the poor Roex fits in the precursor condition, since the Roex model cannot fit a filter that has a very shallow slope near the tip followed by a steep slope in the tail. This is the kind of pattern that occurs in S1 (45 dB), S2 (45 dB) on the low-frequency side of the PTCs and in S2 (40 dB), S3 (55 dB), and S4 (50 and 55 dB) on the high-frequency side of the PTCs.

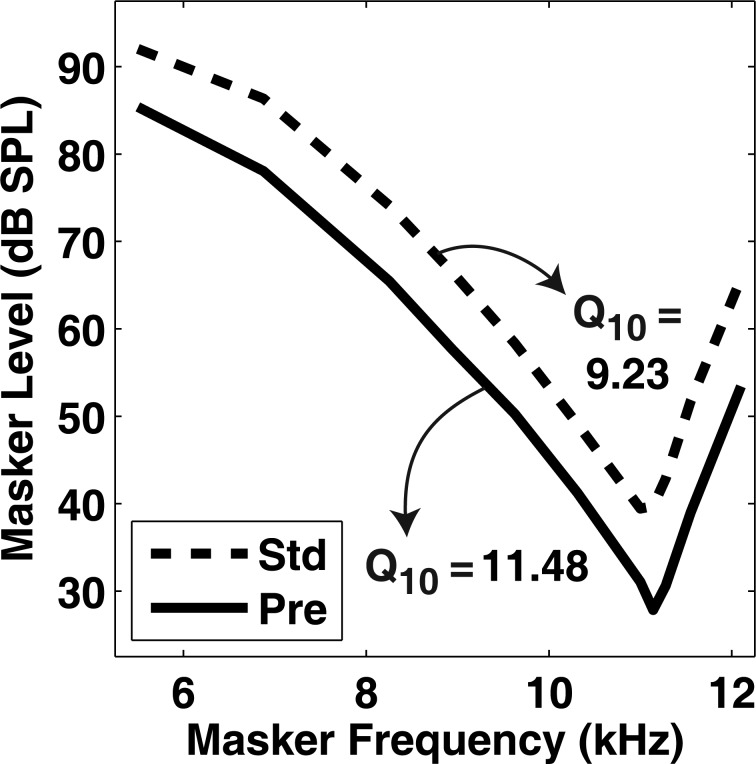
The modeling section evaluated the additivity of masking and gain reduction hypotheses in terms of accounting for the effects of the precursor on PTCs. The model that included gain reduction, in addition to additivity, qualitatively captured the reduction in $Q_{10}$ seen in the behavioral PTCs measured with a precursor. These results support the hypothesis that the precursor elicited the MOC reflex or some other mechanism that reduces gain. The influence of additivity of masking was less than expected in the simulated PTCs. Since the precursor level was held constant, masking due to the precursor should be largest at low signal levels and result in a decrease in masker level relative to the standard condition. Although this pattern was observed, the decrease was only a few dB and not large enough to account for the behavioral data. The smaller-than-expected additivity effect may be due to the relatively high signal levels (15–20 dB SL) tested, suggesting that the precursor energy made a small contribution to the total energy needed to mask the signal. Even though the precursor shifted quiet threshold for the signal by 10 dB, the signal level for the lowest PTC was still 5–10 dB above masking threshold for the precursor. This suggests that simulated PTCs at lower stimulus levels (e.g., 25–40 dB SPL) should exhibit stronger additivity effects, as the precursor energy should account for much of the total energy needed to masker the signal. Figure 9 displays a simulated PTC obtained under the additivity hypothesis where the signal level was 40 dB SPL. As expected, the influence of additivity of masking is large (∼10 dB); however, unlike the behavioral data, the bandwidth of the PTC is narrower in the precursor condition. These narrower bandwidths may arise from the differences in the amount of compression applied to maskers near and remote from the signal frequency. Since greater compression is applied near the signal frequency, thresholds for these frequencies tend to decrease at a relatively faster rate than those for remote masker frequencies, resulting in narrowing of the bandwidth. These results suggest that while additivity does predict a large shift in masker threshold, it does not predict a broadening in filter bandwidth.

Figure 9.

Predicted PTCs in the standard (dashed line) and precursor (solid line) condition at a low signal level (40 dB SPL) and under the additivity hypothesis. Filter sharpness ($Q_{10}$) is shown for each PTC as indicated by the arrows.

In some cases, the tip of the behavioral PTCs shifted away from the signal frequency in the precursor condition (e.g., S1 at 40 and 45 dB SPL, S2 at 40 and 45 dB SPL). This shift is interesting because it was similarly reported by Jennings et al. (2009), but was not observed in the model simulations. Previous studies suggest that a PTC with a shifted tip is indicative of off-frequency listening (Moore and Alcantara, 2001; Kluk and Moore, 2004). This may explain why the model simulations did not predict PTCs with shifted tips, as only the CF at the signal frequency was simulated. One problem with this explanation is the observation that PTCs with shifted tips occurred at relatively low signal levels (∼15–20 dB SL). The influence of off-frequency listening is expected to be greatest at high levels where the signal’s excitation spreads to adjacent CFs. Thus, it appears that off-frequency listening cannot explain why PTCs at high levels did not have shifted tips. In a similar model simulation, Jennings (2011) found that off-frequency listening was not expected to play a large role in determining the bandwidth of PTCs measured with a precursor.

Overall, the results of the present experiment suggest that auditory gain and frequency selectivity adapt during the course of acoustic stimulation. The mechanisms of this adaptation may occur at several locations along the auditory pathway, from the periphery to the auditory cortex (Robinson and McAlpine, 2009). Given the purely psychophysical approach, it is difficult to prove that temporal effects in masking (e.g., Schmidt and Zwicker, 1991; von Klitzing and Kohlrausch, 1994; Strickland, 2001; Krull and Strickland, 2008; Jennings et al., 2009; Roverud and Strickland, 2010) are primarily due to the MOC reflex. Despite this, using the MOC reflex as a framework has proven useful in accounting for effects of the precursor across a variety of stimulus manipulations including: precursor level (Strickland, 2008), precursor duration and delay from masker onset (Roverud and Strickland, 2010; Jennings et al., 2011), and masker frequency (Jennings et al., 2009). Based on the results of the current experiment, this list can be expanded to include technique for measuring frequency selectivity (NNTC vs PTC) and signal level.

If the MOC reflex does play a primary role in masking, as suggested by the current results, there are obvious issues to consider regarding masking theories and techniques. For example, the temporal window model (Oxenham and Moore, 1994) has proven to be effective in predicting a wide variety of data in forward and backward masking. Explicit in the architecture of this model is the assumption that the “compressive non-linearity” (or basilar membrane response) does not adapt with time. Any predicted “temporal effects” in forward masking are a result of the model’s temporal integration window, which occurs after basilar membrane compression. In this context “temporal effects” include changes in threshold associated with masker duration, masker delay from signal onset, and adding an additional masker (or precursor). Given the integration operation, the temporal window model predicts that the precursor and masker energies will add after being processed by the basilar membrane. In other words, the model assumes additivity of masking. The modeling results in the present study show that reducing the gain of the basilar membrane, in addition to additivity, improved the model’s ability to account for the reduction in frequency selectivity observed in the behavioral PTCs. Furthermore, certain changes in threshold associated with precursor duration and delay from masker onset are not predicted by the temporal window model (Roverud and Strickland, 2010). Finally, integration-based models of masking are unable to predict temporal effects in simultaneous masking such as overshoot (Zwicker, 1965) and the effects of gated and continuous maskers (see Oxenham, 2001). Effects such as these are well accounted for by a masking model based on gain reduction (Strickland, 2001; Jennings et al., 2011).

Taken together, these finding suggest that models of masking may be improved by explicitly modeling the effects of the MOC reflex. This interpretation differs from Plack and Arifianto (2010), who used an additivity of masking paradigm and found that masker duration minimally influenced derived cochlear I/O functions and estimates of gain. From these findings they concluded that the MOC has only a weak influence on the temporal aspects of masking. As stated earlier, similar small effects of masker duration are present in the literature involving frequency selectivity (e.g., Kidd et al., 1984; Bacon and Jesteadt, 1987). The present study and previous studies using precursors have shown that the MOC may play a large role in temporal masking (Strickland, 2001; Krull and Strickland, 2008; Jennings et al., 2009; Roverud and Strickland, 2010). Thus, the presumed role of the MOC in a given study depends on whether the study used a precursor or manipulated masker duration. The reason why these two approaches produce different conclusions is currently unknown, but may be related to the experimenter’s ability to control the amount of gain reduction when a precursor is used (see Jennings, 2011).

Forward masking techniques have been used to infer the cochlear I/O function in human listeners (Oxenham and Plack, 1997; Nelson et al., 2001). These techniques rely on a series of assumptions in order to interpret the data in terms of cochlear processing. For example, it is often assumed that the cochlear I/O function is static and does not change with manipulations of masker duration or masker-signal time delay. The present study and other recent studies suggest this assumption may be violated (Roverud and Strickland, 2010). It may be possible to avoid such a violation by restricting the masker duration to be less than 20–25 ms and to avoid techniques that rely on signal-masker delay [e.g., the temporal masking curve (TMC) technique]. These suggestions are based on Backus and Guinan (2006) who reported an onset delay of roughly 20 ms when measuring the MOC reflex using otoacoustic emissions. Another option is to select a method that may be less influenced by gain reduction after certain transformations are employed. For example, in the variant TMC technique (Lopez-Poveda and Alves-Pinto, 2008) masking curves are measured and compared for two slightly different signal levels. If the gain reduction influenced both curves equally, the influence of gain reduction would be canceled in the comparison and thus result in an accurate estimate of the cochlear I/O function.

In addition to separating sound into individual channels, the cochlea (via the MOC reflex) reduces gain in response to the local acoustic environment. The benefit of this gain reduction is primarily evident in auditory nerve fibers, which have a limited dynamic range. As discussed by Guinan (2006), the MOC reflex reduces the influence of neural adaptation, neural saturation, and transmitter depletion on auditory nerve fibers. In addition, the MOC reflex may preserve the dynamic range spanned by high, medium, and low spontaneous rate fibers. These findings suggest that in a noisy environment, the MOC reflex is able to reduce the cochlea’s response to noise, while maintaining a large dynamic range in auditory nerve fibers. With the dynamic range preserved, the auditory system can effectively encode modulated stimuli such as speech (Kawase et al., 1993; Brown et al., 2010; Chintanpalli et al., 2012).

APPENDIX A: TABULATED Q VALUES FOR NNTC AND PTC EXPERIMENTS

Tables TABLE II. (NNTC) and TABLE III. (PTC) display the $Q_3$ and $Q_{10}$ values obtained from all subjects in the perceptual experiments.

APPENDIX B: TABULATED THRESHOLDS FOR ASYMMETRIC NOTCH CONDITIONS

Table TABLE IV. displays thresholds obtained in asymmetric notch conditions in the NNTC experiment.

TABLE IV.

Thresholds for masker’s with asymmetric notches in the NNTC experiment. Subjects are labeled in the first column. The level of the signal or “probe” is presented in the column labeled “Lp.” In the remaining columns, the normalized notch-width values are presented in pairs, where the first number is the notch-width for the low-frequency noise band and the second is for the high-frequency noise band.

Subject a	std/pre	Lp	0.1,0.3	0.2,0.4	0.3,0.1	0.4,0.2
S1	std	40	64.89	76.37	79.12	84.33
		45	76.36	80.76	—	—
		50	80.50	—	—	—
	pre	40	50.99	57.91	56.40	49.56
		45	57.53	64.96	60.60	68.10
		50	64.74	75.06	72.87	78.70
		55	75.10	82.62	78.29	—
S3	std	45	72.35	80.04	78.42	—
		50	77.83	—	83.60	—
		55	80.34	—	—	—
	pre	45	38.45	61.17	53.30	59.98
		50	64.62	77.27	64.57	75.94
		55	75.64	79.32	74.30	82.97
		60	81.84	—	81.80	—
S4	std	45	71.26	—	—	—
	pre	45	51.70	68.20	60.60	71.33
		50	68.78	86.21	60.21	78.58
		55	73.48	86.42	80.61	—
		60	83.13	—	87.33	86.38

^aS2 and S5 did not complete the asymmetric notch measurements.