Abstract
Ishizaka and Flanagan’s classic two-mass model of vocal fold motion is applied to small oscillations where the equations become linear and the aerodynamic driving force is described by an effective stiffness. The solution of these equations includes an analytic formula for the two eigenfrequencies; this shows that conjugate imaginary parts of the frequencies emerge beyond eigenvalue synchronization and that one of the imaginary parts becomes zero at a pressure signaling the instability associated with the onset of threshold. Using recent measurements by Fulcher et al. of intraglottal pressure distributions [J. Acoust. Soc. Am. 129, 1548–1553 (2011).] to inform the behavior of the entrance loss coefficients, an analytic formula for threshold pressure is derived. It fits most of the measurements Chan and Titze reported for their 2006 physical model of the vocal fold mucosa. Two sectors of the mass-stiffness parameter space are used to produce these fits. One is based on a rescaling of the typical glottal parameters of the original Ishizaka and Flanagan work. The second requires setting two of the spring constants equal and should be closer to the experimental conditions. In both cases, values of the elastic shear modulus are calculated from the spring constants.
INTRODUCTION
Introducing a wave that propagated along the medial surface of the vocal fold and examining the motion of its center of mass in the approximation of small amplitudes, Titze1 derived an analytic formula for the threshold pressure of the rectangular glottis, namely,
| (1) |
where kt is the transglottal pressure coefficient,2, 3B is the damping factor for motion of the vocal fold, c is the speed of the mucosal wave, Lg is the glottal length (anterior-posterior direction), T is the glottal thickness (inferior-superior length of the glottal duct), and ξ0 is the prephonatory glottal half-width. During the 1990s and earlier in this century, physical models of the vocal fold mucosa were constructed to test the predictions of this formula.4, 5, 6 Experiments found a range of glottal half-widths for which the threshold data were consistent with the linear trend of Eq. 1 and qualitative behavior consistent with the direct dependence on the viscous damping of the vocal folds and the inverse dependence on the vocal fold thickness. However, the observed values for threshold pressure did not approach zero for any of the experiments with small glottal widths4, 6 as required by the formula of Eq. 1.
A recent study7 showed that the key to resolving this discrepancy lies in recognizing that the entrance loss coefficient8, 9, 10, 11 is not constant at small half-widths but becomes large as the half-width becomes small. There it was also shown that a reasonable parameterization of this coefficient is
| (2) |
where the coefficients E and F are to be determined from the experiment under consideration. If the exit coefficient is assumed to be small,12 then when the viscosity in the glottis is neglected, and Eq. 1 may be put into the form
| (3) |
which does not approach zero as the half-width approaches zero and which produces much better fits7 to the data collected by Chan and Titze6 in 2006 than Eq. 1 with a constant value for kt.
The purpose of this paper is to show that the classic two-mass model of Ishizaka and Flanagan can produce a formula similar to Eq. 3 that is equally effective in reproducing the phonation threshold data collected by Chan and Titze.6 These fits are achieved using two distinct sectors of the parameter space for oscillator stiffnesses and masses. One sector includes values of the stiffness and mass ratios that are the same as those of the original set Ishizaka and Flanagan10 spoke of as typical glottal parameters. Thus it is similar in spirit to a recent approach based on a scaling factor to account for the fundamental frequency differences between men and women’s voices.13
The second sector is defined by choosing two of the spring constants equal with the aim of more closely approximating a homogeneous vocal fold cover. For both sectors of the parameter space, the connections between spring constants and the elastic shear modulus derived by Titze and Story14 are used to calculate elastic shear moduli. The frequencies of the oscillations at phonation threshold were not given by Chan and Titze, but it was stated that these were between 100 and 150 Hz. For all of the calculations presented in the following text, it is assumed that the fundamental frequencies are 100 Hz. Thus it is possible to compare the shear moduli derived from the 2006 experiments with recent rheometer measurements of the shear moduli of vocal fold tissue15 at this frequency.
ESSENTIALS OF THE TWO-MASS MODEL
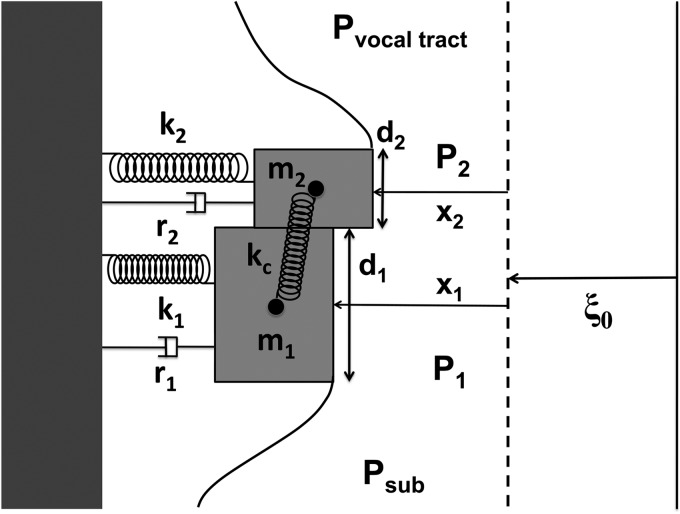
The geometry of the two-mass model is shown in Fig. 1, where the masses m1 and m2 and the spring constants k1, k2, and kc are identified. Thus the oscillator coordinates x1 and x2 obey the coupled equations of motion,
| (4) |
| (5) |
where r1 and r2 are the damping constants for the two oscillators, and F1 = P1Lg d1 and F2 = P2Lg d2, the aerodynamic forces driving the oscillators.
Figure 1.
Schematic diagram of the two-mass model. The quantity ξ0 denotes the prephonatory glottal half-width.
Glottal aerodynamics
The pressure at the glottal entrance P1 is related to the subglottal pressure Psub by
| (6) |
where ρ is the density of air, Ug is the glottal flow rate or volume velocity, A1 is the area at the glottal entrance, and kent is the entrance loss coefficient.8, 9, 10, 11 The pressure at the glottal entrance is connected with the pressure at the glottal exit P2 by the Bernoulli equation,
| (7) |
where A2 is the area of the glottal exit because viscous forces within the glottis are neglected here. In many circumstances,8, 10, 11, 16 an exit coefficient is used to describe pressure recovery, which occurs between the glottal exit and the entrance to the vocal tract. Results presented in Table II of Ref. 8, which were based on pressure distributions17, 18 taken with the physical model M5, showed that the exit coefficients were small in comparison with the entrance loss coefficients,12 and thus we set the exit coefficient kex = 0. If no vocal tract is present, then the pressure at the glottal exit P2 is equal to atmospheric pressure (taken to be zero). Adding Eqs. 6, 7 leads to the equation that determines the glottal flow rate from the subglottal pressure, the entrance loss coefficient, and the areas at the glottal entrance and the glottal exit:
| (8) |
where the time dependence of the areas has been made explicit. Using Eq. 8 to eliminate the factor in Eq. 7 yields an expression for the pressure acting on the first oscillator, viz.,
| (9) |
One noteworthy feature of Eq. 9 is that it depends only on the ratio of areas, and these are the same for an experiment done with a hemilarynx6 as for one done with a full larynx.17, 18 Thus the equations presented in the following text pertain to either a hemilarynx or a full larynx, provided that kent is taken from the appropriate experimental source. As stated in the preceding text, the driving pressure P2 = 0 because the exit coefficient is set equal to zero. The areas in Eq. 9 are connected with the glottal length Lg, the prephonatory half-width ξ0, and the oscillator coordinates x1 and x2, namely,
| (10) |
for the hemilaryngeal geometry of the experiments in Ref. 6. Substituting Eqs. 10 into Eq. 9 gives the following expression for the driving pressure P1:
| (11) |
where the time dependence of the oscillator coordinates has been suppressed.
Small amplitude approximation
Because our interest is confined to phonation threshold, we follow Titze’s lead and assume that the oscillator coordinates x1 and x2 are small in comparison with the prephonatory half-width ξ0. Then one can carry out an expansion of Eq. 11 in powers of x1/ξ0 and x2/ξ0. Retaining only the lowest order terms yields
| (12) |
Substituting this into Eq. 4 and setting P2 = 0 in Eq. 5 results in the following linear forms for the equations of motion:
| (13) |
| (14) |
where
| (15) |
is the flow-induced stiffness19, 20, 21, 22 of the fluid structure interaction. The effect of the flow induced stiffness is to produce linear forces that act opposite to those associated with the resoring forces of Eq. 13, and they destabilize the solutions of Eqs. 13, 14 when they become large enough. If Eqs. 13, 14 are divided by the masses that appear in their respective first terms, it affords an opportunity to introduce the angular frequencies, = (k1 + kc)/m1, = (k2 + kc)/m2, = kc/m1, and = kc/m2, and the damping constants γ1 = r1/(2m1) and γ2 = r2/(2m2). Searching for solutions of the form x1(t) = a1eiωt and x2(t) = a2eiωt yields a set of coupled equations for the amplitudes a1 and a2 that may be expressed in matrix form,
| (16) |
The requirement for a nontrivial solution of Eq. 16 is that the determinant of coefficients be equal to zero. This leads to a fourth degree algebraic equation with complex coefficients that determines the eigenfrequencies ω, that is,
| (17) |
It will be convenient to separate ω into real and imaginary parts so that ω2 = (ωr + i ωi)2 = − + 2 i ωr ωi. Then Eq. 17 can be separated into real and imaginary parts, and the equations determining ωr and ωi take the forms,
| (18) |
| (19) |
where the damping parameters have been restricted so that γ = γ1 = γ2. The ratio of the amplitudes for the two oscillators may be determined from the bottom row of Eq. 16, which may be expressed
| (20) |
for each value of the complex eigenfrequency ω the real and imaginary parts of which satisfy Eqs. 18, 19.
Below threshold
If the values of the subglottal pressure are small enough, then one can find a solution of Eq. 19 by setting the first factor in parenthesis there equal to zero so that ωi = γ. Then Eq. 18 simplifies to
| (21) |
the solutions of which are determined by the two sets of frequencies, , where
| (22) |
and the relationship between the amplitudes of the two oscillators is given by a real factor because
| (23) |
from Eq. 20.
To illustrate the properties of the solutions of Eqs. 21, 22, the mass and stiffness parameters are taken to be those of the typical glottal set of Ishizaka and Flanagan.10, 13, 23, 24, 25 The glottal length Lg = 1.2 cm, the thickness associated with the lower oscillator d1 = 0.25 cm, ξ0 = 0.04 cm, and kent = 1.37, a value9 frequently used for the entrance loss coefficient. The dimensionless damping parameter ζ = 0.3 defines the damping parameter γ by the relation γ = ζ (k1/m1)1/2. The solutions of Eq. 22 as functions of subglottal pressure are shown in Fig. 2. There the real parts of the two solutions approach each other as the subglottal pressure is increased from zero while the imaginary part retains its constant value. These two real parts become equal when the expression in the square brackets of Eq. 22 becomes equal to zero. This point determines a quadratic equation for the effective stiffness of the fluid-structure interaction ϕ, the solutions of which are given by
| (24) |
The pressure at which the real parts of the frequencies in Fig. 2 become equal is determined from the smaller of the solutions of Eq. 24, and the frequencies become equal, or synchronized,22 because both of the imaginary parts are equal to γ. This pressure is 444 Pa and is indicated by two arrows in Fig. 2. However, synchronization does not signify the onset of the threshold because each of the identical frequencies has a positive imaginary part γ, which leads to damped solutions.
Figure 2.
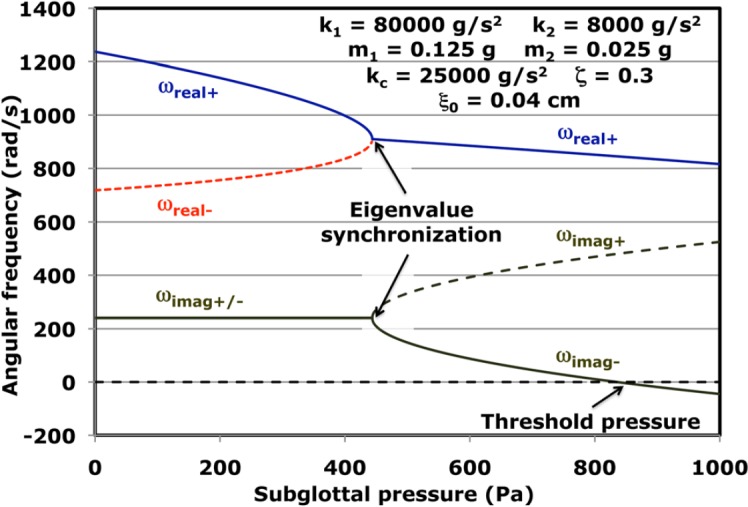
(Color online) The eigenfrequencies as functions of the subglottal pressure. Eigenvalue synchronization occurs when the real parts of the two eigenfrequencies are equal. Threshold occurs at a higher pressure where the imaginary part of one of the eigenfrequencies becomes zero. In Ref. 10, the stiffness units are dynes/cm, which we express in the equivalent form of g/s2.
Increasing the subglottal pressure above the synchronization point requires a change of strategy for the solution of Eqs. 18, 19 because the argument of the square brackets in Eq. 22 becomes negative, and thus the square root there gives a pair of conjugate imaginary values. This is not consistent with the original strategy of separating the frequency ω into real and imaginary parts. To deal with pressures in this region, we require the second factor in parentheses of Eq. 19 to be zero. This requirement leads to two solutions for the imaginary part of the frequency that can be expressed in terms of the real part and other parameters, namely,
| (25) |
As shown in Fig. 2, pressures above the synchronization point give rise to a pair of conjugate imaginary roots. Substituting Eq. 25 into Eq. 18 leads to a quartic equation for ωr, the four solutions of which occur in pairs that may be determined from
| (26) |
Only the real roots determined from Eq. 26 are physical because the value for there is negative. The value of ωr+ decreases with increasing pressure. Of more physical significance is the behavior of the conjugate imaginary parts of the roots. One of these roots increases monotonically with increasing subglottal pressure, and the other decreases monotonically. This root becomes zero at the point marked threshold pressure in Fig. 2. Increasing the pressure beyond this value causes the imaginary part of the frequency to become negative, the signal of an exponentially growing solution, instead of a damped solution. The point at which the imaginary part of the frequency changes sign has been studied in detail by Lucero and Koenig,13, 23, 26 who showed that it represents a Hopf bifurcation. The instability associated with this Hopf bifurcation announces the arrival of phonation threshold. This instability of the linearized equations of motion [Eqs. 13, 14] is absorbed by nonlinear terms in more general treatments of phonation that lead to stable oscillations and limit cycles. These nonlinear terms arise from the nonlinear factors in the pressure expression of Eq. 11, nonlinear additions to the spring forces, and the forces associated with vocal fold collisions.
Determination of threshold pressure
The threshold pressure is determined from Eqs. 18, 19 by setting ωi = 0. Then Eq. 19 requires the real part of the frequency and the flow-induced stiffness ϕ− to be connected by the equation,
| (27) |
Substituting this expression into Eq. 18 gives a quadratic equation for the flow-induced stiffness at which ωi = 0, that is, the flow-induced stiffness that determines the phonation threshold pressure. The threshold pressure is determined from the smaller solution of the flow-induced stiffness equation, which takes the form,
| (28) |
Equation 28 yields a value ϕ- = 91 400 g/s2 for the parameters used in Fig. 2. Using Eq. 15 to express the threshold pressure in terms of ϕ− gives
| (29) |
which yields Pth = 835 Pa for the parameters of Fig. 2.
It is interesting to note the behavior of the threshold pressure as the damping parameter ζ is decreased from its value used in Fig. 2. This lowers the height of the ωimag+/− line there above zero. It has no effect on the location of the synchronization pressure because the expression for the effective stiffness of the fluid-structure interaction in Eq. 24 makes no reference to γ. However, lowering the value of γ does move the point of intersection of the curve ωimag− with the horizontal axis closer to the synchronization pressure; this means that the threshold pressure decreases. If there is no damping (γ = 0), then the threshold occurs at the synchronization pressure because the ωimag+/− line for pressures below synchronization becomes the horizontal axis in this case, and the curve for ωimag− gives a negative value for any pressure above the synchronization pressure.
Results for the oscillator coordinates as functions of time are presented in Fig. 3. These were obtained from the numerical solution of Eqs. 13, 14. It is straightforward to verify that the results of Fig. 3 agree with the analytic formulas presented in the preceding text. For example, substituting the value of ϕ− obtained from Eq. 28 into Eq. 27 gives ωr = 845.1 rad/s. This value agrees with that determined from the time difference between the third and the eighth peak for x2(t) in Fig. 3 to a precision of better than 0.1%. According to Eq. 20, the two amplitudes of the oscillators are related by
| (30) |
when ωi = 0, and thus the phase shift between the two oscillators is given by
| (31) |
Equation 31 yields β = 0.590 for the parameters used in Fig. 3, and the ratio of a1 to a2 can be expressed as the complex number 0.606 + 0.406 i = 0.729 e0.590i. The positive value of β means that the phase of the lower oscillator leads that of the upper oscillator by about 34°. Equation 30 predicts the ratio of the magnitude of the two maxima in Fig. 3 to be 0.729. Both the phase and the magnitude of the ratio of the two amplitudes a1 and a2 agree with those inferred from the numerical results presented in Fig. 3.
Figure 3.
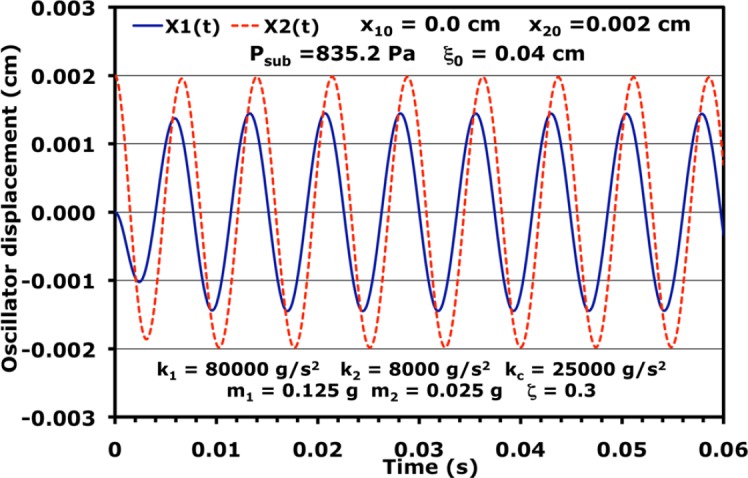
(Color online) Oscillator coordinates as functions of time at phonation threshold from the numerical solution of Eqs. 13, 14.
RESULTS FOR THRESHOLD PRESSSURES
Substituting the parameterization of Eq. 2 for the entrance loss coefficient into Eq. 29 yields
| (32) |
a threshold pressure formula for the two-mass model that is the counterpart of Eq. 3 for the surface wave model. The form of Eq. 32 makes it clear that the slope and intercept of a linear fit to the glottal half-width dependence of the threshold pressure are sensitive to the parameters of the two-mass model only through the combination of these parameters embodied in the expression for ϕ− given by Eq. 28. Thus one might expect that the parameters of the two-mass model represent more freedom than required to give a reasonable fit to any given set of the phonation threshold data collected by Chan and Titze.6 Nevertheless one consequence of our treatment of the two-mass model is apparent from the numerator of Eq. 32, where both the slope and the intercept are directly proportional to ϕ−. An increase in ϕ− means both a larger slope and a larger intercept. Failure to find such a correlation between the slope and the intercept in phonation threshold data would indicate that Eq. 32 is too great a simplification to account for the observed trends in the data.
The first decision to be made when trying to compare with the data of Chan and Titze is how to determine the entrance loss parameters E and F. Because their experiments were based on a hemilaryngeal geometry instead of the symmetric geometry of model M5, one would expect these parameters to be different from those of Ref. 8. However, the large glottal width behavior of the entrance loss coefficients reported there is not much different from unity, and thus we choose F = 1.0 for all of the calculations reported here. We will further assume that the entrance loss coefficient is determined mainly by the geometry, and hence the value of E will be taken as the same for all of Chan and Titze’s 2006 experiments. The choice E = 0.385 cm and ϕ− = 12 880 g/s2 gives the fit to the 0.01% hyaluronic acid data shown by the lower dashed line (visible under the solid line) of Fig. 4 after the geometric parameters are changed to consider the dimensions of the apparatus used by Chan and Titze6 (Lg = 2.22 cm, T = 1.1 cm, and d1 = 5 T/6, to be consistent with the m1 to m2 ratio of the set of typical glottal parameters of Ishizaka and Flanagan10). To fit the 0.1% hyaluronic acid data requires a larger value of ϕ−, which produces a larger intercept and a larger slope, both of which seem consistent with the data.
Figure 4.
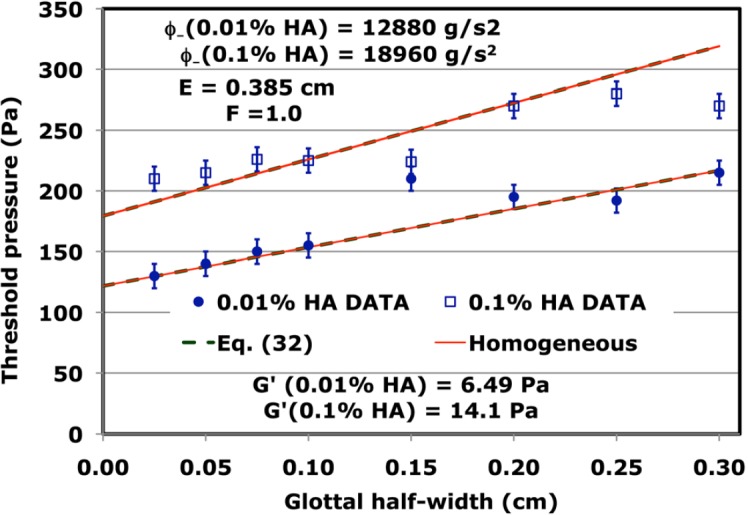
(Color online) Threshold pressures as functions of glottal half-width for two concentrations of hyaluronic acid. The dashed curves there are calculated from Eq. 32 with the values of ϕ− listed near the top of the figure. The (onset) data are taken from Fig. 4 of Chan and Titze.6 The error bars (±10 Pa) are added to the data to consider the accuracy of the pressure resolution of the water manometer used by Chan and Titze. Results (not shown) identical to the dashed curves are obtained from the elastic shear moduli and damping parameters listed in Table TABLE I. of Sec. 4. The solid straight lines were obtained with the elastic shear moduli and the depths of the oscillating mass listed in Table TABLE III. under the assumption of identical spring constants k1 and k2.
Figure 5 shows the results of adding fibronectin to a 0.01% concentration of hyaluronic acid. There it is seen that fibronectin increases the threshold pressure for each glottal width. Such an increase requires a larger value of ϕ− as shown by the higher dashed line of Fig. 5. As discussed in the preceding text, an increased value of ϕ− requires a larger intercept and a steeper slope, and both of these features seem to be present in the data. Figure 6 shows the results of adding fibronectin to a 0.1% concentration of hyaluronic acid. There it is seen that the threshold pressure at each half-width is increased by adding fibronectin. In an attempt to accommodate these increases, the value of ϕ− is raised by about 30%. Thus the intercept of the dashed fibronectin line is about 30% larger than the dashed line for no fibronectin. However, this increase in ϕ− also increases the slope by 30%, a trend not consistent with the data. Because this is the only clear discrepancy reported between our calculations and the experiments done by Chan and Titze, it might be worthwhile to consider some additional measurements with the 0.1% hyaluronic acid with fibronectin implant. If further experiments confirm this discrepancy, then it would represent a substantial challenge to our approach to the two-mass model.
Figure 5.
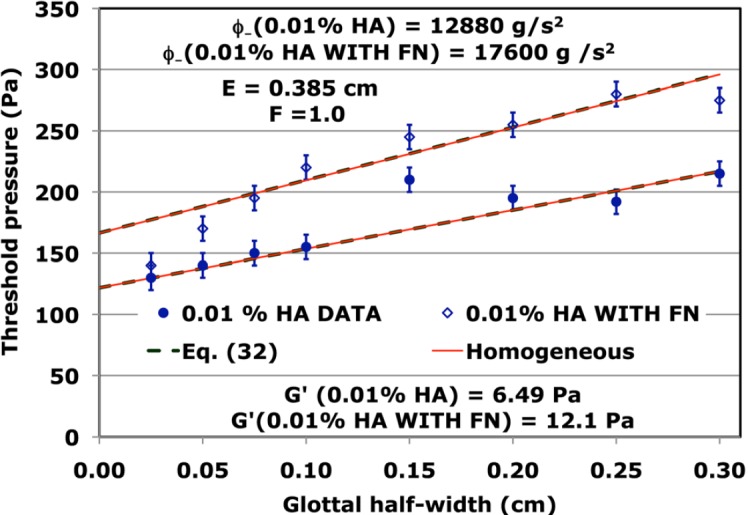
(Color online) Threshold pressures as functions of glottal half-width for 0.01% concentrations of hyaluronic acid with and without fibronectin. The (onset) data are taken from Fig. 6 of Chan and Titze.
Figure 6.
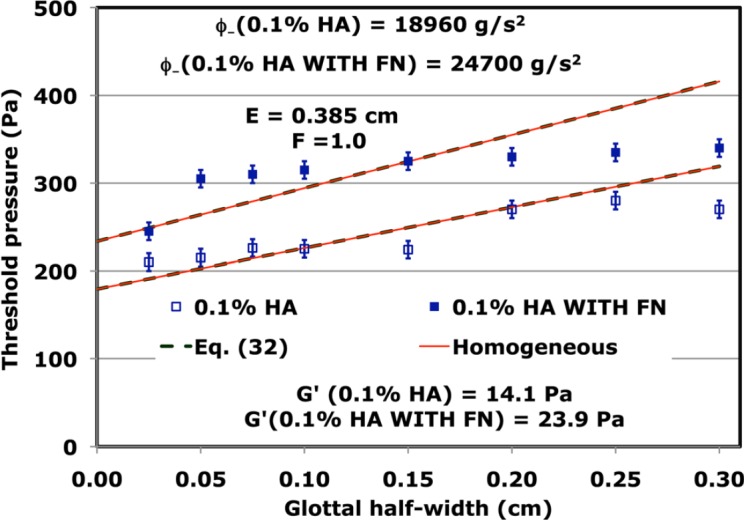
(Color online) Threshold pressures as functions of glottal half-width for 0.1% concentrations of hyaluronic acid with and without fibronectin. The (onset) data are taken from Fig. 7 of Chan and Titze.
The 1995 experiments done by Titze, Schmidt, and Titze4 were done with a different apparatus. Instead of implanting biomechanical materials under the silicone membrane as Chan and Titze did, the physical model of the vocal fold mucosa was designed so that fluids could circulate under the silicone membrane. Threshold pressures were reported for water and water with two concentrations of sodium carboxymethyl cellulose (CMC) powder (to change the viscosity of the fluid) as shown in Fig. 7. These data show the predicted linear increasing trend for half-widths of 0.10 cm or greater. However, there is an increase with decreasing half-width at smaller half-widths, contrary to the trends expected from either Eqs. 3 or 32. Titze, Schmidt, and Titze noted this inconsistency with their expectations and suggested that the upward trends at small half-widths were a consequence of collisions between the oscillating membrane and the opposing Plexiglas wall. This situation was explored further in Ref. 7, where Lucero’s suggestion27 of using Poiseuille’s approach to describe viscous effects of the flowing air within the glottis to explain the upward trends was analyzed. There it was shown that Poiseuille’s approach to viscous effects should also lead to upward trends in Chan and Titze’s 2006 measurements at small glottal widths. Because no such upward trends were reported in the 2006 experiments, it was concluded that collisions with the opposing Plexiglas wall were a more likely explanation of the upward trends of Fig. 7 than viscous effects. The implication of this conclusion is that one would not expect calculations based on the linearized equations [Eqs. 13, 14] to apply to the anomalous small width behavior of the data in Fig. 7 because these equations do not include any collision effects.
Figure 7.
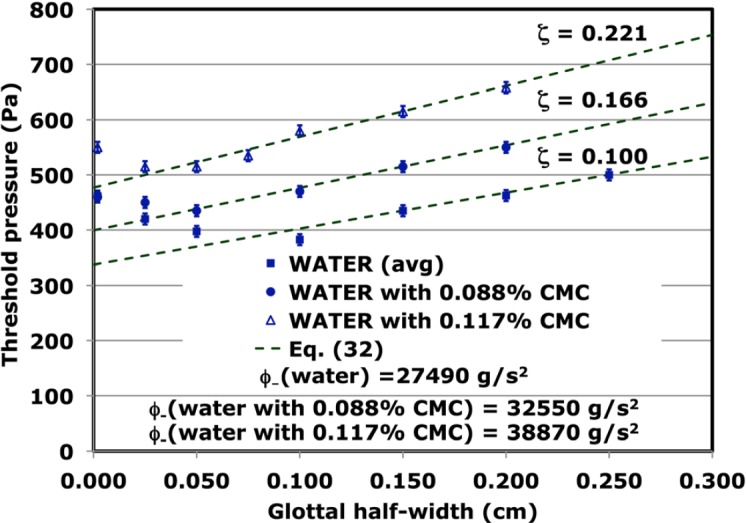
(Color online) Threshold pressures as functions of glottal half-width for water and water with two concentrations of CMC powder flowing under the silicone membrane of the experimental apparatus described in Ref. 4. The dashed lines were obtained with the values of ϕ− listed near the bottom of the figure. Identical results (not shown) were obtained for the damping parameters and the depths of the oscillating mass listed in Table TABLE II., with the elastic shear modulus G′ = 88.4 Pa being the same for all three cases. The data for water without the CMC powder are taken as the average of the two runs presented in Figs. 2 and 3 of Ref. 4. The differences between those two runs average about 15 Pa and thus fall within the 10 Pa error bars alloted to consider the limitations of the pressure resolution of the water manometer.
Because the experimental setup28 for the 1995 experiments was different from that of Chan and Titze, one would expect different values for the parameters E and F. Again F is taken to be 1.0 and E = 0.517 cm for all of the 1995 experiments. The values for ϕ− in Fig. 7 are considerably larger than those required for the calculations of Figs. 456, a consequence of higher threshold pressures. It is worth noting that these larger values of ϕ− lead to steeper slopes in addition to larger values for the magnitudes of the threshold pressures in the linear regime and that both of these trends are readily accommodated by a single parameter ϕ− for each experiment. In the next section, we show that one can fit all of the linear trends of Fig. 7 with the same value of the elastic shear modulus but with different values of the damping parameters ζ, as indicated in Fig. 7. One might expect this to be true for the 1995 experiments because each experiment used the same silicone membrane, which presumably accounted for most of the shear properties, but different fluids, the viscosities of which would probably have a greater influence on the damping parameters than on the elastic shear properties.
SPRING CONSTANTS AND ELASTIC SHEAR MODULI
Before outlining the strategies used to connect the observed threshold pressures of Figs. 4567 to the appropriate values of the elastic shear moduli, it will be convenient to rewrite Eqs. 27, 28 in terms of the spring constants, masses, and damping parameter using the definitions following Eq. 15 and the connection between γ and ζ listed above Eq. 24. Thus
| (33) |
| (34) |
According to the analysis presented by Titze and Story,14 the spring constant k1 is connected with the elastic shear modulus of the cover by the equation,
| (35) |
where D is the depth of the oscillating mass in the 1995 and the 2006 experiments. Our goal of writing Eqs. 33, 34 in terms the elastic shear modulus G′, the depth of oscillating mass D, and the damping parameter ζ requires ratios for the spring constants k1, k2, and kc and the masses m1 and m2. The first strategy chosen is based on the same choice of these ratios as those of the set of typical glottal parameters listed in Fig. 2, namely, k2/k1 = 1/10, kc/k1 = 5/16, and m2/m1 = 1/5. It is denoted as the scaled IF72 approach in the captions of Tables TABLE I. and TABLE II. in the following text. Then Eqs. 33, 34 take the forms,
| (36) |
| (37) |
Using Eq. 35 for the spring constant k1 and the connection between m1 and the average density ρ of the oscillating mass, namely, m1 = ρ Lg T D, Eqs. 36, 37 may be expressed as
| (38) |
| (39) |
Assuming that the fundamental frequency for each of the threshold measurements in Figs. 456 is 100 Hz and using the values of the effective stiffness ϕ− presented there, one may calculate the depths of the oscillating masses and the elastic shear moduli listed in Table TABLE I.. The results for D and G′ listed in columns 3 and 4 were obtained with ζ = 0.1, and those in columns 5 and 6 were obtained with ζ = 0.2. Because each of the depths D listed in Table TABLE I. is several times the thickness of the silicone membrane (70 μm = 0.0070 cm), in retrospect it seems reasonable to use a value of ρ (1.02 g/cm3) close to that of the vocal fold cover.6 On the other hand, the calculation may be done in reverse order. One may assume that the values for G′, D, and ζ are known, use Eq. 39 to determine the effective stiffness ϕ−, and then use Eq. 32 to determine the threshold pressures. Results (not shown) calculated in this manner are almost identical to the dashed lines in Figs. 456.
TABLE I.
Parameters for the scaled IF72 fit to the 2006 experiments of Chan and Titze. The frequency at threshold is assumed to be 100 Hz for each of the experiments.
| ζ = 0.1 | ζ = 0.2 | ||||
|---|---|---|---|---|---|
| Experiment | ϕ (g/s2) | D (cm) | (Pa) | D (cm) | (Pa) |
| 0.01% HA | 12 880 | 0.0265 | 20.9 | 0.0194 | 12.0 |
| 0.1% HA | 18 960 | 0.0390 | 45.2 | 0.0285 | 26.0 |
| 0.01% HA | |||||
| with FN | 17 600 | 0.0362 | 38.9 | 0.0265 | 22.4 |
| 0.1% HA | |||||
| with FN | 24 700 | 0.0508 | 76.8 | 0.0371 | 44.0 |
TABLE II.
Parameters for the 1995 experiments of Titze, Schmidt, and Titze based on the scaled IF72 approach. The elastic shear modulus = 88.4 Pa, and the frequency is assumed to be 100 Hz for each of the experiments.
| Experiment | ϕ (g/s2) | ζ | D (cm) |
|---|---|---|---|
| Water | 27490 | 0.100 | 0.0545 |
| Water with 0.088% CMC | 32550 | 0.166 | 0.0534 |
| Water with 0.117% CMC | 38870 | 0.221 | 0.0521 |
Equations 38, 39 may also be used to calculate depths of the oscillating mass and elastic shear modulus for each of the values of ϕ− listed in Fig. 7, again assuming that the fundamental frequency of oscillation to be 100 Hz. In fact, it was possible to account for all of the linear trends in Fig. 7 with the same value of the elastic shear modulus (88.4 Pa) and different values of the damping parameter ζ as summarized in Table TABLE II.. This choice is motivated by the consideration that it would seem more likely for an increase in the viscosity of the fluid flowing under the silicone membrane to change the damping parameter than the shear modulus. The values of D listed in Table TABLE II. are reasonable because they are more than a factor of two larger than the thickness (200 μm = 0.020 cm) of the silicone membrane used in the 1995 experiments.
The second strategy for determining the elastic shear moduli and the depths of oscillating tissue begins with the assumption that k1 = k2, an attempt to model the more uniform properties of the oscillating masses of Chan and Titze’s 2006 experiments. This choice is referred to as the homogeneous strategy in Figs. 456. Making this substitution in Eq. 34 yields
| (40) |
where β is the mass ratio m2/m1. Minimizing ϕ− with respect to kc determines a ratio of kc to k1, that is,
| (41) |
From the argument of the square root factor in Eq. 40, it is clear that the choice of equal masses m1 and m2, (β = 1) is not an option because the argument of the square root factor then becomes 4 ζ2 (ζ2 − 1), which is negative for ζ < 1. Thus an important requirement for the validity of the homogeneous strategy is that the mass of the upper oscillator of the physical model be greater than that of the lower oscillator.
A choice of β also requires a recalculation of ϕ-, because one would expect the ratio of d1 to d2 to be proportional to the mass ratio. From the β = 3/2, one finds d1 = 0.44 cm. Values for the effective stiffness ϕ-, the depth of the oscillating mass, and the elastic shear modulus obtained with the choice β = 3/2 are listed in columns 2–4 of Table TABLE III.. One would expect these values for the elastic shear modulus to be closer to those of the biomechnaical implants used in the 2006 experiments than the results of Table TABLE I. because Chan and Titze made an effort to distribute the biomaterial under the silicone membrane evenly. Thus, the values of G′ in column 4 may be interpreted as predictions for the elastic shear moduli of the four biomaterials used in the 2006 experiments. They are the basis of the solid lines in Figs. 456, which were obtained from Eqs. 41, 40, and 32 and are labelled with the appropriate values of G′. In each case, the solid lines are identical to the corresponding dashed lines in Figs. 456, emphasizing the mathematical equivalence of using either the first or second strategy to determine the connections between the spring constants and the more physical elastic shear moduli. To get some idea of the sensitivity of the values for G′ to the assumptions made in implementing the second strategy, results for β = 5/4 are also presented in Table TABLE III.. A new value of β also requires a new value of d1 (0.489 cm), and the values of ϕ− thus determined are listed in column 5. The results for D and G′ in columns 6 and 7 are rather close to those in columns 3 and 4, suggesting a mild dependence of the predicted values on the ratio β.
TABLE III.
Parameters for the homogeneous approach to fitting the 2006 experiments of Chan and Titze. The frequency is assumed to be 100 Hz, and the damping parameter ζ is taken to be 0.1.
| m2 = 3m1/2 | m2 = 5m1/4 | |||||
|---|---|---|---|---|---|---|
| Experiment | ϕ (g/s2) | D (cm) | (Pa) | ϕ (g/s2) | D (cm) | (Pa) |
| 0.01% HA | 6180 | 0.0112 | 6.49 | 6869 | 0.0120 | 6.66 |
| 0.1% HA | 9097 | 0.0165 | 14.1 | 10 111 | 0.0177 | 14.4 |
| 0.01% HA | ||||||
| with FN | 8445 | 0.0153 | 12.1 | 9386 | 0.0164 | 12.4 |
| 0.1% HA | ||||||
| with FN | 11 852 | 0.0215 | 23.9 | 13 173 | 0.0230 | 24.5 |
The elastic shear moduli for hyaluronic acid compounds do not seem to have been measured for phonatory frequencies. Nevertheless, it is worthwhile to compare the predictions in Table TABLE III. with recent measurements15 at 100 Hz of several human vocal fold cover specimens. In Fig. 12 of Ref. 15, these rheometer measurements give values between about 220 and 500 Pa, and thus these measurements are more than an order of magnitude higher than the values listed in Table TABLE III.. To consider whether this order of magnitude difference is reasonable, it is instructive to examine two sets of measurements done at 10 Hz. Chan and Titze29 reported rheometer measurements of the human vocal fold mucosa at this frequency for 10 male subjects. Their results ranged from about 25 Pa to about 700 Pa (Fig. 9 of Ref. 29). These were at least an order of magnitude larger than some measurements of the elastic shear properties of a 0.01% concentration of HA and a 0.1% concentration of HA (about 1.5 and 3 Pa, respectively) reported in Fig. 1 of Ref. 30. Moreover, the ratio of the 0.1% case to the 0.01% case is about a factor of 2, which is close to this ratio in Table TABLE III..
The work presented in this and the preceding section makes it clear that Eq. 32 gives reasonable fits to most of the phonation threshold pressures measured in the 2006 and 1995 experiments. The developments based on Eqs. 38 to 41 show that one can infer reasonable values for the elastic shear moduli and the depths of oscillating tissue from these experiments.
CONCLUSIONS
Although much of the previous work with Ishizaka and Flanagan’s two-mass model has been based on the assumption that the entrance loss coefficient is a constant, this assumption is not necessary. Such an assumption has the consequence that the phonation threshold pressure is required to approach zero as the glottal half-width becomes very small. This prediction is not consistent with Chan and Titze’s 2006 measurements,6 where the linear trend of the threshold pressure data clearly does not approach zero. As shown in our earlier work with Titze’s surface wave model,7 the key to resolving this discrepancy is to introduce a parameterization of the entrance loss coefficient that includes an inverse dependence on the glottal half-width. It is shown that this parameterization may be readily incorporated into the two-mass model of Ishizaka and Flanagan.
With the new parameterization, one can obtain an analytic formula for the threshold pressure [Eq. 32], which enjoys considerable success in accounting for the threshold pressures taken in the 2006 experiments that Chan and Titze did with biomechanical materials implanted under the silicone membrane of their physical model of the vocal fold mucosa. In particular, the formula gives a good account of the threshold pressures for the 0.01% and 0.1% hyaluronic acid implants (Fig. 4) and also for the case where fibronectin was added to the 0.01% implant (Fig. 5). The only serious discrepancy is the case of the fibronectin implant with 0.1% hyaluronic acid, where the increase of the threshold pressure with glottal half-width is considerably less than the slope of the line calculated with the analytic formula of Eq. 32 (Fig. 6). It was explained that this failure might potentially be a shortcoming of the approach to the two-mass model employed here because the connection between larger intercept and larger slope given by Eq. 32 is intrinsic to the formulation of the two-mass model described in Secs. 2 and 3. Perhaps more data collected in this case might ameliorate the disagreement between calculations and experiment, but if the discrepancy persists, more sophisticated modeling may be called for.20, 21, 22, 25 It is also shown that the treatment of the two-mass model described here gives a satisfactory explanation of the 1995 threshold pressures (Fig. 7) measured by Titze, Schmidt, and Titze above glottal half-widths of 0.1 cm, where the linearized equations of motion are expected to apply [Eqs. 13, 14].
Several analytic formulas are derived for the frequencies of the oscillations from the linearized equations of motion for the two oscillators. Using parameters typical of those defined in the classic paper of Ishizaka and Flanagan,10 the eigenfrequencies are shown to synchronize at a value of the subglottal pressure around 440 Pa when ζ0 = 0.04 cm. About 400 Pa above the synchronization pressure, the imaginary part of one of the eigenfrequencies crosses the axis and becomes negative, which signals the advent of threshold. An analytic formula is derived for the effective stiffness of the fluid-structure interaction at which this imaginary part crosses the axis [(Eq. 28)]. From this formula, one can determine the threshold pressure [Eq. 29 or Eq. 32].
Two strategies are implemented to connect the spring constants, masses, and damping constants required to explain the experiments with potentially observable quantities, such as, the elastic shear modulus [Eq. 35, which comes from Ref. 14]. One of these is modeled on the same ratios as the set of typical glottal parameters used by Ishizaka and Flanagan, and it is described as a scaled IF72 approach. The second strategy is based on the assumption k1 = k2, which is appropriate for a more homogeneous vocal fold cover. It is expected that results from this strategy should be closer to the actual situation with the 2006 experiments by Chan and Titze because they spread the biomaterial under their silicone membrane evenly along the axial direction. The depths of the oscillating mass with both strategies seem reasonable because they are several times the thickness of the silicone membrane. Predictions for the elastic shear moduli of the biomechanical implants used in the 2006 experiments (Table TABLE III.) tend to be more than an order of magnitude below recent measurements of human vocal tissue at 100 Hz. This finding may be reasonable because a comparison of measurements at a lower frequency suggests there may be an order of magnitude difference for the elastic moduli of hyaluronic acid implants and human vocal fold tissue. Because the shear rheometer described in Ref. 15 represented a considerable technological advance, it may soon be possible to do measurements that will test the predictions of Table TABLE III..
The equations described in Sec. 4 make it clear that one can predict the phonation threshold pressure of models of the vocal folds given their elastic shear moduli, the frequency at which the observation is to be made, and the geometric parameters describing the vocal folds. Since Klemuk et al.31 have recently reported measurements of the elastic shear moduli of nine injectibles at a range of frequencies from 0.1 to more than 1000 Hz, one might employ the formalism of Sec. 4 to obtain predictions of the phonation threshold pressure for vocal fold models made of a given injectible material. Such a follow up calculation is planned, and it will be interesting to compare the results with those reported in Ref. 31 the results of which were based on the surface wave model formulas of Ref. 6.
ACKNOWLEDGMENTS
The authors gratefully acknowledge support of this project by NIH 2R56DC003577. The participation of J.W. was supported by the SETGO Program (NSF Grant DUE 0757001). The authors also are thankful for the independent checks of the numerical results presented in Fig. 2 by Jason Kaminski.
References
- Titze I., “ The physics of small amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83, 1536–1552 (1988). 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
- Scherer R. and Guo C., “ Laryngeal modeling: Translaryngeal pressure for a model with many laryngeal shapes,” in ICSLP Proceedings, 1990 International Conference on Spoken Language Processing (The Acoustical Society of Japan, Tokyo: ), Vol. I, pp. 3.1.1–3.1.4.
- Scherer R. and Guo C., “ Generalized translaryngeal pressure coefficient for a wide range of laryngeal configurations,” in Vocal Fold Physiology: Acoustical, Perceptual, and Physiological Aspects of Voice Mechanisms, edited by Gauffin J. and Hammarberg B. (Singular, San Diego, CA, 1991), pp. 83–90. [Google Scholar]
- Titze I., Schmidt S., and Titze M., “ Phonation threshold pressure in a physical model of the vocal fold mucosa,” J. Acoust. Soc. Am. 97, 3080–3084 (1995). 10.1121/1.411870 [DOI] [PubMed] [Google Scholar]
- Chan R., Titze I., and Titze M., “ Further studies of phonation threshold pressure in a physical model of the vocal fold mucosa,” J. Acoust. Soc. Am. 101, 3722–3727 (1997). 10.1121/1.418331 [DOI] [PubMed] [Google Scholar]
- Chan R. and Titze I., “ Dependence of phonation threshold pressure on vocal tract acoustics and vocal fold tissue mechanics,” J. Acoust. Soc. Am. 119, 2351–2362 (2006). 10.1121/1.2173516 [DOI] [PubMed] [Google Scholar]
- Fulcher L. and Scherer R., “ Phonation threshold pressure: Comparison of calculations and measurements taken with physical models of the vocal fold mucosa,” J. Acoust. Soc. Am. 130, 1597–1605 (2011). 10.1121/1.3605672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fulcher L., Scherer R., and Powell T., “ Pressure distributions in a static physical model of the uniform glottis: Entrance and exit coefficients,” J. Acoust. Soc. Am. 291, 1548–1553 (2011). 10.1121/1.3514424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg J., Zantema J. T., and Doornenbal P., “ On the air resistance and the Bernoulli effect of the human larynx,” J. Acoust. Soc. Am. 29, 626–631 (1957). 10.1121/1.1908987 [DOI] [Google Scholar]
- Ishizaka K. and Flanagan J., “ Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Sys. Tech. J. 52, 1233–1268 (1972). [Google Scholar]
- Gauffin J., Binh N., Ananthapadmanabha T., and Fant G., “ Glottal geometry and volume velocity waveform,” in Vocal Fold Physiology: Contemporary Research and Clinical Issues, edited by Bless D. and Abbs J. (College-Hill, San Diego, CA, 1983), pp. 194–201. [Google Scholar]
- The calculations presented in Ref. showed that typically the exit coefficients were an order of magnitude smaller than the entrance loss coefficients for a given glottal diameter and transglottal pressure.
- Lucero J. and Koenig L., “ Simulations of the temporal patterns of oral airflow in men and women using a two-mass model of the vocal folds under dynamic control,” J. Acoust. Soc. Am. 117, 1362–1372 (2005). 10.1121/1.1853235 [DOI] [PubMed] [Google Scholar]
- Titze I. and Story B., “ Rules for controlling low-dimensional vocal fold models with muscle activation,” J. Acoust. Soc. Am. 112, 1064–1076 (2002). 10.1121/1.1496080 [DOI] [PubMed] [Google Scholar]
- Chan R. and Rodriquez M., “ A simple-shear rheometer for viscoelastic characterization of vocal fold tissues at phonatory frequencies,” J. Acoust. Soc. Am. 124, 1207–1219 (2008). 10.1121/1.2946715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Story B. and Titze I., “ Voice simulation with a body-cover model of the vocal folds,” J. Acoust. Soc. Am. 97, 1249–1260 (1995). 10.1121/1.412234 [DOI] [PubMed] [Google Scholar]
- Scherer R., Shinwari D., DeWitt K., Zhang C., Kucinschi B., and Afjeh A., “ Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees,” J. Acoust. Soc. Am. 109, 1616–1630 (2001). 10.1121/1.1333420 [DOI] [PubMed] [Google Scholar]
- Scherer R., Shinwari D., DeWitt K., Zhang C., Kucinschi B., and Afjeh A., “ Intraglottal pressure distributions for a symmetric and oblique glottis with a uniform duct (L),” J. Acoust. Soc. Am. 112, 1253–1256 (2002). 10.1121/1.1504849 [DOI] [PubMed] [Google Scholar]
- Ishizaka K. and Matsudaira M., “ Fluid mechanical considerations of vocal cord vibration,” in Speech Communication Research Monograph No. 8 (Speech Communication Research Library, Santa Barbara, CA, 1972), pp. 1–76. [Google Scholar]
- Zhang Z., Neubauer J., and Berry D., “ Physical mechanisms of phonation onset: A linear stability analysis of an aeroelastic continuum model of phonation,” J. Acoust. Soc. Am. 122, 2279–2295 (2007). 10.1121/1.2773949 [DOI] [PubMed] [Google Scholar]
- Zhang Z., “ Characteristics of phonation onset in a two-layer vocal fold model,” J. Acoust. Soc. Am. 125, 1091–1102 (2009). 10.1121/1.3050285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., “ On the difference between negative damping and eigenmode synchronization as two phonation onset mechanisms,” J. Acoust. Soc. Am. 129, 2163–2167 (2011). 10.1121/1.3543989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucero J., “ Dynamics of the two-mass model of the vocal folds: Equilibria, bifurcations, and oscillation region,” J. Acoust. Soc. Am. 94, 3104–3111 (1993). 10.1121/1.407216 [DOI] [Google Scholar]
- Steinecke I. and Herzel H., “ Bifurcations in an asymmetric vocal fold model,” J. Acoust. Soc. Am. 97, 1874–1884 (1995). 10.1121/1.412061 [DOI] [PubMed] [Google Scholar]
- Tokuda I., Horacek J., Svec J., and Herzel H., “ Comparison of biomechanical modeling of register transitions and voice instabilities with excised larynx experiments,” J. Acoust. Soc. Am. 122, 519–531 (2007). 10.1121/1.2741210 [DOI] [PubMed] [Google Scholar]
- Lucero J. and Koenig L., “ Phonation thresholds as a function of laryngeal size in a two-mass model of the vocal folds (L),” J. Acoust. Soc. Am. 118, 2798–2801 (2005). 10.1121/1.2074987 [DOI] [PubMed] [Google Scholar]
- Lucero J., “ Relation between the phonation threshold pressure and the prephonatory glottal width in a rectangular glottis,” J. Acoust. Soc. Am. 100, 2551–2554 (1996). 10.1121/1.417365 [DOI] [PubMed] [Google Scholar]
- Reference lists Lg = 2.3 cm instead of 2.22 cm.
- Chan R. and Titze I., “ Viscoelastic properties of human vocal fold mucosa: Measurement methodology and empirical results,” J. Acoust. Soc. Am. 106, 2008–2021 (1999). 10.1121/1.427947 [DOI] [PubMed] [Google Scholar]
- Chan R. and Titze I., “ Hyaluronic acid (with fibronectin) as a bioimplant for the vocal fold mucosa,” Laryngoscope 109, 1142–1149 (1999). 10.1097/00005537-199907000-00026 [DOI] [PubMed] [Google Scholar]
- Klemuk S., Lu X., Hoffman H., and Titze I., “ Phonation threshold pressure predictions using viscoelastic properties up to 1400 Hz of injectibles intended for Reinke’s space,” Laryngoscope 120, 995–1001 (2010). [DOI] [PubMed] [Google Scholar]