Set-size procedures for controlling variations in speech-reception performance with a fluctuating masker

Abstract

Adaptive signal-to-noise ratio (SNR) tracking is often used to measure speech reception in noise. Because SNR varies with performance using this method, data interpretation can be confounded when measuring an SNR-dependent effect such as the fluctuating-masker benefit (FMB) (the intelligibility improvement afforded by brief dips in the masker level). One way to overcome this confound, and allow FMB comparisons across listener groups with different stationary-noise performance, is to adjust the response set size to equalize performance across groups at a fixed SNR. However, this technique is only valid under the assumption that changes in set size have the same effect on percentage-correct performance for different masker types. This assumption was tested by measuring nonsense-syllable identification for normal-hearing listeners as a function of SNR, set size and masker (stationary noise, 4- and 32-Hz modulated noise and an interfering talker). Set-size adjustment had the same impact on performance scores for all maskers, confirming the independence of FMB (at matched SNRs) and set size. These results, along with those of a second experiment evaluating an adaptive set-size algorithm to adjust performance levels, establish set size as an efficient and effective tool to adjust baseline performance when comparing effects of masker fluctuations between listener groups.

INTRODUCTION

Psychometric functions for speech intelligibility in noise are often steep. Speech recognition in noise can improve from near chance to near perfect over a range of signal-to-noise ratios (SNRs) as narrow as 10 dB for high-context speech materials (French and Steinberg, 1947). As a result, when examining how various factors affect speech scores, it can be difficult to determine an appropriate test SNR that avoids floor and ceiling effects across all stimulus conditions for all listeners. This problem can be avoided by using adaptive-tracking procedures to estimate the SNR required for a listener to achieve 50% correct performance (often referred to as the speech-reception threshold or SRT) for each individual condition (Levitt and Rabiner, 1967; Plomp and Mimpen, 1979a,b). These adaptive procedures have been widely adopted for research and clinical applications because they can provide fast, reliable measures of speech-reception ability in noise while generally avoiding ceiling and floor effects.

The SRT has proven particularly useful when comparing speech-reception performance for listening conditions that yield very different levels of performance at the same SNR. For example, normal-hearing (NH) listeners typically demonstrate much better performance for speech presented in a background of modulated noise than for speech presented in a stationary noise at the same long-term-average SNR (e.g., Miller and Licklider, 1950; Festen and Plomp, 1990). This phenomenon is thought to reflect the ability to extract speech information during brief dips in the level of a fluctuating masker (dip listening). In another example, speech reception performance in the presence of competing talkers varies depending on the degree of perceptual similarity of target and interferer (e.g., Brungart, 2001; Brungart et al., 2001; Freyman et al., 2001, 2004). This effect has been described in terms of “informational masking” (IM), whereby both the target and masker are audible, but the listener experiences difficulty in determining which portions of the complex acoustic mixture are associated with the target and which represent the masker. Dip listening and IM effects can be quite large, resulting in ceiling and floor effects where some stimulus conditions produce 0% performance and others produce 100% performance at the same SNR value (e.g., Festen and Plomp, 1990). In such cases, it would be virtually impossible to make meaningful comparisons across different listening conditions without an adaptive metric such as the SRT.

The SRT has also been used to examine speech perception across different listener groups that vary substantially in overall performance. A classic example is the case where NH listeners are compared to hearing-impaired (HI) listeners who might score close to 0% correct in many speech conditions where the NH listeners score close to 100% correct at the same SNR. Thus, to compare the differences in difficulty across different masking conditions for the NH and HI groups, it is often necessary to use SRT values rather than percentage-correct scores. For example, numerous studies have sought to determine whether hearing loss affects the specialized processes involved in listening in the dips of a fluctuating masker to extract speech information (Festen and Plomp, 1990; Eisenberg et al., 1995; Bacon et al., 1998; Peters et al., 1998; Dubno et al., 2003; George et al., 2006; Jin and Nelson, 2006; Wilson et al., 2007). These studies have typically estimated the fluctuating masker benefit (FMB) for NH and HI listeners by taking the difference between SRTs measured for a fluctuating-masker condition and for a baseline stationary-noise condition, and suggest that hearing loss tends to reduce the FMB. The SRT has also been used to examine the effects of hearing loss on IM by comparing performance for NH and HI listeners under assumed high- and low-IM conditions, in some cases showing less IM for the HI listeners (e.g., Arbogast et al., 2005).

The use of the SRT to measure the effect that a particular masker manipulation has on speech recognition is only valid if one assumes that the impact of that manipulation is independent of the SNR of the stimulus in the baseline condition. However, there is evidence that this assumption is generally invalid, both for studies evaluating the magnitude of the FMB and for those where the masker interference is dominated by IM. Oxenham and Simonson (2009) measured psychometric functions for speech presented in stationary and modulated maskers, and found that the slope of the function was steeper for the stationary-noise case. FMB varied with SNR and was largest at very low SNRs, where the two curves deviated the most. IM effects also appear to be SNR-dependent, tending to decrease as SNRs diverge from 0 dB (in either direction), possibly based on the use of target-masker level differences as a segregation cue (Brungart, 2001). HI listeners have poorer speech-reception performance overall, which means that their SRTs will be higher for the baseline condition than baseline SRTs for NH listeners. Because the estimate of FMB or IM is based on different baseline starting points for the two listener groups, effects of hearing loss and effects of SNR cannot be disassociated from one another. Bernstein and Grant (2009) and Bernstein and Brungart (2011) argued that the reduction in FMB associated with hearing loss (e.g., Festen and Plomp, 1990), or signal processing intended to simulate aspects of hearing loss (e.g., ter Keurs et al., 1993; Baer and Moore, 1994; Qin and Oxenham, 2003; Gnansia et al., 2009; Hopkins and Moore, 2009) could be due, at least in part, to SRT differences between NH and HI listeners for the baseline (stationary-noise) condition. Likewise, SNR differences between NH and HI listeners for baseline (non-IM) conditions could confound estimates of IM for NH and HI listeners (Arbogast et al., 2005).

Although SNR confounds pertain to both IM and modulation-based masking release, the current study focused on the issue of FMB in situations where little IM is expected. Bernstein and Brungart (2011) proposed a method of adjusting the relative difficulty of a speech-identification task to avoid SNR confounds in the measurement of FMB. Their method was based on the results of Miller et al. (1951) who showed that word-identification performance improved with decreasing response set size. The idea was to test the two listener groups with different set sizes to yield performance (in the baseline stationary-noise condition) that was equivalent across groups. SRTs for a fluctuating-masker condition, measured using these two different set sizes for the two groups, could then be examined to evaluate group differences in FMB without the influence of an SNR confound. Bernstein and Brungart (2011) applied this approach to investigate whether FMB is affected by certain stimulus-processing algorithms intended to simulate aspects of hearing loss. They examined a spectral-smearing algorithm (Baer and Moore, 1994) simulating the loss of frequency selectivity that often accompanies hearing loss and a noise-vocoding algorithm (Hopkins et al., 2008) that simulates an inability to use temporal fine-structure information. The FMB for processed stimuli was compared to the FMB for the unprocessed stimuli. When estimating FMB using the traditional method—where listeners were tested using the same set size for both processed and unprocessed stimuli—stimulus processing was found to reduce FMB, consistent with previous results. The unprocessed conditions were then tested using a larger set size to reduce stationary-noise performance to be equal to that for the processed conditions. The FMB for processed stimuli (estimated using the smaller word set) turned out to be equal to the FMB for unprocessed stimuli (using the larger word set) across a range of fluctuating-masker types. This led Bernstein and Brungart (2011) to conclude that the signal-processing algorithms did not directly affect dip-listening ability, and that the apparent reductions in FMB using the traditional method were likely due to an SNR confound. While Bernstein and Brungart (2011) applied the set-size method to equalize performance across processing conditions for NH listeners, the same method could be used to equalize stationary-noise performance to compare FMB between NH and HI listener groups (see Bernstein, 2012, for a detailed discussion of approaches to avoid SNR confounds in the measurement of speech intelligibility in fluctuating maskers).

An important assumption underlying use of the set-size method to control SNR effects when estimating FMB is that set size does not affect the ability to extract speech information from dips in the level of a fluctuating masker. Based on the framework of the Articulation Index (French and Steinberg, 1947; Kryter, 1962; ANSI, 1969), it is assumed that a certain amount of speech information is available to the listener, and that set size affects only the transformation from available speech information to performance in the speech task. If instead, the set-size manipulation differently affects the amount of relevant audible speech information available for a stationary-noise versus a fluctuating-masker condition, this would invalidate this approach as an acceptable method for estimating FMB.

Bernstein and Brungart (2011) tested this assumption by examining the relationship between performance for a large and a small response set. In the large-set condition, stimuli were selected at random from a set of 1000 words in an open-response paradigm where listeners were not given the set of word choices. In the small-set condition, a set of 72 possible word responses were displayed on a touchscreen. Performance for these two response paradigms was compared across a range of SNRs for each of three masker types (stationary noise, an interfering talker and a speech-modulated noise). The results indicated that response set size did not affect dip-listening ability at matched SNRs for the maskers tested. Instead, the set-size manipulation affected only the transformation from available speech information to performance. Nevertheless, it was noted that this pattern might not always hold. In particular, a study by Buss et al. (2009) suggested that the size of the response set might have an effect on dip-listening ability at certain modulation rates. They measured the FMB for words presented in sinusoidally amplitude-modulated (SAM) noise with modulation rates ranging from 2.5 to 40 Hz. The FMB was estimated by comparing the SRT for stationary-noise and each SAM masker for an open-set and a three-alternative forced-choice word-identification task. The set-size manipulation had a very large effect for low modulation rates, reducing the FMB by as much as 10 dB, whereas the effect was much smaller for high rates, reducing the FMB by a couple of dB or not at all.

These results conflict with those of Bernstein and Brungart (2011), suggesting instead that set size can influence the FMB. However, it should be noted that there were a number of important differences between the studies. The two studies explored different fluctuating maskers and set-size ranges, which might account for their divergent conclusions. Bernstein and Brungart (2011) examined the effect of set size on the FMB for speech-based maskers, whereas Buss et al. (2009) examined SAM-noise maskers across a range of modulation rates. Bernstein and Brungart (2011) compared performance for set sizes of 72 monosyllabic words (in a closed-set paradigm) and 1000 words (in an open-set paradigm), whereas Buss et al. (2009) compared performance for set sizes of 3 (closed-set) and 500 words (open-set). It was hypothesized that set size might only affect the FMB for very small set sizes (e.g., the three-alternative forced-choice task of Buss et al., 2009) and as a function of modulation rate. For very small set sizes, listeners might often be able to rely on vowel information alone, whereas word identification for larger set sizes would require that both the consonants and vowels be identified correctly. Phatak and Grant (2009) showed that the rate dependence of the FMB in SAM noise was different for consonants than for vowels. There might be an unwanted interaction between set size, modulation frequency, and FMB in cases where the set size is reduced to the point where only vowel information is required to identify the stimulus.

The first goal of the present study was to extend the study of Bernstein and Brungart (2011) to determine the extent to which its results, which showed that FMB and set size were roughly independent of one another, can be generalized to other combinations of masker and set size. Of particular concern in this regard were the results of the study by Buss et al. (2009), which showed that FMB was not independent of set size in conditions with a very small response set (three alternatives) and low modulation rates.

The second goal was to refine the methodology for using set-size adjustment to control SNR effects in estimating FMB. Although Bernstein and Brungart (2011) were able to use this method to investigate FMB for NH listeners presented with simulated aspects of hearing loss (as described above), there were several methodological drawbacks associated with this technique that might discourage its more general use. One major drawback was that the method required extensive training to familiarize the listener with each randomly-selected response set. Several different response sets were chosen during the course of an experiment to limit measurement variability, thereby necessitating several training periods throughout the experiment. This drawback was addressed in the present study by changing the target stimuli to a fixed set of consonant-vowel (CV) and vowel-constant (VC) tokens, with the idea that this stimulus set should require less training and familiarization time than the word-identification test employed by Bernstein and Brungart (2011). NH listeners participated in a single training session to become familiar with a single set of 160 VC and CV tokens, and smaller sets were created by pseudo-random selection of subsets of these 160 tokens. Experiment 1 measured identification accuracy as a function of SNR and set size for the VC and CV tokens presented in stationary noise, an interfering-talker masker, and 4- and 32-Hz SAM noise.

A second drawback of the method employed by Bernstein and Brungart (2011) was that it required a lengthy pilot-testing phase to determine the set size required to yield a given performance level for a particular SNR. The procedure also required further adjustments to refine the set-size selection because the first pilot phase yielded an inaccurate estimate. Experiment 2 investigated the accuracy and reliability of a method of adaptively tracking on set size to determine the appropriate set size for a given listener or test condition.

EXPERIMENT 1: EFFECTS OF SNR, SET SIZE AND MASKER TYPE ON PERFORMANCE

Methods

Experiment 1 measured CV/VC identification performance as a function of SNR and set size. Target syllables were presented in stationary noise, interfering speech from a talker of opposite gender from the target talker or SAM noise (4 or 32 Hz).

Target speech materials

Stimuli consisted of CV or VC tokens, similar to the set described by Vestergaard et al. (2009) and Ives et al. (2005). The set included 160 tokens consisting of all combinations of five vowels (“ah” as in rod, “ay” as in raid, “ee” as in reed, “oh” as in road, and “oo” as in rude) and 16 consonants (“b,” “ch,” “d,” “f,” “g,” “j,” “k,” “l,” “m,” “n,” “p,” “r,” “s,” “t,” “v,” and “z”) in both CV and VC contexts. Response alternatives were arranged in a grid with 16 columns (one for each consonant) and 10 rows. The upper five rows in the response matrix contained the CV responses for the five vowel contexts; the lower five rows contained the VC responses for the same five vowels. Each virtual button in the response matrix was labeled with the phonetic spelling of the appropriate token. These labels were created by combining the consonant and vowel phonetic spellings shown above (e.g., “bah,” “chay,” “eep,” “ohd”), with the exception that the VC tokens ending in “s” were spelled with a double “ss” (e.g., “ahss,” “ayss,” “ohss”) to avoid confusion with the “z” sound that is often associated with an orthographic final “s.” Recorded stimuli were taken from the Linguistic Data Consortium LDC-2005S22 corpus (Fousek et al., 2004), with each token in the set spoken by seven different male talkers and recorded at a sampling rate of 16 kHz. Some of the individual recorded tokens were judged as poor exemplars of the intended token and discarded. As a result, each of the 160 CV or VC stimuli was spoken by four (one token), five (six tokens), six (35 tokens), or seven (118 tokens) individual talkers. Some of the recorded stimulus files contained long silent periods before the onset or after the offset of speech energy. Large discrepancies across tokens in the duration of these silent periods were reduced by limiting the silent periods to no more than 150 ms (onset) or 250 ms (offset) in each stimulus file. The resulting stimulus files ranged in duration from 291 to 1339 ms (mean = 678 ms, standard deviation = 113 ms).

Maskers

Four different maskers were tested: a stationary speech-shaped noise, a 4-Hz and a 32-Hz SAM noise, and a female interfering talker. For each masker type, a long-duration (94-s) masker signal was generated at a sampling rate of 16 kHz and saved on hard disk. The speech-shaped stationary noise was generated by zero-padding each of the 160 tokens spoken by each of the seven talkers (a total of 1120 tokens) to equalize their durations, summing together the resulting waveforms, taking the fast-Fourier transform (FFT), randomizing phase, and zero-padding the spectrum before computing the inverse FFT. The SAM noises were generated by multiplying the speech-shaped stationary noise by a raised 4- or 32-Hz sinusoid (full modulation depth). The interfering-talker masker was derived from a recording of a female speaker of American English reading the “The Unfruitful Tree” by Freidrich Adolph Krummacher (translated from German). To remove pauses between words, the amplitude of the speech was calculated using a 30-ms moving average window. Segments that were more than 20 dB below the long-term average level of the speech for more than 150 ms were removed, with 2.5-ms raised-cosine ramps applied to the speech offset and onset on either side of the removed segment. The resulting speech-masker waveform was then spectrally shaped to match the long-term average spectrum of the target speech that was recomputed in 256 linearly spaced frequency bins. The magnitude spectrum of the masker signal was multiplied by the ratio between the interpolated 256-point long-term spectrum of the masker and the mean spectrum of the 1070 target stimuli (160 tokens, four to seven talkers per token).

Stimuli

Target stimuli were presented at 55 dB sound-pressure level (SPL). For each stimulus presentation, a segment of the appropriate long-duration masker was chosen at random, adjusted in level to yield the target SNR, and then summed with the target stimulus. This masker selection process randomized the timing of masker peaks and valleys relative to the target speech on each trial of the experiment. The masker was ramped on and off 300 ms before the start and 300 ms after the end of the target stimulus.

Apparatus

Listeners were seated in a sound-treated booth equipped with a control computer running matlab. All stimuli were presented diotically through an RME Hammerfall sound card connected to Beyerdynamic DT990 headphones. Listeners responded to the stimuli by clicking on a graphical user interface with a computer mouse.

Procedure

For a set size of 160, all of the buttons in the response matrix were available as response choices. For smaller sets, available responses were pseudo-randomly chosen from the 160 tokens. Available responses were marked with a blue background, while responses that were not available were marked in grey. These smaller sets were chosen in such a way as to simultaneously minimize the number of choices for any one vowel, consonant and phoneme order (VC or CV). For example, for a set size of 40, the available responses were divided equally between VC and CV tokens (20 choices each), the five vowels (eight choices each) and the 16 consonants (two or three choices each). Furthermore, the available choices for one attribute (i.e., vowel, consonant, or phoneme order) were distributed across the other attributes as uniformly as possible. For the example of the set size of 40, the eight available responses for a given vowel were assigned to four consonants in CV context and four different consonants in VC context. The idea was to reduce the number of easily confusable tokens for a given target stimulus so as to increase the impact that the set-size manipulation had on performance. The target token was randomly selected from the subset, and the target talker was chosen randomly from the four to seven talkers for which a stimulus was available for that token. For set sizes smaller than 160, a new response subset was generated on every trial. The listener was first presented with the auditory stimulus, and then presented with the set of available choices. Following the response, feedback was provided by highlighting the correct response in green before the next trial was presented.

Each masking condition was tested with all combinations of seven set sizes (2, 5, 10, 20, 40, 80 and 160 possible responses) and nine SNRs (stationary noise: −30, −15, −12, −9, −6, −3, 0, 3 and 6 dB; fluctuating maskers: −30, −24, −18, −12, −9, −6, −3, 0 and 3 dB). For each listener, 20 trials were presented for each combination of masker, SNR and set size, for a total of 5040 trials. Stimuli were presented in blocks of 72 trials (one or two trials for each combination of SNR and set size presented in random order), with masker type fixed throughout each block. Blocks were presented in pseudo-random order, ensuring that a comparable number of trials was completed for each masker type before an additional block was presented for any given masker. Before data collection began, each listener was provided with a training block, consisting of one trial for each of the 160 tokens presented in quiet in random order. The talker was selected at random for each trial. All 160 tokens were available as possible responses during the training block.

Listeners

Eleven NH listeners (five female) participated in this experiment. Their ages ranged from 20 to 29 years (mean 23.9 years). All had normal audiometric thresholds, defined as 15 dB hearing level or better for octave frequencies between 250 and 8000 Hz in both ears. Participants were paid for their participation.

Results

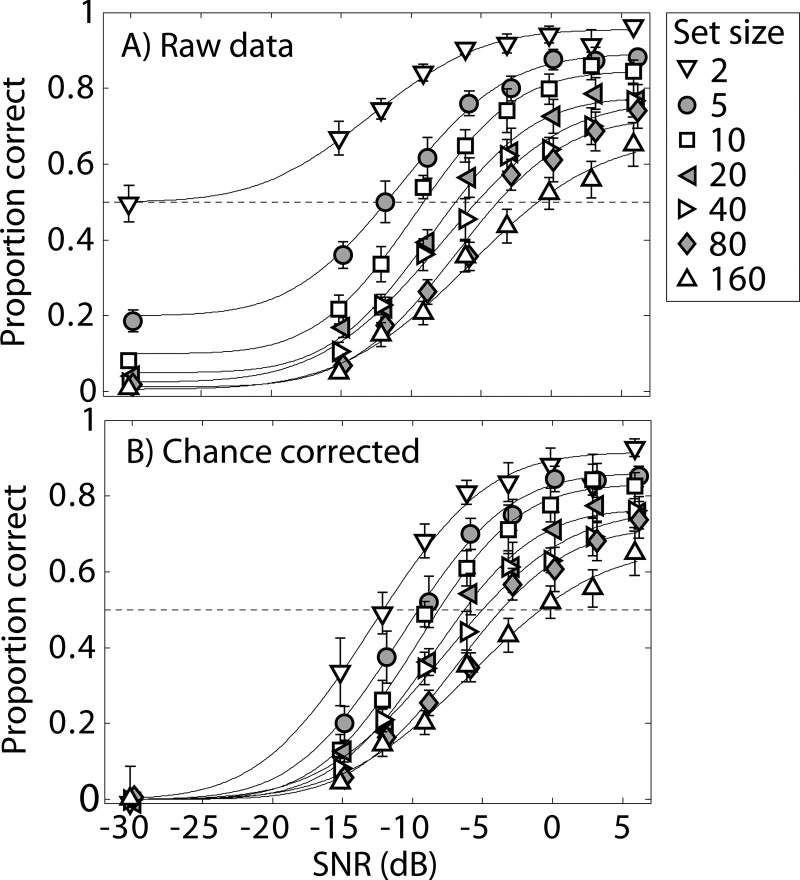
The stationary-noise data are considered first. Figure 1a plots mean speech-identification performance as a function of SNR for each of the seven set sizes tested. Generally, performance improved with decreasing set size (consistent with previous results, Miller et al., 1951) and with increasing SNR. Figure 1b shows the relationship between set size and SNR for the stationary-noise conditions after the results have been corrected for the increased effects of guessing with decreasing set size. For each set size (N), the corrected proportion of correct responses (p_c) is equal to the original proportion of correct responses (p) minus a correction for guessing equal to (1 − p)/(N − 1). As would be expected, this correction tended to reduce the differences in performance across the different set-size conditions, particularly for low SNRs and the smallest set sizes where the effects of guessing on overall performance were substantial. A repeated-measures analysis of variance (ANOVA) was conducted on the chance-corrected stationary-noise data after the application of a rationalized arcsine unit (RAU) transformation (Studebaker, 1985) to stabilize the variance across conditions. Data at the lowest SNR of −30 dB were not included in the analysis because performance at this SNR was at chance for all set sizes. The reported degrees of freedom reflect a Huynh–Feldt (1976) correction for sphericity applied wherever necessary. The analysis showed significant main effects of set size [F(6,60) = 86.3, p < 0.0005] and SNR [F(5.0,49.5) = 195, p < 0.0005], reflecting the expected effects of these variables on performance. The interaction between set size and SNR was not significant (p = 0.87).

Figure 1.

Stationary-noise results of experiment 1, showing (a) group-mean CV/VC identification performance and (b) mean chance-corrected performance for each set-size condition. Solid curves represent sigmoidal fits to the data. The horizontal dashed line indicates the 50% correct level of performance. Error bars indicate standard errors of mean values across listeners.

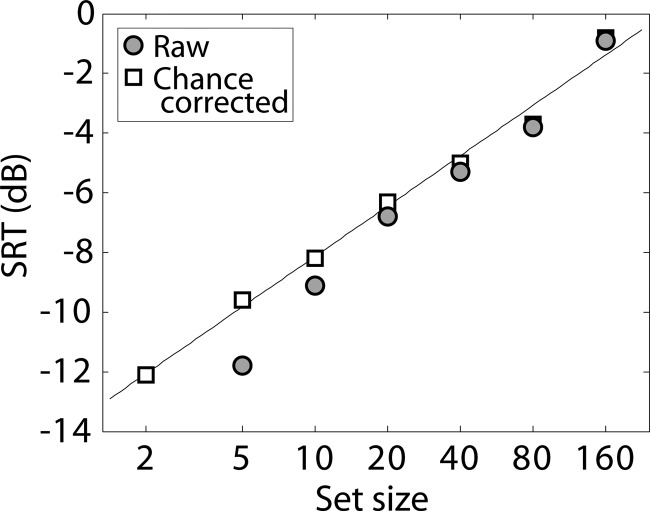
Estimating the stationary-noise SRT (i.e., the SNR required to yield a given performance level, usually 50% correct) gives an idea of the degree to which manipulating the set size can adjust the test SNR for a given listener. SRTs were estimated by fitting sigmoidal functions (curves in Fig. 1) to the raw [Fig. 1a] and chance-corrected data [Fig. 1b] using three free parameters (representing the slope, horizontal position and maximum plateau value of the function) for each set-size condition. The minimum plateau value for each curve was fixed at chance level (the inverse of the set size for the raw data and zero for the chance-corrected data). SRTs were then extracted from the resulting fits by determining the SNR required for 50%-correct (raw or chance-corrected) performance. Figure 2 shows the SRTs (in dB) estimated from the raw (grey circles) and chance-corrected data (white squares) as a function of set size (on a log scale). The SRT for the chance-corrected data increased linearly as a function of the logarithm of the set size, with the best-fitting line depicted in the plot indicating a slope of 1.7 dB for every doubling of set size. The SRT for the raw data deviated slightly from this linear trajectory for set sizes smaller than 20, where the effects of guessing were greatest. For both the raw and chance-corrected data, stationary-noise SRTs ranged from about −12 to −1 dB across the range of set sizes tested. This suggests that stationary-noise SRT differences as large as 11 dB can be offset by manipulating set size. For example, if SRTs for a group of NH and a group of HI listeners differed by 11 dB, equal (uncorrected) stationary-noise performance for the two groups might be achieved by testing the NH listeners with a set size of 160 and the HI listeners with a set size of 5. The results also indicate that the set-size manipulation can be used to elevate performance above floor levels or to reduce performance below ceiling levels, thereby increasing the dynamic range of the speech-intelligibility test. Figure 1b shows that at an SNR of −15 dB, performance was near chance (i.e., corrected performance near zero) for the largest set sizes, but well above chance for set sizes of 20 or smaller. At an SNR of +6 dB, performance was near ceiling for a set size of 2, but below ceiling for larger set sizes.

Figure 2.

SRTs (the SNR required for 50%-correct performance) derived from the group-mean psychometric functions shown in Fig. 1.

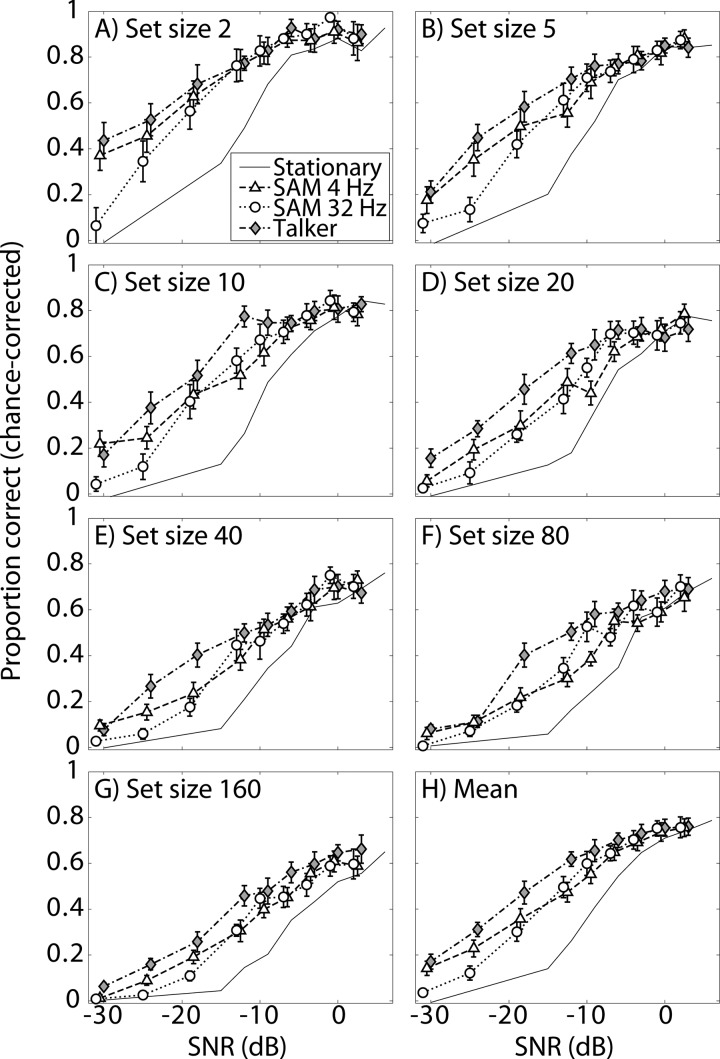
The fluctuating-masker data are considered next. Figure 3 plots chance-corrected performance for each of the maskers tested as a function of SNR, with the results for each set size plotted in separate panels [Figs. 3a, 3b, 3c, 3d, 3e, 3f, 3g]. Figure 3h shows the data averaged across the seven set-size conditions. The chance-corrected stationary-noise data from Fig. 1b are replotted in Fig. 3, but without symbols or error bars for clarity. Several trends that were evident in the data are discussed along with the results of a repeated-measures ANOVA with three factors (masker, set size, SNR) conducted on the chance-corrected, RAU-transformed fluctuating-masker data. (The stationary-noise data was not included in this ANOVA because different SNRs were tested in this condition.) First, performance generally increased with increasing SNR [F(2.9,29.1) = 316, p < 0.0005] and decreasing set size [F(4.4,44.2) = 124, p < 0.0005], as expected. Second, performance differed among the fluctuating-maskers [F(2,20) = 88.1, p < 0.0005], with the interfering-talker condition yielding a larger FMB than the each of the SAM-noise conditions. Third, there was a significant interaction between SNR and masker condition [F(12.2,122) = 11.2, p < 0.0005]. Performance was better for the 4-Hz than for the 32-Hz condition at very low SNRs, while at higher SNRs performance was more similar for the two modulation rates or better for the 32-Hz conditions. This trend was consistently observed for all set sizes tested, and was also clearly observed when the data were averaged across set-size conditions [Fig. 3h]. Fourth, there were no significant interactions between set size and any other variable (set size and masker type: p = 0.41; set size and SNR: p = 0.29; set size, SNR and masker type: p = 0.15).

Figure 3.

Results of experiment 1, showing (a)–(g) group-mean CV/VC identification performance as a function of SNR for the four tested maskers with the seven set-size conditions plotted in separate panels and (h) mean performance across set-size conditions. Error bars indicate standard errors of mean values across listeners.

To address the question of whether set size affects the FMB at a given SNR, stationary and fluctuating-masker conditions should be included in the same analysis. A significant interaction between set size and masker type would suggest that the FMB (i.e., the difference in performance between the stationary-noise and a given fluctuating-masker condition) is not independent of set size. For example, if set size had a large impact on performance for a fluctuating-masker condition, but little impact on stationary-noise performance, this would suggest that FMB depended on set size. An additional ANOVA was conducted on the chance-corrected, RAU-transformed data for all masker types at the six SNRs that were common to the stationary-noise and fluctuating-masker conditions (−12, −9, −6, −3, 0, and 3 dB). The lowest SNR (−30 dB) was not included in the analysis because stationary-noise performance at this SNR was at chance for all set sizes. The results were the same as for the ANOVA that included only the fluctuating-masker data. There were significant main effects of SNR [F(4.4,44.2) = 154, p < 0.0005], set size [F(3.0,30.4) = 148, p < 0.0005] and masker type [F(2.1,20.7) = 75.7, p < 0.0005] and a significant interaction between masker type and SNR [F(9.8, 98) = 16.5, p < 0.0005]. There were no significant interactions between set size and any other variable (set size and masker type: p = 0.11; set size and SNR: p = 0.20; set size, SNR and masker type: p = 0.62).

The main question posed in this experiment was whether there exists a range of set sizes and fluctuating-masker types for which set size affects only the transformation from available speech information to percentage-correct performance and not the underlying FMB. The lack of interactions between set size and masker type in the above analyses provides some indication that set size and FMB were independent for the maskers tested here. Another way to address this question was to plot chance-corrected performance for the same stimuli but different set-size contexts against one another for each masker type. If set size affected only the transformation from speech information to percentage-correct performance level, the curves for each masker type should overlap one another, reflecting the common relationship between percentage-correct scores for the two set-size contexts in question. If, on the other hand, the set-size manipulation affected the FMB for a particular fluctuating masker, then the resulting curve for that masker should differ from that for stationary noise. If the set-size manipulation had a variable effect on the FMB across fluctuating maskers, then the resulting curves for these maskers should differ from one another.

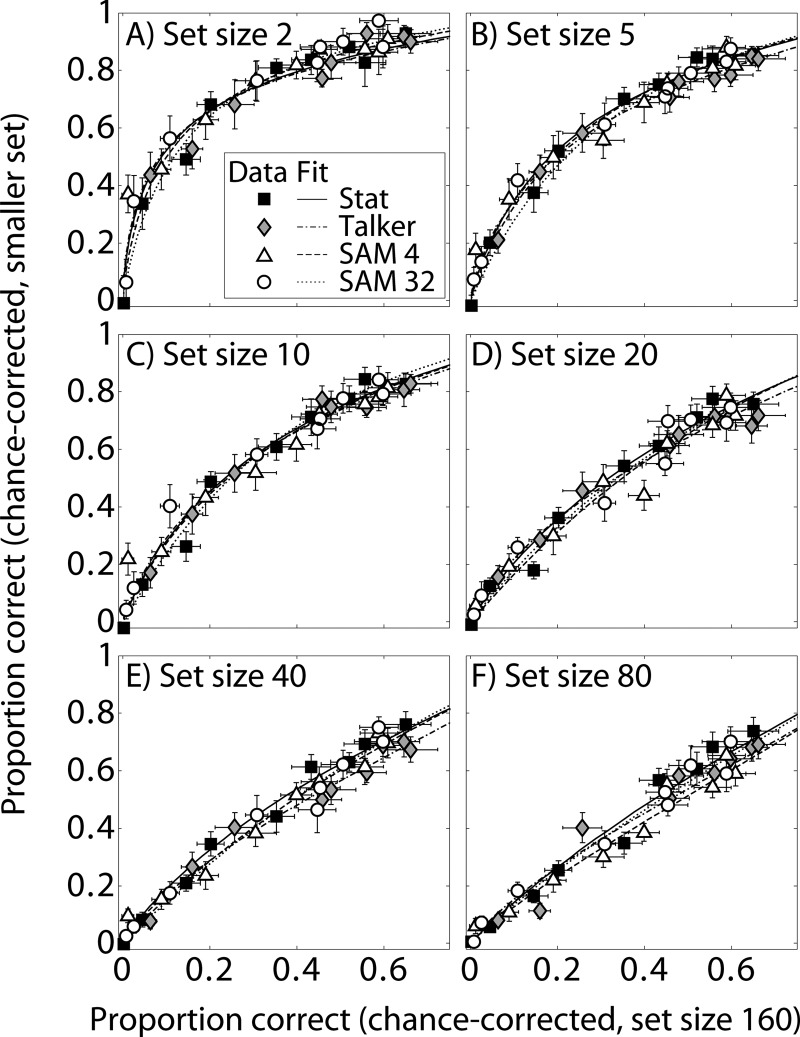
Each panel of Fig. 4 shows chance-corrected performance for one set size (2–80) plotted against chance-corrected performance for a set size of 160 for each of the four maskers. In each panel, the functions for all four maskers follow the same curve. There were no obvious systematic differences across masker type between these functions for any of the set sizes tested. To statistically test for differences in these functions, the percentage-correct data were pooled across listeners, chance-corrected [Eq. (1)], logit transformed, and analyzed using linear regression. The curves in Fig. 3 represent the resulting fits to the data for each masker type. The functions describing the relationships between performance for the largest set size (160) and performance for each of the smaller set sizes (2–80) were statistically compared (Chow, 1960) to determine whether the sets of best-fitting regression coefficients (slope and intercept) were equal across masker types. No significant effects of masker type were found (p > 0.40 for all six comparisons between a set size of 160 and smaller set sizes). This analysis suggests that the functions comparing performance between set-size conditions were independent of masker type.

Figure 4.

Separate panels show CV/VC identification performance for different set size conditions (from 2 to 80) plotted against performance for a set size of 160. Each data point represents a particular SNR and masker condition. Solid curves represent fits to the data for each masker type. Vertical and horizontal error bars indicate standard errors of mean values across listeners.

The two analyses presented above suggest that for these maskers, set size manipulation affected only the transformation from available speech information to percentage-correct performance, consistent with the basic assumption of the Articulation Index. The Fig. 3 showed no interaction between set size and masker type, while the analysis of the data as presented in Fig. 4 suggested that set size affected percentage-correct performance equally for all masker types. The set-size manipulation did not affect performance for a given fluctuating-masker condition any differently than for any other fluctuating masker or for stationary noise. This suggests that this technique can be used to measure the FMB for different listener groups at the same SNR and performance level. Since set-size adjustments between 2 and 160 did not appear to affect the benefit that a listener received from listening in the gaps, this method can be used to equalize stationary-noise performance between listener groups without concern that the manipulation affects the FMB at a given SNR.

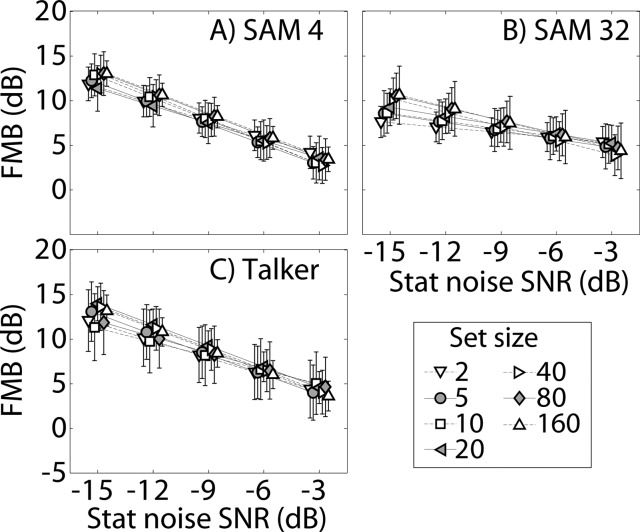
To further demonstrate this point, estimates of FMB were derived from the psychometric functions shown in Fig. 3. For each masker type and set size, the chance-corrected data were logit transformed and fit with a line. Only data for SNRs equal to or less than −3 dB were included in the fit, as the data tended to flatten out for higher SNRs, leading to poor linear fits to the logit-transformed data. The FMB was calculated as the horizontal distance (in dB) between the fitted functions for stationary noise and a given fluctuating masker. Figure 5 plots the FMB estimates as a function of the stationary-noise SNR for each fluctuating masker [panels (a)–(c)] and set size (symbols within each panel). These functions represent the FMB calculated by estimating the performance level associated with a given stationary-noise SNR, then estimating the fluctuating-masker SRT associated with that same performance level. (Although SRT often refers to the SNR required for a 50% correct performance level, here it is defined as the SNR required for any given level of performance that is common across maskers.) The data are shifted horizontally for clarity, with each cluster of points representing the FMB estimates at the same stationary-noise SNR. Error bars represent one standard deviation of the error in the FMB estimates. The results show that for each fluctuating masker, the FMB at a given stationary-noise SNR was not affected by set size, with any differences in FMB between set-size conditions smaller than the standard deviation of the FMB estimate. Note that although the FMB estimates for each set size are plotted at a common stationary-noise SNR, the performance levels associated with that stationary-noise SNR were different for each set size (see Fig. 4).

Figure 5.

Estimates of the FMB for each set size for the (a) 4-HZ SAM, (b) 32-Hz SAM and (c) interfering-talker masker conditions. FMB estimates were derived by fitting curves to the psychometric-function data (Fig. 3) and determining the difference in SNR (relative to stationary noise) required in a given fluctuating-masker to achieve the performance level associated with a given stationary-noise SNR. Error bars indicate standard deviations of the FMB estimation error.

EXPERIMENT 2: ADAPTIVE TRACKING ON SET SIZE

Rationale

Bernstein and Brungart (2011) proposed a two-step procedure to compare FMB for two listener groups or two signal processing conditions at a fixed SNR. The first step was to determine the set size required to yield a given stationary-noise performance level at a particular SNR. Performance was estimated as a function of set size, and the resulting data was fit with a curve to determine the appropriate set size to yield the desired level of performance. The second step was to fix the set size for each listener group and use an adaptive-tracking algorithm to determine the SNR required to achieve a given level of performance for both stationary and fluctuating maskers. This method proved successful as a way to estimate and compare the FMB at the same stationary-noise SNR for unprocessed stimuli and stimuli processed to simulate aspects of hearing loss. However, the first step of the process was cumbersome, requiring a great deal of training and iteration to determine the appropriate set size for each processing condition. Furthermore, the method required that the first step be completed for the entire group of listeners to fix the set sizes for the second step.

Experiment 2 explored an alternative procedure that uses an adaptive-tracking technique to determine the set size required to yield a given level of performance in stationary noise. The goal was to improve on the methodology of Bernstein and Brungart (2011) by developing a technique to quickly and accurately determine the appropriate set size for an individual listener. Adaptive tracking was used to estimate the set-size needed for a given listener to achieve a fixed performance level in stationary noise across a range of SNRs. The set size was then fixed at this tracked value, and performance was measured in terms of percentage correct or adaptively tracked SNR to determine the accuracy of the adaptive set-size tracking in yielding the intended performance level or SNR.

Methods

Experiment 2 used the same stimuli as experiment 1 but with a different test procedure. Only the stationary-noise masking condition was tested. The idea was that set-size adjustment would be employed to equalize stationary-noise performance across listeners before testing a variety of masker conditions using these individually-determines set sizes. One block consisted of 100 trials. For the first 60 trials, set size was varied using an adaptive-tracking procedure with one of two tracking rules. For the one-up, one-down (1u1d) condition (tracking the 50% correct point), set size increased following every correct response and decreased following every incorrect response (Levitt, 1971). For the two-up, one-down (2u1d) condition (tracking the 66.7% correct point), set size increased following every second correct response (consecutive or non-consecutive responses) and decreased following every incorrect response [similar to the three-up, one-down method described by Zwislocki and Relkin (2001) to track 75% correct performance]. The initial nominal set size was 10, changed by a factor of 2 during the first 10 trials, and changed by a factor of √2 for the next 50 trials. The threshold set size was taken to be the geometric mean of the nominal set sizes on each of the last 40 trials. For integer-valued nominal set sizes, the actual set size on a given trial was equal to the nominal value. For non-integer nominal set sizes, the actual set size for a given trial was randomly selected to be the integer value just greater than or just less than this non-integer value, with the probability of each selection weighted based on the decimal portion of the nominal value. Thus, the expected value of the actual set size was equal to the nominal set size. For example, the actual set size for a nominal value of 20.3 was either 20 (with probability 0.7) or 21 (with probability 0.3). The nominal set size was not allowed to be less than 2.5 or greater than 160. If the adaptive-tracking algorithm would have required a nominal set size outside of these bounds, the nominal set size was maintained at the boundary value. If a listener obtained 12 correct responses with the maximum set size of 160 or 12 incorrect responses with the minimum nominal set size of 2.5 within any block, the block was terminated without calculating a threshold set size. Blocks that did not terminate early due to this rule are referred to as valid measurement blocks.

After the adaptive-tracking portion of a block was completed (i.e., the first 60 trials), the nominal set size was held fixed at the threshold value estimated by the tracking procedure for an additional 40 “post-measurement” trials. The purpose of the post-measurement trials was to evaluate the accuracy of the adaptive algorithm in determining the set size required for a given percentage-correct performance level (at a fixed SNR) or SRT (for a given fixed performance level). For the percent-correct post-measurement conditions, the 40 trials were presented at a fixed SNR to evaluate whether the adaptive set-size estimate yielded the intended percentage-correct score. For the adaptive-SNR post-measurement condition, SNR was varied adaptively over the last 40 trials to evaluate whether the set-size estimation procedure yielded the intended SRT. The initial SNR was set at the value that had been fixed for the adaptive set-size portion of the block. The SNR was then increased or decreased in 1-dB steps according to the same adaptive-tracking rule used for the set-size tracking portion of the block. The SRT was taken to be the mean SNR across these 40 trials. [Although “SRT” often refers to the SNR required for 50% correct performance (e.g., Plomp and Mimpen, 1979a,b), here the SRT was tracked at either the 50 or 66.7% correct level.]

Two blocks were completed for each combination of two adaptive rules (1u1d or 2u1d), six SNRs (1u1d: −12 to +3 dB in 3-dB steps; 2u1d: −9 to +6 dB) and two post-measurement conditions (adaptive-SNR or percentage-correct). Test blocks were presented in pseudo-random order, with one block completed for each condition before a second block was presented for any condition. Ten paid NH listeners participated (age range 19 to 29 years, mean 23.4 years, five female). Seven of these listeners had also participated in experiment 1.

Results

General trends

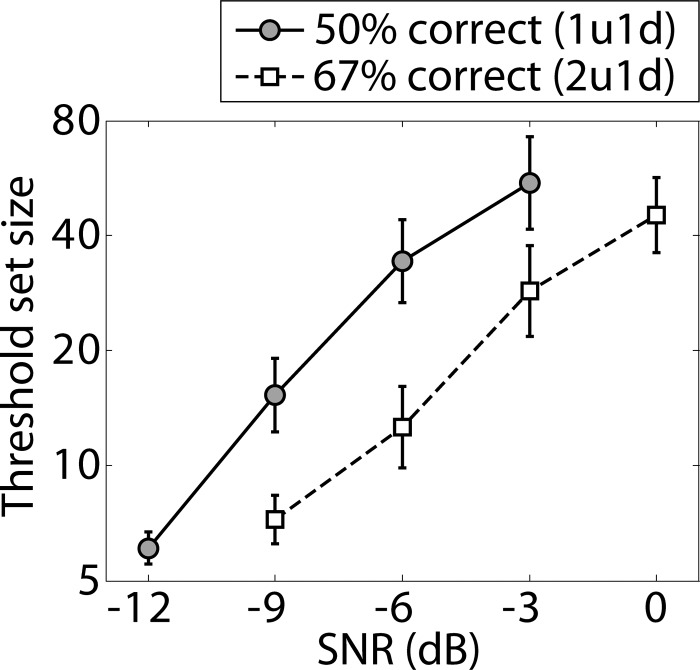
Geometric means of the threshold set-size estimates are plotted as a function of SNR in Fig. 6 for each combination of SNR and adaptive rule. Data are plotted only for conditions where at least two (out of four) valid measurements per listener were obtained for at least eight (out of ten) listeners. As expected, smaller set sizes were required to achieve threshold levels of performance for conditions involving lower SNRs (horizontal axis) or an adaptive rule that tracks a higher level of performance (i.e., the 2u1d tracking rule, 66.7% correct, Fig. 6, open squares). These results indicate that set-size adjustment would allow the group-mean SRT to be adjusted over at least a 9-dB range, between −12 and −3 dB for the 1u1d condition or between −9 and 0 dB for the 2u1d condition. Thus, the SRT for a given performance level for this group of NH listeners could be adjusted to match any SRT for a different group of listeners (e.g., HI) over this 9-dB range.

Figure 6.

Results of experiment 2, showing group-mean threshold set sizes as a function of SNR and adaptive rule. Error bars indicate standard errors of mean values across listeners.

Reliability and accuracy

The reliability and accuracy of the adaptive set-size estimation method were assessed. Test-retest reliability was evaluated to determine the repeatability of the set-size estimate. The accuracy of the estimate was evaluated by comparing the post-measure percentage-correct score and SRT to the target performance levels and SNRs, respectively. Both analyses were performed for the group-mean data, giving an indication of how well the set size manipulation achieved the target performance level for the group as a whole, and for the individual data, giving an indication of the accuracy of the set size estimates for an individual listener and condition. Often, an FMB experiment will focus on group-mean effects rather than individual performance, for example, when addressing the question of whether hearing loss affects the FMB (e.g., Festen and Plomp, 1990). In this case, the group-mean statistics would be relevant. However, it is also sometimes of interest to compare the performance for individual listeners, for example, to ask a question about which psychoacoustic attributes contribute to intersubject differences in FMB (e.g., Dubno et al., 2003; George et al., 2006). For such applications, statistics regarding set-size estimates for individual listeners are pertinent.

Test-retest reliability was evaluated by considering only the adaptive set-size estimates, ignoring the post-measurement data. It is proposed that for general use in future research studies, two tracking blocks would be completed for a given listener and condition, and the resulting threshold set sizes geometrically averaged. In the current experiment, a total of four adaptive set-size estimation blocks were completed for each combination of listener, SNR and tracking rule. To examine the test-retest reliability of the proposed two-block-average estimation procedure, the threshold set sizes obtained by geometrically averaging the first two (of four) estimates for each listener and condition in the current data set were compared to the thresholds obtained by averaging the last two estimates. An important caveat to the proposed two-block-average estimation method is that each adaptive block did not always produce a valid threshold set-size estimate. Thus, an exception to the two-block-average procedure is proposed for the situation where only one of the two blocks produces a valid estimate, whereby the invalid block would be discarded and the set-size threshold estimate would be taken to be that produced by the valid block. To address this situation in the evaluation of test-retest reliability from the current data set (four attempted blocks per listener and condition), the following procedure was used. For those listeners and conditions where four reliable measurements were completed, the geometric means of the threshold set sizes for the first two blocks were compared to the geometric-mean thresholds for the last two blocks. In cases where three reliable blocks were completed, the geometric-mean threshold across the first two blocks was compared to the threshold for the third block. In cases where only two valid blocks were completed, the thresholds for these two blocks were compared. In cases where zero or one valid blocks were completed, that particular condition was not considered in the calculation of test-retest reliability.

To evaluate test-retest reliability for individual listeners, the data were pooled across listeners, SNRs, and adaptive-rule conditions, yielding a total of 89 test-retest pairs. The test-retest Pearson correlation coefficient (R) of the log-transformed set-size thresholds was 0.80 (p < 0.005). Furthermore, there was no evidence of any training effects, with no significant differences between the first and second set-size estimates [t(88) = 1.03, p = 0.31]. To evaluate the reliability of group-mean estimates using the adaptive set size procedure, the test-retest threshold estimates were averaged across listeners for those conditions where at least eight (out of 10) listeners produced at least two valid threshold estimates. The test-retest R across these eight conditions was 0.98 (p < 0.0005), with no significant differences between the two group-mean estimates [t(7) = 0.35, p = 0.74], suggesting a highly repeatable group-mean set-size estimate.

The accuracy of the set-size estimation method was evaluated by considering only the post-measurement data, ignoring the set-size threshold estimates. Figure 7 illustrates the accuracy with which the adaptive set-size algorithm yielded the intended group-mean percentage-correct performance level [Fig. 7a] and SRT [Fig. 7b]. These data were obtained from the last 40 trials of each block, when set size was held constant at the estimated set-size threshold. Data are plotted only for those conditions where at least eight (out of 10) listeners had at least one valid threshold measure for a given post-measurement condition. Error bars indicated ± one standard error of the mean percentage correct or SRT across listeners. The horizontal lines in Fig. 7a indicate the target scores of 66.7% (2u1d) and 50% correct (1u1d). The diagonal line in Fig. 7b indicates the target SNR. In Fig. 7a, the group-mean percentage-correct scores were within 5 percentage points of the target scores for all conditions except for one (2u1d, −9 dB) where the score was about 7 percentage-points lower (59.6%) than the target value (66.7%). In Fig. 7b, the group-mean SRT was within 1 dB of the target SNR for all conditions. Across all adaptive-rule and SNR conditions plotted in Fig. 7, the rms deviation of group-mean performance from the intended score was 3.8 percentage points, while the rms deviation from the intended SNR was 0.90 dB.

Figure 7.

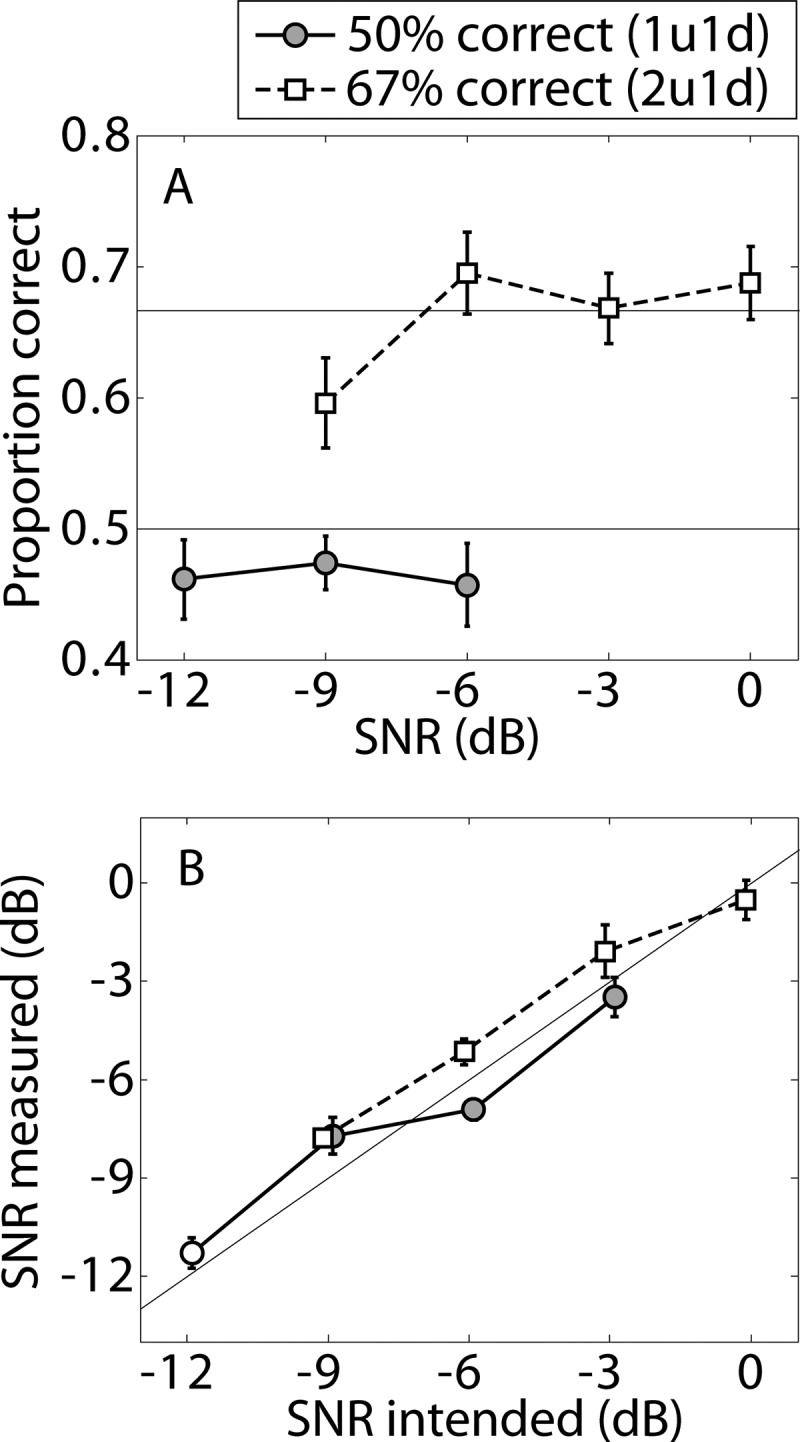
Results of experiment 2, showing group-mean VC/CV identification performance when the nominal set size was fixed at the value determined by the adaptive threshold set-size estimation algorithm. Separate panels show results for measurements of (a) proportion-correct performance level and (b)SRT. Error bars indicate standard errors of mean values across listeners. The accuracy of the adaptive set-size estimation method is indicated by the difference between measured performance and (a) the target performance level (50% or 66.7% correct) or (b) the target SNR represented by the thin lines in each panel.

The accuracy of individual estimates of threshold set-size was examined by pooling data across listeners, SNRs and adaptive rules. The rms deviation across all of these set-size estimation blocks was 11.9 percentage points for the percentage-correct data and 2.3 dB for the adaptive-SNR data (data not plotted). Although these rms deviations suggest fairly inaccurate performance for a given set-size estimation block, it should be noted that a substantial proportion of this variability can be ascribed to variability in the percentage-correct or threshold-SNR measures. Based on a binomial probability model, the expected rms errors for percentage-correct measurements across 40 trials are 7.4 and 7.9 percentage points for mean performance levels of 66.7% correct and 50% correct, respectively. Given the relationship between percent-correct and SNR (Fig. 1) of about 7%/dB, this translates to an expected rms error of about 1 dB for the SRT.

GENERAL DISCUSSION

Two experiments were carried out to test the feasibility of varying response set size to control SNR effects in the measurement of FMB for different listener groups or stimulus-processing conditions. The idea, based on a critical component of the theory underlying the Articulation Index (French and Steinberg, 1947; Kryter, 1962; ANSI, 1969) is that the difficulty or linguistic context of a speech task does not change the underlying amount of speech information available in the acoustic signal; rather, it changes the transformation from this fixed amount of speech information to performance level. If this assumption is correct, then performance differences between listener groups (or stimulus-processing conditions) can be offset by adjusting the difficulty of the task—here, the number of response choices available—without affecting the underlying amount of speech information available. Although articulation theory makes this claim, there are examples from the literature suggesting that this basic assumption does not always hold. In one important example, the widely used Speech Intelligibility Index (SII; ANSI, 1997) provides a range of frequency band-importance functions that depend on the nature of the speech task, rather than assuming a constant frequency allocation of speech information. This is based on results from the literature showing that lower frequencies gain in relative importance as the complexity of the speech materials increases from isolated syllables, to words, sentences and connected discourse (French and Steinberg, 1947; Duggirala et al., 1988; Studebaker and Sherbecoe, 1991; Sherbecoe and Studebaker, 2002). These results suggest that, contrary to the assumptions of articulation theory, the relative importance of various speech cues is indeed affected by context, with different parts of the acoustic signal increasing or decreasing in importance depending on the context. For example, prosodic cues carried in the low frequencies might be important in a connected-speech task but not an isolated-syllable task.

Another example from the literature where this assumption has been questioned is in the impact of speech context on the FMB (Buss et al., 2009), the question addressed here. This study was inspired by differences between the results of Bernstein and Brungart (2011) and Buss et al. (2009) suggesting that the FMB was immune to set-size manipulations under certain conditions (Bernstein and Brungart, 2011), but not others (Buss et al., 2009). Experiment 1 sought to determine the range of set-size and fluctuating-masker conditions for which set size and FMB were independent. The results showed that FMB was immune to set size manipulations for the full range of set sizes and fluctuating maskers that tested. The present results demonstrate that set size can be used to adjust stationary-noise performance at a given SNR to a specified level without affecting performance differently for the other masking conditions tested. This is an essential feature that should allow this manipulation to be used to adjust performance differences between groups without affecting the FMB being measured.

The lack of interaction between set size and masker type suggests that any changes in the speech features required or available to perform the task in the various masking conditions were independent of set size. On the other hand, it should be pointed out that set size, and the particular responses available as choices within a set-size condition, changed on a trial-by-trial basis. Even if the set of speech cues required to correctly identify the speech did vary as a function of set size, the continuously changing nature of the task might have made it difficult to make use of such cues. A different result might have been obtained had the response set been held fixed for a longer period of time, thereby allowing the listener to make use of any possible cues that varied between response sets. Although Bernstein and Brungart (2011) found no interaction between masker type and set size with the response set was held fixed for over 500 consecutive trials, they did not examine very small sets involving only a few response choices, nor did they compare low- and high-rate modulated maskers.

The lack of interaction between set size and fluctuating-masker type in experiment 1 contrasts with the results of Buss et al. (2009) who found a very large interaction between set size and SAM modulation rate on FMB in conditions similar to those tested in the current study. One possible reason for this discrepancy could be the different measurement and analysis methods used to investigate the relationship between set size and modulation rate. The current study measured psychometric functions. Relationships between percentage-correct scores and set size were examined for various maskers (Fig. 4) and the FMB was compared across set sizes at the same baseline stationary-noise SNR (Fig. 5). Buss et al. (2009) measured and compared the FMB across set sizes and masker types without controlling for the effects of set size on the baseline stationary-noise SNR. Although SRTs were not measured in the current study, an examination of the psychometric functions can give an idea of the results that might have been obtained by an adaptive-tracking procedure that does not control for differences in baseline stationary-noise SNR. Recall from the results of experiment 1 that there was a significant interaction between SNR and fluctuating-masker type (Fig. 3). At very low SNRs below about −15 dB, performance was better for the 4-Hz (open triangles) than for the 32-Hz masker (open circles), while for higher SNRs, performance was slightly better for the 32-Hz masker or was roughly equal for the two conditions. Importantly, this interaction occurred for all of the set sizes tested, and was also observed when the data were averaged across set size [Fig. 3h]. This interaction, together with the lack of a significant interaction between set size and masker type, suggests that the effect of modulation rate on performance was dependent on SNR, but not on set size.

If SRTs were extracted from the curves shown in Fig. 3, the interaction between modulation rate and SNR, combined with the main effect of set size, would have generated a result similar to that described by Buss et al. (2009). For very small set sizes, where percentage-correct performance was relatively good for a given SNR, an SRT tracking procedure would have converged on a very low SNR, where the FMB was considerably larger for the low-rate than for the high-rate SAM masker. For very large set sizes, where performance was relatively poor, the SRT tracking procedure would converge on a relatively high SNR, where the FMB was more comparable for the low- and high-rate SAM maskers. This should yield a result similar to that observed by Buss et al. (2009), whereby the FMB difference between the low- and high-rate SAM maskers was much greater for small set sizes than for large set sizes.

To examine this possibility, the FMB was estimated from the current data set by extracting SRTs from psychometric functions fit to the data (uncorrected for chance) from experiment 1. The FMB was calculated by subtracting the SRTs for each SAM masker from the SRT for stationary noise. FMB was estimated for set sizes of 2 and 160 for comparison with the three-alternative and open-set conditions of Buss et al. (2009). SRTs were extracted at the 60% performance level because 50% correct corresponded to chance performance for a set size of 2. As in the Buss et al. (2009) study, the FMB for a small response set (here, a set size of 2) was found to be much larger for the 4-Hz (18.1 dB) than for the 32-Hz SAM masker (9.1 dB). For a large response set (here, a set size of 160) the FMB was similar for the two maskers: 2.0 dB for the 4-Hz and 2.9 dB for the 32-Hz masker. It is important to stress that this apparent interaction between set size and modulation rate was not an effect of set size per se, but instead an effect of SNR, as the interaction between SNR and modulation rate was observed across all set sizes. When the FMB was instead estimated at a common stationary-noise SNR (but different performance level) for each set-size condition, there was no observed influence of set size on the FMB (Fig. 5). The current results therefore can be interpreted as corroborating this aspect of the results of Buss et al. (2009), but shedding doubt on their main conclusion that the context of the speech task affects the nature of the cues needed to perform the task and therefore the FMB. Bernstein and Grant (2009) and Bernstein and Brungart (2011) described how an adaptive SNR-tracking algorithm can lead to erroneous conclusions regarding differences between listener groups in the ability to listen in the gaps of a fluctuating masker. The interaction between SNR and masker type observed in experiment 1 points to yet another situation where an adaptive-tracking algorithm could lead to an erroneous conclusion regarding the influence of an experimental parameter on the benefit that listeners receive from masker fluctuations. This result further underscores the potential pitfalls of using an adaptive-tracking algorithm in the estimation of the FMB or other SNR-dependent effects.

The set of results presented here are also seemingly at odds with the results of two studies by Dirks and colleagues. Dirks et al. (1969) and Dirks and Bower (1971) showed that the relationship between the modulation frequency of an AM masker and performance differed depending on the nature of the speech materials. For spondees and sentences, performance was generally better for a 1-Hz than for a 10-Hz interrupted-noise masker. In contrast, the best modulation rate depended on SNR for monosyllabic and non-spondee bisyllabic speech materials, with better performance observed for a 10-Hz masker at more favorable SNRs, and for a 1-Hz masker at less favorable SNRs. Although Dirks and colleagues measured psychometric functions rather than SRTs, their results were nevertheless susceptible to an SNR confound because the ranges of SNRs tested differed across speech materials. A closer examination of the data of Dirks et al. (1969) reveals that a crossover effect between the 1-Hz and 10-Hz conditions was also present for the spondee and sentence materials. This crossover point occurred at an SNR comparable to the crossover point for the monosyllables and non-spondee bisyllable speech tests (about −20 dB in the conditions involving a 50-dB SPL masker level). This crossover was not as visually apparent in the sentence and spondee data because it occurred at a performance level that was near ceiling (about 90% correct) for these easier speech tasks. In the more difficult monosyllabic and non-spondee bisyllabic tests, performance at the (−20 dB SNR) crossover point occurred at a performance level of about 40% correct, and was therefore much more visually apparent. Thus, the apparent differences between these previous results and those of current study might also be attributable to an SNR confound in the data of Dirks and colleagues.

The above discussion points to an interaction between SAM rate and SNR as the cause of the apparent interactions between SAM rate and speech task identified in previous studies (Dirks et al., 1969; Dirks and Bower, 1971; Buss et al., 2009). One possible contributor to the interaction between SAM rate and SNR in their effect on speech identification performance (Fig. 3) is the limited temporal resolution of the auditory system, which would limit a listener’s ability to extract information from dips in the level of a modulated masker, especially at high modulation rates. The effects of limited temporal resolution should be greatest at the lowest instantaneous masker levels (i.e., the bottom of the valleys), because the duration of the glimpses at these very low levels are very short, making them more audible for a smaller proportion of the SAM period than glimpses occurring at higher-level portions of the SAM cycle. At very low SNRs, more of the dynamic range of the target speech will be similar in level to the noise levels during the masker valleys, thereby increasing the impact of limited temporal resolution on the ability to benefit from masker dips for higher-rate modulated maskers.

Experiment 2 tested the feasibility of an adaptive method to determine the set size required to yield a given performance level at a given SNR. Test-retest reliability of the set-size estimate was fairly good for individual listeners (R = 0.80) and nearly perfect for the group mean (R = 0.98). The accuracy of this estimate was evaluated by fixing the set size and estimating the percentage-correct performance level or SRT. The tracking procedure was found to be fairly accurate in achieving the desired group-mean performance-levels, with scores generally falling within 5 percentage points of the tracked performance level and SRTs falling within 1 dB of the target SNR. Estimates of the required set size for individual listeners were somewhat less accurate and less repeatable, but potentially still useful in a correlational study involving many listeners. Together with the results of experiment 1, these results are encouraging for the feasibility of using set size to offset performance differences in studies examining FMB across listener groups.

Although the current study focused on the relationship between set size and FMB, set-size adjustment might also be useful in controlling SNR in the assessment of differences in informational masking (IM) across listener groups or processing conditions, another situation susceptible to an SNR confound. To apply this approach in an IM context would require evidence that the set-size manipulation does not affect IM. It is not known under which circumstances this might occur. It has been proposed that IM includes two possible sources—stimulus uncertainty and target-masker similarity (e.g., Durlach et al., 2003; Watson, 2005). Changes to the response set would not affect the acoustic similarity of the target and masker, but such changes might affect stimulus uncertainty, and thereby IM, by limiting the range of possible stimuli from which the target can be selected. Although IM in speech perception has been demonstrated both in situations with a small, closed response set (e.g., Brungart, 2001; Brungart et al., 2001; Freyman et al., 2001, 2004; Arbogast et al., 2005), and in an open-set sentence-perception paradigm (e.g., Helfer and Freyman, 2009), these two situations have not been directly compared. Before the set-size technique can be applied to investigations of IM, further work is needed to characterize the effect of set size on IM and to determine whether there is a set of conditions for which IM is not affected by set size.

Another area where set-size adjustment could be a useful tool is in the evaluation of hearing-aid signal-processing algorithms, whose effects can also be SNR dependent. For example, for a speech-on-speech masking situation, Naylor and Johannesson (2009) found that fast compression improved the effective SNR at the output of the hearing aid for unfavorable (generally negative) input SNRs, but reduced the effective SNR for more favorable (generally positive) input SNRs. As in the case of FMB estimation discussed in the current study, an SRT measurement would allow the SNR to vary freely, thereby complicating the evaluation of the benefits of such an algorithm for particular patient. The set-size procedures developed here could be applied to the hearing-aid evaluation process to give the experimenter or clinician more control over the SNR range while still allowing the benefits of an adaptive-tracking procedure. As in the cases of IM and FMB estimation, such an application would first require evidence that set-size adjustments do not affect the benefit provided by a particular signal-processing algorithm at a given SNR.

SUMMARY AND CONCLUSIONS

In stationary noise, HI listeners generally show speech-reception performance deficits relative to NH listeners. As a result, adaptive-tracking algorithms converge to different SNRs for NH and HI listeners. This can complicate the interpretation of data in experiments that compare FMB for NH and HI listeners, because differences in SNR for the baseline (stationary-noise) condition has an influence on the amount of FMB observed. The experiments presented here tested the feasibility of a set-size adjustment method to control stationary-noise performance in comparisons of speech intelligibility in stationary and fluctuating maskers. The idea was that this adjustment could equalize recognition scores at a given SNR, thereby removing this confound. In the first experiment, it was found that the set-size manipulation had the same effect on performance for stationary-noise and several fluctuating-masker conditions, indicating that set size can be used as a tool to adjust baseline performance without affecting FMB. A second experiment showed that an adaptive procedure was able to accurately estimate the set size required to yield a given performance level or SRT for listeners, especially in the group-mean case. Together, these results demonstrate the feasibility of using set size as a tool to equalize performance levels between listener groups and avoid SNR confounds in the measurement of FMB.