Robust methods for automatic image-to-world registration in cone-beam CT interventional guidance

Abstract

Purpose: Real-time surgical navigation relies on accurate image-to-world registration to align the coordinate systems of the image and patient. Conventional manual registration can present a workflow bottleneck and is prone to manual error and intraoperator variability. This work reports alternative means of automatic image-to-world registration, each method involving an automatic registration marker (ARM) used in conjunction with C-arm cone-beam CT (CBCT). The first involves a Known-Model registration method in which the ARM is a predefined tool, and the second is a Free-Form method in which the ARM is freely configurable.

Methods: Studies were performed using a prototype C-arm for CBCT and a surgical tracking system. A simple ARM was designed with markers comprising a tungsten sphere within infrared reflectors to permit detection of markers in both x-ray projections and by an infrared tracker. The Known-Model method exercised a predefined specification of the ARM in combination with 3D-2D registration to estimate the transformation that yields the optimal match between forward projection of the ARM and the measured projection images. The Free-Form method localizes markers individually in projection data by a robust Hough transform approach extended from previous work, backprojected to 3D image coordinates based on C-arm geometric calibration. Image-domain point sets were transformed to world coordinates by rigid-body point-based registration. The robustness and registration accuracy of each method was tested in comparison to manual registration across a range of body sites (head, thorax, and abdomen) of interest in CBCT-guided surgery, including cases with interventional tools in the radiographic scene.

Results: The automatic methods exhibited similar target registration error (TRE) and were comparable or superior to manual registration for placement of the ARM within ∼200 mm of C-arm isocenter. Marker localization in projection data was robust across all anatomical sites, including challenging scenarios involving the presence of interventional tools. The reprojection error of marker localization was independent of the distance of the ARM from isocenter, and the overall TRE was dominated by the configuration of individual fiducials and distance from the target as predicted by theory. The median TRE increased with greater ARM-to-isocenter distance (e.g., for the Free-Form method, TRE increasing from 0.78 mm to 2.04 mm at distances of ∼75 mm and 370 mm, respectively). The median TRE within ∼200 mm distance was consistently lower than that of the manual method (TRE = 0.82 mm). Registration performance was independent of anatomical site (head, thorax, and abdomen). The Free-Form method demonstrated a statistically significant improvement (p = 0.0044) in reproducibility compared to manual registration (0.22 mm versus 0.30 mm, respectively).

Conclusions: Automatic image-to-world registration methods demonstrate the potential for improved accuracy, reproducibility, and workflow in CBCT-guided procedures. A Free-Form method was shown to exhibit robustness against anatomical site, with comparable or improved TRE compared to manual registration. It was also comparable or superior in performance to a Known-Model method in which the ARM configuration is specified as a predefined tool, thereby allowing configuration of fiducials on the fly or attachment to the patient.

INTRODUCTION

Image-guided surgery (IGS) has become increasingly prevalent in clinical practice over the past 20 years for procedures such as orthopaedic, head and neck, and neuro-surgery. Systems for IGS provide geometrically registered information to aid navigation, visualization, targeting, and avoidance of critical anatomy.¹ Conventional navigation systems rely on preoperative images and can be prone to target registration error arising from morphological change imparted during surgery, such as tissue deformation and excision. Such limitations have motivated the development of intraoperative imaging systems to provide updated anatomical information that properly reflects anatomical change during the procedure. Cone-beam computed tomography (CBCT) on a mobile C-arm with a flat-panel detector (FPD) is among such intraoperative imaging technologies, allowing sub-mm isotropic 3D spatial resolution and soft tissue visualization at low radiation dose.^{2, 3, 4} Such systems have the potential to improve surgical precision and patient safety, and as reported below, can be used to improve and streamline the process of image-to-world registration that is essential to surgical navigation.

Background

Conventional (manual) image-to-world registration

Surgical navigation requires a registration of image and world coordinate systems (referred to as image-to-world registration), with methods including markerless and marker-based paired-point and surface registration.⁵ Markerless paired-point registration involves identification of characteristic “anatomical landmarks” in image data and on the patient using a tracked pointer based on optical or electromagnetic tracking. This method does not require fiducial screws or markers affixed to the patient, but exhibits limited accuracy since distinct landmarks are not always available or reliable due to skin surface deformation. A more common method involves marker-based paired-points in which extrinsic fiducial markers (e.g., affixed to the cranium) are clearly identifiable in image data and on the patient's body. However, manual colocalization of markers in image data and on the patient can be time consuming and prone to manual error. Additionally, the markers must be affixed prior to the imaging session, requiring logistical coordination in fiducial placement prior to preoperative scanning. Finally, surface registration involves segmentation of the anatomical surface in image data and correlation to the patient in the world coordinate system using a tracked pointer traced along the skin surface. Iterative closest point (ICP) techniques or variants thereof are employed to register the two surfaces.⁶ Since the skin surface is prone to shift and deformation between planning and surgery, surface registration suffers some of the same drawbacks as markerless point-based registration.⁷

Automatic image-to-world registration: Markerless

Manual image-to-world registration typically requires minutes for a clinician or OR technologist to perform and can be a bottleneck to surgical workflow. It is also somewhat impractical to update (i.e., repeat) the registration or recover from perturbations during surgery. Furthermore, the manual process is prone to human error, often requires several attempts to achieve an acceptable registration, and is subject to changes in the patient anatomy. A variety of efforts have sought to automate image-to-world registration. In the context of markerless registration, work by Grimson et al.⁸ used a laser striping device to obtain 3D measurements of the patient surface and applied computer vision techniques to match the surface to segmentation of the skin from MRI or CT, essentially automating the markerless surface-based approach. Klein et al.⁹ developed a method for automatic registration in navigated bronchoscopy based on the trajectory recorded during routine examination of the airways at the beginning of an intervention. Lee et al.¹⁰ used computer vision techniques applied to frameless cranial IGS to compute image-to-world registration using natural features of the patient.

Automatic image-to-world registration: Marker-based

Similar advances have been made in automatic marker-based registration. For example, specially designed patient masks and headsets potentially improve registration accuracy,¹¹ although the need to remove the device (and replace it each time the registration is to be updated) narrows the range of application and can present a barrier to workflow. For intraoperative C-arm imaging, tracking the C-arm^{12, 13} can provide automatic registration with each C-arm image, since both the patient and C-arm are visible to the tracker, but can be prone to registration errors associated with suboptimal positioning of the tracking system and nonidealities in C-arm gantry rotation.

Several groups have developed means for automatic localization of fiducial markers. Kozak et al.¹⁴ described a new marker design and an automated segmentation algorithm for locating the centroid of markers in 3D image space, demonstrating improved registration accuracy, although the method only automated marker identification in the 3D image data (and marker localization in the world coordinates – i.e., on the patient – was still performed manually). A commercial electromagnetic navigation system, iGuide CAPPA (Siemens AG Healthcare, Erlangen, Germany), provided automatic registration in a similar manner: spherical markers were automatically localized in a CBCT volume and electromagnetically tracked to update the image-to-world registration with each scan.¹⁵ Yaniv^{16, 17} described a method for localizing markers that are outside the reconstructed field of view (FOV) in CBCT by localizing markers in a subset of projection images. This method demonstrated the ability to localize markers accurately in CBCT projections, but involved a degree of manual interaction (e.g., manual definition of a region of interest (ROI) in projection data). Similarly, Hamming et al.¹⁸ described a system for automatic registration directly from CBCT projection data (or subsets thereof for markers outside the FOV) and demonstrated accuracy and reproducibility equivalent or superior to the conventional manual technique in a variety of marker configurations for CBCT-guided head and neck surgery.

Such automatic marker-based registration approaches require automatic segmentation of markers in either the volume or projection domain and can utilize a variety of segmentation methods. Papavasileiou et al.¹⁹ proposed an automatic algorithm for localizing markers in the CT volume, treating the cross section of external markers as protrusions of the slice contour, and localizing 3D marker centroids using an intensity-weighted algorithm following segmentation. Mao et al.²⁰ proposed a method capable of detecting implanted metallic markers (spherical and cylindrical) in both kilovoltage (kV) and megavoltage (MV) images in image-guided radiotherapy. Several marker segmentation algorithms specifically for CBCT projection image sequences have also been reported. Template matching or circle fitting^{18, 21, 22} has demonstrated good performance on spherical markers and involves a fairly simple implementation. Jain et al.²³ designed a marker consisting of a mathematically optimized set of ellipses, lines, and points to segment markers semiautomatically and determine the pose of an x-ray projection using single-frame fluoroscopy (FTRAC). More sophisticated methods have recently been reported, such as creating a 3D marker model from image sequences to address the problem of changing marker shape with projections^{24, 25} or using score functions to track multiple markers.²⁶

Outline of the current work

The work reported below develops two types of automatic, marker-based, image-to-world registration. The first involves a technique in which the marker configuration is specified a priori (similar to defining a tracked tool, referred to as the “Known-Model” method), and knowledge of the marker configuration is employed in 3D-2D registration between the projection image and world coordinate systems. The second extends the projection-based method reported by Hamming et al.¹⁸ (referred to herein as the Free-Form method), which demonstrated the potential for improved registration accuracy and surgical workflow in CBCT-guided procedures, but initial results exhibited some sensitivity to error in (template-based) marker segmentation and focused specifically on implementations appropriate to head and neck surgery. The work below extends the Free-Form methodology to a more robust algorithmic form, employing a Hough transform segmentation of markers, modified search windows, and rejection of false-positive marker detections with improved robustness in comparison to a circular template. Both the Known-Model and Free-Form methods were tested using a simple automatic registration marker (ARM) suitable to various surgical procedures and anatomical sites and evaluated in comparison to manual registration in three anatomical sites (head, thorax, and abdomen) and at variable distance between the ARM and C-arm isocenter (i.e., the patient) as may be necessitated by the anatomical site, body habitus, and auxiliary surgical equipment. The first method requires precise geometric definition of the ARM as a known “tool” in the tracking system, whereas the second method allows a freely defined ARM or, alternatively, markers placed freely on the patient. Finally, the methodologies are translated from prototype form (MATLAB, The Mathworks, Natick, MA) to a C++ implementation using open-source libraries common in IGS—specifically, the cisst libraries²⁷ and 3D Slicer interface²⁸ as implemented in the TREK architecture²⁹ for CBCT-guided surgery.

MATERIALS AND METHODS

Experimental setup

The experimental setup is illustrated in Fig. 1 and consisted of two main systems: a prototype mobile C-arm for intraoperative CBCT and a surgical tracking system with passive retroreflective markers. The C-arm prototype has been previously reported^{2, 3, 4} and was developed in collaboration with Siemens Healthcare (Erlangen, Germany) for high-quality intraoperative 3D imaging at low radiation dose. The mobile isocentric C-arm was modified to include a large-area FPD (PaxScan 3030+, Varian Imaging Products, Palo Alto, CA), a computer-controlled orbital drive, methods for geometric calibration,³⁰ and processing of projection data for CBCT reconstruction.³¹ The FPD has 1536 × 1536 pixels at 0.194 mm pitch, binned upon readout to 768 × 768 pixels in dual-gain readout mode.³² The orbital range of the gantry is ∼178°, and nominal CBCT imaging involves 200 projections acquired in ∼60 s, with fast-scan and slow-scan protocols also available (100 and 600 projections, respectively, giving 32–192 s scan time). Volumetric reconstruction is performed using a variation of the Feldkamp-Davis-Kress (FDK) algorithm,³³ implemented on a graphics processing unit (GPU), providing 512³ volumes within ∼10–20 s. Nominal volumetric FOV is 15 × 15 × 15 cm³ at 0.3 mm voxel size. Potential applications include spine surgery,^{34, 35} head and neck surgery,^{3, 36, 37} thoracic surgery,³⁸ brachytherapy,³⁹ and abdominal interventions⁴⁰ – motivating the studies below of automatic image-to-world registration for a broad variety of anatomical sites.

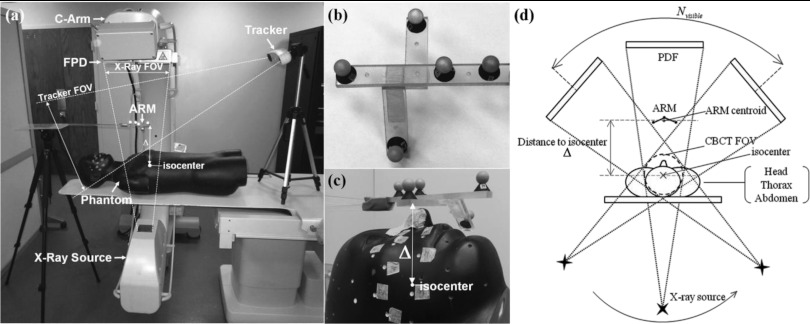
Figure 1.

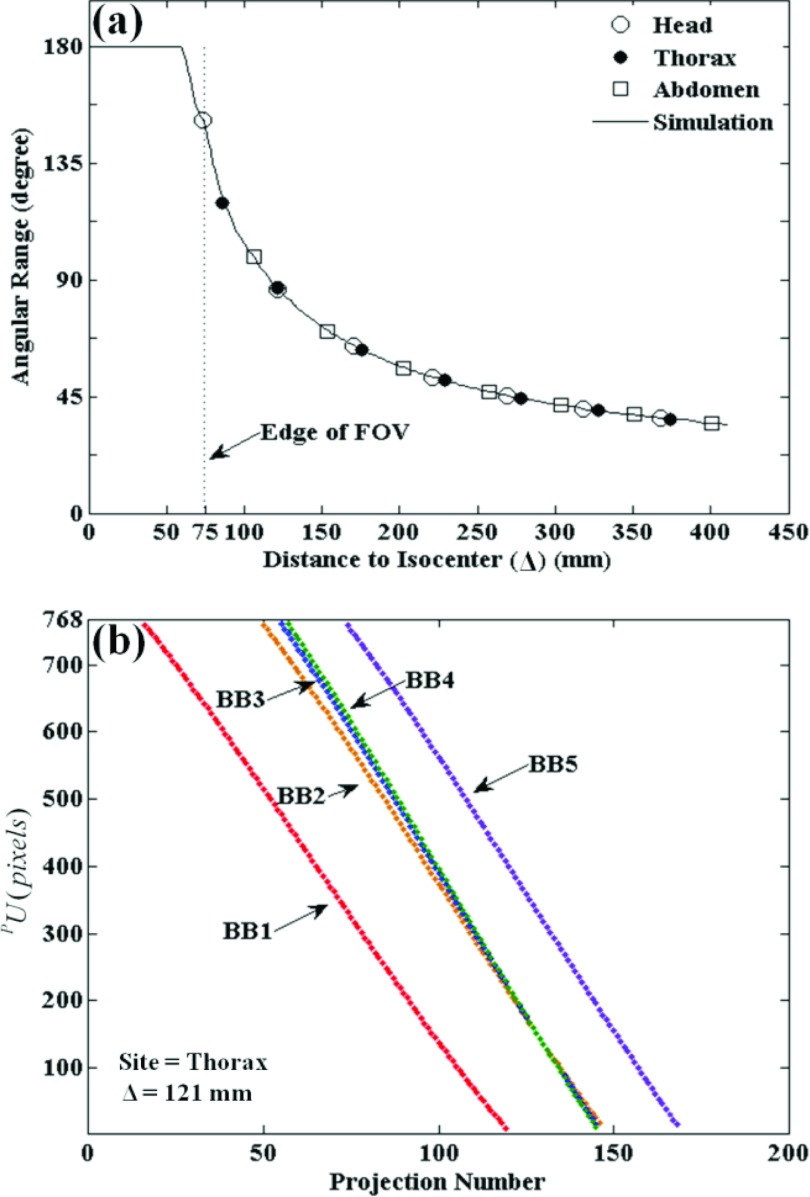
(a) Illustration of the experimental setup, including the C-arm, tracking system, ARM (automatic registration marker), and phantom. The ARM is placed in the FOV of the tracker and a subset of x-ray projections (e.g., above the patient and visible in posterior-anterior projection). (b) Closeup of a simple ARM configuration. Each MM marker consists of a reflective spherical marker with a tungsten sphere (BB) placed at the center and mounted on an x-ray translucent post. (c) Closeup of the ARM placed immediately above a head phantom at minimum separation (Δ) from isocenter (where Δ is the distance from the centroid of the five MM markers to C-arm isocenter). (d) Illustration of system geometry. With the ARM placed at a distance Δ, the MM markers are visible in a subset of projections (N_visible) across the semicircular source-detector orbit.

The tracking system was a stereoscopic infrared (IR) camera (Polaris Vicra, NDI, Waterloo, ON) capable of measuring the locations of up to 50 passive retroreflective spherical markers with a specified accuracy of 0.25 mm root mean square (RMS). The tracker measurement volume described as a rectangular frustum offset from the face of the camera by 55 cm, with a 49 × 39 cm² proximal FOV and 94 × 89 cm² distal FOV separated by 78 cm, thereby sufficient to encompass a large envelope within the C-arm gantry.⁴¹ The tracker was integrated within custom navigation software (“TREK”) for surgical navigation.²⁹

Conventional (manual) image-to-world registration

The IR tracking system measures the location of individual spherical markers (referred to as “strays”) and/or rigid configurations of 3 or more markers affixed to trackable tool (e.g., a pointer, drill, or suction). As briefly summarized in Sec. 1A, in conventional (manual) image-to-world registration, a tracked pointer is used to localize points on the patient [the world coordinate system (x_world, y_world, z_world)], which are then matched to corresponding points in CBCT [the 3D image coordinate system (x_image, y_image, z_image)]. The procedure typically consists of placing the tip of the pointer on a uniquely identifiable point on the patient surface (e.g., a divot in a skin marker or fiducial marker rigidly affixed in bone), simultaneously identifying the corresponding point in the CBCT image, and repeating for at least four points (typically 6–12 points). Alternatively, the pointer can be continuously traced in freehand over the skin surface, and the measured trajectory is fit to a surface which is in turn registered to a segmentation of the patient skin surface. The process is prone to manual error and intraoperator variability, with registration accuracy (target registration error, TRE) typically reported in the range ∼2 mm under best circumstances,^{42, 43} and ∼4 mm under clinical conditions.⁴⁴

In studies reported below, manual registration was performed using a rigid pointer (Polaris Passive 4-Marker Probe, NDI, Waterloo, ON) placed in conical divots (fiducials) drilled in the surface of the rigid head, chest, and abdomen phantom shown in Fig. 1. The corresponding position of each divot was manually localized five times in CBCT using the TREK navigation system, and the average defined the “true” position in CBCT coordinates. A total of 6 or 7 fiducials were used for each manual registration. The point sets colocalized in the world and image coordinate systems were registered using the rigid point-based method described by Horn.⁴⁵ The methodology is common to laboratory testing of surgical tracking systems, and the resulting registration accuracy is recognized as “best-case” and likely superior to that achieved in actual clinical settings. The comparison of manual registration under laboratory conditions to automatic registration techniques that do not rely on manual dexterity and surface fiducials is therefore considered conservative (i.e., advantageous to the manual technique).

Automatic image-to-world registration using a known registration marker

For some applications, an ARM can be designed with a well-defined distribution of markers, allowing the ARM to be defined as a tool recognized by the tracking system. In such circumstances, knowledge of the predefined ARM configuration can be leveraged in the registration process to improve robustness and accuracy in comparison to a Free-Form marker configuration in which the distribution of markers is unknown to the tracker, and individual markers are instead tracked as “strays.”

Automatic registration using the Known-Model method employed an approach similar to the 3D template as in Poulsen et al.²⁴ Instead of a simplified 3D shape template based on back-projection (convex-hull) of a few manually selected binarized x-ray images, we incorporated a priori knowledge of the shape and material composition (x-ray attenuation coefficient) of the arbitrarily shaped radio-opaque marker structures and applied intensity-based 3D-2D registration to localize the structures in the image space. The image similarity based optimization eliminates the need for segmentation, which tends to require additional tuning parameters, and directly localizes the known marker structure using information contained in all projection images simultaneously. Hence, the method is expected to be robust to noisy backgrounds (e.g., surgical tools and the operating table as shown in experiments below) with fewer tuning parameters. The radio-opaque structures are rigidly connected to a tracking fiducial (e.g., retroreflective spheres, checker-board patterns, magnetic coils, etc.) that defines the world coordinate system, and the combined tool is calibrated preoperatively to obtain the relative transformation between the radio-opaque structures and the tracking fiducial. Note that this step is straightforward (or unnecessary) when multimodality markers (MM, defined below) are used, since each radio-opaque structure (BB) is aligned at the center of each tracking marker (reflective sphere). Thus, the 3D-2D registration result and the preoperative calibration provide the image-to-world registration.

The Known-Model method begins with creation of a 3D model (volume) describing the geometry and x-ray attenuation coefficient of the ARM. The center of each optical marker is precisely identified with respect to the coordinate frame associated with the volume: the “model” coordinate system, M, can be generated by various means, for example: (i) precise geometric alignment of each marker derived from a CAD model or measurement by a coordinate-measurement-machine (e.g., a Faro arm or a precise tracker); or (ii) identification of marker locations in a high-resolution CT or CBCT of the ARM. The latter was used in the current work, and the center of each marker was defined by repeat localization in TREK to determine M with respect to the volume. The attenuation volume contains all features that are rigidly connected to the ARM (e.g., the support frame, marker posts, etc.) and are additionally included in the 3D-2D registration step. The tracker measured the position of the model coordinate system with respect to the world coordinate system, with transform between the two denoted ^MT_W.

The image-to-model transformation (^IT_M) was estimated by registering the 3D attenuation volume of the ARM associated with M to the projection image coordinate system (denoted I) using an intensity-based 3D/2D registration in multiple projection views. The registration approach followed Otake et al.³⁴ Based on an approximate estimate of ^IT_M and the geometric calibration of the C-arm, digitally reconstructed radiographs (DRRs) of the attenuation volume were generated. The ^IT_M that maximizes a similarity metric (viz., gradient information⁴⁶) between the DRRs and the real projection images was found with a nongradient stochastic optimizer [viz., the covariance matrix adaptation evolution strategy, CMA-ES (Ref. ⁴⁷)]. The population size in the CMA-ES was 30 transformations, which was chosen to be fairly small for purposes of computational speed. Higher values of population (e.g., 60) did not demonstrate an improvement in registration accuracy. Initialization was estimated from a simple classical pose estimation algorithm such as POSIT (Ref. ⁴⁸), where a rough segmentation based on morphological filtering was first used to identify projected 3D points in one image, and then POSIT was applied to obtain a rough initial guess. Finally, the image-to-world transformation (denoted as ^IT_W) was computed as ^IT_W = ^IT_M^MT_W.

Automatic image-to-world registration by detection of markers in projection data

Previous work¹⁸ described a process for automatic image-to-world registration using markers that were visible to the tracking system and detectable in x-ray projections. The so-called “multimodality” markers (MM, implying detection by both the infrared tracking and x-ray imaging systems) involved 11.6 mm diameter retroreflective spheres modified to include a 2 mm tungsten BB at the center. The method demonstrated accuracy and reproducibility equivalent or superior to manual registration using a variety of marker configurations suitable to CBCT-guided head and neck surgery. Yaniv used a comparable method^{16, 17} and reported similar advantages in accuracy, reproducibility, and speed of registration. In comparison to the Known-Model method, automatic detection of markers in the projection data allows image-to-world registration from freely configurable marker configurations, i.e., does not rely on a specific marker arrangement. The location of each marker is localized independently by the tracker as a “stray,” and no additional knowledge of the geometric relation between markers is required. The approach therefore permits variations in which markers are freely configured in the operating room or even attached to the patient surface.

The relationship between fiducial marker arrangement and registration accuracy is well known^{49, 50} and suggests guidelines for good fiducial configurations, for example, maximum separation between individual markers (consistent with other constraints, such as attachment sites on the patient and tracker line of sight); minimum separation between the centroid of the marker distribution and the surgical target; and multiple markers (at least four, typically 6–12) to reduce TRE. With these guidelines in mind, we designed a simple ARM tool analogous to the various marker configurations described by Hamming et al.⁵⁰ (e.g., “cloud” distributions etc.) – not necessarily as an optimal configuration, but one that was reasonably small (comparable to typical rigid body markers), light-weight, potentially sterilizable, and x-ray translucent. The resulting ARM is illustrated in Fig. 1b, consisting of five MM markers mounted on a rigid, acrylic support, in turn positioned within the x-ray and tracker FOV by an acrylic rod supported by a floor-mounted tripod or table-mounted arm. There are certainly alternative tool designs that could offer comparable or superior configurations with respect to the guidelines intending to minimize registration error, but for purposes of the current work (focusing on robust algorithms for automatic registration, rather than optimal tool design), the simple ARM was used for all studies reported below. More optimal ARM designs could include a more distended arrangement of MM markers and/or a concave arrangement intended to place the marker centroid deeper within the patient (i.e., closer to the surgical target). However, symmetric fiducial configurations should be avoided, which could confound both the Free-Form and Known-Model automatic methods. (This is not an issue for manual localization, since the operator incorporates additional contextual information in fiducial identification.)

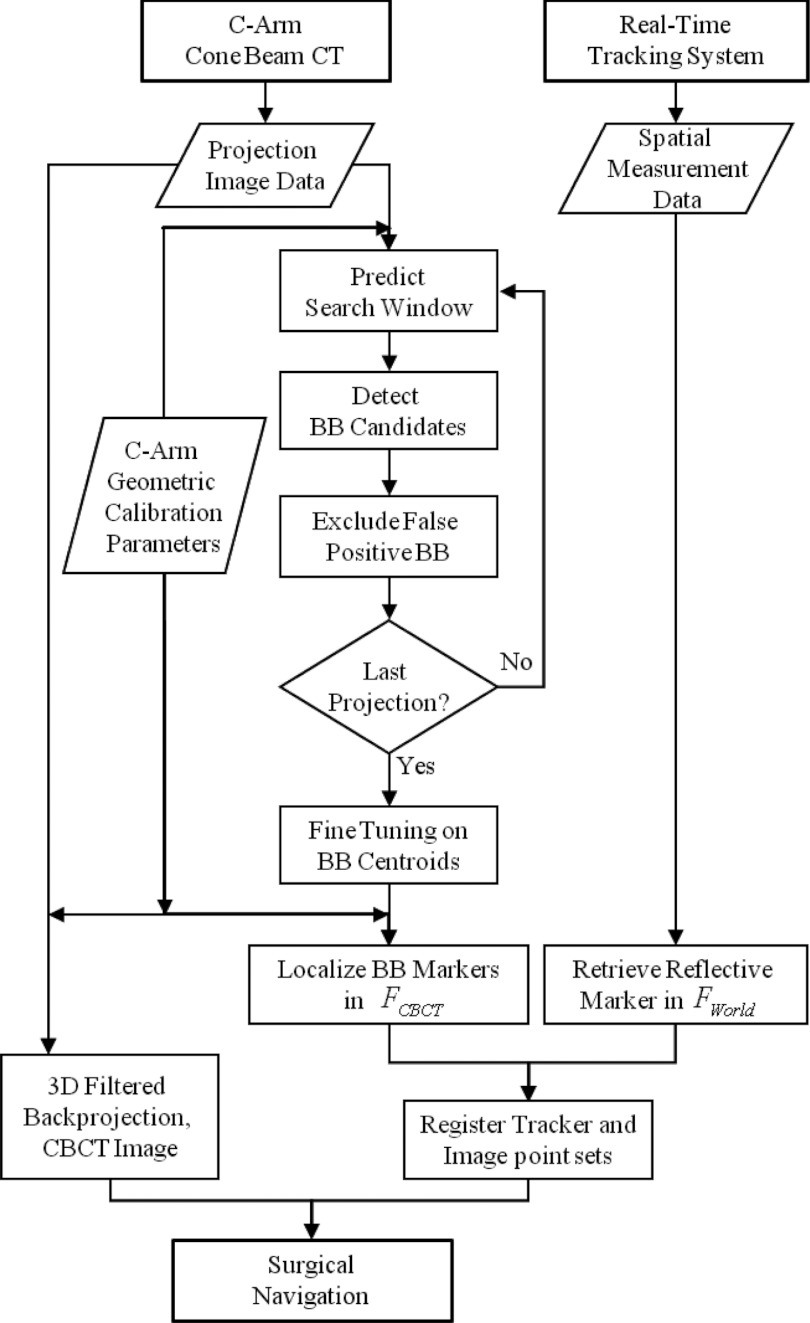
The basic method of Hamming et al.¹⁸ was extended to a more robust form detailed below and summarized in Fig. 2, with primary modifications including: MM marker detection using a Hough transform (improved robustness in comparison to a circular template); modified search windows (reducing the search space and allowing recovery from missed detections); trimming of false positives (i.e., detections not satisfying consistency conditions of continuous motion in the sinogram); and implementation in C++ (improved speed in comparison to MATLAB and compatibility with TREK and associated cisst²⁷ and 3D Slicer²⁸ libraries).

Figure 2.

Summary of the Free-Form automatic image-to-world registration algorithm.

A Hough transform method for robust 2D localization of markers

The Hough-transform-based 2D localization of MM markers consists of two major steps. First, a CBCT projection (or subregion identified by a search window) is transformed into a 2D accumulator space via Hough transform (wherein voting is only with regard to the marker center) in which marker candidates are selected according to accumulated votes. Second, a small region surrounding each candidate is selected, and the centroid of the candidate is calculated by image morphology operations with subpixel precision. The two-step process provides robustness (via the Hough transform at geometric accuracy of ∼1 pixel) as well as precision (centroid calculation at subpixel accuracy).

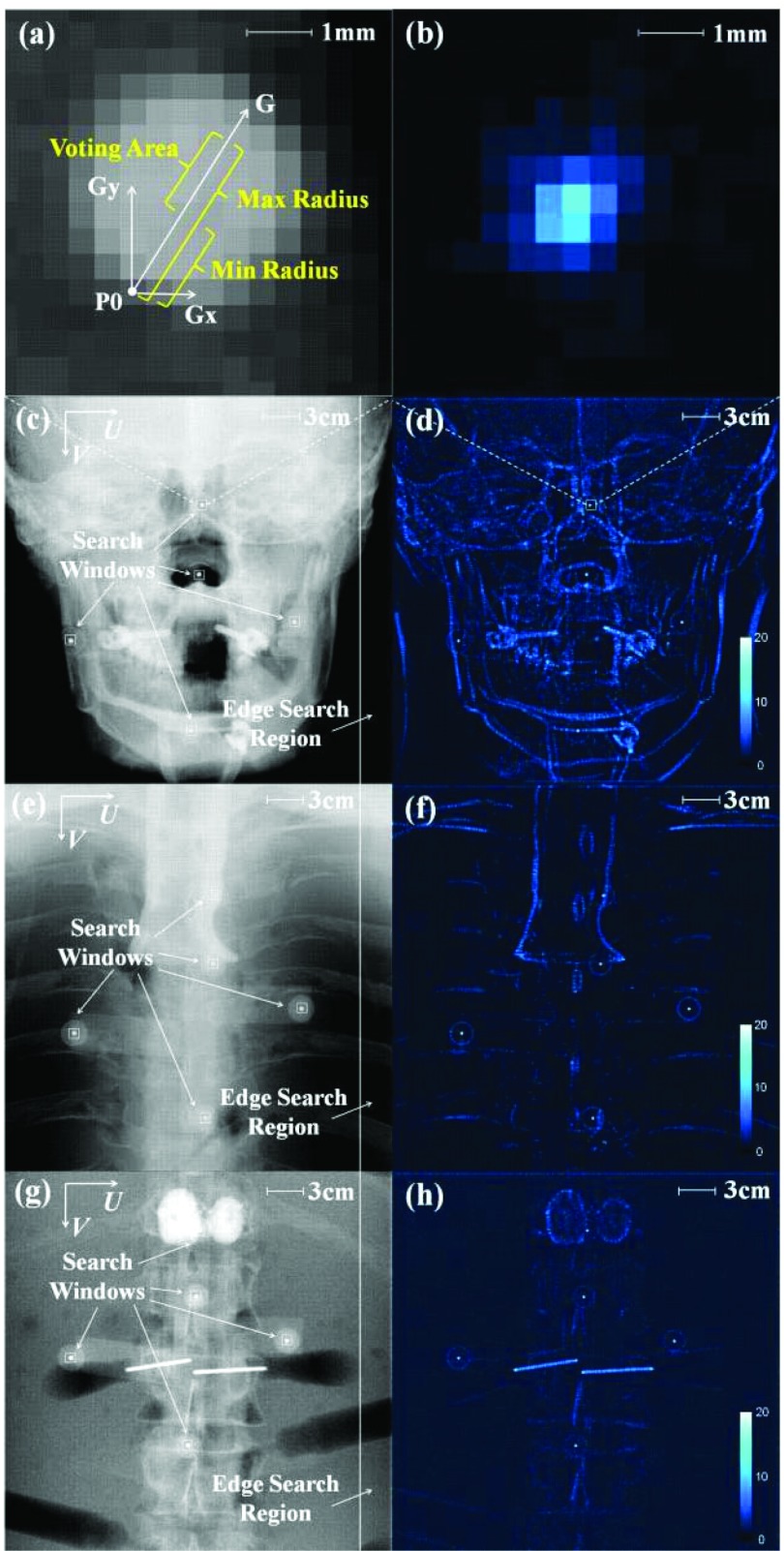
Figure 3 shows the Hough transform method on an anthropomorphic head, thorax, and abdomen phantom (The Phantom Labs, Greenwich, NY). The process first applies a gradient threshold to a CBCT projection (or a search window subregion). The gradient threshold is freely adjustable, and a value of 0.1 ADU/pixel was found experimentally to provide reasonable thresholding in both horizontal and vertical directions for all three body sites. Next, along the gradient direction of each surviving pixel [e.g., vector G of pixel P₀ in Fig. 3a] any pixel that falls within the voting area (bounded by min and max radius) adds one vote to its corresponding pixel in accumulator space. The min and max radius were chosen as 3 and 6 pixels, respectively, according to the size of BB markers in projections. The voting procedure on each surviving pixel generates an accumulator array [Fig. 3b] which is subsequently blurred by a Gaussian kernel (σ = 0.26 pixels). A threshold is applied to the accumulator array to eliminate noisy votes corresponding to background features, with a threshold of 20 votes found sufficient to suppress background noisy votes in all studies below. Finally, pixels exhibiting the votes in accumulator space are chosen as BB marker candidates.

Figure 3.

A robust Hough-transform-based marker localization method. (a) Illustration of the voting mechanism in the Hough transform applied to a small search window about a BB. The voting area of each pixel is generated in the direction of its intensity gradient and constrained by the size of BB markers in projections. (b) The corresponding search window from (a) after Hough transform. Example PA projections of the ARM are shown in the context of the (c) head phantom, (e) thorax phantom, and (g) abdomen phantom. The accumulator space generated by the Hough transform is illustrated in (d), (f), and (h), respectively. The BB markers along with some anatomical structures and surgical implants survive the Hough transform accumulation, but the BB markers consistently demonstrate the highest vote accumulation due to their specific size and circular shape.

The Hough transform method takes advantage of the size and circular shape of BB markers via the voting procedure, providing robustness against high-contrast anatomical structures and interventional devices. Another advantage was that thresholding in accumulator space was more robust in detecting BBs in complex scenes [the head, Fig. 3c] and in large body sites [the abdomen, Fig. 3g] compared to intensity thresholding.¹⁸

Search windows

Rather than computing the Hough transform and accumulation matrix over the entire image for each projection, search windows and edge search regions (Fig. 3) considerably accelerated marker localization. Typically, the first few projections (as few as three) were segmented in their entirety as an initialization. Then, for each BB marker detected, the position determined in the three preceding projections was used to predict the location of a small search window in the next projection. The search window prediction first backprojected the three locations from preceding projections to constrain the 3D location of the BB and then forwardprojected an estimate of the BB location in the next projection (including C-arm geometric calibration). The size of the search window was just 20 × 20 pixels, still large enough to capture the entire BB marker in next projection for nominal CBCT acquisition (200 views over 178°). In addition to these small, predictive search windows, an edge search region (80 pixels wide, as shown in Fig. 3) along one side of the projection was used to detect BB markers entering the 2D projection from one side, with width sufficient to cover the first three projections of a BB marker after entering 2D projection FOV (viz., 80 detector columns). Therefore, after initialization, the marker localization process is performed only on the search regions instead of the entire projection, considerably accelerating the workflow. Introduction of search windows also improved robustness by excluding high-contrast structures outside the search window.

Trimming false-positive detections

False-positive BB marker detections occurred rarely in the small predictive search windows due to their small size; however, erroneous detections did occasionally occur in the edge search region or during initialization when the entire projection was segmented. These detections were automatically rejected based on a consistency condition: only detections that followed a sinusoidal path in the (^PU, ^PV, θ) sinogram domain were maintained as true detections. Specifically, false-positive candidates were identified as excursions from the sinogram (δV > 3 pixels) or (δU > 5–30 pixels), where the δU threshold was selected in proportion to Δ (larger excursion in ^PU for the ARM placed farther from isocenter). (As mentioned in Sec. 4, the marker configuration deduced by the tracking system could also be helpful in eliminating false positives.) If a true BB marker was missed due to a false-positive detection, the predicted BB marker location was still computed and carried along, allowing recovery of missed BBs, for example, if the BB traverses behind a dense metal implant. In the end, all marker locations not satisfying sinusoidal consistency were excluded from the segmentation results.

Fine-tuning 2D centroid locations

Following BB marker detections by the Hough transform (geometrically accurate to the level of 1 pixel by way of accumulated votes), a fine-tuning step localizes the BB centroid to subpixel accuracy. For each BB marker, a square ROI is selected and binarized into a few connected components via intensity thresholding. For the 2.0 mm diameter BBs, an 11 × 11 pixel square was sufficient to capture the entire BB marker in all cases. Among the resulting components, that with highest compactness (i.e., the circularity quotient given by the ratio of the component area to that of a circle) corresponded to the BB marker. Finally, the centroid location of the BB marker was calculated as the center of mass computed on pixel intensities for the corresponding component.

Linear-least-squares method for 3D localization of markers

The location of each BB marker in 3D CBCT image coordinates was then calculated from the centroids localized in projection sequences by a linear least-squares (LLS) method. Each BB centroid location was backprojected to generate a line toward the x-ray source using the C-arm geometric calibration projection matrix. Ideally, all lines for a BB marker would intersect at the location of the BB marker in 3D CBCT image coordinates. However, due to nonidealities in C-arm gantry rotation, the lines do not perfectly intersect at a point. A LLS method was therefore employed to determine an optimal solution point that minimized the sum of the distances from the point to all lines. This can be formulated as

$$\left\{P\left(x,y,z\right),d_i\right\}={\mathrm{argmin}}_{P,d_i}\sum _{i=1}^N‖P-\left(t_i+d_i·l_i\right)‖,$$ (1)

where P represents the solution point, t_i is the source position of the ith projection image, l_i is the direction from t_i to the BB centroid on the ith projection image, and d_i is an undetermined scalar. For a given t_i and l_i for N images, a closed form solution can be found by LLS estimation.

With this solution, the BB marker location was then forward-projected to subsequent projections to guide the placement of search windows. After all BB marker centroids were localized over the full gantry rotation, the final 3D locations of BB markers were calculated by LLS method and assigned as the “image point set” [(x, y, z)_image] for image-to-world registration.

Localization of MM markers in tracker coordinates

As mentioned above, MM markers on the ARM could be independently localized as strays with no additional knowledge regarding the geometric relation between markers. Custom software was created to retrieve the locations of the stray markers from the Vicra tracker through application program interface (API) commands provided by the manufacturer. In studies reported below, the location of each stray marker was recorded ten times and averaged to define the “tracker point set” [(x, y, z)_world] for image-to-world registration.

Registration of image and tracker point sets

The “image point set” [(x, y, z)_image] defined in the 3D CBCT image coordinate system and the “tracker point set” [(x, y, z)_world] defined in the 3D tracker coordinate system were registered by rigid-body point-based registration as described by Horn.⁴⁵ This quaternion-based method yields a closed-form solution of the rotation, translation, and scale that best matches two Cartesian coordinates in a least squares sense. The pairing of two point sets was done by sorting the distances of fiducial points to their fiducial configuration centroid in both coordinate systems. If the distances between some fiducial points were very similar (i.e., differences below a certain threshold, namely, 5 mm), then their distance to fiducial points already sorted was used to discriminate them. This pairing method was found to yield accurate correspondences in all cases considered below.

Experimental methods

Anatomical site (head, thorax, and abdomen)

To investigate the feasibility of automatic registration techniques over a broader range of possible clinical applications, including thoracic and abdominal surgeries, the methods were tested in the context of various anatomical sites using an anthropomorphic head, thorax, and abdomen phantom as illustrated in Fig. 1. The various sites optionally involved pertinent interventional devices (e.g., transpedicle needles and screws) to challenge the BB marker localization method.

The phantom contained a natural human skeleton and soft-tissue simulating material constructed in a manner similar to that described in Chiarot et al.⁵¹ For each anatomical site, the Known-Model and Free-Form registration methods were evaluated using a total of 11 divot markers distributed on the surface of the phantom as target points for measurement of TRE. For the conventional manual method, ∼7 fiducial points (6 to 8 fiducials distinct from target points) were used for manual registration, and the remaining ∼4 points were used as target points in measurement of TRE.¹⁸

Distance from marker to C-arm isocenter

In many clinical scenarios, the ARM would necessarily be placed at some distance from the volume of interest, depending, for example, on the size of the patient and required clearance from surgical devices. The TRE was evaluated for the automatic registration methods as a function of distance (Δ) between the ARM and C-arm isocenter over a range ∼75–400 mm. For each distance, the ARM was placed directly above the phantom as shown in Figure 1d, recognizing that C-arm isocenter (and therefore the distance Δ) is a surrogate for the distance between the ARM and the surgical target. That is, we assume the C-arm is positioned such that the surgical target is at or near isocenter (which is typically the case in order for the target to be within the CBCT field of view). The TRE was expected to degrade with increased Δ for at least two reasons: (i) reduction in the total number of projections in which BB markers are in the x-ray FOV, resulting in fewer backprojected rays for each BB marker and challenging the accuracy of BB marker localization in 3D CBCT image coordinates; and (ii) increase in the distance from the ARM centroid to the target points, causing an increase in TRE as predicted by the analysis of Fitzpatrick et al.⁵² and detailed below. To investigate the dependence of registration accuracy on Δ, the automatic registration methods were repeated with the ARM placed at variable distance from C-arm isocenter or each body site. As illustrated in Fig. 1d, the minimum Δ corresponded to the edge of the CBCT FOV (Δ = 75 mm), and the maximum considered in current experiments was ∼400 mm, with measurements performed in increments of ∼50 mm.

Analysis of registration accuracy

The automatic and manual image-to-world registration methods were evaluated in terms of TRE, describing the Euclidean distance between corresponding target points delineated in the CBCT reconstruction (the “true” position) and the position recorded on the physical phantom using a tracked pointer and transformed to the 3D CBCT image domain by image-to-world registration. As described in Sec. 2E1, ∼11 well distributed divot markers on each anatomical site were used as target points to compute TRE for the automatic method, and a subset of ∼4 of these divot markers were used to compute TRE for the manual method. The TRE for each target point was computed, and the ensemble over all target points was considered in terms of the median, 25th percentile, 75th percentile, and total range of measurements (excluding outliers) to characterize the distribution of TRE.

Note that the 11 divots used in the automatic and manual methods were located at the same positions with respect to the phantom. Since the registration varies depending on the spatial distribution of the registration fiducials in the manual method, we computed TRE using all possible choices of 4 divots [$\left(\begin{array}{c}11\\ 4\end{array}\right)$ = 330 combinations] and averaged the resulting TREs. In the resulting 330 combinations, each divot appears exactly the same number of times (4 × 330 / 11 = 120 times). Thus, when the registration does not vary depending on the choice of the registration fiducials, as in the automatic method where markers on the ARM were used as registration fiducials, it is equivalent to averaging simply the TREs of the 11 divots.

The TRE for a target point at location r can be expressed in terms of the number and location of the registration fiducials as described by Fitzpatrick et al.,⁵²

$$⟨{\mathrm{TRE}}^2\left(r\right)⟩\approx \frac{{\mathrm{FRE}}^2}{(N-2)}\left(1+\frac{1}{3}\sum _{k=1}^3\frac{d_k^2}{f_k^2}\right),$$ (2)

where FRE is the mean fiducial registration error (i.e., the distance between corresponding fiducial points after registration), N is the number of fiducial points (∼7 registration fiducial divots for the manual method and 5 MM markers in the automatic methods), d_k is the distance of the target point r from the kth principal axis of the fiducial point set, and f_k is the RMS distance of the fiducials from the kth axis. Based on this relationship, the TRE was computed as a continuous function of position in the FOV, and the expected dependence of TRE on the location of the ARM (i.e., distance Δ) was compared to measurement.

Analysis of registration reproducibility

The reproducibility of conventional manual registration was compared to the Free-Form automatic method, recognizing that laboratory measurements of the former are likely advantageous in comparison to realistic scenarios in the OR. Both methods were repeated ten times using the thorax phantom with the ARM placed at a nominal distance of Δ = 185 mm. For the reproducibility studies, in each of ten repetitions, six surface divot markers were used for manual registration, and seven divots were used as target points for evaluation of TRE. The same seven divots were used as target points for the Free-Form automatic method.

Challenging scenarios: Marker detection in the presence of metallic devices

As a final challenge to the methodology in addition to various anatomical sites, specific scenarios involving metallic devices/implants were considered to emulate possible challenging scenarios that may be encountered in realistic clinical situations wherein the BB markers are eclipsed by metallic objects in the projections. Cases in which such implants did not directly eclipse the BBs (viz., the head phantom and transaxial screws in the cervical spine as shown in Fig. 3) were found to be robust by virtue of the Hough transform and search windows and are not shown below. For the most challenging case of the abdomen phantom and large values of Δ (∼250–400 mm), the ARM was placed such that some BB markers were directly eclipsed by a steel transpedicle needle, and the BBs closely traversed the length of the needle in numerous consecutive projections. This challenging scenario tested the Free-Form automatic method under conditions where the marker may be difficult to detect and, if lost on a given projection, is recovered in subsequent projections.

RESULTS

Comparison of Known-Model and Free-Form automatic registration methods

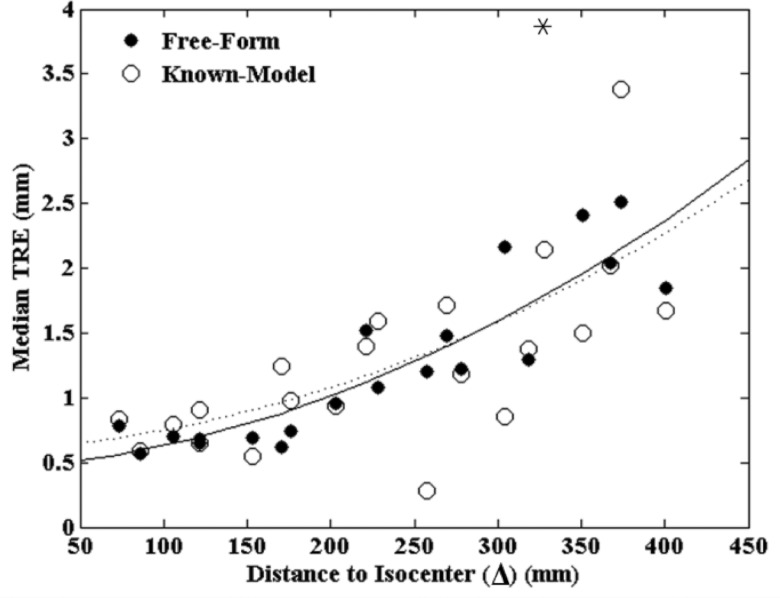
The Known-Model 3D-2D registration and the Free-Form projection-based method were compared in terms of TRE as a function of ARM location (Δ) in three anatomical sites. The Free-Form method yields a deterministic solution and was therefore run once for each case, but the Known-Model method involves an optimizer with a stochastic component³⁴ and was therefore run 20 times, and the results were averaged. As shown in Fig. 4, the results for all three anatomical sites were pooled, and a second-order polynomial was fit to the data as a simple guide to the eye. The TRE increased with Δ as expected for both methods [predicted by Eq. 2] and exhibited comparable registration accuracy over different anatomical sites and distances. A p-value of 0.764 computed between the datasets suggests no statistically significant difference between the Known-Model and Free-Form methods. The variance (overall spread in the data) appears somewhat improved for the Free-Form method, with a mean distance from the polynomial fit of (0.21 ± 0.18) mm compared to (0.35 ± 0.35) mm for the Known-Model method (p-value = 0.057).

Figure 4.

TRE measured for the Known-Model and Free-Form automatic registration methods. A second-order polynomial is fit to each case (solid and dashed, respectively). The methods exhibit comparable TRE with the Free-Form method demonstrating somewhat reduced variability and the advantage of not requiring a 3D model of the ARM as a prior. The asterisk indicates a single outlier outside the plot.

While comparable in registration accuracy, an advantage of the Free-Form method is that it does not require a known 3D model of the ARM as prior information. Ignoring the known model within the 3D-2D registration approach (i.e., taking the marker locations as “strays” as in the projection-based approach) increased the TRE significantly: 274% increase for the head, 174% increase for the thorax, and 86% increase for the abdomen as compared to the results in Fig. 4 (each at Δ ∼300 mm). These results indicate that the Free-Form method enjoys greater flexibility in MM marker configuration and may be preferable in clinical scenarios for which markers need to be constructed on the fly in the OR and/or distributed directly on the patient so that model information is not available.

Accuracy of BB marker localization

The sections below focus on the performance of the Free-Form automatic registration method, considering first the BB marker localization process and including steps related to the Hough transform, search window, trimming of false positives, fine tuning of 2D centroid locations, and 3D localization.

As mentioned above, the accuracy of BB marker localization in 3D is expected to degrade with increasing Δ due to a reduced number and angular range of projections in which BBs are contained in projections. The continuous curve in Fig. 5a shows the number of projections in which BBs are expected to project based on the C-arm geometric calibration, independent of the anatomical site. The curve is constant (N_visible = N_total) when the ARM is within the CBCT FOV and decreases sharply as the ARM moves to greater distances from isocenter. The experimental data points for all body sites show close (perfect) alignment with the simulated curve, demonstrating that the number of BB markers detected by the algorithm matched the theoretical ideal (i.e., for any projection in which the BB marker was within the detector FOV, it was successfully detected).

Figure 5.

Evaluation of 2D BB marker detection in the Free-Form automatic method for various anatomical sites and distance to isocenter. (a) Illustration of the angular range over which BB markers are visible in projections versus distance to isocenter. The solid curve is a calculation based on the C-arm geometry, and the discrete points mark experimental results for each anatomical site. (b) Sinogram plot of ^PU coordinates for each BB marker detected versus projection number for the thorax phantom evaluated at a nominal distance, Δ = 121 mm.

As shown in Fig. 5b, the ^PU coordinates of each marker detected versus the projection number traces a sinogram illustrating that markers enter from one side of the projection FOV and exit at the other during gantry rotation. Each point in the ^PU coordinates represents a backprojected line from the BB centroid to the x-ray source. For the head, thorax, and abdomen phantoms, all markers were successfully detected in all available views (no gaps in the sinograms), with the exception of the purposely challenging cases described below in Sec. 3C4 involving interventional devices. These results indicate that the marker localization method was robust in various anatomical sites, and the number of projections presenting BB markers for detection behaves as expected.

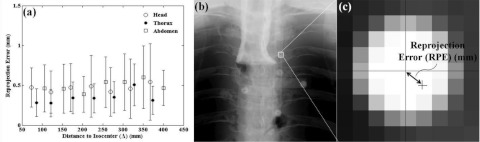
A quantitative evaluation of BB marker localization accuracy in the Free-Form automatic method (including both 2D localization and 3D ray intersection by LLS) is given by the reprojection error (RPE) as shown in Fig. 6. The RPE of a BB marker is defined as the distance in the 2D projection domain between the position of the BB centroid and the position as estimated by forward-projection from the 3D location determined by LLS calculation of backprojected rays. The mean and standard deviation in RPE in Fig. 6 were computed from the set five BBs on all available projections. As shown in Fig. 6a for each anatomical site, there was little or no significant increase in RPE at higher values of Δ, with a mean and standard deviation over all distances of (0.47 ± 0.04) mm for the head, (0.35 ± 0.08) mm for the thorax, and (0.49 ± 0.07) mm for the abdomen. This result indicated that the accuracy of localizing BB markers in 3D is fairly well maintained even for reduced angular range, for example, as little as 0.47 mm for a distance Δ ∼ 400 mm.

Figure 6.

(a) RPE of BB marker localization in the Free-Form automatic method for various anatomical sites and distance to isocenter. (b, c) Illustration of RPE—the distance in the 2D projection domain between the position as localized by the centroid and the position as forward-projected from the estimated 3D location. The small dependence on distance to isocenter suggests that markers are fairly well localized in 3D even for smaller angular ranges for which BBs are present in fewer projections.

Evaluation of TRE: Manual versus Free-Form registration

Dependence on ARM-to-isocenter distance

The theoretical dependence of TRE on the distance to isocenter is shown in Fig. 7 according to the analysis of Fitzpatrick et al.⁵² [Eq. 2]. The FRE was estimated to be (0.37 ± 0.03) mm from measurement of the Free-Form method over all distances. The TRE is smallest when the ARM is closest to the surgical target, for example, Δ ∼ 75 mm, for which TRE is in the range ∼0.2–0.6 mm over the CBCT FOV. As the ARM is placed farther from isocenter, TRE increases, for example, TRE ∼ 1.5–2.5 mm over the CBCT FOV for the ARM placed at a distance of Δ ∼ 325 mm. This dependence is intrinsic to the fiducial configuration and its distance from the patient and has nothing to do with the automatic registration technique. It could be reduced by designing an ARM with a more distended fiducial arrangement or one that “wraps” around the patient, although such extended configurations may introduce line of sight issues when working with optical tracking. However, an objective in the current study was to use as simple an ARM design as possible. The manual registration technique (involving fiducials directly on the patient) has the advantage of lower TRE associated with a smaller fiducial centroid-to-target distance, whereas a freely positioned ARM (typically at greater values of Δ) must contend with the intrinsic increase in TRE associated with the longer geometry.

Figure 7.

Predicted TRE computed throughout the CBCT FOV at various settings of ARM-to-isocenter distance, Δ. A CBCT sagittal slice of the head phantom is superimposed for scale. The TRE increases with Δ due to a greater distance from the fiducial centroid to target as predicted by Eq. 2.

Dependence on anatomical site

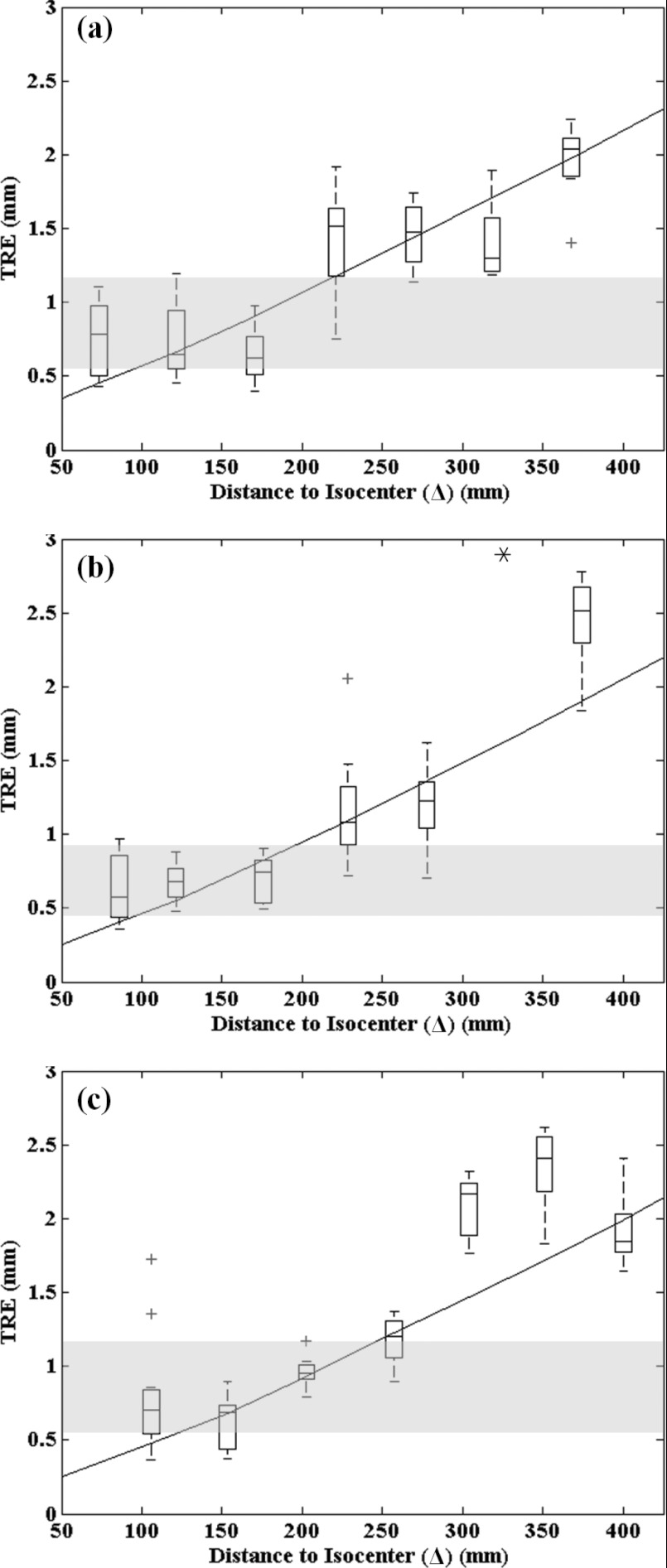
The TRE measured for the Free-Form automatic registration method was evaluated in comparison to that of conventional manual registration as shown in Fig. 8 for the head, thorax, and abdomen phantoms. The continuous curve represents the TRE predicted by Eq. 1. For the manual registration method, since the registration accuracy depends on the particular configuration of fiducial points, all permutations of the 7 fiducial points available from the 11 surface divots were analyzed, and the resulting range in TRE is shown as the horizontal gray region in Fig. 8, showing the lowest and highest TRE the manual method could be expected to achieve.

Figure 8.

TRE for the Free-Form automatic registration method (boxplots), the conventional manual registration method (gray region), and theoretical calculation [solid curve, Eq. 2] for various anatomical sites: (a) head, (b) thorax, and (c) abdomen. For all boxplots, the central mark represents the median TRE, the box represents the 25th and 75th percentiles, and the whiskers cover the range in TRE, excluding outliers (marked by a cross). The asterisk in (b) marks an outlier outside the plot.

For the head phantom, the TRE for the manual technique ranged 0.55–1.16 mm, with a median of 0.82 mm. This is consistent with the level of TRE achieved by infrared tracking systems in a laboratory setting,⁴⁹ although it is better than expected in clinical settings.^{42, 43} The TRE for the automatic technique followed an increase with Δ as expected, with a median TRE of 0.78 mm at the smallest distance (Δ = 73 mm) and increasing to 2.04 mm at Δ = 367 mm. The TRE for the automatic technique was comparable to or lower than that of the manual technique out to a distance of Δ ∼ 200 mm, which is a consistent with a variety of anatomical sites and patient setups. Furthermore, since the TRE closely followed the theoretical curve, and the RPE of Fig. 6 suggests that localization error was nearly independent of the angular range for which BB markers were present in the projections, the registration error is attributable almost entirely to the particular fiducial configuration of the ARM [i.e., to the fundamental relationship described by Eq. 2]. This suggests that possible sources of error in the registration technique (e.g., segmentation, localization in 2D projections, backprojected position estimate, etc.) have a minor effect on the overall TRE, which appears to be governed predominantly by the configuration and position of the ARM. As mentioned above, more distended ARM configurations would therefore be expected to reduce TRE.

The TRE for the thorax and abdomen phantoms exhibited similar results and demonstrated that the Free-Form method was independent of anatomical site, i.e., that the complexity of overlying anatomy and the attenuation (low signal) associated with large body sites did not confound the BB detection process. For both the thorax and abdomen, the automatic technique achieved equivalent or superior TRE compared to the manual technique out to a distance of Δ ∼ 200 mm. In each case, the measurements followed the theoretical form of Eq. 2 and could likely be improved with alternative ARM designs. The single outlier point in Fig. 8b exhibited anomalously high error attributed to possible movement of the phantom, OR table, or C-arm during the scan and was excluded.

The results of Fig. 8 are encouraging overall, indicating: (1) feasibility of the automatic registration technique in a broader range of anatomical sites than previously investigated; (2) a robustness to against complex, high-attenuation projection data; and (3) performance matching or exceeding that of the manual technique out to distances of Δ = 200 mm. Modified ARM designs are expected to reduce TRE further and/or extend the distance (Δ) to which performance is comparable or superior to manual registration.

Reproducibility

The reproducibility of the Free-Form automatic and manual methods was also evaluated by repeating both methods ten times on the thorax phantom with the ARM placed at a fixed distance (Δ ∼185 mm), where the automatic method was found to achieve approximately equivalent registration as the manual method. The standard deviation of TRE for the Free-Form automatic method was consistently lower than that of the manual method over ten repeat trials, with an average standard deviation of 0.22 mm for the automatic registration and 0.30 mm for the manual method. The reduction in standard deviation was statistically significant (p = 0.004 analyzed in a two-tailed, heteroscedastic student t-test), suggesting superior reproducibility of the automatic method compared to manual. The manual method also likely enjoys an unrealistically high level of reproducibility in a laboratory setting, whereas the automatic method is free from such sources of human variability; therefore, the improved reproducibility may be anticipated to be even greater for the automatic technique under more realistic clinical settings.

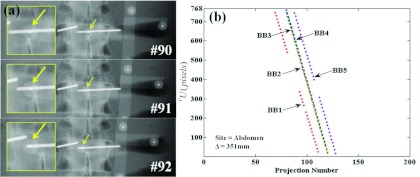
Challenging scenarios: BBs behind implants

The challenging scenarios described in Sec. 2E5 were created by placing the ARM such that one or more BBs were eclipsed by transpedicle needles in consecutive projections. Example images are shown in Fig. 9, where the ARM was placed above the abdomen phantom at Δ ∼ 350 mm, and one BB marker is entirely eclipsed by a needle in consecutive projections. The Free-Form automatic registration method was used here. The resulting sinograms in Fig. 8b show gaps for BB #1 [missed detections corresponding to the projections in Fig. 8a] and BB #5 (which traversed the other transpedicle needle in projections #108–111). Note, however, that the BB localization method was able to recover detection of both BBs when they emerged from behind the needles in subsequent projections. Specifically, as described in Sec. 2D3, the algorithm continued to predict the location of search windows even when detections were missed, providing detection of BBs along the entire C-Arm rotation, even when some were lost temporarily to highly attenuating implants. The Known-Model method tested on the same scenario was similarly not interrupted or degraded by the presence of the implant. Both methods demonstrated similar robustness in these challenging scenarios of implant obstruction.

Figure 9.

A challenging scenario in which BB markers are eclipsed by interventional devices. (a) Projection images showing one BB marker traversing the length of a transpedicle needle in consecutive projections. (b) The resulting sinograms exhibit gaps in which BB detections are lost when traversing the needles; however, the segmentation algorithm in the Free-Form automatic method is capable of recovering detection, since it continues to predict the projected location of search windows and finds the BBs when they emerge from the shadow of highly attenuating implants.

DISCUSSION

Relative advantages and sources of error among three methods

The experiments overall suggest that (i) the Free-Form automatic registration technique performs as well as the Known-Model automatic registration technique but with no requirement for an exactly defined marker configuration; (ii) with the ARM placed within a certain distance from isocenter (Δ up to ∼200 mm) the Free-Form automatic registration technique achieves equivalent or superior registration to the conventional manual technique and with improved reproducibility; and (iii) across a wider distance of ARM placement (Δ up to ∼300 mm), the automatic technique performs within the registration accuracy (TRE ∼2.5 mm) typical of current surgical navigation systems under realistic clinical conditions but with greater reproducibility.

The conventional manual method has been shown to provide registration accuracy at the level of ∼2 mm by a trained OR technologist or surgical fellow.^{42, 43} However, the process can be prone to manual error, intraoperator variability, and requires several repeats to obtain an acceptable registration. Updating the registration during a procedure (requiring several minutes) presents a bottleneck to surgical workflow. The Known-Model method could obviate many of these limitations with a faster, more reproducible registration with comparable geometric accuracy automatically updated with each CBCT scan. This method leverages the knowledge of a predefined marker configuration to improve robustness and accuracy, but necessitates the use of predefined ARM tools and would not allow fashioning of an ARM on the fly or attachment of fiducials to the patient during the procedure. The Free-Form automatic registration method shares these speed, reproducibility, and automation characteristics method and further enables registration using a freely configurable marker arrangement formed in the operating room or attached to the patient.

The sources of error contributing to the overall geometric accuracy of the manual and automatic methods are distinct. Errors contributing to the Free-Form method include: (i) 2D localization error of BB centroids in projections; (ii) error in the LLS estimated intersection point of backprojected rays; (iii) the error associated with the ARM fiducial configuration and distance from the target point [Eq. 2]; and (iv) fiducial localization error (FLE) associated with tracker localization of stray markers. The conventional manual method includes errors analogous to (iii) – i.e., the arrangement of fiducials, recognizing that the TRE for fiducials on the patient is likely improved due to a shorter distance to the target – as well as (iv) the FLE associated with the tracker and tool, recognizing that the FLE for a tracked tool is likely better than that of strays. The conventional method also includes error due to human variability in manually localizing markers in both the 3D image (by mouse click) and with the handheld tracked tool (manually placed on each fiducial). The Known-Model method in principle obviates errors associated with (i) and (ii), reduces errors associated with (iv), and introduces potential variability associated with 3D-2D registration (and stochastic nature of the CMA-ES optimization). Considering the results of Figs. 67, the automatic registration methods are seen to be dominated by errors associated with (iii) – the configuration and location of the ARM as described by Eq. 2 – and not by the various detection, segmentation, localization, and 3D-2D registration processes. Therefore, more sophisticated, application-specific ARMs than the simple tool shown in Fig. 1 can be expected to improve registration accuracy beyond the results shown here. The current work also demonstrates close correspondence between experimental measurements of TRE and calculations according to the Fitzpatrick equation [Eq. 2], whereas previous work⁴⁹ showed discrepancies attributed in part to manual registration error. Besides being eliminated directly in 2D projections, false-positive detections could also conceivably be eliminated in the 3D CBCT image coordinate system based on the relative positions of markers as measured by the tracking system. The 3D location constrained from false-positive detections might represent an object other than markers (e.g., anatomical structures or an interventional device) and would not match the marker configuration measured by the tracking system.

Limitations of the current study

The studies described are not without limitations. First, the automatic registration methods were evaluated using a single, simple ARM design. Although this configuration considered basic guidelines and clinical constraints for marker tool design, it is certainly not “optimal,” and ARM tools that contain more fiducials, a more distributed configuration of fiducials, and place the fiducial center of mass closer to the target would improve the N, f_k, and d_k terms, respectively, in Eq. 2 which are the dominant source of TRE in the experiments shown above. ARM tools befitting specific clinical applications can be envisioned, analogous to the “cloud” configuration proposed by Hamming et al.⁴⁹ in head and neck surgery, and reimplemented in separate forms appropriate to the thorax, abdomen, pelvis, or extremities.

Second, the measurements of TRE were performed in a laboratory environment using a rigid anthropomorphic phantom. This likely benefitted the conventional manual registration approach more than the automatic methods, so the TRE measured for the conventional technique is probably optimistic. The automatic registration methods are limited by factors less related to the laboratory setup and may be expected to maintain registration accuracy closer to the levels reported under realistic clinical conditions, recognizing other possible sources of error such as additional hardware present in the projection images, etc.

Finally, although the results suggest the potential for improved surgical workflow, a rigorous workflow analysis was not performed in the current work, which focused on the algorithms more than actual clinical application. The computational load associated with the Free-Form automatic registration method is fairly light, allowing the registration to be computed in less than ∼1 min on a modern desktop computer with our initial implementation on a single CPU thread. Since all computationally intensive operations in the Free-Form method (viz., the Gaussian derivative, Hough transform, and Gaussian blur) are highly parallelizable, significant speed-up (perhaps an order of magnitude) is expected with a more sophisticated multithreaded GPU implementation. The Known-Model method is much more computationally intense, requiring ∼2 min on a modern desktop computer even with implementation of forward-projection and back-projection steps on a midrange GPU.

CONCLUSIONS AND FUTURE WORK

Real-time surgical navigation requires image-to-world registration to align the image and world systems in order to localize and visualize tools in image coordinates. Conventional manual registration methods require several minutes to complete and are prone to error, intraoperator variability, and poor workflow. In this study, two automatic methods – a Known-Model and a Free-Form method – were implemented and exhibited comparable registration accuracy, with greater flexibility in marker configurations allowed by the latter. Across a spectrum of various anatomical sites (viz., head, thorax, and abdomen), the Free-Form method exhibited equivalent or superior registration with higher reproducibility compared to the manual method when the ARM-to-isocenter distance was within ∼200 mm. The method may support clinically acceptable registration accuracy (TRE < ∼2.5 mm) out to ∼300 mm. The dominant source of registration error for the automatic registration methods was the configuration of fiducials on the ARM and the distance from the target as predicted by the Fitzpatrick equation [Eq. 2].⁵² Alternative ARM configurations can therefore be expected to improve TRE. The automatic registration method was robust under challenging scenarios in which BB markers were eclipsed by interventional tools. Within the scope of these experiments, the Free-Form method was superior to Known-Model method in each respect (i.e., there was little to be gained from having a Known-Model method). Future work includes the translation and testing of the Free-Form automatic method clinical studies involving intraoperative CBCT guidance. With intraoperative imaging systems such as C-arm CBCT becoming more common in image-guided interventions, such automatic registration methods could offer more streamlined and accurate incorporation of navigation systems in routine surgical workflow.