Integration of data from multiple sources for simultaneous modelling analysis: experience from nevirapine population pharmacokinetics

Abstract

AIMS

To propose a modelling strategy to efficiently integrate data from different sources in one simultaneous analysis, using nevirapine population pharmacokinetic data as an example.

METHODS

Data from three studies including 115 human immunodeficiency virus-infected South African adults were used. Patients were on antiretroviral therapy regimens including 200 mg nevirapine twice daily and sampled at steady state. A development process was suggested, implemented in NONMEM7 and the final model evaluated with an external data set.

RESULTS

A stepwise approach proved efficient. Model development started with the intensively sampled data. Data were added sequentially, using visual predictive checks for inspecting their compatibility with the existing model. Covariate exploration was carried out, and auxiliary regression models were designed for imputation of missing covariates. Nevirapine pharmacokinetics was described by a one-compartment model with absorption through two transit compartments. Body size was accounted for using allometric scaling. The model included a mixture of two subpopulations with different typical values of clearance, namely fast (3.12 l h⁻¹) and slow metabolizers (1.45 l h⁻¹), with 17% probability of belonging to the latter. Absorption displayed large between-occasion variability, and food slowed the absorption mean transit time from 0.6 to 2.5 h. Concomitant antitubercular treatment including rifampicin typically decreased bioavailability by 39%, with significant between-subject variability. Visual predictive checks of external validation data indicated good predictive performance.

CONCLUSIONS

The development strategy succeeded in integrating data from different sources to produce a model with robust parameter estimates. This work paves the way for the creation of a nevirapine mega-model, including additional data from numerous diverse sources.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Integrating individual data from multiple sources in one simultaneous population analysis (sometimes called a mega-model) can address novel research questions and add power for covariate detection without requiring new clinical studies. However, the development of this type of model can be challenging and time consuming.

• Nevirapine is a non-nucleoside reverse transcriptase inhibitor commonly used for treatment of human immunodeficiency virus infection in resource-limited settings.

WHAT THIS STUDY ADDS

• This study outlines a strategy for integration of data from multiple sources for modelling analysis. It provides suggestions on handling of missing covariates in the context of several data sources and a starting point for development of a multinational nevirapine mega-model.

Introduction

Simultaneous analysis of raw data from multiple sources (different clinical studies) can address novel research questions and add power for covariate detection without requiring new clinical studies. Pharmacometricians have termed the resulting model a ‘mega-model’, and the approach has been described as ‘individual participation data meta-analysis’ when applied in other areas [1, 2]. This type of approach is increasingly popular but poses challenges, for example handling the large amount of data (which may lead to long run times), investigating and characterizing a larger number of potential effects (more covariates and with a larger range of values) and properly managing the heterogeneity present in data obtained in different studies. Traditional methods of analysing aggregate data (i.e. meta-analysis and systematic reviews) are statistical examinations of scientific studies and typically rely on published results and summary statistics. Assumptions about common treatment effects and random effects between studies and the difficulty in using covariates to explain this variability may limit their interpretation. Another option for combining data from multiple sources consists in using previously obtained parameter estimates for the analysis of new data. This can be done either by fixing the parameters in the new analysis or by employing the Bayesian priors. Both methods may be problematic when the populations in the different studies are not exchangeable [3, 4].

Nevirapine (NVP), a non-nucleoside reverse transcriptase inhibitor, is one of the most commonly used antiretroviral drugs for treatment of human immunodeficiency virus (HIV) infection in resource-limited settings [5]. Nevirapine has been available since 1996 and is extensively studied, hence large amounts of pharmacokinetic (PK) data have been generated and several population PK models have been previously published [6–14]. Although these models present a similar structural component, other areas require further investigation. Several models were unable to characterize absorption parameters, because the studies lacked sufficient information in the absorption phase. Numerous and varying covariate effects were detected, sometimes with contradictory results, such as the effect of age and ethnicity on clearance (CL). These uncertainties and other unresolved issues in NVP PK could be addressed with the potential construction of a mega-model, with the advantage of much broader data support.

Nevirapine is administered orally. The recommended adult dose is 200 mg once daily during the first 2 weeks and thereafter increased to 200 mg twice daily. Nevirapine is subject to auto-induction; it increases the levels of metabolic enzymes in the body and thereby also the rate of its own elimination [15]. Nevirapine is readily absorbed (bioavailability >90% after single dose [16]), lipophilic and not ionized at physiological pH [15]. Nevirapine is extensively metabolized in vivo by cytochrome p450 isoenzymes, mainly CYP3A4 and CYP2B6[17, 18], and is affected by genetic polymorphism in these CYP enzymes [19–22]. Notably, the 516G>T point mutation in CYP2B6 is associated with significant loss of function [19, 23]. Although highly active antiretroviral treatment (HAART) including NVP has proved to be both effective and relatively safe [24, 25], several concerns regarding NVP remain, including the risk of hepatotoxicity [26], the development of drug resistance [27], interactions with concomitant medications [26, 28] and the effects of genetic polymorphisms [19].

The objective of this work was to learn about technical challenges that arise during modelling of data from multiple sources and to suggest an efficient development path for this type of model. In doing so, we aimed to initiate the development process and demonstrate the feasibility of a mega-model of NVP population PK.

Methods

Data

The data used for model building included 1270 samples from 115 patients and were obtained from three different sources (Table 1). Data were excluded from the analysis when information about dosing or sampling times was missing. All patients were HIV-infected adults, received the same NVP dosage regimen (200 mg twice daily) and were sampled at steady state. The NVP formulation and the other antiretroviral drugs included in the therapy varied between and within studies.

Table 1.

Summary of study and patient characteristics, as median and range (in parenthesis) when applicable

	Study 1[29]	Study 2[30]	Study 3[31]	Study 4[6, 32]
Type of study	Interaction with TB treatment, including rifampicin	Therapeutic drug monitoring of DOT-HAART	Interaction with antimalarial artemether/lumefantrine	Therapeutic drug monitoring/compare QID and BID dosing
Number of included patients	49	50	16	173
Number of excluded patients	6*	4	2	0
Number of samples	645 rich, 74 sparse	105	446	570 rich, 759 sparse
Rich sampling day (hours after observed morning dose)	(n ID = 25) Predose, 0.5, 1, 1.5, 2, 4, 6 and 10	–	Predose, 0.5, 1, 1.5, 2, 3, 4, 5, 6 and 8	0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 5, 6, 8, 10 and 12 QID: 14, 16 and 24
Rich sampling night (hours after observed evening dose)	(n ID = 25) 0, 0.25, 0.75, 2, 10 and 12	–	Predose, 1.5, 2, 3, 4, 5, 6, 8, 10 and 12	BID: 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 5, 6, 8, 10 and 12
Sparse sampling (hours after dose)	(n ID = 24) two samples 0–12, median: ∼3 h (observed dose)	one sample 0–12, median: ∼2 h (unobserved dose)	14, 24, 96, 120 and 144 h after first observed morning dose	(n ID = 173) one sample 0–12, median: ∼3 h (unobserved dose)
Visits for sampling	Patients with TB: one during and one after TB treatment	One to four per subject, 6 months apart	One	One to 12 per subject
	Patients without TB: one
Male/Female	12/37	4/46	3/13	155/18
Weight (kg)	67 (43–102)	72 (47–128)	60 (45–80)	72 (45–113)
Age (years)	34 (21–58)	32 (19–57)	32 (28–60)	42 (24–69)

^*All sparsely sampled. Excluded patients are not included in the summary statistics. BID, twice daily dosing; DOT-HAART, directly observed therapy for highly active anti-retroviral treatment; n ID, number of individuals; QID, once daily dosing; TB, tuberculosis.

The first study was a study on interaction with tuberculosis (TB) treatment and included patients with and without TB co-infection [29]. The co-infected patients were sampled in the continuation phase of the TB treatment (including rifampicin and isoniazid and, for five patients with relapsing TB, also ethambutol) and 3 months after concluding TB treatment. The sampling was rich for about half of the patients and sparse for the others. The rich sampling included both a day and a night profile, with the morning dose fasted and the evening dose fed.

The second study examined the effect of directly observed therapy (DOT-HAART) in out-patients and utilized therapeutic drug monitoring samples [30]. A single sample was collected at routine visits to the clinic at 6, 12, 18 and 24 months after initializing antiretroviral treatment.

The third study was an interaction study with the antimalarial artemether-lumefantrine [31]. The patients were not co-infected with malaria. The sampling included rich and sparse sampling, with day and night profiles for all patients.

A fourth data set was used for external validation (Table 1). The data included 1329 samples from 173 Dutch HIV-infected adult patients [6, 32]. The majority of the data were therapeutic drug monitoring samples, but 13 of the patients were also richly sampled over both day and night. The nevirapine dosing regimen varied between patients, and sampling was carried out at steady state.

Studies one, two and three were approved by the Research Ethics Committee of the University of Cape Town and the Medicines Control Council of South Africa (where appropriate) and study four by the Institutional Review Board of the Slotervaart Hospital before initiation of screening procedures. The study information was provided in the participants' preferred language, with the aid of a translator if necessary. All study participants were given a copy of patient information and signed a consent form, which included the contact details for the investigator and the entity responsible for the approval of the study. The risks to the patients of participation in the PK studies were considered minimal.

Sample collection and quantification assay

Venous blood was collected in heparinized tubes and stored on ice until centrifugation. The plasma was then stored at −80°C (−30°C in study four) until analysis. For the three studies used in model development, the drug quantification was conducted by the same laboratory using a validated liquid chromatography–tandem mass spectrometry method [33]. For study four a validated high-performance liquid chromatography–ultraviolet method [34] was employed.

Modelling

The population PK of NVP was described with nonlinear mixed effects models. This modelling technique is able to separate the variability in the data to identify fixed effects (the deterministic components of the model, describing the concentration–time profile of a typical subject) and random effects (the stochastic components of the model, accounting for the variability between individuals or occasions as well as measurement errors).

Tested structural models for disposition were one- and two-compartment models with first-order elimination from the central compartment. First-order absorption was tested with and without lag time, and with transit compartments as suggested by Savic et al. [35]. A log-normal distribution for the between-subject (BSV) and between-occasion variability (BOV) in the parameters was assumed, as described by Equation 1, where θ_i is the parameter value for the i^th individual (or occasion), θ is the typical value in the population and η is the patient- (or occasion)-specific random effect from a normal distribution with mean 0 and variance ω². The typical values of θ and the variance ω² are estimated.

(1)

Each dosing interval was regarded as a separate occasion. Allometric scaling with body weight (BW), fat-free mass (FFM; also called lean body weight, described by Equation 2) or normal fat weight (NFW; described by Equation 3) were evaluated as size descriptors to account for effect of body size on clearance and volume of distribution [36].

(2)

WHS_max and WHS₅₀ are constants with the empirically derived values of 37.99 and 35.9, respectively, in women and 42.92 and 30.93 in men.

(3)

The FFAT is the fat weight fraction reflecting the contribution of fat to the apparent body weight, a constant to be estimated for each drug. Both estimated and fixed coefficients for the allometric scaling were evaluated. The fixed values used were 0.75 for clearance and 1 for volume of distribution (V) [36].

Other potential parameter–covariate relationships were tested using a stepwise approach. Covariates were evaluated to avoid co-linearity, and the physiological and scientific plausibility and clinical relevance of the results were assessed.

Model selection was based on the objective function value (OFV), graphical analysis (goodness-of-fit plots and visual predictive checks; VPCs), precision of parameter estimates, scientific plausibility and clinical relevance. The model performance was evaluated by VPCs, simulations and re-estimation and bootstraps. The model was finally evaluated with an external data set obtained in a different population to investigate compatibility of the results and generalizability to a multinational mega-model. Development of an appropriate modelling strategy to integrate the data from the different data sets in a mega-model is part of the aim of the present work and will be outlined in the Results section.

Handling of missing covariates

Study two (therapeutic drug monitoring data) lacked information about patients' heights. To enable evaluation of the impact of FFM and body mass index (BMI), separate models to describe the relationship between weight, sex and FFM or BMI were developed [37]. Data from studies one and three plus another study [38] in an ethnically similar population were used (203 patients in total). The FFM and BMI were imputed from these models, and the estimated level of prediction error was used as variability in the imputation step. The external validation data lacked information about patients' heights. To mimic that population, another data set with matched proportions of ethnicities was generated using the P3M software (Physiological parameters for PBPK modelling [39]) and used to develop a corresponding imputation model.

Prediction- and variability-corrected VPCs (pvcVPCs)

Prediction correction of a VPC aims to adjust for the variability due to independent variables, such as covariates and doses. Prediction and variability correction of a VPC is achieved by normalizing the observed and simulated dependent variables with the typical population prediction (PRED) and variability. Prediction- and variability-corrected VPCs have been shown to increase the ability to diagnose model misspecifications [40]. Prediction correction of a VPC for a model including a mixture cannot be handled in the standard way. For each individual, several different population predictions are generated, one for each subpopulation to which the subject can be assigned. The average of the predictions in the different populations weighted by the estimated proportion of each population was calculated and used for the correction (Equation 4).

(4)

Software

The data were analysed with NONMEM® 7.1.2 (ICON Development Solutions, Hanover, MD, USA) [41], and estimations were conducted with the first-order conditional estimation method with eta–epsilon interaction. The following tools were used to aid the model development process: PsN [42] to automate a diverse range of scripts; Piraña [43] to structure and document the development work; and Xpose [44] for graphic evaluation.

Results

A schematic diagram of the development process described in this section is shown in Figure 1. As a first step, the data from each study were explored separately, with the purpose of deciding the order of priority for inclusion and to identify study-specific features. The latter was done so that covariates to account for such effects could be included early in model development to harmonize the data. Two richly sampled individuals from study three with results only below the limit of quantification were identified; no explanation was found for their low concentrations, and they were excluded from further analysis. The model building started by analysing the intensive sampling data from study one. A provisional structural model was designed, and a temporary set-up for the stochastic component was used. Large covariate effects arising from the study design, in this case the effect of concomitant TB treatment, were included in the model at this early stage. In addition, a significant difference in absorption was detected between the morning dose (fasted) and the evening dose (fed). Allometric scaling was used for CL and V. The intensive sampling data from study three were subsequently added, after assessing their agreement with the existing model by using a VPC. Decisions on the structural component of the model were then taken, when all the richly sampled data had been included. The combined data allowed the rejection of a diurnal effect, showing that the observed differences in absorption were due to food. The stochastic model was then reassessed. Next, the sparse sampling data were included study by study, using a similar approach. The stochastic and covariate parts of the model, including the size descriptor for allometric scaling, were continuously re-evaluated as more data were added. Finally, when all data had been integrated, a more meticulous optimization and evaluation of the model was performed, retesting inclusion of covariates and additional random effects.

Figure 1.

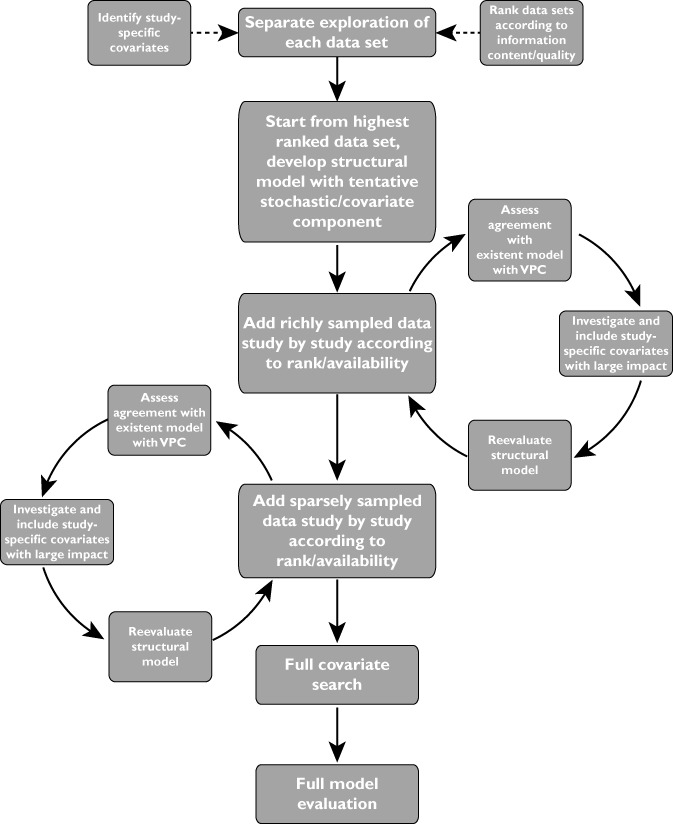
Schedule of the work flow during the mega-model development process. Abbreviation: VPC, visual predictive check

The parameter estimates for the final model and their precision are reported in Table 2. The values for the disposition parameters agree well with the results in earlier analysis [6, 9, 10, 12, 13, 45, 46]. Nevirapine population PK was best described by a one-compartment model with first-order elimination and a transit compartment model for absorption. In the final model, the number of transit compartments was fixed to two without significant loss of goodness of fit. This also enabled the use of a faster ADVAN routine in NONMEM, which accelerated run times significantly; an important aspect when dealing with large data sets. The data included four richly sampled patients with markedly higher NVP concentrations which no recorded covariate could explain. Parameter estimation excluding these four individuals showed that they had a strong influence on the estimate of the typical values of oral clearance (CL/F). A mixture model estimating two typical values of CL/F and the probability of belonging to the low-clearance population improved the predictive performance of the model, decreasing BSV in CL from 38 to 25%, and prevented these outlying data from unduly biasing the estimation of the typical value of CL/F of the majority of the population. The 95% confidence intervals for the lower and higher typical CL/F value were 1.0–1.9 and 2.8–3.4 l h⁻¹. Between-subject variability was supported for CL/F and BOV for absorption mean transit time (MTT) and bioavailability (F). The residual error structure was proportional and estimated as 8.41%.

Table 2.

Final parameter estimates (variability as CV, precision as RSE%) and bootstrap results (n= 200, stratified on study, precision as RSE%)

Parameter	Parameter estimates (RSE%)		Bootstrap (RSE%)
CL/F pop. 1 (l h−1)	3.12	(5.10)	3.16	(6.0)
CL/F pop. 2 (l h−1)	1.45	(14.70)	1.45	(15.8)
Probability (%) of belonging to pop. 2	17.30	(45.30)	19.30	(48.1)
V/F (l)	105	(4.90)	105	(5.4)
MTT (h) fed	2.46	(7.50)	2.46	(7.1)
MTT (h) fasted	0.596	(8.70)	0.60	(9.0)
F (%) when TB treatment	61.30	(8.70)	61.70	(8.7)
Proportional error (%)	8.41	(5.40)	8.39	(4.8)
BSV CL/F (%)	24.90	(13.90)	23.90	(16.0)
BSV F when TB treatment (%)	34.10	(27.00)	31.20	(33.2)
BOV F (%)	26.90	(9.60)	26.50	(10.7)
BOV MTT (%)	64.00	(9.10)	63.30	(9.1)

The values of CL/F and V/F refer to a typical person of 42 kg fat-free mass and 70 kg body weight. BOV, between occasion variability; BSV, between subject variability; CL/F, oral clearance; F, bivalent; MTT, meant transit time; pop., population; TB, tuberculosis; V/F, apparent volume of distribution.

The covariates evaluated during the stepwise model building are summarized in Table 3. The physiologically plausible covariate–parameter relationships with significant impact were the effect of concomitant TB treatment on bioavailability {a decrease of 39% [95% confidence interval (CI) 29–49%] with a BSV of 34%} and effect of fed or fasted dosing on absorption MTT [2.5 h (95% CI 2.1–2.8 h) when fed and 0.60 h (95% CI 0.50–0.69 h) when fasted].

Table 3.

Included and evaluated but rejected parameter–covariate relationships

Included parameter–covariate relationships
Relationship	ΔOFV	ΔBOV
Fed/fasted dosing on MTT	−90.4	−29.2%
TB treatment on F	−65.4	−3.8%
TB treatment with BSV on F	−84.6	−9.8%

Evaluated but not included parameter–covariate relationships
Parameter	Covariates
CL	age, sex, CD4 count, day/night, TB treatment, AL treatment, WHO-stage
V	age, sex, CD4 count
MTT	TB treatment, AL treatment, day/night
F	AL treatment, fed/fasted dosing

Included relationships are listed together with the drop in OFV and the change in between occasion variability when comparing the final model with a model without the specified relationship. Abbreviations: AL, artemether/lumefantrine; ΔBOV, difference in between subject variability; BSV, between subject variability; CL, clearance; F, bioavailability, MTT, mean transit time; ΔOFV, difference in objective function value; TB, tuberculosis; V, volume of distribution.

Allometric scaling with BW was found to be the best size descriptor to account for the effect of body size on apparent volume of distribution (V/F), while FFM was the best size descriptor for CL/F. For BW a reference value 70 kg was used, while for FFM the reference was 42 kg, corresponding to a woman of 70 kg and 1.6 m. A model to impute FFM based on weight and sex was developed for use in subjects with missing height information (studies two and four). The FFM was best described by an exponential model (Equation 5) with proportional error model.

(5)

The parameters FFM_max and K were estimated as 104 kg and 0.0107 and 69.6 kg and 0.0131 for males and females, respectively, in the South African population and as 106 kg and 0.0106 and 73.2 kg and 0.0126 for males and females, respectively, in the population from the P3M database mimicking the Dutch patients in the external validation data. The residual errors were 2.0% for males and 4.7% for females in the South African population (0.1% for both sexes in the validation population). A prediction- and variability-corrected VPC of the final model is shown in Figure 2. The model was evaluated with a bootstrap (n= 200) stratified by study. A prediction- and variability-corrected VPC of the final model applied to the external data set is shown in Figure 3. Estimating the allometric coefficients instead of using ¾ for CL and 1 for V fixed did not improve the OFV convincingly (−6.9 points, 2 degrees of freedom) and did not decrease the variability in the parameters, hence scaling with the fixed coefficient was found to be sufficient.

Figure 2.

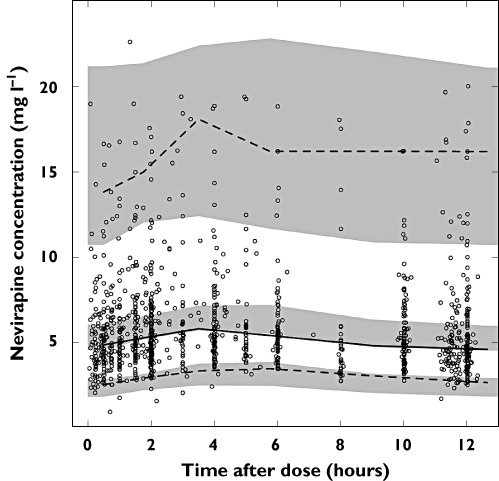
Prediction and variability corrected VPC of final model showing the observations (open circles), the fifth (dashed line), 50th (continuous line) and 95th percentile (dashed line) of the observations and the simulated confidence intervals for the fifth, 50th and 95th procentiles (shaded areas)

Figure 3.

Prediction and variability corrected VPC of final model applied to the external validation data set showing observations (open circles), the fifth (dashed line), 50th (continuous line) and 95th percentile (dashed line) of the observations and the simmulated confidence intervals for the the fifth, 50th and 95th procentiles (shaded areas). Fat-free mass was imputed with the model developed on P3M data

Discussion

Simultaneous modelling of individual data from numerous sources is one of several possible methods for combining information collected in separate studies. In conventional meta-analyses, the parameter estimates obtained in different studies are compared and combined, taking into account their relative precision. A significant drawback is that this approach can only combine results obtained in the original studies, so any test that was not performed in the original investigation, e.g. the exploration of a covariate effect, cannot be re-addressed. This approach is generally only viewed as appropriate when individual data are impossible to obtain [47]. Another approach to propagate information across studies is to fix parameters to values obtained in another study, which has been used in existing NVP models [12, 14]. While this may be useful to stabilize a model, it may also result in biased estimates of the other model parameters and it may mask potential difference between the values of the fixed parameter in the separate populations [4]. Another option is to use a Bayesian approach with priors. This has been shown to generate results in good agreement with simultaneous analysis (a mega-model) and to shorten run times significantly [48]. However, as the priors are dependent on the previous analysis, new hypotheses cannot be evaluated on all the data, and when the population used to generate the priors is not exchangeable with the population in the current analysis or when the variability is large, this approach may be inappropriate [48, 49]. Integrating data from nonhomogeneous populations may be one of the goals when combining data, hence this weakness represents a significant limitation for the use of this method. It has been addressed by using an alternative, more restrictive form of the prior or by modelling the systematic differences with covariates or other parameters to make the populations exchangeable in the extended parameter space [48, 49]. Modelling the differences would be a simultaneous analysis in itself, and the time-saving advantage over the mega-model approach would probably be lost. One advantage of the Bayesian approach is that it can be used when only summary results of a study are available. A disadvantage is that the result of the new analysis is dependent on the quality of the earlier analysis and its results. Alternatively, a penalty function based on summary information from earlier analysis may be applied to the OFV for the current data; a strategy similar to the Bayesian and sometimes called ‘frequentist’ priors [4].

A way to manage random differences between studies, which may be applied to the methods described above except the meta-analysis, is to add another level of random effects [3, 47, 49]. This interstudy variability (ISV) corresponds to a new level in the hierarchy of variability that already includes the commonly used BSV or BOV and would be estimated in an equal way. It has been shown that failure to address ISV results in inflated BSV estimates, but also that it is only valid to incorporate ISV when the number of studies to combine is large [47]. As the number of studies included in this work is still low, we have not investigated ISV further but would certainly do so if the model was to be extended to include a larger number of data sets.

A simultaneous analysis of all information is the most straightforward option when individual data are available and relies on the smallest number of assumptions, but it may be cumbersome and time consuming to perform. In this work, we suggest and evaluate a strategy for integration of data from multiple sources for modelling analysis to optimize the development work and counter the drawbacks mentioned as much as possible. This suggested approach proved useful and effective for modelling nevirapine pharmacokinetic data from heterogeneous studies. The stepwise addition of data made the analysis easier to handle by reducing the number of options to explore at once. The initial exploration of the individual studies and the evaluation of VPCs including data to be added in the subsequent step contributed to the identification of study-specific features and guided decisions on how to account for them by fixed effects. When many data sets are available, the initial exploration could also be used to create a ranking to determine the order of inclusion based on information content (for example, the number of subjects and richness of sampling schedule) and quality (for example, amount of missing data and number of samples below the limit of quantification). Development of the structural part of the model based only on the rich data decreased the run times without substantial loss of information, because sparsely sampled data are unlikely to contribute to defining the structure of the model. The combined analysis of the data enabled us to draw conclusions we could not draw from the studies separately. The following discussion focuses on the features of the final model and how they relate to the concept of model development with multisource data.

The data included a number of individuals (across all studies and some sampled on two occasions) with NVP concentrations markedly higher than average. We handled this by implementing a mixture model with two typical values of clearance. The mixture model allowed for inclusion of those patients with higher steady-state concentrations without biasing the clearance estimate for the general population. There are several reports in the literature of genetic polymorphisms affecting NVP PK [19–21]. The 516G>T mutation in CYP2B6 is associated with substantial loss of metabolic function [19, 23], and the frequency of 516TT homozygotes in a South African population has been reported to be 13–23% [23, 50]. The estimate of the probability of belonging to the low-clearance population (17.3%) agrees well with the reported proportion of CYP2B6-516-TT homozygotes in the South African population, implying biological plausibility of two populations with different clearance rates.

Other possible explanations for the high concentrations observed were considered; for example, interactions with concomitant medications or food. Studies one and three had exclusion criteria to avoid such interactions, and no potentially interacting nonstudy drugs were found on review of concomitant medications. The studies also captured data on co-administration of food, and no connection between foods ingested and the high concentrations were found. Hence, it is likely that the high concentrations observed were caused by polymorphisms in metabolizing enzymes. If genotyping information were available, the performance of the mixture model could be evaluated by comparing how the patients were assigned to the two populations with their genotypes. Genotyping data are rarely available, because they are costly and technically demanding to produce, but some studies have recently been conducted and models accounting for genotype developed [9, 13, 14]. It would be most interesting to include such data in the mega-model to assess the performance of the mixture model.

The effect of concomitant TB treatment was best incorporated as a decrease in bioavailability (ΔOFV −84.6 points). Earlier work [8] has described the effect as an increase in clearance (ΔOFV −59.7 points when tested in our model), due to induction of metabolic enzymes by rifampicin. Hence, our result was somewhat surprising. Incorporating the effect on both CL/F and F resulted in the same OFV as when applying the effect on only CL/F and the estimate for the effect on F was very small. From what is known about NVP PK and rifampicin enzyme induction, it is possible that rifampicin affects both the clearance and the bioavailability of NVP. Rifampicin is known to increase CYP3A4, CYP2B6 and P-glycoprotein (P-gp, a transporter protein) activity [51, 52]. Nevirapine is mainly cleared hepatically and is a substrate of CYP3A4 and CYP2B6[17, 18], whereas it is to a low extent (if at all) a substrate of P-gp[46, 53]. CYP3A4 is present both in the gut wall and in the liver, hence the induction will affect both bioavailability (through metabolism in the enterocytes and the first-pass metabolism) and clearance. The first-pass metabolism is not expected to have a great impact, because NVP is reported to be a low-extraction compound, based on the findings of bioavailability being above 90% after a single dose [16]. However, as NVP shows profound auto-induction [15], it is possible that the bioavailability is somewhat lower at steady state. The increased P-gp activity due to rifampicin induction is expected to play a small role, because NVP is a weak substrate. In a model of data following only an oral route of administration, absolute bioavailability cannot be estimated, but a change in bioavailability could be implied by a relative change impacting on both CL/F and V/F. In conclusion, the literature supports the hypothesis that both clearance and bioavailability of NVP can be affected by rifampicin co-administration. We chose to include the effect on the parameter where it improves the fit the most, in this case the bioavailability. As only one of the studies included concomitant TB treatment, we were unable to benefit from the ability of models based on multisource data to strengthen decisions on the characterization of the covariate inclusion in this case.

Food was found to impact the rate (ΔOFV −90.449) but not the extent of the absorption, in agreement with earlier findings [54]. Absorption in fasted conditions was estimated to be about four times faster than during fed conditions, which is expected for a lipophilic drug such as NVP. We were able to separate the food effect from a diurnal effect when combining data from studies with different protocols, demonstrating the usefulness of a mega-model.

Allometric scaling was incorporated early in the model development and, as no significant improvement was obtained with the re-estimation of the coefficients, they were fixed to the customary values of ¾ for CL and 1 for V. For clearance, FFM was found to be the best size descriptor. Bodyweight as size descriptor performed significantly worse in terms of OFV and goodness-of-fit plots, but could still be a more practical option for clinical model applications (for example, in therapeutic drug monitoring) where height data are often missing (parameter estimates for this alternative model are available online). For volume of distribution, BW and NFW performed almost equally well. The fat weight factor (FFAT) was estimated as 2.7, indicating an accumulation of NVP in fatty tissues in agreement with the lipophilic properties of NVP. However, the improvement in OFV obtained by scaling with NFW (and then estimating an additional parameter) rather than simply scaling with BW was not convincing and thus, for reasons of parsimony, the simpler scaling with BW was used in the final model. To enable evaluation of scaling with FFM on all data, we performed an imputation for those data that were missing information about patients' heights. The imputation was conducted using a model developed on the data that included all necessary covariates. We made use of information we had to predict missing covariates in part of the data, a possibility that is often available when analysing multisource data.

No other covariates were included in the final model. It is worth noticing that the concomitant artemether–lumefantrine administration in study three had no effect on nevirapine pharmacokinetic parameters.

The proportional residual error was estimated as 8.4%, which we regard as small, indicating that the structural and the stochastic models describe the data and its variability well. The most imprecise estimate (relative standard error 45%) was the probability of belonging to the less frequent low-clearance population. The estimate of the BSV in the effect of TB treatment on bioavailability was somewhat imprecise (RSE 27%). In both cases, the parameter was estimated on a small part of the data, which is likely to be the reason for the imprecision. All the other parameters had RSE values lower than 15%.

The data included few samples outside the limits of quantification. Two richly sampled individuals from study three with all samples below the limit of quantification for unknown reasons were excluded from the start. Besides these, there were a total of three samples below and five samples above the limit of quantification, all belonging to sparse PK profiles. Owing to the low number and the limited information contained in individual sparse samples, it was decided to exclude these samples from the analysis, rather than implementing more advanced (and time-consuming) methods to account for them.

Conclusions

A model of NVP population PK in a diverse population of South African HIV-infected patients has been successfully developed based on data from three separate sources. A stepwise data integration procedure for simultaneous analysis of multisource data was tested and found to be efficient. The procedure included the following stages:

• Separate exploration of the data sets to identify study-specific features.

• Development of the model, starting from richly sampled data.

• Integration of further data, study by study, giving priority to more richly sampled data and data considered to be of higher quality.

Study-specific covariates with a large impact, such as the effect of TB treatment in study one, were incorporated at an early stage to harmonize the data. Allometric scaling to account for size effects was also incorporated early. Decisions about the structural model were mainly based on the analysis of the rich data, and the stochastic model and the covariate model were continuously re-evaluated as the sparse data were added. The performance of the model at each stage was evaluated with goodness-of-fit metrics and VPCs.

The amount of data included in this model so far is not much larger than what has been analysed previously, and therefore the additional insight provided by our model for covariate detection is limited. However, it is a good starting point for development of a larger NVP population PK model, i.e. a mega-model. It would be of interest to include multinational data, other concomitant medications, specific patient groups (for example, pregnant women or children) and information about genetic polymorphisms, inter alia. Such an extended model could, without new clinical studies, contribute to a better understanding of NVP population PK and potentially help to address the current concerns regarding NVP therapy.

Competing Interests

There are no competing interests to declare.

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Table S1

Parameter estimates for alternative model

Please note: Wiley-Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.