Scaling of pharmacokinetics across paediatric populations: the lack of interpolative power of allometric models

Abstract

AIM

The objective of this investigation was to assess the performance of an allometric model as the basis for interpolating drug exposure in the context of pharmacokinetic bridging across paediatric subpopulations.

METHODS

Midazolam was selected as a paradigm compound. Two nonlinear mixed effects models were developed to describe midazolam pharmacokinetics in infants, toddlers and adults (model 1) and in children and adolescents (model 2). Subsequently, systemic drug exposure, expressed in terms of the area under the concentration vs. time curve (AUC), in children and adolescents was interpolated based on pharmacokinetic parameter distributions obtained from the model describing infants, toddlers and adults (model 1). Results were compared with the values obtained from modelling of the data in the corresponding population (model 2).

RESULTS

The two pharmacokinetic models accurately described midazolam exposure in the population on which they were built. However, the model based on data from infants, toddlers and adults failed to predict the exposure observed in children and adolescents: the mean difference between the predicted and estimated AUC_0–180 was of −17.8%, with a range of −6.8 to −38.4%.The discrepancy between estimated and interpolated exposure increased proportionally with body weight.

CONCLUSIONS

The current results indicate that irrespective of whether extrapolation or interpolation methods are to be applied during paediatric drug development, model predictions beyond the range of the data used for parameter estimation may be biased. For accurate inter- or extrapolation to different populations, the assumption of identical parameter–covariate correlations across age groups may not be taken for granted.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• No consensus has been reached so far on the suitability of different methodologies for dose selection in children.

• In paediatric drug development, initial estimation of the paediatric dose is obtained by extrapolation. This is usually performed using the dosing regimen in another population as reference. This approach also implies the possibility of using interpolations across age groups.

• Midazolam, the paradigm compound selected for the purposes of our investigation, is a short-acting imidazobenzodiazepine used for inducing sedation before medical procedures.

WHAT THIS STUDY ADDS

• The results of this analysis show that the use of allometric models to interpolate pharmacokinetics between paediatric subpopulations has limitations and drawbacks.

• Estimation of covariate effects is critical, but not sufficient to interpolate parameter distributions and drug exposures from a reference population to another population.

• The covariate–parameter relationship does not remain constant beyond the range of observations. Exponential relationships used by allometry do not correct for these discrepancies.

Introduction

The development of new drugs for paediatric indications needs careful consideration of potential differences in pharmacokinetics, efficacy and safety. These differences may result from or be compounded by the developmental changes that occur throughout childhood and adolescence and have major implications for the dose rationale in early clinical trials. On the other hand, every effort must be made to decrease the burden on paediatric patients, minimizing the risk and discomfort which are always present in a clinical trial. The aforementioned considerations are reflected in the Best Pharmaceuticals for Children Act (BPCA) and the Pediatric Research Equity Act (PREA) in the US [1] and, most recently, the 2007 Paediatric Regulation in the EU [2], which have boosted clinical research activities in children and prompted the development of regulatory and scientific guidelines for the design of paediatric clinical trials.

An opportunity exists in some indications and disease conditions for pharmacokinetic bridging, which would represent an exemption for formal demonstration of efficacy in children. The feasibility of such an approach depends on the appropriate dose selection for a pharmacokinetic trial [3]. Given that formal dose escalation studies similar to those carried out in adults are not appropriate in children, starting a trial at the effective dose range is of crucial importance in paediatric pharmacology [4]. Extrapolation methods are therefore often used to address this requirement, providing some initial estimation of dose to be administered to paediatric patients. This is normally done by scaling the dose from adults or from one paediatric subgroup (pre-term newborns, term newborns, infants, toddlers, children and adolescents) [5] to another. Different approaches have been proposed for the purposes of extrapolating pharmacokinetic data [6–9]. A discussion over the benefits and problems associated to each of these approaches is beyond the scope of this article. However, we would like to keep in mind that all of them rely on the use of data from a reference population as the basis for inferences about potential differences in pharmacokinetics.

Assuming that the exposure–effect relationship is independent of age, differences in PK parameter distributions across populations should be used as a basis for the dose rationale. Such an approach must identify which physiological factors alter pharmacokinetics and how these (might) differ across the paediatric population(s), without relying on a priori assumptions about the correlation between pharmacokinetic parameters and demographic covariates. For these reasons, we strongly suggest the use of a physiologically-based scaling approach, which we describe as scaling for function[3]. In addition, one must realize that nonlinearity may exist between pharmacokinetics and demographic factors. Different examples show the implications of non-linearity for dosing regimens in children [7, 10, 11] and how non-linear mixed effects and Bayesian hierarchical modelling can take into account such non-linearity, yielding appropriate estimates of the differences in pharmacokinetics [12, 13].

Recently, we have shown how a parametric approach can be used to characterize changes in drug exposure due to developmental growth [14]. Based on the predicted differences in parameter distributions, it is possible to define doses in the paediatric population. In this paper we focus on the predictive value of allometric models, allegedly the most used method for initial dose estimation in paediatric drug development [15]. Given that historically pharmacokinetic modelling has been used to analyze existing compounds (e.g. therapeutic monitoring), it remains unclear whether the approach has comparable performance when applied prospectively in drug development.

It was our objective to evaluate the performance of a model-based approach to interpolate rather than extrapolate. Whilst most paediatric drug development programmes involve staggering procedures in which age groups are included in a trial in a decreasing order (i.e. from adolescents to newborns), the trigger for considering the predictive value of models for interpolations between age groups was the requirement for age stratification. In addition, in paediatric oncology and some rare, genetic diseases for which prognosis is limited to a few years of life, there is a need to treat young children before any evidence is available in an older group, who may be more vulnerable or refractory to treatment. In this case, the only available clinical data are from adult patients or volunteers and neonates, infants and toddlers.

From a methodological point of view, interpolation and extrapolation are not very different, except for the fact that intuitively one may take for granted the continuity of covariate–parameter correlations when dealing with interpolations and assume the validity of approximation by linearization methods [16, 17]. Here we assess whether parameter values estimated in a reference population can be used to make inferences about the dose requirements in a paediatric subgroup that has not been investigated yet. In this particular case, the focus is on those groups which have not contributed to the data supporting initial model fitting and validation.

As a paradigm compound for the purposes of our investigation, we have selected midazolam, a short-acting water-soluble imidazobenzodiazepine [18, 19]. The pharmacokinetics of midazolam have been previously described by many authors in adults [20–23], pre-term newborns [24, 25], neonates [26–28], infants [29], children [30, 31] and adolescents [32]. Despite the availability of numerous models describing the pharmacokinetics of midazolam, these efforts were aimed at evaluating the implication of different dosing recommendations for the same population used to develop the model. Irrespective of whether data analysis was limited to a specific subgroup or whether modelling involved meta-analysis, validation procedures have not included the assessment of model performance on a different group or sub-populations.

Methods

Patients

Adult data were obtained from three studies performed by the Centre for Human Drug Research (CHDR, Leiden, the Netherlands). Study 89110-pilot was a pilot dose validation study in which six healthy volunteers received 0.15 mg kg⁻¹ of midazolam intravenously. Study 89110 was a randomized, double-blind, placebo controlled, four-way crossover experiment in eight healthy volunteers. Each subject received four treatments: (1) placebo, (2) midazolam 0.1 mg kg⁻¹ over 15 min by intravenous infusion, (3) midazolam 5 mg for subjects weighing less than 60 kg, 7.5 mg for subjects weighing 60–80 kg or 10 mg for subjects weighing more than 80 kg, by oral administration and (4) 1-hydroxy-midazolam 0.15 mg kg⁻¹ over 15 min by intravenous infusion. Study 94113 was a randomized, double-blind, five-way crossover trial in 20 healthy males, in which midazolam was used as comparator for an investigational drug. Each subject received 0.1 mg kg⁻¹ over 20 min by intravenous infusion [33, 34].

Data from infants and toddlers were obtained from the Erasmus MC – Sophia's Children Hospital (Rotterdam, the Netherlands), where infants admitted to the paediatric surgical intensive care unit (PSICU) were studied during the first 24 h after elective craniofacial surgery. Twenty-three infants and toddlers between 3 months and 2 years of age were administered a bolus of midazolam 0.1 mg kg⁻¹ followed by an infusion of 0.05 mg kg⁻¹ h⁻¹. COMFORT [35] and visual analogue scale were assessed every 2 h and used as the basis for dose titration during the course of treatment when needed [36].

Data from children and adolescents were obtained from a collaborative investigation between the Purdue University in Indianapolis, USA, and the Sophia Children's Hospital in Rotterdam, the Netherlands. The cohort (3–17 years old) comprised 18 paediatric oncology patients who were administered midazolam intravenously (average dose was 0.12 mg kg⁻¹) prior to invasive procedures [37]. A summary of the demographic variables and treatment regimens for all trials is shown in Table 1.

Table 1.

Studies characteristics and demographics. Mean (range) values are shown for all three groups of patients involved in the analysis

	Infants and toddlers mean (range)	Children and adolescents mean (range)	Adults mean (range)
n	23	18	34
Age	10.9 months (3.2–24.7)	7.7 years (3.2–16.2)	23.8 years (19.9–29.7)
Body weight (kg)	9.2 (5.1–12)	29.0 (12.6–60.1)	72.3 (59–91)
n. samples	8.8 (3–13)	4.6 (3–5)	19.3 (14–31)
Dose and administration route	0.1 mg kg−1 bolus +0.05 mg kg−1 h−1 i.v.	0.12 mg kg−1 i.v.	0.1 mg kg−1 i.v. or 5–7.5 – 10 mg oral

The aforementioned study protocols were approved by local Ethical Committees and written informed consent was obtained from the healthy volunteers or from legal guardians prior to participation into the trial.

Pharmacokinetic analysis

Nonlinear mixed-effects modelling was used to analyse the pharmacokinetics of midazolam. The first order conditional estimation with interaction method in NONMEM VI (release 2.0) [38] was used to fit all concentration data described later in this section. Given the objective of this exercise, different model building and validation steps were involved. A PK model was built based on infants, toddlers and adult data together (model 1). A second PK model, built on data from children and adolescents, was used as control for validation purposes (model 2). In other words, pharmacokinetic parameter estimates derived from infants, toddlers and adults were used to simulate midazolam concentration profiles in children and adolescents. The predicted concentration profiles were subsequently compared with those derived from the data in children and adolescents.

Different approaches were evaluated during the development of a model describing infant, toddlers and adult data. Initially, the use of adult data as prior information for the analysis of paediatric data in a Bayesian framework was considered [14], but it was soon discarded due the lack of convergence. This clearly suggested that parameter distributions in the younger patients were considerably different from the healthy subjects included in the analysis. Therefore, an attempt was made to integrate infant, toddler and adult data in a single dataset and analyzing this population using a covariate model, in which the demographic covariates would have described the differences between the subgroups.

The effects of body weight and age (the only covariates available in the datasets) were investigated as potential covariates on pharmacokinetic parameters. Significant correlations between covariates and parameters were incorporated using an exponential relationship for continuous variables, according to the formula:

Equation 1

where θ_i represents the parameter of interest for the individual, θ the population value for the parameter, COV the covariate of interest for the individual, median is the median of the covariate in the population and EXP the exponent.

The change in the objective function (OFV; equal to −2 log likelihood) as determined by NONMEM was used as a goodness-of-fit diagnostic for covariate inclusion (Δ= 3.84, P= 0.05, χ² distribution with one degree of freedom). The contribution of each covariate was confirmed by a stepwise backward deletion (ΔOFV = 6.89, P= 0.01, χ² distribution). In addition, goodness-of-fit plots, including observed (OBS) vs. individual prediction (IPRED), OBS vs. population prediction (PRED), conditional weighted residuals (CWRES) vs. time and CWRES vs. OBS were used for diagnostic purposes [39]. Given that the accuracy of model predictions also depends on the variance structure, special attention was paid to the evaluation of model misspecifications for the random effects. Mirror plots from simulated datasets were produced and results compared with the original data. In addition, the normalized prediction distribution errors (NPDE) method was applied for an in-depth diagnosis of potentially poor behaviour [40]. This method was implemented using the NPDE add-on software package [41], which was run in R [42].

In a subsequent step, the parameter estimates obtained from this model were used to predict midazolam plasma concentrations in the 18 children and adolescents available in the control group. The exposure to the drug, expressed as AUC_0–180, was selected as a clinically relevant endpoint for comparison purposes. Although the original idea was to directly compare the results from model-based predictions with the observed pharmacokinetic profiles in children and adolescents, estimated exposures based on a separate model (model 2) were used instead of actual observations. This was caused by the use of a very sparse sampling scheme in children and adolescents (4.6 samples on average), which did not allow for accurate estimation of the individual AUCs. In addition, the use of model-based estimates mitigates the potential impact of outliers in a small group of only 18 patients, which could lead to misinterpretation of observed AUC distributions. In short, AUCs in children and adolescents as predicted by model 1 were compared with the AUCs in the same subjects as estimated by model 2.

Therefore, a separate pharmacokinetic model for the analysis of midazolam concentrations in children and adolescents was built in the same manner as previously described for infants, toddlers and adults. In this case, informative priors were used to stabilize the model and to minimize the variability caused by the sparse sampling and the small population [43]. This method was previously applied to abacavir and was aimed at integrating prior information about parameter distributions in the analysis of small datasets [14]. Parameter estimates were obtained based on the posterior distribution, rather than the likelihood, as defined by the available data. This is an effective approach to challenge the validity of assumptions regarding the magnitude of the differences in parameter distributions. Data analysis was implemented with the PRIOR subroutine [44] using the Wishart distribution for parameter priors. Prior information about midazolam parameter distribution in children and adolescents was taken from De Wildt (CL = 5 ml kg⁻¹ min⁻¹, V_c= 0.38 l kg⁻¹, V_p= 1.7 l kg⁻¹) [45].

Prediction of pharmacokinetics in children and adolescents

Based on the parameter estimates obtained from this second model, individual AUCs were simulated 200 times for each of the 18 children and adolescents in the original trial. The resulting AUC distribution for each patient was then plotted as whisker plots and used to assess the accuracy of model-based interpolations. AUCs were calculated in NONMEM by integrating the amounts in a dummy compartment, according to the equation:

Equation 2

where C_t is the concentration at time t, dt is the time derivative.

We evaluated whether drug exposure in children and adolescents can be predicted accurately under the assumption of continuity in the correlations between pharmacokinetic parameters and covariates across the age range of interest. Using the parameter estimates obtained from the model built with data on infants, toddlers and adults, concentration vs. time profiles were simulated 200 times for each patient in the group of children and adolescents (n= 18). Predicted AUCs were summarized for each patient as mean and 95% confidence intervals and then compared with the AUCs obtained from the model built on the data from the actual children and adolescents in the trial. The discrepancy between the estimated and the predicted exposure was expressed as percentage, according to equation 3:

Equation 3

Results

PK model in infants, toddlers and adults (model 1)

The pharmacokinetics of midazolam in infants, toddlers and adults was described by a two-compartment model with first order absorption and first-order elimination. Inter-individual variability (IIV) was estimated for clearance (CL) and peripheral volume of distribution (V_p). Residual variability was characterized by a proportional error model. The incorporation of BW as covariate on clearance according to an exponential model showed the highest drop in objective function and improvement in goodness-of-fit. The exponent was fixed to the classic allometric value of 0.75 [46]. All attempts to estimate this parameter resulted in unsuccessful minimizations. This is explained by the narrow range of body weights in the infant and toddler population, and the gap between this latter group and adults. The highest value for body weight in infants was 12 kg, whilst the lowest value for body weight in adults was 59 kg.

Bearing in mind the objective of interpolation across populations, focus was given to model validation steps, which yield information about the variance structure and variance-covariance matrix. As shown in Figure 1, goodness-of-fit plots reveal that the model provides an accurate description of the data. Of particular interest are the mirror plots which showed that the model was able to simulate data with a variance structure similar to the original data. In addition, NPDE summaries indicate that the discrepancy between predicted and observed values can be assumed to be normally distributed. In spite of minor misspecification of the variance, overall these diagnostic techniques confirm that the infants and adult model is suitable for simulation purposes.

Figure 1.

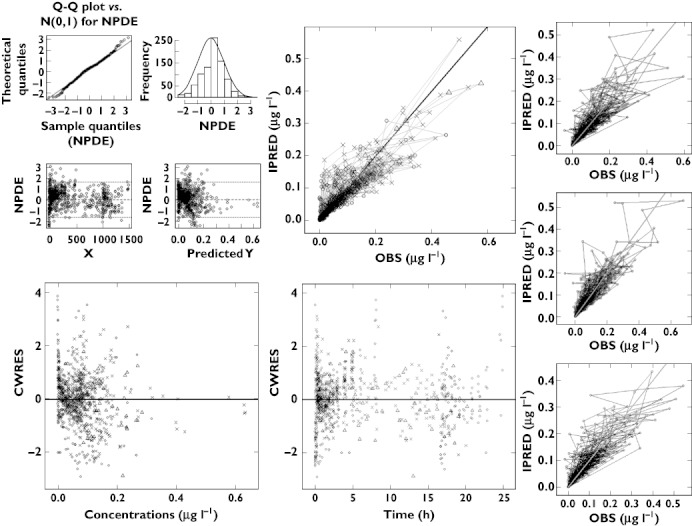
Diagnostic plots of model 1, i.e., based on data from infants (✗), toddlers (▵) and adults (○). (Top, left) NPDE; (top, centre) Post hoc predictions vs. observed concentrations; (bottom, left) CWRES vs. predicted concentrations; (bottom, centre) CWRES vs. time; (right hand side) mirror plots. All diagnostic measures indicate acceptable goodness of fit and model performance for simulation purposes. All three populations are depicted by open circles in the NPDE panels and in the mirror plots

PK model in children and adolescents (model 2)

The pharmacokinetics of midazolam in children and adolescents was also described by a two compartment model with first order elimination. Inter-individual variability was estimated for clearance and central volume of distribution (V_c). Residual variability was characterised by a proportional error model. In contrast to the covariate model in infants and adults, it was the normalization of V_p by age using a linear function that caused the highest drop in objective function and improvement in goodness-of-fit. As shown in Figure 2, diagnostic plots show that the model accurately described the observed data. In addition, NPDE confirms that the difference between predicted and observed values is normally distributed. The inclusion of informative priors did not appear to affect the final parameter estimates. Final parameter estimates for both models are shown in Table 2.

Figure 2.

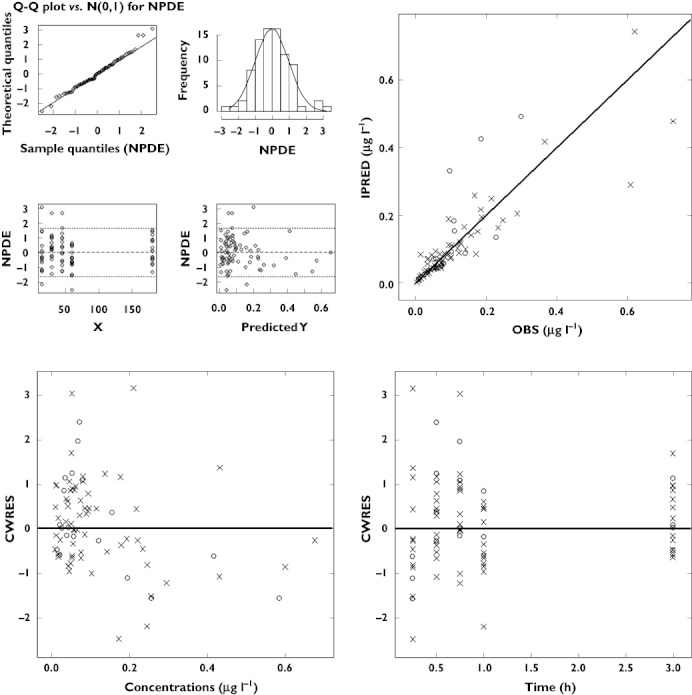
Diagnostic plots of model 2, i.e., based on data from children (○) and adolescents (✗). (Top, left) NPDE; (top, right) Post hoc predictions vs. observed concentrations; (bottom, left) CWRES vs. predicted concentrations; (bottom, right) CWRES vs. time. All diagnostic measures indicate acceptable goodness of fit and model performance. Both populations are depicted by open circles in the NPDE panels

Table 2.

Final pharmacokinetic parameter estimates for midazolam, as estimated from data on infants, toddlers and adults (Model 1) and on children and adolescents (Model 2)

Parameters (units)	Model 1 Infants, toddlers and adults		Model 2 Children and adolescents
	Mean	Bootstrap mean (CV%)	Mean	Bootstrap mean (CV%)
Fixed effects
CL (l min−1)	–	–	0.19	0.12 (20.4)
CL (l min−1 kg 0.75)	0.234	0.232 (9.6)	–	–
Vc (l)	0.312	0.310 (9.6)	1.95	2.07 (47.7)
Q (l min−1)	1.34	1.33 (10.3)	0.105	0.107 (32.8)
Vp (l)	16.5	16.2 (8.7)	–	–
Vp (l × months/74)	–	–	7.14	7.38 (31.2)
Ka (h−1)	8.21	8.29 (14.7)	–	–
Inter-individual variability (%)
CL	39.9	39.3 (28.2)	32.7	32.9 (26.0)
Vc	–	–	31.5	32.4 (22.6)
Vp	58.5	58.9 (17.0)	–	–
Residual variability
ε (%)	40.0	40.0 (12.4)	39.0	37.2 (21.1)

CL, apparent oral clearance; K_a, absorption rate constant; V_c, volume of distribution (central compartment); V_p, volume of distribution (peripheral compartment).

Interpolation of midazolam exposure from infants, toddlers and adults to children and adolescents

To evaluate the predictive power of a model-based approach to characterize the exposure to midazolam in a different paediatric population, the parameter estimates from the model based on infants, toddlers and adults were used to predict the AUC_0–180 in a population of 18 children and adolescents. The mean difference between the predicted and extrapolated AUC_0–180 was of −17.8%, with a range of −6.8–−38.4%. More interestingly, as can be seen in Figure 3 and in Table 3, this discrepancy seems to increase proportionally with body weight. By splitting the study population into two subgroups across the median body weight, i.e. the first including nine subjects up to 21.5 kg and the second including nine patients above this threshold, the discrepancy is of 11.4% for the first subgroup and of 24.1% for the second one. A summary of individual exposures obtained by either model is shown in Table 3.

Figure 3.

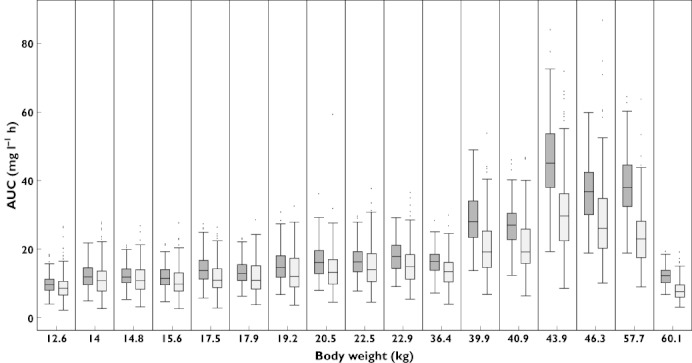
Whisker plots of the exposure to midazolam in children and adolescents, as estimated by modelling of the original data (dark grey) and as predicted by the model 1, i.e., based on data from infants and adults (light grey). Subject 7 has been excluded from the graph because of the extreme values (see Table 3 for details)

Table 3.

Individual exposure to midazolam in children and adolescents ranked by body weight

Subject	Body weight (kg)	Predicted exposure	Interpolated exposure	Relative difference (%)
		(mg l−1 min)	(mg l−1 min)
1	12.6	9.78	9.12	−6.75
2	14.0	12.29	11.12	−9.52
3	14.8	12.25	11.27	−8.00
4	15.6	11.80	10.58	−10.34
5	17.5	14.15	11.45	−19.08
6	17.9	13.17	11.74	−10.86
7	18.8	78.18	70.10	−10.34
8	19.2	15.24	13.20	−13.39
9	20.5	16.19	13.83	−14.58
10	22.5	16.40	15.23	−7.13
11	22.9	17.81	15.23	−14.49
12	36.4	16.25	13.62	−16.18
13	39.9	29.14	20.54	−29.51
14	40.9	27.24	20.89	−23.31
15	43.9	45.65	31.03	−32.03
16	46.3	36.53	28.30	−22.53
17	57.7	38.80	23.89	−38.43
18	60.1	12.00	7.95	−33.75

The presented values indicate the AUC_0–180vs. time curve obtained by the original model (i.e. estimated exposure) and as predicted from the model built on data from infants, toddlers and adults (model 1). The relative difference between estimated and predicted values appears to become larger with increasing body weight.

Discussion

The use of pharmacokinetic bridging studies represents an important opportunity for the development of new drugs for paediatric indications. However, the rationale for dose selection and dose adjustment remains a challenge when new compounds are first tested in children. Historically, dosing recommendations and dose adjustment have been based on empirical methods, most of which assume a linear relationship between drug exposure and body weight (i.e., mg kg⁻¹). We have used midazolam pharmacokinetic data to exemplify the concept of bridging and explore the predictive value of allometric models to support dose selection in children.

In contrast to retrospective analysis of pharmacokinetic data, there are two issues that require further attention to ensure accurate decisions are made with regard to the dose rationale in prospective trials with new compounds. First is the recognition that model-based (parametric) approaches are required to ensure unbiased description of pharmacokinetic properties. Noncompartmental analysis and various nonparametric methods do not warrant characterization (in a mechanism-based manner) of the physiological factors underlying the changes in pharmacokinetics induced by developmental growth [47, 48]. Second is the need to define model validation requirements for subsequent use of parameter estimates in simulations, extrapolation and /or interpolation of results, i.e., prediction of drug behaviour in new subjects or patients yet to be investigated [49, 50].

The aforementioned methodological aspects are very pertinent to research protocols in early clinical development. In these circumstances, the use of interpolation or extrapolation assumes the existence of a continuous function for the parameter−covariate correlation. This implies that identification of covariates and selection of a covariate model during data fitting are performed under the assumption that the correlation between parameter and covariate holds true for the overall population. Unfortunately, most of the ongoing debate in paediatric pharmacology has been focused on the choice of the scaling factor of allometric models. The issues regarding extrapolation and interpolation have been left aside [51]. Therefore, the main point of our analysis was the validity of non-linear mixed effects models to describe the population of interest when data on the variable of interest and corresponding covariates are limited or not available.

We have characterized the pharmacokinetics of midazolam by combining infant, toddler and adult data and analyzing them in an integrated manner. A two compartment model was identified, with body weight affecting clearance according to an exponential function. The use of a fixed allometric correlation between clearance and body weight turned out to be a necessity. However, we defend the view that fixing model parameters is only justifiable if evidence is irrefutable about the validity of such an assumption. This is particularly important if parameters are used subsequently for making predictions related to data which have not been used during model fitting. The implications of data driven methods become evident by the differences in the covariate model structure observed when fitting the data from children and adolescents. Age was identified as the most significant covariate on the peripheral volume, instead of body weight on clearance. Even if age and body weight are highly correlated during developmental growth (co-linearity), it must be recognized that the diagnostic criteria for goodness-of-fit used with maximum likelihood methods may overrule the evidence of another plausible or even mechanistic correlation, if the data do not support such a correlation.

The degree of accuracy required from model predictions, irrespective of whether they relate to interpolations or extrapolations, depends on the purpose of the model in the first place. In our case, predictions were aimed at defining dosing recommendations in a new population, under the assumption that target systemic exposure was known and should be reached to guarantee efficacy and safety in those patients. Our results show that the model built on infants, toddlers and adults systematically under-predicts midazolam exposure in children and adolescents and these under-predictions become larger with increasing body weight. This means that the differences between estimated vs. extrapolated exposures are small when the body weight is low, but differ considerably for heavier subjects. For midazolam, discrepancies observed for smaller children may have limited clinical impact, and therefore the model could be considered useful, although not accurate. On the other hand, in heavier subjects these discrepancies can be as large as 38% and cannot be overlooked in the context of the dose rationale for a paediatric protocol. The difference between observed and predicted exposures indicates that the interpolation cannot rely on the assumption that covariate−parameter interactions remain constant in different paediatric subpopulations.

The discrepancies observed between the parameter–covariate correlations across the two groups raise two important questions. The first one refers to the distinction between ‘mechanistic’, ‘descriptive’ and ‘predictive’ models, i.e. models whose parameters correspond to physical or conceptual entities, models applicable only to a restricted set of circumstances and models that explicitly incorporate variables quantifying design features so as to be able to predict outcomes, respectively [52]. It is clear that the use of more physiological parameters does not circumvent the limitations imposed by current model building criteria, which rely, among other things, on parsimony (Occam's razor). Hence, no matter how plausible it may be, the notion of a common, continuous correlation between parameter and covariate across populations does not survive the criteria used by maximum likelihood estimation methods. In this sense, mechanistic and mechanism-based models remain primarily descriptive of the data used to develop them. Given the accuracy of the deterministic and stochastic components of a hierarchical model, it can also be said that simulations can be predictive of new individuals or patients under the assumption that they come from the same parameter distributions (i.e. the same population), and that study design factors do not have a significant effect on these distributions. These requirements underpin the concept of Bayesian forecasting and other similar approaches used for therapeutic drug monitoring [53].

The second question regards both the approximation and inference methods which are required to make predictions about a new population or group. Subjects in the new population may not share the same parameter distributions, or the parameter distributions may be comparable, but influenced by design factors or experimental conditions. Given the criteria for maximum likelihood methods, it is evident that these questions cannot be addressed by typical modelling algorithms. To this purpose, model building and validation techniques are required which account for model uncertainty and permit parameter estimation irrespective of parsimony. This requirement is critical for the evaluation of a common, continuous correlation between parameter and covariate across populations, an assumption which may be plausible and defendable from a mechanistic point of view [54]. There are two possible alternatives to solve this conundrum: an adaptation procedure to ensure updates of previously estimated parameter distribution, so that inaccuracies or model mis-specification are mitigated as new data are acquired, or alternatively, to obtain parameter estimates which reflect not a single model but all plausible ones. The ability to evaluate multiple models is quite appealing from a statistical point of view. In addition, it offers advantages as compared with adaptive protocols, which cannot always be implemented. In contrast to maximum likelihood methods, a more comprehensive approach to addressing model uncertainty is Bayesian model averaging (BMA), which allows us to assess the robustness of results to alternative specifications by calculating posterior distributions over coefficients and models [55]. It should be clear that in the presence of model uncertainty, model averaging procedures provide better predictive performance than any single model which might reasonably have been selected [56].

Our analysis may have some limitations with regard to accepted model diagnostic requirements, but do reflect the reality with regard to the type and amount of data available during early clinical development. We have not delved into the discussion of the possible reasons for the under-predictions of systemic exposure. Based on our current understanding of processes underlying the disposition of midazolam, various factors could play a role in the changes in pharmacokinetics. It should also be noted that the increase in metabolic capacity in CYP3A4 associated with increase in body weight may not be fully discriminated in a quantitative manner without assessment of different dose levels (e.g. inclusion of exposure levels approaching V_max). Given the current therapeutic dose recommendations, it may not be possible or ethical to explore this clinically. These limitations may be generalizable to other compounds.

In summary, our findings show that the accuracy of model-based predictions depends not only on the characterization of surrogate measures of function which reflect the changes induced by developmental growth, but also on the choice of diagnostics and validation procedures. Whilst the use of model-based approaches is vital for the implementation and analysis of paediatric clinical trials, the current results also indicate that model predictions based on maximum likelihood methods are valid as long as the same parameter distributions can be warranted across the population. Bayesian averaging methods should be further evaluated for the development of truly inter- and extrapolative models. The development of predictive models imposes not only novel parameterisations but also new statistical concepts.

Competing Interests

There are no competing interests to declare.