Caffeine and Sugars Interact in Aqueous Solutions: A Simulation and NMR Study

Abstract

Molecular dynamics simulations were carried out on several systems of caffeine interacting with simple sugars. These included a single caffeine molecule in a 3 molal solution of α-D-glucopyranose, at a caffeine concentration of 0.083 molal; a single caffeine in a 3 molal solution of β-D-glucopyranose, and a single caffeine molecule in a 1.08 molal solution of sucrose (table sugar). Parallel Nuclear Magnetic Resonance titration experiments were carried out on the same solutions under similar conditions. Consistent with previous thermodynamic experiments, the sugars were found to have an affinity for the caffeine molecules in both the simulations and experiments, and that the binding in these complexes occurs by face-to-face stacking of the hydrophobic triad of protons of the pyranose rings against the caffeine face, rather than by hydrogen bonding. For the disaccharide, the binding occurs via stacking of the glucose ring against the caffeine, with a lesser affinity for the fructose observed. These findings are consistent with the association being driven by hydrophobic hydration, and are similar to the previously observed binding of glucose rings to various other planar molecules, including indole, serotonin, and phenol.

Introduction

Caffeine is an important active constituent of beverages like coffee, tea and various kinds of soft drinks. In such beverages, caffeine is in solution with many other constituents. Coffee, for example, also contains, among other compounds, polysaccharides, lignans, polyphenolics, lipids, melanoidins and chlorogenic acid.¹ Caffeine is known to interact directly with some of these constituents, such as the chlorogenic acid, to which it weakly binds.^2,3 While caffeine has significant dipole and quadrupole moments, its flat and weakly-hydrating non-polar faces make it only sparingly soluble in water at room temperature,^4,5 although it becomes more so at elevated temperatures. Caffeine is a purine derivative, and its heteronuclear, fused bicyclic structure qualitatively resembles the nucleotide bases and the aromatic indole molecule of the tryptophan side chain. Face-to-face nucleotide stacking is of course important in the double helical structure of DNA, and all of these planar species exhibit self-association in water.^6–8

Because of its limited solubility, caffeine is surface-active and also undergoes significant self-aggregation in an aqueous environment, as has been established from calorimetric data.⁴ Recent molecular dynamics simulation studies have characterized this aggregation in terms of stacking interactions between the flat faces, with many molecules forming extended aggregates like stacks of coins.^9–11 This limited aqueous solubility and self-aggregation is the basis for the commercial decaffeination of coffees and teas using non-polar solvents or supersaturated CO₂.¹ Similar stacking aggregation is presumed to be the mechanism of the interaction of caffeine with other molecules, such as the planar aromatic ring of chlorogenic acid, as was determined from NMR experiments.² Since many caffeinated beverages are also consumed with added sugar, it is important to characterize the interactions, if any, between sugar molecules and caffeine.

Unlike caffeine, most simple sugars like glucose, fructose, and sucrose are very soluble in water and exhibit little detectable tendency to associate in aqueous solution.¹² However, they have different solubilities in water, with fructose being significantly more soluble than glucose or the disaccharide sucrose.¹³ As osmolytes in a Hofmeister sense,¹⁴ sugars hydrate strongly and generally are excluded from the surfaces of proteins, promoting conformational stability. However, a variety of proteins have been designed by evolution to bind specifically to sugars like glucose,^15,16 and the binding sites of these proteins usually contain the planar aromatic side chains of the amino acids phenylalanine, tyrosine, histidine, or particularly tryptophan.^17,18 Both experimental and simulation studies have demonstrated a weak binding affinity between the hydrophobic face of glucose, consisting of non-polar aliphatic-like protons, and the planar face of indole rings.^19–21 These findings suggest that glucose might exhibit a similar weak binding affinity for caffeine as well, as was found from thermodynamic studies, which have also established that the presence of sucrose in aqueous solution decreases the solubility of caffeine,^4,5 as would be expected if the sugar osmolyte increases the chemical potential and surface tension of the solution, further promoting caffeine self-aggregation.

Analysis of simulations of pure caffeine in water has demonstrated that the tendency for self-aggregation at room temperature is driven by the nature of the hydration of the individual caffeine molecules, and in particular, by the way that the planar faces of caffeine structure adjacent water molecules.¹¹ The thermodynamics of this solution can be understood in terms of recent theories of the hydration of extended planar hydrophobic faces, which structure water differently from smaller non-hydrogen-bonding species.^22–27 Small hydrophobic groups, like the low atomic number rare gases, methane, and the methylene groups of lipids, force adjacent water molecules to adopt geometries that on average resemble the orientations of water molecules in crystalline clathrate hydrates, where the water molecules do not point either hydrogen atoms or lone pairs directly at the solute, since this would involve the loss of a strong hydrogen bond. Instead, they straddle the solute, without pointing either of their protons or lone pairs directly at the methane. However, this arrangement restricts the rotational freedom of the water molecules, thus lowering the entropy and increasing the heat capacity. When two such methane molecules come together, this structured water is released, regaining its rotational freedom, so that the hydrophobic aggregation of these species is entropy-driven.²⁸

Caffeine’s flat, non-hydrogen-bonding face is sufficiently wide such that water molecules directly above or below the center of the molecular plane cannot straddle it and make hydrogen bonds to other water molecules off to the side.¹¹ Thus, due to its size, caffeine hydrates differently from smaller hydrophobic species like methane. In this situation, the water molecules actually will point a hydrogen atom directly at the surface, since losing one hydrogen bond is less energetically costly than losing the two to three that would result from adopting the straddling geometry. Thus, when caffeine molecules aggregate, and these water molecules are liberated, they regain not only their rotational entropy, but also, and more importantly, the lost hydrogen bond, so that the free energy of aggregation is dominated by the enthalpic contribution, as has been observed calorimetrically.^4,29 It seems likely that the associations of sugars with caffeine would take place by such face-to-face pairing, and thus be enthalpy driven as well. It seems much less likely that there would be a significant concentration of caffeine-sugar hydrogen-bonded dimers, due to the competition with water molecules for the hydroxyl groups, but such an assumption requires testing.

We report here new molecular mechanics (MM) simulations of caffeine in aqueous solutions of both D-glucose and sucrose (Figure 1) to characterize the nature and extent of any interactions between these molecules and how they might depend on the sugar structure and the relative hydration characteristics of both the sugars and caffeine. NMR experiments of the same co-solutes in water have also been conducted. In an aqueous medium, glucose undergoes mutarotation to produce several structural isomers, or tautomers, although only two of these, the α-D-glucopyranose and β-D-glucopyranose anomers, are present in significant amounts.^30,31 Since these anomers have previously been shown to interact somewhat differently with a tryptophan side chain in a model protein,²¹ separate simulations were conducted for each anomeric species, although experimentally, a pure solution of either transforms to a 36/64% α/β equilibrium mixture over a period of about 2 hours at room temperature and neutral pH.³¹ As a non-reducing disaccharide, however, sucrose does not undergo any such transformations, and only one form of this molecule needed to be simulated.

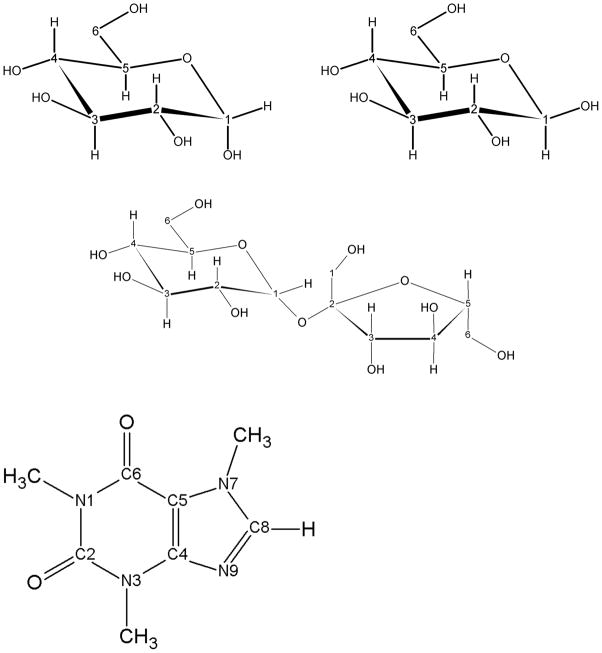
Figure 1.

The molecular structures of a) α-D-glucopyranose; b) β-D-glucopyranose; c) sucrose; and d) caffeine, showning the conventional atomic numbering used here.

In this context, it should also be noted that the tendency to aggregate discussed above is a hydrophobic association, driven by the constraints imposed on adjacent water molecules as they are forced to adopt specific structure relative to the solute molecules dictated by their topological details. However, it has recently been suggested that these types of associations are strengthened by interactions between the C-H bonds and the π-clouds of aromatic rings such those of caffeine.^32–35 Quantum-mechanical studies have been used to estimate the magnitude of this increase in interaction energy that might result from such interactions. While any such effects would of course be present in the NMR experiments reported here, they would appear in the MM simulations only to the extent that they are captured by the force field parameterization, primarily through the choice of atomic partial charges and van der Waals radii.

Methods

Modeling

Molecular dynamics simulations were carried out using the general molecular mechanics program CHARMM.^36,37 The caffeine solute was modeled using the same force field employed previously.¹¹ The glucose anomers were modeled using the CHARMM36 carbohydrate force field,³⁸ and water was modeled using the TIP4P model.³⁹ Covalent bonds involving hydrogen atoms were kept fixed in length using the general SHAKE algorithm.⁴⁰ The general systems studied consisted of single caffeine molecules in concentrated aqueous solutions of sugars. Each simulation was implemented following the general procedures previously used to simulate pure aqueous solutions of caffeine. For the cases of the glucose anomers, this procedure produced a cubic, periodic primary simulation box containing 1 caffeine molecule, 36 glucose molecules and 667 TIP4P water molecules. The size of the box was fixed to 30.0281 Å to achieve the atom number density of 0.1067 atoms Å⁻³, with a caffeine concentration of 0.083 m and a β-D-glucopyranose or α-D-glucopyranose concentration of 3.0 m. The system was energy-minimized through 500 steps of steepest descent minimization. It was then heated from 0 K to 300 K over 10 ps and equilibrated for 50 ps with velocities reassigned every 30 fs. The van der Waals interactions were smoothly truncated on an atom-by-atom basis using switching functions from 10.5 to 11.5 Å. Electrostatic interactions were calculated using the particle-mesh Ewald method.⁴¹ The system was then simulated in the NVE ensemble and trajectory data were collected for 80 ns. Previous experience with similar binding systems has found that the choice of ensemble (NPT vs NVE) makes no difference in observed association tendencies.²¹

Similar procedures were used for the caffeine/sucrose simulation. The cubic simulation box contained 1 molecule of caffeine, 13 molecules of sucrose and 666 molecules of TIP4P water, again giving a caffeine concentration of 0.083 m as in the glucose studies, but the sugar concentration was lower, 1.08 m instead of 3.0 m, in order to prevent an excessive increase in the system viscosity. The size of the box was set to 29.2562 Å to obtain an atom number density of 0.1041 atoms Å⁻³. Initial coordinates were first energy-minimized with 500 steps of steepest descent minimization, after which the system was heated from 0 K to 300 K in 6 ps and equilibrated for 20 ps with velocities being reassigned every 30 fs. The simulation was run in the NVE ensemble for 100 ns. The glycosidic torsion angle averages φ and ψ were −28° and −4°, respectively, where φ is defined as H1g-C1g-O2f-C2f and ψ is defined as C1 g-O2f-C2f-O5g.

The calculated trajectories were analyzed for sugar-caffeine binding using the density of sugar protons in a unit volume as a measure of sugar concentration. Alternatively, the density of ring heavy atoms could also have been employed. Using a coordinate frame fixed with respect to the caffeine solute, the non-hydroxyl proton density of the sugar molecules was computed as a function of position with respect to the solute and contoured at different density levels compared to the bulk density of these protons in order to define the occupancy of the sites. Because of the symmetry of the two faces of the caffeine, the densities for both faces were combined when computing binding affinities. Relative binding energies for the sites were computed using the Gibbs equation as in our previous studies.^11,21

NMR Experiments

Caffeine and D-glucose were obtained from Sigma-Aldrich (St Louis, MO, USA) and sucrose from Nordic Sugar AB (Malmö, Sweden). All chemicals were freeze-dried once from D₂O prior to use. For the saccharide titrations a stock solution of caffeine (35 mM) in D₂O was prepared at neutral pD. Two titration solutions were prepared by adding the caffeine stock solution to either D-glucose or sucrose in order to obtain a saccharide concentration of 500 mM and caffeine of 35 mM at neutral pD. Sucrose titration experiments were performed by measuring the ¹H chemical shifts (fast exchange) as a function of saccharide concentration by adding small amounts of either titration solution to 0.3 mL of stock solution thereby increasing the saccharide concentration while keeping the caffeine concentration constant. The NMR experiments were carried out at 298 K on a Bruker AVANCE 500 MHz spectrometer equipped with 5 mm TCI Z-Gradient CryoProbe. An insert tube containing a sodium 3-trimethylsilyl-(2,2,3,3-²H₄)-propanoate (TSP) solution (0.1 mg·mL⁻¹) was used as a reference since caffeine induces a chemical shift change in TSP. ¹H NMR spectra were recorded with eight scans, a spectral width of 9.0 ppm and 64k data points. The FIDs were zero-filled once and an exponential weighting function employing a line-broadening factor of 2 Hz was applied prior to Fourier transformation.

1D ¹H,¹H-NOESY experiments⁴² were performed with a zero-quantum suppression filter⁴³ on samples containing either D-glucose (214 mM) or sucrose (250 mM) in caffeine stock solution (35 mM) without the insert tube. Selective excitation of different resonances was performed using r-SNOB shaped pulses⁴⁴ of 30 – 60 ms duration and a cross-relaxation delay (mixing time) of 1 s. Spectra were recorded with either 1536 or 2048 scans, a spectral width of 9.0 ppm, 32k data points and a relaxation delay of 10 s. The FIDs were zero-filled once and an exponential line-broadening factor of 5 Hz was applied prior to Fourier transformation.

For the caffeine titrations two stock solutions of either D-glucose (10 mM) or sucrose (10 mM) in D₂O at neutral pD were prepared. Each stock solution was added to caffeine in order to obtain two titration solutions, one of D-glucose (10 mM) together with caffeine (80 mM) and one of sucrose (10 mM) together with caffeine (80 mM). Titration experiments were performed by adding small portions of either titration solution to 0.3 mL of the corresponding stock solution. The NMR experiments were carried out at 298 K on a Bruker AVANCE 700 MHz spectrometer equipped with 5 mm TCI Z-Gradient CryoProbe. An insert tube containing TSP was once again used as a reference. ¹H NMR experiments were recorded with twelve scans, a spectral width of 9.4 ppm and 64k data points. The FIDs were zero-filled once and an exponential weighting function employing a line-broadening factor of 0.3 Hz was applied prior to Fourier transformation. 1D ¹H,¹H-TOCSY experiments were carried out for the caffeine to D-glucose titration. Each one of the two anomeric protons was targeted in separate experiments with a 180° Gaussian shaped refocusing pulse of 80 ms. An MLEV-17 spin-lock was used with a mixing time of 80 ms. Spectra were recorded with 64 scans, a spectral width of 8.0 ppm and 14k data points. The FIDs were zero-filled to 128k data points and an exponential weighting function employing a line-broadening factor of 1 Hz was applied prior to Fourier transformation. Multiplicity-edited ¹H,¹³C-HSQC spectra were measured for each caffeine to saccharide titration. Spectra were recorded with 8 scans and with 1k × 256 points in the F₂ × F₁ dimensions using an echo-antiecho method. Zero-filling was performed to achieve 16k × 2k points and 90° shifted squared sine-bell functions were applied in each dimension. Processing and analysis for all NMR experiments were carried out using Bruker TopSpin^™ version 3.0.

Results and Discussion

Simulations

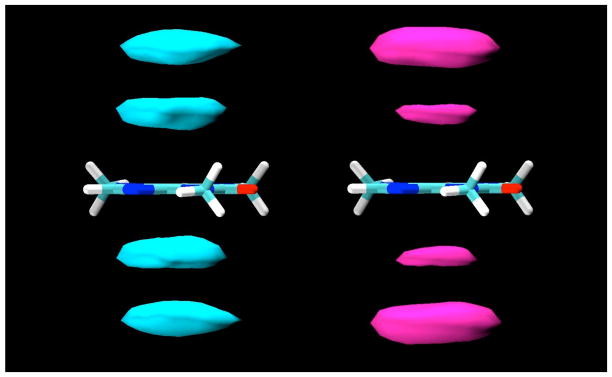
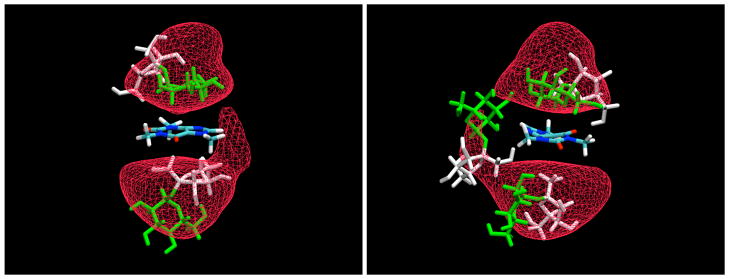
In the simulations, all of the sugars studied were indeed found to bind to the caffeine molecule, interacting by stacking of their ring faces against its non-polar, planar faces, as shown for a typical example configuration of the β-anomer of D-glucopyranose in Figure 2. In these stacked pairings, the glucose molecules typically have their axial protons in contact with the van der Waals surface of the caffeine ring faces. In the example displayed in Figure 2, both glucose molecules have their H1-H3-H5 proton triad directed toward the caffeine, with their H2 and H4 protons pointing away toward the bulk solution. The glucose molecules are well-localized with respect to the caffeine, indicating that this type of face-to-face pairing is by far the preferred form of interaction, as can be seen from the contours of glucose proton density relative to the caffeine shown in Figure 3, calculated in a reference frame fixed with respect to the molecule at its center of mass. As can be seen from these density maps, there is a slight preference for the glucose molecules to have the geometry shown in Figure 2, with the H2 and H4 protons pointing out.

Figure 2.

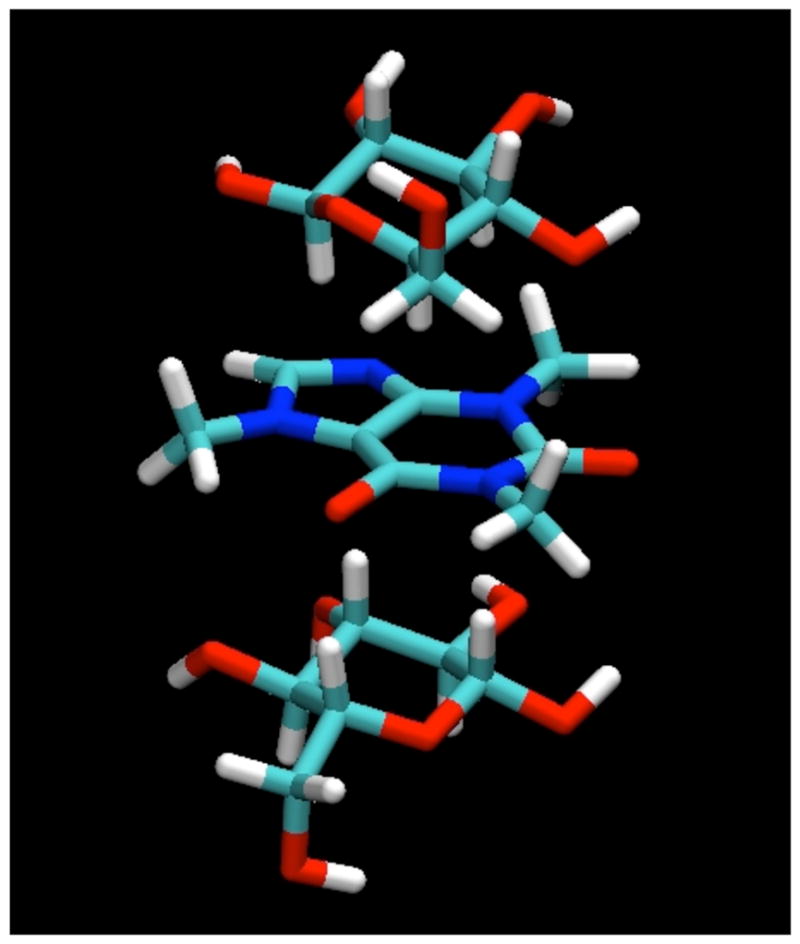
A “snapshot” of a typical configuration for β-D-glucopyranose molecules interacting with caffeine by stacking as found in the MD simulations.

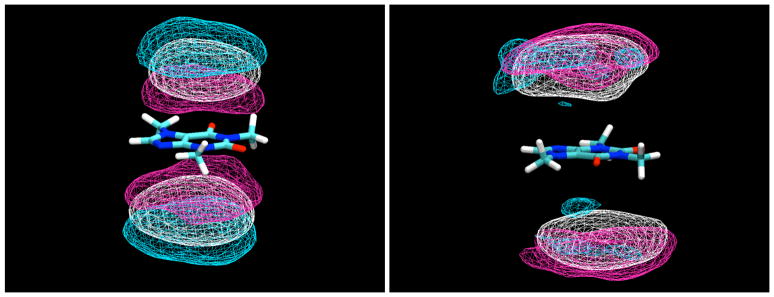
Figure 3.

Contour density maps for β-D-glucopyranose protons around caffeine, calculated in a reference frame fixed with respect to the caffeine at its center of mass. On the left, contours for protons H3 and H5, and on the right, contours for H2 and H4. In both, the contours enclose regions with proton density 3 times those of the bulk solution.

When contoured at a lower density level, two arms of density extend out from the density caps for glucose molecules stacked against the caffeine faces, encaging the caffeine molecule (Figure 4). These density arms represent glucose molecules that are significantly localized by their interactions with the caffeine to positions that lie closer to the plane of the caffeine. One of these density arms represents glucose molecules that are hydrogen bonded to the O6 atom of the caffeine through one of their hydroxyl groups (see Table 2). Another such density band, however, is adjacent to the H8 atom. Ordinarily this proton might not be thought of as a hydrogen bond donor. However, the valence situation of this atom results in it having an unusually large partial charge of 0.216,¹¹ more than half of that of a hydrogen bonding proton and twice that of a typical aliphatic proton, allowing it to make hydrogen-bond-like interactions as a “donor” with oxygen atoms of glucose hydroxyl groups. Similar interactions to water were observed in previous simulations of pure caffeine in water.¹¹ As can be seen from Table 2, there is somewhat limited hydrogen bonding between sugar hydroxyl groups and the hydrogen bonding atoms O2, O6, and N9, each of which makes approximately one hydrogen bond on average, which is predominantly to water molecules.

Figure 4.

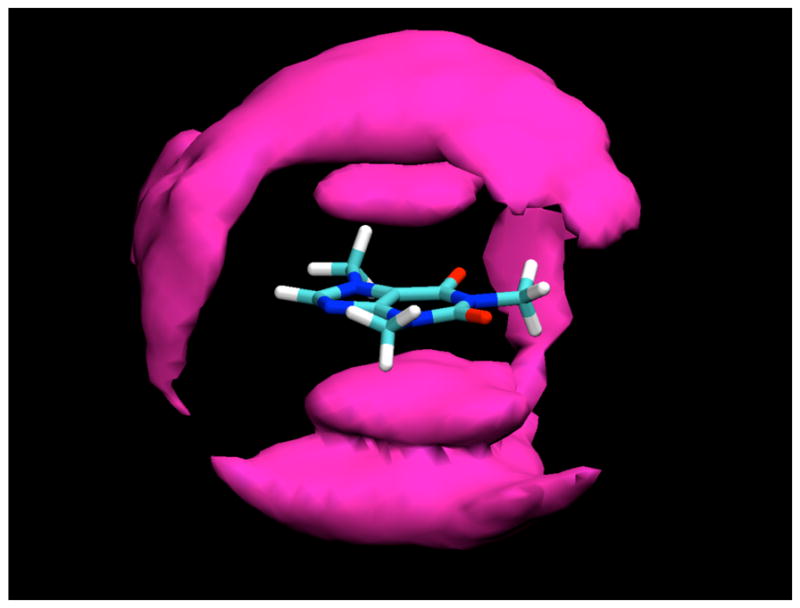
Contours of glucose H2 and H4 proton density around caffeine, averaged over the entire simulation, contoured at a density 1.5 times bulk density. As can be seen, at this lower density contour, bands of glucose density encage the molecule, reaching from the density caps representing the predominant stacked positions to the equatorial plane, where the glucose makes a hydrogen bond to the O6 atom of the caffeine molecule.

Table 2.

The trajectory-averaged number of hydrogen bonds made by caffeine in each of the present simulations, with a hydrogen bond distance cutoff of 3.4 Å and an angle cutoff of 150°.

Caffeine acceptors	Water	β-glucose*	β-glucose donors
			HO1	HO2	HO3	HO4	HO6
O6	0.854	0.145	0.039	0.029	0.024	0.027	0.025
O2	0.845	0.150	0.031	0.028	0.030	0.034	0.029
N9	0.837	0.201	0.040	0.029	0.038	0.038	0.056

Caffeine acceptors	Water	α-glucose*	α-glucose donors
			HO1	HO2	HO3	HO4	HO6
O6	0.839	0.179	0.024	0.029	0.030	0.036	0.061
O2	0.846	0.158	0.031	0.023	0.031	0.028	0.046
N9	0.827	0.218	0.038	0.037	0.450	0.046	0.053

Caffeine-Sucrose Solution
Caffeine acceptors	Water	α-glucose moiety	α-glucose donors
			HO2	HO3	HO4	HO6
O6	0.865	0.062	0.009	0.015	0.016	0.023
O2	0.885	0.049	0.010	0.008	0.010	0.020
N9	0.815	0.094	0.012	0.019	0.013	0.050
Caffeine acceptors	Water	β-fructose moiety	β-fructose donors
			HO1	HO3	HO4	HO6
O6	0.865	0.060	0.010	0.005	0.012	0.033
O2	0.885	0.048	0.012	0.007	0.008	0.020
N9	0.815	0.098	0.026	0.005	0.021	0.045

^*Note that these hydrogen bonded partners give rise to the density arms extending around the sides of the molecule in Figure 4.

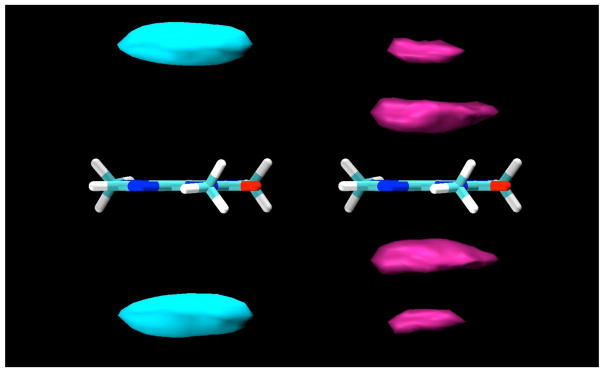
For the β-D-glucopyranose simulation, there was only a small difference between the sugar molecules stacking their H1-H3-H5 faces or their H2-H4 faces against the flat surfaces of the caffeine solute. However, in the case of the α-D-glucopyranose simulation, there is a stronger preference for the glucose molecules to bind with the H3 and H5 protons pointing away from the caffeine molecule (Figure 5). In this arrangement, the axial O1 hydroxyl group is also pointing away from the caffeine, which explains the stronger preference for this arrangement, since if it points toward the caffeine its ability to make hydrogen bonds to solvent is reduced.

Figure 5.

Contour density maps for α-D-glucopyranose protons around caffeine, calculated in a reference frame fixed with respect to the caffeine at its center of mass. On the left, contours for protons H3 and H5, and on the right, contours for H2 and H4. In both, the contours enclose regions with proton density 3 times those of the bulk solution.

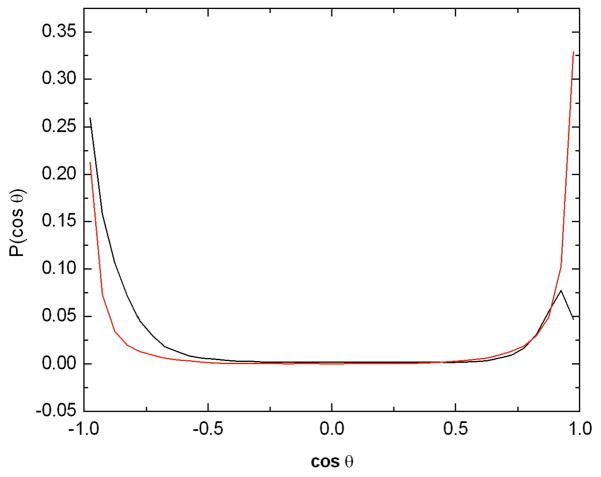
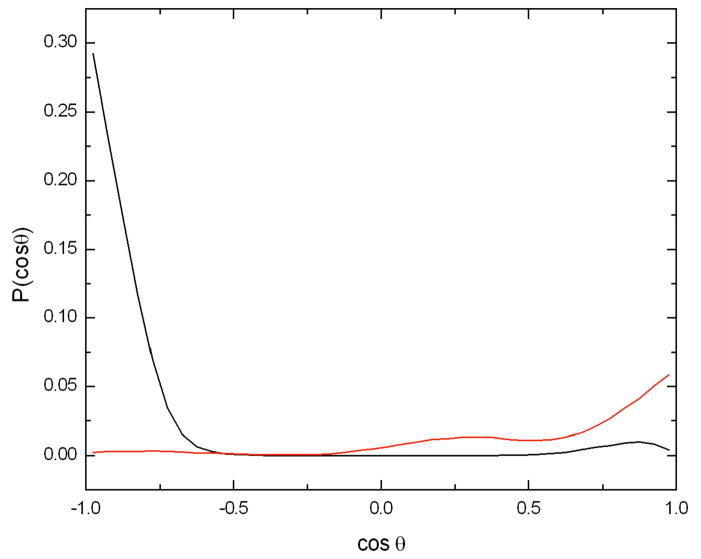
The different behavior between the two anomers of glucose is more evident in Figure 6, which shows the probability distribution of the orientation of the glucose molecules with respect to the caffeine molecule. In the case of the β anomer the cosine of the angle between the normal to the caffeine plane and the plane defined by the glucose ring exhibits a maximum at cos(θ) = 1 which is only slightly higher than the peak at cos(θ) = −1, whereas for the α anomer there is a clear preference for the configuration given by the proton atoms H2 and H4 pointing towards the caffeine ring (cos(θ) = −1).

Figure 6.

Probability of the cosine of the angle between the normal vector to the caffeine plane and the normal vector to each of the glucose anomers whose centers of mass were within 5 Å of the center of mass of the caffeine molecule. The caffeine plane was defined using the atoms N3, N1, and C5, the glucose plane was defined using the atoms C1, C3, and C5. The angular distribution for the α anomer is shown in black and that for the β is shown in red. A value of 1.0 corresponds to a proton pointing away from the caffeine plane, while −1 corresponds to pointing directly toward it.

Like glucose, sucrose was also found to bind weakly to the planar faces of the caffeine (Figure 7). Often this binding was again the result of stacking of the sugar rings against the caffeine, as can be seen from typical examples displayed in Figure 8. However, as can be seen from these figures, the binding was more complex in the case of the disaccharide than for the glucose monomers, in many cases involving other types of interactions. Both rings of the disaccharide were found to stack against the planar caffeine faces. Such an arrangement necessarily then places the other monomer of the disaccharide at a nearly perpendicular angle with respect to the caffeine. Figure 9 displays density contours for individual groups of atoms for both rings. For the glucose, there is a strong tendency for the H3 and H5 atoms to point away from the caffeine plane, and for the H2 and H4 atoms to point toward it, with the ring atoms neatly sandwiched in between as would be expected from the relatively rigid geometry of the pyranose ring. However, for the fructose ring there is no such tendency, due to the much greater flexibility of the the furanoid ring, which can easily undergo pseudorotation to sample a range of conformations which place the protons in varying positions with less regular relative orientations. In spite of this difference, there does appear to be a significant tendency for the fructose ring to adhere to the caffeine plane.

Figure 7.

Left: Density contours calculated from the sucrose trajectory for the ring atoms of the component monomers α-D-glucopyranose and β-D-fructofuranose, enclosing regions with a density level 5 times the bulk value; orange, α-D-glucopyranose residue; blue, β-D-fructofuranose residue. Right: Density contours for the same ring atoms (with the same color scheme) shown at a level 1.5 times the bulk value.

Figure 8.

Snapshots of the interaction between caffeine and sucrose. The glucose moiety of the disaccharide is represented in green, while the fructose is displayed in white. The contour density map refers to the ring atoms of α-D-glucopyranose residue, shown at a level 1.5 times the bulk value.

Figure 9.

Contours of atomic density for atoms of the individual monomer residues of sucrose, shown at a level 3.5 times the bulk value. Left: glucose atoms; blue: H3, H5; white: C1, C2, C3, C4, C5, O5; pink: H2, H4. Right: densities for the atoms of the fructose residue, also shown at 3.5 times the bulk value; blue: H3, H5; white: C2, C3, C4, C5, O5; pink: H4.

Figure 10 displays the probability distribution for angular orientations of the sugar rings of sucrose relative to the caffeine, defined as the angle between the normal to the caffeine plane and planes defined by the rings of both sugars. As can be seen, the pyranoid glucose ring stacks in a very parallel manner against the caffeine plane, with a strong peak in the angluar probability at cos(θ) = −1, corresponding to a very small angle between the two vectors, and with the glucose vector pointing away from the caffeine, as can be surmised from the H3 and H5 densities shown in Figure 9. The opposite orientation is strongly disfavored by the steric clashes for the attached fructose ring that would result from that orientation for the glucose ring. For the case of the fructose monomer, however, the rippling structure of the furanoid ring as it undergoes facile pseudorotation causes the normal vector calculated using the chosen atoms to rotate significantly, giving a much flatter distribution. The broad, weak peak near cos(θ) = 1 indicates that when the ring is adjacent to the caffeine plane, it tends to point in the opposite direction from that adopted by the glucose ring, and is restricted from orienting in the other direction by the clashes that would result for its attached glucose ring.

Figure 10.

Probability of the cosine of the angle between the normal vector to the caffeine plane and the normal vector to each of the sucrose monomers whose centers of mass were within 5 Å of the center of mass of the caffeine molecule. The caffeine plane was defined using the atoms N3, N1, and C5; the glucose plane was defined using the atoms C1, C3, and C5; and the fructose plane was an average of the planes defined by the atoms C3, C5, O5 and C2, C4, O5, respectively. The angular distribution for the glucose ring is shown in black and that for the fructose ring is shown in red.

The binding energy for the association of these sugars with caffeine can be estimated from the occupancies of the density clouds, as a simple equilibrium between bound and unbound states, using the Gibbs equation.²¹ In this approach, the calculated energy will then depend upon the arbitrary selection of the contouring boundary. However, if the site is well-defined, the density will fall off steeply moving away from the center of the site, making the calculated energy only weakly dependent on the arbitrary boundary. As seen from Figures 3–5 and 7, the sites do become more diffuse as the selected contour is significantly lowered, but at high densities, corresponding to highly localized sugar molecules, the density does fall off quite steeply (Figure 11), allowing a qualitative estimate of the binding energy, as can be seen from the data presented in Tables 3 and 4. The calculated energies are relatively low, only about ~2 to 2.5 kJ/mol per binding face, or ~0.5 to 0.6 kcal/mol, with total binding energies for both faces being twice this amount in each case. These values are small, on the order of k_BT, but are similar to those previously estimated from free energy simulations for the binding of glucose to indole and para-methyl-phenol in aqueous solution.²⁰ It is interesting to note that the binding energies are about the same for both anomers of glucose, and for both the glucose and fructose rings of sucrose. Literature data on caffeine in aqueous sucrose solutions refer to the caffeine Gibbs transfer energy⁵ and to caffeine enthalpy of transfer properties.⁴⁵ These values (ΔG_tr = −1.15 kJ mol⁻¹ and ΔH_tr = −0.88 kJ mol⁻¹) are in qualitative agreement with those estimated in this work.⁵

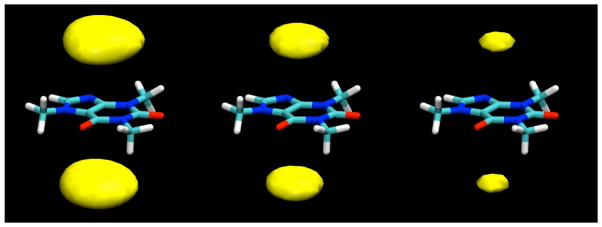
Figure 11.

Examples of the contour levels for β-D-glucopyranose used in the calculation of the binding energies shown in Table 3; left: density cutoff of 0.03 atoms/ų, middle: cutoff of 0.04 atoms/ų, right: cutoff of 0.05 atoms/ų.

Table 3.

The dependence of the glucose-caffeine binding energies calculated from the simulations as a function of the contour level selected to define the binding site.

density cutoff (atoms/Å3)	β-D-glucopyranose		α-D-glucopyranose
	ΔGbind (J/mol)	ΔGbind/2 (J/mol)	ΔGbind (J/mol)	ΔGbind/2 (J/mol)
0.0300	−3970	−1985	−3989	−1995
0.0325	−4070	−2035	−4126	−2063
0.0350	−4179	−2089	−4206	−2103
0.0375	−4291	−2145	−4309	−2154
0.0400	−4388	−2194	−4412	−2206
0.0425	−4464	−2232	−4508	−2254
0.0450	−4546	−2273	−4607	−2303
0.0475	−4632	−2316	−4681	−2340
0.0500	−4706	−2353	−4766	−2383

Table 4.

The dependence of the sucrose-caffeine binding energies calculated from the simulations as a function of the contour level selected to define the binding site. Since both rings exhibited binding affinity for the caffeine, the monomer units of the disaccharide are listed separately.

density cutoff (atoms/Å3)	glucose ring		fructose ring
	ΔGbind (J/mol)	ΔGbind/2 (J/mol)	ΔGbind (J/mol)	ΔGbind/2 (J/mol)
0.0100	−4209	−2104	−4060	−2030
0.0125	−4539	−2269	−4388	−2194
0.0150	−4811	−2406	−4664	−2232
0.0175	−5207	−2514	−4899	−2450
0.0200	−5229	−2615	−5130	−2565

NMR Experiments

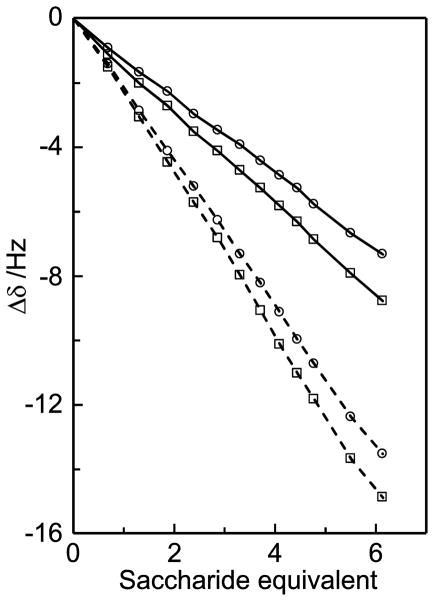
Titrations were based on ¹H NMR chemical shift changes using a constant concentration of caffeine (35 mM) in D₂O at neutral pD. Upfield displacements (towards lower chemical shift) are observed upon addition of D-glucose and sucrose (Figure 12), in agreement with studies on similar systems.^46,47 The magnitudes of the chemical shift changes were similar for the protons within each saccharide but they differed between the molecules, with larger chemical shift displacements for sucrose compared to D-glucose. The chemical shift changes for the three methyl groups in caffeine were of the same magnitude whereas the effect for the H8 proton was smaller. Also the caffeine chemical shift displacement were larger in the glucose titration compared to the sucrose titration. These results are exemplified by the chemical shift changes as a function of added saccharide (Figure 13).

Figure 12.

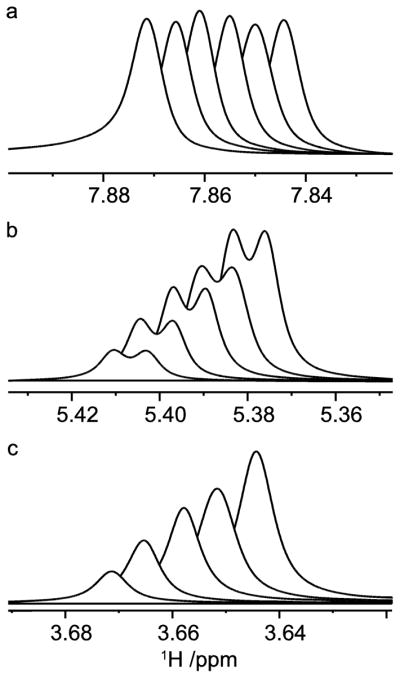
¹H NMR resonances from a titration of sucrose in D₂O containing 35 mM caffeine; H8 of caffeine (a), H1g (b) and H1f (c) of sucrose. Spectra are stacked according to increasing sucrose concentration (0, 1.3, 2.4, 3.7, 4.8 and 6.1 equivalents). Scalar spin-spin coupling between H1g and H2g results in the splitting into doublets.

Figure 13.

¹H NMR chemical shift changes of protons H8 (○) and Me1 (□) in caffeine (35 mM solution in D₂O) upon addition of D-glucose (solid lines) or sucrose (dashed lines).

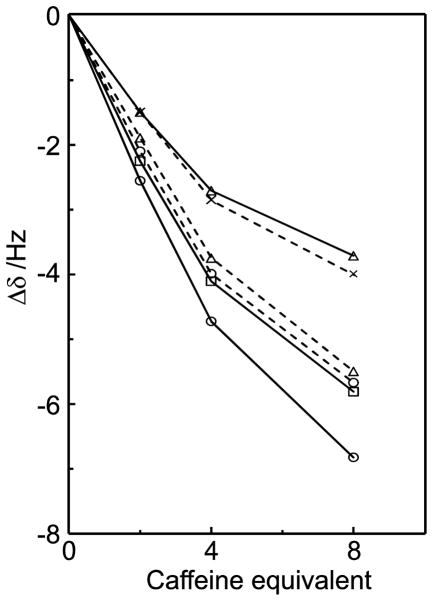
Additional titration experiments were carried out at constant saccharide concentrations (10 mM) with variable caffeine concentrations in order to investigate ¹H NMR chemical shift displacements for the saccharides. In this case the resonances also displayed an upfield displacement behavior. For sucrose the magnitude of the chemical shift changes differed for different protons (Figure 14). Protons H3g and H4f experienced a relatively small chemical shift change while H2g, H1f and H3f displayed a realtively large chemical shift change. Since the shielding effect decreases with a larger distance⁴⁸ between the saccharide proton and the aromatic caffeine surface, this would imply that H2g, H1f and H3f are in closer proximity to the caffeine surface than H3g and H4f, in good agreement with the molecular dynamics simulations. H1g displayed the highest degree of chemical shift displacement. Other sucrose proton signals could not be extracted from a 1D ¹H spectrum due to spectral overlap. Therefore, 2D ¹H,¹³C-HSQC experiments were conducted in order to resolve these resonances; the chemical shift displacements followed the same trend as predicted by the molecular dynamics simulations.

Figure 14.

¹H NMR chemical shift changes of sucrose protons upon addition of caffeine for H1g (○), H2g (□) and H3g (△) of the glucose residue (solid lines) and for H1f (○), H3f (□) and H4f (×) of the fructose residue (dashed lines). The titration was made with a 10 mM sucrose solution in D₂O.

Due to the extent of spectral overlap in the 1D proton spectra, only data for H1 and H2 in αD-glucopyranose and H1, H3 and H4 in β-D-glucopyranose were extracted from the glucose titration. Additional 1D ¹H,¹H-TOCSY experiments were carried out to resolve the H1-H4 signals for each anomeric form. For α-D-glucopyranose the magnitude of the H1 and H3 chemical shift displacements were slightly lower then for H2 and H4 indicating an association behavior suggested in the molecular dynamics simulations. For β-D-glucopyranose differences between the corresponding magnitudes of the chemical shift change were negligable.

Inter-molecular interactions were investigated using 1D ¹H,¹H-NOE experiments in which a targeted proton is selectively inverted. Besides intra-molecular cross-relaxation to other protons in the sugar, inter-molecular NOEs may be observed thereby supporting the presence of inter-molecular complex formation. Selective inversion was carried out separately on the α- and β-anomeric proton resonances from D-glucose as well as on the H1g and H1f resonances of sucrose and in all cases weak and positive NOEs were observed to H8 and Me1 in caffeine, supporting the presence of sugar-caffeine complexes.

Caffeine – Sugar interaction

Both the molecular dynamics simulations and the NMR experiments showed that sugars have an affinity for caffeine molecules. NOE measurements suggested the presence of sugar-caffeine complexes. The nature of the interaction exhibited between sugar and caffeine molecules is a stacking of the hydrophobic faces produced by the ring proton atoms of the sugar against the caffeine plane. This is revealed by the shape of the contour of the sugar proton atom densities (Figures 3, 5, and 9) and the angular distribution of the sugar rings (Figures 6 and 10) obtained from the MD simulations. Indeed the ¹H NMR caffeine titration experiments reported that within each saccharide the magnitudes of the chemical shift changes varied for protons depending on which face of the sugar ring is next to the caffeine surface. The similar magnitudes of chemical shift changes for the methyl groups of caffeine in the ¹H NMR sucrose titration also are in agreement with a face-to-face stacking of sugar and caffeine molecules as seen in the MD simulations.

Sucrose and both the α- and β-anomers of glucose had similar behavior, although some differences were evident. The β-anomer of glucose has no preference for pointing either the face defined by the proton atoms H1, H3, and H5 or that defined by H2 and H4 toward the caffeine plane, whereas for the α-anomeric form of glucose the arrangement having the proton atoms H2-H4 pointing toward the caffeine ring has a higher probability. This is due to the presence of the anomeric hydroxyl group. Sucrose tends to interact with the caffeine molecule by the glucose moiety even though there is a significant affinity for caffeine of the fructose moiety. The predominant configuration of interaction having glucose close to the caffeine molecule has the face described by the proton atoms H2g and H4g facing the caffeine ring. Due to the conformation of the disaccharide, when fructose is adjacent to the caffeine plane, the face oriented towards the caffeine ring is that produced by the proton atoms H3f and H5f. The present results were confirmed by ¹H NMR caffeine titration experiments. The strong preference of sucrose for having one face of each residue towards caffeine is supported by the large difference in chemical shift displacements between protons of opposite sides of the sugar plane. For β-D-glucopyranose, on the other hand, the chemical shift change differences between the protons on opposite sides of the sugar plane are smaller since the β-anomer does not have a preferential binding side. The moderate differential binding preference of the α-anomer gives rise to the small chemical shift changes between protons observed in the ¹H NMR caffeine titrations.

Conclusions

Caffeine is known from thermodynamic measurements to self-associate,⁴ and from MD simulations of caffeine in water the nature of the aggregation has been characterized as face-to-face stacking.¹¹ Caffeine is also known from experiment to associate weakly with sucrose in water, although those studies demonstrate that the presence of sugar lowers the solubility of caffeine in water as the sugar concentration increases.⁵ This latter observation is not unexpected, given that sugars are osmolytes that raise the chemical potential of a solution, favoring self-aggregation of a sparingly soluble species like caffeine. The present results show that sugars weakly bind to caffeine by face-to-face stacking, similar to the binding of caffeine molecules to each other. This mode of interaction does not interfere with the hydrogen bonding of the sugar molecules to water, so that their effect on the surface tension is undiminished by the binding. Since there was only one caffeine molecule in each of the present simulations, caffeine-caffeine stacking not observable, and so it was thus not possible to evaluate the competition between caffeine binding to other caffeine molecules and that to the sugars, or the effect of sugar concentration on caffeine solubility.

Although all of the sugars studied here are osmolytes and highly soluble in water, they do contain hydrophobic patches due to the weak polarity of the C-H bonds, which are not able to compete with water molecules as hydrogen bond partners. The principal means of association of these sugars with the caffeine is for their nonpolar regions to pair against the hydrophobic faces of the caffeine, displacing the unfavorably structured water molecules over the caffeine. Recently we demonsrated that the flat hydrophobic faces of caffeine are sufficiently large that they hydrate somewhat like extended hydrophobic surfaces,^22,24–27 with water molecules directly over the center pointing a proton directly down at the surface, even though this involves the loss of a hydrogen bond, since the alternate orientations would involve the loss of two to three hydrogen bonds.¹¹ This solvent structuring drives the aggregation of caffeine in solution, since the pairing of two caffeine faces liberates these unfavorably structured water molecules, which regain not only their rotational entropy, but also the lost hydrogen bond, explaining why caffeine aggregation is enthalpically driven even though it is a hydrophobic association. On the other hand, sugars like glucose are not sufficiently large to structure water molecules in this manner, and thus exhibit no self-aggregation tendency at normal concentrations in aqueous solution. However, by pairing with caffeine molecules, they are able to liberate the water molecules structured over the caffeine face, promoting the aggregation. The pairing energy is weak, and the dominant effect of adding sugars to caffeine solutions appears to be the promotion of caffeine aggregation, which is stronger than caffeine-sugar binding, by raising the chemical potential and thus the surface tension.

These MM simulations do not include any possible C-H/π interactions such as have been reported from recent ab initio calculations,^32,34,35,49 beyond those effects included implicitly through the choice of force field parameters. The absence of these effects might explain the smaller binding energies calculated here compared to the 2.5 – 5.4 kcal/mol estimated from ab initio calculations.³² Such C-H/π interactions would be present in the experimental systems, but it was not possible to use the NMR results to calculate the binding energies. The binding energies reported here are due primarily to hydration effects resulting from the liberation of structured water molecules.

The practical effects of such association in beverages sweetened with sugar are unclear. For example, does this pairing affect the taste perception of such beverages, and is the adsorption across the intestinal lumen (i.e., the bioavailability) affected? And how might this association compete with interactions with other components of beverages like coffee, such as tannins or chlorogenic acid? Furthermore, the association might affect the stability of the bubbles in the foams of drinks such as espresso.⁵⁰ All of these questions merit further study in the light of the present results.

Table 1.

The simulations conducted in the present study.

	β-D-glucopyranose	α-D-glucopyranose	sucrose
N° of caffeine molecules	1	1	1
N° of sugar molecules	36	36	13
N° of water molecules	667	667	666
Box size [Å]	30.0281	30.0281	29.2562
Caffeine conc. [mol kg−1]	0.083	0.083	0.083
Sugar conc. [mol kg−1]	3.0	3.0	1.08
Density [atoms Å−3]	0.1067	0.1067	0.1041
Time [ns]	80	80	100