Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Oct 22;2:759. doi: 10.1038/srep00759

Theoretical Investigation of the Magnetic Exchange Interactions in Copper(II) Oxides under Chemical and Physical Pressures

Xavier Rocquefelte 1,a, Karlheinz Schwarz 2, Peter Blaha 2
PMCID: PMC3477650  PMID: 23091699

Abstract

It remains a challenge to understand the unconventional mechanisms that cause high-TC superconductivity in cuprate superconductors, high-TC multiferroicity in CuO, or low-dimensional magnetism in the spin-Peierls transition compounds such as CuGeO3. A common feature of all these copper oxide compounds (containing Cu2+ ions) is the presence of large magnetic superexchange interactions J. It is a general strategy to apply chemical and/or physical pressure in order to tune these exotic properties. Here we show theoretically, for the first time, the impact of physical pressure on J on CuO, for which we predict a strong enhancement of the low-dimensionality of the magnetic interactions and the spin-frustration at high-pressures. Such modifications are expected to strongly influence the multiferroic properties of CuO. We finally demonstrate that PBE0 hybrid DFT calculations provide reliable J values for a wide range of copper(II) oxides compounds, i.e. CuGeO3, BaCu2Si2O7, BaCu2Ge2O7, and La2CuO4.

The interest for CuO has been revived in 2008 by the discovery by Kimura et al. of magnetically induced electric polarization at 230 K1. Indeed, CuO exhibits a type-II multiferroic behavior, i.e. the ferroelectric polarization is triggered by a specific magnetic order. Recently, several efforts have been carried out to elucidate the relationship between the magnetic properties and the high-temperature mutiferroicity in CuO2,3. In particular, one important ingredient explaining the high-TC value of CuO is the existence of a high Néel temperature (TN = 230 K), which is due to the presence of large antiferromagnetic superexchange interactions J. Thus, tuning TC towards room-temperature implies to be able to tune the magnetic exchange interactions in CuO. However, the experimental estimation of the J values is not straightforward and strongly depends on the technique. On the other side, a theoretical estimation of the J values could be realized by using the Heisenberg spin Hamiltonian. Here, based on PBE0 hybrid density functional calculations, we propose an efficient and reliable evaluation of the impact of physical pressure on J in CuO. In addition, we also apply these calculations to a series of low-dimensional cuprate compounds, allowing to estimate the impact of the chemical pressure on J.

Results

CuO at ambient pressure and temperature

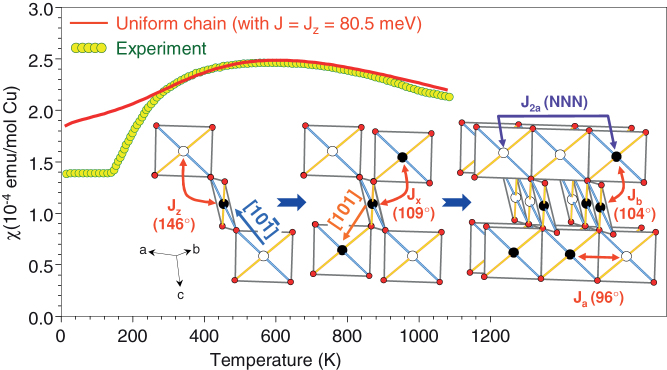
CuO is a particularly interesting case because it exhibits at least four superexchange interactions9,10, namely Ja, Jb, Jx, Jz, and three super-superexchange interactions, namely J2a, J2b, J2c(Fig. 1). Recently we have shown that J2a > J2b ≫ J2c11. In the present study we focus on the global effect of the next nearest neighbour (NNN) interactions, i.e. J2 = J2a + J2b + J2c. Such complexity is due to the three-dimensional nature of the atomic structure of CuO12. This structure can be seen to consist of corner- and edge-sharing square-planar CuO4 units, which form (-Cu-O-)∞ zigzag chains running along the [10-1] and [101] directions of the chemical unit cell (Fig. 1).

Figure 1. Structural and magnetic properties of CuO at ambient pressure.

Figure 1

Open in a new tab

The experimental magnetic susceptibility14 is compared to a simulated one based on an S = 1/2 Heisenberg uniform chain model with J = Jz = -80.5 meV. The experimental susceptibility has been corrected by the temperature independent contribution χ0, i.e. χexp(T) = χmol(T) – χ0, with χ0 = +20 × 10-6 emu/mol, as found from the fit of the high-temperature magnetic susceptibility and a g factor of 2.095 obtained from EPR measurements24. A progressive construction of the crystal structure and the magnetic ground state of CuO is shown, indicating the most important (Jz) and other (smaller) magnetic exchange couplings (Jx, Ja, Jb and J2a). At low temperature (T < TL), the CuO magnetic structure consists of FM and AFM arrangements along the [101] and [10-1] crystallographic directions The oxygen atoms are represented by small red circles, and the Cu2+ sites are depicted as filled and empty circles, representing up-spin and down-spin, respectively.

Before discussing how physical pressure affects the 5 essential J values of CuO a validation of our method is needed. It was demonstrated that our PBE013 hybrid calculations are able to accurately reproduce both J values and magnetic susceptibility data14 (Fig. 1). More specifically, the reported experimental J values15,16 J[10-1] = Jz = 80 meV and J[101] = Jx = 5 meV, are in excellent agreement with the calculated ones, namely Jz = 80.5 meV and Jx = 3 meV. The magnetic susceptibility modelling has been based, to a first approximation, on a S = 1/2 AFM uniform Heisenberg chain model17 using the Jz deduced from our PBE0 hybrid calculations, i.e. Jz = 80.5 meV. However, at low temperature (T < 260 K), the 1D uniform chain model overestimates the magnetic susceptibility of CuO. This result indicates an onset of 2D spin correlations18, which can be used to roughly estimate the interchain couplings, i.e. Jinter ≈ 260 K ≈ 22 meV. Indeed, the second largest J value in our calculations is J2 = 19.6 meV, which couples the (-Cu-O-)∞ zigzag chains, defined by the intrachain term Jz.

Effect of chemical pressure on J in low-dimensional cuprates

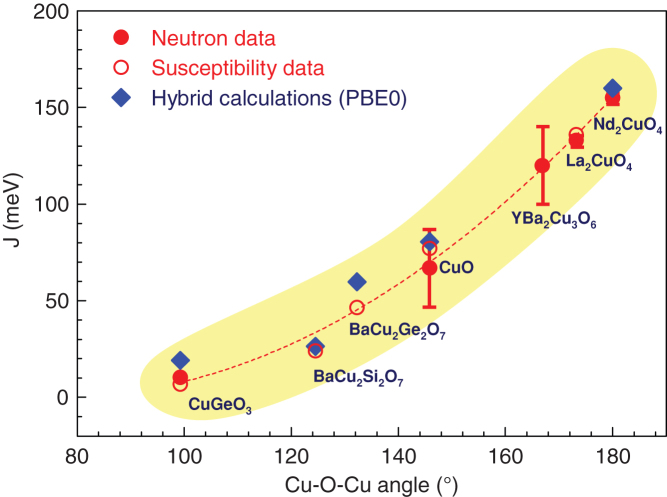
For over half a century, the Goodenough-Kanamori-Anderson rule4,5,6 is routinely used to qualitatively explain the relation between J and the atomic arrangement of the magnetic centers in a given system. For instance, in copper oxide compounds, the nearest-neighbor (NN) Cu-Cu spin interaction J is expected to change from antiferromagnetic (AFM) to ferromagnetic (FM) when the angle φ of the Cu-O-Cu bond goes from 180° to 90°. Recently Shimizu et al. have proposed such a correlation between J and the Cu-O-Cu bond angle φ in low-dimensional cuprates7,8, based on neutron and Raman scattering, and susceptibility measurements. By tuning the chemical composition, i.e. the chemical pressure, copper oxide compounds give access to the full range of Cu-O-Cu bond angles from 90° to 180°. Figure 2 shows how the magnetic exchange coupling in a series of copper oxide compounds depends on the Cu-O-Cu bond angle. For this study we considered the spin-Peierls transition compound CuGeO3, the quasi-one-dimensional AFM compounds BaCu2Si2O7 and BaCu2Ge2O7, and the 2D AFM cuprate La2CuO4, which under doping becomes an high-TC superconductor. For simplicity the small buckling of the Cu-O-Cu bonds in the CuO2 sheets in La2CuO4 has been neglected in the present PBE0 hybrid calculations (i.e. a Cu-O-Cu bond angle of 180° is assumed), as in Nd2CuO4. The agreement between available experimental data7 and these calculations is very good and validates that the PBE0 hybrid functional is well-suited to estimate the magnetic exchange parameters in all these copper(II) oxide compounds.

Figure 2. Principal superexchange interaction Jz as a function of the Cu-O-Cu bond angle φ for various low-dimensional cuprates.

Figure 2

Open in a new tab

Our calculations are compared to experimental data taken from neutron and Raman scattering, and susceptibility measurements7.

Effect of physical pressure on J in CuO

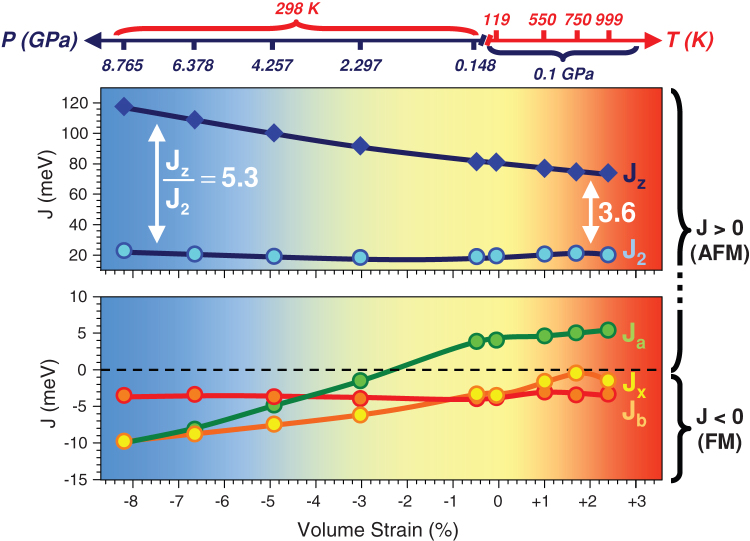
An alternative to probe the correlation between J and the Cu-O-Cu bond angle φ in cuprates would be physical pressure applied to a specific compound. However, to our knowledge, no experimental and/or theoretical investigations of the physical pressure dependence of J have been reported so far. In Fig. 3 we show the calculated pressure and temperature dependence of the J values in CuO. For this purpose, we have considered the atomic structures that were refined at different temperatures19 and pressures20. The new J values for each temperature and pressure have been deduced using the same strategy as reported in ref. 9. By increasing pressure or decreasing temperature, CuO undergoes a volume contraction, leading to significant modifications in the Cu-O-Cu bond angles. The present calculations show how these structural rearrangements affect the J values of CuO. For instance, the intrachain Jz value undergoes a reduction of 8% when the temperature is raised up to T = 999 K, but an increase of 46% when the pressure is increased up to 8.8 GPa. Thus Jz can be tuned from 74 to 117 meV by varying these two variables, T and P. The interchain coupling J2, however, is nearly insensitive to both pressure and temperature. As a consequence, the ratio Jz/J2 increases from 3.6 to 5.3 when pressure is increased from 0.1 GPa to 8.8 GPa. Similar effects of P and T are observed for the smaller J parameters, namely Ja, Jb and Jx. As pressure is increased the FM couplings are enhanced, and an additional FM coupling appears, i.e. Ja.

Figure 3. Pressure and temperature dependence of the magnetic exchange couplings of CuO.

Figure 3

Open in a new tab

In this figure, P and T are increasing to the left and to the right, respectively. The volume strain of CuO is given by the volume variation divided by the initial volume (at ambient pressure and temperature). By convention positive and negative J values represent AFM and FM interactions, respectively.

It should be noted that Ja and J2 correspond to the NN and NNN interactions in the chains based on edge-sharing CuO4 plaquettes (Fig. 1). Under high-pressure, the NN coupling Ja becomes FM, while the NNN J2 coupling remains AFM, with a ratio J2(NNN) ≈ −2 Ja(NN), i.e. the spin frustration is increased by a factor of two compared to ambient conditions. Consequently, the present calculations show that applying high-pressure on CuO will induce: (i) an increase of the larger AFM coupling (Jz) implying an increase of the Néel temperature (TN) with pressure, (ii) a larger stability of the incommensurate phase, directly related to the increase of 1D magnetic character and spin frustration in CuO. Our results are consistent with recent neutron diffraction experiments21,22, revealing that TN increases slightly from 230 K (ambient pressure) to 235 K (P = 1.8 GPa), and the stability range of the incommensurate spiral magnetic phase is increased, with a lock-in temperature TL decreasing from 213 K (ambient pressure) to 207 K (P = 1.8 GPa).

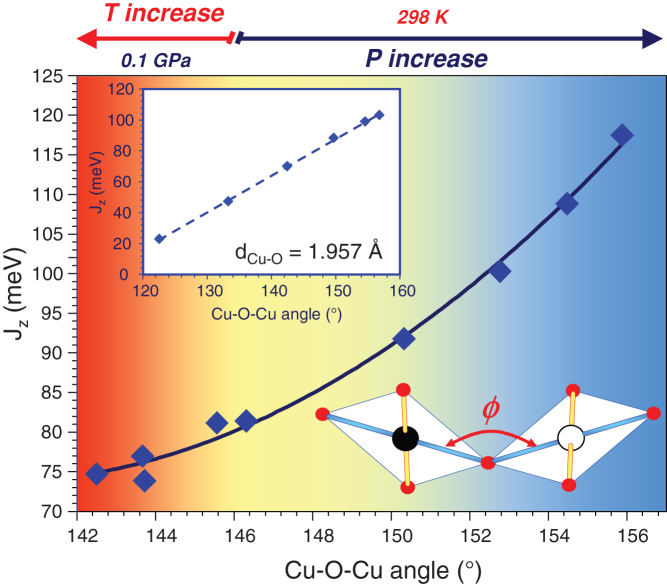
The large increase of Jz under high pressure emerges mainly from an increase of the Cu-O-Cu bond angle from 143.7° (at T = 999 K and P = 0.1 GPa) to 155.9° (at T = 298 K and P = 8.8 GPa), as evidenced in Fig. 4. This non-linear correlation between J and φ is very similar to the one previously proposed by Shimizu et al.7 (see also Fig. 2). However, in their case the angle variation is a consequence of chemical pressure whereas in our case it is physical pressure. In this context it is of interest that previous works7,8 found no correlation between the Cu-O bond length and J. In order to analyze the effects on the magnetic exchange interactions, namely the contribution from the bond length and bond angle, we have generated artificial CuO atomic structures, under positive and negative pressure but keeping the Cu-O distances constant inside the CuO4 plaquette (dCu-O = 1.957 Å), i.e. the volume change induces only bond angle variations (Fig. 3 inset). In this hypothetical situation, the correlation between Jz and φ becomes linear over the whole angle range from 120° to 160°. This shows that the influence of the bond length variation on J is smaller than the bond angle variation, but is significant, leading to the non-linear correlation between J and φ. The analogy shown here between physical and chemical pressures is very pronounced.

Figure 4. Principal superexchange interaction Jz as a function of the Cu-O-Cu bond angle φ for CuO under high-temperature and high-pressure.

Figure 4

Open in a new tab

In this figure, P and T are increasing to the right and to the left, respectively. The inset shows the evolution of Jz in CuO as a function of the Cu-O-Cu bond angle φ for CuO under positive and negative pressure, while keeping constant the Cu-O bond length in the CuO4 plaquettes (dCu-O = 1.957 Å).

Discussion

In the present work, we demonstrate that an efficient and reliable estimation of the magnetic exchange parameters of a wide variety of copper oxide compounds is achievable by using the PBE0 hybrid functional. Moreover, the present theoretical investigation shows that by applying 8.8 GPa to CuO, an increase of 46% of the largest J value is expected, implying that the Néel temperature will be also enhanced under pressure, paving the way for the first room-temperature multiferroic material.

Methods

DFT calculations were performed using the WIEN2k program package23 with the PBE013 hybrid functional. For each temperature and pressure, the magnetic exchange couplings of CuO have been evaluated considering nine ordered spin states depicted in ref. 9, and assuming collinear arrangements of the magnetic moments. A similar strategy has been applied to the six hypothetical CuO structures in which the Cu-O bond length were kept constant (for positive and negative pressure – see inset of Fig. 3). The magnetic exchange couplings of CuGeO3, BaCu2M2O7 (with M = Si, Ge) and La2CuO4 have been evaluated using magnetic unit cells consisting of 4, 4 and 2 formulae units, respectively.

Author Contributions

X.R. designed and performed the calculations, and drafted the manuscript. X.R., K.S. and P.B. analysed and discussed the results.

Acknowledgments

X.R. thanks the CCIPL (Nantes) computing center for computational facilities. P.B. was supported by the Austrian Science Fund (SFB F41, “ViCoM”). We thank C. Ewels for a critical reading of the manuscript.

References

  1. Kimura T., Sekio Y., Nakamura H., Siegrist T. & Ramirez A. P. Cupric oxide as an induced-multiferroic with high-TC. Nature Materials 7, 291–294 (2008). [DOI] [PubMed] [Google Scholar]
  2. Giovannetti G. et al. High-TC Ferroelectricity Emerging from Magnetic Degeneracy in Cupric Oxide. Phys. Rev. Lett. 106, 026401 (2011). [DOI] [PubMed] [Google Scholar]
  3. Tolédano P. et al. Theory of high-temperature multiferroicity in cupric oxide. Phys. Rev. Lett. 106, 257601 (2011). [DOI] [PubMed] [Google Scholar]
  4. Goodenough J. B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 100, 564–573 (1955). [Google Scholar]
  5. Kanamori J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 10, 87–98 (1959). [Google Scholar]
  6. Anderson P. W. Theory of Magnetic Exchange Interactions:Exchange in Insulators and Semiconductors. Solid State Phys. 14, 99–214 (1963). [Google Scholar]
  7. Shizmizu T. et al. Spin susceptibility and superexchange interaction in the antiferromagnet CuO. Phys. Rev. B 68, 224433 (2003). [Google Scholar]
  8. Mizuno Y. et al. Electronic states and magnetic properties of edge-sharing Cu-O chains. Phys. Rev. B 57, 5326–5335 (1998). [Google Scholar]
  9. Rocquefelte X. et al. Short-range magnetic order and temperature-dependent properties of cupric oxide. J. Phys. Condens. Matter 21, 045502 (2010). [DOI] [PubMed] [Google Scholar]
  10. Filippetti A. & Fiorentini V. Magnetic ordering in CuO from first principles: a cuprate antiferromagnet with fully three-dimensional exchange interactions. Phys. Rev. Lett. 95, 086405 (2005). [DOI] [PubMed] [Google Scholar]
  11. Rocquefelte X., Schwarz K. & Blaha P. Comment on “High-TC Ferroelectricity Emerging from Magnetic Degeneracy in Cupric Oxide”.. Phys. Rev. Lett. 107, 239701 (2011). [DOI] [PubMed] [Google Scholar]
  12. Asbrink S. & Norrby L.-J. A refinement of the crystal structure of copper(II) oxide with a discussion of some exceptional e.s.d.'s. Acta Crystallogr. B 26, 8 (1970). [Google Scholar]
  13. Perdew J. P., Ernzerhof M. & Burke K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996). [Google Scholar]
  14. O'Keffe M. & Stone F. S. The magnetic susceptibility of cupric oxide. J. Phys. Chem. Solids 23, 261–266 (1962). [Google Scholar]
  15. Aïn M., Reichardt W., Hennion B., Pepy G. & Wanklyn B. M. Magnetic excitations in CuO. Physica C 162-164, 1279–1280 (1989). [Google Scholar]
  16. Boothroyd A. T. High-Energy magnetic excitations in CuO. Physica B 234-236, 731–733 (1997). [Google Scholar]
  17. Johnston D. C. et al. Thermodynamics of spin S = ½ antiferromagnetic uniform and alternating-exchange Heisenberg chains. Phys. Rev. B 61, 9558–9606 (2000). [DOI] [PubMed] [Google Scholar]
  18. Tsirlin A. A., Zinke R., Richter J. & Rosner H. Spiral ground state in the quasi-two-dimensional spin-1/2 system Cu2GeO4. Phys. Rev. B 83, 104415 (2011). [Google Scholar]
  19. Yamada H., Zheng X. G., Soejima Y. & Kawaminami M. Lattice distortion and magnetolattice coupling in CuO. Phys. Rev. B 69, 104104 (2004). [Google Scholar]
  20. Ehrenberg H., McAllister J. A., Marshall W. G. & Attfield J. P. Compressibility of copper-oxygen bonds: a high-pressure neutron powder diffraction study of CuO. J. Phys. Condens. Matter 11, 6501–6508 (1999). [Google Scholar]
  21. Chatterji T., Brown P. J. & Forsyth J. B. High pressure neutron diffraction investigation of CuO. J. Phys. Condens. Matter 17, S3057–S3062 (2005). [Google Scholar]
  22. Ohashi M., Tashiro A., Oomi G., Maeda E. & Zheng X. G. Effect of pressure on the magnetic phase transition in cupric oxide. Phys. Rev. B 73, 134421 (2006). [Google Scholar]
  23. Blaha P., Schwarz K., Madsen G., Kvasnicka D. & Luitz J. WIEN2k: An Augmented Plane Wave + LO Program for Calculating Crystal Properties, TU Wien, Vienna., (2001).
  24. Azzoni C. B., Paleari A. & Parravicini G. B. On the low-temperature magnetic properties of CuO single crystals. J. Phys. Chem. Solids 4, 1359–1366 (1992). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES