Bayesian hierarchical modeling for a non-randomized, longitudinal fall prevention trial with spatially correlated observations

Abstract

Because randomization of participants is often not feasible in community-based health interventions, non-randomized designs are commonly employed. Non-randomized designs may have experimental units that are spatial in nature, such as zip codes that are characterized by aggregate statistics from sources like the U.S. census and the Centers for Medicare and Medicaid Services. A perennial concern with non-randomized designs is that even after careful balancing of influential covariates, bias may arise from unmeasured factors. In addition to facilitating the analysis of interventional designs based on spatial units, Bayesian hierarchical modeling can quantify unmeasured variability with spatially correlated residual terms. Graphical analysis of these spatial residuals demonstrates whether variability from unmeasured covariates is likely to bias the estimates of interventional effect.

The Connecticut Collaboration for Fall Prevention is the first large-scale longitudinal trial of a community-wide healthcare intervention designed to prevent injurious falls in older adults. Over a two-year evaluation phase, this trial demonstrated a rate of fall-related utilization at hospitals and emergency departments by persons 70 years and older in the intervention area that was 11 per cent less than that of the usual care area, and a 9 per cent lower rate of utilization from serious injuries. We describe the Bayesian hierarchical analysis of this non-randomized intervention with emphasis on its spatial and longitudinal characteristics. We also compare several models, using posterior predictive simulations and maps of spatial residuals.

Introduction

Second-stage translational public health interventions often entail the dissemination of new information to communities in ways designed to facilitate people's adoption of constructive behaviors. In addition to relevant clinical knowledge, community-based interventions often involve elements of learning theory, psychology, and sociology. Because of the concerns of policy, logistics, and feasibility, community-based interventions are often necessarily restricted to non-randomized designs. Non-randomized designs are vulnerable to bias from unmeasured sources of variability that have not been theoretically balanced as in a randomized trial.

Sometimes these non-randomized designs are based on geographical units, such as school districts, census tracts, or zip code tabulation areas (ZCTAs) [1]. The analysis of such `spatial' entities is increasingly based on Bayesian hierarchical spatial models that go beyond traditional regression approaches. Because covariate information on individual participants is often limited, the model is supplemented with spatial random effects that account for all variability not explained by the covariates. Mapping these spatial residuals allows for a comparison between study arms of a non-randomized design to graphically assess potential biases contributed by the unmeasured variables.

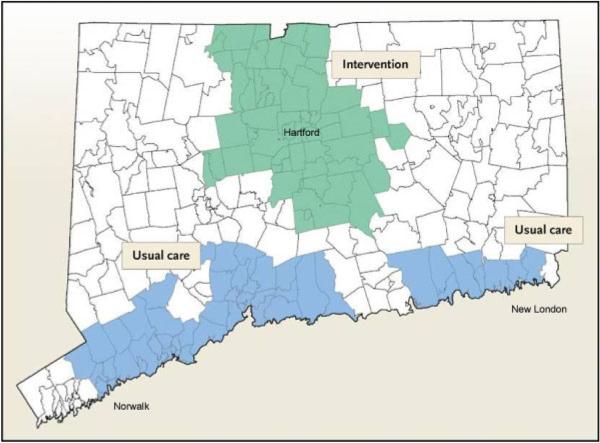
The Connecticut Collaboration for Fall Prevention (CCFP) was a non-randomized, longitudinal trial which ran from October 2001 through October 2006 and compared two regions of Connecticut (CT) to test whether dissemination of the evidence of proven efficacy [2, 3] for reducing the rate of fall-related injury among older people was effective at the community level. For each six-month interval, counts of fall-related outcomes and population at risk were obtained from the Connecticut Hospital Association and Medicare denominator files [4], respectively, with ZCTA-level estimates of covariates provided by the U.S. Census [5]. The study was divided into a three-year `intervention' phase allowing for dissemination of educational materials and their subsequent integration within clinical practice, and a two-year phase of formal `evaluation'. CCFP used a quasi-experimental design that compared a treatment area receiving the intervention and a usual care area which did not. As shown in Figure1, the intervention region consisted of 58 contiguous ZCTAs in north central CT (i.e. the greater Hartford region) while the usual care area comprised a discontinuous stretch of 53 ZCTAs along the southern coastline (i.e. the I-95 corridor from Norwalk to New London).

Figure 1.

Connecticut Collaboration for Fall Prevention.

The discontinuity in the usual care area was necessary to prevent the contamination of the intervention because the catchment areas of healthcare providers from both study arms overlapped in that south-central coastal region. The design of the study arms balanced aggregate characteristics of important explanatory variables and a two-year pre-intervention analysis verified that baseline rates of fall-related events were not significantly different. The design, content, and pre-intervention analysis of the CCFP are described elsewhere [6, 7].

During the two-year evaluation phase of the CCFP, adjusted rates of serious fall-related injury and fall-related use of medical services were respectively 9 per cent and 11 per cent lower in the intervention region relative to usual care [8]. From a community health perspective, the 11 per cent relative reduction in the use of fall-related medical services translated into approximately 1800 fewer medical treatment events and avoidance of commensurate physical distress. Based on an average acute care cost of $12 000 per event, this decrease in medical treatment represents a potential savings of $21 million in health care costs [9]. These findings suggest that in addition to conserving precious medical resources, the dissemination of evidence about fall prevention may well prevent falls and related physical hardship.

In this paper we describe the analytical model used to evaluate the CCFP intervention and discuss ways of checking model fit. These include the Deviance Information Criterion [10], posterior predictive simulations, and maps of spatial residuals that quantify spatially related variability not captured by the ZCTA-level covariates. We use these criteria to demonstrate their utility for evaluating non-randomized interventions and for appraising potential models.

Description of analysis

For CCFP, units of analysis were the age–gender subgroups of ZCTAs whose outcome was the number of fall-related utilizations (f _jklt), where the indices j, k, l, and t respectively indicate the ZCTA, age, gender, and time period under consideration. We assumed a Poisson distribution as follows:

$$f_{jklt}~\text{Poisson}(E_{jklt}\ast \text{exp}\left({\mu }_{jklt}\right))$$

where E_jklt are the internally standardized expected fall counts and μ_jklt the log relative risk of fall-related utilization. For CCFP the latter term was modeled as follows,

$$\left({\mu }_{j,k,l,t}\right)=\mu +(I_j\beta +P^{\left(t\right)}\delta +I_j{P}^{\left(t\right)}\epsilon )+F_j\rho +A_k\nu +G_{l\gamma }+{\mathbf{X}}_j^{\mathrm{T}}\Omega +{\varphi }_j^{\left(t\right)}+{\theta }_{jkl}^{\left(t\right)}$$ (1)

where the three terms on the right-hand side in parentheses collectively evaluate the intervention. Respectively, I _j is the treatment applied to ZCTA j (0 if usual care, 1 if intervention), P^(t) is the phase of the study at time (t) (0 for dissemination and 1 for the evaluation), and I _j P^(t) represents the treatment-by-phase interaction. The remaining terms on the right-hand side adjust the estimated effect of intervention. Among the fixed effect covariates, F_j is the average fall-rate of ZCTA j over the two-year pre-dissemination phase, A_k is age group (1, 2, 3, or 4 corresponding to ranges of 70–74, 75–79, 80–84, and 85 years and older), G_l is gender (0 if male, 1 if female), and X_j is a vector of ZCTA-level covariate information whose specific covariates are defined in the row of Table I labeled `Clinical'. Thus μ is an intercept, and the other fixed effects are spatial regression coefficients where the combined values of the A_k and G_l define the eight age–gender subgroups.

Table I.

Four candidate models to evaluate the CCFP.

Model*	Model terms†	Value of Deviance Information Criterion.10
	μj,k,l,t =μ+(I jβ+P(t)δ+I j P(t)ε)+F j ρ+Akυ+Glγ
Fixed effects‡	I j is intervention (0=usual care, 1=intervention)
	P(t) is phase at time t (0=intervention, 1=evaluation)
	I j P(t) is the interaction of intervention and phase at time t	1230
	Fj is the pre-intervention fall rate of ZCTA j
	Ak is age group (ordinal 1–4 in five year increments)
	Gl is gender (0=male, 1=female)
Random effects‡	${\mu }_{j,k,l,t}=\mu +\left(I_j\beta \right)+P^{\left(t\right)}\delta +I_j{P}^{\left(t\right)}∊+F_j\rho +A_k\upsilon +G_{l\gamma }+{\varphi }_j^{\left(t\right)}+{\theta }_{\mathrm{jkl}}^{\left(t\right)}$	130
	${\varphi }_j^{\left(t\right)}$ is ZCTA level spatial variability
	${\theta }_{\mathrm{jkl}}^{\left(t\right)}$ is ZCTA specific age–gender stratum (nominal 1–8)
Clinical§	μj,k,l,t =Random Effects+XjΩ	125
	where XjΩ includes ZCTA-level specific values for :
	Proportion 65+ households with income ≤15000
	Proportion 65+ households with income ≤75000
	Proportion 65+ persons living in institutions
	Proportion 65+ non-institutionalized with physical disability
	Proportion 65+ self-reported race as non-white
Statistical§	μj,k,l,t =Random effects+XjΩ	119.6
	where XjΩ includes ZCTA-level specific values for :
	Proportion 65+ households with income ≤15000
	Proportion 65+ persons living in institutions

^*Four candidate models for evaluating effectiveness of the intervention from the CCFP where observations are ZCTA in either an intervention or usual care area, which were respectively exposed and not-exposed to a treatment to prevent falls among older persons.

^†Stratified analysis where model terms define analytical units as specific age-gender subgroups with indices defined as follows: j =ZCTA, k=ordinal age, l=binary gender, and t =six-month period of observation (ordinal) over a five-year period and where μ_j,k,l,t is the rate of fall-related utilization for specific ZCTA-level age–gender subgroup and time period.

^‡Terms in parentheses on right-hand side of model collectively evaluate intervention.

^§Proportions are ZCTA-level estimates obtained from the U.S. Census of 2000.

The last two terms in the right-hand side of (1) are random effects that account for potential bias from non-randomized designs based on our correlated geographical units (ZCTAs). First, the random effects ${\theta }_{jkl}^{\left(t\right)}$ account for the unstructured heterogeneity of each ZCTA's sub-population for the eight specific age and gender combinations within each six-month time period t. More specifically, we assume ${\theta }_{jkl}^{\left(t\right)}~N(0,1∕{\tau }_H)$ where ${\tau }_H$ is a precision term allowing for unstructured heterogeneity on a statewide basis. This is an enhancement of the model used by Waller et al. (1997) who calculated a random effect ${\theta }_j^{\left(t\right)}$ for the unstructured heterogeneity of each spatial unit within each time period [11]. Complementing the terms for unstructured heterogeneity, the random effects ${\varphi }_j^{\left(t\right)}$ account for the spatial variability of ZCTA j not captured by other model terms for each six-month time period t. The use of these two types of random effects provides a rigorous accounting of unmeasured variability, accommodates experimental units which have few or no falls, and allows for maps showing the geographical distribution of the unmeasured variability. This Bayesian hierarchical approach also provides appropriate levels of shrinkage for parameters corresponding to units with very large or very small outcome counts.

Suppressing the (t) superscript for the moment, we now describe the distribution of the spatial random effects [12]. Suppose the spatial random variable ϕ_j is observed at J areal locations, to define the vector ϕ=(ϕ₁,…ϕ_j)^T Assuming the ϕj form a Markov random field [13], the J full conditional distributions of the ϕj are defined as

$$p({\varphi }_j\mid {\varphi }_{i\ne j,{\tau }_j})=N(\alpha {\Sigma }_{i~j}{b}_{ij}{\varphi }_i,{\tau }_j^{-1}),j=1,\dots J,$$ (2)

where i ~ j denotes that region j is a neighbor of region i, i.e. i and j are spatially adjacent, and τ_j are precision terms determining the degree of spatial clustering. The full conditional distributions then uniquely determine the joint distribution of the vector φ=(ϕ₁, …_J)^T as follows [14]:

$$\phi ~N(0,{\left[D_{\tau }(\mathbf{I}-\alpha B)\right]}^{-1}),$$ (3)

where B is an J × J matrix with b_jj=0, D_τ =Diag(τ_j) and is usually taken as τ_cD where τ_c>0 is a spatial clustering parameter, D is a diagonal matrix, and α is a smoothing parameter of value between 0 and 1 that controls spatial dependence. Contingent upon the weighting matrix W (defined in next paragraph) being row stochastic, it has been shown that constraining |α|<1 preserves propriety of the joint distribution of (3) [15]. This joint distribution is known as the conditional autoregressive (CAR) formulation [13].

Different values of α, D, and B provide various CAR model structures. The most popular CAR implementation is the pairwise difference formulation in which α=1 and D=Diag(m_j) where m_j is the number of neighbors of region j, and B=D⁻¹W where W is a weighting matrix whose values w_ij define the neighbors of each region. In this same CAR implementation, W is specifically an adjacency matrix for the map (i.e. w_jj=0 and w_ij=1 if i ~ j and 0 otherwise) [16]. The joint distribution of φ=(ϕ₁, …ϕ_J)^T then becomes

$$\phi ~N(0,{\left[{\tau }_c(D-W)\right]}^{-1}),$$ 4

which is improper because of the singularity of [τ_c(D–W)].

We chose the CAR model of (4) as implemented in WinBUGS software, which employs Gibbs sampling (see Section 3.4.1 in Carlin and Louis [17]). We initially assigned separate precision terms for each study arm, i.e. τ_c(I) and τ_c(UC) for the intervention and usual care arms respectively, which produced higher values of the DIC and nearly complete overlap of the credible intervals for the main effects in (1) as well as for τ_c(I) and τ_c(UC). For purposes of better fit and model parsimony we retained a single spatial distribution (τ_c) in the candidate models. The fixed model effects were given flat priors and the precision terms τ_H and τ_c were given gamma priors whose parameters were assigned mildly informative values to expedite Markov chain Monte Carlo (MCMC) convergence. Five Markov chains initialized at disparate values were each run for 6000 iterations with convergence confirmed by the Gelman–Rubin statistic as modified by Brooks [18, 19]. Following burn-in, an additional 5000 iterations were run to obtain estimates of posterior distributions of all model parameters.

Defining four candidate models

Because model selection is often a matter of concern in the analysis of non-randomized interventions, we examined four models that are defined in Table I.

The four models were conceived as follows. In addition to adjustment for each ZCTA's pre-intervention rate of fall-related utilization, the fixed effects model consists of only those fixed effects necessary for evaluating the intervention (indicators for intervention, phase, and their interaction) with strata defined by the age–gender subgroups and adjustment for ZCTA-level pre-intervention fall rates. The random effects model contains all the terms of the fixed-effects model as well as the two random effects on the right-hand side of (1). The clinical model augments the random effects model with five ZCTA-level covariates defined in Table I that were deemed essential for clinical plausibility, and generated the results formally reported for the CCFP intervention [8]. Finally, the statistical model is simply the clinical model pruned back to achieve the minimal relative value of the deviance information criterion (DIC) [10]. The DIC is a generalization of the Akaike Information Criterion (AIC) that can be applied to Bayesian hierarchical models. Note that the latter three models, i.e. the random effects, clinical, and statistical, have comparable values of the DIC with the lowest pertaining to the statistical model. In stark contrast, the DIC of the fixed effects model is 1000 points higher than values from the models containing random effects. This highlights the very tangible improvement in model fit afforded by the addition of the two random effects to the fixed effects model.

In Table II we present posterior estimates of the parameters needed to evaluate the intervention, i.e. β, δ, and ε, as well as the precision terms τ_c and τ_H. Note that the three models containing the random effects, i.e. the random effects, clinical, and statistical, yielded significant, negative associations of comparable magnitude between the intervention and the rate of fall-related outcomes in the CCFP. On the contrary, the fixed effects model yielded a non-significant negative association of about half the magnitude of the three models containing random effects. The precision term τ_H is more than double the τ_c, indicating that the spatial random effect due to the clustering of each ZCTA with its adjacent neighbors has greater variability than the undefined heterogeneity across the age-gender strata of the ZCTAs.

Table II.

Posterior distributions of parameters from four models of fall utilization data from the CCFP.

Parameter	Factor	Model	Mean	95% credible interval
β	Intervention	Fixed effects	−0.02349	(−0.04858,0.00124)
		Random effects	−0.04294	(−0.07435,−0.01134)
	(0=Usual Care, 1=Intervention)	Clinical	−0.04769	(−0.07822, −0.01562)
		Statistical	−0.05122	(−0.08222, −0.02039)
δ	Study phase	Fixed effects	0.08566	(0.05931,0.1122)
		Random effects	0.08848	(0.0552,0.1203)
	(0=Dissemination, 1=Evaluation)	Clinical	0.08864	(0.05706,0.1224)
		Statistical	0.0892	(0.05674,0.1216)
ε	Interaction of Intervention and Study	Fixed effects	−0.06708	(−0.09985,−0.0336)
		Random effects	−0.07411	(−0.1161,−0.03082)
	Phase	Clinical	−0.07409	(−0.1193,−0.0291)
	(1=Intervention during evaluation, 0=otherwise)	Statistical	−0.07597	(−0.1193,−0.03445)
τ C	Precision for spatial	Random effects	8.304	(5.032,12.76)
	clustering	Clinical	8.221	(5.044,12.43)
		Statistical	8.219	(5.055,12.8)
τ H	Precision for undefined heterogeneity	Random effects	20.48	(15.81,26.4)
	undefined heterogeneity	Clinical	20.24	(15.94,25.98)
		Statistical	20.43	(15.65,26.38)

Two criteria for Bayesian hierarchical model checking

Table I shows that the statistical model had lowest DIC followed in increasing order by the clinical, random effects, and fixed effects models. We further evaluate the four candidate models using two criteria enabled by Bayesian hierarchical methods, namely posterior predictive simulation (see Chapter 8 of Gelman and Hill [20]) and maps of spatial residuals. Note that neither of these techniques is possible with traditional regression approaches. Posterior predictive simulation provides an arguably more rigorous appraisal of the predictive ability of a specific model than traditional goodness-of-fit statistics. Vectors consisting exclusively of the model coefficients for the fixed effects are randomly sampled from their posterior distributions and then multiplied by the design matrix of the explanatory variables to yield the log relative risk of falls. Poisson draws then convert these model coefficients into posterior simulations of the original outcome data. Descriptive statistics are calculated from a large sample of such simulations and compared against the corresponding statistics of the actual outcome data.

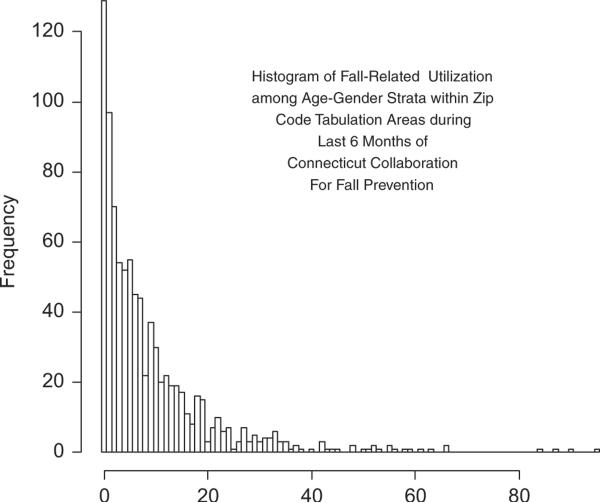
Figure 2 is a histogram of the counts of fall-related utilizations for the age-gender subgroups in the CCFP analysis from the last six months of the study. In order to check across a representative range of outcome values, we examine each model's performance in predicting the proportion of units with values of 0, 3, 10, 15, 25, and 35 falls. Note that because the frequency of units with 25 units is strikingly small compared to its neighboring values, this value will be problematic for models to replicate.

Figure 2.

Histrogram of fall-related utilization among age-gender strata within zip code tabulation areas during last 6 months of Connecticut Collaboration for Fall Prevention.

The second criterion is mapping of the spatial residuals to see whether there is a gross imbalance in the unmeasured, spatial variability between the study arms. Analogous to residual plots from regression models, maps of spatial residuals provide conceptual insight regarding assumptions and model fit. We expect better models to have fewer `outliers' among the spatial residuals, as well as a balanced distribution between study arms. This graphical evidence speaks to the uncertainty regarding imbalance of unmeasured covariates in a non-randomized design.

Results of posterior predictive simulations

In Table III we present the results of posterior predictive simulations from the four candidate models. The top half of the table compares the proportion of units with the following outcome values, 0, 3, 10, 15, 25, and 35, in the recorded data from the last six months of CCFP with the corresponding proportions yielded by samples of 1000 randomly generated posterior predictive models. A floor function was utilized in the R-based simulations across all three models so that model predictions were rounded down to the nearest integer value. The 95 per cent credible intervals of the proportion of units with the specific predictive values show how well each of the candidate models covered the true proportion of outcome values in the data.

Table III.

Posterior predictive simulations of CCFP outcome data in the last six months.

Test Statistic	Proportion of units in the last six Months with (#) outcomes	95% credible intervals from fixed effects model	95% credible intervals from random effects model	95% credible intervals from clinical model	95% credible intervals from statistical model
		Specific predictive outcome values
Prop(0)	0.15	(0.13,0.14)*	(0.14,0.15)	(0.13,0.16)	(0.14,0.16)
Prop(3)	0.061	(0.061,0.072)	(0.063,0.072)†	(0.056,0.073)	(0.059,0.07)
Prop(10)	0.034	(0.033,0.048)	(0.023,0.041)	(0.023,0.051)	(0.019,0.045)
Prop(15)	0.019	(0.014,0.020)	(0.012,0.020)	(0.0079,0.021)	(0.010,0.021)
Prop(25)	0.0011	(0.0034,0.011)‡	(0.0034,0.012)‡	(0.0023,0.012)‡	(0.0023,0.012)‡
Prop(35)	0.0034	(0.00,0.0034)	(0.00,0.0034)	(0.00,0.0056)	(0.00,0.0045)
	Percentile value in data	Distributional characteristics of posterior simulations
2.5 pctl	0	(0,0)	(0,0)	(0,0)	(0,0)
25 pctl	1	(1,2)	(1,1)	(1,1.8)	(1,1.8)
50 pctl	5	(5,6)	(5,5)	(4,6)	(4,6)
75 pctl	12	(11,12)	(10, 12)	(9,12)	(10,12)
97.5 pctl	43	(40,44)	(37,44)	(35,46)	(37,44)
IQR	11	(9.5,11)	(9,10)§	(9,11)	(9,11)

Prop(#)=proportion of units in samples with the value #.

^*Fixed Effects model under-predicts units with 0 falls.

^†Random Effects model over-predicts number of units with 3 falls.

^‡All models over-predict number of units with 25 falls.

With the exception of Prop(25), clinical and statistical have good coverage with statistical more precise.

pctl = percentile.

IQR = interquartile range (75–25 pctl).

^§Random effects model under-predicts IQR.

Not surprisingly, all models under-predict the proportion of units with 25 falls, which clearly contradicts the localized trend of the frequency distribution depicted in Figure 2. Note however that the clinical and statistical models present lower bounds of their respective credible intervals for Prop(25) that are closer to inclusion of the observed value of Prop(25) than those of the fixed and random effects models. Otherwise, the clinical and statistical models exhibit consistently good coverage with slight gains in precision for the statistical. On the contrary, the fixed effects model under-predicts the proportion of units with 0 falls, i.e. the mode of the distribution, while the random effects model over-predicts the proportion of units with three outcomes. This is consistent with the DIC's suggestion that the fixed effects, random effects, clinical, and statistical models exhibit progressively better fit.

The lower half of Table III compares overall distributional characteristics of the posterior predictive simulated values from the four models. The fixed effects, clinical, and statistical models have very similar ability to describe the distribution across a range of percentiles, whereas the random effects model underestimates the inter-quartile range.

Maps of spatial residuals

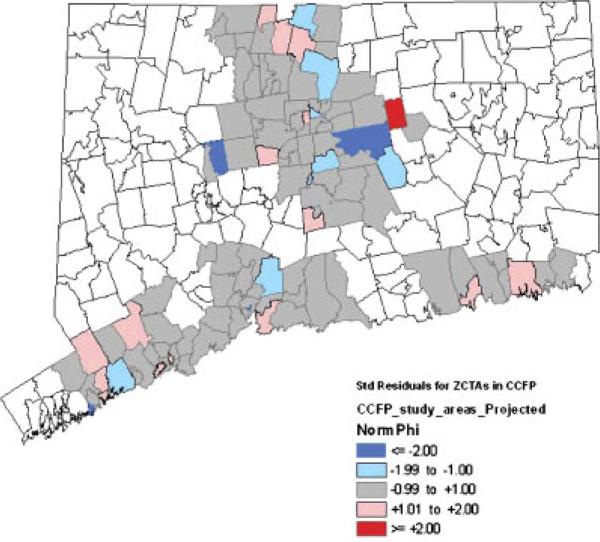
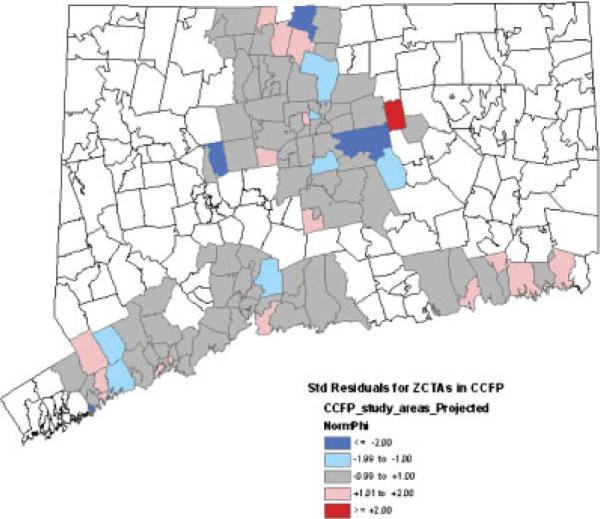
Maps of standardized values of the spatial residuals from the random effects and statistical models are depicted in Figures 3 and 4 respectively. Because the clinical model yielded a map nearly identical to that of the statistical model, and because the fixed-effects model does not contain spatial residuals, corresponding maps for these two models are not presented. In Figures 3 and 4 we are looking for evidence of imbalance in the distributions of standardized spatial residuals between the study arms, and wish to see a fairly random distribution of the values as evidence that small-scale variability is being accommodated by our spatial random effects. Overall, the two maps show the random effects and statistical models presenting fairly random distributions of unmeasured spatial variability across the study arms and do not suggest any gross imbalance that might be indicative of important covariates missing from the model. In both maps all but one of the significant standardized residuals (values ≥ 2 in absolute value) occur in the intervention arm, where several ZCTAs have highly negative standardized residuals and a single ZCTA has a highly positive standardized residual.

Figure 3.

Standardized spatial residuals from random effects model.

Figure 4.

Standardized spatial residuals from statistical model.

The magnitudes of the significant standardized residuals reflect the models' tendencies to respectively over- and under-predict the fall rates of these particular ZCTAs. The highly positive standardized residual came specifically from the town of Bolton, which with 416 persons of age 70 and older in 2003 had one of the smallest populations at-risk in the entire dataset. Even a handful of additional falls will cause a very significant shift in the local fall rate in such a small at-risk population. It is also plausible that the significant standardized residuals reflect a more variable spatial distribution of the fall rate due to highly localized differences in the implementation of the intervention.

Concluding remarks

In this paper we have shown the specific analytical model (the clinical model) used to evaluate a non-randomized, longitudinal trial on fall prevention and have compared four alternative models using criteria facilitated by hierarchical Bayesian analysis. Notice that the hierarchical Bayesian approach has provided additional tools not available from traditional regression approaches. The DIC is a special form of the AIC which can be used to evaluate the relative fit of multi-level models within a Bayesian framework. The spatial residuals and posterior predictive checks are directly enabled by the hierarchical Bayesian approach. These tools and the model checking they facilitate are of special importance in the evaluation of community health interventions, which typically preclude randomized designs because of constraints on data gathering or administration of the intervention.

While it must be noted that the techniques demonstrated here do not address the issue of causality, they demonstrate that a significant array of informative techniques exist that lend themselves to the analysis of non-randomized designs. Future work is needed to expand the use of these tools in a way that will strengthen claims of causality for interventions applied in the context of non-randomized designs. Building on the strengths demonstrated in this paper, it is foreseeable that the combination of hierarchical Bayesian with traditional techniques for adjusting the bias in non-randomized designs, such as propensity scores, will yield feasible approaches in this increasingly valuable area of statistical research.