Data-based theoretical identification of subcellular calcium compartments and estimation of calcium dynamics in cardiac myocytes

Abstract

In cardiac cells, Ca²⁺ release flux (J_rel) via ryanodine receptors (RyRs) from the sarcoplasmic reticulum (SR) has a complex effect on the action potential (AP). Coupling between J_rel and the AP occurs via L-type Ca²⁺ channels (I_Ca) and the Na⁺/Ca²⁺ exchanger (I_NCX). We used a combined experimental and modelling approach to study interactions between J_rel, I_Ca and I_NCX in porcine ventricular myocytes. We tested the hypothesis that during normal uniform J_rel, the interaction between these fluxes can be represented as occurring in two myoplasmic subcompartments for Ca²⁺ distribution, one (T-space) associated with RyR and enclosed by the junctional portion of the SR membrane and corresponding T-tubular portion of the sarcolemma, the other (M-space) encompassing the rest of the myoplasm. I_Ca and I_NCX were partitioned into subpopulations in the T-space and M-space sarcolemma. We denoted free Ca²⁺ concentrations in T-space and M-space Ca_t and Ca_m, respectively. Experiments were designed to allow separate measurements of I_Ca and I_NCX as a function of J_rel. Inclusion of T-space in the model allowed us to reproduce in silico the following important experimental results: (1) hysteresis of I_NCX dependence on Ca_m; (2) delay between peak I_NCX and peak Ca_m during caffeine application protocol; (3) delay between I_NCX and Ca_m during Ca²⁺-induced-Ca²⁺-release; (4) rapid I_Ca inactivation (within 2 ms) due to J_rel, with magnitude graded as a function of the SR Ca²⁺ content; (5) time delay between I_Ca inactivation due to J_rel and Ca_m. Partition of 25% NCX in T-space and 75% in M-space provided the best fit to the experimental data. Measured Ca_m and I_Ca or I_NCX were used as input to the model for estimating Ca_t. The actual model-computed Ca_t, obtained by simulating specific experimental protocols, was used as a gold standard for comparison. The model predicted peak Ca_t in the range of 6–25 μm, with time to equilibrium of Ca_t with Ca_m of ∼350 ms. These Ca_t values are in the range of LCC and RyR sensitivity to Ca²⁺. An increase of the SR Ca²⁺ load increased the time to equilibrium. The I_Ca-based estimation method was most accurate during the ascending phase of Ca_t. The I_NCX-based method provided a good estimate for the descending phase of Ca_t. Thus, application of both methods in combination provides the best estimate of the entire Ca_t time course.

Key points

• Ca²⁺ release from intracellular stores affects the cardiac action potential via currents through L-type Ca²⁺ channels (I_Ca) and the sodium/calcium exchanger (I_NCX).

• Dynamic interactions between released calcium, I_Ca and I_NCX occur in a restricted subcellular compartment, close to Ca²⁺ released sites, where calcium concentration (Ca_t) cannot be measured.

• We used a computational model and experimental data to define this compartment and to provide a theoretical basis for estimating Ca_t.

• We estimated Ca_t from recordings of I_Ca and I_NCX and optical recordings of whole-cell calcium concentration (Ca_m).

• Estimated peak Ca_t ranged from 6 μm to 25 μm, depending on calcium load. Time to equilibrium between Ca_t and Ca_m was ∼350 ms. The Ca_t values are in the range of I_Ca and I_NCX sensitivity to calcium, implying that there is significant effect of Ca²⁺ in this restricted domain on their kinetics and on the action potential during cell excitation.

Introduction

Ca²⁺ release flux (J_rel) from the sarcoplasmic reticulum (SR) via ryanodine receptors (RyRs) exerts a complex effect on the cardiac action potential (AP) via Ca²⁺-dependent inactivation of L-type Ca²⁺ channels (LCCs) (repolarizing effect) and activation of 3Na⁺/Ca²⁺ exchangers (NCXs) (depolarizing effect). It has been shown that abnormality of J_rel due to genetic defects in RyR, heart failure, or excessive phosphorylation during exercise and stress could cause abnormal cellular electrical activity and arrhythmic behaviour. For example (1) beat-to-beat alternans in J_rel is associated with arrhythmogenic AP alternans, with amplitude that depends on the balance between Ca²⁺ flux via LCCs (I_Ca) and NCX (I_NCX); this process is modulated by the Ca²⁺/calmodulin-dependent protein kinase II (CAMKII) (Sato et al. 2006, Livshitz & Rudy, 2007); (2) I_Ca recovery from Ca²⁺-dependent inactivation following J_rel is implicated in the development of early afterdepolarizations (EADs) (Antoons et al. 2007); and (3) diastolic J_rel underlies the formation of delayed afterdepolarizations (DADs) and triggered activity at high levels of β-adrenergic tone (e.g. Belevych et al. 2011; Priori & Chen, 2011).

The mechanism of coupling between J_rel, I_NCX, I_Ca and the AP is not completely understood, even under normal physiological conditions. Consensus exists that the interactions are mediated by the free Ca²⁺ sensed by these channels, and are modulated by the CaMKII signalling pathway. However, optical recordings of the whole-cell (global) Ca²⁺ transient (Ca_m) show dynamics which correlate poorly with the much faster kinetics of the ionic currents (I_Ca and I_NCX). This implies that these channels are experiencing different local Ca²⁺ transients (Ca_t) that cannot be measured with current experimental techniques with sufficient temporal and spatial resolution. Consequently, combined experimental/computational methods were developed for estimating local Ca²⁺ from measurements of whole-cell Ca²⁺ using fluorescence imaging, together with recorded I_NCX (Egan et al. 1989; Trafford et al. 1995; Weber et al. 2001) or I_Ca (Sipido et al. 1995; Sham, 1997; Zahradnikova et al. 2004; Antoons et al. 2007) as local Ca²⁺ sensors (reporters). Early work used Ca_m and mathematical modelling to calculate J_rel in skeletal (Melzer et al. 1987) and cardiac (Sipido & Wier, 1991) fibres. These indirect (inverse) methods for estimating local Ca²⁺ from I_NCX and I_Ca recordings rely heavily on the mathematical models employed and the quality of recorded I_NCX and I_Ca data.

Due to tight coupling between Ca²⁺ cycling and membrane voltage (V) in cardiac myocytes, it is difficult to control I_NCX and I_Ca independently and separate Ca²⁺-dependent from V-dependent processes in experiments. For example, it is extremely challenging to separate effects of Ca²⁺-dependent (CDI) and voltage-dependent (VDI) inactivation of I_Ca, or effects of Ca²⁺-dependent and voltage-dependent modulation of I_NCX. In addition, modulation of I_Ca by Ca²⁺ is due to both CDI and changes in the driving force. Moreover, there is strong interaction (mediated by Ca²⁺ changes) between I_Ca and I_NCX during an AP and therefore caution should be taken in extrapolating estimates of local Ca²⁺ from each individual current to the physiological environment of the myocyte during excitation. Ca²⁺ fluxes have been measured under experimental conditions (voltage clamp, dialysed whole cell, cocktails of blockers, non-physiological ion concentrations, artificial ion buffers, non-physiological levels of protein phosphorylation, etc.) which differ from those in intact functioning cardiac cells. Additional complexity arises from the fact that different cardiac cells (e.g. ventricular, atrial, purkinje) exhibit distinct structural organization, which is also age and species dependent (Bootman et al. 2006; Soeller et al. 2007, 2009; Li & Rudy, 2011).

In ventricular myocytes, RyRs, NCXs and LCCs are distributed non-uniformly (Fig. 1A) in the SR membrane (RyRs) and sarcolemma (NCXs and LCCs) (Pasek et al. 2008; Jayasinghe et al. 2009; Smyrniasa et al. 2010). Not all LCCs and only a fraction of NCXs sense the same Ca²⁺ as RyRs (Adachi-Akahane et al. 1996), underscoring the importance of considering subcellular compartments for Ca²⁺ dynamics in mathematical models of the cell. Experimental data and model simulations suggest that Ca²⁺ flux per unit time through LCCs and RyRs is several orders of magnitude greater than the diffusion flux towards the core of the cell, resulting in local subcellular Ca²⁺ gradients (Allbritton et al. 1992). In addition, local Ca²⁺ buffers contribute to a relatively slow (tens of milliseconds) dissipation of these Ca²⁺ gradients (Naraghi & Neher, 1997; Higgins et al. 2007).

Figure 1. Compartmental model of Ca²⁺ cycling, based on structural organization of a ventricular myocyte.

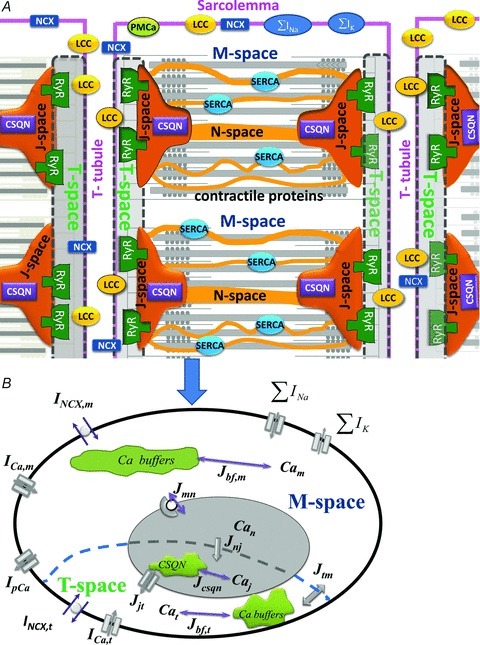
A, schematic diagram of the structural organization of a ventricular myocyte. Sarcolemmal Ca²⁺-ATPase (PMCa), L-type Ca²⁺ channels (LCC), 3Na⁺/Ca²⁺ exchanger (NCX) and Ca²⁺ binding proteins (buffers) are expressed throughout the sarcolemma. T-Tubules run radially and flank each sarcomere. Ca²⁺ release channels (RyRs) are expressed in the junctional portion of the SR membrane which faces the T-tubular portion of the sarcolemma and bounds the calsequestrin (CSQN) containing J-spaces. The junctional portion of the SR membrane and corresponding T-tubular portion of the sarcolemma form the T-spaces (grey spaces enclosed by dashed boundaries). During uniform activation of all RyR, identical Ca²⁺ distribution can be assumed in all J-spaces and in all T-spaces. Given the structural periodicity of the myocyte, a cell average Ca²⁺ concentration in J-space (Ca_j) and T-space (Ca_t) can be defined. SR Ca²⁺-ATPase (SERCA) is expressed in the network portion of the SR membrane which encloses the N-space. M-space is separated by the network portion of the SR membrane from the N-space and contains Ca²⁺ sensitive contractile (troponin) and regulatory (calmodulin) proteins. ∑I_K and ∑I_Na are sum of trans-sarcolemmal K⁺ and Na⁺ fluxes, respectively. B, compartmental model of Ca²⁺ cycling based on the structural organization in panel A, when synchronized activation of RyR generates a uniform Ca²⁺ flux (J_jt) from J-space to T-space. The transsarcolemmal Ca²⁺ fluxes, which include currents via LCC (I_Ca) and NCX (I_NCX), are partitioned between T-space and M-space. The effects of the contractile and regulatory proteins on Ca²⁺ dynamics is accounted for by buffering fluxes in the M-space (J_bf,m), T-space (J_bf,t), and J-space (J_csqn). Ca²⁺ flux between M-space and N-space (J_mn) is carried by SERCA. Transfer of Ca²⁺ between T-space and M-space (J_tm) is proportional to the difference between Ca_t and Ca_m. Similarly, J_nj is proportional to the difference between Ca_n and Ca_j. Additional symbols are defined in the text. Computer code is available on the website http://rudylab.wustl.edu/research/cell/lrd2.htm.

Unfortunately, using numerical models of the reaction-diffusion system in the realistic, detailed geometry of the cell requires precise knowledge of the intracellular structure and of Ca²⁺ diffusion properties in this structure. It involves many parameters that cannot be constrained precisely and is computationally very demanding (e.g. Chen-Izu et al. 2006; Soeller et al. 2009).

The representation of spatial organization in a compartmental model is a simplification that makes computation possible (Atkins, 1969). It has been used extensively in modelling calcium cycling in cardiac myocytes (Standen & Stanfield, 1982; Adler et al. 1985; Luo & Rudy, 1994). Here, we use this approach to better define functional cellular compartments for Ca²⁺ interactions and to provide a theoretical basis for estimation of dynamic Ca²⁺ concentrations in these compartments. We hypothesize that under normal physiological conditions (i.e. uniform whole cell J_rel), the interaction between J_rel, I_Ca and I_NCX can be formulated, to a very good approximation, as occurring in four functional compartments of Ca²⁺ distribution, two in the myoplasm and two in the SR. One myoplasmic compartment (denoted T-space) is associated structurally with the RyRs and enclosed by the tubular portion of the sarcolemma and the junctional portion of the SR membrane (enclosed by the dashed curve in Fig. 1A). The other myoplasmic compartment (M-space) encompasses the rest of the myoplasm, enclosed by the non-tubular sarcolemma and non-junctional SR membrane. LCCs and NCXs are present in the sarcolemma of both T-space and M-space, but with different density in each compartment. We denote free Ca²⁺ concentrations in T and M spaces Ca_t and Ca_m, respectively. Similarly, the SR is also divided into two compartments of Ca²⁺ distribution. One compartment (denoted J-space) is associated structurally with the RyRs and the junctional portion of the SR membrane. The other compartment (N-space) encompasses the rest of SR (network SR) as we have done previously (Luo & Rudy, 1994). We employ mathematical modelling together with experimental measurements to explore the interactions of J_rel, I_Ca and I_NCX in the T-space and to provide a theoretical basis for estimating the Ca_t dynamic properties in this functional space, where J_rel, I_Ca and I_NCX interact.

The choice of compartments was dictated by the assumptions of a uniform Ca²⁺ distribution in each compartment and a spatially uniform Ca²⁺ flux between communicating compartments. It was guided by structural and functional considerations and differs from ‘subspace’ and ‘bulk myoplasm’ used in many previous compartmental models. In these models, ‘subspace’ has been used to define a continuous subsarcolemmal space in the entire cell. In certain models, it was subdivided to contain a ‘dyadic’ space (Shannon et al. 2004; Higgins et al. 2007; Mahajan et al. 2008); the dyadic space communicated with the subsarcolemmal subspace, which in turn communicated with the bulk myoplasm. This implies that dyads are distributed uniformly beneath the sarcolemma, and all NCXs are affected identically by J_rel via a Ca²⁺ diffusion flux from the dyadic space. Based on structural and functional properties, including the non-uniform distribution and partition of LCCs and NCXs between T-tubular and non-T-tubular portions of the sarcolemma, and of RyRs in the SR membrane, Ca²⁺ distribution cannot be assumed uniform in a subsarcolemmal ‘subspace’ compartment. Rather, RyRs interact with LCCs and NCXs in a functional compartment near the RyR, which we label T-space. Figure 1 depicts two populations of LCCs and NCXs, one interacting with RyRs in the T-space (via a common pool of Ca²⁺, Ca_t), and the other communicating directly with the M-space. Based on experimental data, we estimate the fraction of NCXs that are coupled functionally to RyRs via Ca_t.

Methods

Symbols and definitions are given in Table 1.

Table 1.

Symbols and definitions

V	Transmembrane potential	mV
Cat	Free Ca2+ concentration in T-space	mm
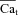	Inverse estimated Ca t
Cam	Free Ca2+ concentration in M-space
Caj	Free Ca2+ concentration in junctional SR (J-space)	mm
Can	Free Ca2+ concentration in network SR (N-space)	mm
Cacmdn	Ca2+ bound to calmodulin in M-space	mm
Cacsqn	Ca2+ bound to calsequestrine in J-space	mm
Catrpn	Ca2+ bound to troponin in M-space	mm
Cab,f	Ca2+ bound to fast buffer in T-space	mm
Cab,s	Ca2+ bound to slow buffer in T-space	mm
JCa,m	Trans-sarcolemmal Ca2+ flux in M-space	mm ms−1
JCa,t	Trans-sarcolemmal Ca2+ flux in T-space	mm ms−1
Jnj	Ca2+ between N-space to J-space	mm ms−1 s
τtr	Time constant of Jnj	ms
Jtm	Ca2+ flux between T-space and M-space	mm ms−1 s
τdiff	Time constant of Jtm	ms
Jmn	Ca2+ flux between M-space and N-space	mm ms−1
AP	Action potential
ICa	L-type Ca2+ current	μA μF−1
fCa	Ca2+-dependent inactivation gate of ICa
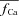	Inverse estimated fCa
β	Fraction of NCX in T-space
INCX	Na+-Ca2+ exchanger current	μA μF−1
NCXmax	Maximal turnover rate of INCX	μA μF−1
Kncx	INCX affinity to Ca2+	mm
	ICa in the absence of Jrel	μA μF−1
ΔICa=ICa–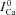	Difference current (presence-absence of Jrel)
tmax	Time of maximal ΔICa	ms
IpCa	Ca2+ current via PMCA	μA μF−1
ICab	Background Ca2+ current	μA μF−1
Jrel	Ca2+ flux via RyRs	mm ms−1
∑INa	Sum of transsarcolemmal Na+ fluxes	mm ms−1
∑IK	Sum of transsarcolemmal K+ fluxes	mm ms−1
JSERCA	Ca2+ flux via SERCA	mm ms−1
Jleak	Ca2+ leak flux from J-space	mm ms−1
Jb,x	Ca2+ flux from and to Ca2+ buffers ‘x’	mm ms−1
v,x	Volume of compartment ‘x’	μl
Cm,Ct	M-space and T-space capacitances of sarcolemma, μF
F	Faraday constant, 96,487 C mol−1
R	Gas constant, 8314 J mmol−1 K−1
T	Temperature, 310 K
Nao	External Na+ concentration
Cao	External Ca2+ concentration

Ethical approval

All experiments were conducted at the University of Leuven, Belgium, according to the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health (USA). Experimental protocols were approved by the ethical committee of the University of Leuven. The current study conforms to the ethical standards set by The Journal of Physiology (Drummond, 2009). Killing of the pigs was done under full anaesthesia (premedication with tiletamine and zolazepam, 4 mg kg⁻¹ i.m. and xylazine 0.25 mg kg⁻¹ i.m., maintenance anaesthesia with propofol i.v., 7 mg kg⁻¹ h⁻¹); pigs were intubated and ventilated with a 1:1 oxygen–air mixture. After an additional bolus of pentobarbital (100 mg kg⁻¹ i.m.), hearts were excised quickly and placed in oxygenated Tyrode solution.

Experimental considerations

The experiments were conducted in porcine ventricular myocytes and described in detail in Acsai et al. (2011). Briefly, experiments were designed to allow separate measurements of I_Ca and I_NCX as a function of J_rel, which was controlled by regulation of SR Ca²⁺ load using caffeine and voltage-clamp protocols. Whole-cell Ca²⁺ was measured optically. The size of the T-space compartment is orders of magnitude smaller than that of the M-space. Therefore, contribution from Ca_t to the optically measured Ca²⁺ signal can be regarded as negligible and the cell-average Ca²⁺ signal reflects Ca_m. The experimental protocols were conducted under voltage clamp conditions, with all ion concentrations, except Ca²⁺, maintained constant. In addition, we utilized a depolarizing step to +10 mV which ensures maximal spatially uniform activation of J_rel to reflect normal conditions in non-failing myocytes (see Fig. 2A in Acsai et al. 2011). In addition, large concentrations of caffeine were used (10 mm) to ensure spatial uniformity of caffeine-evoked J_rel. Also, the state of the cell (SR Ca²⁺ load, depolarizing V pulses) in both the I_Ca and I_NCX experiments was identical to yield identical estimations of Ca_t. Experimental recordings of I_Ca, Ca_m and I_NCX were used as an input to the model for estimating Ca_t; the mathematical formulation and simulation procedures are described below.

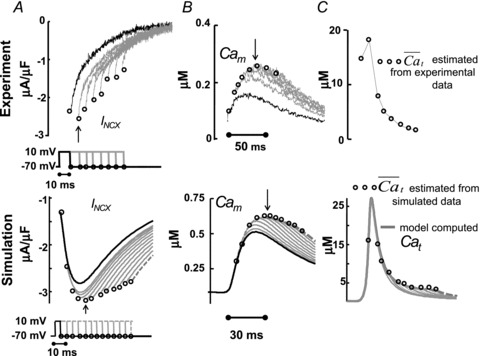
Figure 2. Ca_m and I_Ca inactivation increase with increasing SR load.

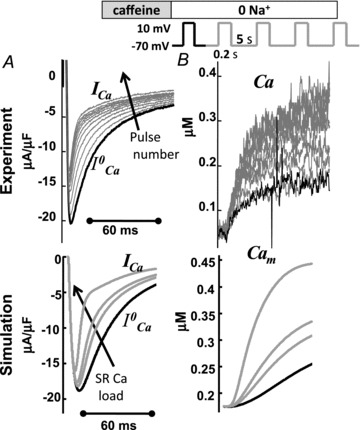
A, superimposed traces of I_Ca evoked by depolarizing pulses to 10 mV for 200 ms (inset on top show the experimental protocol). B, corresponding traces of the global Ca²⁺ transient (Ca_m). Experimental recordings are shown at the top, model simulations at the bottom. The first trace of I_Ca and of Ca_m after caffeine application (i.e. for depleted SR) is depicted in black. Arrows indicate increasing number of depolarizing pulses.

Myocyte isolation

In the current study we used ventricular myocytes isolated from the mid-myocardial layer of the posterior wall of healthy pigs. Animals (n= 12, weight 35–45 kg) were housed and treated according to the Guide for the Care and Use of Laboratory Animals (National Institutes of Health, USA) and experimental protocols were approved by the in-house ethical committee at the University of Leuven. Killing of the pigs was done under full anaesthesia, hearts were excised quickly and placed in oxygenated Tyrode solution. The circumflex coronary artery was cannulated and the myocardium was perfused with Ca²⁺-free Tyrode solution and subsequently enzyme solution. Isolated cells were stored at room temperature and used within 12 h. The isolation procedure was as described before (Heinzel et al. 2002).

Chemical solutions

Chemicals were purchased from Sigma, fluorescent probes from Invitrogen, Belgium. Tyrode solution for cell storage contained (in mm) NaCl 130, KCl 5.4, Hepes 11.8, MgCl₂ 0.5, CaCl₂ 1.8, and glucose 10, pH 7.40 with NaOH. For recording I_CaL and I_NCX, the extracellular solution contained (in mm): NaCl 130, CsCl 10, Hepes 11.8, MgCl₂ 0.5, CaCl₂ 1.8, glucose 10, pH 7.4 adjusted with NaOH. To block the fast Na⁺ current, 200 μm lidocaine was included in the external solution. In order to increase the amplitude of the I_CaL and facilitate study of Ca²⁺-dependent inactivation and recovery by increasing SR Ca²⁺ content, 5 μm forskolin was added to the external solution. The pipette solution contained (in mm): caesium aspartate 120, TEACl 10, NaCl 5, Hepes 10, MgCl₂ 0.5, MgATP 5, pH 7.2 adjusted with CsOH with 50 μm K5Fluo-3 was added as a fluorescent Ca²⁺ indicator for measurement of the global cytosolic Ca²⁺ concentration. In the experiments carried out in Na⁺ free conditions, the external solution contained N-methyl-d-glucamine 120, TEACl 20, Hepes 11, MgCl2 0.5, CaCl2 1.8, glucose 10, pH 7.4 with HCl.

Cardiac myocytes were placed in a perfusion chamber on an inverted microscope (Nikon Diaphot). The set-up for epifluorescence recording, calibration of the Ca²⁺-dependent fluorescence and measurement of membrane currents were as described previously (Acsai et al. 2011). Fluorescence signals were recorded from the entire cell and calibrated to [Ca²⁺] after obtaining F_max at the end of the experiments. All experiments were performed at 36°C.

Model geometry and calcium compartments

Typical spatial organization of a non-failing ventricular myocyte is shown in Fig. 1A. The cell membrane (sarcolemma) invaginates to form transverse tubules (T-tubule) which run predominantly radially across the muscle fibre. These tubules are situated between the sarcomeres, which consist of a regular array of Ca²⁺ binding myofilaments, forming the basic unit of the contractile machinery (Adrian, 1983; Bootman et al. 2006). Given the structural periodicity of the myocyte, only two sarcomeres in the radial direction (out of many) are shown. Approximately half of the sarcolemmal surface area is associated with the T-tubular system, where LCCs and NCXs are expressed at higher density. Ca²⁺-binding calsequestrin (CSQN) and RyRs are expressed in the J-space membrane and lumen, respectively. SR Ca²⁺-ATPase (SERCA) is expressed in the N-space membrane, in close proximity to the contractile proteins in the myoplasm.

When all RyRs are activated in synchrony to generate J_rel flux from J-spaces to T-spaces, uniform Ca²⁺ distributions can be assumed in these compartments and represented in the model by average Ca_j and Ca_t (Fig. 1A and B).

Compartmental model based on structural organization of a ventricular myocyte

A schematic diagram of the model is shown in Fig. 1B. The Luo–Rudy dynamic (LRd) model (Luo & Rudy, 1994) was used as the template for modelling Ca²⁺ cycling; it was modified to fit porcine data, as experiments were conducted in porcine myocytes. The LRd model includes three intracellular Ca²⁺ compartments (myoplasm, network SR and junctional SR). Each compartment is characterized functionally by the bound and free Ca²⁺ concentrations, and Ca²⁺ fluxes in and out of the compartment (Hund & Rudy, 2004; Faber et al. 2007). Bound Ca²⁺ in each compartment is associated with endogenenous Ca²⁺ buffers. For the purpose of this study (and to better represent the structural organization of a ventricular myocyte), the original myoplasmic Ca²⁺ compartment of the LRd model was subdivided into two compartments: T-space and M-space (Fig. 1B). Following Winka et al. (1999), we assumed that SR calcium is divided between two functionally discrete pools, one is available for release during normal I_Ca-triggered J_rel (J-space), while the other is releasable by caffeine application but unavailable for release during normal triggered release (N-space).

Also, note that the T-space is not separated by a membrane from the M-space (nor is J-space from N-space); rather, they are separated functionally by Ca²⁺ diffusion barriers which result in faster and larger Ca²⁺ transients in the T-space (J-space) than in the M-space (N-space). Ca²⁺ diffusion barriers between T-space and M-space and between J-space and N-space (dashed curve, Fig. 1B) are accounted for by diffusion fluxes J_tm and J_nj, respectively.

The mathematical model

Free Ca²⁺ concentration (mm) in T-space, M-space, N-space and J-space are denoted Ca_t, Ca_m, Ca_n and Ca_j, respectively. Ca²⁺ efflux from compartment ‘x’ to compartment ‘y’ (J_xy) has units of millimolar of x volume (v_x) per ms. Consequently, to ensure Ca²⁺ conservation, Ca²⁺ influx into compartment y is normalized by the volume fractions v_xy=v_x/v_y. The balance of fluxes for each compartment in terms of free Ca²⁺ concentrations is as follows:

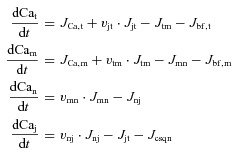(1)

where subscripts t, m, n, and j indicate the corresponding quantities for T-space, M-space, N-space and J-space, respectively. Trans-sarcolemmal Ca²⁺ fluxes into M-space and T-space are denoted J_Ca,m=ψ _m(I_Ca,m+I_Cab,m+I_pCa,m− 2I_NCX,m) and J_Ca,t=ψ _t(I_Ca,t+I_Cab,t+I_pCa,t− 2I_NCX,t), respectively. ψ _m=−C_m/(2v_mF) and ψ _t=−C_t/(2v_tF) are Ca²⁺ current to flux conversion factors for T-space and M-space, respectively. F= 96,485 is the Faraday constant. Membrane capacitance in M-space (C_m) and T-space (C_t) is the same. I_pCa is current via PMCA (plasma membrane ATPase) and I_Cab is background leak current (Livshitz & Rudy, 2009).

M-space and T-space, and N-space and J-space communicate via diffusion fluxes, J_tm= (Ca_t– Ca_m)/τ_diff (v_tm= v_t/v_m≍ 0.0152) and J_nj= (Ca_n−Ca_j)/τ_tr (v_nj=v_n/v_j≍ 11.5), respectively. Ca²⁺ flux between J-space and T-space (J_jt) has two components, J_rel and J_leak. Formulations of these fluxes are provided in the Appendix eqn (A2).

Ca²⁺ binding sites (buffers) are defined in terms of Ca²⁺ fluxes between a buffer and its corresponding compartment (J_bf,m, J_bf,t and J_csqn in Fig. 1B). In M-space, J_bf,m includes a fast component (calmodulin) and a slow component (troponin). Similarly, J_bf,m in T-space has fast (J_b,f) and slow (J_b,s) Ca²⁺ anionic binding sites. J_mn is carried by SERCA. Formulations of fluxes are provided in the Appendix eqns (A1)–(A3).

Parametrization of the model

Experimental data were used to fit the model parameters, including the activation and inactivation kinetics of I_Ca, partition of NCX between the T and M spaces, density of Ca²⁺ binding sites on the SR membrane and sarcolemma, calmodulin partition between the T and M compartments, and intra-compartmental Ca²⁺ diffusion rates. Whenever possible, we used different sets of experimental data for the forward model validation and for inverse model estimation. The parameter τ_tr (200–600 ms) was set to reproduce experimentally measured Ca_m restitution (Luo & Rudy, 1994). The time constant of Ca²⁺ flux between the T-space and M-space was fitted to reproduce the experimentally observed delay between peak Ca_m and the onset of I_Ca inactivation due to J_rel. The parameter τ_diff (0.1–0.2 ms) and T-space buffering parameters were set to reproduce the experimentally measured rate of rise of Ca_m (4–8 mm ms⁻¹, as in Sipido & Wier (1991)) and its time to peak. Several model parameters, such as compartment volumes and total concentrations of Ca²⁺ buffers, were constrained by conservation of total Ca²⁺ in the cell.

The state variables of the model are membrane voltage, free ion concentrations, and ion channels gating variables. Computation of ionic currents (e.g. I_Ca and I_NCX) from these state variables constitutes a forward problem. Estimation of Ca_t (the estimate is denoted 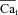) from Ca_m together with I_Ca or I_NCX constitutes an inverse problem (Keller, 1976). Note that Ca_m, I_Ca or I_NCX can be either measured experimentally or generated by the model in a forward simulation. In the approach presented here, the forward-calculated Ca_t (obtained by simulating specific experimental protocols in silico) is used as a standard for comparison and evaluation of 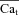. This allows us to critically validate and evaluate different experimental methods and protocols that have been used to estimate Ca_t.

It should be noted that the sensitivity of the inverse model to variations in parameter values is much greater than that of the forward model, especially at saturating levels of Ca²⁺.

Current through L-type Ca²⁺ channels, I_Ca

LCCs were partitioned between the T-space and M-space, with a large fraction (85–95%) in T-space; total I_Ca=I_Ca,m+ I_Ca,t. We assumed that the intrinsic LCC properties are independent of their location and dropped the subscripts m and t for notational convenience. The L-type channel current is as in Luo & Rudy (1994):

(2)

where P_Ca is the maximal conductance, d is a V-dependent activation gate, f is a V- and Ca²⁺-dependent inactivation gate, and f_Ca is a Ca²⁺-dependent inactivation gate. E_Ca denotes the driving force for Ca²⁺ flux through the LCC as a function of trans-sarcolemmal Ca²⁺ and V gradients, given by the Goldman–Hodgkin–Katz relation (GHK) (Hille, 2001),

(3)

where ϕ=F/R/T= 0.0374 (V⁻¹), R= 8314 (J mol⁻¹ K⁻¹) is the universal gas constant, T= 310 is the absolute temperature (K), and γ_Ca and γ_Cao are activity coefficients for free intracellular (Ca) and extracellular (Ca_o) concentrations, respectively. By definition γ_Cai > γ_Cao if Ca < Ca_o. γ_CaCa_i can be viewed as an effective concentration of Ca²⁺ (Hille, 2001). I_Ca inactivation is represented by the product of two time-dependent processes: (1) voltage-dependent inactivation modulated by free Ca²⁺ ions, f-gate, and (2) a Ca²⁺-dependent process, f_Ca-gate.

Steady-state voltage dependence of I_Ca activation (d-gate)

Formulation of the voltage-dependent activation d-gate was derived using peak values of I_Ca measured in porcine ventricular myocytes (Stengl et al. 2010). I_Ca elicited by test voltage pulses was normalized by the driving force E_Ca (eqn (3)) at each voltage step. A best-fit analytical expression for steady-state d_∞ was obtained using the Matlab (The Mathworks, Natick, MA, USA) subroutine ‘lsqcurvefit’ and is as follows:

(4)

Supplemental Fig. S1A shows simulated (continuous trace) and measured (circles) I–V curves. Supplemental Fig. S1B shows model simulated d_∞ (eqn (4), continuous black curve). Ca²⁺ was set to 0.1 μm in these simulations. The time constant of I_Ca activation, τ_d, is fast and was set to its average value of 1 ms (Luo & Rudy, 1994).

Steady-state dependence of f-gate on V and Ca²⁺

Following Morad & Soldatov (2005) we assumed that I_Ca inactivation is V-dependent and is not complete in the absence of Ca²⁺

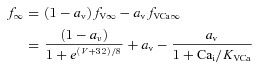(5)

0 < a_v < 1 is a factor that defines the contribution of Ca²⁺ (f_VCa∞) and voltage (f_V∞) to steady-state f_∞. Typically, a_v was set to 0.25. f_V∞ and f_VCa∞ are saturating functions of V and Ca²⁺, respectively. K_VCa= 3–5 μm is a half-saturation coefficient. Supplemental Fig. S1B shows measured (circles) and simulated (grey curve) f_V∞ (Stengl et al. 2010). Note that a_v was set to 0 in this simulation.

Time-constant of I_Ca inactivation (τ_f) with Ca²⁺-dependent acceleration

We assumed that I_Ca inactivation is V dependent and is accelerated in the presence of Ca²⁺:

(6)

τ_fVca is a Ca²⁺-dependent acceleration factor; its maximal value equals Ca_Vτ= 55 ms, and half-saturation constant K_Vτca= 1 μm. The best fit of τ_f (V-dependent term in eqn (6)) to experimental data is shown in Supplemental Fig. S1C. In the simulations, τ_f values beyond experimentally recorded voltages (i.e. more than 40 mV and less than −10 mV) were set to 143 ms and 95 ms, respectively. Ca_Vτ was set to zero in the simulation of Fig. S1C.

Ca²⁺-dependent inactivation gate f_Ca

Steady-state (f_Ca∞) and time constant (τ_fCa) of Ca²⁺-dependent inactivation were formulated as follows:

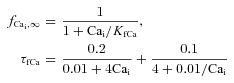(7)

where K_fCa= 4 μm is the half-saturation constant. Parameters in eqns (6) and (7) were fitted to reproduce the time course of I_Ca with and without J_rel. Supplemental Fig. S1D shows a measured trace of I_Ca just after caffeine application (i.e. depleted SR Ca²⁺) (dotted grey trace) and for a Ca²⁺ loaded SR (dotted black trace). Comparison of the I_Ca traces shows significant acceleration of inactivation and decrease of peak I_Ca due to J_rel. In addition, a long lasting effect of J_rel on the I_Ca time course is observed even after 60 ms. These features are well replicated by the I_Ca model (see continuous traces in Supplemental Fig. S1D).

Ca_t estimation using J_rel modulation of I_Ca

Estimation of free Ca²⁺ in the T-space requires formulation of its estimate, 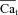, as a function of J_rel-dependent inactivation (RDI) of I_Ca. Assuming that J_rel is the major Ca²⁺ flux that contributes to Ca_t, the kinetics of I_Ca inactivation in the presence of different RDI levels could be used to estimate Ca_t. We assume that RDI is a saturating function of Ca²⁺, denoted 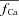, with a half-saturation constant K_Δfca. With this assumption, 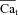is given by:

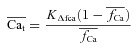(8)

RDI is a very fast process, with a time constant less than 4 ms (Antoons et al. 2007); thus, an instantaneous relation between and 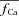was assumed. Note that the estimation of Ca_t using eqn (8) does not depend on the protocol used for estimating 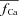. To estimate , we utilized the protocol of Acsai et al. 2011, shown in Fig. 2. Briefly, after depletion of SR Ca²⁺ with caffeine, the cell was repeatedly stimulated with a voltage pulse of duration 200 ms (i.e. typical AP duration, APD), from a holding potential V_h (−70 mV) to a depolarized potential V_d (10 mV). The magnitude and time course of the resulting I_Ca were influenced by VDI and CDI. However, the difference between the first I_Ca trace immediately after caffeine application (black trace, denoted 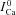) and the following traces of I_Ca (ΔI_Ca=I_Ca–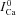) reflects I_Ca inactivation due to J_rel only. Note that due to the long (>4 s) interpulse interval, no accumulation of diastolic Ca²⁺ was detected, i.e. the initial phases of Ca_m (<10 ms) were almost identical for all pulses. This implies that most of the Ca²⁺ that entered through LCCs during the 200 ms depolarizing voltage pulses was sequestered by the SR and did not contribute directly to I_Ca inactivation. The decline of I_Ca was therefore attributed to an augmented J_rel due to increased SR Ca²⁺ load with each consecutive pulse. Thus, in forward model simulations (Fig. 2, bottom panels) we generated the data using different (graded) initial values of SR Ca²⁺ content (Ca_j= Ca_n) to modulate J_rel and, in turn, I_Ca. Note that zero SR Ca²⁺ content (Ca_n= Ca_j= 0) corresponds to experimental conditions after caffeine application. Other Ca_j values were varied from 0.62 to 1.3 mm. As was shown previously (e.g. Shannon et al. 2004) and modelled in this study (eqn (A2)), J_rel is a steep non-linear function of the SR Ca²⁺ content. Therefore, relatively small changes in Ca_j result in large changes of J_rel. The time course of Ca²⁺ in the J-space and N-space is shown in Supplemental Fig. S2.

In the protocol of Fig. 2, any effect due to a small fraction of Ca²⁺ carried via LCCs in the M-space was eliminated by the 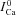subtraction procedure. Because J_rel is much larger (10 times; see Fig. 3B) than J_Ca,_t, ΔI_Ca is a good surrogate for the time-dependent Ca_t transient. To convert ΔI_Ca into the dimensionless units of 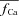, we normalized it by the value of 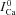when ΔI_Ca was maximal:

Figure 3. The relative contributions of different Ca²⁺ fluxes to Ca_t is SR-load dependent.

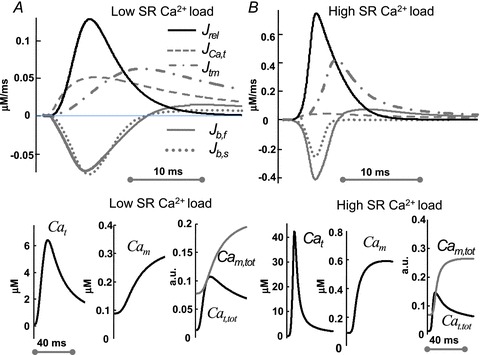
The time course of Ca²⁺ fluxes in the T-space (top) and Ca²⁺ redistribution between Ca_t and Ca_m (bottom) as a function of J_rel (SR Ca²⁺ load). Top: J_rel (black trace), trans-sarcolemmal Ca²⁺ influx, J_Ca,t (dashed grey trace), Ca²⁺ efflux from T-space to M-space, J_tm (grey dashed-dot trace) and fast (J_b,f, continuous grey trace) and slow (J_b,t, dotted grey trace) buffering fluxes. Bottom (left to-right): corresponding free Ca_t, free Ca_m and total (free and buffered) Ca²⁺ content in M-space (Ca_m,tot, grey) and T-space (Ca_t,tot, black) as fractions of the total cell Ca²⁺ content. A, at low SR Ca²⁺ load, Ca_j= Ca_n= 0.875 (small J_rel). B, at a large SR Ca²⁺ load, Ca_j= Ca_n= 1.167 mm (large J_rel). Note that panels A and B use different scales and J_rel is normalized by v_jt (eqn (1)).

(9)

where 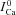(t_Δmax) is the value of 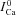at the time (t_Δmax) when the effect of J_rel on the I_Ca time course is maximal. This normalization procedure eliminates a possible effect of the time onset of J_rel on the relative contribution of Ca²⁺ and V to I_Ca inactivation. Previously, ΔI_Ca was normalized by peak ; we will discuss the benefits of the new normalization procedure in connection with Fig. 7. It is clear from eqn (8) that in order to accurately estimate 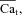K_Δfca must be known with sufficient accuracy. Values of f_Ca affinity to Ca²⁺ (which is largely dependent on calmodulin affinity to Ca²⁺) were reported in the range 2–10 μm (Saucerman & Bers, 2012); we set the value of K_Δfca=K_fCa= 4 μm.

Figure 7. Model-based validation of the ΔI_Ca method for estimating Ca_t.

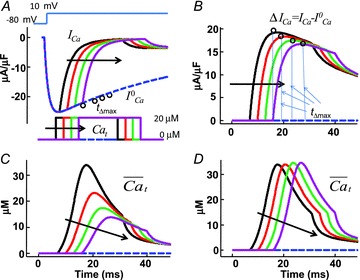
A, model simulated traces of I_Ca evoked by a depolarizing step to 10 mV (inset on top) in the presence of controlled (calcium clamp) Ca_t pulses of 20 μm amplitude and 25 ms duration, with progressively delayed onset by 5 ms (arrows; inset on bottom). 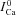, blue dashed trace, is subjected to V-dependent inactivation only (Ca_t set to zero). Circles indicate the values of 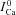at time t_Δmax. Note that all traces coincide prior to application of the Ca_t pulse. B, difference current, ΔI_Cav=I_Ca–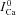. Circles indicate the maximal values of ΔI_Ca, occurring at time t_Δmax. C, 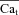estimated with ΔI_Ca normalized by peak 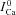(old method). D, 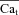estimated by normalizing each ΔI_Ca trace by the corresponding value of at time t_Δmax (eqn (8); new method).

Ca_t estimation using I_NCX and Ca_m: forward and inverse relations between I_NCX, Ca_m and Ca_t

Experimental data suggest that I_NCX is a saturating function of the intracellular Ca²⁺ concentration, at given values of V and other ion concentrations (Trafford et al. 1995; Ottolia et al. 2009); it is expressed as follows:

(10)

where the Ca²⁺-dissociation constant and maximal turnover rate are denoted K_ncx and NCX_max, respectively. K_ncx is estimated to be around 3.6 μm (e.g. Weber et al. 2001). This value indicates that NCX responds to Ca²⁺ in T-space dynamically, without saturation. For forward model simulations, NCX_max and K_ncx in eqn (10) were determined by best fit to data simulated using eqn (1) in Weber et al. 2001 (Supplemental Fig. S3A). NCX_max and K_ncx depend on V and intracellular sodium concentration (Na_i), respectively. Our simulation shows that K_ncx increases from 3 to 11 μm as Na_i increases from 4 to 16 mm (Supplemental Fig. S3B) and is not sensitive to V in the range from −90 to −50 mV. NCX_max magnitude decreases from 7.5 to 5 μA μF⁻¹ when V increases from −90 to −50 mV (Supplemental Fig. S3C) and is not sensitive to Na_i in the range from 4 to 16 mm.

Unlike the original formulation (Weber et al. 2001), eqn (10) can be readily inverted to calculate Ca²⁺ in terms of I_NCX, as required for inverse Ca²⁺ estimation. Assuming that total I_NCX is the sum of two populations (in T-space and M-space), eqn (10) is represented as follows:

(11)

where β is the fraction of I_NCX in the T-space (sensing Ca_t). Manipulating eqn (11) leads to the following expression for :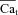

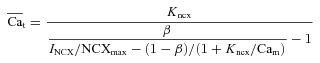(12)

The value of β can be estimated directly using immunohistochemical methods. Here, the parameter β was determined from the best fit of simulated Ca_m and I_NCX to those measured experimentally using the caffeine induced J_rel protocol. NCX_max was calibrated during the phase of Ca_m when both I_NCX populations sense the same Ca²⁺ (i.e. Ca_t= Ca_m) and eqn (11) reduces to eqn (10). Time to equilibrium of Ca_t with Ca_m was estimated using model simulations.

Ca_t estimation using I_NCX and Ca_m: Ca_t estimation using I_NCX and Ca_m during J_rel induced by a caffeine pulse

A commonly used intervention to study I_NCX activity is the caffeine pulse experiment, where rapid application of caffeine depletes the SR Ca²⁺ content and produces a Ca_m rise that activates I_NCX (e.g. Trafford et al. 1995). We simulated the application of caffeine by increasing the sensitivity of J_rel to Ca_t, reducing its refractoriness and decreasing its regulation by SR Ca²⁺ eqn (A2) in Appendix) (Kong et al. 2008). In addition, SERCA activity was inhibited (Blinks et al. 1972). The time course of caffeine-induced J_rel and consequently of Ca_m and I_NCX were different from those induced by voltage and I_Ca. During caffeine induced J_rel, both the J-space and N-space Ca²⁺ pools were depleted. Taking advantage of the fully controlled in silico conditions, we utilized a J_rel-clamp protocol to simulate caffeine application; the J_rel waveform was represented by a Gaussian function, J_rel=Aexp[–(t–μ)²/σ], where the parameters A, μ, and σ were fitted to match the I_NCX and Ca_m measured in the experiment, while keeping the total amount of Ca²⁺ released (∫J_reldt) constant and equal to the initial total SR Ca²⁺ content.

Ca_t estimation using I_NCX and Ca_m: Ca_t estimation using I_NCX tail current and Ca_m

We also simulated an I_NCX-tail current experiment, which activates J_rel by the CICR mechanism via I_Ca (Egan et al. 1989). Square depolarizing pulses were applied from holding (V_h) to depolarizing (V_d) potentials to ensure cell-wide J_rel. The I_NCX tail current, measured a few milliseconds after return to V_h, allows for separation of I_NCX from all other Na⁺- and Ca²⁺-dependent currents, which inactivate very rapidly at negative voltages (V_h) and do not contribute significantly to the total current. Optically assessed Ca_m was sampled simultaneously. This procedure was repeated with a progressively increased duration of depolarizing pulses (with increments of Δt ms), which were allowed to cover the entire duration of the Ca²⁺ transient elicited by J_rel. The values of the I_NCX and Ca_m were used as input to eqn (12). This method relies on the assumption that J_rel is independent of the depolarizing pulse duration.

Results

Relative contributions of Ca²⁺ fluxes to Ca_t are SR-load dependent

Model simulations were conducted to test the assumptions made with regard to contributions of different Ca²⁺ fluxes to the time course of Ca_t. The top panels in Fig. 3 show the time course of Ca²⁺ fluxes in T-space during depolarization to 10 mV for 200 ms, for a small (Fig. 3A) or large (Fig. 3B) J_rel (note that J_rel in Fig. 3 is normalized by v_jt; eqn (1)). Ca²⁺ contribution to Ca_t from trans-sarcolemmal Ca²⁺ flux into the T-space, J_Ca,t (dominated by I_Ca, dashed grey) is almost 50% that of J_rel (black trace) when J_rel is small (due to a small SR Ca²⁺ load, Ca_j= Ca_n= 0.875 mm). In contrast, the contribution from J_Ca,t is negligible when J_rel is large (large SR Ca²⁺ load, Ca_j= Ca_n= 1.167 mm). This verifies that J_rel is a good surrogate for Ca_t at larger SR Ca²⁺ loads. The time course of Ca²⁺ in the J-space and N-space is shown in Supplemental Fig. S2. Note that small changes in Ca_j result in large changes of J_rel. J_rel lags slightly behind J_Ca,t, reflecting the typical CICR sequence. Contributions of the fast (J_b,f dotted grey) and slow (J_b,s continuous grey) buffers are also J_rel dependent. The relative contribution of J_b,f increases with increased J_rel. Note that initially J_b,f and J_b,s act as Ca²⁺ sinks (negative fluxes), decreasing Ca_t; later, the buffering fluxes reverse direction, increasing Ca_t. The buffering fluxes reverse direction earlier (by 5 ms) when J_rel is large. The peak of the Ca²⁺ flux from T-space to M-space (J_tm, dashed-dot grey curve) coincides with the reversal of the buffering fluxes, demonstrating the importance of including Ca²⁺ buffering sites in the model.

Magnitude and time course of Ca_t and Ca_m are different and SR load dependent

The bottom panels in Fig. 3A show, for small J_rel (small SR Ca²⁺ load), Ca_t, Ca_m and the total Ca²⁺ content (free and bound) in M-space (Ca_m,tot= Ca_m+ Ca_trpn+ Ca_cmdn, grey) and T-space (Ca_t,tot= Ca_t+ Ca_b,f+ Ca_b,s, black), normalized by the total cell Ca²⁺ content. Figure 3B shows similar data, but for a large J_rel (large SR Ca²⁺ load). Importantly, the results show that even Ca²⁺ flux via I_Ca alone has sufficient capacity to increase Ca_t up to ∼5 μm and thus to induce inactivation of LCCs in T-space. LCCs in M-space are exposed to smaller Ca²⁺ values and the relative contribution of CDI to their inactivation is smaller.

The time course of Ca_m,tot and Ca_t,tot indicates that the total amount of Ca²⁺ in the T-space can reach similar values to those in the M-space for a brief period of time, during both small and large J_rel, in spite of a large (∼70 fold) difference in the compartments’ volumes. This indicates that buffering capacitance is more important in determining the balance of Ca²⁺ fluxes during dynamic Ca²⁺ transients than the compartmental volumes per se.

Partition of NCX between T-space and M-space

To investigate the effect of I_NCX localization on Ca_i and to estimate the fraction of NCX in T-space (β), we simulated a caffeine pulse protocol and compared the results to experimental data. The amplitude of the simulated caffeine-induced intracellular calcium transient agrees well with the measurements (compare Fig. 4A right and left panels).

Figure 4. An NCX partition of 25% in T-space and 75% in M-space provides the best fit to experimental data.

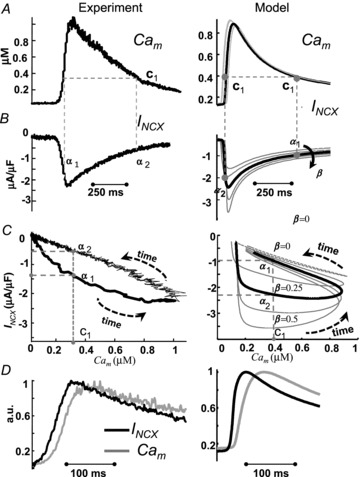
Peak Ca_m lags by 25 ms relative to peak I_NCX, reflecting the NCX partition. The fraction of NCX in T-space, β (right panels), estimated from best fit to experimental data (left panels). Experimentally recorded Ca_m (A, left) and I_NCX (B, left) evoked by caffeine pulse; V was held at −80 mV. Phase plots of I_NCX vs. Ca_i are constructed in C from the data in A and B. It is clear from panel C that I_NCX is a bi-valued function of Ca_m; that is, one value of Ca_m (e.g. c₁) is associated with two values on I_NCX (α₁ and α₂). In panel C, right, β (fraction of NCX in T-space) is varied from 0 to 0.5. The continuous black trace is for 25% of I_NCX (β= 0.25) in the T-space, which provides the best fit for the experimental data. Note that for β= 0 (grey dashed trace), I_NCX is a single-valued function of Ca_m. D, I_NCX (black) and Ca_m (grey), corresponding to the traces in panels A and B, are shown on an expanded time scale. Ca_m, normalized to its peak value, is superimposed on normalized and inverted I_NCX. Note that peak I_NCX precedes peak Ca_m by about 25 ms in both simulation and experiment.

The left panels in Fig. 4 show experimentally recorded Ca²⁺ transient (Ca_m) (Fig. 4A) and I_NCX (Fig. 4B) after caffeine induced J_rel. A phase plot of I_NCX vs. Ca_m is provided in Fig. 4C (same data as in Fig. 4A and Fig. 4B). I_NCX is a bi-valued function of Ca_m; that is, one value of Ca_m (e.g. c₁) is associated with two values of I_NCX (a₁ and a₂). Figure 4D shows that I_NCX precedes global Ca_m by 25 ms. The right panels in Fig. 4 show the corresponding simulated Ca_m (Fig. 4A) and I_NCX (Fig. 4B) as a function of I_NCX fractional population in T-space, β (arrow in Fig. 4B indicates increasing β). The corresponding simulated phase plots of I_NCX vs. Ca_m are shown in Fig. 4C (right). As in the experiment, I_NCX is a bi-valued function of Ca_m; for example Ca_m= 0.4 μm (c₁) is associated with two values of I_NCX (α₁=−1 μA μF⁻¹ and α₂=−2.3 μA μF⁻¹). Note that for β= 0 (all I_NCX in M-space), I_NCX is a single-valued function of Ca_m (dashed grey trace). Thus, the hysteresis and delay between the peaks of Ca_m and I_NCX are due to the existence of a population of I_NCX that senses Ca_t, which rises faster and reaches higher values than the cell-average Ca²⁺. The area of the hysteresis loop was chosen as a criterion for determining the best fit to experimental data; it reflects the difference between the ascending (due to increase of Ca_m) and descending (due to decrease of Ca_m) limbs of the I_NCX curves and the relative contribution of Ca_t to whole-cell I_NCX. The continuous black curve is for β = 0.25; it provides the best fit for the experimental data and a similar delay (Fig. 4D) to that measured experimentally. Based on this fit, all estimations of Ca_t were conducted for 25%I_NCX in T-space (75% in M-space; β= 0.25).

Estimation of Ca_t using I_NCX and Ca_m due to caffeine induced J_rel

Figure 5 shows estimation of Ca_t (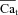) during a caffeine pulse experiment similar to that in Fig. 4, but from a different cell. V was held constant throughout at −70 mV. The top panels in Fig. 5 show experimentally recorded Ca_m (Fig. 5A) and I_NCX (Fig. 5B) after caffeine induced J_rel. A phase plot of I_NCX vs. Ca_m is provided in Fig. 5C (same data as in Fig. 5A and Fig. 5B). Figure 5D shows measured Ca_m (grey trace) and inverse-estimated 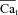(black trace) using Ca_m and I_NCX as input to eqn (12). Na⁺-sensitive K_ncx was set to 3.6 mm and NCX_max was estimated to be 11 μA μF⁻¹. These results predict a peak Ca_t in the range of 10 μm, with time to equilibrium with global Ca_m of 250–350 ms. The Ca_t peak value is an order of magnitude larger than global Ca_m (1 μm).

Figure 5. The time course of Ca_t can be estimated from caffeine-induced I_NCX and Ca_m; it shows different dynamics from Ca_t generated by CICR.

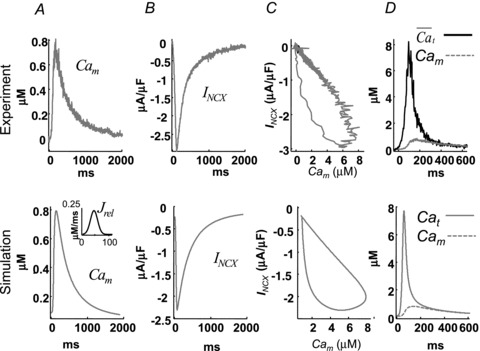
Experimentally recorded Ca_m (A, top) and I_NCX (B, top) evoked by a caffeine pulse; V was held at −70 mV. Phase plots of I_NCX vs. Ca_m are constructed in C from the data in A and B. D, estimated Ca_t, 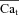, using eqn (12) with I_NCX from A and Ca_m from B as input. For the model-generated data (bottom panels), the J_rel waveform shown in the inset to panel A, bottom, was used as input. Model generated (D, bottom) Ca_t (black) and Ca_m (grey) are shown for comparison with those estimated from experimental data (D, top).

The bottom panels of Fig. 5 show model-generated data. As explained in Methods, a J_rel-clamp protocol was used (waveform in inset to panel A). The duration of J_rel was set so that the time course of Ca_t estimated using experimental data matched that of Ca_t generated by the model. The best fit was achieved with J_rel= 400exp[–(t– 45)²/200]. Model generated Ca_t (black) and Ca_m (dashed grey) are shown in Fig. 5D, bottom; both are very similar to experimental Ca_m and 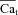(Fig. 5D, top). The model predicts that the time course of Ca_m and I_NCX during caffeine-pulse experiment is V dependent (Supplemental Fig. S4). Peak Ca_m (Supplemental Fig. S4A) increases and peak I_NCX decreases (Supplemental Fig. S4A) with depolarizing voltage. Time to equilibrium between Ca_t and Ca_m shows a moderate V-dependence (Supplemental Fig. S4D); it is shorter for negative V. This is important, because to calibrate NCX_max, Ca_m and Ca_t should reach equilibrium.

Ca_t estimation using I_NCX tail current and Ca_m due to CICR

Figure 6 shows experimental (top) and simulated (bottom) results of the I_NCX tail current protocol. During the simulations, similar to experimental protocols, V pulses were applied from a holding (−70 mV) to a depolarizing (10 mV) potential. The depolarizing step was interrupted at different time intervals (increments of 10 ms in the experiment), stepping back to −70 mV (see inset in Fig. 6A). In the simulations (bottom panels of Fig. 6), the time increments were decreased to 5 ms in order to increase sampling and thus the quality of the estimation; traces for the first and last V pulses are shown as continuous and dashed black lines, respectively. In Fig. 6A changes of I_NCX tail current amplitude with pulse duration (circles) reflect changes of Ca_t sensed by I_NCX. Corresponding values of Ca_m were sampled at the same time and are indicated by circles in Fig. 6B; note that the locus of sampled Ca_m values coincides with the Ca_m transient during the last (dashed black) pulse. This indicates that the same J_rel (and consequently Ca_t) is evoked by each pulse, ensuring that the estimation of is unique. Figure 6C shows estimated from experimental (top) and model generated (bottom) I_NCX and Ca_m data. In the bottom panel, the actual model-computed Ca_t traces (grey) are also shown as a gold standard for comparison. Importantly, the I_NCX-based method is able to recover both the ascending and descending limbs of Ca_t. However, it is difficult to estimate the value of peak Ca_t using this method with sufficient accuracy due to the limited number of sampling points, which limits its temporal resolution.

Figure 6. The time course of Ca_t, estimated from the I_NCX tail current.

Estimation of free Ca²⁺ in T-space,, using experimentally measured (top) and model generated (bottom) I_NCX and Ca_m, generated by V pulses as shown in the inset. A, I_NCX tail current traces. Raw current traces were truncated before the voltage was returned to the holding potential. Simulated traces, corresponding to the first and last V pulses, are shown in continuous and dashed black lines, respectively. B, corresponding optically measured (top) or model simulated (bottom) Ca_m. Circles in panels A and B indicate peaks of I_NCX tail currents and corresponding Ca_m values. Arrows in A and B indicate peak I_NCX and Ca_m, respectively. C, estimated Ca_t, 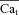, using eqn (12) with I_NCX from A and Ca_m from B as input. For the model-generated data (bottom panel), the actual model computed Ca_t is shown (grey traces) together with the estimated 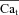(circles).

Note that the first three model simulated I_NCX tail current traces (bottom of Fig. 6A) are biphasic (increasing then decreasing in magnitude) and reach their peaks after the end of the V pulse. This non-monotonic behaviour is because Ca_t is still increasing during the first 30 ms of simulation (Fig. 6C). This early phase was not covered by the experimental protocol (top of Fig. 6A). Note that I_NCX reaches its maximum negative magnitude earlier than peak Ca_m, reflecting the existence of a T-space population of I_NCX which is activated by Ca_t. Ca_m reaches its peak value at 50 ms, 25 ms later than I_NCX (arrows in Fig. 6A and B), which corresponds well to the results of the caffeine pulse simulations in Fig. 4D.

Estimation of Ca_t using I_Ca inactivation as reporter (ΔI_Ca -based method)

Model-based validation of the ΔI_Ca method

To elucidate the effect of the normalization procedure in eqn (9) on 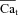, we simulated V and Ca_t clamp protocols in Fig. 7. The model cell was depolarized to 10 mV for 200 ms (Fig. 7A top, inset) and Ca_t was also clamped to 20 μm for 20 ms, with a progressive 5 ms shift of Ca_t pulse onset (Fig. 7A bottom, inset) as indicated by arrow. Figure 7A shows five I_Ca traces elicited by the V step, with four Ca_t pulses following the I_Ca descending limb. The first I_Ca trace (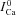, blue dashed curve) was simulated without applying a Ca_t pulse, and thus shows inactivation by only a V-dependent mechanism. Figure 7B shows the difference current ΔI_Ca=I_Ca–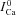; note that peak ΔI_Ca is progressively decreased as Ca_t pulses are progressively delayed relative to the V pulse (circles in Fig. 7B). This indicates that the contribution of Ca_t to I_Ca inactivation decreases with the delay, despite the identical waveforms of Ca_t pulses. Consequently, calibration of ΔI_Ca by peak 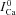results in the 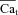shown in Fig. 7C, which is progressively underestimated as the onset of the Ca_t pulse is increasingly delayed relative to the onset of the V step. This is because I_Ca is subjected to V-dependent inactivation immediately after onset of the depolarizing pulse; the longer delay between the V and Ca_t pulses results in greater I_Ca inactivation by VDI (not CDI, which is the basis of the ΔI_Ca method), smaller ΔI_Ca, and consequently a smaller estimate of 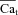. To correct for this artifact of pulse delay, we calibrated each ΔI_Ca trace by 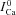values at the time when ΔI_Ca was maximal (i.e. contribution of Ca_t to I_Ca inactivation was maximal). The resulting 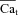traces are shown in Fig. 7D; note that with this calibration, the peaks of 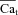are identical (time-invariant), independent of the Ca_t pulse time delay.

Estimation of Ca_t from experimental data and comparison to model simulation

Figure 8 shows estimation of 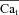by the ΔI_Ca-based method, using experimental (top panels) and model simulated (bottom panels) data. The experimental data set was from a different cell from the one in Fig. 2; however the V-clamp protocol was identical (inset in Fig. 2). Both experimental and simulated I_Ca show similar dependence on J_rel. That is, both peak amplitude and residual current decrease as J_rel increases. In Fig. 8A the current trace evoked by the first pulse after SR depletion by caffeine is denoted by 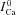(black trace). J_rel significantly inactivates and decreases I_Ca immediately (∼2 ms) after J_rel initiation, while maximal inactivation of I_Ca is reached after 5–10 ms. The model data were generated using graded initial values of Ca_j= Ca_n from 0 to 1.5 mm.

Figure 8. Estimation of Ca_t from J_rel-dependent inactivation of I_Ca using the ΔI_Ca method.

Estimation of free Ca²⁺ in T-space (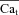) using experimentally measured (top) and model simulated (bottom) I_Ca. A, superimposed traces of I_Ca evoked by depolarizing pulses to 10 mV (V-clamp protocol is identical to that in the inset of Fig. 2); levels of SR Ca²⁺ load increase with the number pulses (arrows). 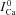is the current trace evoked by the first pulse after SR depletion by caffeine (black trace). B, difference current, ΔI_Ca=I_Ca–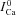; the ΔI_Ca trace which corresponds to 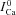(depleted SR; J_rel= 0) (continuous black) is equal to zero. Circles indicate the maximal values of ΔI_Ca, occurring at time t_Δmax. C, estimate of RDI, 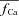. Each ΔI_Ca trace was normalized by the 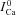value at the time of maximal ΔI_Ca (t_Δmax, indicated by circles in panel A). In the bottom panel, model computed CDI curves, f_Ca (grey traces), are also shown for comparison. and f_Ca traces which correspond to 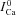are indicated by a star and a square, respectively. The f_Ca trace indicated by a square shows contribution to CDI from Ca²⁺ fluxes other than J_rel. D, 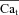estimated via eqn (8) using 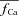as input. In the bottom panel, model computed Ca_t (grey traces) are also shown for comparison. 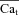and Ca_t traces which correspond to are indicated by a star and a square, respectively. The trace indicated by a square shows contribution to Ca_t from Ca²⁺ fluxes other than J_rel (via LCC and NCX). Arrows indicate increasing number of depolarizing pulses (SR load).

Figure 8B shows the difference current ΔI_Ca=I_Ca–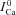. The traces exhibit a biphasic behaviour, with a fast initial increase reaching a maximum at around 10 ms, followed by a slow decrease which lasts for more than 60 ms. Model-based analysis of these data clarifies that the first phase of ΔI_Ca is dominated by an increase of Ca_t due to J_rel, while the second phase is dominated by Ca²⁺ diffusion from T-space to M-space, J_tm.

Figure 8C shows estimated 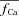using experimental (top) and simulated (bottom, dashed black) data as input to eqn (9). Circles in Figure 8A and B indicate 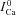at t_Δmax and maximal ΔI_Ca, respectively. Model computed f_Ca traces (continuous grey) are shown in (8) (top panel is from experimental data; bottom panel from model generated data). In addition, Fig. 8C as a gold standard for comparison. The trace of f_Ca which corresponds to CDI in the absence of RDI (J_rel= 0) is denoted by a square symbol. Note that the 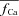trace which corresponds to 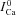(indicated by a star) is equal to unity, i.e. it predicts correctly the absence of I_Ca inactivation due to RDI. In contrast, the model computed f_Ca trace, indicated by a square, is different from unity. Unlike 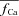, which is estimated via RDI (due to J_rel only), f_Ca accounts for CDI due to all Ca²⁺ fluxes into the T-space. Fluxes other than J_rel (via LCC and NCX) contribute to CDI (compare traces indicated by square and star symbols). Clearly, 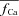underestimates CDI of I_Ca because it does not consider Ca²⁺ fluxes other than J_rel. However, as SR load increases (arrow), J_rel increases and the accuracy of 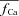estimation improves, especially during the descending limb of f_Ca. Figure 8D shows 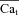(dashed black traces) estimated using 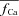as an input to eqn (8) (top panel is from experimental data; bottom panel from model generated data). In addition, Fig. 8D (bottom) shows the actual model computed Ca_t (grey traces) for comparison. Note that the 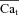trace which corresponds to 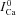(star) is equal to zero (depleted SR, J_rel= 0), while the corresponding Ca_t (square) is not (it reaches peak values of 2–3 μm) due to contribution from LCC and reverse-mode NCX. As SR load increases, J_rel increases and the accuracy of Ca_t estimation (assessed as the ratio of peak Ca_t to peak 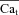) improves. This is due to an increased contribution of J_rel-dependent RDI to total CDI. Using normalized peak differences of the corresponding Ca_t and 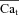in Fig. 8D (bottom), the estimation error decreases from 47% to 7% as SR load increases.

The ascending phase of Ca_t is estimated with a greater accuracy than the descending phase. This is because the method is based on the J_rel component of inactivation and peak J_rel coincides with the steepest ascending portion of Ca_t. In addition, a large J_rel accelerates inactivation, which makes the instantaneous approximation between Ca_t and inactivation more accurate. However, the I_Ca-based method tends to underestimate the descending portion of Ca_t when the relative contribution of J_rel to total inactivation is smaller.

Discussion

In this study, we verified that the minimal model for interactions between J_rel, I_Ca and I_NCX requires two myoplasmic functional compartments for Ca²⁺ distribution, T-space and M-space. This compartmental organization differs from the compartmentalization used in previous models (Hund & Rudy, 2004; Shannon et al. 2004; Faber et al. 2007; Mahajan et al. 2008) primarily due to a different partition of LCCs, NCXs and Ca²⁺ buffers. Inclusion of the T-space, which is structurally associated with RyRs, in the compartmental model of Ca²⁺ cycling allowed us to reproduce in silico the following important experimental results. (1) Hysteresis of I_NCX dependence on Ca_m during a caffeine application protocol (Fig. 4C). (2) A delay between peak I_NCX and peak Ca_m during a caffeine application protocol (Fig. 4D). (3) A delay between I_NCX and Ca_m during CICR (Fig. 6). (4) A rapid I_Ca inactivation (∼2 ms) due to J_rel, with a graded inactivation magnitude as a function of the SR Ca²⁺ content (Fig. 8). (5) A delay between I_Ca inactivation due to J_rel and due to Ca_m (Fig. 8).

A rapid I_Ca inactivation due to J_rel indicates a strong functional coupling between LCCs and RyRs in ventricular myocytes, which is not surprising because structurally most of the LCCs and RYRs are located in close proximity to each other. NCXs are usually considered to be expressed outside the Ca²⁺ microdomain of interaction between LCCs and RyRs. However, using the experimental results from the non-failing ventricular myocytes as an input to the compartmental model, we found that a small but significant (∼25%) fraction of NCXs is functionally coupled to RyRs via a common pool of Ca²⁺ (Ca_t).

The study provides a theoretical basis for estimating the dynamic properties of Ca_t using measured I_Ca, I_NCX and Ca_m as input to the compartmental model. The model was used to generate Ca_t transients, simulating specific experimental protocols, and the simulated Ca_t was used as a gold standard for evaluation of inverse-estimated Ca_t using I_Ca, Ca_m and I_NCX. The simulations confirmed estimations by previous investigators (Egan et al. 1989; Trafford et al. 1995; Weber et al. 2002; Acsai et al. 2011), demonstrating that peak Ca_t is an order of magnitude larger than the corresponding peak Ca_m and that Ca²⁺ gradients between T-space and M-space could persist into the late phase of the AP. Previous procedures to estimate Ca_t from Ca²⁺-dependent currents used a reductionist approach by employing each current in isolation. Here we used data from both I_Ca and I_NCX, where J_rel was induced by either CICR or by caffeine application. The results revealed that the I_Ca-based method is more accurate during the rising phase of Ca_t, while the I_NCX-based method is more accurate during its slow descending phase. Combined application of both methods provides a close estimate of both phases and a more accurate estimate of the entire Ca_t than the application of each method alone.

Characteristics of free Ca²⁺ in T-space (Ca_t)

The model predicts peak Ca_t in the range of 6–25 μm; these values are similar to computed Ca²⁺ transients averaged over many dyadic spaces (15 μm, Bondarenko et al. 2004; Greenstein et al. 2006), but significantly lower than the maximal values computed for a single dyad (>50 μm, Stern, 1992; Langer & Peskoff, 1998; Higgins et al. 2007; Gaur & Rudy, 2011). These results are consistent with our definition of T-space, which assumes a uniform whole-cell J_rel and an average Ca_t over many dyads. We also found that the time to equilibrium between Ca_t and Ca_m was strongly dependent on the experimental conditions, including the amount of Ca²⁺ released via RyRs (SR Ca²⁺ load) and the magnitude of the depolarizing V pulses (the driving force for I_NCX) (Supplemental Fig. S4). An increase of J_rel and/or of V increased the time to equilibrium, which was in the range of 50–350 ms, depending on J_rel and V. The lower bound of these values are consistent with those previously computed in models for CICR (Shannon et al. 2004; Greenstein et al. 2006; Faber et al. 2007). The caffeine pulse protocol shows significant prolongation of Ca_t duration (Fig. 5).

We found that the time course of Ca_t is strongly regulated by fast and slow Ca²⁺ buffers (Fig. 3). We also found that J_rel significantly inactivates and decreases I_Ca immediately (∼2 ms) after J_rel initiation, while maximal inactivation of I_Ca due to J_rel is reached after 5–10 ms.

The compartmental model of Ca²⁺ cycling

The success of inverse Ca_t estimation depends on the accuracy of the mathematical model used, and how well constrained is the model by experimental data. The model should describe quantitatively the relationship between the time course of Ca²⁺-dependent currents and the time course of Ca²⁺ which modulates them. Below we discuss modelling considerations for I_Ca and I_NCX.

Accuracy of the I_Ca model

In the I_Ca model development, we utilized experimental data from porcine ventricular myocytes. Using the Hodgkin–Huxley formalism, model activation and inactivation gates were fitted to reproduce the recorded I_Ca I–V curve (Supplemental Fig. S1). Note that the I–V curve is SR Ca²⁺ load dependent (Sham, 1997). I_Ca inactivation was assessed by the conventional two-step voltage-clamp protocol (Stengl et al. 2010) (Supplemental Fig. S1). Following (Kass & Sanguinetti, 1984; Lee et al. 1985; Hadley & Hume, 1987) we assumed that I_Ca inactivation is V dependent and is not complete in the absence of Ca²⁺. In the model, I_Ca inactivation was characterized by the product of two time-dependent processes: (1) voltage-dependent inactivation modulated by Ca²⁺, and (2) a pure free Ca²⁺-dependent process. Ca²⁺-dependent parameters were fitted to reproduce the magnitude and time course of I_Ca and its dependence on J_rel (variable SR Ca²⁺ load) (Fig. 2). To validate the model in the context of whole cell Ca²⁺ cycling, we verified that it reproduces experimentally recorded whole cell Ca²⁺ transients and I_Ca at different levels of SR Ca²⁺ load. Model simulated results match simultaneously the experimentally recorded I_Ca (Fig. 2A) and Ca_m (Fig. 2B) at different levels of J_rel (SR Ca²⁺ load).

Accuracy of the I_NCX model

Bidirectional flux of Ca²⁺ through NCX depends on V, intracellular concentration (Na_i) and extracellular concentration (Na_o) of Na⁺ and extracellular concentration of Ca²⁺ (Ca_o), which complicates the analysis. To keep I_NCX operating in the forward (Ca²⁺ extrusion) mode, experimental protocols were conducted at constant V close to the resting values (∼−80 mV) and at low Na_i (<5 mm). Since Na_o and Ca_o can be controlled in experiments, measured I_NCX can be regarded as a function of Ca_m and Ca_t only. An independent measurement of Ca_m (whole-cell optical signal) allows for a unique estimate of Ca_t. The formulation proposed by Weber et al. (2001) was used as a starting point for I_NCX modelling here. The slow allosteric dependence of I_NCX on intracellular Ca²⁺ was eliminated based on the recent study of Reeves & Condrescu (2003). We show that the resulting I_NCX model (eqn (10)) can be approximated by a Hill equation with a variable intracellular Ca²⁺ at fixed Na_o, Ca_o, Na_i and V, conditions that can be realized experimentally. This formulation (eqn (10)) was inverted to calculate Ca_t in terms of I_NCX, as required for inverse estimation (eqn (12)).

Spatial constraints

In ventricular myocytes, Ca²⁺ concentration gradients exist between SR dyads, a subsarcolemmal space (including caveolae) and the bulk myoplasm (Trafford et al. 1995; Weber et al. 2002; Higgins et al. 2007). The model used here does not consider the dynamics of Ca²⁺ in individual dyadic spaces (Shannon et al. 2004; Gaur & Rudy, 2011); instead all dyads are incorporated into the T-space and their Ca²⁺ concentration is assumed to be in rapid equilibrium. This implies that no Ca²⁺ gradients exist between dyads. Consistently, the experimental protocols evaluated here rely on the cell-average Ca²⁺ and are not designed to estimate Ca²⁺ in a single dyad. Therefore, we implemented protocols for which RyRs are activated uniformly throughout the cell, either by CICR (via LCC flux) or by caffeine-induced-Ca²⁺ release.

The physical characteristics of T-space

Unlike structurally defined, membrane delimited organelles such as the myoplasm, sarcoplasmic reticulum, nucleus, or mitochondrion, subsarcolemmal compartments have been considered as functional, with little correspondence to the actual structural organization of the cell (e.g. Standen & Stanfield, 1982; Shiferaw et al. 2003; Shannon et al. 2004). Here, T-space and M-space are functional compartments; however, their physical characteristics, i.e. size, localization of Ca²⁺ sensitive proteins (LCC, NCX, RyR), buffers, and Ca²⁺ fluxes into and out of the compartments were determined based on the structural organization of the porcine ventricular myocyte and using best fit to experimental data. T-space is enclosed by the T-tubules portion of the sarcolemma and the junctional portion of the SR membrane. M-space is enclosed by the non-tubular sarcolemma and the non-junctional SR membrane. LCCs and NCXs reside with different densities in the sarcolemma of T-space and M-space. Note (Fig. 1A) that a portion of the T-tubular membrane can be outside the T-space and LCCs and NCXs there sense M-space Ca²⁺.

The effects of the spatial localization of I_NCX on Ca_m were investigated with a simulated caffeine induced J_rel (Fig. 4). Experiments show that the time course of global Ca²⁺ lags (>30 ms) behind I_NCX. Interpretation of this result is not unique and is model dependent. For example, Weber et al. (2002) and Trafford et al. (1995) showed that the existence of a single diffusion barrier between the subsarcolemmal space (where all I_NCX were located in their models) and the bulk myoplasm is sufficient to account for this phenomenon; the time constant of Ca²⁺ diffusion flux between the subsarcolemmal space and global myoplasm was used as a fitted parameter in these studies. We used a different approach in this study; instead of fitting the time constant of J_tm, we used the fraction of I_NCX in the T-space, β, as a parameter. Best fit to the experimental data was obtained for 25% of I_NCX in the T-space, 75% of I_NCX in the M-space.

The quantity of sarcolemmal and SR membrane anionic Ca²⁺ binding sites (‘buffers’) in the T-space defines the functional ‘size’ of this compartment. Note that, the effective buffering capacity depends strongly on the kinetics of the buffers (dissociation constants) and not only on the number of available binding sites per se. This effective size depends on the membrane surface area that encloses this compartment (which is large) and not on the myoplasmic volume that it encloses (which is small). The effective size of the T-space compartment depends on the Ca²⁺ sensitivity (half-saturation constants) of J_rel, I_Ca and I_NCX; it is estimated to be in the range of 0.5–10 μm (units of concentration; Hofer et al. 1997; Bers, 2001; Ottolia et al. 2009). An increase of sensitivity (i.e. a decrease of half-saturation constants) will increase the effective size of the T-space. In fact the T-space merges with the M-space when the half-saturation constants drop below the average Ca_m. A similar merger occurs if J_tm is large and time to equilibrium between Ca_t and Ca_m is short.

The use of I_NCX and I_Ca as Ca²⁺ sensors requires that their sensitivity to Ca²⁺ (half-saturation constants, K_d) is in the range of expected values of the local Ca²⁺ concentration. If the local Ca²⁺ concentration is too low (≪K_d) its ability to affect these currents is blunted. Similarly, if it is too high (≫K_d) the dependence of these currents on Ca²⁺ reaches saturation and sensitivity is lost.

Number of compartments in the model

The representation of the structure in Fig. 1A by the compartmental model in Fig. 1B is not unique. Obviously, during the transition from a 3D structure to a compartmental model certain assumptions must be made. Several studies used three-compartment myoplasmic models (dyads, subsarcolemmal space and bulk myoplasm) or two-compartment models (subsarcolemmal space and bulk myoplasm). Inter-compartmental fluxes and partition of major Ca²⁺-sensitive proteins vary greatly between models. We assumed that regardless of the number of compartments in the model, the total amount of Ca²⁺ and total trans-sarcolemmal Ca²⁺ flux should be conserved. This conservation relation greatly decreases the parameter space of the model (Livshitz & Rudy, 2009). The strategy to include only two Ca²⁺ myoplasmic subcompartments was motivated by the need to ensure that the model is tractable and its parameters are experimentally verifiable. Importantly, it allowed us to formulate an analytic inverse relation between the Ca²⁺-dependent currents (I_Ca and I_NCX) and Ca_t.

Evaluation of methods for estimating Ca_t

We evaluated the validity of the experimental methods for Ca_t estimation by simulating the experimental protocols and comparing the inverse-estimated with the model-computed Ca_t. The results show that under ideal and fully controlled in silico conditions, all methods that use a V-clamp protocol to activate J_rel result in similar estimates of Ca_t, providing that the SR Ca²⁺ load and the depolarizing pulses are the same. Not surprisingly, the amplitude and duration of Ca_t induced by caffeine varies greatly from that induced by depolarization (compare Figs 4–5 and 7–8). Typically, Ca_t induced by caffeine has a significantly longer duration than its depolarization-induced counterpart.

Estimation of Ca_t using tail I_NCX current and Ca_m

We show (Fig. 6) that estimation of Ca_t using the I_NCX-based method provides a good estimate for the descending phase of Ca_t. This method is less sensitive to the SR Ca²⁺ load than the I_Ca-based method, as it does not require modulation of the SR Ca²⁺ load. The quality of the estimation increases when the number of sampling points increases (duration of testing pulses decreases), a condition that can be difficult to achieve in experiments. An advantage of the I_NCX-based method is that pharmacological interventions are not required. However, in this method a greater number of parameters must be fitted. Parameter sensitivity analysis indicates that the accuracy is strongly dependent on the specified fraction of I_NCX in the T-space. In addition, the model used for the estimation should be re-calibrated for each set of ion concentrations (Na_o, Ca_o, Na_i) and test potential V.

Estimation of Ca_t using I_Ca

To derive an analytical expression for Ca_t as a function of I_Ca, several assumptions were made. Since J_rel provides the dominant contribution to Ca_t in ventricular myocytes, its contribution to I_Ca inactivation (denoted RDI) was used as a surrogate for Ca_t (Sham, 1997). To isolate the J_rel-dependent component from I_Ca traces, the I_Ca trace in the absence of J_rel (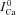) was subtracted from those in the presence of J_rel (Acsai et al. 2011). The ΔI_Ca-based method does not depend on the partition of LCCs between the T-space and M-space, because the effects of M-space LCCs is eliminated by the subtraction procedure. We formulated the Ca²⁺-dependent inactivation of I_Ca as a function of free Ca²⁺ concentration assuming that the contributions of Ca²⁺ fluxes to changes in the Ca²⁺ concentration are additive (eqn (1)). To convert the resulting difference current, ΔI_Ca (μA μF⁻¹), into the dimensionless units of Ca²⁺-dependent inactivation, f_Ca, we calibrated ΔI_Ca by the value of 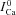at the time when ΔI_Ca reached its maximum (i.e. contribution of Ca_t to I_Ca inactivation was maximal, Fig. 7B). Taking advantage of the completely controlled in silico conditions, we simulated a double (V and Ca²⁺) clamp protocol (Fig. 7) to study the effect of the delay between depolarization (V step) and CICR (Ca²⁺ pulse) on the relative dynamics of VDI and CDI of I_Ca. We found that an increased delay between the onset of the V step and the Ca²⁺ step (which can happen under pathophysiological condition that impair J_rel; Bito et al. 2008) reduced the relative contribution of CDI to total I_Ca inactivation, even when the Ca²⁺ pulse shape and duration were held constant. Thus, calibrating ΔI_Ca by peak 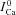(eqn (9)) and using the resulting 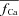as an input to eqn (8) underestimates . The proposed new calibration procedure does not suffer from this artifact (compare Fig. 7C and D).

The method presented here is based on steady state (time-independent) approximations of Ca²⁺-dependent inactivation of I_Ca and Ca²⁺-dependent activation of I_NCX. It was shown that inactivation of I_Ca induced by J_rel is a fast process (e.g. Antoons et al. 2007; Puglisi et al. 1999), especially at high SR Ca²⁺ loads (i.e. large J_rel and Ca_t) and therefore this assumption is well justified. The steady-state approximation allowed us to use an analytic expression for Ca_t as a function of f_Ca. During a voltage pulse, the inverse estimation of Ca_t using the ΔI_Ca-based method provided the best accuracy at high SR Ca²⁺ load, when I_Ca is sufficiently small relative to J_rel and does not contribute substantially to Ca_t, i.e. when the gain of CICR (i.e. J_rel/J_Ca,t ratio) is high, which is true under normal physiological conditions.

With the I_Ca-based method, the ascending phase of Ca_t is estimated with a greater accuracy than the descending phase (Fig. 8D) (the opposite is true for the I_NCX-based method). This is an expected result, because this method is based on the J_rel-component of inactivation and peak J_rel coincides with the steepest ascending portion of Ca_t. However, during the descending portion of Ca_t the contribution of J_rel to inactivation is decreased, resulting in a less accurate estimate. Therefore, combination of the I_Ca and I_NCX-based methods provides an estimate for the entire Ca_t time course.

New insights and potential future applications of the model

Beyond estimation of Ca_t, the compartmental model presented here provides a conceptual framework for studying the interactions between dynamic Ca²⁺, I_Ca and I_NCX in the functional microdomain where they interact physiologically (T-space). The functional compartmentalization is different from that in previous models; it does not employ a uniform subsarcolemmal ‘subspace’, but a functional volume near RyR (Acsai et al. 2011), where subpopulations of I_Ca and I_NCX (estimated here at 90%I_Ca and 25%I_NCX) interact with RyR through a common Ca²⁺ pool. The compartmentalization and partition are based on an interpretation of experimental data obtained under voltage clamp conditions and controlled SR Ca²⁺ load. For this compartmentalization, we estimated a peak Ca_t in the range of 6–25 μm, with time to equilibrium between Ca_t and Ca_m of about 350 ms. The Ca_t values are in the range of LCC and RyR sensitivity to Ca²⁺, which implies that there is a significant effect of Ca²⁺ in this domain on their kinetics and, in turn, on the action potential during physiological cell excitation. A natural continuation of the work presented here will be an implementation and application of the model to study cellular excitation and Ca²⁺ cycling under physiological conditions (i.e. an expansion from the controlled, clamped protocols implemented here) and during disease states associated with various pathologies.

Glossary

AP

action potential

CDI

Ca²⁺-dependent inactivation

DAD

delayed afterdepolarization

EAD

early afterdepolarization

LCC

L-type Ca²⁺ channel

NCX

3Na⁺/Ca²⁺ exchanger

PMCA

plasmalemmal Ca²⁺-ATPase pump

RDI

J_rel-dependent inactivation of I_Ca

RyR

ryanodine receptor

SERCA

SR Ca²⁺-ATPase pump

SR

sarcoplasmic reticulum

VDI

voltage-dependent inactivation of I_Ca

Appendix

Units and equations

Physical units are as in the original LRd paper (Luo & Rudy, 1994): time (t) in milliseconds (ms), membrane voltage (V) in millivolts (mV), current through channel X (I_X) in microamperes per cell capacitance (μA μF⁻¹), channel conductance (G_X) and maximal channel conductance (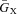) in millisiemens per microfarad (mS μF⁻¹), intracellular and extracellular ion concentrations (X_i, X_o) in millimoles per liter (mm). Inter-compartmental Ca²⁺ fluxes are defined in terms of millimoles per liter (of the compartment indicated by the first subscript) per milisecond (mm ms⁻¹). Gating variables are given by their steady state and time constant expressions x_∞ and τ_x (ms), or by forward α_x and backward β_x rate constants (ms⁻¹) as follows: d x/d t= (x_∞−x)/τ_x=α_x(1 −x) −β_x x. Model equations and computer code can be found in the research section of http://rudylab.wustl.edu. The notations ϕ=F/R/T= 0.0374 (V⁻¹) and ψ=Vϕ are used in equations, where R= 8314 (J mol⁻¹ K⁻¹) is the universal gas constant, F= 96,485 is the Faraday constant (C mol⁻¹) and T= 310 is the absolute temperature (K); z_Ca= 2 is the valence of Ca²⁺ ions.

Geometrical considerations

Following the LRd model structure (Luo & Rudy, 1994), the M-space volume was set to v_m= 25 × 10⁻⁶μl, leaving 30% of the total cell volume (v_cell= 38e–6 μl) inaccessible to ions due to the presence of mitochondria and other organelles. The SR volume (6% of v_cell) was subdivided into J-space (v_j= 0.138e–6 μl) and N-space (v_n= 2.1 × 10⁻⁶μl), v_t was set conservatively to 0.38 × 10⁻⁶μl, 1% of v_cell. To ensure Ca²⁺ conservation, any change in a compartment volume should be accompanied by a change in the total Ca²⁺ concentration. Thus, a decrease of v_t should be accompanied by a corresponding increase in concentration of Ca²⁺ binding sites (buffers) to preserve the total amount of cell Ca²⁺.

Due to cell size variability, experimental recordings of I_Ca and I_NCX (μA μF⁻¹) were normalized by the total cell capacitance C_cell (μF), which varied from 0.09 to 0.2 μF. To convert Ca²⁺ currents into units of Ca²⁺ fluxes, an average value of C_cell= 0.15 μF was assumed, which is very close to the value used in LRd (0.1534 μF). Note that the capacitive areas of the T-tubular and non-tubular portions of the sarcolemma are assumed equal C_m=C_t= 0.075 μF. Extracellular ion concentrations were set to the values in corresponding experiments.

Ca²⁺ buffering fluxes

The Ca²⁺ flux to and from a buffer protein X (J_b,x) is formulated as a first order kinetic equation:

(A1)

where Ca_x is bound Ca²⁺ to buffer x; Ca_y is free Ca²⁺ in compartment y. The buffering fluxes in M-space (J_bf,m) include binding–unbinding to troponin and calmodulin Ca²⁺ binding sites. The buffering flux in T-space involves fast and slow components (J_bf,t=J_b,f+J_b,s). These are composed of sarcolemmal anionic binding sites (Post & Langer, 1992), and Ca²⁺/calmodulin binding sites to LCC, RyR and CaMKII (Saucerman & Bers, 2012). Kinetics of the fast and slow buffers were adjusted to best fit I_Ca inactivation. Volumes of functional Ca²⁺ compartments, their buffering capacity, and Ca²⁺ fluxes between compartments are interdependent. Therefore, conservation of total cell Ca²⁺ was imposed as an additional constraint. Calsequestrin (J_csqn) is located in J-space. Forward () and backward rate constants and total concentration () of protein X binding sites are summarized in Table 2.

Table 2.

Ca²⁺ buffers (Bers, 2001)

Name of buffer	kd=k−/k+ (mm)	k− (1/ms)	k+ (1/mm ms−1)	Maximal concentration (mm)
M-space troponin	0.5e–3	0.02	40	50e–3
M-space calmodulin	2.4e–3	0.24	100	70e–3
T-space fast	0.5e–3	0.05	100	0.7
T-space slow	10e–3	0.1	100	1.32
J-space calsequestrin	0.8	80	100	10

Ca²⁺ flux from J-space to T-space (J_jt)

J_jt has two components, J_rel and J_leak. J_leak is an intrinsic RyR Ca²⁺ leak, which depends on the Ca²⁺ gradient: J_leak=k_leak(Ca_j–Ca_t). The J_rel model is based on a previously published model (Livshitz & Rudy, 2007). Following Faber & Rudy (2000), J_rel is activated by the flux of free Ca²⁺ into the T-space, regardless of its origin (I_Ca, I_NCX, J_tm). In addition, to simulate caffeine-induced J_rel, we included luminal (SR) activation of RyR in the model. The differential equation that describes J_rel is of the form:

(A2)

J_rel,∞=α_rel(A_rel+B_rel)D_rel represents the steady-state value of J_rel; τ_rel=β_τ/(1+K_rel,τ/Ca_j) is the time constant, K_rel,τ= 0.0123, β_τ= 4.75 is the maximal value of τ_rel, α_rel= 12 β_τ is the amplitude coefficient. J_rel,∞ is expressed as a product of the sum of cytosolic (A_rel) and luminal (B_rel) Ca²⁺-dependent activation with luminal deactivation (D_rel). A_rel= dCa_t/dt when dCa_t/dt is positive, and A_rel= 0 otherwise. Similarly, B_rel is not zero only above a certain level of Ca_j (threshold). This formulation involves logical expressions that introduce singularities which can cause problems for implementation in a problem solving environment such as MATLAB and for numerical analysis. To remove singularity, we follow the method in Livshitz & Rudy (2009) and introduce an auxiliary function λ(x) = 1/[1+exp(–xγ)], where γ is a small (e.g. 1 × 10⁻⁸) number. λ(x) is equal to unity for a positive argument and zero otherwise. Formulations of A_rel and B_rel in terms of λ(x) are A_rel= (dCa_t/dt)·λ(dCa_t/dt) and B_rel=λ (Threshold – Ca_j). Ca_j-dependent deactivation was modelled as a steep saturating function of Ca_j: D_rel= 1/[1+(K_rel,∞/Ca_j)^h], where K_rel,∞= 1 mm is the half-saturation coefficient and h= 9. Application of caffeine was simulated by a gradual decrease of K_rel,∞ to zero, and by simultaneous increase of α_rel and k_leak.

J_mn (bidirectional) flux between the M-space and the N-space

J_mn is described by a phenomenological equation, as proposed in Shannon et al. (2004)

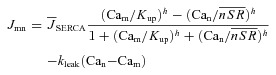(A3)

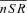(maximal affinity to SR Ca) = 15 mm, 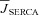= 0.875 × 10⁻³ mm ms⁻¹, K_up=0.8 × 10⁻³ mm, h= 1.7.

Author contributions

L.L. participated in data analysis, provided the theoretical basis for the computations, and contributed to manuscript writing. K.A. performed experiments and data analysis and participated in manuscript writing. K.A. developed the computational methods together with L.L. and Y.R. G.A. performed experiments and data analysis and participated in manuscript writing. K.S. contributed to the experimental study design and the final manuscript writing. Y.R. participated in data analysis, provided the theoretical basis for the computations, and participated in manuscript writing. All authors approved the final version of the manuscript. The experimental work was conducted at the laboratory in Leuven, Belgium, with additional analysis performed at the University of Szeged and at Washington University in St Louis.

Supplementary material

Supplemental Figure S1

Supplemental Figure S2

Supplemental Figure S3

Supplemental Figure S4