Analysis of factors affecting Ca²⁺-dependent inactivation dynamics of L-type Ca²⁺ current of cardiac myocytes in pulmonary vein of rabbit

Abstract

L-type Ca²⁺ channels (ICaLs) are inactivated by an increase in intracellular [Ca²⁺], known as Ca²⁺-dependent inactivation (CDI). CDI is also induced by Ca²⁺ released from the sarcoplasmic reticulum (SR), known as release-dependent inhibition (RDI). As both CDI and RDI occur in the junctional subsarcolemmal nanospace (JSS), we investigated which factors are involved within the JSS using isolated cardiac myocytes from the main pulmonary vein of the rabbit. Using the whole-cell patch clamp technique, RDI was readily observed with the application of a pre-pulse followed by a test pulse, during which the ICaLs exhibited a decrease in peak current amplitude and a slower inactivation. A fast acting Ca²⁺ chelator, 1,2-bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA), abolished this effect. As the time interval between the pre-pulse and test pulse increased, the ICaLs exhibited greater recovery and the RDI was relieved. Inhibition of the ryanodine receptor (RyR) or the SR Ca²⁺-ATPase (SERCA) greatly attenuated RDI and facilitated ICaL recovery. Removal of extracellular Na⁺, which inhibits the Na⁺–Ca²⁺ exchange (Incx), greatly enhanced RDI and slowed ICaL recovery, suggesting that Incx critically controls the [Ca²⁺] in the JSS. We incorporated the Ca²⁺-binding kinetics of the ICaL into a previously published computational model. By assuming two Ca²⁺-binding sites in the ICaL, of which one is of low-affinity with fast kinetics and the other is of high-affinity with slower kinetics, the new model was able to successfully reproduce RDI and its regulation by Incx. The model suggests that Incx accelerates Ca²⁺ removal from the JSS to downregulate CDI and attenuates SR Ca²⁺ refilling. The model may be useful to elucidate complex mechanisms involved in excitation–contraction coupling in myocytes.

Key points

• L-type Ca²⁺ channels are inactivated by an increase in intracellular [Ca²⁺], known as Ca²⁺-dependent inactivation (CDI), and are inhibited by Ca²⁺ released from the sarcoplasmic reticulum (SR), known as release-dependent inhibition (RDI).

• RDI was greatly enhanced by the removal of Na⁺–Ca²⁺ exchange (Incx), and attenuated by blocking Ca²⁺ release from the sarcoplasmic reticulum (SR), and abolished by Ca²⁺ chelator.

• We analysed the role of ICaL, SR and Incx and found Incx prevented CDI by controlling [Ca²⁺] in the junctional subsarcolemmal space ([Ca²⁺]_JSS).

• With previously developed model and the addition of Ca²⁺ binding kinetics of L-type Ca²⁺ channels (ICaLs), we successfully reproduced CDI and RDI.

• From this simulation, we found Incx actively participated in controlling CDI by the regulation of [Ca²⁺]_JSS and by controlling SR Ca²⁺ refilling.

Introduction

Excitation–contraction (E-C) coupling is a process that links action potentials to myocardial contraction (Bers, 2001). Action potential-induced depolarisation activates L-type Ca²⁺ channels (ICaLs), and the subsequent influx of Ca²⁺ activates ryanodine receptors (RyRs) located in the sarcoplasmic reticulum (SR) membrane. RyR activation in the SR then triggers Ca²⁺-induced Ca²⁺ release (CICR), which in turn induces the actin–myosin response to bring about myocardial contraction. ICaLs are modulated by a variety of factors, including membrane potential, intracellular Ca²⁺ and ATP levels, pH and phosphorylation status. ICaLs are inactivated either in a voltage-dependent manner (voltage-dependent inactivation, VDI) or by increased [Ca²⁺]. The latter mechanism, which was first described as Ca²⁺-dependent inactivation (CDI) by Brehm & Eckert (1978) in Paramecium, is considered to be the principal mechanism under a variety of physiological conditions (Anderson, 2001).

Current evidence suggests that clusters of RyRs form individual release units in the SR membrane and are locally activated via Ca²⁺ influx through single ICaLs juxtaposed across the 15 nm-wide dyadic gap of the junctional subsarcolemmal nanospace (JSS) (Cannell et al. 1995; Lopez-Lopez et al. 1995; Wang et al. 2001). It is difficult to precisely measure changes in Ca²⁺ levels in this region using current experimental tools. These changes are predicted, however, based on the analysis of phenomena such as alterations in the Ca²⁺-dependent current and Ca²⁺ sparks at the plasma membrane. Previous simulation studies predicted that the [Ca²⁺] will increase to a level over 100 μm upon release (Smith et al. 1998; Leem et al. 2006). During the E-C coupling process, ICaLs not only accelerate Ca²⁺ release from the SR, but also regulate its extent. However, the ICaL itself is negatively regulated by Ca²⁺ itself (Haack & Rosenberg, 1994). The ICaL may be negatively regulated by the Ca²⁺ influx through ICaLs and also be negatively regulated by Ca²⁺ released from the SR; the latter model, known as release-dependent inactivation (RDI), was previously thought to be the dominant mechanism of ICaL inactivation (Sham, 1997). Calmodulin was suggested to play a role as a Ca²⁺ sensor in RDI (Peterson et al. 1999).

In 1975, ICaLs in ventricular muscle were found to be inactivated in a voltage- and current-dependent manner (Kohlhardt et al. 1975); the current-dependent process was the basis for considering CDI to be the principal mechanism of inactivation. With respect to RDI, depleting the SR of Ca²⁺ by means of caffeine or ryanodine significantly attenuated the inactivation of ICaLs (Balke & Wier, 1991; Sham et al. 1995; Adachi-Akahane et al. 1996). On the other hand, the gradual accumulation of Ca²⁺ in the SR increased the magnitude of CICR and led to faster inactivation (Sipido et al. 1995). Further complicating findings was that the type of Ca²⁺-containing buffer used in the experimental pipettes also affected the inactivation of ICaLs by changing the radii of Ca²⁺ microdomains (Sham, 1997; Kreiner & Lee, 2006; Leem et al. 2006).

CDI or RDI phenomena may be affected by factors that affect the Ca²⁺ concentration in the JSS ([Ca²⁺]_JSS), such as (1) Ca²⁺ influx through ICaLs, (2) Ca²⁺ release from the SR, (3) the activity of a Ca²⁺ removal mechanism in the plasma membrane, such as Na⁺–Ca²⁺ exchange (Incx), (4) the action of a plasma membrane Ca²⁺ pump, (5) Ca²⁺ diffusion into the cytoplasm, or (6) the Ca²⁺ concentration in the experimental buffer. Ventricular myocytes contain a complicated t-tubular network (Soeller & Cannell, 1999) and analyses of RDI and changes in Ca²⁺ concentration in the dyadic nanospace are not easy. Recently there was an attempt to estimate microdomain [Ca²⁺] near RyRs using ICaL inactivation and Incx activation in rat ventricular myocytes (Acsai et al. 2011). In the present study, we used cardiac myocytes isolated from the pulmonary vein (PV) of the rabbit, which were shown to have virtually no t-tubules and are simpler in structure than ventricular myocytes (Leem et al. 2006). Using these myocytes, we tried to elucidate the contributions of various factors to CDI or RDI, the mechanism of ICaL inactivation, and the Ca²⁺ dynamics in the JSS by exploiting a computational model based on experimental data. Our work will assist in developing an understanding of the physiological regulatory aspects of ICaLs in the dyadic nanospace.

Methods

Isolation of cardiac myocytes

Rabbits (1.5 kg) were anaesthetised with ketamine and a thoracotomy was performed to insert a catheter into the ascending aorta. The heart was excised and mounted on a Langendorff-type perfusion system and normal Tyrode (NT) solution was perfused to wash out the blood. Afterwards, normal Tyrode solution without Ca²⁺ was perfused for 4 min to relax the heart muscle and to remove residual Ca²⁺ from the tissue. The same solution containing the enzymes collagenase (35 mg/50 ml; Worthington Biochemical Corp., Lakewood, NJ, USA) and pronase (2 mg/50 ml, Sigma-Aldrich) was then perfused for 15 min. After the enzymatic digestion, the left atrium was resected from the digested whole heart. Confirming its branch, the pulmonary vein was resected along the margin where the light brown colour of the artrial tissue disappears. The dissected tissue was immersed in fresh enzyme-containing solution for 15 min and dispersed in modified Kraft–Brühe (KB) medium, which is high in K⁺ and low in Cl⁻ (Isenberg & Klockner, 1982), and stored at 24–26°C.

All experimental procedures were reviewed and approved by the Institutional Review Board (IRB) for animals, University of Ulsan College of Medicine, and the procedure was carried out in accordance with the guidelines of the IRB on ethical use of animals.

Experimental solutions and protocols

We recorded and analysed changes in current using the whole-cell patch-clamp method. The basic composition of the glass pipette solution was as follows: 40 mm tetraethylammonium chloride (TEACl), 5 mm MgATP, 5 mm Tris creatine phosphate, 10 mm N-[2-hydrozyethyl]piperazine-N′-[4-butanesulfonic acid] (Hepes), 3 mm malate, and 3 mm pyruvate. Additionally, 0.1 mm ethylene glycol-bis(2-aminoethylene)-N,N,N′,N′-tetraacetic acid (EGTA) or 10 mm 1,2-bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA) were used as Ca²⁺ chelators, and CsCl and CsOH were added to regulate the osmolarity and pH, respectively. The extracellular solution contained 2 mm CaCl₂, 0.5 mm MgCl₂, 40 mm TEACl, and 10 mm Hepes. NaCl and NaOH were used to adjust the osmolarity and pH, respectively, for solutions containing Na⁺, while N-methyl-d-glucamine and HCl were used, respectively, for solutions without Na⁺. All reagents were purchased from Sigma-Aldrich, and all experimental procedures were performed at 37°C.

The double pulse protocol used to induce RDI was as follows: a step pulse to 50 mV with 2.5 ms duration was applied first from a holding potential of −40 mV, and then a second step pulse to 50 mV with 50 ms duration was applied after an interval of 25 ms. The extent of RDI was analysed based on the change in amplitude of the ICaL and the inactivation time constant of the ICaL during the second pulse. The purpose of the 25 ms interval was to allow sufficient time for the other Ca²⁺-induced currents to decline to a negligible level and, therefore, to not contribute to the ICaL current during the second pulse. To analyse the time-dependent dynamics of RDI, the time interval between the first and second step pulse was increased stepwise in 5 ms increments every 30 s. The RDI dynamics were analysed under various conditions, such as 0.1 mm EGTA in the pipette solution to allow intracellular Ca²⁺ change, 10 mm BAPTA in the pipette solution to completely prevent any Ca²⁺ changes in the myocytes, 150 μm ryanodine to block Ca²⁺ release from the SR, 10 μm thapsigargin to block the SR Ca²⁺-ATPase (SERCA) to inhibit Ca²⁺ refilling in the SR, and the removal of extracellular Na⁺ to block Incx. Under these various conditions, the time interval-dependent changes in peak current amplitude and the inactivation time constant of the ICaLs were monitored and analysed.

Model establishment

Previous reports recorded and analysed the Ca²⁺-dependent Cl⁻ current (I_Ca,Cl) and developed a computational model to simulate the current in relation to the change in [Ca²⁺]_JSS (Leem et al. 2006). The model was improved to simulate the spontaneous action potential (Seol et al. 2008). We adopted all model components from those reports. In this report, only the kinetics of Ca²⁺ binding to the ICaL were constructed to reproduce the experimental results under various experimental conditions, and the mechanism of RDI was identified. The detailed model structure and equations are shown in the appendix of the previous reports. The additional description of ICaL is added in the Appendix. All programs were written using C++ builder 2010. The combination of the Runge–Kutta algorithm and a noble algorithm developed in our laboratory (Lee et al. 2010) was used to solve all ordinary differential equations with an adaptive time step smaller than 0.03 ms, so that the maximum change among all time-dependent variables is within a range of ±4% of the previous value in the Runge–Kutta cycle. To find Ca²⁺ binding kinetic constants, the time courses of ICaL were compared and fitted to get the best least square values.

Statistical analysis

All results are presented as mean ± S.E. Statistical analyses were performed using Student-t test. p <0.05 was considered significant.

Results

CDI

The most appropriate way to observe CDI is to change the concentration of a Ca²⁺ chelator inside the glass electrode to adjust for any change in intracellular Ca²⁺ concentration. ICaLs were compared in the presence of 0.1 mm EGTA or 10 mm BAPTA in the pipette solutions. The Ca²⁺ buffering effect of 0.1 mm EGTA should be negligible because of its slow speed in chelating Ca²⁺. In contrast, BAPTA affords a buffering rate 100-fold faster than that of EGTA (Naraghi, 1997), which makes it possible to prevent spike-like changes in Ca²⁺ concentrations. Figure 1 shows the difference in the rate of inactivation of ICaLs when 0.1 mm EGTA versus 10 mm BAPTA was used as the chelator. The mean current amplitudes of 0.1 mm EGTA and 10 mm BAPTA were −441.7 ± 44.8 and −1032.5 ± 211.1 pA (n= 5), respectively. Mean current density was −15.3 ± 1.7 pA pF⁻¹ and −30.6 ± 4.3 pA pF⁻¹ (P < 0.01, n= 5). With BAPTA, the inactivation was much slower than with EGTA because changes in [Ca²⁺]_i were prevented (15.47 ± 1.06 ms, n= 5 vs. 5.6 ± 0.5, n= 6, P < 0.01). Based on this result, we conclude that CDI exists in cardiac myocytes isolated from the PV.

Figure 1. Inactivation of ICaLs with 0.1 mm EGTA (A) or 10 mm BAPTA (B) as the Ca²⁺ chelator.

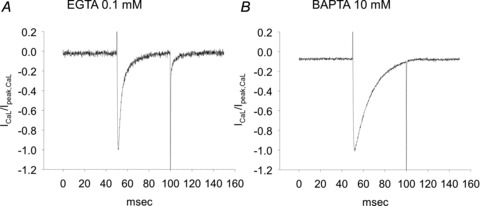
The rate of inactivation was much slower with BAPTA than with EGTA.

RDI

In the presence of 0.1 mm EGTA, ICaLs did not show any change with repetitive step pulses to 10 mV from a holding potential of −40 mV at 30 s intervals (Fig. 2A). To induce Ca²⁺ release from the SR and minimise VDI, a 2.5 ms pre-pulse with the same amplitude was given to the cells. During the pre-pulse, the ICaLs were accompanied by other transient inward currents which were activated by Ca²⁺ release from the SR, as shown in Fig. 2B. These currents have been identified as Incx and I_Ca,Cl, respectively (Leem et al. 2006). After 25 ms, the transient currents had completely disappeared. When the second step pulse was applied, the current amplitude decreased and the inactivation rate slowed (Fig. 2B), which are characteristics of RDI.

Figure 2. Characteristics of release-dependent inactivation (RDI).

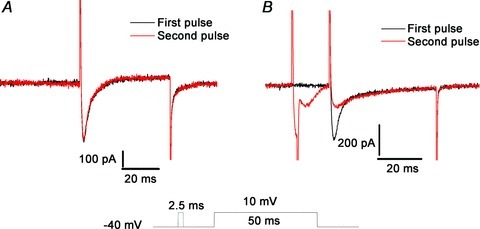
A, repetitive step pulses separated by 30 s intervals did not induce any change in the ICaLs. B, when a pre-pulse was applied, the inward current activated by Ca²⁺ appeared, after which RDI of the ICaLs was observed with a reduced peak current and slower rate of inactivation.

The RDI completely disappeared in the presence of 10 mm BAPTA in the pipette solution and was greatly attenuated in the presence of 0.1 mm EGTA and 150 μm ryanodine (Fig. 3). These results suggest that Ca²⁺ release from the SR is a prerequisite for RDI. In addition, transient inward currents appearing during the pre-pulse disappeared with either of the above treatments, suggesting that Ca²⁺ release from the SR was responsible for the generation of those currents.

Figure 3. Effect of altering the change in intracellular [Ca²⁺] on release-dependent inactivation (RDI).

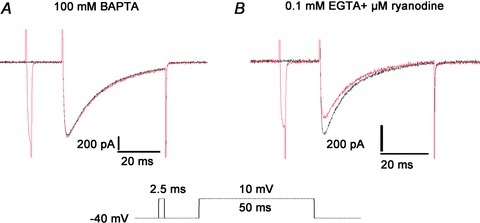
A, suppression of the intracellular [Ca²⁺] change by 10 mm BAPTA eliminated the RDI. B, suppression of Ca²⁺ release from the SR by ryanodine caused a significant decrease in the RDI.

Time-dependent and extracellular Na⁺ deprivation-induced changes in RDI

Once RDI appears, the ICaL should recover rapidly to maintain the normal E-C coupling of the heart. To test this hypothesis, we monitored the degree of RDI using increasing time intervals between the pre-pulse and test pulse in the presence of 0.1 mm EGTA (Fig. 4A). Although RDI, as monitored by the decrease in amplitude of the ICaL current during the test pulse, was initially clear, the ICaL gradually recovered as the time interval between the pre-pulse and test pulse increased. The inactivation rate also increased (Fig. 4C and D, •). Because RDI is dependent on [Ca²⁺], and because the ICaLs are located in the sarcolemma, such changes must be associated with variations in [Ca²⁺] in the JSS and/or the Ca²⁺ binding/dissociation kinetics of the ICaLs.

Figure 4. Effects of increasing the time interval between pre-pulse and test pulse on the extent of RDI.

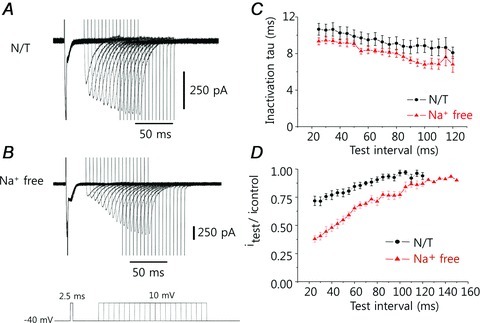
The traces from subsequent experiments are overlapped to illustrate the trend. A, the amplitude of the ICaL current initially decreased as a result of the pre-pulse; as the time interval between the pre-pulse and test pulse increased, the amplitude of the ICaL current recovered to that of the control, and the inactivation rate also increased. B, under conditions of Na⁺ deprivation (Na⁺-free solution), the current amplitude was smaller and recovery was slower than in normal physiological (NT) solution. C, the inactivation time constant for the ICaL was always less in the Na⁺-free solution than in NT solution, meaning the rate of inactivation of ICaL was faster in the absence of Na⁺. D, the decrease in current amplitude attributable to RDI was larger and recovered more slowly in Na⁺-free solution than in NT solution.

Cardiac myocytes maintain intracellular Ca²⁺ equilibrium by balancing the actions of the Ca²⁺ import (i.e. ICaL) and export mechanisms (i.e. Incx and the sarcolemmal Ca²⁺ pump). Because the activity of the sarcolemmal Ca²⁺ pump is much less than that of Incx (Bers, 2001), we focused on Incx as a Ca²⁺ export mechanism in our analyses. We sought to determine the effect of extracellular Na⁺ removal (and hence, abolition of Incx) on RDI (Fig. 4B). Under such conditions, the pre-pulse still generated transient inward currents that were activated by SR Ca²⁺ release. These inward currents were presumably due to I_Ca,Cl (Leem et al. 2006). Compared with the data obtained using normal physiological solution (normal Tyrode, NT), the amplitude of the ICaL current was greatly reduced, although it slowly recovered to the control level (Fig. 4D, ▴). The time constants for recovery of the peak current, measured in NT or Na⁺-free solution, were 49 and 60 ms, respectively. The inactivation time constant for ICaL was always less in the Na⁺-free medium than in NT solution, indicating that the rate of ICaL inactivation was faster in the absence of Na⁺ (Fig. 4C, ▴). Since the rate of inactivation is primarily regulated by [Ca²⁺]_JSS, it suggests that the change in [Ca²⁺]_JSS is larger in the absence of Na⁺. Ca²⁺ release from the SR may have increased, or the removal of Ca²⁺ from the JSS may have been retarded due to an inhibition of Incx.

Time-dependent changes in RDI in the presence of BAPTA or suppression of SR function

Figure 5 shows the changes in the peak current amplitude and the inactivation time constant of the ICaL when 10 mm BAPTA was present in the pipette solution. Under this condition of fast Ca²⁺ chelation, neither transient currents induced by the pre-pulse, nor changes in the ICaL were seen (Fig. 5A). Identical results were observed in the absence of Na⁺ (Fig. 5B). Thus, BAPTA prevented changes in the [Ca²⁺]_JSS. This may be attributable to either SR Ca²⁺ depletion or the fast-chelating action of BAPTA. Although the inactivation time constant was unchanged (Fig. 5C), the peak current amplitude of the ICaLs was slightly decreased immediately after the pre-pulse (Fig. 5D) in both the presence and absence of Na⁺, suggesting some involvement of VDI or probably CDI by Ca²⁺ influx through ICaL.

Figure 5. Effect of fast Ca²⁺ chelation by BAPTA on the time-dependent change in release-dependent inactivation (RDI).

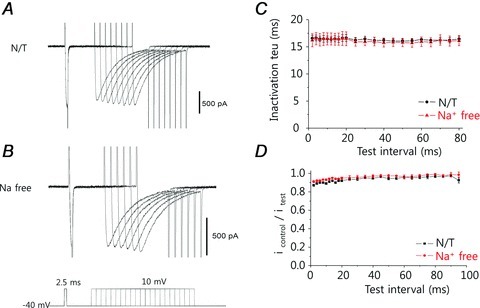
A and B, with the intracellular [Ca²⁺] change suppressed by 10 mm BAPTA, the L-type Ca²⁺ channel (ICaL) was little changed, as seen by a series of step pulses, regardless of the presence (A) or absence (B) of extracellular Na⁺. C, the inactivation time constant of the ICaL was unchanged. D, the amplitude of the ICaL current was slightly decreased when the time interval between the pre-pulse and test pulse was less than 20 ms; this effect may be due to voltage-dependent inactivation (see text).

Ryanodine is an activator of RyRs at concentrations below 10 μm and is an inhibitor at higher concentrations. At a concentration of 150 μm, ryanodine will completely block RyRs. We compared the extent of RDI in the presence of 150 μm ryanodine and 0.1 mm EGTA under both NT and Na⁺-free conditions (Fig. 6A). Although the changes in peak current amplitude were similar to those seen in the presence of BAPTA, the inactivation time constant slowly decreased as the time interval between the pre-pulse and test pulse increased. Under Na⁺-free conditions, the inactivation time constant tended to be smaller. Similar results were obtained when thapsigargin, a potent SERCA blocker, was used (Fig. 6B). Since SR function was inhibited, any decrease in the inactivation time constant could have been mediated only via Ca²⁺ influx through the ICaLs. The decrease in the inactivation time constant under Na⁺-free conditions may be attributable to a larger [Ca²⁺]_JSS, and Incx may play a role in removing Ca²⁺ from the JSS.

Figure 6. Time-dependent changes in release-dependent inactivation (RDI) when SR function is suppressed.

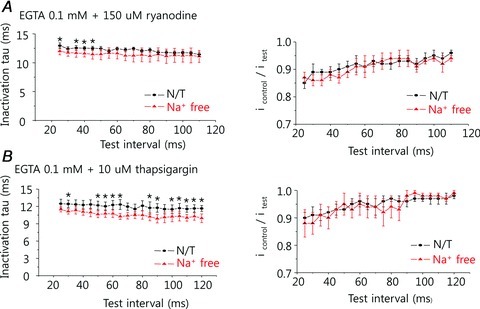
A, in the presence of 150 μm ryanodine, the peak current amplitude was little changed, similar to the pattern seen in the presence of BAPTA (see Fig. 5C), although the inactivation time constant was smaller and decreased slightly as the time interval between the pre-pulse and test pulse increased. Removal of extracellular Na⁺ decreased the inactivation time further. B, similar findings were observed in the presence of 10 μm thapsigargin.

Contribution of each factor to the change in RDI

Time-dependent changes in the peak current amplitude under various test conditions are shown in Fig. 7A. The extrapolated trace of BAPTA (Fig. 7A, ▵) showed the amplitude at 0 ms was about 88% of the control ICaL. VDI and CDI by Ca²⁺ influx through ICaL should contribute to this decrease. In the presence of ryanodine to block SR function (Fig. 7A, ▾), only small differences from the trace of BAPTA are identified and the extrapolated trace indicates that the amplitude was about 85% of the control current. Since SR function was suppressed, the differences is likely to have resulted from changes in [Ca²⁺]_JSS by Ca²⁺ influx through the ICaL. Under NT conditions (Fig. 7A, •), in which the SR is active, the peak amplitude was decreased to about 49%. In the absence of Na⁺ to inhibit Incx (Fig. 7A, ○), it was decreased to about 1.5% of the control ICaL. Since the extrapolated values indicated virtually no ICaL activity in Na⁺-free conditions, we assumed the total ICaL activity in BAPTA accessible space is the subtraction of the normalised amplitude of Na⁺-free conditions from the normalised amplitude of BAPTA. Based on this assumption, the contribution of each factor in BAPTA accessible space was calculated by the following equation. The resultant graph is shown in Fig. 7B.

Figure 7. Influence of each factor on time-dependent changes in the peak current of L-type Ca²⁺ channels (ICaLs).

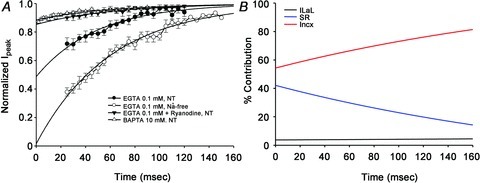
A, the current amplitudes were normalised to the control amplitude. The X-axis denoted the time interval between the pre-pulse and the test pulse. Extrapolating to zero time between pre-pulse and test pulse, in BAPTA accessible space, the relative contributions of ICaLs, SR, and inhibition of Incx to the decrease of peak current were approximately 4%, 42% and 54%, respectively. B, relative contributions of the ICaLs (black), SR (blue), and inhibition of Incx (red) to the decrease of ICaL current as a function of the time interval between the pre-pulse and test pulse.

• Total ICaL activity =% amplitude with BAPTA –% amplitude of Na⁺-free conditions

• ICal dependent change =% amplitude with BAPTA –% amplitude with ryanodine

• SR dependent change =% amplitude of ryanodine –% amplitude of NT conditions

• Incx dependent change =% amplitude of NT conditions –% amplitude of Na⁺-free conditions

From this analysis, the contributions made by the ICaLs, SR and Incx inhibition to the initial decrease in peak amplitude were calculated to be 4%, 42% and 54%, respectively. The relative contributions of these three components changed during the recovery from RDI; the relative contribution of Incx became larger, while that of the SR gradually decreased, and the contribution of the ICaLs themselves remained relatively constant (Fig. 7B).

With respect to changes in the inactivation time constant of the ICaL caused by CDI, the contributions of each factor are shown in Fig. 8. Figure 8A demonstrates the changes in inactivation time constant in the presence of BAPTA, ryanodine, thapsigargin, and none under NT conditions, while Fig. 8B demonstrates those under Na⁺-free conditions. Both clearly show that the inactivation became faster as Ca²⁺ increasing factor was added. The control inactivation time constants obtained every 30 s are shown in Fig. 8C. Black bars denote NT conditions and grey bars show Na⁺-free conditions. Each values of the paired experiments in NT conditions and Na⁺-free conditions in the presence of BATPA, ryanodine, thapsigargin, and none were 15.5 ± 1.1 vs. 15.6 ± 1.0 ms (n= 5), 11.4 ± 0.3 vs. 10.5 ± 0.3 ms (n= 6, P < 0.01), 9.6 ± 0.4 vs. 6.8 ± 0.5 ms (n= 7, P < 0.01), 5.6 ± 0.5 vs. 3.9 ± 0.2 ms (n= 6, P < 0.01), respectively. They are presumably the contributions of each factor to the inactivation of ICaL. The inactivation under the Na⁺-free conditions, which blocked Ca²⁺ efflux through Incx but kept both Ca²⁺ influx through ICaLs and Ca²⁺ release from SR, was about 4 times faster than that of BAPTA. If we normalised the inactivation speed based on this increment, in the presence of Incx, Ca²⁺ influx through ICaL and Ca²⁺ release from SR contributed 12.3% and 47.2%, respectively. Therefore, Incx prevented the inactivation by 40.5%. In the absence of Incx, Ca²⁺ influx through ICaL and Ca²⁺ release from SR contributed 16.2% and 83.8%, respectively. It clearly showed the majority of the inactivation caused by Ca²⁺ release is from SR. The CDI was faster in the presence of 10 μm thapsigargin than in the presence of 150 μm ryanodine (P < 0.01), indicating that 10 μm thapsigargin was insufficient to completely block SR function. This could be confirmed under Na⁺-free conditions, in which the removal of Incx accelerated CDI only 8.6% in ryanodine but approximately 41% in thapsigargin.

Figure 8. Influence of each factor on the inactivation time constant.

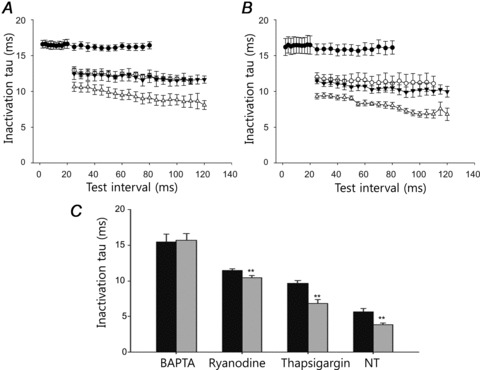
A, under physiological (NT) conditions, the changes in the inactivation time constant as a function of the time interval between the pre-pulse and test pulse in the presence of BAPTA (•), ryanodine (○), thapsigargin (▾) and none (▵). B, under Na⁺-free conditions, the changes in the inactivation time constant in the presence of BAPTA (•), ryanodine (○), thapsigargin (▾) and none (▵). C, the control inactivation time constants obtained by the single pulse applied at every 30 s. Black bars denotes NT conditions and grey bars show Na⁺-free conditions. Those were the paired experiments and ** denoted P value < 0.01.

Model development

Although we have analysed the contribution of each factor based on experimental data, our observations are basically phenomenological. The factors governing [Ca²⁺] in the subsarcolemma are complex, and a model simulation was required to confirm our analyses. A simulation model of I_Ca,Cl in cardiac myocytes from the PV has been developed (Leem et al. 2006), and its basic structure is shown in Fig. 9. This model is useful for simulating changes in [Ca²⁺]_JSS, but it is limited in that it does not consider the kinetics of Ca²⁺ binding to the ICaLs. Therefore, we have modified the model to incorporate components related to the Ca²⁺-binding kinetics of ICaLs.

Figure 9. Model structure of cardiac myocytes in the pulmonary vein, showing components involved with the change of Ca²⁺ concentration in the junctional subsarcolemmal space (JSS).

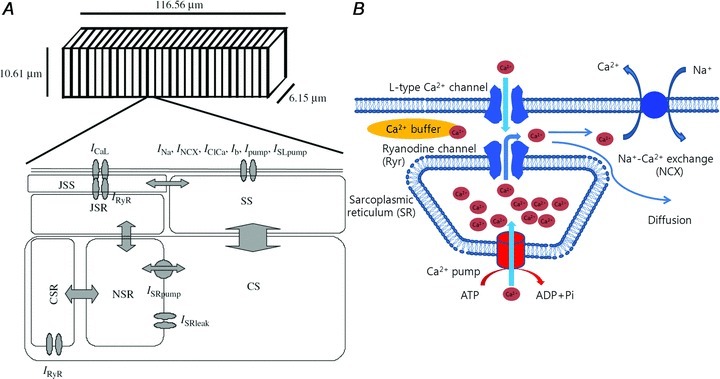
A, the diagram shows half a sarcomere (adapted from Leem et al. 2006). B, sources of Ca²⁺ ingress and egress in the JSS.

Shirokov et al. (1993) showed that the sites responsible for VDI and CDI of ICaLs are located separately. The model for CDI proposed by Markevich et al. (2005) featured two separate Ca²⁺-binding sites, a fast-binding site and a slow-binding site. According to this model, the binding of Ca²⁺ to either site would inactivate the ICaL. As VDI simulation had already been developed in the previous model (Leem et al. 2006; Seol et al. 2008), we tried various Ca²⁺-binding kinetics to fit our experimental results in this study. As suggested by Markevich et al. (2005), we assumed two different types of Ca²⁺-binding sites, a low-affinity site and a high-affinity site. The low-affinity site must have faster kinetics than the high-affinity site because, if high-affinity site was faster, the ICaLs might be promptly closed by the increase up to the tens of micromolar level of Ca²⁺ in JSS. Therefore we could assume two binding sites, a low-affinity fast-kinetic site (LAFK) and a high-affinity, slow kinetic site (HASK). However, we further assumed that the ICaL has four of these sites, of either type to obtain the best fit to the experimental results. We assumed that each Ca²⁺-binding site could exist in two simple states, as follows, and that occupation of any site by Ca²⁺ would close the ICaL:

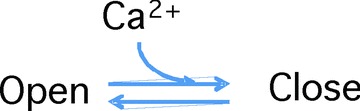
K_d values for the best fit were 14.3 μm in LAFK and 1.2 μm in HASK, respectively. Detailed ICaL kinetics is shown in the Appendix. The model simulation results (Figs 10 and 11) reproduced RDI very well (Fig. 10). The predicted recovery from RDI was also in excellent agreement with our experimental results (Fig. 11).

Figure 10. Results from a model simulation of release-dependent inactivation (RDI).

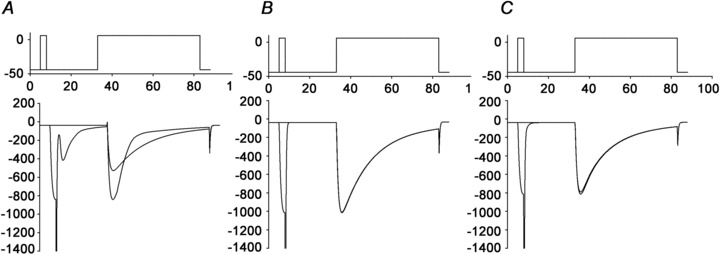
The model simulation satisfactorily reproduced the experimental measurements of RDI in the presence of 0.1 mm EGTA/NT (A), 10 mm BAPTA/NT (B), and 0.1 mm EGTA/Ryanodine (C) (see text). Top, depiction of the voltage pulse train given to the L-type Ca²⁺ channels (ICaLs). Bottom, simulated ICaL currents resulting from the voltage pulses.

Figure 11. Model simulation of the recovery from release-dependent inactivation (RDI).

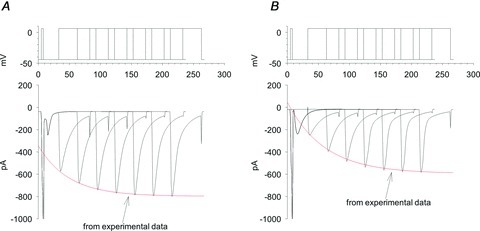
The model simulation satisfactorily reproduced the experimental measurements of RDI recovery in the presence of 0.1 mm EGTA under physiological conditions (A), and 0.1 mm EGTA in Na⁺-free medium (B). Top, depiction of the voltage pulse train given to the L-type Ca²⁺ channels (ICaLs), with varying times between the pre-pulse and test pulse. Bottom, simulated ICaL currents resulting from the voltage pulses. The traces from separate simulations are overlapped to show the trend. Red lines are from the experimental data.

Model analysis

Our experimental results suggested that Incx makes quite a large contribution to RDI; it appears that Incx activity is crucial for the control of [Ca²⁺]_JSS near the ICaL. However, the model analysis shown in Fig. 12 indicates that this is not the sole mechanism. Figure 12A shows changes in SR refilling during RDI recovery. Before pre-pulsing, the Ca²⁺ content in the SR was greater under Na⁺-free condition. In addition, the resting [Ca²⁺]_JSS under Na⁺-free conditions was higher as compared with that under NT conditions (140 nm vs. 57 nm). When the pre-pulse was applied under Na⁺-free conditions, Ca²⁺ released from the SR generated a much larger increase in [Ca²⁺] in the JSS near the ICaL channels (Fig. 12B). Further, it decreased the open probability of the Ca²⁺ binding site having LAFK much more than in NT conditions (Fig. 12C). The other Ca²⁺ binding sites with HASK determined the level of available ICaL channel activity, and this value decreased under Na⁺-free conditions because of the increased level of resting [Ca²⁺]_JSS.

Figure 12. Model simulations of the Ca²⁺ concentration in the junctional subsarcolemmal (A) region ([Ca²⁺]_JSR) or (B) space ([Ca²⁺]_JSS), and (C and D) the corresponding L-type Ca²⁺ channel (ICaL) current due to Ca²⁺ binding at two different types of Ca²⁺-binding sites in a series of double-pulse experiments (see text).

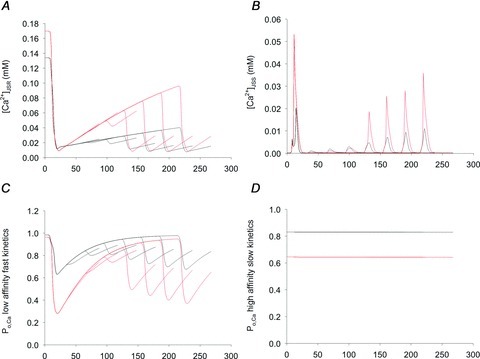
The traces from several simulations at different time intervals between the pre-pulse and test pulse are overlapped to show the trends. A, before the pre-pulse, the Ca²⁺ content of the SR was greater in the Na⁺-free medium (red) than under physiological (NT) conditions (black) because Ca²⁺ refilling was facilitated in the absence of Na⁺. B, the Ca²⁺ released from the SR during the pre-pulse and subsequent pulses generated a much larger increase in [Ca²⁺]_JSS near the ICaL when Na⁺-free medium (red) was used as compared with NT conditions (black). C, the higher [Ca²⁺]_JSS in the absence of Na⁺ (red) as compared with NT conditions (black) decreased the open probability of LAFK sites with bound Ca²⁺, leading to lesser ICaL activity. D, the HASK Ca²⁺-binding site contributed less to the overall ICaL activity because the slow kinetics but determined the availability of ICaLs. Black line: NT, Red line: Na⁺-free.

The simulation results clearly show that the Na⁺-free condition facilitated SR Ca²⁺ refilling. The initial larger decrease in ICaL amplitude under Na⁺-free conditions was principally due to a greater accumulation of Ca²⁺ in the SR and an elevated release of Ca²⁺ from the SR. The faster inactivation of the ICaL during RDI recovery was also attributable to facilitation of Ca²⁺ refilling and a greater release of Ca²⁺ from the SR. Therefore, removal of Incx activity facilitates the SR Ca²⁺ refilling process and the main role of Incx is to control the extent of Ca²⁺ refilling in SR. When we removed SR function under the Na⁺-free condition, RDI did not occur and Incx virtually had no role (Fig. 13A).

Figure 13. Model simulation of release-dependent inactivation (RDI) under specific conditions.

A, with the SR function removed, RDI did not occur under Na⁺-free conditions, indicating that Na⁺–Ca²⁺ exchange (Incx) had virtually no role in the absence of an active SR. B, with an active SR, the RDI in the absence of Na⁺ (inactive Incx) is greater than that under physiological conditions (active Incx). Top, depiction of the voltage pulse train given to the L-type Ca²⁺ channels (ICaLs), with varying times between the pre-pulse and test pulse. Middle (B), simulated [Ca²⁺] in the junctional subsarcolemmal space. Bottom, simulated ICaL currents resulting from the voltage pulses. The traces from separate simulations are overlapped to show the trends. Red lines are the experimental results from control ICaL current amplitude measurements during RDI.

As removal of Incx increased the SR Ca²⁺ content, it was of interest to examine whether Incx played any role in the control of [Ca²⁺]_JSS if the initial SR Ca²⁺ content remained the same as NT conditions. This is a hypothetical situation because Incx removal also changes the SR Ca²⁺ content. Figure 13B shows the effect of Incx removal under the same SR [Ca²⁺] level as that under NT with 0.1 mm EGTA, where ICaL amplitude decreased even more during RDI as compared with that in control RDI. This suggests that, when Ca²⁺ is released from SR, Incx actively modulates [Ca²⁺]_JSS and affects CDI.

Discussion

Physiological implications of CDI and RDI

ICaLs not only initiate E-C coupling but also modulate Ca²⁺ recruitment for the contraction of cardiac myocytes (Bers, 2001). Therefore, an understanding of the mechanisms by which ICaLs are modulated is important. In general, CDI could be a mechanism for the self-regulation of ICaL activity. When [Ca²⁺]_JSS is high or low, CDI decreases or increases ICaL activity, respectively. Consequently, CDI may be a means to control [Ca²⁺]_i for the maintenance of intracellular Ca²⁺ balance. Ca²⁺ involved in CDI came from two different sources, Ca²⁺ influx through ICaLs and Ca²⁺ release from SR. Our results suggested that the latter mechanism called RDI may be the major one for the CDI because Ca²⁺ release from SR contributed about 84% of the inactivation and Ca²⁺ influx through ICaLs contributed the rest (about 16%) in Na⁺-free conditions. However, the role of Ca²⁺ through ICaLs must be underestimated because those figures were calculated under the assumption that BAPTA chelated Ca²⁺ in JSS completely. The inactivation time constant measured with Ba²⁺ instead of Ca²⁺ was about 58 ms (data not shown). If we calculated the contribution of ICaL based on that, it was about 33%. Therefore, RDI is still the dominant component for CDI.

CDI may be a negative-feedback mechanism to attenuate Ca²⁺ influx through the ICaL. From our results, the inactivation in the presence of BAPTA occurred with a time constant of 16 ms. If we assume the shape of a cardiac myocyte to be a cylinder 10 μm in diameter and 100 μm in length, then the total increase in intracellular Ca²⁺ in 100 ms is 21.1 μm. When CDI was allowed, the inactivation time constant was approximately 6 ms. In this case, the total increase in intracellular Ca²⁺ was 1.32 μm, which is approximately 16 times smaller. For intracellular Ca²⁺ balance, the majority of influxed Ca²⁺ is exported through Incx, which brings a Na⁺ influx. This Na⁺ must be removed by a Na⁺,K⁺-ATPase. Another mechanism for Ca²⁺ efflux is the sarcolemmal Ca²⁺-ATPase. In any case, myocytes must use ATP for maintaining intracellular Ca²⁺ balance. From this point of view, CDI is beneficial for the cardiac myocytes because less ATP is consumed.

Localized control of [Ca²⁺]_JSS and its measurement

ICaLs are regulated by a variety of mechanisms, such as voltage, phosphorylation, ATP, pH, and Ca²⁺ (Bers, 2001). In the case of Ca²⁺, an ICaL is usually juxtaposed against a RyR in cardiac myocytes to form a dyad, between which is the JSS (Scriven, 2000). Factors that may affect a change in [Ca²⁺] in the dyadic space include (1) Ca²⁺ influx through the ICaL, (2) Ca²⁺ release from the SR, (3) Ca²⁺ removal by Incx, (4) Ca²⁺ pumping by the SERCA, (5) diffusion of Ca²⁺ into the cytoplasm, and (6) buffering of [Ca²⁺] by the medium. Precise values are difficult to obtain experimentally for the factors, such as diffusion rate or buffering capacity, and could only be estimated or assumed. Ideally, one would measure the change of [Ca²⁺] directly in the JSS between the ICaL and RyR. However, current technology is not sufficient to access and measure the Ca²⁺ in JSS.

The analysis of [Ca²⁺]_JSS dynamics from measurements of Ca²⁺-sensitive ionic currents has several advantages: (1) the recording is obtained under physiological conditions; (2) if the electrodes are positioned in the sarcolemma at a specific location, the measurement reflects the specific change of [Ca²⁺] at that location; and (3) because of the time scales involved, the measurements are not affected by Ca²⁺ diffusion. Nevertheless, this method does have some problems. The kinetics of Ca²⁺ binding to Ca²⁺-sensitive ion channels is difficult to measure. Ionic currents are obtained from the whole membrane, and the recorded currents do not reflect the change in [Ca²⁺] at a specific binding site. Additionally, the location of ion channels themselves may not be specific. However, with a reasonable model structure and parameters, analysis of ionic currents seems to be the most practical approach at present for determining the dynamics of Ca²⁺ within the JSS. We tried to estimate Ca²⁺ dynamics in JSS and SS with the recordings of Ca²⁺-activated Cl⁻ currents and the reasonable model based on electron microscopic structure (Leem et al. 2006). Recently, there was also an attempt to estimate microdomain [Ca²⁺] near RyRs using ICaL inactivation and Incx activation in rat ventricular myocytes (Acsai et al. 2011). In their report, [Ca²⁺] near release site was between 10 and 15 μm. Our present report is also an extension of the previous work to explore Ca²⁺ dynamics in JSS using ICaL kinetics and the peak Ca²⁺ concentration reached about 20 μm by the activation of ICaL and the release of Ca²⁺ from SR.

RDI of the ICaL

Using a unique pulse protocol, Zahradnikova et al. (2004) claimed to observe only CDI without any VDI, based on the observation that the inactivation occurred in a Ca²⁺-dependent manner within the SR. The decrease in amplitude of the ICaL peak current caused by the pre-pulse-induced SR Ca²⁺ release was termed RDI. The inactivation rate during the test pulse was slowed because Ca²⁺ release from the SR was abolished or decreased. These two phenomena were mutually exclusive because one was due to an increase in [Ca²⁺]_i, while the other is due to a decrease in [Ca²⁺]_i.

The decrease in amplitude of the ICaL peak current after a pre-pulse was clearly caused by Ca²⁺ because those phenomena were abolished by the presence of BAPTA in the pipette solutions. However, even the presence of BAPTA failed to prevent the small decrease of ICaL after the prepulse even though there was no activation of Ca²⁺-dependent current. We thought this decrease could be caused by two mechanisms, VDI and CDI by Ca²⁺ influx through ICaL. We believe the latter mechanism is more feasible because Ba²⁺ instead of Ca²⁺ increased the inactivation time constant of ICaL (58 ms vs. 16 ms in 10 mm BATPA conditions). Therefore, a BAPTA inaccessible space may be present. A previous report also suggested these possibilities (Sham, 1997). Since this space is not controllable, we only consider the Ca²⁺ dynamics in BAPTA accessible space in the present study.

We assessed the contribution of each factor (ICaL, SR and Incx) to the RDI in Fig. 7. Interestingly, the contribution of the ICaLs themselves remained relatively constant at about 4 % during the recovery from RDI. These figures indicated a contribution only in BAPTA accessible space. As described in the previous section, the contribution of ICaL should be larger. The relative contributions of these three components changed during the recovery from RDI and the relative contribution of Incx became larger. These results suggested that Incx activity relatively became more important in regulating [Ca²⁺]_JSS as [Ca²⁺]_JSS became smaller. From these results, we could conclude that that Incx actively participated in regulating ICaL by controlling [Ca²⁺]_JSS in physiological conditions.

The peak amplitude and the time course are excellent indicators of Ca²⁺ dynamics of JSS. And also, changes in the inactivation time constant of ICaL during RDI recovery are very good indicators of SR Ca²⁺ content changes. However, RDI is a complex phenomenon, and an estimation of parameters and a simulation were required to analyse it.

Model structure and Ca²⁺-binding behaviour of the ICaL

In cardiac myocytes from the PV, the dyad between the ICaL and RyR is located principally on the surface of the sarcolemma because there is no complicated t-tubule structure (Leem et al. 2006) like ventricular myocytes (Soeller & Cannell, 1999). The results of Scriven et al. (2000) were employed to develop a basic model. A more complex and detailed model was developed based on the electron microscopic data and I_Ca,Cl currents were simulated by Leem et al. (2006). This model is composed of three cytosolic compartments, including the JSS and cytosolic space. The ICaLs exist exclusively in the JSS to trigger Ca²⁺ release from the SR, while all of the other ion channels are located on the cell membrane facing the sarcoplasmic space (SS). Previous studies have confirmed that I_Ca,Cl is a Ca²⁺-dependent phenomenon inside the cardiac myocyte and the model accurately reconstructed the experimentally observed I_Ca,Cl, which reflects changes in [Ca²⁺]_SS, which, in turn, reflects [Ca²⁺]_JSS. This model was further improved to reconstruct a spontaneous action potential usually seen in cardiac myocytes of the PV (Seol et al. 2008).

From the simulation, the resting [Ca²⁺]_JSS was greater in Na⁺-free medium than in NT solution. The peak ICaL current induced by a step pulse was smaller in Na⁺-free medium than in NT solution (data not shown), and was larger in the presence of 10 mm BAPTA than 0.1 mm EGTA. These results suggest that the ICaL is constitutively inactivated by the resting [Ca²⁺]_JSS, which must, therefore, be sufficient to affect ICaL availability. A difference of 100 nm could affect such availability. Therefore, at least one binding site must be active at this level of [Ca²⁺] to inactivate ICaL. Its Ca²⁺-binding affinity must be high to work with submicromolar change in [Ca²⁺]_JSS. There must also be at least one other binding site of lower affinity because SR Ca²⁺ release would increase [Ca²⁺]_JSS up to several tens of micromolar (Fig. 12B). Apparently, the binding of Ca²⁺ to either of these sites is sufficient to inactivate the ICaL. This suggestion differs markedly from the hypothesis of Markevich et al. (2005), in which sequential binding of Ca²⁺ to two separate sites is necessary to inactivate the ICaL.

The reaction rate of ICaL when Ca²⁺ is bound to the putative high-affinity site must be considerably less than when Ca²⁺ is bound to the putative low-affinity site. Otherwise, the high-affinity binding sites would be saturated by Ca²⁺ released from the SR, and the channels would not become available again until the [Ca²⁺]_JSS fell enough. Based on these considerations, we presume the ICaL must have, at a minimum, two types of Ca²⁺-binding sites, a high-affinity with slow kinetics site, and a low-affinity with fast kinetics site. We cannot exclude other types of Ca²⁺-binding sites, but our simulation featured only these two. Further, we assumed that the binding sites function independently of any Markov chain reaction. With these assumptions, we fitted the Ca²⁺ binding constants that would best reconstruct our experimental results.

Several models have been developed to reproduce the VDI and CDI. Shirokov et al. showed there were three modulating sites, an extracellular divalent-ion-binding site that controls VDI, a voltage sensor, and an intracellular Ca²⁺-binding site responsible for CDI (Shirokov et al. 1993). Another model, designed specifically for reconstructing CDI, was proposed by Markevich et al. (2005). This model assumed two Ca²⁺-binding sites, with high and low affinity, and required sequential binding of Ca²⁺ to the sites. These two models were successful at reproducing the features of ICaL currents under the limited conditions of those studies, but it remained uncertain whether they would also be appropriate for conditions in which Ca²⁺-induced Ca²⁺ release occurred. Neither of them could accurately predict the RDI seen in our experiments.

Model simulation and its implications

Our simulation successfully reconstructed RDI. Our first question was: What role does Incx play? Our experimental data showed that Incx substantially influenced ICaL activity. The initial decrease in ICaL activity during a test pulse following a pre-pulse under Na⁺-free conditions was presumably due to a higher SR Ca²⁺ content when Na⁺ was absent. This implies a role of Incx in modulating the [Ca²⁺]_JSS. When the SR function was removed, there was little decrease in ICaL activity during the test pulse (Fig. 13A), implying again that [Ca²⁺]_JSS is the determining factor in the decrease of ICaL activity. Removal of Incx by using a Na⁺-free medium facilitated SR Ca²⁺ refilling, leading to faster inactivation of the ICaL.

The above considerations suggest that Incx plays no direct role in RDI, but rather an indirect role by modulating the initial [Ca²⁺]_JSS. Experimentally, we could not prove this supposition because it was not possible to make the initial SR Ca²⁺ contents of the NT and Na⁺-free conditions the same. Thus, we could not examine the contribution of Incx by itself or make direct comparisons. The merit of modelling is that imaginary situations that are impossible to attain experimentally can be explored. Thus, through modelling, we could theoretically remove Incx without affecting the initial SR Ca²⁺ content. In this simulation, removal of Incx clearly decreased ICaL amplitude (Fig. 13B), but only when the SR was active (Fig 13A). These results indicate that Incx actively participates in ICaL modulation by controlling [Ca²⁺]_JSS.

The dynamics of [Ca²⁺]_JSS control over ICaL are complex. Our modelling shows that various factors interact to modulate ICaL activity. In any pathological condition in which Ca²⁺-related factors are concerned, simple intuition is inadequate. For example, when Incx activity is decreased, its impact on basal [Ca²⁺]_i and SR Ca²⁺ content is not obvious. Nor is it obvious how a transient change in Ca²⁺ levels would affect contraction. Although it might be expected that an impairment of a Ca²⁺ efflux mechanism would increase the overall cellular [Ca²⁺], the situation is not so simple. An increase in [Ca²⁺]_i can decrease ICaL availability, causing a fall in Ca²⁺ influx; the [Ca²⁺]_i will then be determined by the new balance established between ICaL and Incx activities. In real situations, changes in [Ca²⁺]_i-related factors are diverse; however, useful results can be obtained by computation and simulation using an appropriate model.

Limitations of the model

To retain model simplicity, we assumed the existence of only two different types of Ca²⁺-binding sites. For adequacy of fit, we assumed that four binding sites of either kind are present, although we have no experimental evidence to support this assumption. Even though Ca²⁺ binding has been simplified in the model, we take the view that the role of SR and Incx derived from the model are not greatly affected by these assumptions.

We also did not incorporate Ca²⁺-dependent facilitation (CDF) mechanisms into the model. CDF was first noted upon augmentation of ICaL action by a cardiac glycoside (Marban & Tsien, 1982). CDF was reported to be dependent on the Ca²⁺/calmodulin system and the action of a protein kinase (Anderson, 2001). If CDF mechanisms were to be included in the model, the calculation of Ca²⁺ content in the myocytes would probably change, and the Ca²⁺ dynamics would likely be affected. In our analyses, we normalised the ICaL current amplitudes during RDI to the ICaL current amplitude induced by the pre-pulse. The variation in ICaL amplitudes during the pre-pulse was negligible. Even if ICaL activity was increased by CDF, the intrinsic ICaL run-down would compensate for it.

Another limitation of the model is the short recording time, which may not have been long enough for the intracellular Ca²⁺ balance to change; this could affect our entire scheme. In short, we have assumed many parameters, as described in our previous report (Leem et al. 2006; Seol et al. 2008), and acknowledge that these assumptions are intrinsic weaknesses of the model. Despite these shortcomings, however, we consider the mechanistic explanation afforded by the model to be valid.

Conclusions

Based on our experimental results, we assumed that two types of Ca²⁺-binding sites exist in the ICaL: high-affinity sites with slow kinetics and low-affinity sites with fast kinetics. The decrease in ICaL amplitude seen during RDI is mediated by the basal [Ca²⁺]_JSS, CDI rate, Incx and SR Ca²⁺ content. Incx seems to play two roles: it downregulates Ca²⁺ refilling of the SR and it also accelerates Ca²⁺ removal from the JSS to prevent inactivation of the ICaL. By pumping intracellular Ca²⁺ to the extracellular space, Incx seems to be dynamically involved in CDI and modulates ICaL activity. Our physiomic model successfully reconstructed the RDI phenomenon and interpreted the dynamic interrelationships between various factors modulating Ca²⁺ levels in the SR. The model is useful to explain why, during myocardial cell contraction, Ca²⁺ dynamics are affected by ICaL levels and Incx activity, and what may occur if a specific ion channel is overexpressed or underexpressed. Our data should be useful to establish the dynamic Ca²⁺ physiome of the myocardial cell. The dynamics of [Ca²⁺]_JSS is complex, and diverse factors, including the steady-state [Ca²⁺]_i, CDI, and the activities of Incx, RyR and SERCA, are all involved. By allowing permutations of these factors, the model presented here can be employed to analyse changes affecting the CDI and RDI, Ca²⁺ dynamics, and their impact on [Ca²⁺]_JSS.

Glossary

CDI

Ca²⁺-dependent inactivation

CICR

Ca²⁺-induced Ca²⁺ release

ICaL

L-type Ca²⁺ channel

Incx

Na⁺–Ca²⁺ exchange

NT

normal Tyrode

RDI

release-dependent inhibition

SR

sarcoplasmic reticulum

Appendix

Basic geometry and the simulation system were the same as those reported previously (Leem et al. 2006; Seol et al. 2008). Here only ICaL kinetics were described with new Ca²⁺-dependent kinetics

Equation of steady state activation curve:

Equation of activation time constants:

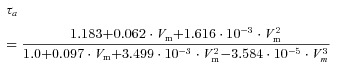Fast inactivation three state:

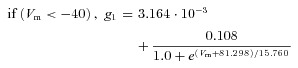Very slow inactivation three state:

Ca²⁺ concentration in JSS in the vicinity of Ca²⁺channel and RyRs will be increased to induce Ca²⁺ release from SR by the activity of L-type Ca²⁺channel.

Ca²⁺-dependent inhibition Inf_Ca, Inf_Ca2 : Ca²⁺-dependence of the steady state open probability of each Ca²⁺ binding site τ_Ca, τ_Ca2: Ca²⁺-dependence of the time constant of each Ca²⁺ binding site:

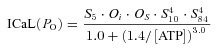Author contributions

The experiments were performed by J.S.R., W.T.K., J.H.L., J.H.K., and H.A.K. in the laboratory of C.H.L. The model development was made by C.H.L. with the support of E.B.S. and J.B.Y. The manuscript was written by J.S.R. and C.H.L. with the assistance of J.B.Y. All authors have read and approved the final version.