Theoretical study of L-type Ca²⁺ current inactivation kinetics during action potential repolarization and early afterdepolarizations

Abstract

Sarcoplasmic reticulum (SR) Ca²⁺ release mediates excitation–contraction coupling (ECC) in cardiac myocytes. It is triggered upon membrane depolarization by entry of Ca²⁺ via L-type Ca²⁺ channels (LTCCs), which undergo both voltage- and Ca²⁺-dependent inactivation (VDI and CDI, respectively). We developed improved models of L-type Ca²⁺ current and SR Ca²⁺ release within the framework of the Shannon–Bers rabbit ventricular action potential (AP) model. The formulation of SR Ca²⁺ release was modified to reproduce high ECC gain at negative membrane voltages. An existing LTCC model was extended to reflect more faithfully contributions of CDI and VDI to total inactivation. Ba²⁺ current inactivation included an ion-dependent component (albeit small compared with CDI), in addition to pure VDI. Under physiological conditions (during an AP) LTCC inactivates predominantly via CDI, which is controlled mostly by SR Ca²⁺ release during the initial AP phase, but by Ca²⁺ through LTCCs for the remaining part. Simulations of decreased CDI or K⁺ channel block predicted the occurrence of early and delayed afterdepolarizations. Our model accurately describes ECC and allows dissection of the relative contributions of different Ca²⁺ sources to total CDI, and the relative roles of CDI and VDI, during normal and abnormal repolarization.

Key points

• The L-type Ca²⁺ current (I_Ca) plays an important role in regulation of excitation–contraction coupling and development of cardiac arrhythmias.

• We studied theoretically I_Ca inactivation and the relative contributions of voltage-dependent inactivation (VDI) and Ca²⁺-dependent inactivation (CDI) to total inactivation, and we present an improved mathematical model of rabbit ventricular I_Ca.

• The model proposes that inactivation observed when Ba²⁺ is the charge carrier includes a small contribution from ion-dependent inactivation (in addition to pure VDI), usually neglected by other modelling studies.

• The model, identified and validated against a broad set of experimental data, is applied to study the relative roles of VDI and CDI (and the relative contributions of different Ca²⁺ sources to total CDI) during normal and abnormal repolarization.

• The model predicts that CDI is crucial for repolarization, and that impairment of CDI may be arrhythmogenic by affecting intracellular Ca²⁺ cycling, through its effect on the I_Ca time course and Na⁺–Ca²⁺ exchanger activity.

Introduction

The L-type Ca²⁺ current (I_Ca) critically regulates excitation–contraction coupling (ECC) (Bers, 2001) by triggering sarcoplasmic reticulum (SR) Ca²⁺ release, and modulating action potential (AP) shape and duration (APD), i.e. maintaining the long AP plateau.

I_Ca plays an important role in the development of cardiac arrhythmias. Indeed, at the single myocyte level it has been implicated in the development of early afterdepolarizations (EADs) in classical studies by January and colleagues (January et al. 1988; January & Riddle, 1989), who presented evidence linking EADs in Purkinje fibres with reactivation of Ca²⁺ current during the AP plateau. Several modelling studies have highlighted the importance of I_Ca in EAD formation in different animal species and cardiac cell types (Zeng & Rudy, 1995; Tanskanen et al. 2005; Corrias et al. 2011). Under a number of pathophysiological conditions that tend to prolong APD (as in hypertrophic and failing hearts), I_Ca may become arrhythmogenic (Benitah et al. 2010), even in the absence of disease-induced alteration of the current itself, as the longer AP plateau provides more time for Ca²⁺ channel reactivation and facilitates the occurrence of EADs.

L-type Ca²⁺ channels (LTCCs) are activated by membrane depolarization and provide the main source of Ca²⁺ influx. The decay of I_Ca during depolarization due to current inactivation is both Ca²⁺ and voltage dependent (Lee et al. 1985). Intracellular Ca²⁺-dependent inactivation (CDI) is mediated by Ca²⁺ binding to calmodulin (CaM) tethered to the C-terminus of the channel (Peterson et al. 1999; Zuhlke et al. 1999). Current decay through LTCCs is markedly prolonged when Ba²⁺ is the charge carrier (Peterson et al. 2000; Bers, 2001). Ba²⁺ current inactivation has been considered widely to be purely voltage dependent (VDI) in both experimental and theoretical studies (Peterson et al. 2000; Findlay, 2002b; Faber et al. 2007; Mahajan et al. 2008b). However, a residual ion-dependent inactivation (IDI) does influence Ba²⁺ current (I_Ba) decay (Brunet et al. 2009; Grandi et al. 2010), given the ability of Ba²⁺ to bind CaM weakly (Ferreira et al. 1997). This has been neglected by previous studies and incorporated here. CDI is an important negative feedback mechanism that limits Ca²⁺ influx during APs, and may constitute a physiological safety mechanism against harmful Ca²⁺ overload (Benitah et al. 2010). Elimination of CDI in guinea pig ventricular myocytes via expression of Ca²⁺-insensitive CaM (CaM₁₂₃₄) produced ‘ultralong’ APs, and suggested a paradigm of AP control, whereby LTCCs attain dominance in controlling APD due to the faster kinetics of CDI compared with ongoing K⁺ channel activation during the plateau (Alseikhan et al. 2002).

We present here an improved theoretical model of LTCC kinetics that accounts for the weak Ba²⁺-dependent inactivation and the greater efficacy of I_Ca to trigger SR Ca²⁺ release at negative potentials. The model was validated extensively and recapitulates faithfully the relative importance of VDI and CDI in I_Ca inactivation. The model includes a small contribution of Ba²⁺-dependent inactivation that is observed when Ba²⁺ is the charge carrier, in addition to pure VDI. Thus the overall contribution of VDI to I_Ca inactivation is somewhat reduced compared to previous models. We incorporated this I_Ca model within the framework of the Shannon–Bers rabbit ventricular ECC model (Shannon et al. 2004). The formulation of SR Ca²⁺ release was modified to reproduce the experimentally measured membrane potential (E_m) dependence of ECC gain. With this updated myocyte model, which was validated against a broad range of experimental data, we showed that CDI, dominated by SR Ca²⁺ release at the beginning of the AP and by Ca²⁺ via LTCCs for the remaining part, outweighs VDI in physiological conditions. Impairment of CDI is predicted to cause AP prolongation and triggered activity depending on its degree of reduction. New insights into EAD formation were obtained using the model, and I_Ca kinetics was analysed during these abnormal APs.

Methods

The Shannon–Bers model of a rabbit ventricular myocyte (Shannon et al. 2004) provided the computational framework for this study, where the only changes are on the I_Ca and ryanodine receptor (RyR) properties (Fig. 1), as described here and in the Supplemental Material.

Figure 1. RyR and IC_a models.

A, schematic diagram of dyadic cleft fluxes of the rabbit ventricular myocyte AP model of Shannon et al. (2004). Voltage dependence of SR Ca²⁺ release was introduced as in inset. B, structure of the Mahajan et al. (2008b) LTCC model as modified for this study.

We modified the SR Ca²⁺ release formulation by adding an E_m-dependent factor that reduces RyR Ca²⁺ flux at positive E_m (Fig. 1A, inset). This is not meant to imply that RyR has intrinsic E_m dependence, but this phenomenological adjustment allows our common pool model to recapitulate experiments showing lower efficacy of macroscopic I_Ca to trigger SR Ca²⁺ release at more positive E_m (Supplemental Fig. S1A) (Beuckelmann & Wier, 1988; Bers, 2001; Altamirano & Bers, 2007). At more negative E_m, fewer Ca²⁺ channels open, but the unitary flux is larger (due to larger driving force), causing more efficient Ca²⁺-induced Ca²⁺ release and higher ECC gain (measured as the ratio of Ca²⁺ transient, CaT, amplitude to peak I_Ca in Fig. S1B). Gain at negative E_m is high, in part, because a single Ca²⁺ channel opening may trigger junctional release but as more channels are recruited (e.g. approaching 0 mV) there is more trigger redundancy of LTCC opening per release unit (and a consequently smaller denominator in the gain equation) (Altamirano & Bers, 2007). At increasingly positive E_m (where unitary currents are small), multiple openings are needed to assure RyR opening, which results in lower gain. This circumvents the need here for local stochastic interactions between LTCCs and RyRs in thousands of Ca²⁺ release units (Restrepo et al. 2008; Lee et al. 2011). The modified formulation predicted higher CaT amplitude for a given I_Ca at negative E_m and lower amplitude at positive E_m (Fig. S1C) and the expected decreasing ECC gain with stronger depolarization (Fig. S1D).

The seven-state I_Ca model (Fig. 1B) by Mahajan et al. (2008b) was incorporated into the ECC model and parameters were constrained to match experimental data obtained under various Ba²⁺/Ca²⁺ homeostasis conditions. I_Ba was simulated by replacing Ca²⁺ with Ba²⁺ in the extracellular solution composition, and Ba²⁺ entering the cell via LTCC was assumed to affect local [Ba²⁺] (i.e. sub-sarcolemmal and cleft) without altering bulk [Ba²⁺] or triggering SR Ca²⁺ release (Fig. 1A) (Ferreira et al. 1997). With Ba²⁺ as the charge carrier, Mahajan et al. (2008b) modelled inactivation to occur only via the VDI pathway. That is, during I_Ba the two upper states in Fig. 1B (CDI) are never visited, and the model is effectively reduced to the lower five states. In contrast, we obtained our I_Ba model parameters by fitting the voltage and Ba²⁺ dependence of VDI and CDI rate constants to the measured I_Ba with 8-fold weaker apparent affinity of Ba²⁺ vs. Ca²⁺ for CaM (Grandi et al. 2010). These parameters were also constrained to fit I_Ca data (with Ca²⁺ as the charge carrier) with normal CaT, or without SR Ca²⁺ release and with the Ca²⁺ buffers EGTA or BAPTA. We made simplifying assumptions that, in the absence of release and presence of Ca²⁺ buffers, Ca²⁺ entering the cell via LTCC affects sub-sarcolemmal and cleft [Ca²⁺] without altering bulk [Ca²⁺] (for EGTA), or [Ca²⁺] is clamped at diastolic values in all compartments (for BAPTA).

LTCC permeability values for Ba²⁺ and Ca²⁺ were set to reproduce the experimental peak current values measured by Mahajan et al. (2008b) at physiological temperature. Model rate parameters were chosen to reproduce kinetics at 37°C, and a Q₁₀ of 2 (Faber et al. 2007) was used to scale the duration of voltage pulses of experimental data obtained at room temperature. The full list of model equations and parameters can be found in the Supplemental Material (Tables S1, showing the expressions of the transition rates in Fig. 1B, and S2 respectively).

CaM₁₂₃₄ expression was simulated by assuming that the overexpressed CaM₁₂₃₄ displaced the wild-type (WT) CaM in a fraction α of LTCCs in the cell, such that this population of channels exhibited VDI but not CDI (i.e. I_Ca,VDI with the reduced 5-state model), as done previously by Mahajan et al. (2008a). Thus, total I_Ca,CaM1234 is given by:

Ionic concentrations were set to the following values (in mm): [Cl⁻]_i 5, [Cl⁻]_o 146, [K⁺]_i 140, [K⁺]_o 5.4, [Na⁺]_o 135, [Ca²⁺]_o 2 (or [Ba²⁺]_o 1.8), as in Mahajan et al. (2008b). During EAD-like AP-clamp, the following values were changed: [Cl⁻]_i 15, [Cl⁻]_o 150, [K⁺]_i 135, [Na⁺]_o 140, [Ca²⁺]_o 1.8, as in Shannon et al. (2004). The reduced Cl⁻ driving force diminished background Cl⁻ currents, thus reducing the repolarization reserve.

Model equations were implemented in Simulink (The Mathworks Inc., Natick, MA, USA) and solved numerically with a stiff variable order solver (ode15s) based on the numerical differentiation formulas (NDFs) with an adaptive time step ranging from 1 ms to 1 ps. The digital cell was stimulated in voltage- or AP-clamp to replicate experimental protocols. AP-clamp simulations were performed with a command AP simulated by pacing the cell in current-clamp (15 A F⁻¹ current stimulus lasting 3 ms) at 0.33 Hz to steady-state with normal CaT. APs showing EADs were also used as a command voltage.

A gapped double-pulse (GD-P) protocol was implemented in which the AP-clamp was interrupted at defined potentials. E_m was then stepped back to −40 mV for 2 ms, followed by a 200 ms rectangular test pulse to 5 mV. The fraction of available channels at each time during the AP was calculated by normalizing peak I_Ca evoked by the corresponding test pulse to the peak I_Ca elicited by a rectangular clamp step from −80 to 5 mV (when the channels are fully available). Inactivation (i.e. 1-availability) was plotted against the time elapsed between AP upstroke and interruption.

Results

I_Ca model parameterization

The I_Ca model was parameterized using voltage-clamp data from previous studies in isolated ventricular myocytes from rabbit (Yuan et al. 1996; Linz & Meyer, 2000; Mahajan et al. 2008b), guinea pig (Hadley & Hume, 1987; Zhong et al. 1997; Sonoda & Ochi, 2001), rat (Sun et al. 2000) and mouse (Sako et al. 1998). Results are shown for Ba²⁺ current, and for Ca²⁺ currents with and without SR Ca²⁺ release.

Current–voltage relationship

Dependence of (normalized) current on E_m is depicted in Fig. 2A–C. Simulated I_Ba and I_Ca (lower panels) peak at +5 mV, independent of charge carrier and SR function. At 5 mV, peak I_Ba equals −2.00 nA, peak I_Ca equals −2.14 nA and −2.17 nA with and without SR Ca²⁺ release, respectively (vs.−2.06 nA at 0 mV, −1.98 nA at 0 mV, and −2.14 nA at +10 mV, in experiments by Mahajan et al. (2008b)). Normalized experimental current–voltage (I–V) curves are shown for comparison (upper panels) and exhibit some variability, possibly due to differences in species, intra- and extracellular solution compositions, and experimental protocols. Details on the experimental data used in the development and validation of the model are provided in the Supplemental Table S3. As a guideline, we favoured experiments obtained in rabbit at physiological temperature and solutions vs other species and less physiological conditions.

Figure 2. Experimental (top) and simulated (bottom) I–V relationships and quasi-steady-state inactivation (SSI) for I_Ba (A and D), I_Ca without SR Ca²⁺ release (B and E), and I_Ca with CaT (C and F).

I–V curves were obtained by stimulating the cell with voltage steps from a resting potential of −80 mV to various test potentials. Quasi-SSI curves were obtained by measuring the available current after inactivation prepulses of various (indicated) durations. Results for simulated I_Ba with a reduced 5-state model (only VDI) are also shown (dashed lines).

Quasi-steady-state inactivation

Simulated current availability curves (Fig. 2D–F) indicate that inactivation is more complete the longer the inactivating prepulse, in agreement with experimental data (upper panels). A slightly U-shaped curve is obtained for I_Ba (Fig. 2D), with the largest inactivation corresponding to the largest Ba²⁺ influx, near +5 mV, consistent with modest Ba²⁺-dependent inactivation (Brunet et al. 2009). Moreover, this U-shaped region is not seen with the reduced five-state model lacking IDI (dashed lines). Inactivation is more markedly U-shaped when simulating I_Ca (Fig. 2E and F), and is especially pronounced with SR function intact (compare Fig. 2E vs. 2F) as seen experimentally.

Kinetics of inactivation

The kinetics of I_Ba and I_Ca inactivation can be assessed by the ratio of pedestal to peak current (I_Ped/I_Peak) at different times after depolarization to different E_m for experimental (Mahajan et al. 2008b) and simulated traces (Fig. 3C). Pedestal currents (and I_Ped/I_Peak) decrease with longer pulses and inactivation is faster and deeper for I_Ca vs. I_Ba, and with larger ion influx and/or Ca²⁺ release, in agreement with experiments (left panel). Again, the dependence of I_Ped/I_Peak on E_m is U-shaped (Fig. 3C) around the peak potential of 0 to +10 mV (Fig. 2A and C) for both I_Ba and I_Ca. In contrast, simulated I_Ba curves with the five-state model (VDI) are relatively flat (dashed lines at right). Previous results have shown that I_Ba inactivation depends on Ba²⁺ influx (Brunet et al. 2009; Grandi et al. 2010). For a given peak current at different E_m, the kinetics of I_Ba inactivation are comparable. For example, experimental (Mahajan et al. 2008b) and simulated I_Ba at −10 and +20 mV reach similar peak values (simulated: −8.75 and −9.12 A F⁻¹) and inactivate similarly (Fig. 3A). On the other hand, when SR Ca²⁺ release occurs, for a given peak I_Ca, inactivation is faster at negative E_m, where ECC gain and release are larger. For example, experimental (Mahajan et al. 2008b) and simulated I_Ca at −10 and +20 mV reach similar peak values (simulated: −9.58 and −10.1 A F⁻¹) but inactivation is much faster at −10 mV (Fig. 3B). This is further illustrated in Supplemental Fig. S2, where E_m values are chosen symmetrically with respect to peak current, such that the currents reach the same peak value and inactivation kinetics are easily compared.

Figure 3. Kinetics of LTCC current inactivation.

Experimental (top) (Mahajan et al. 2008b) and simulated (bottom) I_Ba (A) and I_Ca (B) traces evoked by voltage pulses from −80 mV to −10 mV (left) and +20 mV (right). C, experimental (left) (Mahajan et al. 2008b) and simulated (right) ratios of pedestal to peak current (I_Ped/I_Peak) at varying times (indicated) during voltage pulses from −80 mV to various test potentials for I_Ca and I_Ba. Results for simulated I_Ba with a reduced 5-state model (only VDI) are also shown.

Recovery from inactivation

Time constants of recovery from inactivation were assessed for I_Ba and I_Ca at various holding potentials, and are depicted in Fig. 4 with experimental results (Mahajan et al. 2008b). Recovery is faster at more negative E_m, with no differences between I_Ca and I_Ba.

Figure 4. Experimental (symbols) and simulated (lines) time constants of I_Ba and I_Ca recovery from inactivation obtained at varying holding potentials.

Recovery from inactivation assessed using a 250 ms long voltage-clamp pulse to +10 mV (P1) followed by repolarization to the various holding potentials for a variable time interval and a second pulse to 0 mV (P2). The time constant was estimated by fitting the recovery curve (ratio of the peak P2/P1 currents plotted as a function of recovery interval) to a monoexponential function.

I_Ca model validation

In Fig. 5 we assessed the robustness of the model by validating it in more physiological settings against experimental AP-clamp data from isolated ventricular myocytes from rabbit (Yuan et al. 1996; Puglisi et al. 1999; Linz & Meyer, 2000) and guinea pig (Linz & Meyer, 1998). Ca²⁺ influx via LTCC during an AP differs notably from that evoked by a square voltage pulse (Yuan et al. 1996), and our simulations confirm this (left vs. right). I_Ca peaks and inactivates more slowly during an AP (Fig. 5B), but the current integral is larger at the end of the AP command pulse (Fig. 5C). Supplemental Fig. S3 shows comparable simulated and experimental I_Ca (Linz & Meyer, 1998) (Fig. S3B) elicited by APs with different amplitudes (Fig. S3A). I_Ca peak decreases as AP amplitude (and upstroke potential) increases. The reduced influx also causes slower inactivation in each case.

Figure 5. Differences between step and AP-clamp.

Simulated (left) and experimental (right) (Yuan et al. 1996) E_m (A), I_Ca (B), and running integral of Ca²⁺ influx via LTCC (C). Simulated voltage step was from −80 mV to 5 mV, and AP waveform was obtained by pacing the virtual cell at 0.33 Hz to steady-state (with normal CaT).

The time courses of I_Ba and I_Ca during an AP (Fig. 6A) are depicted in Fig. 6B. When SR Ca²⁺ release is prevented, I_Ca inactivates more slowly (Fig. 6B), and the integral of Ca²⁺ influx through the channel is augmented (Fig. 6C). Furthermore, when addition of BAPTA is simulated, CDI is nearly absent, and I_Ca exhibits a prominent plateau and causes a much larger Ca²⁺ influx (Fig. 6B and C). Model predictions agree well with experimental results (Linz & Meyer, 1998) reported in Fig. 6A–C, right panels. In Fig. 6B and C, left, I_Ba is simulated with either the seven-state or the non-IDI five-state LTCC model.

Figure 6. Influence of Ca²⁺ homeostasis on I_Ca during AP-clamp.

AP waveform was obtained by pacing the virtual cell at 0.33 Hz to steady-state (with normal CaT). Simulated (left) and experimental (right) (reproduced from Linz & Meyer (1998) with permission) command AP (A), evoked current (B), and running flux integral (C) with normal CaT, without SR Ca²⁺ release, and BAPTA. I_Ba was also simulated with the baseline model and a reduced 5-state (VDI only) model. Experimental (top) (Linz & Meyer, 1998) and simulated (bottom) time course of current inactivation (E–G) during an AP was obtained with the GD-P protocol depicted in D. E, inactivation of I_Ca with CaT, I_Ca without SR Ca²⁺ release, I_NS, and I_Ba. F, experimental and simulated VDI, and CDI. G, experimental and simulated CDI_SR and CDI_LTCC.

Cell model validation

We also validated the comprehensive cellular AP and CaT model. To allow a direct comparison with existing rabbit models, time courses of AP and CaT (Fig. S4A), APD restitution properties (Fig. S4B), APD rate-adaptation (Fig. S4C) after sudden changes in cycle length, and frequency-dependent increase of systolic [Ca²⁺]_i and [Na⁺]_i (Fig. S4D) obtained with our model are superimposed to those obtained with the Shannon et al. (2004) and the Mahajan et al. (2008b) models as compared by Romero et al. (2011). Our model performs well when comparing simulated values of cardiac biomarkers (APD₉₀, APD triangulation, slow time constant of the temporal APD₉₀ adaptation to the accelerating rate, and maximal slopes of S1S2 and dynamic restitution curves) to the experimental range reported by Romero et al. (2011) (Table S4). Alternans developed in our model at a pacing cycle length ≤180 ms (Fig. S4E).

Analysis of inactivation mechanisms and sources of CDI

To estimate the contribution of VDI and CDI to total inactivation and further validate the model, we reproduced the experimental GD-P protocol designed by Linz & Meyer (1998) and illustrated in Figs 6D and S3B, inset. This protocol, by interrupting the AP at different times (see Methods), reveals the fraction of channels inactivated during an AP (1-availability; see Fig. S3C–E). Figure 6E–G show the progression of Ca²⁺ channel inactivation during the AP and how VDI and CDI contribute to it (experiments at top and simulations at bottom).

The time course of inactivation (Fig. 6E, lower panel) was assessed using this protocol for simulated I_Ca with and without SR Ca²⁺ release and I_Ba. Figure 6F shows the accumulation of CDI and VDI, estimated assuming that LTCC availability is the product of Ca²⁺- and voltage-dependent availability, as in (Linz & Meyer, 1998). The contribution of Ca²⁺ released from the SR to I_Ca inactivation (CDI_SR) was calculated as the difference between availabilities measured with and without SR Ca²⁺ release (Fig. 6G). Finally, the contribution of Ca²⁺ entry via I_Ca to inactivation (CDI_LTCC) was calculated by subtracting CDI_SR from CDI (Fig. 6G). We infer that SR Ca²⁺ release accounts for most of CDI during the initial AP phase, whereas Ca²⁺ through LTCC controls CDI later during the AP. Experimental results (Linz & Meyer, 1998) are shown in the upper panels of Fig. 6E–G. Non-specific monovalent current (I_NS, carried by Na⁺ and Cs⁺) via LTCC was used experimentally to assess VDI, rather than using our five-state VDI model (Fig. 1B).

The importance of SR Ca²⁺ release for CDI was also highlighted in AP-clamp experiments in rabbit ventricular myocytes at 35°C (Puglisi et al. 1999). Analogous to experiments, I_Ca traces evoked by APs subsequent to an initial SR depletion show increasingly faster inactivation (Supplemental Fig. S5A and B) as the SR is replenished and SR Ca²⁺ release increases (Fig. S5C). Normalized integrals of I_Ca during each pulse reveal that inactivation due to SR Ca²⁺ release decreases net Ca²⁺ influx by about 40%, similar to experimental data (Fig. S5D).

Effects of reduced VDI

Changes in the VDI transitions (as described in the Supplemental Material) caused a striking reduction in the steady-state inactivation curve (Fig. 7A), and led to AP prolongation (Fig. 7B). Notably, this reduced VDI did not modify I_Ca during the early repolarization and initial plateau phase, but rather during late AP phase 2 and 3 (Fig. 7C). Indeed, VDI monotonically increases during the AP and makes a larger contribution during repolarization (Fig. 6F vs. 7E). The time courses of CDI_SR and CDI_LTCC do not appear appreciably modified by removal of VDI (Fig. 7F).

Figure 7. Effects of reduced VDI.

A, quasi-SSI curves depict the available I_Ba (5-state model) after 1000 ms-long inactivation prepulses to the indicated voltages in control and reduced VDI conditions. Action potentials (B) and I_Ca (C) with normal CaT in control and reduced VDI conditions. D, simulated time course of current inactivation during an AP with reduced VDI for I_Ca with CaT, I_Ca without SR Ca²⁺ release, and I_Ba. E, simulated VDI and CDI. F, simulated CDI, CDI_SR and CDI_LTCC.

Effects of reduced CDI

We assessed the effects of impaired CDI on the cardiac AP by simulating the expression of CaM₁₂₃₄, which eliminates CDI of native LTCCs by displacing WT CaM that is otherwise normally prebound to the channels. LTCC inactivation slowed with increasing expression of CaM₁₂₃₄ (Fig. 8A and B) (Alseikhan et al. 2002; Mahajan et al. 2008a), which caused significant AP prolongation (Fig. 8C), as reported experimentally (Alseikhan et al. 2002), e.g. larger than that produced by comparable reduction of VDI in Fig. 7.

Figure 8. Effects of Ca²⁺-insensitive CaM overexpression.

A, experimental (reproduced from Mahajan et al. (2008a) with permission of Elsevier) normalized currents evoked by a voltage step from −80 mV to +10 mV for I_Ca without SR Ca²⁺ release (WT and CaM₁₂₃₄) and I_Ba. B, simulated normalized I_Ca without SR Ca²⁺ release (baseline, and with various degrees of impaired CDI). I_Ba traces are shown with the baseline model and a reduced 5-state model. C, simulated AP obtained when pacing the digital myocyte at a basic cycle length of 3 s in baseline conditions and with various degrees (indicated) of impaired CDI. D–S, simulated AP, I_Ca, I_NaCa, CaT, [Ca²⁺] in sub-sarcolemmal and cleft compartments, free SR Ca²⁺ content and SR Ca²⁺ release obtained when pacing the digital myocyte at a basic cycle length of 3 s in baseline conditions and with reduced CDI (20% reduction in D–K, and 50% in L–S). Insets in panels D and F show results obtained for the mutant condition by reducing instantaneously NCX density by 10% and 30%.

When 20% of the channels have Ca²⁺-insensitive CaM prebound, the model predicts the occurrence of EADs, as shown in Fig. 8D and 9A. We monitored the time courses of LTCC open probability, the opening rate (dO/dt), and contributions to dO/dt of transitions between open and closed states (activation/deactivation) or open and inactivated states (inactivation/recovery) during a control AP (Supplemental Fig. S6) and during the CaM₁₂₃₄-induced EAD (Fig. 10, left). Insets show enlargement of AP plateau near the EAD takeoff (i.e. when dE_m/dt became positive during AP plateau). This phenomenon does not depend on I_Ca reactivation (Figs 9A and B and 10B–D, left). In fact, LTCC open probability progressively declines (dO/dt is always negative) during the entire AP plateau and EAD (Fig. 10D, left, inset); channels are leaving the open state. Instead, these EADs are likely to be due to enhanced Ca²⁺ extrusion via inward Na⁺/Ca²⁺ exchange (NCX) current (I_NaCa, Fig. 8F). This I_NaCa is due to enhanced SR Ca²⁺ loading and spontaneous SR Ca²⁺ release (Fig. 8J) and elevated subsarcolemmal [Ca²⁺] ([Ca]_SL; Fig. 8H). We tested the role of I_NaCa by reducing NCX density instantaneously during the arrhythmogenic AP just before EAD takeoff. When I_NaCa was reduced by 10%, EAD amplitude was reduced (Fig. 8D and F, inset), whereas a 30% NCX reduction completely eliminated the EAD (Fig. 8D and F, inset).

Figure 9. Kinetics of I_Ca (B, F and J) during AP-clamp with EAD-like stimuli (A, E and I) assessed with the GD-P protocol.

Total I_Ca (with and without release) inactivation (C, G and K), VDI, CDI (D, H and L), and CDI_SR and CDI_LTCC were computed with 20% expression of CaM₁₂₃₄ (A–D), and block of I_Kr and I_Ks (E–H, simulations vs. experiments (reproduced from Yamada et al. (2008) with permission from Springer), I–L).

Figure 10. Time course of E_m (A), I_Ca (B), LTCC open probability (C) and its rate of changes (D), and contributions to dO/dt of channel transitions between open and closed (O-C), open and CD-inactivated (O-CDI), open and VD-inactivated (O-VDI), and open and inactivated (O-VDI and CDI) during an EAD caused by either CaM₁₂₃₄ overexpression (left) or K⁺ current blockade (right).

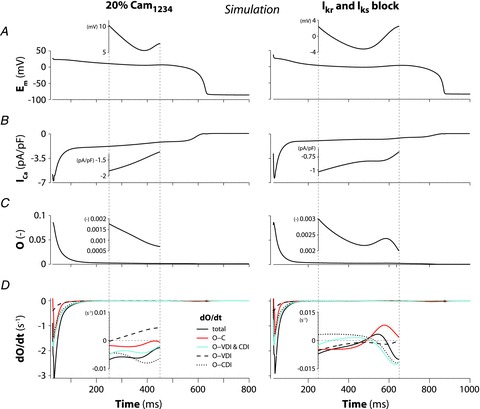
Insets show the time window corresponding to EAD takeoff (x axis limits are indicated with dotted lines in the main panels).

As CDI reduction increased to 40%, APD was futher prolonged, but no EADs occurred (Fig. 8C). Our explanation for the disappearance of EADs is that as CDI decreases the AP plateau potential becomes more depolarized, thus opposing inward I_NCX (the more depolarized E_m the less inward I_NCX), which is not large enough to cause membrane after-depolarization.

When the fraction of Ca²⁺/CaM-insensitive channels was increased to 50%, the AP prolonged further (Fig. 8L) due to the increased depolarizing I_Ca (Fig. 8M), which also further loaded the SR with Ca²⁺ (Fig. 8R). The high [Ca²⁺]_SR causes a large spontaneous Ca²⁺ release (Fig. 8R-S) which activates a large inward I_NaCa (Fig. 8N), sufficient to cause a delayed afterdepolarization (DAD) and triggered AP (Fig. 8L). A second DAD occurs after the first triggered AP, but the spontaneous SR Ca²⁺ release is slightly smaller, and fails to trigger an AP.

Effects of I_Kr and I_Ks block

We also examined AP prolongation due to complete block of both rapid and slow components of delayed-rectifier K⁺ current (I_Kr and I_Ks, Fig. 9E). As with the CaM₁₂₃₄-modified AP, we monitored the time courses of LTCC open probability and state transitions (Fig. 10B-D, right). In contrast with CaM₁₂₃₄ expression, under I_Kr and I_Ks block we clearly detected LTCC reactivation during EAD takeoff. In this case dO/dt turned positive (Fig. 10D, right, inset), indicating that more channels entered the open state (unlike the CaM₁₂₃₄ case). Further, this I_Ca reactivation during the EAD was not due to recovery from inactivation, but rather to reopening from the closed state. While the transition between inactivated and open states in Fig. 10D, right, inset, moved negative, indicating inactivation did increase (negative dO/dt), that between closed and open states moved more strongly positive, indicating a more than compensatory reactivation (resulting in dO/dt > 0).

I_Ca inactivation kinetics during EADs

We next evaluated I_Ca inactivation during APs that showed EADs. We used GD-P protocols based on the two types of exemplar APs described above, obtained at 0.33 Hz, one with 20% expression of CaM₁₂₃₄ (Fig. 9A) and the other with complete block of I_Kr and I_Ks (Fig. 9E).

As originally found by January & Riddle (1989), in our simulations EAD amplitude inversely correlated with takeoff potential (the more negative the takeoff potential the larger the EAD amplitude, as indicated in Fig. 9A and E). I_Ca decayed smoothly throughout the CaM₁₂₃₄-induced EAD (Fig. 9B), whereas it exhibited a notch upon EAD initiation (Fig. 9F) with inhibition of K⁺ currents. Notably, a similar hump in I_Ca was detected experimentally during the same type of protocol in guinea pig ventricular myocytes (Fig. 9I and J) (Yamada et al. 2008). I_Ca inactivation increased monotonically during the CaM₁₂₃₄-induced EAD (Fig. 9C), and so did its E_m- and Ca²⁺-dependent components (Fig. 9C and D respectively). On the other hand, with the EAD induced by K⁺ current block, I_Ca inactivation increased during the AP plateau, decreased slightly just before EAD takeoff, and increased again thereafter (Fig. 9G), as observed experimentally (Fig. 9K) (Yamada et al. 2008). In both simulations and experiments, VDI did not display any clear notch (Fig. 9G and K), whereas CDI showed a notch before EAD takeoff (Fig. 9H and L). Both CDI_LTCC and CDI_SR (defined as described in Methods) exhibited a hump prior to EAD initiation (Fig. 9H). However, we observed only a modest recovery of LTCCs from CDI before EAD takeoff.

Discussion

In the present study we developed improved LTCC and SR Ca²⁺ release models within the framework of the rabbit ventricular ECC model of Shannon et al. (2004). A recent paper investigated the differences between the Shannon et al. (2004) and Mahajan et al. (2008b) models of the rabbit ventricular AP, and showed that the former performs better at slow rates, the latter at fast rates (Romero et al. 2011). We conducted a model evaluation taking into consideration frequency-dependency mechanisms, and showed that steady-state APD and Ca²⁺ rate dependence (Fig. S4) are similar to those predicted by the parent Shannon et al. (2004) model, in good agreement with experimental data. Although we did not perform a systematic sensitivity analysis, we also expect the ionic mechanisms modulating electrophysiological properties to be similar.

Our main goal was to dissect the relative importance of VDI and CDI to total I_Ca inactivation during normal and abnormally prolonged APs. The AP model reproduces faithfully experimental properties of ventricular myocytes, including (1) the higher ECC gain at negative E_m, (2) the kinetics of LTCC inactivation (measured with both voltage steps and AP-clamps) under different Ca²⁺ homeostasis conditions and during EADs, (3) the SR Ca²⁺ release contribution to I_Ca inactivation during an AP, (4) the effects of Ca²⁺-insensitive CaM expression, and (5) the effects of delayed-rectifier K⁺ current inhibition. We used this improved model (1) to predict the effects of removal of VDI, (2) to study arrhythmogenic mechanisms in the presence of impaired CDI, and (3) to assess the involvement of I_Ca in EADs.

To differentiate VDI from CDI of macroscopic I_Ca, replacement of Ca²⁺ by other charge carriers (e.g. Ba²⁺, (Zhong et al. 1997; Sako et al. 1998; Sun et al. 2000; Sonoda & Ochi, 2001; Mahajan et al. 2008b) or Na⁺ and Cs⁺ (Hadley & Hume, 1987; Hryshko & Bers, 1992; Yuan et al. 1996)) has been widely used. In these studies, inactivation of I_Ba or I_NS has been assumed to reflect purely VDI. It is well known that Ba²⁺ can weakly mimic Ca²⁺ (Ferreira et al. 1997), and it seems clear now that Ba²⁺ can recapitulate a weak version of CDI. Indeed, I_Ba inactivation depends on Ba²⁺ influx, while it has been shown that I_NS inactivation is independent of the triggering current peak (see Fig. 1 in Brunet et al. (2009)). However, in a previous study (Grandi et al. 2010), we found that I_NS inactivation at physiological temperature is faster (vs. I_Ba) and complete, perhaps reflecting some intrinsic difference vs. VDI occurring during I_Ca or I_Ba. We concluded that both approaches lead to an overestimation of VDI. Here, we constrained our LTCC model parameters by accounting for reduced, but not eliminated, IDI when Ba²⁺ is the charge carrier, and adopted the reduced I_Ba model (5 lower states in Fig. 1B) to represent pure VDI.

We simulated the GD-P protocol to quantify the contributions of CDI and VDI to total inactivation, and to study the importance of different Ca²⁺ sources involved in this process (Fig. 6D–G), as in Linz & Meyer (1998). We found that I_Ca inactivation during an AP is predominantly CDI, which is mostly controlled by SR Ca²⁺ release during the initial AP phase, but mainly by Ca²⁺ entering through LTCCs for the remaining part. Linz & Meyer (1998) showed similar results in guinea pig cells, although they estimated a smaller contribution of the SR to CDI. Discrepancies between simulated and experimental results in Linz & Meyer (1998) may be explained by the authors’ choice of measuring I_NS to assess pure VDI, since we have shown this assumption leads to overestimation of VDI (Grandi et al. 2010). Furthermore, there may be differences in LTCC control by Ca²⁺ in guinea pig vs. rabbit myocytes. In fact, we found that I_Ca inactivation due to SR Ca²⁺ release decreases net Ca²⁺ influx by about 40%, which is just a little less than that which Puglisi et al. (1999) showed in rabbit myocytes (Fig. S5).

We based our analysis of CDI and VDI on the classic Hodgkin–Huxley formulation, where the activation and inactivation gating parameters do not represent specific kinetic states of ion channels and are independent, and their product modulates the current (as I_Ca in the original Shannon et al. (2004) model, inherited from the Luo–Rudy model (Luo & Rudy, 1994a)). However, the structure of the Mahajan et al. (2008b) Markovian model here adopted allowed us to discriminate the contributions of CDI and VDI by monitoring transitions from the open state to closed and inactivated states (Figs 10 and S6), as further discussed below.

Several computational studies have acknowledged the importance of developing a detailed kinetic model of LTCC (Imredy & Yue, 1994; Jafri et al. 1998; Sun et al. 2000; Findlay, 2002a,b; Faber et al. 2007; Mahajan et al. 2008b; Hashambhoy et al. 2009), due to its fundamental role in ECC in cardiac myocytes (Bers, 2001). Imredy & Yue (1994) first introduced a Ca²⁺-dependent mode (‘Ca²⁺ mode’) to separate CDI and VDI in a rat LTCC model, which was extended by Jafri et al. (1998) with two mirroring ‘normal’ structures and a ‘Ca²⁺’ gating mode structure. Faber et al. (2007) conserved the two-mode ‘mirror’ structure with a more complex description of the inactivation pathways, whereas Mahajan et al. (2008b) proposed the minimal Markovian LTCC formulation that is extended in the present paper. The latter models were accompanied by improved formulations of SR Ca²⁺ release and integrated into existing AP models (respectively, guinea pig (Luo & Rudy, 1994a) and rabbit (Shannon et al. 2004)). In both models I_Ba was used for fitting of VDI. Faber et al. (2007) and Mahajan et al. (2008b) found that CDI plays a greater role at negative E_m during voltage pulses, due to higher ECC gain. In fact, Mahajan et al. (2008b) indicated that CDI_SR is more important at negative voltages, while Ca²⁺ entering the cell dominates CDI at positive E_m. As for the time course of inactivation, Faber et al. (2007) reported an early dominance of SR Ca²⁺ release in controlling CDI, and a late dominance of sarcolemmal Ca²⁺ influx, in agreement with our findings with AP-clamp.

The need for a faithful characterization of the roles of VDI and CDI has been underlined by experimental studies showing the deleterious effects of inhibiting one of the two mechanisms. Alseikhan et al. (2002) showed the effects of CaM₁₂₃₄ expression, which inhibits CDI and produces dramatic AP prolongation, whereas Splawski et al. (2004) showed the effects of the G406R mutation that removes VDI and is linked to the Timothy syndrome. The effects of Timothy syndrome have been investigated in simulation studies (Sung et al. 2010; Faber et al. 2007; Zhu & Clancy, 2007; Thiel et al. 2008). The notion that gene mutations linked to disease may interfere both with VDI and CDI is intriguing (Yarotskyy et al. 2009), although not yet fully understood. Also, shifts in VDI could alter intracellular Ca²⁺ handling and signalling, which could in turn contribute to the Timothy syndrome phenotype (Thiel et al. 2008). In this study, removing VDI, while retaining CDI, caused AP prolongation (Fig. 7). Notably, when simulating the expression of CaM₁₂₃₄, which removes CDI without affecting VDI (Alseikhan et al. 2002), we predicted a much more marked APD prolongation (Fig. 8), confirming previously observed experimental (Alseikhan et al. 2002) and simulation (Mahajan et al. 2008a) results.

We predicted the occurrence of EADs when CDI was reduced, or with further CDI reduction, DADs. The latter occurred when residual CDI was small enough so that added Ca²⁺ influx caused SR Ca²⁺ overload and spontaneous release, with consequent activation of enough transient inward NCX current (I_ti) to depolarize the membrane beyond threshold (Priori & Corr, 1990). With a smaller reduction in CDI, not sufficient to harmfully overload the cell, EADs occurred during the AP plateau (phase 2). Depolarization during phase 2 EADs has been attributed to reactivation of I_Ca (January & Riddle, 1989; Luo & Rudy, 1994b; Zeng & Rudy, 1995; Yamada et al. 2008). However, in our simulation of CaM₁₂₃₄ overexpression, I_Ca did not reactivate, but rather continued to inactivate (Fig. 10B–D, left). NCX is typically considered responsible for EADs occurring in AP phase 3 (Luo & Rudy, 1994b; Milberg et al. 2008), where the more negative E_m and increased [Ca²⁺]_i due to spontaneous Ca²⁺ release both favour inward exchange current. Here, we predicted that changes in Ca²⁺ cycling due to reduced CDI caused greater Ca²⁺ extrusion, spontaneous SR Ca²⁺ release (relying on the modified description of RyR gating), and sufficient inward NCX current to cause frank depolarization (Fig. 8). In support of this, when reduced NCX activity was imposed in the simulation, the EAD disappeared (Fig. 8D and F, insets). Indeed, Priori & Corr (1990) proposed that EADs and DADs might share the same mechanism, with NCX-mediated inward current being involved also in the genesis of EADs, as proposed for example in cardiac hypertrophy (Sipido et al. 2000).

Phase 2 EADs most typically occur when repolarization is prolonged due to alterations in K⁺ or Na⁺ currents. We obtained a phase 2 EAD due to I_Ca reactivation by blocking I_Kr and I_Ks (Fig. 9), and used this AP waveform to analyse the kinetics of I_Ca during abnormal repolarization, as done experimentally by Yamada et al. (2008). They have suggested that EADs occur because I_Ca fails to completely deactivate, as opposed to significantly recovering from CDI. Indeed, EADs we obtained with I_Kr and I_Ks blocked were driven by LTCCs reactivating from the closed state (E_m-independent transition, see Fig. 1B) and not by recovery from either inactivated state (Fig. 10D, right). This would be hard to test unequivocally in experiments, but if stable EADs (in current clamp) could be interrupted by a voltage clamp step one could assess I_Ca availability and distinguish between the two. However, since the model fits the experimental kinetics of recovery from inactivation and of activation/deactivation, this interpretation seems most likely. In our simulations with the GD-P protocol we found that I_Ca inactivation exhibited a notch before EAD takeoff, whereas VDI did not (Fig. 9G), as was also found experimentally by Yamada et al. (2008). Despite the fact that CDI (including both CDI_SR and CDI_LTCC components) had a notch, the net recovery afterward near the time of takeoff was at best modest (Fig. 9H). Thus both the state analysis and the GD-P assay call into questions the importance of recovery from inactivation for EAD initiation (Yamada et al. 2008).

Conclusion

Our I_Ca model allowed us to investigate realistically the effects of CDI changes in normal and prolonged APs. We predicted that CDI is crucial for AP repolarization (while VDI is less so), and showed that impairment of I_Ca CDI may be arrhythmogenic by affecting intracellular Ca²⁺ cycling, through its effect on the time course of LTCC Ca²⁺ fluxes and thus NCX. We conclude that our improved model is a useful tool to study the role of I_Ca kinetics during normal and altered repolarization at the single cell level, and given its computational tractability it could be incorporated in tissue-scale/whole heart models to test how these cellular instabilities can induce arrhythmias. Further work will be required to incorporate modulation of I_Ca gating by other molecules involved in its regulation, such as PKA and CaMKII, as has been described in previous studies (Findlay, 2002a; Saucerman et al. 2003; Hashambhoy et al. 2009, 2010; Soltis & Saucerman, 2010).

Glossary

AP

action potential

APD

action potential duration

CaM

calmodulin

CaT

Ca²⁺ transient

CDI

Ca²⁺-dependent inactivation

CDI_LTCC

LTCC-mediated CDI

CDI_SR

SR Ca²⁺ release-mediated CDI

DAD

delayed afterdepolarization

dO/dt

rate of changes of LTCC open probability

EAD

early afterdepolarization

ECC

excitation–contraction coupling

E_m

membrane potential

GD-P

gapped double-pulse

I_Ba

barium current

I_Ca

calcium current

IDI

ion-dependent inactivation

I_Kr

rapid delayed-rectifier K⁺ current

I_Ks

slow delayed-rectifier K⁺ current

I_NaCa

Na⁺/Ca²⁺ exchange current

I_NS

non-specific monovalent current

I_Peak

peak current

I_Ped

pedestal current

I_ti

transient inward current

LTCC

L-type Ca²⁺ channel

NCX

Na⁺/Ca²⁺ exchanger

RyR

ryanodine receptor

SR

sarcoplasmic reticulum

SSI

steady-state inactivation

VDI

voltage-dependent inactivation

WT

wild type

Author contributions

E.G. and D.M.B. conceived and designed the study, S.M., E.G., A.S., K.S.G. and D.M.B. collected, analysed and interpreted the data, S.M. and E.G. drafted the article, K.S.G. and D.M.B. revised the article critically for important intellectual content. All authors have approved the final version. The study was performed at the Department of Pharmacology, University of California Davis, and at the Department of Electronics, Computer Science and Systems, University of Bologna, Cesena.

Supplemental Data

Table S1

Table S2

Table S3

Table S4

Figure S1

Figure S2

Figure S3

Figure S4

Figure S5

Figure S6