A murine experimental model for the mechanical behaviour of viable right-ventricular myocardium

Abstract

Although right-ventricular function is an important determinant of cardio-pulmonary performance in health and disease, right ventricular myocardium mechanical behaviour has received relatively little attention. We present a novel experimental method for quantifying the mechanical behaviour of transmurally intact, viable right-ventricular myocardium. Seven murine right ventricular free wall (RVFW) specimens were isolated and biaxial mechanical behaviour measured, along with quantification of the local transmural myofibre and collagen fibre architecture. We developed a complementary strain energy function based method to capture the average biomechanical response. Overall, murine RVFW revealed distinct mechanical anisotropy. The preferential alignment of the myofibres and collagen fibres to the apex-to-outflow-tract direction was consistent with this also being the mechanically stiffer axis. We also observed that the myofibre and collagen fibre orientations were remarkably uniform throughout the entire RVFW thickness. Thus, our findings indicate a close correspondence between the tissue microstructure and biomechanical behaviour of the RVFW myocardium, and are a first step towards elucidating the structure–function of non-contracted murine RVFW myocardium in health and disease.

Key points

• Right-ventricular (RV) function is an important determinant of cardio-pulmonary performance. How and when RV failure occurs in disease is poorly understood. RV biomechanics provides a means to understand tissue level behavior that links cellular mechanisms to organ level phenotype. RV biomechanics has received little attention.

• We developed 1) rat model for quantifying the structure and biomechanical behavior of viable and transmurally intact RV tissue, and 2) a novel analysis method for obtaining representative scalar strain-energy function from stress-controlled biaxial experiments.

• The mechanical testing revealed a marked mechanical tissue anisotropy with the apex-to-outflow tract direction being the stiffer direction.

• The myo- and collagen fibers show a preferential alignment from the apex to the RV outflow tract direction with little transmural variation.

• We found a strong relationship between normal tissue microstructure and biomechanical behavior, which lays the foundation for a detailed understanding of RV remodeling in response to disease.

Introduction

Myocardial wall stress is of central importance in the understanding and simulation of cardiac function. It is a major determinant of myocardial oxygen consumption, as well as an important signal governing adaptive hypertrophy in otherwise healthy ventricular tissue (Yin, 1981). A mechanistic understanding of this dynamic adaptation requires understanding of how the primary structural constituents (myofibres and collagen fibres) respond, and how their interaction contributes to the overall tissue response. Such mechanistic understanding can lead to time-evolving constitutive models of myocardial function and the remodelling processes. In addition to the more commonly studied left ventricle (LV), right ventricular function is also a major determinant of cardiac performance. Specifically, it is an important predictor of patient outcomes in pulmonary hypertension, which can impose a significant pressure load on the right ventricle (RV) (Voelkel et al. 2006). Such a load can lead to pronounced remodelling, resulting in progressive myocyte enlargement (hypertrophy), extracellular matrix proliferation, chamber dilatation, weakening of the ventricular wall, and ultimately mechanical failure of the ventricle (Bogaard et al. 2009). The structural and functional changes associated with this remodelling process at the tissue level of the right ventricular myocardium can consequently affect the LV, leading to failure of the entire heart. Currently, no organ-level measure exists to monitor the progression of ventricular hypertrophy to failure, as it has been difficult to connect tissue-level changes to organ-level performance, in particular RV biomechanics.

As stress cannot be measured directly but rather must be computed, a constitutive model (stress–strain relation) must be established to determine the time-varying wall stress within a simulation framework (Nordsletten et al. 2011), and has been an active research area (Yin, 1981; Weber et al. 1983; Halperin et al. 1987; Glass et al. 1991; Nash & Hunter, 2000). Driven by the need to understand the cellular and fibrillar mechanisms, current research is focused on the development of constitutive models that are framed in terms of tissue constituents. Termed ‘structural’, these models use the properties of the underlying fibre micro-structure as a foundation (Lanir, 1983). Such approaches simulate tissue-level behaviours using model parameters that have a direct physical meaning, and are therefore ideal to elucidate changes in normal and pathological conditions (Lanir, 1979, 1983; Horowitz et al. 1988; Billiar & Sacks, 2000; Holzapfel & Gasser, 2000; Sacks, 2003; Holzapfel & Ogden, 2009). While such approaches have been attempted in the myocardium (Horowitz et al. 1988; Holzapfel & Ogden, 2009), a key limitation in developing computational models of the RV, and indeed of the heart overall, has been the paucity of experimental data on the multiaxial stress–strain relationships of viable myocardium from which to construct realistic models of ventricular myocardial function. Indeed, the only reported right ventricular multiaxial mechanical data have been from canine (Sacks & Chuong, 1993a) and bovine (Ghaemi et al. 2009) myocardium. These studies utilized techniques similar to the LV (Demer & Yin, 1983; Strumpf et al.; Yin et al. 1986, 1987; Shacklock, 1987; Humphrey et al. 1990a; Smaill & Hunter, 1991; Lin & Yin, 1998; Dokos et al. 2002). In these investigations, the authors utilized partial-thickness myocardial tissue specimens, which resulted in unavoidable tissue damage. Furthermore, in most work to date, no reference to the state of viability of the specimens was made. Lin & Yin (1998) were the only investigators to report multi-axial mechanical data from viable myocardial specimens in their work on the LV free wall, though these investigators also sectioned the myocardium and studied partial-thickness tissue samples. Sectioning both the edges as well as the upper and lower surfaces of the specimens can introduce artifacts in the mechanical responses due to disruption of the connective tissue and damage to the myocytes in the vicinity of the cutting planes. Before realistic constitutive models of viable ventricular myocardium can be developed, a method is first required to obtain reproducible multi-axial mechanical responses of viable, minimally damaged ventricular myocardium.

Much work has also focused on elucidating the detailed myocardial myofibre and connective tissue architecture (Borg & Caulfield, 1981; Robinson et al. 1983; Young et al. 1998; Pope et al. 2008). Chuong et al. (1991) were the first to demonstrate a direct association in the right ventricular free wall (RVFW) between the transmural myofibre architecture and the direction of greatest contraction in a canine experimental model. This relationship was in contrast to the LV, where for example Waldman et al. (1985) demonstrated that transmural variation in the principal axis of strain in the LV did not correlate to the transmural change in fibre orientation. This may be due to the LV's more complex deformation patterns and its interrelations with the local myofibre structure (Streeter et al., 1969). This led us to posit that the close association between the fibre direction and the RVFW mechanical response is due to the unique planar nature of the RVFW fibre structure and its thin-walled geometry. We thus hypothesize that the myofibre and collagenous fibrous components of viable RVFW myocardium, are the primary determinants of the RVFW myocardium mechanical response at the tissue level. Moreover, a complete understanding will ultimately require sophisticated computational biventricular models of the heart. These will require detailed knowledge of the mechanical behaviour of active RFVW myocardium under physiologically realistic multi-axial conditions. We thus further hypothesize that by utilizing structurally consistent, viable murine RVFW specimens a truly representative tissue-level strain-energy function of viable ventricular myocardium can be obtained.

To test these hypotheses, we developed a method to elucidate the biomechanical properties of transmurally intact, viable right ventricular myocardium. We utilized a murine myocardial experimental model that exploits the small size of the resultant tissue samples, allowing for mechanical evaluation of full-thickness RVFW tissue specimens while allowing for specimen viability. We assessed the local myocardial structure by quantifying the transmural myofibre and collagen fibre architecture. Finally, we developed a method to generate a representative scalar strain-energy function from the set of individual specimen stress–strain responses. This allowed us to determine representative characteristics of murine RVFW properties that can be used in our ongoing work on the development of constitutive models for normal and pathological myocardium. The presented structural and functional data in this animal model also help to support specific constitutive models of the RV. Our goal is to use this work to start building the modelling framework of the RV.

Methods

Animal choice and considerations

Several factors entered into our choice of an animal model. First, the choice should allow for sufficiently large full-thickness RVFW tissue samples for mechanical evaluation, yet be sufficiently thin for the viability of the tissue to be maintained ex vivo using a simple oxygen-rich bath (Lipinski, 1989). The small ratio of sample thickness to sample length/width is also important, as it allows for the tissue to be treated as essentially planar, without the need for sectioning the upper and lower surfaces. Being transmurally intact in our ex vivo setting, the specimens have the specific advantage of retaining the full-thickness myocardium (without the need for transmural sectioning as has been done by prior studies). This preparation facilitates greater structural integrity by minimizing the damaged tissue area to the edges of the specimen. Finally, the animal model should allow for the study of myocardial remodelling due to different pathological conditions, especially pulmonary hypertension (Takimoto et al. 2005; Faber et al. 2006). We thus chose a murine model, which satisfied these criteria.

Tissue source and preparation

The experimental protocol of this study was approved by the University of Pittsburgh Institutional Animal Care and Use Committees, and the animals were kept in accordance with the Guide for the Care and Use of Laboratory Animals (Science C.o.L., 1996). A total of 14 male 8-week-old Sprague–Dawley rats were used, each weighing approximately 200–250 g at the time of sacrifice. On the day of testing, the animal was anaesthetized using 5% isoflurane. After a midline thoracotomy, the animal was partially exsanguinated and the heart removed along with the proximal segments of the great vessels. Next, the heart was arrested by placing it in cardioplegic solution (Lin & Yin, 1998) and transported in an iced container to the biomechanical testing facility. We isolated the RVFW by cutting the apex of the heart transversely, identifying the RV chamber, and then dissecting along the inter-ventricular septum. During the isolation process, we placed adhesive markers on the epicardium, identifying the apical region and the outflow tract of the tissue sample with red and black beads, respectively (Fig. 1A).

Figure 1. Specimen preparation and orientation.

A, intact rat heart with sample tissue location indicated, and pulmonary artery (PA) cannulated. The right ventricle is delineated with blue beads, the outflow tract (OT) region with black beads and the right ventricular apical region (Apex) with red beads. The rectangle indicates the selection of the tissue samples; X₁: apex-to-outflow-tract (preferred) direction; X₂: cross-preferred direction. B, example of a full-thick RVFW specimen; the four blue markers delineate the region of structural and mechanical analysis. C, histological section (25 μm thickness) of the midwall RVFW stained with Masson's trichrome. The section shown is 400 μm from the endocardial surface and shows strong preferred myofibre alignment along the apex-to-outflow tract direction (X₁ direction).

From the isolated RVFW, rectangular tissue specimens were cut such that the long axis was aligned from the outflow tract to the apex, and the short axis perpendicular to it. To test our hypothesis that the myofibre and collagenous fibrous components of viable RVFW myocardium are the primary determinants of the RVFW myocardium mechanical response at the tissue level, we also isolated rectangular tissue specimens such that the sample's long axis was at a 45 deg angle to the apex to outflow tract direction. We strived to maximize the area of the tissue sample, while also keeping the thickness as constant as possible. We measured the tissue sample thickness using a dial gauge (Starrett, Athol, MA, USA. No. 1010), and the length and width using a digital caliper (Mitutoyo Kawasaki, Japan).

Viability study

To determine the time window for mechanical testing of viable myocardium, we carried out a viability study in the following preliminary study. Hearts were harvested and immediately placed into a cardioplegic solution of the following composition (in mm): NaCl, 110; NaHCO₃, 10; KCl, 16; MgCl₂, 16; CaCl₂, 1.2 (Lin & Yin, 1998). After 30 min in cardioplegic solution, the RVFW tissue samples were placed in the biaxial testing device (Biotester 5000, CellScale Biomaterials Testing), where the sample was bathed with a modified Krebs solution (without any BaCl₂), oxygenated, and kept at 37°C. The modified Krebs solution consisted of (in mm): NaCl, 127; KH₂PO₄, 1.3; MgSO₄, 0.6; NaHCO₃, 25; KCl, 2.3; CaCl₂, 2.5; dextrose, 11.2; 2,3-butanedione 2-monoxime (BDM), 30 (Lin & Yin, 1998). Under displacement control, a minimal strain level was applied (0.5%) and the elongation was held for 100 s. During the constant displacement control, the device continuously measured the developed force of the tissue. Once the measured force was constant, the tissue was simultaneously chemically and electrically stimulated and the induced force was measured. Chemical stimulation consisted of successively adding BaCl₂ to the modified Krebs solution to reach concentrations of 0.5 mm, 1.0 mm, and 1.5 mm, which resulted in tissue contraction (Lin & Yin, 1998). Electrical stimulation was provided via a voltage pulse train from a pulse stimulator (Grass Technologies, Stimulator Model S48). Electrodes were placed such that homogeneous contractions were observed throughout the myocardium. The applied voltage was varied from 0 V to 4.5 V with a pulse width of 10 ms and a repetition rate of 5 pulses s⁻¹. To confirm contraction in response to the chemical and electrical stimulation, the induced forces were recorded under displacement control. Chemical and electrical stimulation was repeated at regular intervals to determine at what time the tissue ceased to respond.

Mechanical evaluation

Seven total tissue specimens underwent biomechanical testing using a custom-built biaxial device as described in detail in Grashow et al. (2006). Briefly, four graphite markers were attached to the epicardial surface of the central third of the RVFW specimens for optical tracking of displacement (Fig. 1B). The biomechanical testing was therefore focused on the central third region of the specimens. Four stainless steel hooks were attached to each side of the specimens and connected to eight equal-length loops of 000-nylon sutures for force transduction to two load cells. The edges of each specimen were aligned with the principal testing directions of the biaxial testing device. The specimens were bathed in an oxygenated modified Krebs solution containing 30 mm BDM (Lin & Yin, 1998) and kept at room temperature. Weight, thickness and dimension measurements were taken at every step of the tissue sample preparation, and before and after biaxial testing.

To estimate the systolic stress level of the rat RV outflow tract, we utilized Laplace's law for cylindrical geometry and set the maximum load to be 25 kPa, which is approximately five times the estimated stress, to explore the estimated range of normal and hypertensive tissue stress levels. The calculation of peak wall stress on the basis of Laplace's law provides an estimate of wall stress (Fung, 1993b). The calculations are based on a peak systolic pressure of 22 mmHg (Kass et al. 2012), an RV outflow tract diameter of 2 mm, and a wall thickness of 0.6 mm. The results of this calculation were purely used for the purpose of establishing an initial experimental condition.

From the marker positions, the deformation gradient tensor F was calculated for each loading cycle using standard methods (Grashow, 2005). From F, the components of the Green–Lagrange strain tensor E were calculated using E= 1/2(F^TF−I), where I is the identity tensor. We noted that the shear components of F were negligible in all test specimens, the in-plane components of E could be determined using 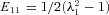and 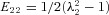, respectively, where the λ_i are the (principal) stretches along the X₁ and X₂ axes, respectively (Fig. 1). The First Piola–Kirchhoff stress tensor P was calculated from the measured loads and the initial specimen dimensions, and the second Piola–Kirchhoff stress tensor S was determined using S=PF^−T (Fung, 1981), which was used to compute the run-time stress levels. We note that due to the loading conditions of the planar biaxial experimental configuration, S₁₃=S₂₃=S₃₃= 0 and E₁₃=E₂₃= 0, with E₃₃ computed using the assumption of isovolumic deformation (i.e. incompressible) due to the high water content of the tissue.

Each specimen first underwent a preconditioning step that consisted of an equibiaxial stress-controlled protocol of 25 kPa. This was followed by a sequence of five stress-controlled biaxial testing protocols of S_11max:S_22max= 5–25, 15–25, 25–25, 25–15, and 25–5 kPa. Each protocol consisted of 10 loading and unloading cycles, from which the data of the 10th loading cycle was used for our analysis. After each cycle the specimen returned to the state corresponding to an initial tare load of 0.25 ± 0.05 g. To determine the level of mechanical stability and reproducibility of the mechanical response, we carried out experiments that additionally included two equibiaxial (S_11max=S_22max= 25 kPa) stress protocols, one right after preconditioning and one at the conclusion of the five-protocol sequence outlined above. The three equibiaxial stress states responses were then compared for consistency.

Representative biomechanical response

In the present work, we sought to determine a representative biomechanical response from the combined data. Note that in the following we adopt the formalism of a constitutive model, but our intent is to utilize this only as a means to assess our ability to determine a representative strain energy function. We first follow the common assumption that biological tissues can be modelled as hyperelastic materials (Fung, 1993a), in which the stress state can be derived from a scalar potential function and is thus independent of loading history. Further assuming tissue incompressibility, we can thus express the tissue-level stresses in terms of the strain and the strain-energy function W according to

(1)

where S is the second Piola–Kirchhoff stress tensor, E the Green–Lagrange strain tensor, p is a Lagrange multiplier to enforce incompressibility, and C=F^TF is the right Cauchy–Green tensor (Sacks, 2003). Since S₃₃= 0, p can be algebraically eliminated so that S₁₁ and S₂₂ are expressed in terms of experimentally measured forces and deformations, as well as the material constants (Sacks, 2000).

While the stress-control protocol was designed to achieve the same stress component space across specimens, the resultant strain responses varied from specimen to specimen. This prevented direct averaging of the W(E) from each specimen since they result in differing strain ranges. Note too that averaging the model parameter values in a non-linear constitutive model is not a valid method to obtain a mean or representative parameter set. To address these issues, we first determined a complementary energy density function W^c=W^c(S), which expresses the stored complementary energy per unit mass, and is determined from the experimental data using:

(2)

For the present study the functional form of W that fit the RVFW data was, in indicial form:

(3)

This form has the advantage of being directly invertible, as opposed to resulting in an implicit function as is the case with the commonly used Fung-type exponential form (Fung, 1993). Since the shear components (S₁₂) were negligible, differentiating eqn (3) with respect to the Green–Lagrange strain yields expressions for the stress components:

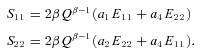(4)

Solving for E₁₁ and E₂₂ yields

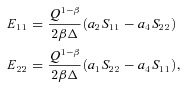(5)

where 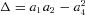. Substituting eqn (5) for E₁₁ and E₂₂ into eqn (3), allowed for Q to be expressed as an explicit function of the stresses S₁₁ and S₂₂

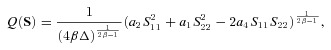(6)

so that the corresponding complimentary strain energy density function is given by

(7)

Using a Gauss–Newton algorithm (Matlab, version 7.12.0, The Mathworks, Inc., Natick, MA, USA), the optimal values for β, a₁, a₂, a₄ for each specimen were obtained using eqn (5). A coefficient of determination R² and the root mean square (RMS) error were used to assess the fits to the individual data sets.

Using these optimal parameter sets, we evaluated each specimen's W^c (eqn (7)) over a grid of equally spaced S₁₁–S₂₂ coordinates that were defined as the Cartesian product of S₁₁ and S₂₂ in which each coordinate ranged between 0 and 25 kPa. We then computed the representative (average) by averaging the individual W^c in a point-by-point manner in the common S₁₁–S₂₂ space. From the resultant average complementary energy function, the representative parameter set was obtained as above. By numerically differentiating the upper and lower bounds of the averaged complementary energy function 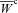, we derived bounds on the average stress–strain relationships and the representative (average) strain-energy .

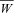Quantitative structural information

To evaluate the key structural features, and in particular the transmural range in fibre structure, we investigated the structure of the two primary tissue constituents: myofibres and the collagenous extracellular matrix (ECM) fibres. Compared to extensive work on other species, little work has been done on murine fibre architecture, and in particular the RVFW. We therefore sought to understand the relationship between myofibre and ECM fibre alignment and how the fibre architecture varies transmurally from endo- to epicardium. Such structural information is a key component of a mechanistic modelling approach of the constitutive relation in normal and remodelled RV myocardium.

We investigated the fibre orientation of both intact and decellularized specimens. In the intact tissue, we quantified the myofibre orientation in two specimens, which were sectioned transmurally at 25 μm thickness and subsequently stained with Masson's trichrome stain. Six measurements of the local average myofibre orientation were performed manually per slide with reference to the apex-to-outflow tract direction (defined as 0 deg from the X₁ axis, Fig. 1). To quantify the fibre orientation of the ECM alone, we decellurized 10 intact specimens using the technique from Nagatomi et al. (2005). Briefly, this protocol consisted of sequential exposure of specimens to a Tris-buffered solution with 0.1% phenylmethylsulfonyl fluoride (PMSF), 1% Triton X-100, and 0.1% SDS for 48 h each. To prevent loss of the graphite markers, the specimens were placed securely in cell strainers, while on a stirring plate at room temperature. At the conclusion of the decellularization procedure, the specimens underwent a phosphate-buffered saline (PBS)–glycerol gradient dehydration protocol (Joyce et al. 2009).

Next, we quantified the collagenous structure utilizing small-angle light scattering (SALS), which has been extensively described (Sacks & Chuong, 1992; Sacks et al. 1997; Sacks & Schoen, 2002). In brief, monochromatic, non-polarized laser light (HeNe laser, λ= 638.2 nm) is passed through the specimen. The spatial intensity distribution of the resulting scattering pattern is recorded and allows determination of the local fibre orientation within the light beam (Sacks, 2004; Joyce et al. 2009). To study the transmural variation in collagen fibre orientation, two decellularized specimens were paraffin preserved and subsequently sectioned from endo- to epicardium into slices of 25 μm thickness. By slicing the full-thickness specimens and repeating SALS measurements on the individual tissue sections, we were able to compare transmural variations in tissue architecture with the results from the full-thickness tissue evaluation. Since the biomechanical measurements are made on the central third of the rectangular specimens, the structural analyses focused on that region. Summary statistics are reported as average and standard deviations across all specimens. The level of local fibre alignment around the dominant fibre orientation from the SALS measurements are reported as a percentage value of the orientation index or normalized orientation index (Joyce et al. 2009).

Results

Viability study

Stable active contraction was found to be inducible and maintained for at least 3 h after harvesting. Peak developed forces of 15 mN were recorded with electrical stimulation of 2 V and 1.5 mm BaCl₂. Two representative examples of the stable active contraction that were obtained in a specimen at 78 and 180 min after harvesting (Fig. 2A and B). The results from this viability study demonstrated that the window for mechanical testing of our specimens is at least 3 h following harvesting of the heart.

Figure 2. Representative results of the viability tests by simultaneous electrical (black bar) and chemical stimulation.

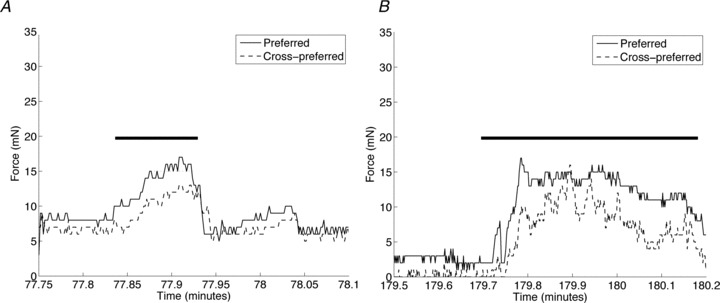
Developed force 78 min post-harvesting (A), and developed force 180 min post-harvesting (B), both showing strong contractile responses, demonstrating tissue viability at three hours post-harvest.

Quantitative structural information

Analysis of the histological slices of the intact RVFW (Fig. 1C) demonstrated a mean preferred myofibre orientation of 5.2 ± 0.3 deg, where 0 deg corresponds to the long axis of the specimen (apex-to-outflow-tract direction). For each specimen, the preferred myofibre orientation varied from –12.7 deg to 22.6 deg in one specimen and –11.8 deg to 18.7 deg in the other, resulting in a range in myofibre orientation across the ventricular wall of 35.3 deg and 30.5 deg, respectively (Fig. 3C). Collagen structural measurements of decellularized specimens revealed an average fibre orientation across all specimens of –16 ± 12.3 deg, as well as a high degree of local fibre alignment (Fig. 3A). Specifically, in the centre third region a mean normalized orientation index of 48.1 ± 5.3% was obtained (Fig. 3B). The dominant collagen fibre orientation varied little from endo- to epicardium. The full range of transmural collagen fibre variation was 46.6 deg and 31.4 deg in the two specimens studied. The range of collagen fibre variation across the RVFW (46.6 deg and 31.4 deg) is similar to that of the myofibres (35.3 deg and 30.5 deg). The results of the myofibre and collagen fibre orientations for one specimen are shown in Fig. 3C. The myofibre and collagen fibre orientations are therefore both closely aligned with the apex-to-outflow tract direction and are consistent with the results from mechanical behaviour.

Figure 3. Structural analysis of RVFW specimen.

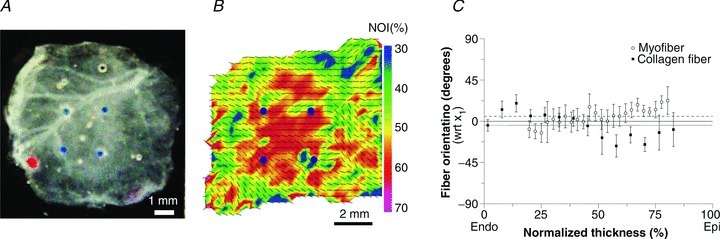
A, RVFW specimen after decellularization. B, collagen fibre architecture of decellularized specimen as measured by SALS. The vector field represents the local dominant collagen fibre orientations, which shows a strong alignment with the apex-to-outflow tract direction. The normalized orientation index (NOI) codes the degree of local fibre alignment, which is very high in the region of mechanical testing, indicating that the local fibre orientation is almost uniformly oriented along the X₁ direction. C, transmural myofibre and collagen fibre orientations showing very little variation around 0 deg line (corresponding to the apex-to-outflow-tract direction).

Mechanical evaluation

Specimens were on average 0.64 ± 0.06 mm thick and had surface dimensions of 7.3 ± 0.6 mm × 9.6 ± 1.2 mm. The mean time between harvesting and initiation of mechanical testing was 89 ± 5 min, with an additional mean time for biaxial testing of 51 ± 2 min. Thus, all testing was completed within the viability time window. Moreover, the testing protocol was reproducible and led to stable mechanical tissue responses.

For each specimen we computed the ratio of the maximum deviation from the mean stress–strain response (numerator) to the mean stress–strain response (denominator) in order to quantify the degree of reproducibility of the equibiaxial protocols. We report the average across all specimens as the mean maximum relative deviation. The responses from the preferred direction were stable (mean maximum deviation of 16%) whereas the responses from cross-preferred direction were remarkably stable (mean maximum deviation of only 6% and no statistically significant difference was found among the three equibiaxial stress protocols among all specimens). Under the equibiaxial stress state (S₁₁=S₂₂), the RVFW myocardial tissue demonstrated a consistent anisotropic behaviour, with a stiffer mechanical response along the long axis or apex-to-outflow-tract direction (Fig. 4A). The specimen's complementary strain energy W^c also demonstrated mechanical anisotropy over the entire stress range (Fig. 4B). The mechanical response also covered a wide range of realized Green–Lagrange strains.

Figure 4. Biaxial mechanical response of an individual specimen.

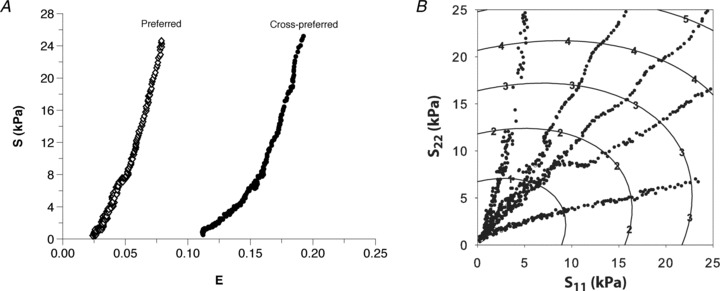
A, equibiaxial stress–strain relationship for an individual specimen, showing anisotropic tissue response with the preferred direction being the mechanically stiffer direction. B, contour levels of the complementary energy W^c for one specimen, along with the measured second Piola–Kirchhoff stress components, indicating an anisotropic tissue response over the entire measured stress range.

Representative (average) biomechanical response

Given the functional form of the strain-energy function W (eqn (3)), the optimization routine fitted the individual specimen stress–strain data well and convergence was achieved for all specimens. The RMS error obtained for the stress–strain fits ranged from 0.61 to 1.13, with an average of 0.84 ± 0.09 (Table 1). Individual specimen strain-energy responses (Fig. 5A) demonstrated mechanical anisotropy over the entire strain range, with the preferred fibre direction (X₁) being mechanically stiffer, as expected. The contour plot also reveals a steep rise in the work required to stretch the specimen beyond strains of 0.15 in either axial direction.

Table 1.

The optimal parameter set for each specimen, the associated RMS errors and R² values, along with the statistical summary for all seven specimen and the optimal parameter set that represents the average response

	β	a1	a2	a4	RMS error	R2
Specimen 1	2.39	52.3	34.5	16.2	0.61	0.91
Specimen 2	2.55	23.7	29.3	7.80	0.64	0.94
Specimen 3	2.62	33.1	18.9	7.60	0.54	0.97
Specimen 4	2.55	23.2	25.8	10.6	0.96	0.95
Specimen 5	2.09	16.3	16.5	6.60	1.00	0.91
Specimen 6	2.24	116.9	13.0	6.54	1.01	0.91
Specimen 7	1.85	20.1	12.8	7.85	1.13	0.91
Mean ± SEM	2.33 ± 0.11	40.8 ± 13.5	21.5 ± 3.2	9.03 ± 1.3	0.84 ± 0.09	0.93 ± 0.01
Average response	2.25	33.7	23.2	9.82

While a representative response cannot be obtained by averaging individual parameter values, the average and associated standard error of the mean of each parameter are provided to demonstrate the consistency of identified parameters across all specimens.

Figure 5. Representative strain and complementary strain energies.

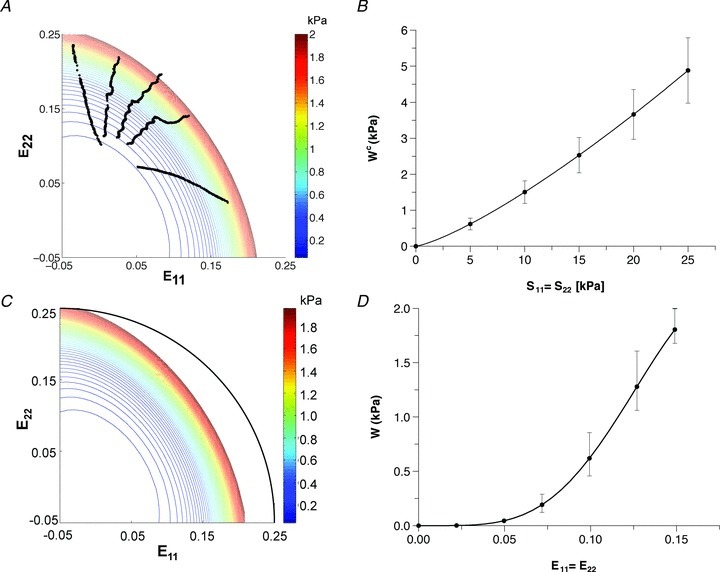
A, the resultant strain-energy function W for an individual specimen along with the measured Green strain components. C, representative (averaged) strain energy derived from all specimen data showing a smooth, distinctly anisotropic mechanical behaviour. The black arc indicates an isotropic tissue behaviour and is used as a reference comparison. B and D, mean ± SEM representative (averaged) complementary strain energy function under equibiaxial stress and representative (average) strain energy function under equibiaxial strain. These results underscore the consistent, anisotropic mechanical response of the RVFW myocardium.

Averaging all specimen's complementary energy functions resulted in small standard errors of the mean equibiaxial response (Fig. 5B). The representative (average) strain-energy demonstrated a consistent anisotropic tissue response with the E₁₁ direction being stiffer than the E₂₂ direction (Fig. 5C). The representative (average) response is therefore similar in behaviour to the individual strain-energy responses (Fig. 5A). We confirmed that the variability in the representative strain energy was small (Fig. 5D). Finally, the representative (average) stress–strain relationship for the equibiaxial stress protocols (Fig. 6), which were obtained by numerically differentiating the averaged complementary energy function, likewise demonstrated the tissue's anisotropic stress–strain response. Comparing the representative (average) stress–strain relationships at every 5 kPa between the two principal axes demonstrated statistically significantly different (P < 0.05) responses, except for the zero-stress state. Thus, the individual specimen responses, as well as the representative (average) biomechanical response across all specimens, demonstrated an anisotropic tissue response under biomechanical testing with the apex-to-outflow-tract direction being the mechanically stiffer tissue axis. To underscore the importance of our approach, we also plot the stress–strain curves from using the mean values (Table 1). While showing a qualitatively similar response, it also unsurprisingly demonstrated large differences from the actual mean responses and underscores the need for processing multi-axial mechanical data correctly.

Figure 6. Representative (average) stress–strain equibiaxial stress responses for all seven specimens of the preferred and cross-preferred directions along with standard errors of the mean (*P < 0.05), demonstrating statistically significant differences between the preferred and cross-preferred mechanical responses.

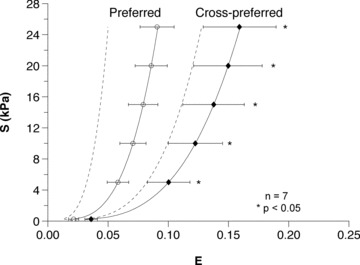
To underscore the importance of our approach, we also show the stress–strain curves derived using the mean values (Table 1). While showing a qualitatively similar response, it also unsurprisingly demonstrated large differences from the actual mean responses and underscores the need for processing multi-axial mechanical data correctly.

Finally, to test our hypothesis that the myofibre and collagen fibres dominated the in-plane mechanical response, we compared the results presented to the experimental results in which the RVFW tissue samples were rotated by 45 deg with respect to the preferred fibre direction (Fig. 7). In contrast to the results when the preferred fibre orientation is aligned with the specimen axis (Fig. 7A, unprimed coordinate axes), the results in Fig. 7B demonstrate an isotropic response, as expected.

Figure 7. To validate our hypothesis that the overall myofibre and collagen fibres dominate the tissue-level mechanical response, we prepared specimens with a preferred fibre orientation at 45 deg with respect to the specimen axis.

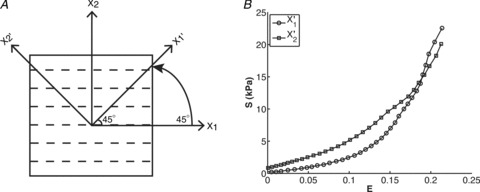
A, the resulting mechanical response demonstrated an isotropic response. This finding lends support to our hypothesis that for RVFW myocardium it is the in-plane fibre architecture that dominates the local mechanical response.

Discussion

The goals of the present study are two-fold: (1) to develop a murine experimental model that allows the study of the mechanical behaviour of full-thickness, viable, ex vivo RVFW tissue, and (2) to develop an analysis method for obtaining the representative scalar strain-energy function summarizing the measured RVFW tissue mechanical behaviour. Thus, we provide the framework to obtain the relevant physiological data on which structure-based constitutive models of RV function can be built. The biomechanical test protocol was developed such that the testing time was short enough to allow for the entire experiment to fit within the time window established for tissue viability. The resultant experimental protocol produced stable, reproducible and consistent data.

When the specimen axis is aligned with the preferred fibre orientation, the biomechanical responses of RVFW myocardium revealed an expected anisotropic mechanical behaviour, with the stiffer direction along the preferred myofibre and collagen fibre (apex-to-outflow-tract) direction (Fig. 6). These results are consistent with the preferred fibre direction (Figs 1C and 3B) in that biological tissue exhibit stiffer biomechanical properties along the preferred structural direction (Billiar & Sacks, 1997; Sacks & Gloeckner, 1999; Sacks & Sun, 2003; Nagatomi et al. 2005; Gilbert et al. 2008; Jor et al. 2010). Moreover, when the specimen axis is rotated by 45 deg with respect to the preferred fibre orientation (Fig. 7A), the resultant tissue-level mechanical response became isotropic. That is, when an orthotropic-like tissue is loaded with its preferred fibre direction (i.e. its material axis) at a 45 deg angle, the resulting mechanical response will be isotropic-like. This finding thus lends support to our hypothesis that for the RVFW myocardium, it is the in-plane fibre architecture that dominates the local mechanical response. Furthermore, anisotropic mechanical behaviour of our full-thickness murine RV myocardium is consistent with the findings in canine (Sacks & Chuong, 1993a) and bovine (Ghaemi et al. 2009) partial-thickness RV specimens, and partial-thickness LV myocardium in leporine (Lin & Yin, 1998), canine (Demer & Yin, 1983; Halperin et al. 1987; Yin et al. 1987; Humphrey et al. 1990a,b; Novak et al. 1994), and bovine (Ghaemi et al. 2009) animal models.

The resultant strain-energy data, as well as the associated best-fit strain-energy surfaces, demonstrate that very little energy is required to stretch the tissue at low strain levels. This behaviour of the passive RVFW is consistent with the chamber's physiological role of efficient filling at low pressure. However, the strain-energy response becomes markedly non-linear as demonstrated by a very steep rise in the strain-energy surface as the strain increases.

A representative response

Quantification of a fully representative biomechanical response from individual specimen data can be challenging when dealing with non-linear mechanical behaviours. Novak et al. (1994) and Lin & Yin (1998) defined common deformation states of their specimens for inter-specimen comparisons. In our study, use of stress-controlled tests results in variations in the realized Green–Lagrange strains, making averaging of the resultant strain-energy functions problematic. Another approach has been taken by Sacks & Chuong (1998) in which they structurally pre-sorted the specimens to reduce variability. However, while demonstrating that consistent averaged properties can be derived, this approach is not practical for general tissue studies wherein structural consistency cannot be strictly controlled.

To arrive at a representative biomechanical tissue-level response for all specimens, without directly averaging the stress–strain relations, we took advantage of the particular design of our stress-control protocols to compute the average complementary strain energy. From it, we then derived the representative scalar strain energy, which represents the net experimentally derived tissue response over the entire measured response range. This approach led to small variation in the mean stress–strain relationship and the preservation of the anisotropic behaviour of the tissue. With this simple yet novel methodology, we determined an actual representative biomechanical response of the healthy control sample population, which cannot be obtained by averaging individual parameter values due to the non-linearity of the constitutive model equation (eqn (3)). Importantly, while simply averaging the parameter values across specimens (as we present in Table 1 to underscore the inherent consistency to our data) appear to yield comparable parameters to those obtained from the average response data, it must be noted that even though the values are similar, due to the non-linearity of the constitutive law, the resulting stress–strain curves would likely be very different. Our results can be used as a reference point for future investigations of disease conditions.

The murine RVFW model – implications of its transmural structure

The myofibre orientation of the LV has been studied extensively (Nielsen et al. 1991b; LeGrice et al. 1995; 1997; Vetter & McCulloch, 1998; Young et al. 1998; Pope et al. 2008; Sands et al. 2005), and substantial changes in endo- to epicardial myofibre orientations have been reported across a spectrum of species. The results of these studies have been incorporated into detailed models of LV function (Nash & Hunter, 2000; Schmid et al. 2006, 2008; Nordsletten et al. 2011; Holzapfel & Ogden, 2009; Usyk et al. 2000). Chuong et al. (1991) reported a large transmural variation in myofibre orientation of about 105 deg in the canine RV. Nielsen et al. (1991a) and LeGrice et al. (1995, 1997) similarly reported large transmural variations. The work by LeGrice et al. (1995), for example, demonstrated a transmural variation in myofibre orientation of about 150 deg in canine RV specimens. In the rat LV, Young et al. (1998) and Sands et al. (2005) reported a 120 deg transmural variation of myofibre orientation, and a close alignment of collagen and myofibres. Recently, Pope et al. (2008) reported that myocyte orientation in murine left ventricles varies transmurally by about 150 deg from endo- to epicardium. But as pointed out by Nielsen et al. (1991a) and Vetter & McCulloch (1998), the transmural variation is larger (by about 20 deg) in the LV than it is in the RV in dogs and rabbits.

However, only limited structural information exists for the RVFW and, to the best of our knowledge, no detailed analysis exists on the transmural myofibre and collagen fibre orientations of the rat RVFW. We found a remarkably small transmural variation in both these fibre orientations across the RVFW. The mean orientation was 5.2 ± 0.3 deg for the myofibres and –4.4 ± 0.2 deg for the collagen fibres (Fig. 3C). Thus, the mean myofibre and collagen fibre orientation are both very close (only about 10 deg apart) and are closely aligned with the apex-to-outflow-tract direction (0 deg by definition of the reference frame). Furthermore, aggregate measurement of the collagen fibre orientation obtained from studying full-thickness decellularized specimens was remarkably consistent with the results from the transmural information (–16 ± 12.3 deg in the full-thickness case versus–4.4 ± 0.2 deg in the slices of transmural sections). Although the level of variability should be confirmed in a larger set of specimens, the current results suggest that another, unanticipated advantage of the murine model is relative transmural uniformity of myo- and collagen fibre structures within the strain measurement region (Fig. 3C). These results have important implications for the modelling of RV biomechanics using this animal model in that it can help simplify structural constitutive (i.e. stress–strain) model development.

Limitations

The decellurized RVFW tissue essentially lumps the endo- and epicardial layers in addition to the intramuscular connective tissue (e.g. endomysium, interfibre struts, etc.) into a single functional unit. However, these layers are relatively thin and do not appear to have a major structural contribution (Fig. 3) with respect to their mass fraction. We note too that we are using biaxial mechanical testing as an approximation of the true 3D stress that the myocardium undergoes (Sacks & Sun, 2003). Given the relatively planar nature of the murine RVFW, this approximation may be sufficient for this portion of the heart. In principle, once a complete, detailed microstructural description of myocardium is obtained, one can presumably predict any geometrical configuration of ventricular myocardium. This is, of course, a big step and will have to be validated in future studies. Finally, we note that the measurement and preservation of the native tissue geometry from its in vivo configuration to the mechanical testing environment remains an open challenge in both experimental and analytical biomechanics.

Future work

A key limitation for the development of anatomically and physiologically accurate computational models of the right ventricle has so far been the paucity of experimental data on the structure and mechanical function of viable, full-thickness RV myocardium. Our work presented here is a step towards filling this gap by providing an experimental and data-analysis framework for obtaining the relevant physiological data for such a structure-based constitutive modelling approach. In future work, we intend to study the biomechanical behaviour of actively contracted, full-thickness, viable RV myocardium, and determine the myofibre and collagen fibre orientation in the contracted state to compare their organization to the passive state of the myocardium. Next, we will incorporate our experimental findings into a structure-based constitutive model of RV function.

Summary

The present work presents a first step towards elucidating the structure–function of non-contractile murine RVFW myocardium. The insights derived here lay the foundation for an understanding of RV remodelling in response to pulmonary hypertension and also provide an important reference for understanding the general process of myocardial hypertrophy. In particular, they will allow us to formulate constitutive relations of the RVFW that summarize the multi-axial (anisotropic) stress–strain relationship and therefore capture the biomechanical properties of the ventricular tissue. Having access to such a mathematical representation of the tissue properties will allow us to test physiological hypotheses about the normal and hypertrophic RV. It is also a key ingredient in developing large-scale heart models that include RV and RV–LV interactions.

Glossary

LV

left ventricle

RVFW

right ventricular free wall

RMS

root mean square

RV

right ventricle

Author contributions

D.V.J. carried out the tissue preparation, viability study, structural and mechanical testing, analysis of mechanical data, and quantification of decellularized RVFW tissue structure; proposed the functional form of the strain-energy function and implemented the analysis of the biomechanical data; and developed the draft manuscript and generated the figures. M.A.S. developed the tissue preparation protocol, carried out histological analysis, and revised the manuscript. H.C.C. provided the animal model and provided critical feedback on the manuscript. M.S.S. conceived the idea of the project, supervised the experiments and data analysis, provided the facility for biomechanical testing and structural investigation of decellularized tissue samples, and supervised the manuscript and figure development.