An examination of effect estimation in factorial and standardly-tailored designs

Abstract

Background

Many clinical trials are designed to test an intervention arm against a control arm wherein all subjects are equally eligible for all interventional components. Factorial designs have extended this to test multiple intervention components and their interactions. A newer design referred to as a ‘standardly-tailored’ design, is a multicomponent interventional trial that applies individual interventional components to modify risk factors identified a priori and tests whether health outcomes differ between treatment arms. Standardly-tailored designs do not require that all subjects be eligible for every interventional component. Although standardly-tailored designs yield an estimate for the net effect of the multicomponent intervention, it has not yet been shown if they permit separate, unbiased estimation of individual component effects. The ability to estimate the most potent interventional components has direct bearing on conducting second stage translational research.

Purpose

We present statistical issues related to the estimation of individual component effects in trials of geriatric conditions using factorial and standardly-tailored designs. The medical community is interested in second stage translational research involving the transfer of results from a randomized clinical trial to a community setting. Before such research is undertaken, main effects and synergistic and or antagonistic interactions between them should be identified. Knowledge of the relative strength and direction of the effects of the individual components and their interactions facilitates the successful transfer of clinically significant findings and may potentially reduce the number of interventional components needed. Therefore the current inability of the standardly-tailored design to provide unbiased estimates of individual interventional components is a serious limitation in their applicability to second stage translational research.

Methods

We discuss estimation of individual component effects from the family of factorial designs and this limitation for standardly-tailored designs. We use the phrase ‘factorial designs’ to describe full-factorial designs and their derivatives including the fractional factorial, partial factorial, incomplete factorial and modified reciprocal designs. We suggest two potential directions for designing multicomponent interventions to facilitate unbiased estimates of individual interventional components.

Results

Full factorial designs and their variants are the most common multicomponent trial design described in the literature and differ meaningfully from standardly-tailored designs. Factorial and standardly-tailored designs result in similar estimates of net effect with different levels of precision. Unbiased estimation of individual component effects from a standardly-tailored design will require new methodology.

Limitations

Although clinically relevant in geriatrics, previous applications of standardly-tailored designs have not provided unbiased estimates of the effects of individual interventional components.

Discussion

Future directions to estimate individual component effects from standardly-tailored designs include applying D-optimal designs and creating independent linear combinations of risk factors analogous to factor analysis.

Conclusion

Methods are needed to extract unbiased estimates of the effects of individual interventional components from standardly-tailored designs.

Introduction

Interventions for geriatric conditions such as injurious falls [1] or disability [2] differ from those corresponding to single diseases because typically more than a single interventional component is used. Accordingly, the interventions often consist of components to modify a number of selected risk factors. To improve generalizability of their clinical trials, geriatric researchers often establish broad inclusion criteria so that a participant need not have all the risk factors or pre-existing conditions corresponding to the multiple interventional components to be eligible. Constraining participants to those having all risk factors limits inference to persons with all risk factors. Such a restriction would make recruitment for trials of interventions consisting of multiple components for geriatric health syndromes much more expensive.

Of the many issues to consider in the design of such trials, [3], one of the most important is how to assign individual interventional components. Clinical trials of multifactorial geriatric conditions commonly assign individual components of the intervention based on a priori risk factor assessment. For example in the FICSIT fall prevention trial postural hypotension was one of seven risk factors and was defined as a drop of ≥20 mm Hg drop in blood pressure when moving from a lying position to standing [4]. Its corresponding interventional components were postural exercises, elevation of patient’s head when in bed, and review and adjustment of medication. This method of assigning the individual interventional components on an ‘as needed’ basis has been referred to as a ‘standardly-tailored’ (ST) design. These differ from ‘customized’ designs in following a protocol for the assessment of the risk factor and assignment of a predetermined intervention component. Some ‘customized’ designs allow for changing the intervention throughout the trial, which is not the case with ST designs. While ST designs are clinically relevant and yield an estimate for the net effect of the multicomponent intervention, it has not yet been shown if individual component effects can be separately estimated in an unbiased manner. The ability to estimate the most potent interventional components has direct bearing on conducting second stage translational research [5].

A topic of great interest to the medical community, second stage translational research involves the transfer of results from a randomized clinical trial (RCT) to a more general setting and is also known as the as the T2 application phase [6,7]. Before second stage translational research is undertaken, synergistic and or antagonistic interactions between the individual component effects should be identified in addition to their main effects. Knowledge of the relative strength and direction of the effects of the individual components and their interactions facilitates the successful transfer of clinically significant findings and may potentially reduce the number of interventional components needed. A large scale example of second stage translational research is the Connecticut Collaboration for Fall Prevention which has been described elsewhere [8,9].

In this paper, we review a variety of factorial designs that facilitate the estimation of component effects, and contrast them with ST designs, which pose significant challenges to the unbiased estimation of the effects of individual interventional components. We use the phrase ‘factorial designs’ to describe full-factorial designs and their derivatives that include the fractional factorial, partial factorial, incomplete factorial, and the modified reciprocal design.

Estimation of individual component effects

Traditionally, RCTs test interventional components that all subjects can potentially receive. For example, if the two interventional components A and B are to be studied, design options include: (1) three 2-arm trials (A vs control, B vs control and A + B vs. control), (2) a single 3-arm trial (A vs. B vs control), and (3) a 2 × 2 full-factorial design (A alone, B alone, A + B, and neither treatment). The three design options are differentiated by the number of participants needed to have the same precision in effect estimates and whether or not interactions can be estimated [10]. Because the interventional component effects are estimated separately in option 1 (e.g., A vs control and B vs control), comparisons among components (e.g., A vs B) cannot be made directly. In the single 3-arm design interventional component estimates are not independent because they are based on the same comparison group and although interactions cannot be estimated, comparisons between A and B may be made. In the full factorial, however, the interventional component effects are independent so that main effects and interactions can be separately estimated. Another strength of factorial designs is that when sample sizes are the same for each arm they are balanced (e.g., every factor appears an equal number of occasions) [10]. Although balanced factorial designs efficiently estimate the main effects by averaging across other effects, their sample sizes grow geometrically as additional interventional components are added.

A key element of these three different design strategies is eligibility to be randomized to a treatment arm. For the three 2-arm trials, a particular subject could be eligible for just one of the trials (subjects that are not candidates for receiving B would only be eligible for the trial A vs control). In the case of the single 3-arm trial, subjects have to be eligible to receive intervention A or B, but not A + B. In the full factorial design each subject must be eligible for intervention A, B and their combination.

As the number of risk factors requiring intervention increases in a geriatric health syndrome, there may be a prohibitively small number of subjects eligible for any particular treatment combination. This affects the generalizability of the results, which depend on the sample in which the trial was conducted. In the falls prevention trial FICSIT [4] there were seven interventional components. If this had been a full factorial design, then there would have been 2⁷ = 128 treatment arms and the results would have been generalizable only to older persons with all seven risk factors.

Another consideration is that factorial designs may be inappropriate for clinical trials when some components are known a priori to have a qualitative interaction or are contraindicated for some participants [11]. McAlister et al. [12] review the use of full factorial designs and caution that their appropriate use assumes independence between the interventional components. They emphasize that substantive interactions between two interventional components bias the estimated effects of the individual components.

Partial factorial designs

As used in the clinical trial literature, the term ‘partial factorial design’ has been used to refer to a trial where the study population is randomized on at least a single factor of interest and a subset of the study population is randomized to one or more factors. The choice of how to restrict the random assignment when using partial factorial designs has been driven by economic, geographic, or clinical constraints. The Women’s Health Initiative [13], CREATE-ECLA [14], and OASIS trials [15] are well-known trials based on partial factorial design.

The Women’s Health Initiative [13] (WHI) had three embedded clinical trials: the Dietary Modification Trial (DM), the Hormone Replacement Therapy Trial (HRT), and the Calcium with Vitamin D trial (CaD). These trials tested interventions aimed at the prevention and control of diseases commonly experienced by postmenopausal women. After determining eligibility, women of ages 50–79 were invited to join a single intervention trial, i.e., DM or HRT, or both. In the DM trial 48,835 women were randomized to either a low fat or control diet. The HRT trial had two separate interventional components depending on whether or not the woman had an intact uterus. At the first and second year anniversary of their assignment within the DM and HRT trials, each woman was screened for eligibility for the CaD trial. The design of the WHI therefore resulted in some women being randomized to a single intervention (one trial), some randomized to two interventions (two trials), and some randomized to three interventions (three trials). Therefore the design used different, overlapping groups of women to estimate the separate effects of the DM and the individual components of the HRT and CaD interventions.

The CREATE-ECLA randomized controlled trial [14] addressed myocardial infarction related to a specific segment of the electrical signal controlling heart pumping as measured by angiogram. Stability of this segment of the heart signal, known as the S-T segment, is associated with lower mortality and better ventricular activity [16]. The CREATE-ECLA randomized controlled trial [14] used a partial 2 × 2 factorial design with two separate randomized assignments of treatment. The first randomization assigned all patients to either treatment (glucose–insulin–potassium infusion) or control while the second randomization applied only to those subjects residing in India and China. This latter subset of patients were therefore randomized to double-blind therapy with reviparin or matching placebo in addition to the treatment assignment they received in the first go-round.

The OASIS-6 trial [15] evaluated the effect of fondaparinux on mortality and reinfarction in patients with myocardial infarction characterized by elevation of the previously described S-T segment of the heart’s controlling electrical signal. The primary design was a full factorial where all patients were stratified by indication for use of unfractionated heparin. The partial factorial was formed by a subset of these patients who were also randomly assigned to receive glucose–insulin–potassium infusion to evaluate association with mortality and nonfatal cardiac arrest.

Fractional factorial designs

One possible approach to the problem when there are a large number of components of an intervention is to consider a fractional factorial design [17,18]. This type of design has been advocated [19,20] but has rarely been used in Phase III medical trials [21,22]. A fractional factorial design is one in which only a specifically selected subset (fraction) of the treatment combinations from the full factorial design is used. The fraction of the treatment combinations is chosen by selecting one or more defining contrasts [23], that define which interactions are confounded with the main effects [17]. Confounded effects cannot be estimated separately or distinguished from one another because the experimental levels of each of the confounded terms are identical in the design matrix of the experiment. Typically, interactions of more than two factors are considered to be harmlessly confounded (e.g., have negligible effects) whereas the confounding of main effects and two-way interactions needs to be carefully considered. The resolution of a design indicates the highest order of interaction that is not confounded with other interactions of the same order [17]. For example, in a resolution III design the estimates of main effects are confounded with those of potentially important two-factor interactions. Fractional factorial designs are based around a defining contrast so that the pattern of confounding can be precisely defined a priori. When there is not an a priori allocation to treatment arms, an inefficient, unbalanced trial can result that leads to effect estimates with ill-defined patterns of confounding. This results in a very limited ability to separate the estimates of main effects from those of interactions of interest.

An example of a 1/2 fractional factorial resolution IV design for an intervention to prevent nursing home acquired pneumonia is provided in Table 1. In these designs the main effects are not confounded with any two-factor interactions, but are confounded with three-factor interactions and two-factor interactions are confounded with each other. This design is based on four factors that were found to be risk factors for nursing home acquired pneumonia in an observational study [24]. The four modifiable risk factors are lack of Pneumococcal vaccination, lack of oral care, problems with swallowing, and feeding the patient when seated <90°. This fractional design allows for estimation of all four main effects while using only 8 treatment arms compared to the 16 treatment arms needed for a full factorial design. The price of this smaller experimental design is that the estimates of the four main effects are each confounded with that of a three factor interaction and the two-factor interactions are confounded with other two-factor interactions. So although the fractional factorial eliminates the larger sample sizes of the full factorial, it requires that same baseline assumption that all participants possess all risk factors and therefore eligible for assignment to all treatment arms. It also assumes that confounding of higher order interactions with main effects adds negligible bias. For example, in Table 1 the main effect of Pneumococcal Vaccination is confounded with the three-way interaction Oral Care × Swallowing Therapy × Feeding Position. Also, the investigator a priori must decide about the confounding of two-way interactions. For example, in Table 1 the two-way interaction Pneumococcal Vaccination × Oral Care is confounded with the two-way interaction Swallowing Therapy × Feeding Position. As the number of factors (components) increases, confounding as well as its consequent risk for biasing estimates grows considerably. We refer the interested reader to texts that provide detail on these designs [10,25].

Table 1.

Design matrix for a 1/2 fractional factorial of resolution IV for four components of a multifactorial intervention to prevent nursing home acquired pneumonia [24]. 0 denotes that the component is absent and 1 that the component is present

	Components of the intervention
Treatment combination	Pneumococcal vaccination A	Oral care B	Swallowing therapy C	Feeding position of <90 degrees D
1	0	0	0	0
2	1	0	0	1
3	0	1	0	1
4	1	1	0	0
5	0	0	1	1
6	1	0	1	0
7	0	1	1	0
8	1	1	1	1

The confounding pattern is:

• Pneumococcal vaccination = Pneumococcal vaccination × (Oral Care × Swallowing Therapy × Feeding Position).
• Oral Care = Oral Care × (Pneumococcal vaccination × Swallowing Therapy × Feeding Position).
• Swallowing Therapy = Swallowing Therapy × (Pneumococcal vaccination × Oral Care × Feeding Position).
• Feeding Position = Feeding Position × (Pneumococcal vaccination × Oral Care × Swallowing Therapy).
• Pneumococcal vaccination × Oral Care = (Pneumococcal vaccination × Oral Care) × (Swallowing Therapy × Feeding Position).
• Pneumococcal vaccination × Swallowing Therapy = (Pneumococcal vaccination × Swallowing Therapy) × (Oral Care × Feeding position).
• Oral Care × Swallowing Therapy = (Oral Care × Swallowing Therapy) × (Pneumococcal vaccination × Feeding position).

Incomplete factorial and modified reciprocal control

There is a variant of the factorial design called the incomplete factorial design [11] that specifically addresses effect estimation when there are ethical considerations or problematic combinations of components. Suppose that a multicomponent intervention had three components where each corresponded to a different medication. As is common in HIV/AIDS or cancer trials, a treatment arm where participants receive all three medications or specific combinations of them may be toxic. Therefore, a full factorial design is not appropriate and so an incomplete factorial excludes problematic treatment arms. The challenge with this design is obtaining unbiased estimates of individual component effects [11]. However, methods for estimating the component variances, covariances and bias of their estimates of component effects have been developed [11,26]. This design has been used in agriculture [27] and pharmacology, but has not been used in medical trials. A hypothetical example of a geriatric trial using an incomplete block design for fall prevention might contain exercise and medication components and would exclude the use of anti-hypertensive medications associated with risk of injurious falls for older patients.

Another variant that could be considered is a modified reciprocal control design, which is applicable when the sample population does not have all the same risk factors. In this design subjects with the same set of risk factors are randomized, as in a full factorial design. That is, a participant with two modifiable risk factors may be randomized to receive interventional components for one of their two modifiable risk factors and serve as a control for the effect estimate of the other [28,29] (Table 2). However, when analyzing this design we must assume that the estimated effect of component A on all subjects eligible to receive it, is independent of all other interventional effects. For example in Table 2, subjects with risk factor combinations AB and AC are used in the estimation of the effect of the intervention component to treat A. We assume that the coexisting risk factor, either B or C, or the corresponding interventional component, has negligible influence on the estimated effect of component A. This form of design has not been published in the medical literature possibly due to the complications of its application.

Table 2.

Modified reciprocal control design for a hypothetical trial with subjects having two of three potential risk factors (A, B or C). Within risk factor combination subjects are randomized to treatment and control for different risk factors. Different combinations of subjects contribute to effect estimation

Risk factor combination	Patient in arm with risk factor combination	Random assignment	Risk factors contributing to effect estimate
			A	B	C
AB	A patient with AB	Treatment A	X	X
		Control B
	Another patient with AB	Control A	X	X
		Treatment B
AC	A patient with AC	Treatment A	X		X
		Control C
	Another patient with AC	Control A	X		X
		Treatment C
BC	A patient with BC	Treatment B		X	X
		Control C
	Another patient with BC	Control B		X	X
		Treatment C

Standardly-tailored designs

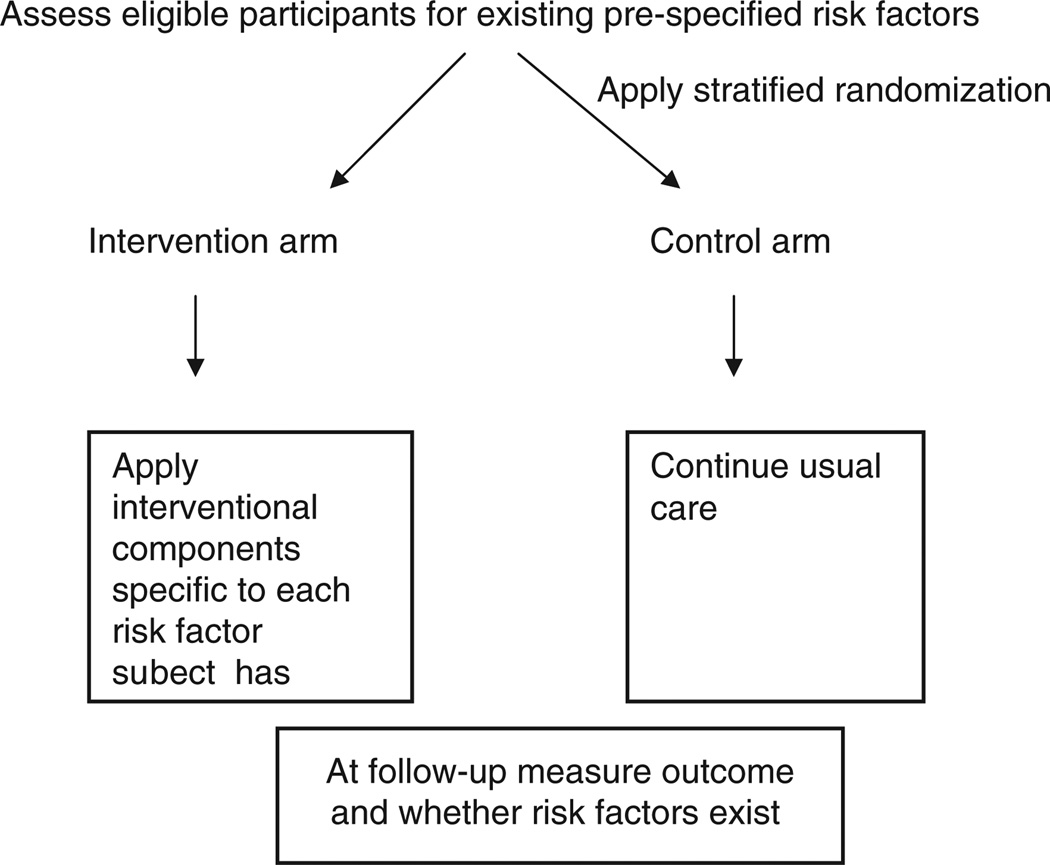
In trials designed to address multifactorial geriatric health syndromes, participants rarely have all risk factors, but rather some subset of them. Consequently, participants are not randomly assigned to all or some pre-planned combination of interventional components as in a factorial design. In the ST design participants randomized to the intervention arms are given only those interventional components that correspond to the risk factors that she or he possesses at the time of enrollment (Figure 1). Although we limit our examples in this article to dichotomous risk factors, the same techniques can be directly extended to ordinal categories. To create ordinal categories of risk from continuous risk factors, such as measures of vision, hearing, and blood pressure, clinical justification or methods such as classification and regression trees can be used to determine cut-points [30].

Figure 1.

Conceptual example of standardly-tailored design

Randomization in standardly-tailored designs

Clinical trials use randomization to control for both measured and unmeasured factors that have an effect on the treatment comparison. The level at which randomization can occur varies from individual participant to group (i.e., clustering at the level of physician, ward, or site). Following their randomized assignment to intervention or control arm in a ST design, those in the intervention arm receive only those interventional components corresponding to the risk factors they have. An important consideration is that the control arm must have the same balance of risk factors and their combinations as the intervention arms. Thus, randomization based on stratification of risk factors present is often the preferred form of randomization. This stratified randomization is depicted in Figure 1.

A major issue in estimating individual component effects is determining the appropriate comparison group. For example, if an individual component effect were to be estimated from a ST design, only those participants in the control arm possessing the corresponding risk factor should constitute the comparison group. This comparison group differs from one consisting of all participants who did not receive the component, because in the latter case participants in the control arm not possessing the risk factor are not candidates for the interventional component.

Comparing estimation of effects in factorial and standardly-tailored designs

In this section, we demonstrate how factorial and ST designs respectively provide estimates representative of net intervention and individual interventional components based on a prospective study of three specific risk factors associated with falls of older persons within a three year follow-up period. The three risk factors are impairment in manual dexterity, impaired ability to perform chair lifts, and presence of depression. Occurrence of each of these dichotomous risk factors is based on exceeding a threshold value on a continuously measured variable. Because this study was observational without intervention, we make a few assumptions to convey the concepts relevant to effect estimation. We refer to the effect of net intervention as that pertaining to an indicator variable showing whether a subject has one or more of the three risk factors. Any subject with none of the three risk factors has a value of 0 for the indicator of net intervention. All re-sampling and analyses of data were performed with SAS statistical software version 9.1. 3 [31].

For demonstration purposes, we illustrate the effects pertaining to individual risk factors as if they were actual individual interventional components. These interpretations allow us to demonstrate how analysis of the data gathered per the two design types respectively estimate interventional effects in a well studied multi-factorial geriatric syndrome.

The data set used to illustrate the analyses presented in Tables 3 (factorial) and 4 (ST design) is based on 831 observations with no missing values from an original cohort of 1103. The 831 complete observations were stratified into 8 subgroups representing the risk factor combinations 1 through 8 indicated in both tables. Table 3 analyzes data based on an assumed factorial design of the data collection process. Sampling with replacement was used to iteratively create 1000 samples of 40 observations from each risk factor combinations. Bootstrapped estimates of the coefficients of Poisson regression of number of falls per subject over a 3 year follow-up period were obtained from the 1000 data sets. In Table 3 effect estimates are presented for Net Intervention, as well as for the distinct risk factors. Because of the assumed independent assignment of the risk factors, the factorial design only requires the same number of subjects for risk factor combination 1, i.e., subjects with no risk factors. Note that in Table 3 Net Intervention does not have a significant association with probability of falling at the 5% significance level. However, Chair lift impairment and depression have significant individual associations with probability of falling.

Table 3.

2³ factorial design (interventional components fully randomized)

Factor combination	Manual dexterity impairment	Chair lift impairment	Depression	Number of data points	Estimated effect contribution [1,2]
1	0	0	0	40	All
2	0	0	1	40	All
3	0	1	0	40	All
4	0	1	1	40	All
5	1	0	0	40	All
6	1	0	1	40	All
7	1	1	0	40	All
8	1	1	1	40	All
				Total data points = 320
Estimated bootstrap effect (95% CI)3	Hand skill impairment 0.28 (−0.05, 0.60)	Chair lift impairment 0.38 (0.05, 0.75)	Depression 0.40 (0.05, 0.79)	Net Intervention 0.23 (−0.43, 1.08)

¹Estimates from Poisson regression on number of falls in 3 years with fixed offset.

²All includes effects for net intervention and individual components for hand, chair, and depression.

³Bootstrap estimates based on 1000 re-samplings of non-missing values of original data set.

Table 4.

Standardly-tailored design (interventional components assigned as needed)

Factor combination	Manual dexterity impairment	Chair lift impairment	Depression	Number of data points	Estimated effect contribution 1
1	0	0	0	280	Net intervention
2	0	0	1	40	Net intervention
3	0	1	0	40	Net intervention
4	0	1	1	40	Net intervention
5	1	0	0	40	Net intervention
6	1	0	1	40	Net intervention
7	1	1	0	40	Net intervention
8	1	1	1	40	Net intervention
				Total data points = 560
Estimated bootstrap effect (95% CI)2	Hand skill impairment Inappropriate due to bias	Chair lift impairment Inappropriate due to bias	Depression Inappropriate due to bias	Net intervention 0.20 (−0.32, 0.65)

¹Estimates from Poisson regression on number of falls in 3 years with fixed offset.

²Bootstrap estimates based on 1000 re-samplings of non-missing values of original data set.

In Table 4 we assume that the interventional components, i.e., risk factors, are assigned on an ‘as needed’ basis implying an ST design. As in the analysis of Table 3 we sample with replacement from the 8 risk factor combinations to iteratively produce 1000 data sets consisting of 40 subjects from risk factor combinations 2 through 8. For purposes of estimating Net Intervention from an equal number of control and treatment subjects, we resample 280 subjects from risk factor combination 1. Note that the assumed independence of risk factor assignment in Table 3 required only 40 subjects from risk factor combination 1, an advantage of the factorial design. Due to the larger number of subjects used to calculate the effect of Net Intervention in Table 4, its 95% confidence interval is smaller while remaining insignificant.

To summarize, Tables 3 and 4 highlight the differences in how factorial and ST designs respectively estimate interventional effects. The factorial is more efficient and allows unbiased estimates of Net Intervention, as well as individual interventional components with smaller sample sizes. Because the factorial requires a condition typically untenable in interventions for multicomponent geriatric syndromes, i.e., independent assignment of interventional components corresponding to specific risk factors, it has limited utility in these circumstances. In contrast analysis based on the ST design in Table 4 requires an overall larger sample size and does not permit unbiased estimation of effects of individual interventional components. For interventions consisting of several interventional components that respectively target specific risk factors of geriatric syndromes, it is often more useful and less expensive due to its less restrictive assumptions regarding treatment assignment.

Future directions for estimation of individual interventional components

Standardly-tailored designs will continue to be employed because of their clinical relevance in geriatric and second stage translational research. However, the complexity introduced by their correlated effect estimates is not easily resolved. We suggest two potential directions for extending ST designs to allow the unbiased estimate of individual component effects. We first suggest that the set of optimal experimental designs commonly used in the engineering disciplines [32] may permit an unbiased separation of the individual estimates of correlated factors. Note that the optimal designs used in engineering are substantively different from the ‘optimal designs’ sometimes referred to in the clinical trial literature. In the clinical trials literature, the phrase ‘optimal design’ typically describes adaptive sampling schemes that provide the investigator with the flexibility to optimize their test resources [33]. In contrast, the optimal class of engineering designs are appropriate when not all combinations of the components are ethical or possible, or when there are resource or implementation limitations which restrict the number of component combinations in the trial, or when analysis requires either a nonstandard linear or nonlinear model.

In the world of engineering design, experiments are typically laid out in a sequential fashion where the first one is a screening experiment that identifies the crucial main effects and two-factor interactions. The pharmaceutical literature presents examples [34–36] of Phase II clinical trials that use D-optimal designs [32] to pick the group of factor combinations, or time points in longitudinal trials [37] that optimize characteristics, such as minimum covariance, of specific model coefficients. Unlike factorial designs, D-optimal designs do not require independent (orthogonal) interventional components, thus parameter estimates may be correlated. D-optimal design minimizes the covariance of the components estimates, which is the same as maximizing the determinant of the design matrix; hence the ‘D’ in the name is from determinant.

D-optimal designs are selected by algorithms where the user chooses the total number of intervention component combinations that can be included in the trial consisting of all possible combinations of various components that one could apply in the trial and the form of the model. Next, an algorithm selects the optimal set of component combinations from those specified. Optimal design methods have yet to be applied to estimates of individual component effects from ST designs.

Our second suggestion for extending the ST design’s ability to yield unbiased estimates of individual interventional components is based on identifying statistically independent linear combinations of the individual risk factors and their corresponding interventional components. In order to accommodate the lack of random assignment of risk factors in ST designs, we start with a simplifying assumption. We assume that for each modifiable risk factor under consideration there is only a single component for which we want to estimate an interventional effect on a final outcome. Because a considerable obstacle to estimating the effect of individual interventional components separately is the correlation among risk factors they are intended to modify, a systematic grouping of risk factors according to their inter-relationships may be worthwhile [1,3,38,39]. We therefore suggest that a promising area of research may be found in the application of factor analysis to the correlated risk factors in multicomponent interventional trials.

Suppose that a medical condition, such as fall-related injury, is associated with a number of modifiable risk factors. From pilot or epidemiologic studies, risk factors associated with fall-related injury might include measures of gait speed, balance, lower body strength, and use of a specific medication. Whether these risk factors are continuous or categorical, the techniques of factor analysis may yield statistically independent linear combinations of the original risk factors. Furthermore, assume that some of these linear combinations can be interpreted as combinations of specific risk factors, e.g., patients with impairment of gait speed and impairment of lower body strength with no other risk factors. A second such combination might be patients with poor balance and using a specific medication. Assuming that only two of the interventional components have significant association with probability of falling, these two statistically independent linear combinations might be solved to yield unbiased estimates of the two significant interventional components.

There are strengths and limitations to such an approach. The main strength is that unconfounded estimates of discrete interventional components applied to risk factors for a health outcome of interest, e.g. fall-related injury, could hypothetically be derived. A second strength is that this approach has a natural conceptual alignment with the ST design where interventional components would be given to participants according to their study arm assignment and possession of specific risk factors.

The limitations include a requirement of a pilot study to estimate the existence of such linear combinations or risk factors in the target population. However, this information might be retrieved from Phase II trials that have already determined which components merit consideration in Phase III testing. Furthermore, the method assumes the existence of linear combinations of the risk factors that can be interpreted and assigned to specific study participants. Sampling plans for such an assignment procedure would need to be developed with associated formulae for power and sample size calculations.

In summary, we suggest the application of optimal designs from the engineering literature and the assignment of interventional components based on factor analysis of risk factors as two potential methods for obtaining unbiased estimates of individual interventional components in ST designs. Both approaches assume an initial pilot study of central importance. From this pilot or Phase II trial, optimal design assumes that the important interventional components have been identified. Likewise the assignment of interventional components based on factor analysis of risk factors assumes that the pilot study is a representative sample of the larger study population. In either approach, bias in the final effect estimates necessarily depends on the validity of the assumed accuracy of estimates derived from the pilot or Phase II study.

Conclusions

The clinical trial literature shows that the vast majority of multicomponent trials are designed with full factorial assignment of interventional components which, by assuming their independence, facilitates the estimation of individual effects. Because there are many geriatric medical syndromes that are multifactorial in nature and effectively treated by intervening upon several correlated risk factors, ST designs have been developed to evaluate the net interventional effect. We suggest two possible directions for unbiased estimation of the effect estimates of individual interventional components from ST designs. Each approach requires a well-designed initial pilot or Phase II study. These estimates are assumed to adequately approximate the larger study population and are used in subsequent experiments to yield the desired estimates.