Abstract
In this study, a correlation matrix based hierarchical clustering (CMBHC) method is introduced to extract multiple correlation patterns from resting-state functional magnetic resonance imaging (fMRI) data. It was applied to spontaneous fMRI signals acquired from anesthetized rats, and the results were then compared with those obtained using independent component analysis (ICA), one of the most popular multivariate analysis method for analyzing spontaneous fMRI signals. It was demonstrated that the CMBHC has a higher sensitivity than the ICA, particularly on a single run data, for identifying correlation structures with relatively weak connections, for instance, the thalamocortical connections. Compared to the seed-based correlation analysis, the CMBHC does not require any priori information and thus can avoid potential biases caused by seed selection, and multiple patterns can be extracted at one time. In contrast to other multivariate methods, the CMBHC is directly based on spatiotemporal correlations of BOLD signals and its analysis outcomes are easy to interpret as the strength of functional connectivity. Moreover, its sensitivity of detecting patterns remains relatively high even for a single dataset. In conclusion, the CMBHC method could be a useful tool for investigating resting-state brain connectivity and function.
Keywords: resting-state functional connectivity, spontaneous BOLD fluctuations, clustering method, thalamocortical connections
Introduction
The development of functional magnetic resonance imaging (fMRI) technique (Bandettini et al., 1992; Ogawa et al., 1990; Ogawa et al., 1992) during the past two decades has made it one of the most popular neuroimaging tools to explore brain functions noninvasively. Recently, the focus of this research field has been largely extended from detecting brain’s activation associated with brain stimulation (or task performance) to exploring spontaneous brain activity at the rest, a condition during which subjects were usually asked to refrain from cognitive, language, or motor tasks as much as possible but not to fall asleep. It has been found that spontaneous fMRI blood oxygenation level-dependent (BOLD) signals acquired during the resting state demonstrated slow (< 0.1 Hz) but strong fluctuations, which are highly synchronized within a variety of specific brain systems, for example, the visual, auditory, language, default mode and attention systems (Cordes et al., 2000; Fox et al., 2006; Greicius et al., 2003; Hampson et al., 2002; Lowe et al., 1998) and across a wide range of brain states, for example, from awake, sleep, lightly sedated or even vegetative human brains (Biswal et al., 1995; Boly et al., 2009; Greicius et al., 2008; Horovitz et al., 2008) to lightly and deeply anesthetized animal brains (Liu et al., 2011; Lu et al., 2007; Shmuel and Leopold, 2008; Vincent et al., 2007). These interesting findings suggest that spontaneous BOLD fluctuation originates from ongoing brain activity fluctuation, their temporal correlations reflect “functional connectivity” between different brain regions (Biswal et al., 1995), and the implied spatial correlation structures represent many resting-state brain networks (Mantini et al., 2007). Understanding these resting networks should be essential for answering many important neuroscience questions, for example, why the majority of brain energy is consumed by spontaneous brain activity (Raichle, 2006)? However, one technical challenge is how to properly analyze the resting-state fMRI data for identifying a large number of coherent networks.
Several statistical methods have been applied to identifying spatial patterns hidden in spontaneous BOLD fluctuation. The seed-based correlation analysis (Biswal et al., 1995; Fox et al., 2005) is the simplest and also the most commonly used technique. This hypothesis-driven method needs to first define a seed voxel (or several voxels) at a specific brain region of interest based on some prior knowledge (e.g., anatomical information), then compute the temporal correlations between the BOLD signal from the seed region and those from all other brain regions to generate a correlation map (called functional connectivity map), which can also be further transformed to other types of parametric maps, such as Z map (Fox et al., 2005). This approach is easy to implement and the resulting correlation values could be interpreted as the strength of functional connectivity. It, however, may have a various degree of bias caused by the selection of the seed regions; moreover, only one specific resting network could be identified each time.
To overcome the limitation of the seed-based correlation analysis, several multivariate, data-driven methods were introduced for functional connectivity analysis. Principle component analysis (PCA) is a statistical method widely used in exploratory data analysis (Pearson, 1901). This non-parametric method compresses the dimension of a dataset and thus can reveal some simplified structures hidden in the dataset. However, the intrinsic orthogonality constraint implied by PCA limits its applicability and efficacy in the analysis of spontaneous BOLD signals. In contrast, independent component analysis (ICA) (Comon, 1994), which decomposes an original dataset into multiple components with maximized independence, does not assume orthogonality between components and has become a popular multivariate methods for resting-state fMRI analysis (Beckmann et al., 2005; Kiviniemi et al., 2003; van de Ven et al., 2004). Compared to the seed-based correlation analysis, PCA and ICA do not need any priori-defined seed region and can extract multiple components at one time once the number of components is specified in advance. Their results, however, are not easy to interpret, because they are not directly based on spatiotemporal correlations of spontaneous BOLD signals. Moreover, there is still no empirical evidence supporting the assumption behind ICA, i.e., spontaneous BOLD signal is a mixture of a set of statistically independent non-Gaussian sources representing multiple resting-state networks (RSNs).
Other than PCA and ICA, clustering analysis is another multivariate method used for resting-state fMRI analysis. It has been applied to classify a set of objects into subsets (clusters) so that objects within the same cluster are more similar to each other. Previous studies applying cluster analysis to spontaneous BOLD signals mainly focused on assigning brain voxels into different clusters according to time courses (Cordes et al., 2002) or spectrograms (Mezer et al., 2009) of fMRI signals. These studies successfully grouped brain voxels into different clusters representing some known RSNs, but failed to provide maps describing relative strength of functional connectivity between different brain regions.
In this study, we introduce a correlation-matrix-based hierarchical clustering (CMBHC) method for analyzing spontaneous fMRI BOLD signals and extracting correlation patterns representing RSNs. The method was applied to spontaneous BOLD signals acquired from anesthetized animals, and the results were then carefully compared with those obtained using the probabilistic independent component analysis (PICA) (Beckmann et al., 2005) to evaluate its strengths and weaknesses. In addition, we also compared this new method to conventional clustering methods for resting-state fMRI analysis, which is based mainly on temporal dynamics of fMRI BOLD signals.
Materials and Methods
Basic Theory
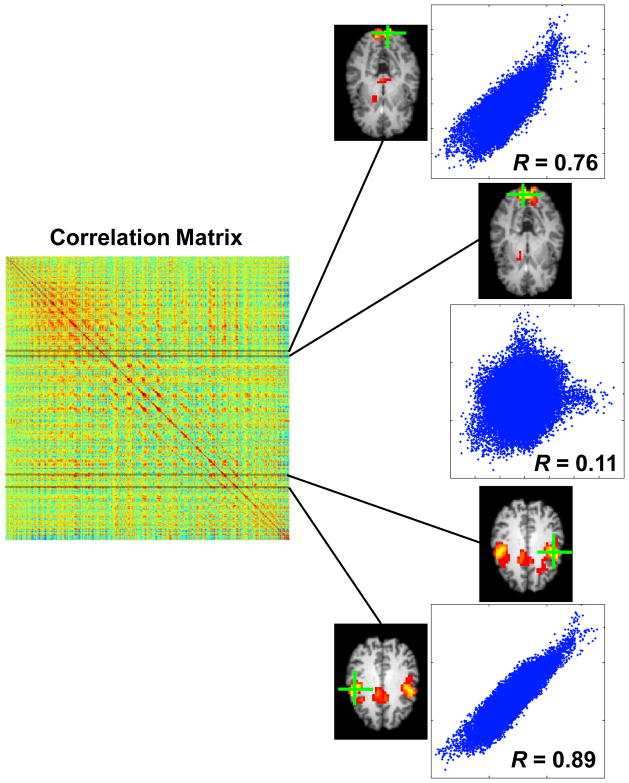
A resting-state fMRI dataset with 3D image volume acquisition can be described as a 4D matrix with one temporal and three spatial dimensions. If three spatial dimensions are compressed to one, the resting-state fMRI dataset can be represented with a 2D (time × voxel) matrix X, where X is an n×p matrix with n and p representing the numbers of time points and voxels, respectively; and each column of X represents a BOLD time course for a corresponding image voxel. The corresponding correlation matrix Cp×p of Xn×p is a symmetric matrix containing correlation between each pair of voxels. Each row (or column) of Cp×p actually includes correlations of a specific voxel to all voxels and is corresponding to a seed-based correlation map with respect to this specific voxel, as illustrated in Figure 1.
Figure 1.
Relationship between correlation matrix and correlation maps. Four rows of the correlation matrix are actually corresponding to four correlation maps representing two brain networks. Scatter plots show (spatial) correlations between different maps, indicating their spatial similarity or dissimilarity.
As discussed previously, a resting-state brain network refers to a set of brain regions showing spontaneous and synchronized neural activity or fMRI signal owing to a tight neurovascular coupling. From the image perspective, it can be regarded as a group of image voxels showing coherent BOLD signal fluctuations. Therefore, correlation maps with respect to voxels belonging to the same RSN would have similar pattern of this network. If the rows/columns of the correlation map could be correctly classified into groups based on their similarity, multiple RSNs can be identified. This is the essential idea behind the correlation matrix based hierarchical clustering (CMBHC) method proposed herein. Even though the CMBHC employed the hierarchical clustering method for classification process, the same goal could also be achieved with other classification methods.
Hierarchical Clustering
Hierarchical clustering is an agglomerative (“bottom-up”) type of clustering method. It begins with regarding each element as a separate cluster and then merge them into larger clusters successively. Specifically, in each particular step of hierarchical clustering, it finds the closest pair of clusters and then merges them into a new parent cluster. The step is repeated until only one cluster formed after N-1 iterations (N is the number of objects). The result of hierarchical clustering could be described with a tree structure plot called dendrogram.
In the present study, the Pearson’s correlation is used to measure the similarity between different rows/columns. The Pearson’s correlation coefficient (cc) between any two n-dimensional row/column vectors u and v can be calculated according to Eq.1.
| (Eq.1) |
Since it is more common to use “distance” (disimilarity) instead of “similarity” for clustering analysis, the distance d between the row/column vectors u and v was defined as 1 minus their correlation coefficient (Eq.2).
| (Eq.2) |
According to this definition, the more similar two vectors are, the shorter their distance will be. The distance will approach 0 as the correlation goes to 1.
For any two vectors u and v, besides their original distance d(u,v) defined in Eq.2, there is another distance measurement called cophenetic distance D(r,s), which is defined as inter-cluster distance between two clusters r and s that u and v belong to when they are first merged into a new cluster (at a joint of the dendrogram). There are different ways to calculate the cophenetic distance, among them the single, complete, and average linkage are the most commonly used three. Their corresponding formulas are shown in Eqs. 3–5, respectively.
| (Eq.3) |
| (Eq.4) |
| (Eq.5) |
The average linkage method was chosen for calculating cophenetic distance in this study, because it yields higher cophenetic correlations than the others. Moreover, it can potentially avoid the “chaining” problem of the single linkage (i.e., the tendency to produce chain-shape clusters) and has a higher tolerance for outliers than the complete linkage.
The correlation between the original and cophenetic distances is called cophenetic correlation, which quantifies how well the dendrogram represents the pattern of similarities (or dissimilarities) among objects and thus the quality of clustering analysis.
The above process only provides the dendrogram representing hierarchical structure of the correlation matrix, and to derive final clusters additional steps are needed to break down the dendrogram tree. We achieved this goal with two different strategies. In our main approach, we first broke down the dendeogram at the joints whose cophenetic distances exceeding a predefined threshold, i.e. the row/column vectors merging at such joints were classified into different final clusters. Then, the final clusters with voxels less than a pre-defined value were further identified and discarded because they are unlikely to represent any meaningful spatial patterns. The threshold on cophenetic distances was set to 0.4 and the final clusters were required to have at least 8 voxels, and these values were chosen based on some preliminary analysis including those shown in Figure S1. With different combination of the cophenetic distance threshold and cluster size constraint, the final clusters could be different to certain degree.
Additionally, we also broke down the dendrogram based on inconsistency coefficients, which quantify to what extent the cophenetic distance of a specific joint is different from those of joints just below it (Zahn, 1971). For example, given a joint f and its two child joints d and c, the inconsistency coefficient ic(f) can be calculated according to Eq.6.
| (Eq.6) |
where D(•) represents the cophenetic distance (Eq.5) at a specific joint. The inconsistency coefficient is sensitive to sudden changes in cophenetic distances along the direction of building up the dendrogram (bottom-up direction) and suitable for finding boundaries between distinct groups. The distribution of inconsistent coefficients for a typical dendrogram (Run 1 of Rat 1) was shown in Figure S2, and there is always a “tail” at the right side of histogram. The thresholds were set to the transition point (red dash line) to this “tail” region. The same constraint on the size of the final clusters, i.e. 8 voxels as a minimum, was also applied to identify and discard the clusters with only a few voxels. This second strategy was also applied to derive final clusters, but the results will only be briefly discussed in the section of Discussion and Conclusion.
Aggregation Index
To quantitatively compare and evaluate the results of the CMBHC and ICA analysis, aggregation index (AI), which was originally proposed in landscape ecology (He et al., 2000), is introduced to automatically quantify and evaluate the patterns obtained by both methods. Figure S3 shows examples of AI values for several different 2D patterns. For a pattern consisting of m voxels, AI value is equal to the ratio between the number of actual shared edges and the largest possible number of shared edges. For example, in a 2D space, 16 pixels can have at most 24 shared edges. The “default mode” pattern in Figure S3B has 16 shared edges, therefore its AI value was calculated as 16/24 = 0.67; while the only 6 shared edges for the random distributed pixels (Figure S3D) make its AI value as low as 0.25. In this study, the computation of the AI values was extended to 3D since the fMRI BOLD signals were acquire from 3D volumes.
The underlying assumption of using AI to evaluate the quality of brain maps is that the “meaningful” maps are likely to show more aggregated patterns than randomly distributed voxels. However, the AI should only be regarded as a coarse quantity rather than an accurate one for non-randomness of resulting maps since the above assumption may validate loosely. Moreover, the maps with non-random pattern are not necessarily representing true neuronal networks.
Datasets
The data were acquired from four male Sprague-Dawley rats under ~1.0% isoflurane anesthesia, and have been used previously for testing other scientific hypotheses. The Institutional Animal Care and Use Committee of the University of Minnesota approved the animal surgical procedures and experimental protocols. All experiments were performed on a 9.4T horizontal magnet (Magnex Scientific, UK) interfaced with a Varian INOVA console (Varian Inc., CA, USA) using a proton radiofrequency (RF) surface coil. The head position of the rat was fixed by a home-built head-holder with a mouth-bar and ear-bars to minimize head motion. Multi-slice T1-weighted anatomical images were acquired from axial, sagittal, and coronal orientations to identify the rat somatosensory cortex and select appropriate image slice positions for fMRI data acquisition. Five consecutive gradient-echo planar image (GE-EPI) (Mansfield, 1977) slices covering somatosensory cortex (Bregma −4.3–0.7 mm (Paxinos and Watson, 1998)) were acquired (Field of view (FOV) = 32×32 mm2; repetition and echo times (TR/TE) = 612/16.5 ms; 64×64 matrix size; 1 mm thickness, 500 image volumes and ~306 seconds per fMRI run) when rats were in uniform darkness (regarded as the resting-state). Ten dummy scans were also added before each run to avoid the transient BOLD signal change during the initial acquisition period. Muscle relaxant was used to minimize the stress of rat. All data were acquired when all monitored physiological parameters were stable and within the normal physiology ranges. For each rat, the fMRI measurements were repeated for 4 runs.
Data Analysis
The fMRI data preprocessing was performed using the FEAT tool in FSL software package (http://www.fmrib.ox.ac.uk/fsl/) (Smith et al., 2004). The following steps were applied: motion correction (MCFLIRT (Jenkinson et al., 2002)), slice timing correction, brain extraction, spatial filtering with FWHM (full width at half maximum) equal to 1 mm. Besides these steps, detrending and temporal filtering was performed in Matlab (MathWorks, Inc., MA, USA) with band-pass filtering ranges of 0.01–0.5 Hz. For each fMRI voxel, the fMRI BOLD signals were also normalized with its mean.
For seed-based correlation analysis on rat, three 2-pixel×2-pixel seeds were selected in the left and right S1FL (primary somatosensory cortex, forelimb; −1.8 mm from the bregma and ~2.5–3 mm from the brain midline), and the right S1BF (primary somatosensory cortex, barrel field; −1.8 mm from the bregma and ~5 mm from the brain midline), and then BOLD signals from all image voxels were cross-correlated (Pearson’s correlation) with the reference time courses extracted from the seed regions to generate three correlation maps.
ICA analysis was carried out with MELODIC tool (Beckmann and Smith, 2004) in FSL, and the number of components was automatically determined by the program. Multi-session Tensor ICA (Beckmann and Smith, 2005) was used for group analysis using data from multiple runs.
CMBHC analysis was performed in Matlab. For each run, the correlation matrix was first calculated based on the preprocessed data and the hierarchical clustering analysis described above was then applied. After determining the final clusters, the rows/columns belonging to same cluster were then averaged to generate a corresponding map for this specific cluster. For multi-run analysis, the correlation matrices were calculated and then averaged across runs, and all other procedures were identical to those used in single run analysis.
To automatically set thresholds for displaying maps and also to provide an input for AI calculation, the 75% percentile was found for each cluster map and independent component (IC) map (the absolute values of maps were used to determine percentiles). All cluster and IC maps used this value as a displaying threshold, with only showing positive values larger than this threshold and negative values smaller than its negative. In this way, a fixed portion (25%) of brain regions will be overlaid with cluster or IC color maps. At the same time, for each map a binary mask was created covering these over-threshold voxels and used as an input for AI calculation.
Results
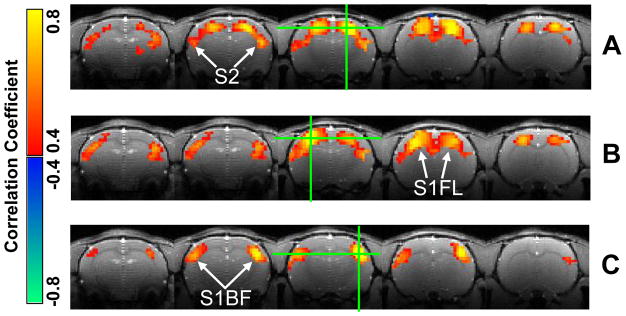
It has been observed previously that under the deep (~1.8%) isoflurane anesthesia, the rat brain shows strong spontaneous and highly synchronized fluctuation over widely distributed cortical areas (Liu et al., 2011). In contrast, functional connectivity in the rat brain with 1.0% isoflurane anesthesia shows multiple networks with distinct spatiotemporal dynamics (Figure 2). Correlation maps with respect to the left and right S1FL seed regions (Figure 2A and 2B) are very similar to each other and indicate the same resting-state brain network mainly covering the bilateral S1FL regions, while the correlation map with respect to the right S1BF region (Figure 2C) demonstrates a different network mainly covering the bilateral S1BF regions. The finding suggests coexistence of multiple RSNs in the rat brain according to a somatotopic organization.
Figure 2.
Three correlation maps from a representative rat (Rat 1) indicating distinct resting-state brain networks. The correlation maps with respect to the right (A) and left (B) S1FL regions show similar patterns covering the bilateral S1FL regions, while the one with respect to the right S1BF region (C) has a different pattern mainly covering the bilateral S1BF regions. The green crosses marked seed locations.
To further explore other network patterns using the CMBHC method, the correlation matrix was calculated and the hierarchical clustering was then applied to classify its rows/columns into different groups (final clusters). A total of 24 clusters were identified for a typical single fMRI run (Run 1 of Rat 1) as shown in the left panel of Figure 3. The cluster maps are arranged from top to bottom with their AI values in a descending order. The clusters with high AI values (>0.5) exhibit distinct and “meaningful” patterns representing multiple RSNs, including the bilateral S1FL (Cluster #4) and S1BF (Cluster #5) networks identified with the seed-based correlation maps in Figure 2, but with superior map quality. Some identified networks mainly cover subcortical regions, e.g., Clusters #2 and #12. More interestingly, a few clusters show distinct connections between cortical and subcortical regions, for example, Cluster #9 showing the motor–CPu (caudate putamen) connection and Cluster #14 reflecting the sensory–TN (thalamic nuclei) circuit. Overall, the results demonstrate effectiveness of the CMBHC method in extracting correlation structures from a single scan of the resting-state fMRI signals.
Figure 3.
Clusters and ICs for a single run of the representative rat (Run 1 of Rat 1). The clusters (left panel) are arranged from top to bottom according to their AI values, while the ICs (right panel) are displayed right next to their similar cluster if they have one, otherwise they are arranged according to their AI values. The AI values are shown next to the corresponding maps. The bottom-right corner shows the anatomical drawings indicating the motor–CPu (blue) and sensory–TN (red) networks (adapt from the reference of (Paxinos and Watson, 1998)).
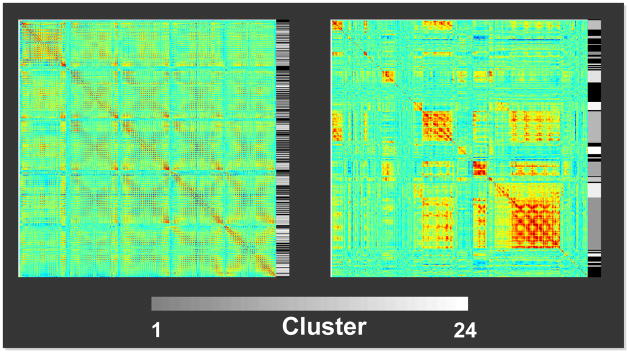
To further examine how successfully the hierarchical clustering grouped the correlation matrix rows/columns according to their similarity, the correlation matrix of the representative run (Run 1 of Rat 1) was rearranged according to the clustering result (Figure 4). The gray scale in the bar right next to the correlation matrices encodes the final cluster numbers, and the rows/columns with similar correlation profiles were successfully grouped together. The black color in the bar is corresponding to the rows abandoned due to the constraint on the final cluster size (see Materials and Methods). Generally, these rows only have elements with small correlation values, suggesting that the constraint on final cluster size successfully exclude voxels without strong coherent fluctuations and probably not belonging to any of networks.
Figure 4.
Correlation matrices without (left) and with (right) arranging their rows/columns according to the CMBHC results (Run 1 of Rat 1). Gray-scale bars right next to the matrices encode the cluster number shown in Figure 3. The black color in the bars is corresponding to rows abandoned due to the cluster size constraint.
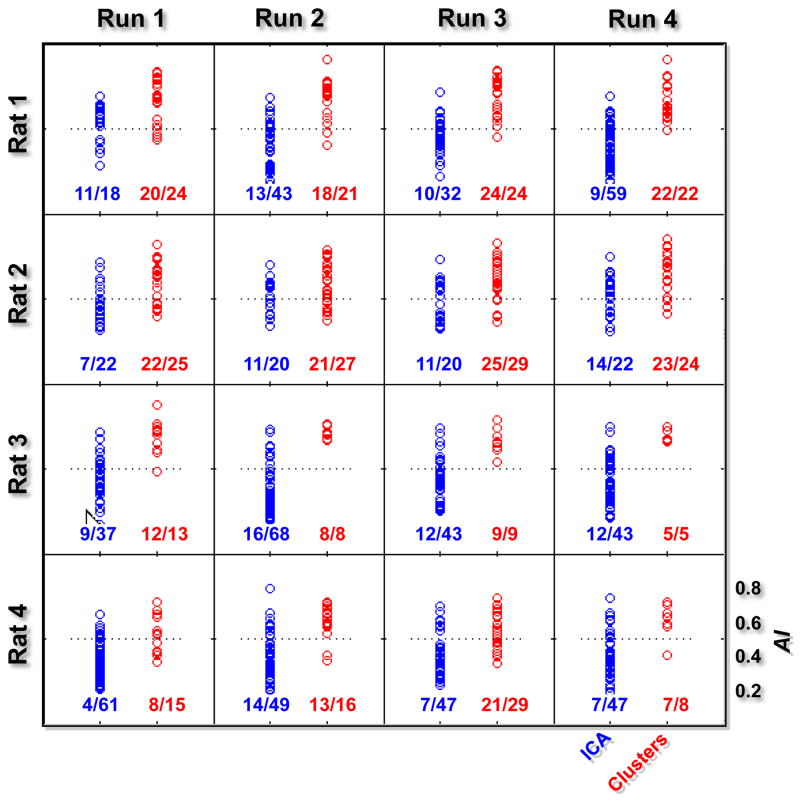
The right panel of Figure 3 shows ICs obtained from the same single-run fMRI dataset. ICs showing patterns similar to those found with the CMBHC (the spatial correlation between the cluster and IC is higher than 0.6, corresponding to the cophenetic distance threshold used for determining final clusters) are plotted right next to their corresponding clusters, while the remaining ICs were then arranged according to their AI values. There are several common patterns found by both methods, including those locating both at cortical and subcortical regions; however, the ICA missed (or failed to provide maps with similar quality for) some patterns showing in the CMBHC results, especially those with cortical-subcortical connections. Moreover, most of ICs showed small brain regions with negative values and relatively random locations, resulting lower AI values. Some of ICs have relatively unilateral (asymmetric) patterns with much higher statistics in one of hemispheres, e.g., ICs #3, #4, #5, and #13. The AI values for maps from all rats are summarized in Figure 5. The cluster maps have significantly higher AI values than IC maps (two sample t test with p < 10−3) for all 16 runs of 4 rats.
Figure 5.
AI values for clusters and ICs from all rats. Each plot represents the AI values for clusters (red points) and ICs (blue points) obtained from a single run, and numbers below give the fraction of clusters (ICs) having AI values higher than 0.5 (the horizontal dash line). The AI values of the clusters are significantly higher than those of ICs for all runs (p < 10−3).
Similar to the ICA, the CMBHC can also be applied for group analysis on multiple runs or even multiple subjects, given a good spatial registration across runs and subjects. The easiest way is to average correlation matrices from different runs or subjects (after spatial registration), and the hierarchical clustering is then performed on this averaged matrix. Figure S4 compared outcomes of the multi-run CMBHC (combining 4 runs from Rat 1) to those of group ICA analysis. Majority of patterns identified with both methods are similar to those from the single run data with subtle improvement on map quality.
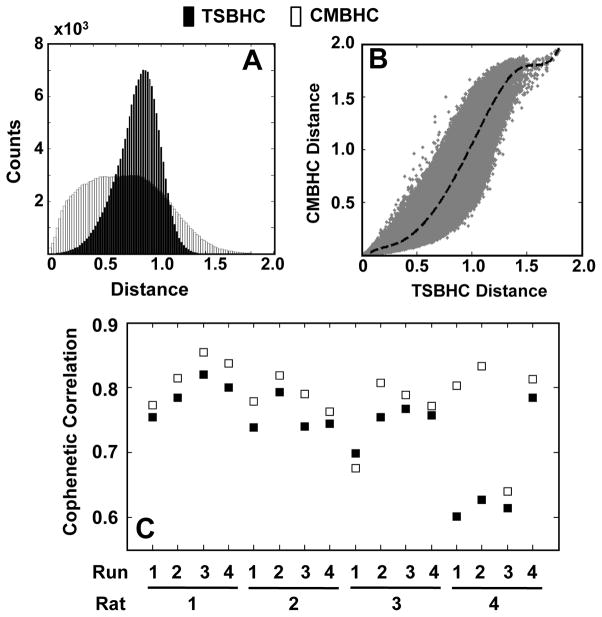
Hierarchical clustering method has been proposed for functional connectivity analysis based on the time series or spectra of fMRI BOLD signals (Cordes et al., 2002; Mezer et al., 2009). While these methods group brain voxels based directly on their fMRI signals, the CMBHC classifies the voxels according to their functional connectivity to others. They may, therefore, give different information regarding the relationships among voxels. Histograms in Figure 6A show distributions of original distances between voxels when applying the time series based hierarchical clustering (TSBHC) or CMBHC to the representative fMRI run. The CMBHC method shows a more uniform distribution than the TSBHC, and there is a nonlinear relationship between them (Figure 6B). Such a distribution can potentially increase sensitivity for identifying RSN patterns with less strong correlations by expanding correlations within a narrow regime to a wider range. The distinct distributions of distances in these two methods also suggest that it is unfair to apply a common threshold (on cophenetic distance) for dividing final clusters and then compare their outcomes. Therefore, the structure of dendrogram was compared instead. Cophenetic correlations, which quantify the goodness of fit of the clustering analysis, were calculated for dendrograms constructed with these two methods (Figure 6C). The CMBHC consistently showed a better fitting (paired t test, p = 0.007) than the TSBHC.
Figure 6.
Comparison between the time series based hierarchical clustering (TSBHC) and the correlation matrix based hierarchical clustering (CMBHC). Compared to the TSBHC (black), the distribution of original distances in the CMBHC (white) is more uniform (A), and the scatter plot suggests a nonlinear relationship between them (B). Moreover, a comparison on cophenetic correlations (from all runs) indicates a better goodness of fit (p = 0.007) with the CMBHC (C). Note: the (A) and (B) are based on the data from Run 1 of Rat 1; and the dash line in (B) represent the mean of CMBHC distances.
Discussions and Conclusion
In this study, the CMBHC method is introduced to identify the RSNs based on the spatiotemporal correlations of spontaneous BOLD signals. By classifying correlation maps for all brain voxels into different clusters according to their spatial similarities, this method can effectively extract spatial patterns representing coherent networks in the resting brain. Although it is based on correlation maps, this method does not require any priori-knowledge about seed regions and is thus exempt from the bias caused by seed selection. Multiple patterns can be identified at one time. Moreover, the resulting cluster maps are averaged over many correlation maps and thus offer high map quality. Compared to the ICA method widely used in functional connectivity analysis, the CMBHC is likely to have a higher sensitivity to identify additional patterns, especially those with relatively weak functional connectivity, e.g., those between cortical and subcortical regions. Moreover, the values of cluster maps are actually averaged correlation coefficients, which can serve as a coarse index for the strength of the functional connectivity, and this merit makes the results based on the CMBHC analysis easier to interpret than other multivariate approaches, in the perspective for quantifying the strength of network coherence.
Neuroscience research has revealed the hierarchical organization of the brain. The cerebral cortex can be divided into many functional modules specialized for different brain functions, while within modules, particularly those processing sensory information, the finer subgroups can be further defined according to more specific functions (e.g., somatotopic organizations) or stages in information processing (e.g., primary versus associated visual cortex). Correspondingly, similar hierarchical organization of functional connectivity has also been reported. For example, as one of robust resting brain networks, spontaneous BOLD fluctuations within the motor cortex exhibit much stronger correlations than other brain regions; nevertheless further analysis in a finer scale indicated stronger correlations between bilateral homologous sub-regions associated with more specific motor functions (van den Heuvel and Hulshoff Pol, 2009). If such a hierarchical organization exists in the brain in general, the dendrogram obtained with the hierarchical clustering analysis will be a good representation for such a hierarchical organization.
Although the ICA is usually regarded as a data-driven, multivariate approach without explicit modeling, it actually has an important assumption that the measured signal is a mixture of multiple statistically independent source signals. To uncover these independent sources from the mixed signal, different ICA algorithms can be applied either to minimizing mutual information between or to maximizing non-Gaussianity of estimated components. Such a model can accurately describe problems with clearly defined source signals, for example, a microphone recording several voices simultaneously from different people, but it may not be perfect for describing resting-state functional connectivity that represents complicated interactions between different brain regions. As shown in our results (Figures 3), the ICs tend to cover spatially focalized regions, because such a pattern is corresponding to high spatial non-Gaussianity. At the same time, the ICA appears to be over conservative, because it failed to identify several “meaningful” patterns found by the CMBHC, especially those with relatively weak cortico-subcortical correlations.
Dividing final clusters is a critical step for the CMBHC method. Two strategies, with setting threshold either on cophenetic distances or on inconsistency coefficients and then breaking down the dendrogram at joints with over-threshold values (see Materials and Methods for details), were tested in this study (only the results using the first strategy were presented). The approach of setting thresholds on cophenetic distance is sensitive to global correlation level (defined as the mean of correlations between each voxel and the global signal averaged over the whole brain). Less final clusters were found in Rat 3 and Rat 4 (especially Run 4) compared to Rat 1 and Rat 2 when using the same threshold (Figure 5), and this is because that the BOLD signals acquired from these two rats have higher global correlation levels than the other two (Figure S5). It has been shown that the global correlation in spontaneous BOLD signals could be neural origin (Liu et al., 2011; Scholvinck et al., 2010). Moreover, the deep anesthesia can significantly increase the global correlation and make spatially specific networks merge into less specific ones. Therefore, the global correlation level could be an important index reflecting the status of brain activity. The number of final clusters automatically determined by this strategy has already incorporated information regarding the global correlation level: with a fixed threshold, the higher the global correlation is, the fewer final clusters are expected.
In contrast, the strategy of setting threshold on inconsistency coefficients is effective on finding boundaries between distinct clusters and less sensitive to the global correlation level. Therefore, this approach may miss some physiological information associated with the global correlation. Furthermore, this strategy is lack of a relatively fixed standard, and the resulting clusters could have quite different correlation strength (within-cluster correlations). Nevertheless, the division according to this strategy may fit better to the natural cluster structure of the fMRI dataset. How to select an optimal strategy for dividing final clusters may depend on specific purposes of studies.
No matter which strategy is applied, the constraint on final cluster size would be essential. According to the datasets used in this study, there are a significant portion of brain voxels that do not have strong correlations with the rest of other brain voxels and tend to be classified into clusters consisting of themselves only or with several others. Without identifying and removing this type of clusters, the meaningful clusters representing RSNs could be buried among them.
With the strategy of setting threshold on cophenetic distances, the threshold will be an important factor determining final results. A low threshold will break down the dendrogram at joints whose children still have significant similarity (correlation), and give a division at a finer spatial scale. Therefore, a higher displaying threshold is required to differentiate cluster maps. For example, Clusters #3 and #5 in Figure 3 are similar to each other with current displaying threshold, but they actually represent different subgroups of S1BF voxels located at anterior and posterior slices, respectively. As discussed previously, functional connectivity at different spatial scales may reflect the hierarchical organization of the brain; but it may also arise for other reasons, e.g., the spatial smoothing effect. With the freedom of setting threshold, certain flexibility is allowed to examine BOLD correlation patterns at different spatial scales.
The displaying threshold for each cluster or IC map was automatically calculated according to a fixed percentile of map values for two reasons. First, it is easy to compare the CMBHC and ICA results with a fixed portion of brain regions being overlaid with color map. Secondly, it would be fair to compare AI values calculated using the binary masks with a fix number of brain voxels. In contrast, a fixed threshold of correlation coefficient or Z score will cause a large variation in the amount of brain regions covered by different clusters or ICs, and this may affect the direct comparison of their spatial patterns.
It should also be noted that the comparison of AI value depends on the displaying threshold. For any map, its AI value will converge up to 1 as the displaying threshold increases, and the AI value difference between cluster and IC maps will become smaller when using a higher displaying threshold. Nevertheless, even though the IC maps become relatively “noisy” at certain brain regions, the cluster maps still show clear patterns, suggesting the threshold we used is still in a reasonable range for comparing AI values.
Previous studies have compared the ICA with the seed-based correlation method or the PCA method (Beckmann et al., 2005; Ma et al., 2007), in which simulation was used as an effective way for quantitative comparisons. In the present study, the comparison is, however, made based only on the real fMRI datasets rather than the simulated one. Although some progresses have been achieved towards understanding the mechanism of the resting-state functional connectivity during the past several years, it is still not fully clear at the current stage. Without this information, it is very difficult to simulate datasets close to real ones; and the way of generating simulated datasets may sometimes bias the comparison by specifically preferring the model of certain methods. This is the major reason why the simulation method was not used in the present study.
Other clustering methods can also be used for grouping the rows/columns of correlation matrix, but the hierarchical clustering has certain advantages over them. The hierarchical clustering is a connectivity-based method, and the resulting dendrogram provides a good representation of relationship of different brain voxels. Moreover, unlike some other clustering methods, which need to specify the number of final clusters in advance, the hierarchical clustering will build the dendrogram first and divide the final clusters later. Different final cluster sets could be re-divided without repeating clustering process; moreover, the criterion of dividing final clusters is still based on similarity measurements (thresholds on cophenetic distances) rather than just an arbitrary number (the number of clusters desired).
Computation intensity of the CMBHC is not high. With optimized script in Matlab, it took less than 3 minutes to finish computation on a dataset with over 20,000 image voxles in a linux workstation (3.0G Quad-Core Intel Xeon). The running time can be further shortened significantly with programs using more efficient algorithm, e.g., fastcluster (only available in R and Python currently, http://math.stanford.edu/~muellner/fastcluster.html). However, the size of correlation matrix is equal to the square of the total voxel number and will increase dramatically for high-resolution fMRI datasets with the whole brain coverage, and the current algorithms of clustering require the full correlation matrix to be loaded into memory for computation. Therefore, the application of the CMBHC to high-resolution datasets will be limited by RAM memory. There are different ways to alleviate this problem without hardware upgrade, for example, identifying and discarding rows/columns without strong correlations before clustering analysis, reducing the total number of 3D image voxels by further eliminating voxels from non-brain regions, or developing new clustering algorithms loading only a small portion of the correlation matrix into RAM for computation.
In conclusion, the CMBHC method provides an alternative and improved statistical method for reliable identification of correlation structures from fMRI signals.
Supplementary Material
Research Highlights.
Correlation-map-based multivariate analysis for fMRI data.
High sensitivity to detect resting-state network patterns with weak connections.
Acknowledgments
This work was partially supported by NIH grants: NS041262, NS041262S1, NS057560, NS070839, P41 RR08079 and P30NS057091; and the Keck Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–7. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci. 2005;360:1001–13. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE transactions on medical imaging. 2004;23:137–52. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Tensorial extensions of independent component analysis for multisubject FMRI analysis. Neuroimage. 2005;25:294–311. doi: 10.1016/j.neuroimage.2004.10.043. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–41. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Boly M, Tshibanda L, Vanhaudenhuyse A, Noirhomme Q, Schnakers C, Ledoux D, Boveroux P, Garweg C, Lambermont B, Phillips C, Luxen A, Moonen G, Bassetti C, Maquet P, Laureys S. Functional connectivity in the default network during resting state is preserved in a vegetative but not in a brain dead patient. Hum Brain Mapp. 2009;30:2393–400. doi: 10.1002/hbm.20672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comon P. Independent Component Analysis, a new concept. Signal Processing. 1994;36:287–314. [Google Scholar]
- Cordes D, Haughton V, Carew JD, Arfanakis K, Maravilla K. Hierarchical clustering to measure connectivity in fMRI resting-state data. Magn Reson Imaging. 2002;20:305–17. doi: 10.1016/s0730-725x(02)00503-9. [DOI] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Wendt GJ, Turski PA, Moritz CH, Quigley MA, Meyerand ME. Mapping functionally related regions of brain with functional connectivity MR imaging. AJNR Am J Neuroradiol. 2000;21:1636–44. [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and biomedical research, an international journal. 1996;29:162–73. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc Natl Acad Sci U S A. 2006;103:10046–51. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–8. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Kiviniemi V, Tervonen O, Vainionpaa V, Alahuhta S, Reiss AL, Menon V. Persistent default-mode network connectivity during light sedation. Hum Brain Mapp. 2008;29:839–47. doi: 10.1002/hbm.20537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003;100:253–8. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampson M, Peterson BS, Skudlarski P, Gatenby JC, Gore JC. Detection of functional connectivity using temporal correlations in MR images. Hum Brain Mapp. 2002;15:247–62. doi: 10.1002/hbm.10022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He HS, DeZonia BE, Mladenoff DJ. An aggregation index (AI) to quantify spatial patterns of landscapes. Landscape Ecology. 2000;15:591–601. [Google Scholar]
- Horovitz SG, Fukunaga M, de Zwart JA, van Gelderen P, Fulton SC, Balkin TJ, Duyn JH. Low frequency BOLD fluctuations during resting wakefulness and light sleep: a simultaneous EEG-fMRI study. Hum Brain Mapp. 2008;29:671–82. doi: 10.1002/hbm.20428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–41. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Kiviniemi V, Kantola JH, Jauhiainen J, Hyvarinen A, Tervonen O. Independent component analysis of nondeterministic fMRI signal sources. Neuroimage. 2003;19:253–60. doi: 10.1016/s1053-8119(03)00097-1. [DOI] [PubMed] [Google Scholar]
- Liu X, Zhu XH, Zhang Y, Chen W. Neural origin of spontaneous hemodynamic fluctuations in rats under burst-suppression anesthesia condition. Cereb Cortex. 2011;21:374–84. doi: 10.1093/cercor/bhq105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe MJ, Mock BJ, Sorenson JA. Functional connectivity in single and multislice echoplanar imaging using resting-state fluctuations. Neuroimage. 1998;7:119–32. doi: 10.1006/nimg.1997.0315. [DOI] [PubMed] [Google Scholar]
- Lu H, Zuo Y, Gu H, Waltz JA, Zhan W, Scholl CA, Rea W, Yang Y, Stein EA. Synchronized delta oscillations correlate with the resting-state functional MRI signal. Proc Natl Acad Sci U S A. 2007;104:18265–9. doi: 10.1073/pnas.0705791104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Wang B, Chen X, Xiong J. Detecting functional connectivity in the resting brain: a comparison between ICA and CCA. Magnetic resonance imaging. 2007;25:47–56. doi: 10.1016/j.mri.2006.09.032. [DOI] [PubMed] [Google Scholar]
- Mansfield P. Multi-planar image formation using NMR spin-echos. J Phys C: Solid State Physics. 1977;10:L55–L8. [Google Scholar]
- Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M. Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci U S A. 2007;104:13170–5. doi: 10.1073/pnas.0700668104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezer A, Yovel Y, Pasternak O, Gorfine T, Assaf Y. Cluster analysis of resting-state fMRI time series. Neuroimage. 2009;45:1117–25. doi: 10.1016/j.neuroimage.2008.12.015. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Lee T-M, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci USA. 1990;87:9868–72. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci U S A. 1992;89:5951–5. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. Academic Press; San Diego, California: 1998. [Google Scholar]
- Pearson K. On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine. 1901:559–72. [Google Scholar]
- Raichle ME. Neuroscience. The brain’s dark energy. Science. 2006;314:1249–50. [PubMed] [Google Scholar]
- Saad ZS, Glen DR, Chen G, Beauchamp MS, Desai R, Cox RW. A new method for improving functional-to-structural MRI alignment using local Pearson correlation. Neuroimage. 2009;44:839–48. doi: 10.1016/j.neuroimage.2008.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholvinck ML, Maier A, Ye FQ, Duyn JH, Leopold DA. Neural basis of global resting-state fMRI activity. Proc Natl Acad Sci U S A. 2010;107:10238–43. doi: 10.1073/pnas.0913110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmuel A, Leopold DA. Neuronal correlates of spontaneous fluctuations in fMRI signals in monkey visual cortex: Implications for functional connectivity at rest. Hum Brain Mapp. 2008;29:751–61. doi: 10.1002/hbm.20580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23 (Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- van de Ven VG, Formisano E, Prvulovic D, Roeder CH, Linden DE. Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Hum Brain Mapp. 2004;22:165–78. doi: 10.1002/hbm.20022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Hulshoff Pol HE. Specific somatotopic organization of functional connections of the primary motor network during resting state. Hum Brain Mapp. 2009;31:631–44. doi: 10.1002/hbm.20893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Patel GH, Fox MD, Snyder AZ, Baker JT, Van Essen DC, Zempel JM, Snyder LH, Corbetta M, Raichle ME. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 2007;447:83–6. doi: 10.1038/nature05758. [DOI] [PubMed] [Google Scholar]
- Zahn CT. Graph-theoretical methods for detecting and describing Gestalt clusters. IEEE Transactions on Computers. 1971;C-20:68–86. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.